LMI-Based Delayed Output Feedback Controller Design for a Class of Fractional-Order Neutral-Type Delay Systems Using Guaranteed Cost Control Approach
Abstract
1. Introduction
2. Prerequisites
3. Problem Statement
4. Theoretical Results
5. Application
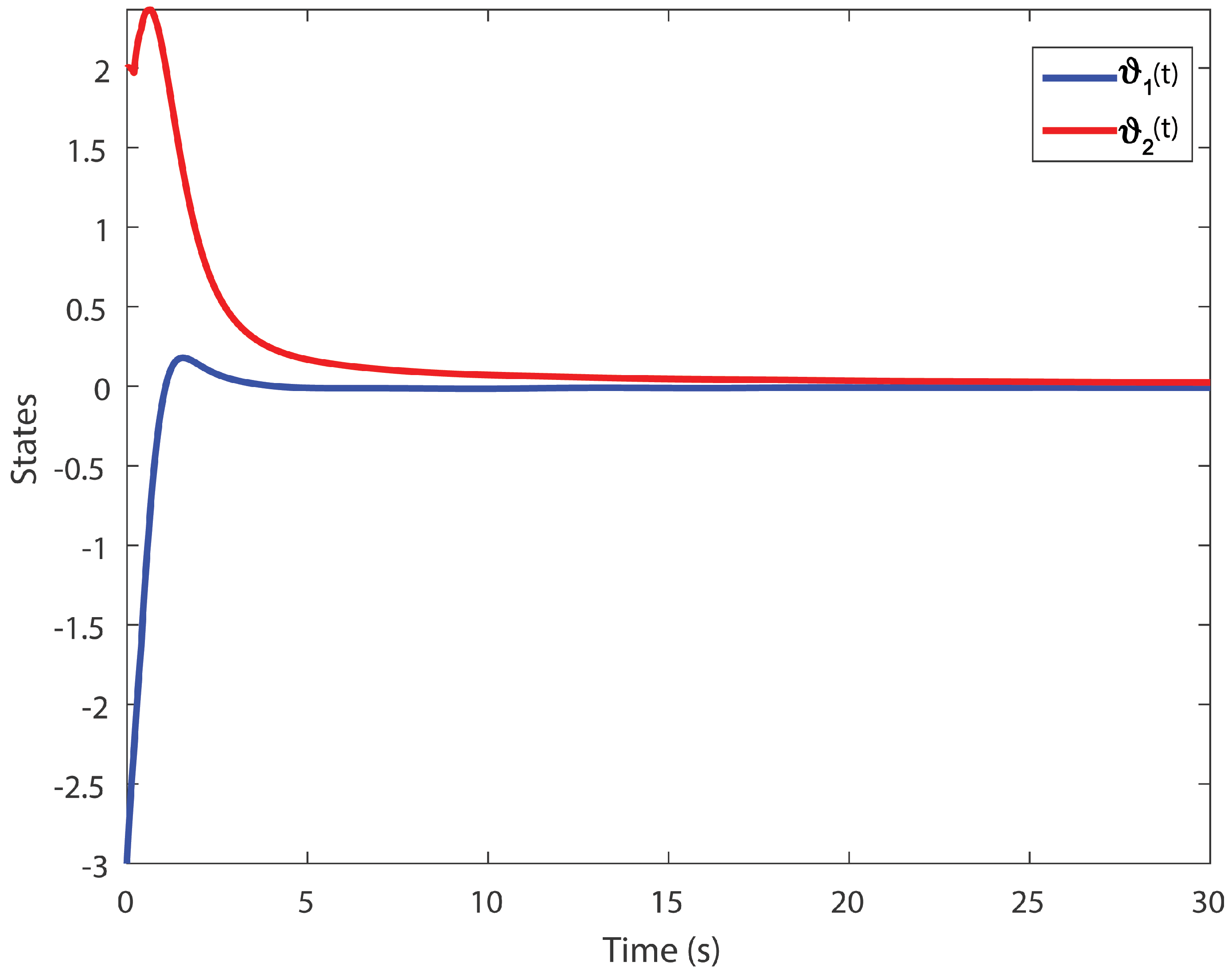
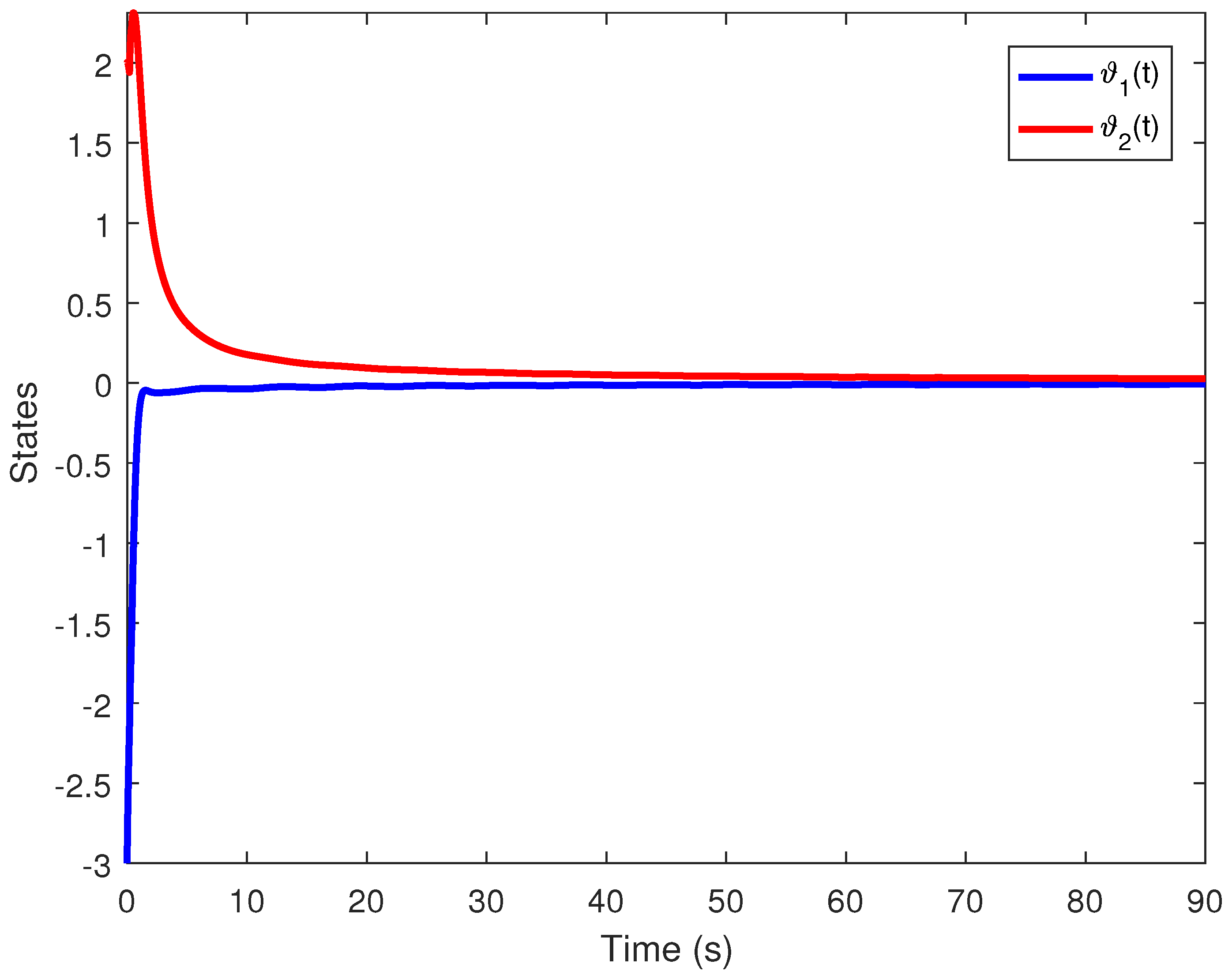
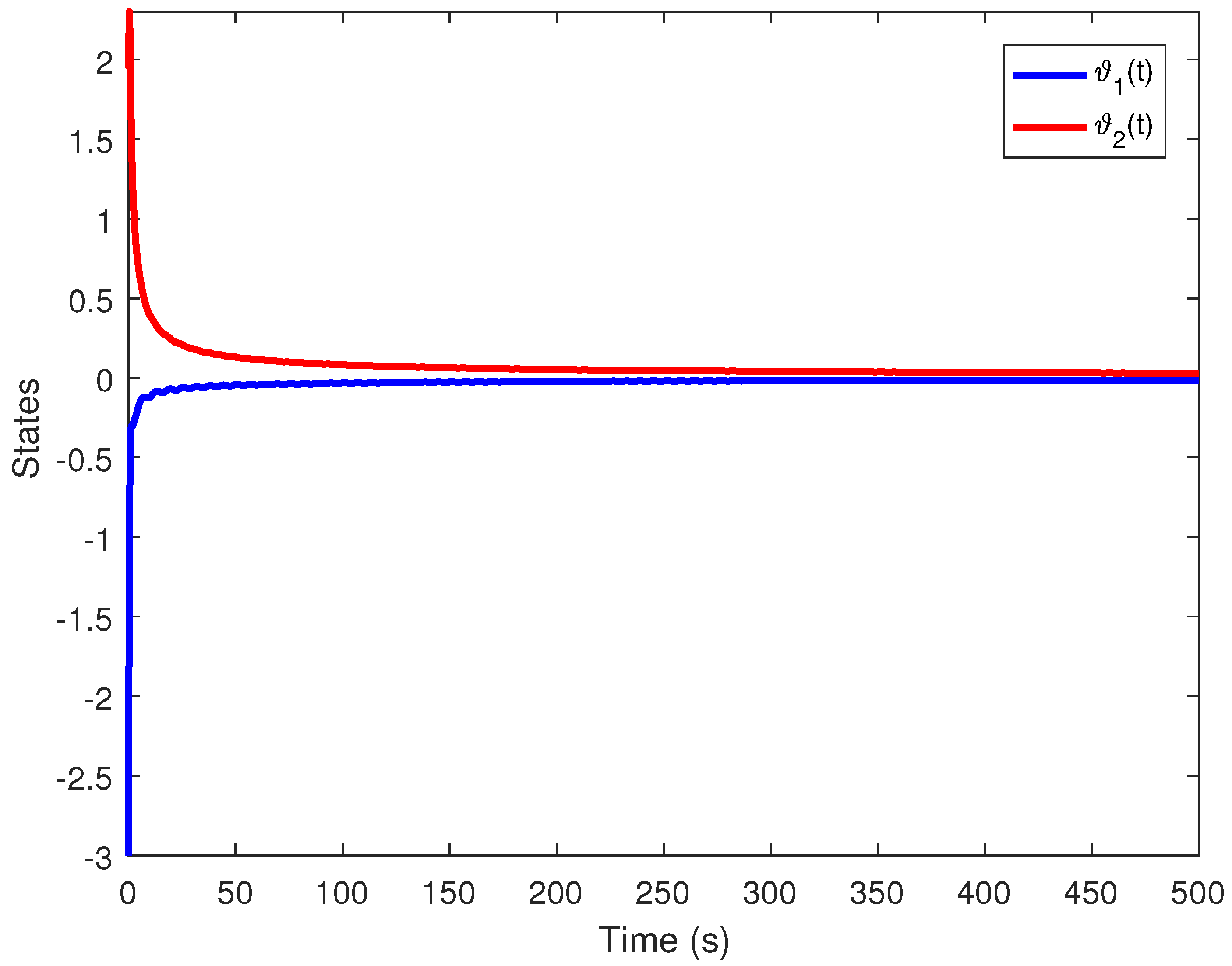
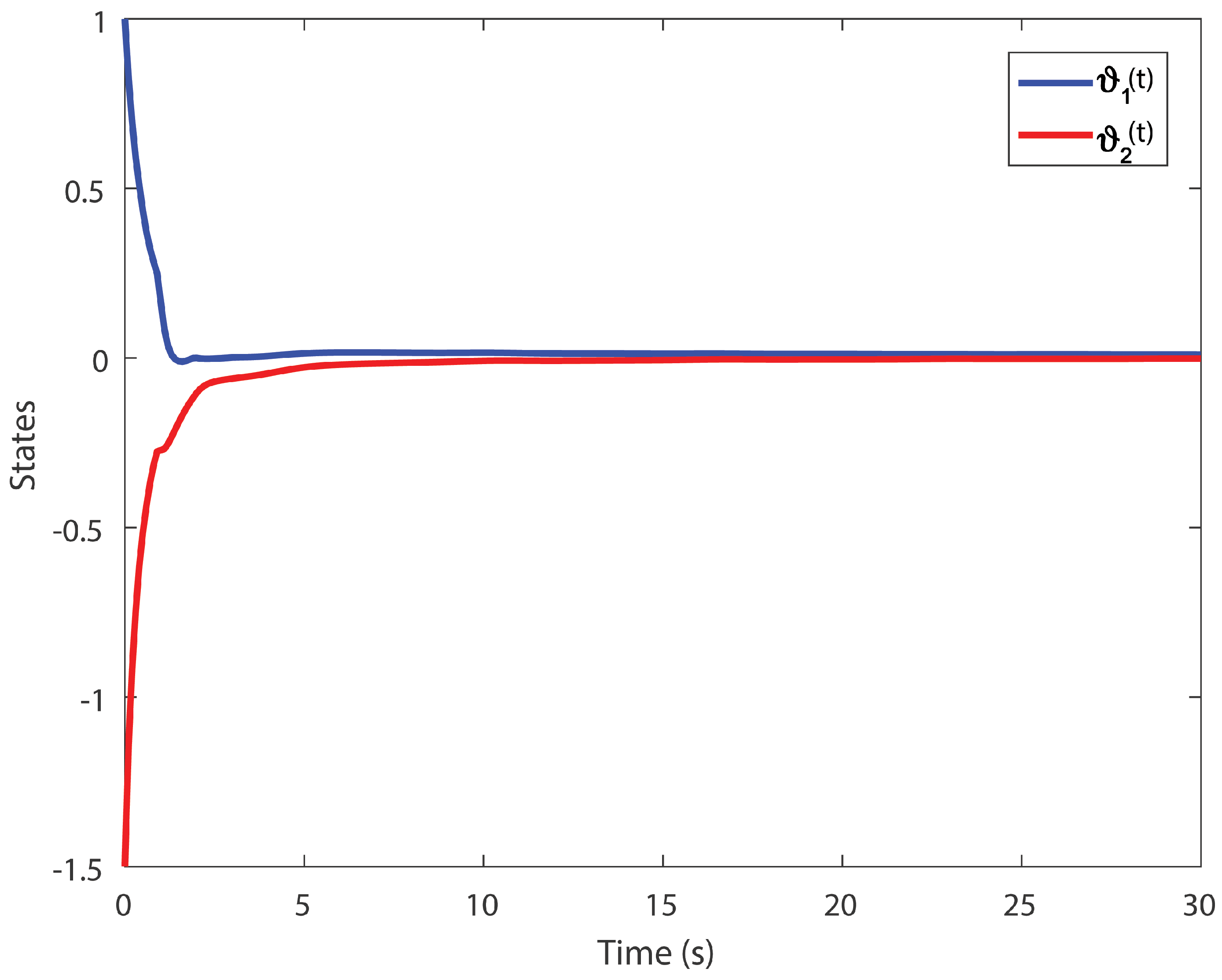
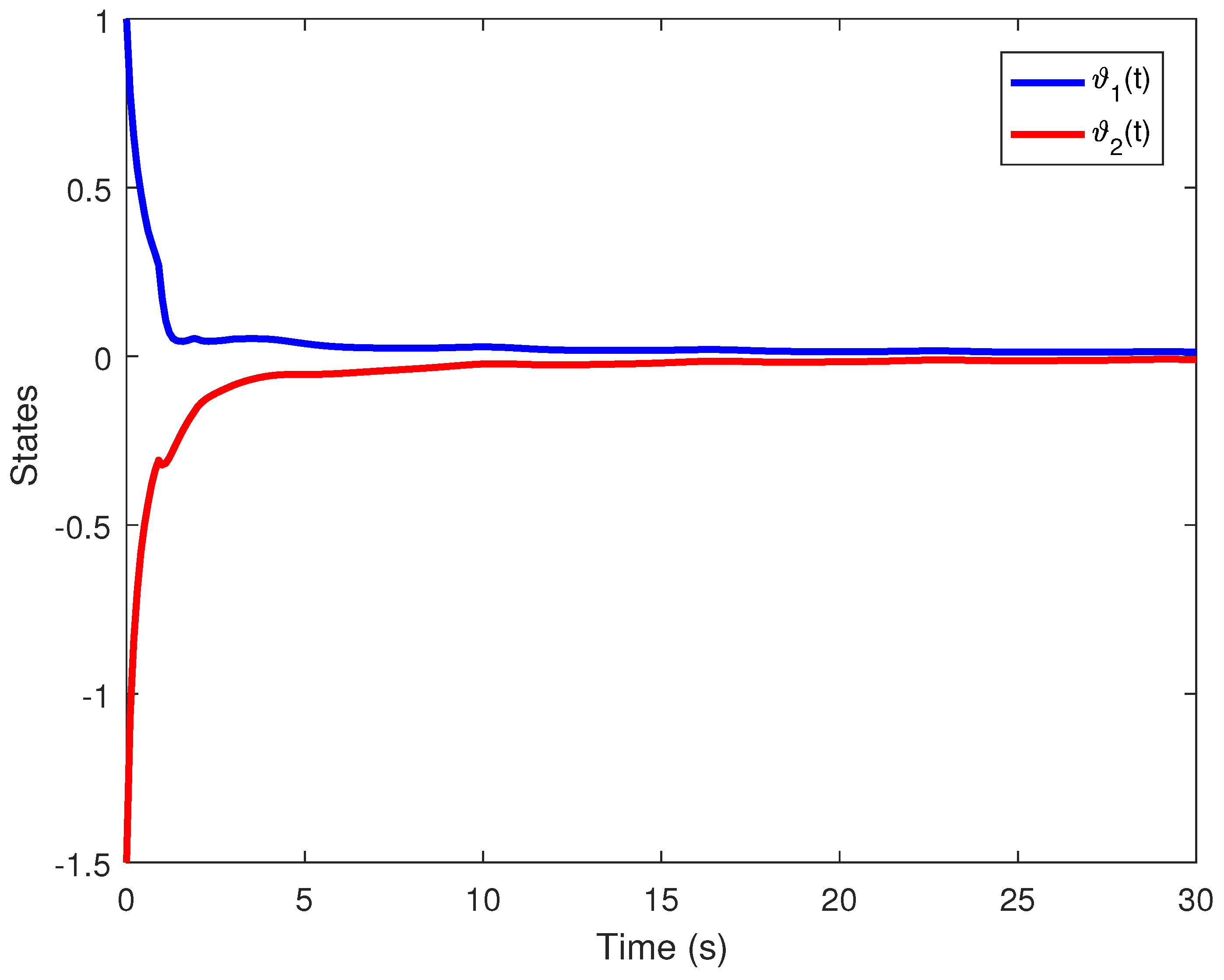
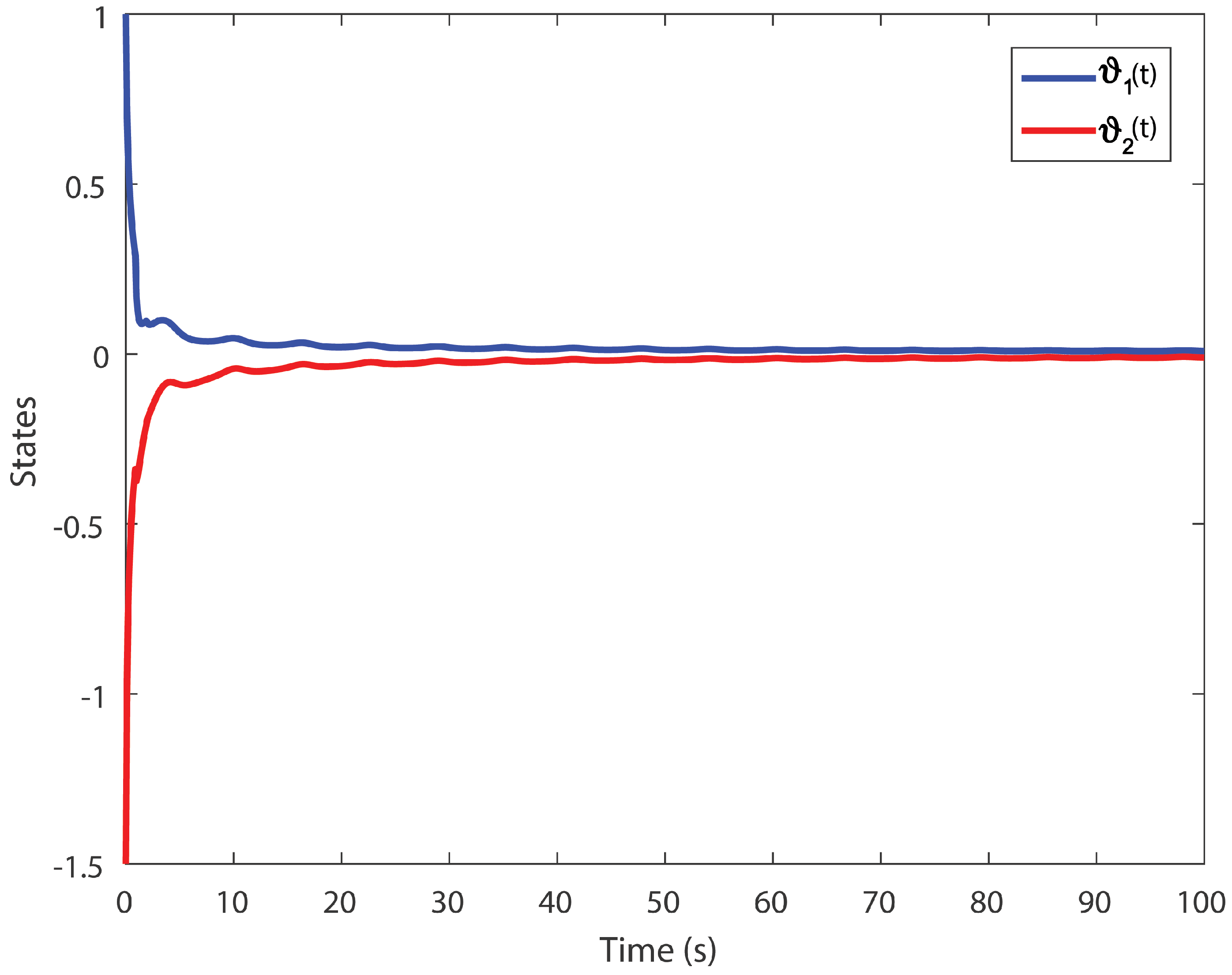
6. Simulation Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Qu, Y.; Kao, Y.; Gao, C. Observer-Based Controller Design for Fractional-Order Neutral-Type Systems. In Recent Advances in Control Problems of Dynamical Systems and Networks; Springer: Berlin/Heidelberg, Germany, 2021; pp. 267–289. [Google Scholar]
- Thanh, N.T.; Niamsup, P.; Phat, V.N. Observer-based finite-time control of linear fractional-order systems with interval time-varying delay. Int. J. Syst. Sci. 2021, 52, 1386–1395. [Google Scholar] [CrossRef]
- Elahi, A.; Alfi, A.; Modares, H. Distributed Consensus Control of Vehicular Platooning Under Delay, Packet Dropout and Noise: Relative State and Relative Input-Output Control Strategies. IEEE Trans. Intell. Transp. Syst. 2022. [Google Scholar] [CrossRef]
- Mokkedem, F.Z. Approximate Controllability for a Class of Linear Neutral Evolution Systems with Infinite Delay. J. Dyn. Control. Syst. 2021, 28, 917–943. [Google Scholar] [CrossRef]
- Barbarossa, M.; Hadeler, K.; Kuttler, C. State-dependent neutral delay equations from population dynamics. J. Math. Biol. 2014, 69, 1027–1056. [Google Scholar] [CrossRef] [PubMed]
- Han, Q.L. Stability analysis for a partial element equivalent circuit (PEEC) model of neutral type. Int. J. Circuit Theory Appl. 2005, 33, 321–332. [Google Scholar] [CrossRef]
- Cui, K.; Lu, J.; Li, C.; He, Z.; Chu, Y.M. Almost sure synchronization criteria of neutral-type neural networks with Lévy noise and sampled-data loss via event-triggered control. Neurocomputing 2019, 325, 113–120. [Google Scholar] [CrossRef]
- Kilbas, A.; Bonilla, B.; Trujillo, J. Fractional integrals and derivatives, and differential equations of fractional order in weighted spaces of continuous functions. Dokl. Nats. Akad. Nauk Belarusi 2000, 44, 18–22. [Google Scholar]
- Heydari, M.; Tavakoli, R.; Razzaghi, M. Application of the extended Chebyshev cardinal wavelets in solving fractional optimal control problems with ABC fractional derivative. Int. J. Syst. Sci. 2022, 53, 2694–2708. [Google Scholar] [CrossRef]
- Xie, L.; Liu, Z.; Zhang, B. A modeling and analysis method for CCM fractional order Buck-Boost converter by using R–L fractional definition. J. Electr. Eng. Technol. 2020, 15, 1651–1661. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, F.; Yu, Q.; Li, T. Review of fractional epidemic models. Appl. Math. Model. 2021, 97, 281–307. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, H.; Stowell, H.H.; Zayernouri, M.; Hansen, S.E. A review of applications of fractional calculus in earth system dynamics. Chaos Solitons Fractals 2017, 102, 29–46. [Google Scholar] [CrossRef]
- Silva, M.F.; Machado, J.T.; Lopes, A. Fractional order control of a hexapod robot. Nonlinear Dyn. 2004, 38, 417–433. [Google Scholar] [CrossRef]
- Ionescu, C.; Lopes, A.; Copot, D.; Machado, J.T.; Bates, J.H. The role of fractional calculus in modeling biological phenomena: A review. Commun. Nonlinear Sci. Numer. Simul. 2017, 51, 141–159. [Google Scholar] [CrossRef]
- Zou, C.; Zhang, L.; Hu, X.; Wang, Z.; Wik, T.; Pecht, M. A review of fractional-order techniques applied to lithium-ion batteries, lead-acid batteries, and supercapacitors. J. Power Sources 2018, 390, 286–296. [Google Scholar] [CrossRef]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Duarte Ortigueira, M.; Tenreiro Machado, J. Fractional signal processing and applications. Signal Process. 2003, 83, 2285–2286. [Google Scholar] [CrossRef]
- Xiao, B.; Luo, J.; Bi, X.; Li, W.; Chen, B. Fractional discrete Tchebyshev moments and their applications in image encryption and watermarking. Inf. Sci. 2020, 516, 545–559. [Google Scholar] [CrossRef]
- Lopes, A.M.; Tenreiro Machado, J. Dynamics of the N-link pendulum: A fractional perspective. Int. J. Control. 2017, 90, 1192–1200. [Google Scholar] [CrossRef]
- Nikan, O.; Avazzadeh, Z.; Machado, J.T. Numerical approach for modeling fractional heat conduction in porous medium with the generalized Cattaneo model. Appl. Math. Model. 2021, 100, 107–124. [Google Scholar] [CrossRef]
- Mohsenipour, R.; Fathi Jegarkandi, M. Robust stability analysis of fractional-order interval systems with multiple time delays. Int. J. Robust Nonlinear Control. 2019, 29, 1823–1839. [Google Scholar] [CrossRef]
- Maurya, R.K.; Devi, V.; Singh, V.K. Stability and convergence of multistep schemes for 1D and 2D fractional model with nonlinear source term. Appl. Math. Model. 2021, 89, 1721–1746. [Google Scholar] [CrossRef]
- Shahri, E.S.A.; Alfi, A.; Machado, J.T. Lyapunov method for the stability analysis of uncertain fractional-order systems under input saturation. Appl. Math. Model. 2020, 81, 663–672. [Google Scholar] [CrossRef]
- Pahnehkolaei, S.M.A.; Alfi, A.; Machado, J.T. Fuzzy logic embedding of fractional order sliding mode and state feedback controllers for synchronization of uncertain fractional chaotic systems. Comput. Appl. Math. 2020, 39, 182. [Google Scholar] [CrossRef]
- Badri, P.; Sojoodi, M. Robust stabilisation of fractional-order interval systems via dynamic output feedback: An LMI approach. Int. J. Syst. Sci. 2019, 50, 1718–1730. [Google Scholar] [CrossRef]
- Guo, Y.; Lin, C.; Chen, B.; Wang, Q.G. Stabilization for singular fractional-order systems via static output feedback. IEEE Access 2018, 6, 71678–71684. [Google Scholar] [CrossRef]
- Jeet, K.; Bahuguna, D. Approximate controllability of nonlocal neutral fractional integro-differential equations with finite delay. J. Dyn. Control. Syst. 2016, 22, 485–504. [Google Scholar] [CrossRef]
- Wang, T.; Li, T.; Zhang, G.; Fei, S. Further triple integral approach to mixed-delay-dependent stability of time-delay neutral systems. ISA Trans. 2017, 70, 116–124. [Google Scholar] [CrossRef]
- Liu, P.L. Improved results on delay-interval-dependent robust stability criteria for uncertain neutral-type systems with time-varying delays. ISA Trans. 2016, 60, 53–66. [Google Scholar] [CrossRef]
- Chartbupapan, W.; Bagdasar, O.; Mukdasai, K. A Novel Delay-Dependent Asymptotic Stability Conditions for Differential and Riemann-Liouville Fractional Differential Neutral Systems with Constant Delays and Nonlinear Perturbation. Mathematics 2020, 8, 82. [Google Scholar] [CrossRef]
- Aghayan, Z.S.; Alfi, A.; Machado, J.T. Robust stability of uncertain fractional order systems of neutral type with distributed delays and control input saturation. ISA Trans. 2021, 111, 144–155. [Google Scholar] [CrossRef]
- Aghayan, Z.S.; Alfi, A.; Machado, J.T. LMI-based stability analysis of fractional order systems of neutral type with time varying delays under actuator saturation. Comput. Appl. Math. 2021, 40, 142. [Google Scholar] [CrossRef]
- Aghayan, Z.S.; Alfi, A.; Tenreiro Machado, J.A. Observer-based control approach for fractional-order delay systems of neutral type with saturating actuator. Math. Methods Appl. Sci. 2021, 44, 8554–8564. [Google Scholar] [CrossRef]
- Aghayan, Z.S.; Alfi, A.; Tenreiro Machado, J. Stability analysis of uncertain fractional-order neutral-type delay systems with actuator saturation. Front. Inf. Technol. Electron. Eng. 2021, 22, 1402–1412. [Google Scholar] [CrossRef]
- Padmaja, N.; Balasubramaniam, P. Mixed H∞/passivity based stability analysis of fractional-order gene regulatory networks with variable delays. Math. Comput. Simul. 2022, 192, 167–181. [Google Scholar] [CrossRef]
- Luo, S.; Lu, J.G. Robust stability and stabilization of fractional-order systems with polytopic uncertainties via homogeneous polynomial parameter-dependent matrix forms. Int. J. Gen. Syst. 2021, 50, 891–914. [Google Scholar] [CrossRef]
- Chang, S.; Peng, T. Adaptive guaranteed cost control of systems with uncertain parameters. IEEE Trans. Autom. Control. 1972, 17, 474–483. [Google Scholar] [CrossRef]
- Aghayan, Z.S.; Alfi, A.; Machado, J.T. Guaranteed cost-based feedback control design for fractional-order neutral systems with input-delayed and nonlinear perturbations. ISA Trans. 2022. [Google Scholar] [CrossRef]
- Mohammadi, L.; Alfi, A. Guaranteed cost control in delayed teleoperation systems under actuator saturation. Iran. J. Sci. Technol. Trans. Electr. Eng. 2019, 43, 827–835. [Google Scholar] [CrossRef]
- Lee, T.H.; Park, J.H.; Ji, D.; Kwon, O.; Lee, S.M. Guaranteed cost synchronization of a complex dynamical network via dynamic feedback control. Appl. Math. Comput. 2012, 218, 6469–6481. [Google Scholar] [CrossRef]
- Yang, X.; Wang, Y.; Zhang, X. Lyapunov Matrix-Based Method to Guaranteed Cost Control for A Class of Delayed Continuous-Time Nonlinear Systems. IEEE Trans. Syst. Man, Cybern. Syst. 2020, 52, 554–560. [Google Scholar] [CrossRef]
- Shen, B.; Wang, Z.; Tan, H. Guaranteed cost control for uncertain nonlinear systems with mixed time-delays: The discrete-time case. Eur. J. Control. 2018, 40, 62–67. [Google Scholar] [CrossRef]
- Thuan, M.V.; Huong, D.C. Robust guaranteed cost control for time-delay fractional-order neural networks systems. Optim. Control. Appl. Methods 2019, 40, 613–625. [Google Scholar] [CrossRef]
- Thuan, M.V.; Binh, T.N.; Huong, D.C. Finite-time guaranteed cost control of Caputo fractional-order neural networks. Asian J. Control. 2020, 22, 696–705. [Google Scholar] [CrossRef]
- Qi, F.; Chai, Y.; Chen, L.; Tenreiro Machado, J.A. Delay-Dependent and Order-Dependent Guaranteed Cost Control for Uncertain Fractional-Order Delayed Linear Systems. Mathematics 2021, 9, 41. [Google Scholar] [CrossRef]
- Niamsup, P.; Phat, V.N. A new result on finite-time control of singular linear time-delay systems. Appl. Math. Lett. 2016, 60, 1–7. [Google Scholar] [CrossRef]
- He, H.; Yan, L.; Tu, J. Guaranteed cost stabilization of time-varying delay cellular neural networks via Riccati inequality approach. Neural Process. Lett. 2012, 35, 151–158. [Google Scholar] [CrossRef]
- He, H.; Xu, W.; Jiang, M. Guaranteed cost anti-windup stabilization of discrete delayed cellular neural networks. Neural Process. Lett. 2017, 46, 343–354. [Google Scholar] [CrossRef]
- Lien, C. Guaranteed cost observer–based controls for a class of uncertain neutral time-delay systems. J. Optim. Theory Appl. 2005, 126, 137–156. [Google Scholar] [CrossRef]
- He, H.; Yan, L.; Tu, J. Guaranteed cost stabilization of cellular neural networks with time-varying delay. Asian J. Control. 2013, 15, 1224–1227. [Google Scholar] [CrossRef]
- Davies, I.; Haas, O.L. Robust guaranteed cost control for a nonlinear neutral system with infinite delay. In Proceedings of the 2015 European Control Conference (ECC), Linz, Austria, 15–17 July 2022; pp. 1255–1260. [Google Scholar]
- Parlakçı, M.A. Robust delay-dependent guaranteed cost controller design for uncertain nonlinear neutral systems with time-varying state delays. Int. J. Robust Nonlinear Control. IFAC Affil. J. 2010, 20, 334–345. [Google Scholar] [CrossRef]
- Yun, S.W.; Choi, Y.J.; Park, P. Dynamic output-feedback guaranteed cost control for linear systems with uniform input quantization. Nonlinear Dyn. 2010, 62, 95–104. [Google Scholar] [CrossRef]
- Balasaheb, W.V.; Uttam, C. Novel intelligent optimization algorithm based fractional order adaptive Proportional Integral Derivative controller for linear time invariant based biological systems. J. Electr. Eng. Technol. 2022, 17, 565–580. [Google Scholar] [CrossRef]
- Alfi, A. Chaos suppression on a class of uncertain nonlinear chaotic systems using an optimal H∞ adaptive PID controller. Chaos Solitons Fractals 2012, 45, 351–357. [Google Scholar] [CrossRef]
- Åström, K.J.; Hägglund, T. PID Controllers: Theory, Design, and Tuning; ISA—The Instrumentation, Systems and Automation Society: Pittsburgh, PA, USA, 1995. [Google Scholar]
- Valério, D.; Trujillo, J.J.; Rivero, M.; Machado, J.T.; Baleanu, D. Fractional calculus: A survey of useful formulas. Eur. Phys. J. Spec. Top. 2013, 222, 1827–1846. [Google Scholar] [CrossRef]
- Zhang, F. The Schur Complement and Its Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006; Volume 4. [Google Scholar]
- Petersen, I.R. A stabilization algorithm for a class of uncertain linear systems. Syst. Control. Lett. 1987, 8, 351–357. [Google Scholar] [CrossRef]
- Liang, S.; Wu, R.; Chen, L. Comparison principles and stability of nonlinear fractional-order cellular neural networks with multiple time delays. Neurocomputing 2015, 168, 618–625. [Google Scholar] [CrossRef]
- Chen, B.; Chen, J. Razumikhin-type stability theorems for functional fractional-order differential systems and applications. Appl. Math. Comput. 2015, 254, 63–69. [Google Scholar] [CrossRef]
- Liao, X.; Chen, G.; Sanchez, E.N. LMI-based approach for asymptotically stability analysis of delayed neural networks. IEEE Trans. Circuits Syst. Fundam. Theory Appl. 2002, 49, 1033–1039. [Google Scholar] [CrossRef]
- Diethelm, K.; Freed, A.D. The FracPECE subroutine for the numerical solution of differential equations of fractional order. Forsch. Und Wiss. Rechn. 1998, 1999, 57–71. [Google Scholar]
- Phoojaruenchanachai, S.; Uahchinkul, K.; Prempraneerach, Y. Robust stabilisation of a state delayed system. IEE Proc. Control Theory Appl. 1998, 145, 87–91. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J. Analysis of fractional differential equations. J. Math. Anal. Appl. 2002, 265, 229–248. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aghayan, Z.S.; Alfi, A.; Lopes, A.M. LMI-Based Delayed Output Feedback Controller Design for a Class of Fractional-Order Neutral-Type Delay Systems Using Guaranteed Cost Control Approach. Entropy 2022, 24, 1496. https://doi.org/10.3390/e24101496
Aghayan ZS, Alfi A, Lopes AM. LMI-Based Delayed Output Feedback Controller Design for a Class of Fractional-Order Neutral-Type Delay Systems Using Guaranteed Cost Control Approach. Entropy. 2022; 24(10):1496. https://doi.org/10.3390/e24101496
Chicago/Turabian StyleAghayan, Zahra Sadat, Alireza Alfi, and António M. Lopes. 2022. "LMI-Based Delayed Output Feedback Controller Design for a Class of Fractional-Order Neutral-Type Delay Systems Using Guaranteed Cost Control Approach" Entropy 24, no. 10: 1496. https://doi.org/10.3390/e24101496
APA StyleAghayan, Z. S., Alfi, A., & Lopes, A. M. (2022). LMI-Based Delayed Output Feedback Controller Design for a Class of Fractional-Order Neutral-Type Delay Systems Using Guaranteed Cost Control Approach. Entropy, 24(10), 1496. https://doi.org/10.3390/e24101496







