Optimized LightGBM Power Fingerprint Identification Based on Entropy Features
Abstract
:1. Introduction
2. The Power Fingerprint Identification Architecture
3. Feature Extraction Based on Time-Domain Analysis and V-I Trajectory
4. Feature Selection Based on the Modified Boruta Algorithm
4.1. Boruta Algorithm
4.2. Modified Boruta Algorithm
- Step 1:
- For each original feature , randomly disrupt the order. Duplicate the original features to obtain the shadow feature matrix , and the new feature matrix is formed by splicing with the original feature .
- Step 2:
- The new feature matrix is used as input and the base learner is trained. Calculate the importance score .where is the evaluated importance of the feature, and is the importance of the feature.
- Step 3:
- Find the maximum value of the importance score in the shadow features and mark it as . Mark the features with importance scores higher than in the original features as important.
- Step 4:
- Marking features with importance scores lower than in the original feature as unimportant and permanently deleting them.
- Step 5:
- Remove all shadow features and repeat the above process until all important features are filtered out.
5. Construction of Power Fingerprint Identification Classifier
5.1. Improved LightGBM Model
5.2. Optuna Optimization Algorithm
- Define-by-run framework: Optuna describes hyperparametric optimization as the process of maximizing or minimizing an objective function given a set of hyperparameters and returning its (validated) score [37]. The function does not depend on externally defined static variables and dynamically constructs the search space of the neural network structure (number of layers and number of hidden units).
- Efficient sampling: Optuna has both relational and independent sampling [38] and can identify trial results. These results provide information for concurrent relationships. The framework can identify potential co-occurrence relationships after a certain number of independent samples and use the inferred co-occurrence relationships for a user-selected relational sampling algorithm.
- Efficient pruning: Optuna periodically monitors intermediate target values and terminates trials that do not meet predefined conditions. It also uses the asynchronous successive halving algorithm [37], and therefore we can perform parallel computations here without much influence on each other.
5.3. Construction of the Optuna–LightGBM Classification Model
- Initialization, and then determining the direction of optimization, the type of parameters, the range of values, and the maximum number of iterations.
- Enter the loop: selecting a set of individuals uniformly within the function defining the range of parameter values, automatically terminating hopeless individuals using a pruner according to the pruning conditions, and determining the value of the objective function for the overall number of uncomputed individuals.
- Repeating the above steps for the loop and jumping out of the loop when the maximum number of iterations is reached.
- Obtaining the best parameter values and the best values of the objective function and output the final model OPT–LightGBM.
5.4. Evaluation Metrics
6. Result and Discussion
6.1. Dataset Selection
6.2. Construction of Optimal Feature Subsets Based on the Modified Boruta Algorithm
6.3. Amount of Data Transmission
6.4. Comparison of Different Hyperparameter Optimization Algorithms
6.5. Comparison of the Impact of Entropy Features on Classification Performance
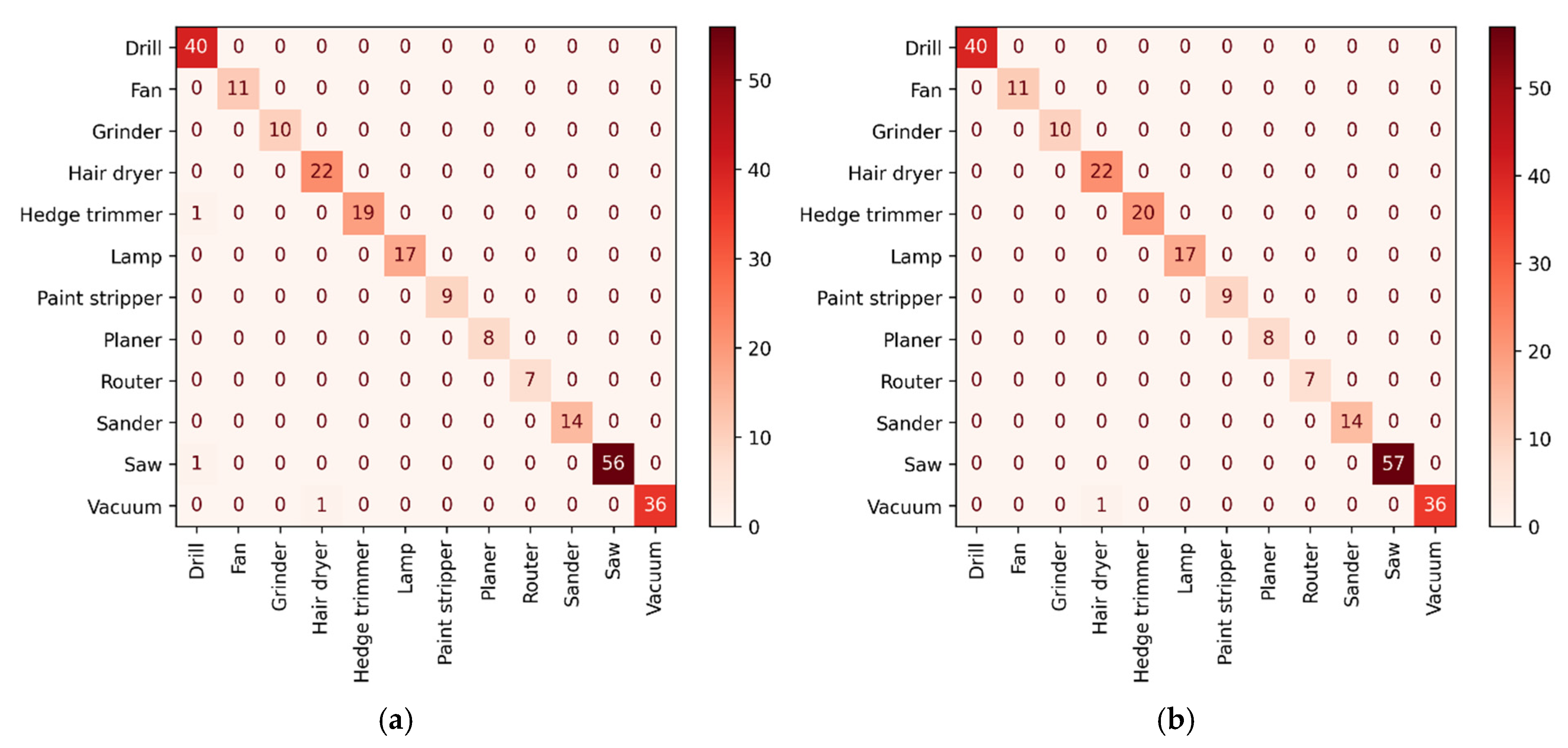
6.6. Comparison of the Performance of Each Classifier under an Imbalanced Dataset
6.7. Analysis and Discussion
7. Conclusions
- A modified Boruta algorithm was used to feature select the original feature set containing six entropy features and to construct the optimal feature subset, which further improved the optimization-seeking efficiency of feature selection and reduced the impact of redundant features on the classification performance of the classifier. The experimental results showed that the five entropy features retained after feature selection significantly improved power fingerprint identification.
- The optimal feature subset replaced the original signal and the original feature set and was uploaded to the upper system, effectively reducing the amount of data transmission and feature computation required for edge devices and reducing the overall communication and hardware cost of the system.
- A lightweight power fingerprint identification model for class-imbalanced samples was constructed. The LightGBM loss function was improved, and its parameters were optimized using the Optuna optimization algorithm. The experimental results show that the method improved the accuracy of power fingerprint identification on imbalanced datasets and effectively verified the model’s generalization ability.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| LightGBM | Light gradient boosting machine |
| NILD | Non-intrusive load disaggregation |
| STFT | Short-time Fourier transform |
| WT | Wavelet transform |
| RFE | Recursive elimination |
| RF | Random forest |
| DT | Decision tree |
| SVM | Support vector machine |
| KNN | K-nearest neighbor |
| CNN | Convolutional neural network |
| RNN | Recurrent neural network |
| GBDT | Gradient boosting decision tree |
| XGBoost | Extreme gradient boosting |
| GA | Genetic algorithm |
Appendix A
| Formula | Formula |
|---|---|
| Formula | Formula |
|---|---|
References
- Fang, Y.; Jiang, S.; Fang, S.; Gong, Z.; Xia, M.; Zhang, X. Non-Intrusive Load Disaggregation Based on a Feature Reused Long Short-Term Memory Multiple Output Network. Buildings 2022, 12, 1048. [Google Scholar] [CrossRef]
- Hadi, M.U.; Suhaimi, N.H.N.; Basit, A. Efficient Supervised Machine Learning Network for Non-Intrusive Load Monitoring. Technologies 2022, 10, 85. [Google Scholar] [CrossRef]
- Enrico, T.; Davide, B.; Andrea, A. Trimming Feature Extraction and Inference for MCU-Based Edge NILM: A Systematic Approach. IEEE Trans. Ind. Inform. 2022, 18, 943–952. [Google Scholar]
- Yu, J.; Liu, W.; Wu, X. Noninvasive Industrial Power Load Monitoring Based on Collaboration of Edge Device and Edge Data Center. In Proceedings of the 2020 IEEE International Conference on Edge Computing (EDGE), Beijing, China, 19–23 October 2020; IEEE: Piscataway, NJ, USA; pp. 23–30. [Google Scholar]
- Chen, J.; Wang, X. Non-intrusive Load Monitoring Using Gramian Angular Field Color Encoding in Edge Computing. Chin. J. Electron. 2022, 31, 595–603. [Google Scholar] [CrossRef]
- Wang, C.; Wu, Z.; Peng, W. Adaptive modeling for Non-Intrusive Load Monitoring. Int. J. Electr. Power Energy Syst. 2022, 140, 107981. [Google Scholar] [CrossRef]
- Houidi, S.; Fourer, D.; Auger, F. On the Use of Concentrated Time–Frequency Representations as Input to a Deep Convolutional Neural Network: Application to Non Intrusive Load Monitoring. Entropy 2020, 22, 911. [Google Scholar] [CrossRef]
- Dowalla, K.; Bilski, P.; Łukaszewski, R.; Wójcik, A.; Kowalik, R. Application of the Time-Domain Signal Analysis for Electrical Appliances Identification in the Non-Intrusive Load Monitoring. Energies 2022, 15, 3325. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, X.; You, W. Non-Intrusive Load Monitoring by Voltage–Current Trajectory Enabled Transfer Learning. IEEE Trans. Smart Grid 2018, 10, 5609–5619. [Google Scholar] [CrossRef]
- Maqsood, A.; Oslebo, D.; Corzine, K. STFT Cluster Analysis for DC Pulsed Load Monitoring and Fault Detection on Naval Shipboard Power Systems. IEEE Trans. Transp. Electrif. 2020, 6, 821–831. [Google Scholar] [CrossRef]
- De Aguiar, E.L.; Lazzaretti, A.E.; Mulinari, B.M.; Pipa, D.R. Scattering Transform for Classification in Non-Intrusive Load Monitoring. Energies 2021, 14, 6796. [Google Scholar] [CrossRef]
- Sadeghianpourhamami, N.; Ruyssinck, J.; Deschrijver, D. Comprehensive feature selection for appliance classification in NILM. Energy Build. 2017, 151, 98–106. [Google Scholar] [CrossRef]
- Bai, H.; Zhan, X.; Yan, H.; Wen, L.; Jia, X. Combination of Optimized Variational Mode Decomposition and Deep Transfer Learning: A Better Fault Diagnosis Approach for Diesel Engines. Electronics 2022, 11, 1969. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Y.; Kong, L.; Niu, Q.; Bai, Y. Improved DBSCAN Spindle Bearing Condition Monitoring Method Based on Kurtosis and Sample Entropy. Machines 2022, 10, 363. [Google Scholar] [CrossRef]
- Sheng, B.; Li, Z.; Xueshan, H. Feature Selection Method for Nonintrusive Load Monitoring With Balanced Redundancy and Relevancy. IEEE Trans. Ind. Appl. 2022, 58, 163–172. [Google Scholar]
- Szul, T.; Tabor, S.; Pancerz, K. Application of the BORUTA Algorithm to Input Data Selection for a Model Based on Rough Set Theory (RST) to Prediction Energy Consumption for Building Heating. Energies 2021, 14, 2779. [Google Scholar] [CrossRef]
- Shi, X.; Ming, H.; Shakkottai, S. Nonintrusive load monitoring in residential households with low-resolution data. Appl. Energy 2019, 252, 113283. [Google Scholar] [CrossRef]
- Wu, X.; Gao, Y.; Jiao, D. Multi-label classification based on random forest algorithm for non-intrusive load monitoring system. Processes 2019, 7, 337. [Google Scholar] [CrossRef] [Green Version]
- Gjoreski, M.; Mahesh, B.; Kolenik, T. Cognitive Load Monitoring With Wearables–Lessons Learned From a Machine Learning Challenge. IEEE Access 2021, 9, 103325–103336. [Google Scholar] [CrossRef]
- Ding, D.; Li, J.; Zhang, K. Non-intrusive load monitoring method with inception structured CNN. Appl. Intell. 2022, 52, 6227–6244. [Google Scholar] [CrossRef]
- Yang, T.; Wai, L.; Thillainathan, L. Load Disaggregation Using One-Directional Convolutional Stacked Long Short-Term Memory Recurrent Neural Network. IEEE Syst. J. 2020, 14, 1395–1404. [Google Scholar]
- Park, J.; Hwang, E. A Two-Stage Multistep-Ahead Electricity Load Forecasting Scheme Based on LightGBM and Attention-BiLSTM. Sensors 2021, 21, 7697. [Google Scholar] [CrossRef]
- Luo, Z.; Wang, H.; Li, S. Prediction of International Roughness Index Based on Stacking Fusion Model. Sustainability 2022, 14, 6949. [Google Scholar] [CrossRef]
- Li, X.; Leung, F.H.F.; Su, S.; Ling, S.H. Sleep Apnea Detection Using Multi-Error-Reduction Classification System with Multiple Bio-Signals. Sensors 2022, 22, 5560. [Google Scholar] [CrossRef] [PubMed]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. Lightgbm: A highly efficient gradient boosting decision tree. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 3146–3154. [Google Scholar]
- Sun, J.; Li, J.; Fujita, H. Multi-Class Imbalanced Enterprise Credit Evaluation Based on Asymmetric Bagging Combined with Light Gradient Boosting Machine. Appl. Soft Comput. 2022, 130, 109637. [Google Scholar] [CrossRef]
- De Baets, L.; Develder, C.; Dhaene, T.; Deschrijver, D.; Gao, J.; Berges, M. Handling Imbalance in an Extended PLAID. In Proceedings of the 2017 Sustainable Internet and ICT for Sustainability (SustainIT), Funchal, Portugal, 6–7 December 2017; IEEE: Piscataway, NJ, USA; pp. 1–5. [Google Scholar]
- Tian, L.; Wang, Z.; Liu, W.; Cheng, Y.; Alsaadi, F.E.; Liu, X. An Improved Generative Adversarial Network with Modified Loss Function for Crack Detection in Electromagnetic Nondestructive Testing. Complex Intell. Syst. 2022, 8, 467–476. [Google Scholar] [CrossRef]
- Bhat, P.C.; Prosper, H.B.; Sekmen, S.; Stewart, C. Optimizing Event Selection with the Random Grid Search. Comput. Phys. Commun. 2018, 228, 245–257. [Google Scholar] [CrossRef] [Green Version]
- Jiang, T.; Hua, M.; Li, Y. Flight delay prediction based on LightGBM. In Proceedings of the 2021 IEEE 3rd International Conference on Civil Aviation Safety and Information Technology (ICCASIT), Changsha, China, 20–22 October 2021; pp. 1248–1251. [Google Scholar]
- Yu, M.; Wang, B.; Lu, L. Non-intrusive adaptive load identification based on siamese network. IEEE Access 2020, 10, 11564–11573. [Google Scholar] [CrossRef]
- Franco, P.; Martinez, J.M.; Kim, Y.C.; Ahmed, M.A. IoT Based Approach for Load Monitoring and Activity Recognition in Smart Homes. IEEE Access 2021, 9, 45325–45339. [Google Scholar] [CrossRef]
- Longjun, W.; Xiaomin, C.; Gang, W. Non-intrusive load monitoring algorithm based on features of V–I trajectory. Electr. Power Syst. Res. 2018, 157, 134–144. [Google Scholar]
- Mulinari, B.; Linhares, R.; Campos, D. A new set of steady-state and transient features for power signature analysis based on V-I trajectory. In Proceedings of the 2019 IEEE PES Innovative Smart Grid Technologies Conference-Latin America (ISGT Latin America), Gramado, Brazil, 15–18 September 2019; pp. 1–6. [Google Scholar]
- Alù, F.; Miraglia, F.; Orticoni, A.; Judica, E.; Cotelli, M.; Rossini, P.M.; Vecchio, F. Approximate Entropy of Brain Network in the Study of Hemispheric Differences. Entropy 2020, 22, 1220. [Google Scholar] [CrossRef]
- Kursa, M.B.; Rudnicki, W.R. Feature Selection with the Boruta Package. J. Stat. Soft. 2010, 36, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Polipireddy, S.; Rahul, K. HyOPTXg: OPTUNA hyper-parameter optimization framework for predicting cardiovascular disease using XGBoost. Biomed. Signal Process. Control. 2021, 73, 103456. [Google Scholar]
- Namoun, A.; Hussein, B.R.; Tufail, A.; Alrehaili, A.; Syed, T.A.; BenRhouma, O. An Ensemble Learning Based Classification Approach for the Prediction of Household Solid Waste Generation. Sensors 2022, 22, 3506. [Google Scholar] [CrossRef] [PubMed]











| Features | Formula | Feature Number | Features | Formula | Feature Number |
|---|---|---|---|---|---|
| Maximum value | F1 | Peak | F10 | ||
| Minimum value | F2 | Peak to peak value | F11 | ||
| Mean value | F3 | Absolute mean | F12 | ||
| Variance | F4 | Square root amplitude | F13 | ||
| Standard deviation | F5 | Waveform index | F14 | ||
| Root mean square | F6 | Peak index | F15 | ||
| Cliffness | F7 | Pulse index | F16 | ||
| Skewness | F8 | Clearance index | F17 | ||
| Sum of maximum and minimum values | F9 | Energy | F18 |
| Features | Formula | Feature Number | Features | Formula | Feature Number |
|---|---|---|---|---|---|
| Shannon entropy | F19 | Fuzzy entropy | F22 | ||
| Renyi entropy | F20 | Permutation entropy | F23 | ||
| Approximate entropy | F21 | Sample entropy | F24 |
| Features | Feature Number | Feature Number |
|---|---|---|
| Transient | Steady State | |
| Current span | F25 | F37 |
| Area | F26 | F38 |
| Direction | F27 | F39 |
| Asymmetry | F28 | F40 |
| The curvature of the mean line | F29 | F41 |
| Self-intersection | F30 | F42 |
| The peak of the middle segment | F31 | F43 |
| The shape of the middle segment | F32 | F44 |
| Area of left and right segments | F33 | F45 |
| Variation of instantaneous admittance | F34 | F46 |
| The angle between the maximum point and the minimum point | F35 | F47 |
| The distance between the maximum point and the minimum point | F36 | F48 |
| Features | Feature Number |
|---|---|
| The difference between the current span of the steady state and transient trajectory | F49 |
| The difference between the area of the steady state and transient trajectory | F50 |
| The difference between the asymmetry of the steady state and transient trajectory | F51 |
| The difference between self-intersection of the steady state and transient trajectory | F52 |
| The difference between the peak of the middle segment of the steady state and transient trajectory | F53 |
| The difference between the area of the left and right segments of the steady state and transient trajectory | F54 |
| The difference between the angle between the maximum point and the minimum point of the steady state and transient trajectory | F55 |
| The difference between the distance between the maximum and minimum points of the steady state and transient trajectory | F56 |
| Appliance Labels | Appliances | Number of Appliances | Number of Signals |
|---|---|---|---|
| A | Drill | 6 | 120 |
| B | Fan | 2 | 40 |
| C | Grinder | 2 | 40 |
| D | Hair dryer | 4 | 80 |
| E | Hedge trimmer | 3 | 60 |
| F | Lamp | 4 | 80 |
| G | Paint stripper | 1 | 20 |
| H | Planer | 1 | 20 |
| I | Router | 1 | 20 |
| J | Sander | 3 | 60 |
| K | Saw | 8 | 160 |
| L | Vacuum | 7 | 140 |
| Model | Optimal Feature Dimension | Accuracy (%) | Recall (%) | Precision (%) | F1-Score (%) |
|---|---|---|---|---|---|
| No feature selection | 56 | 97.62 | 98.24 | 97.62 | 97.77 |
| Correlation coefficient | 30 | 96.83 | 96.83 | 97.72 | 97.03 |
| REF | 25 | 97.22 | 97.22 | 97.87 | 97.36 |
| GA | 28 | 96.43 | 96.43 | 97.57 | 96.70 |
| Embedded (LightGBM) | 23 | 98.81 | 98.90 | 98.90 | 98.82 |
| Modified Boruta | 23 | 99.60 | 99.77 | 99.64 | 99.70 |
| Transmission Data Type | Amount of Data Transmission for a Set of Feature Sets (Byte) |
|---|---|
| Original signal | 2,744,650 |
| Original feature set | 1591 |
| Optimal feature subset | 1118 |
| Model | Optimized Hyperparameters | Default Hyperparameters |
|---|---|---|
| LightGBM | ‘max_depth’: 7, ‘subsample’: 0.8, ‘num_leaves’: 22, ‘learning_rate’: 0.018, ‘min_child_wight’: 1.12, ‘n_estimators’: 146 | ‘lambda_l1’: 0.5, ‘lambda_l2’: 0.5, ‘bagging_fraction’: 1, ‘feature_fraction’: 1, ‘num_threads’: 2 |
| Model | Original Feature Dimension | With or Without Entropy Features | Entropy Feature Type of Original Feature Set | Classification Accuracy (%) | Optimal Feature Dimension | Entropy Feature Number of Optimal Feature Set | Classification Accuracy (%) |
|---|---|---|---|---|---|---|---|
| OPT–LightGBM | 50 | With | 0 | 96.88 | 25 | 0 | 97.81 |
| 56 | Without | 6 | 97.62 | 23 | 5 | 99.60 |
| Model | Feature Subset Dimension | Accuracy (%) | Recall (%) | Precision (%) | F1-Score (%) |
|---|---|---|---|---|---|
| SVM | 23 | 94.44 | 96.97 | 96.14 | 96.47 |
| KNN | 23 | 95.63 | 95.95 | 95.88 | 95.82 |
| DT | 23 | 97.22 | 97.07 | 97.27 | 97.01 |
| RF | 23 | 98.01 | 97.68 | 98.81 | 98.19 |
| GBDT | 23 | 98.02 | 98.94 | 99.07 | 98.99 |
| XGBoost | 23 | 98.41 | 98.46 | 98.26 | 98.27 |
| LightGBM | 23 | 98.81 | 98.90 | 98.90 | 98.82 |
| OPT–LightGBM | 23 | 99.60 | 99.77 | 99.64 | 99.70 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, L.; Zhang, J.; Zhang, N.; Shi, J.; Chen, C. Optimized LightGBM Power Fingerprint Identification Based on Entropy Features. Entropy 2022, 24, 1558. https://doi.org/10.3390/e24111558
Lin L, Zhang J, Zhang N, Shi J, Chen C. Optimized LightGBM Power Fingerprint Identification Based on Entropy Features. Entropy. 2022; 24(11):1558. https://doi.org/10.3390/e24111558
Chicago/Turabian StyleLin, Lin, Jie Zhang, Na Zhang, Jiancheng Shi, and Cheng Chen. 2022. "Optimized LightGBM Power Fingerprint Identification Based on Entropy Features" Entropy 24, no. 11: 1558. https://doi.org/10.3390/e24111558
APA StyleLin, L., Zhang, J., Zhang, N., Shi, J., & Chen, C. (2022). Optimized LightGBM Power Fingerprint Identification Based on Entropy Features. Entropy, 24(11), 1558. https://doi.org/10.3390/e24111558






