Chaotic Mapping-Based Anti-Sorting Radio Frequency Stealth Signals and Compressed Sensing-Based Echo Signal Processing Technology
Abstract
:1. Introduction
2. Principle of Anti-Sorting Signal Design
2.1. Sorting Algorithm Based on the SDIF
| Algorithm 1: Deinterleaving signals via the SDIF |
| Input: TOA |
| Initialization: The order of the histogram C |
| 1: Judge the TOA number of level C |
| 2: Calculate the TOA difference of level C |
| 3: Count the TOA difference of level C and form a histogram |
| 4: Determine the detection threshold and obtain the PRI estimation |
| 5: Check subharmonics |
| 6: Determine the unique PRI estimation |
| 7: Perform sequence search |
| 8: Remove the searched pulse train from the pulse flow |
| 9: Sort the remaining pulses until the number of pulses is less than five or the number of PRIs in the first-level histogram exceeding the threshold is not unique |
| 10: Increase difference level C and repeat the above steps until the sorting is over |
2.2. Sorting Failure Principle
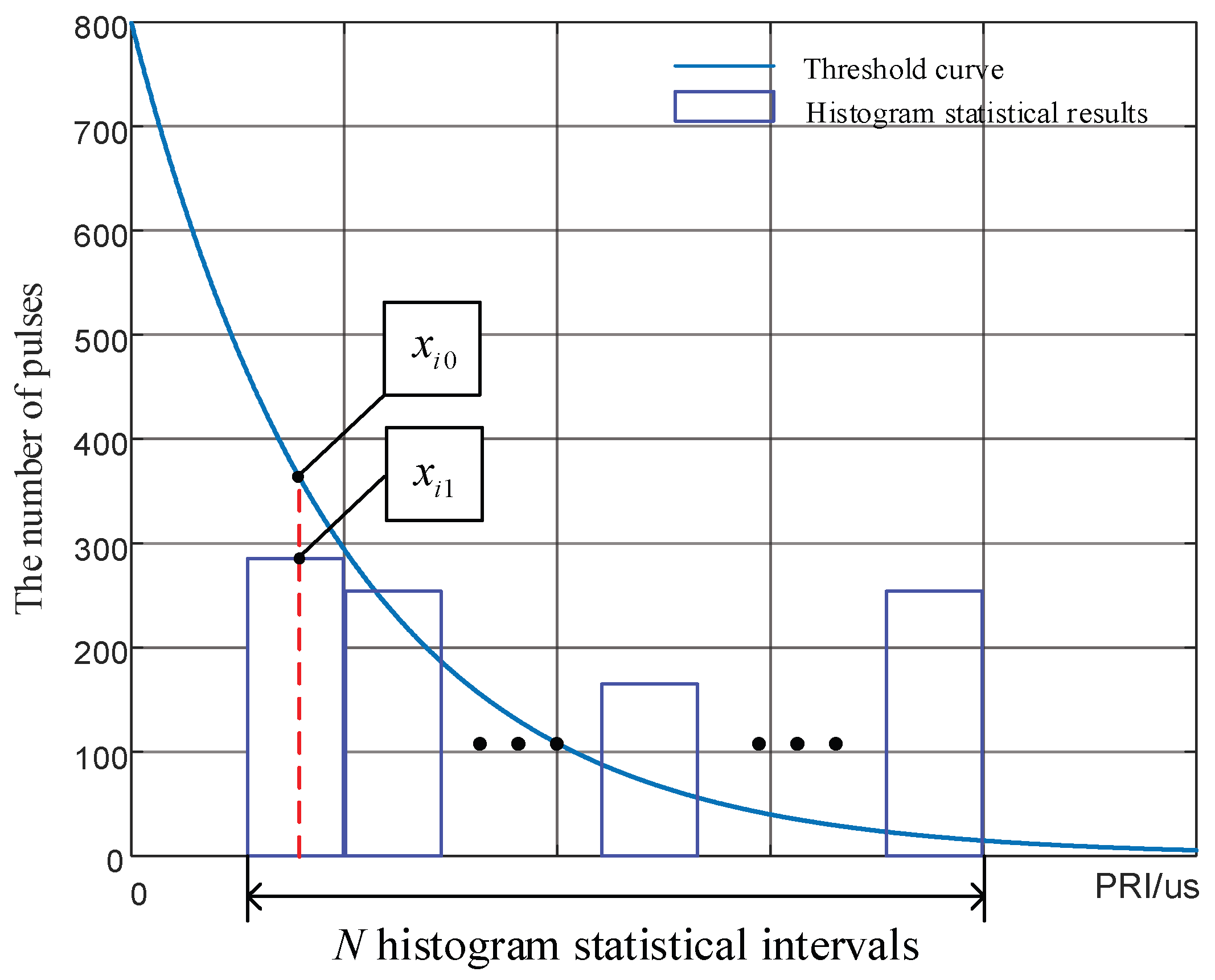
2.2.1. Analysis of the Sorting Failure Principle of the First-Order Histogram
- ①
- The number of PRI values increases from one to a finite number.
- (1)
- The total number of pulses is still
- (2)
- The number of PRI values increases to a finite number, meaning that the signals are multiple staggered signals.
- (3)
- The PRI values are , ().
- (4)
- The number of pulses corresponding to each PRI value is .
- ②
- The signal PRI values follow an interval distribution.
- (1)
- N is the number of cells counted in the histogram, which is usually above 1000.
- (2)
- z is the minimum interval of PRI values. In general, z, , and have the same size scale and all are at the microsecond level.
- (3)
- a and k in Equation (1).
2.2.2. Analysis of the Sorting Failure Principle of the Multi-Order Histogram
2.3. Principles of Signal Design
3. Anti-Sorting Signal Design of the SNP-PLCM Chaotic System Based on Random Disturbance
3.1. Construction of the SNP-PLCM Chaotic System Based on Random Disturbance
3.2. Method for Designing Widely Spaced Signals
4. Anti-Sorting Signal Processing Based on CS
4.1. Multi-Parameter Composite Modulated Signal Model
4.2. Target Parameter Estimation Based on CS
5. Simulation and Analysis
5.1. Simulation of the Signal Design Principle
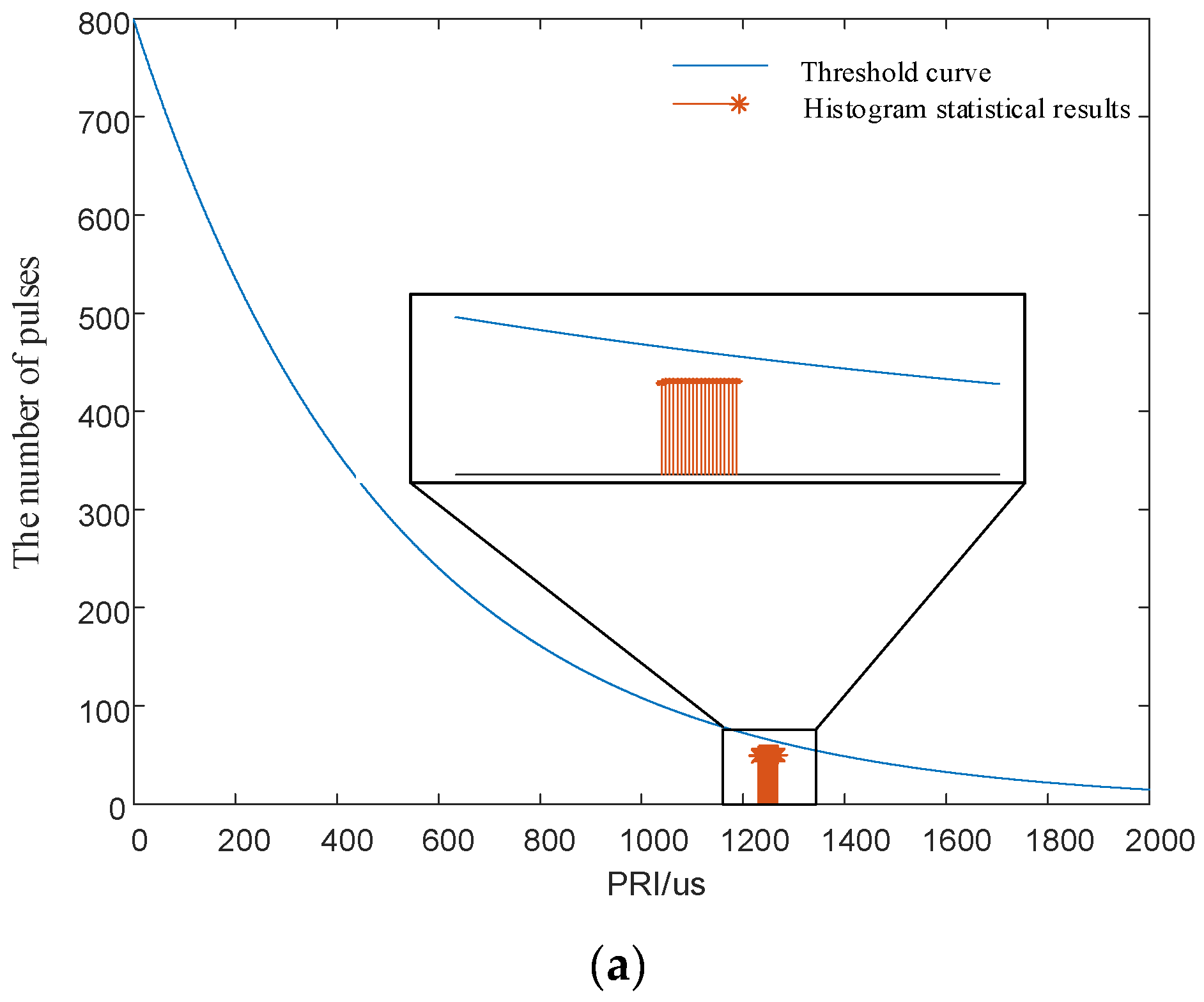
5.1.1. Correctness of the Signal Design Principle
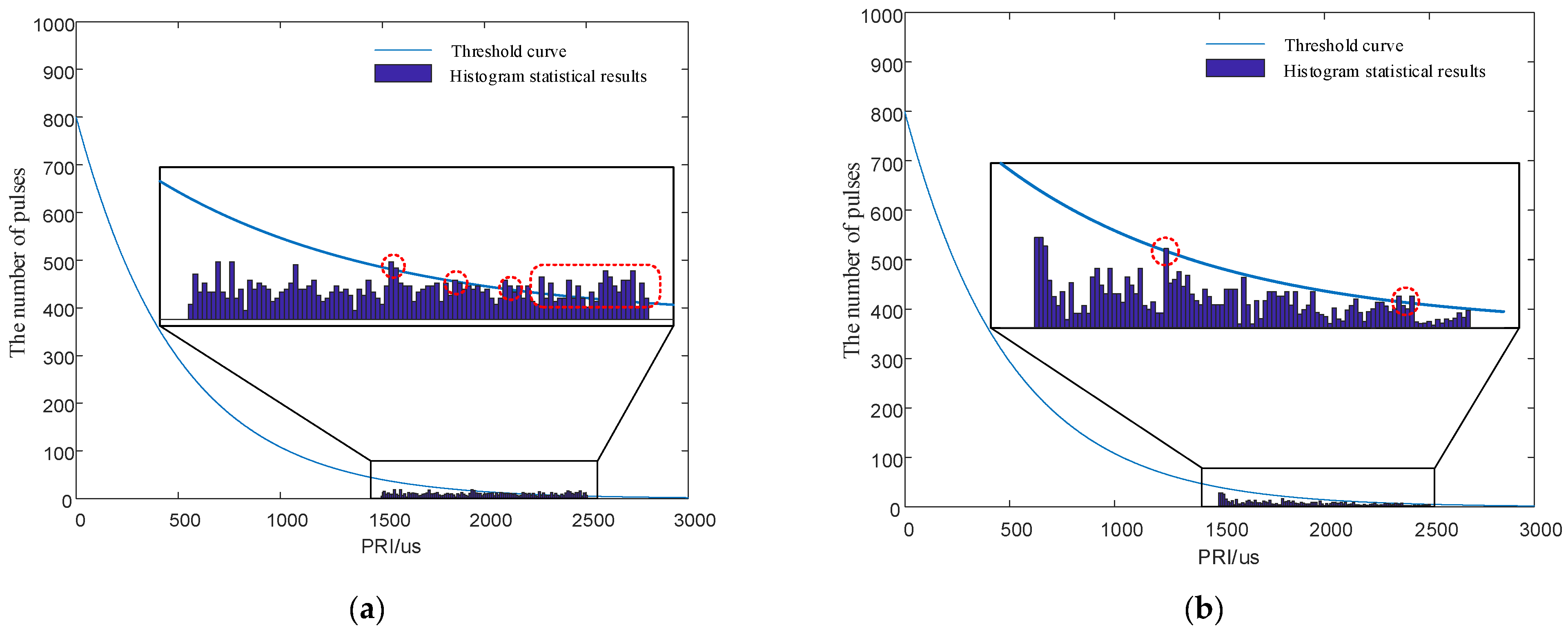
5.1.2. Simulation of the Signal Anti-Sorting
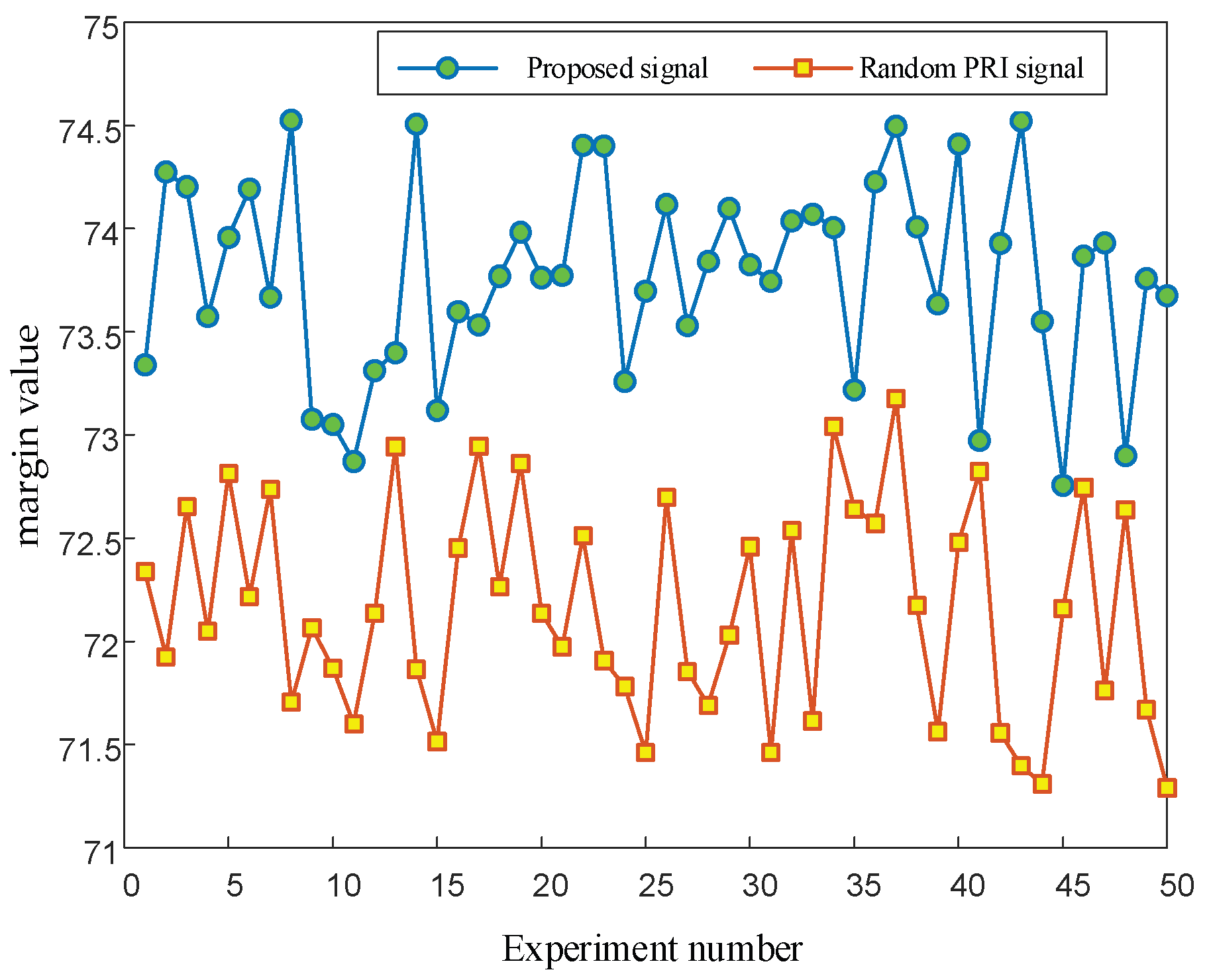
5.1.3. Comparison and Simulation of the Anti-Sorting Performance of PRI Random Jitter Signals
5.1.4. Quantization Simulation of Signal Anti-Sorting Performance
5.2. Performance Simulation of the Chaotic System
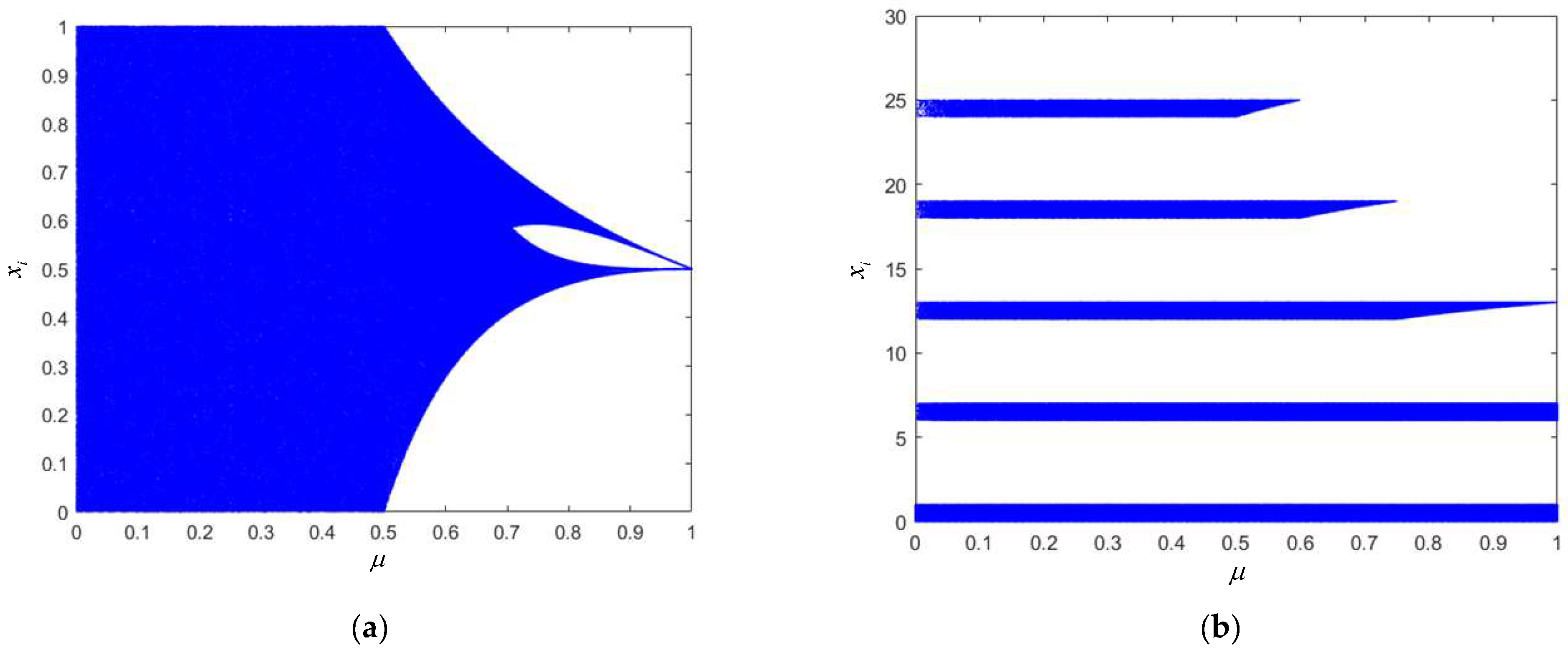
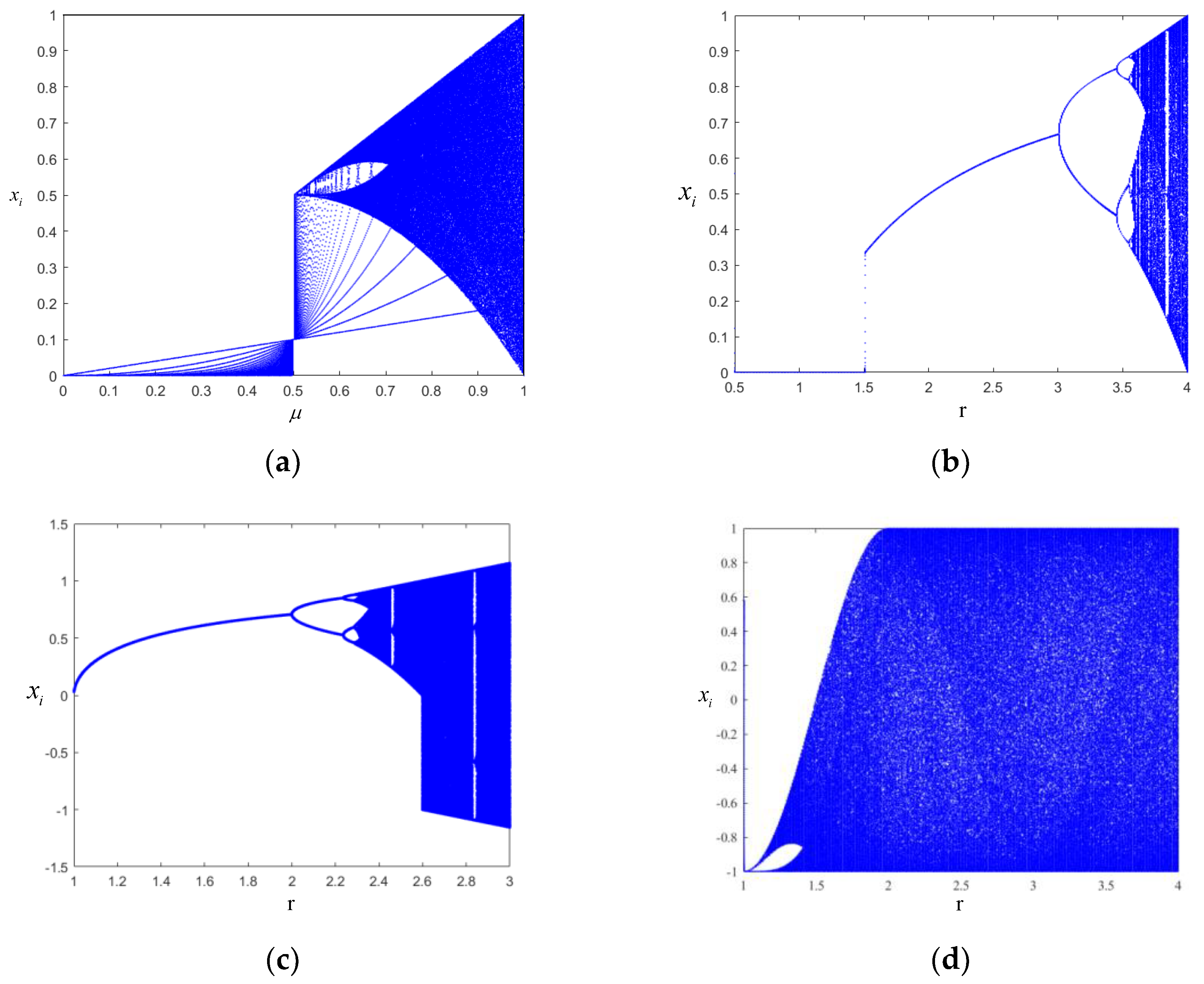
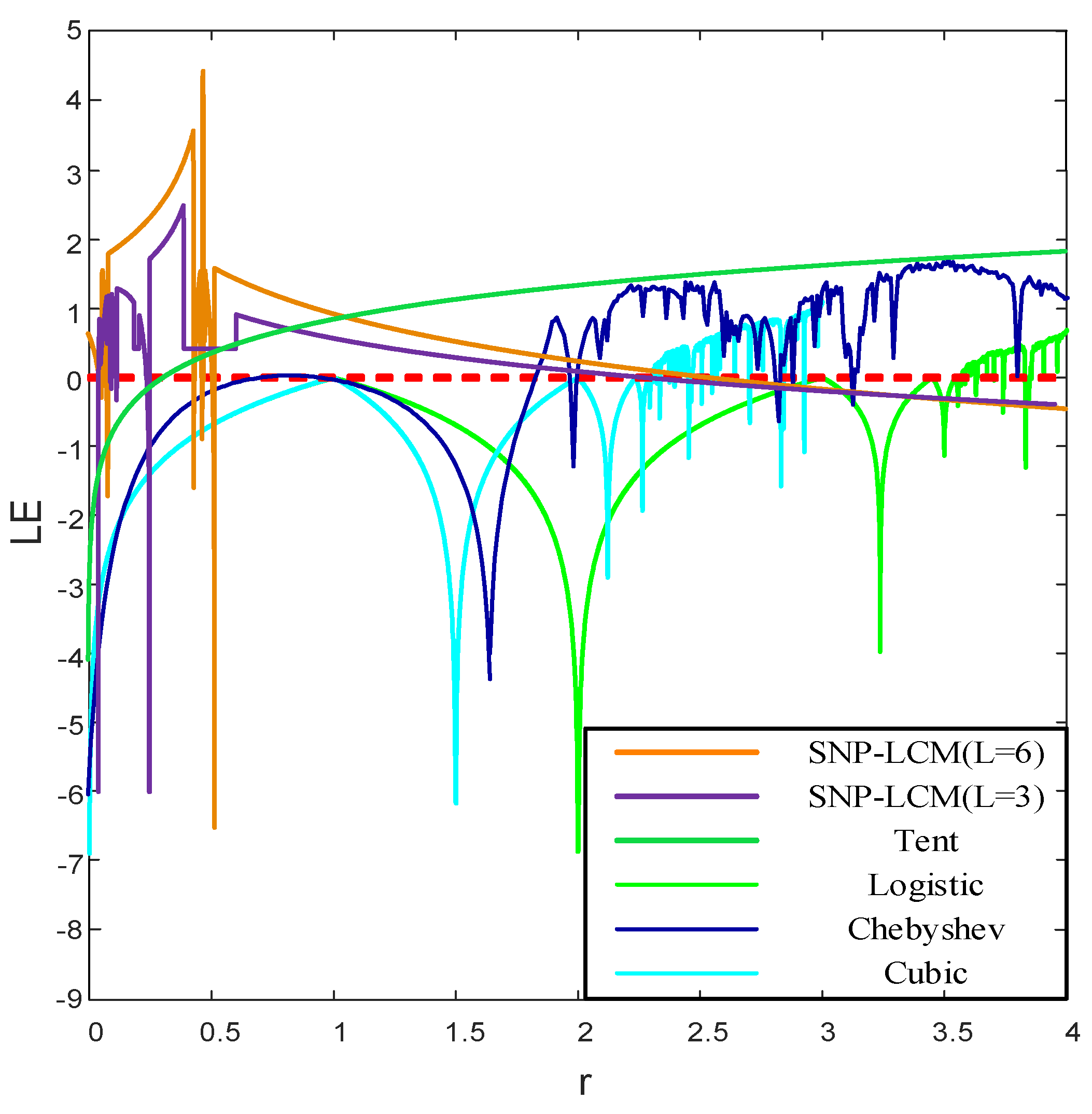
5.2.1. Performance Simulation of the Chaotic Mapping
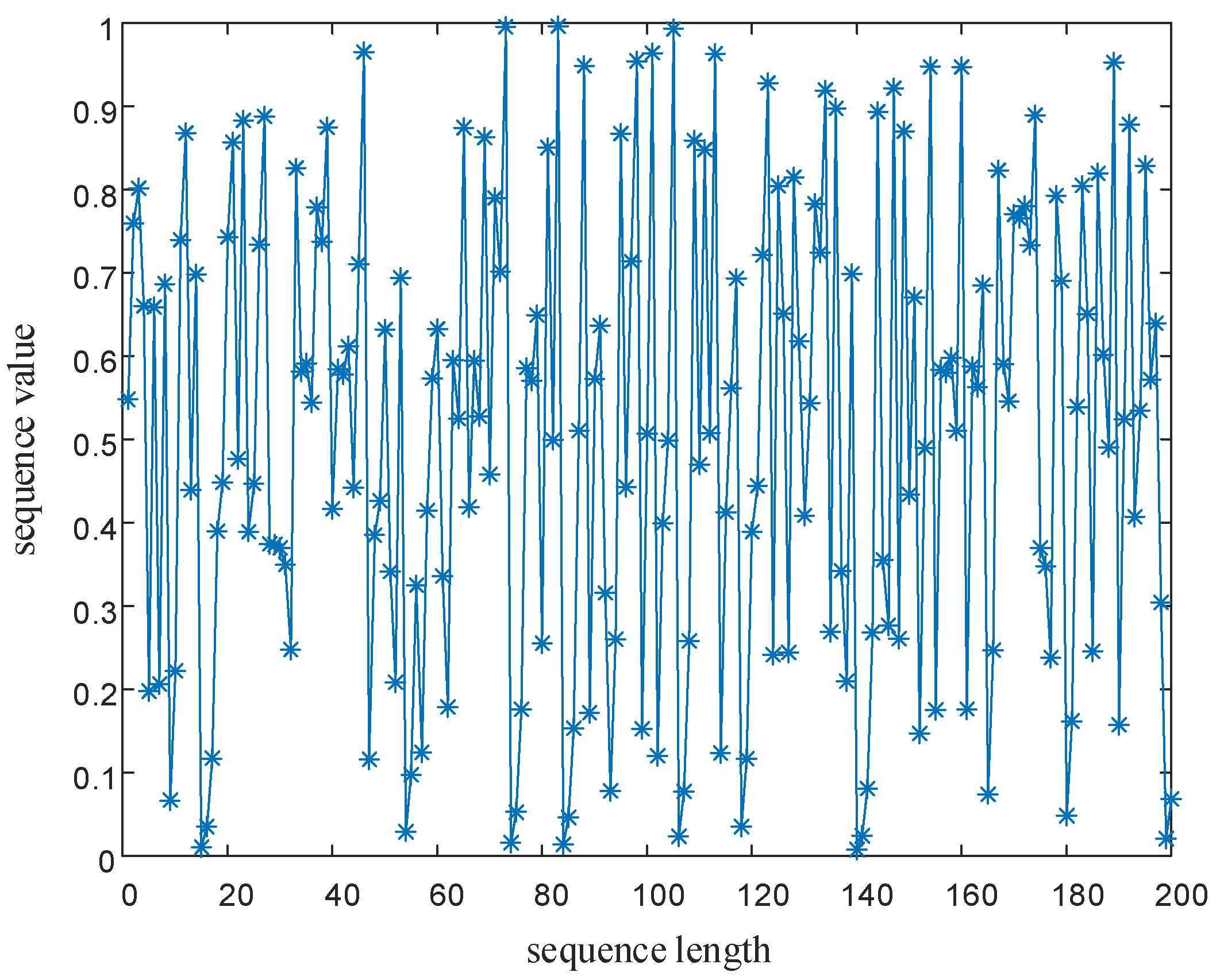
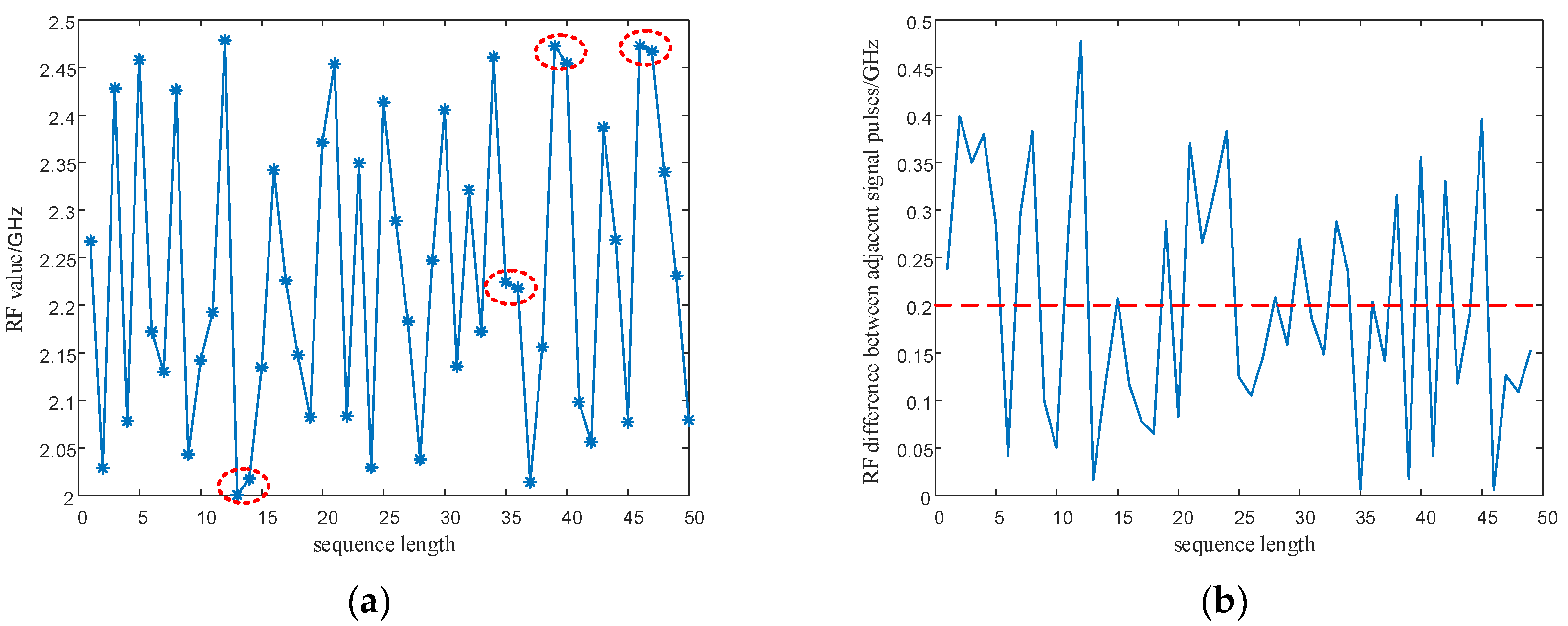
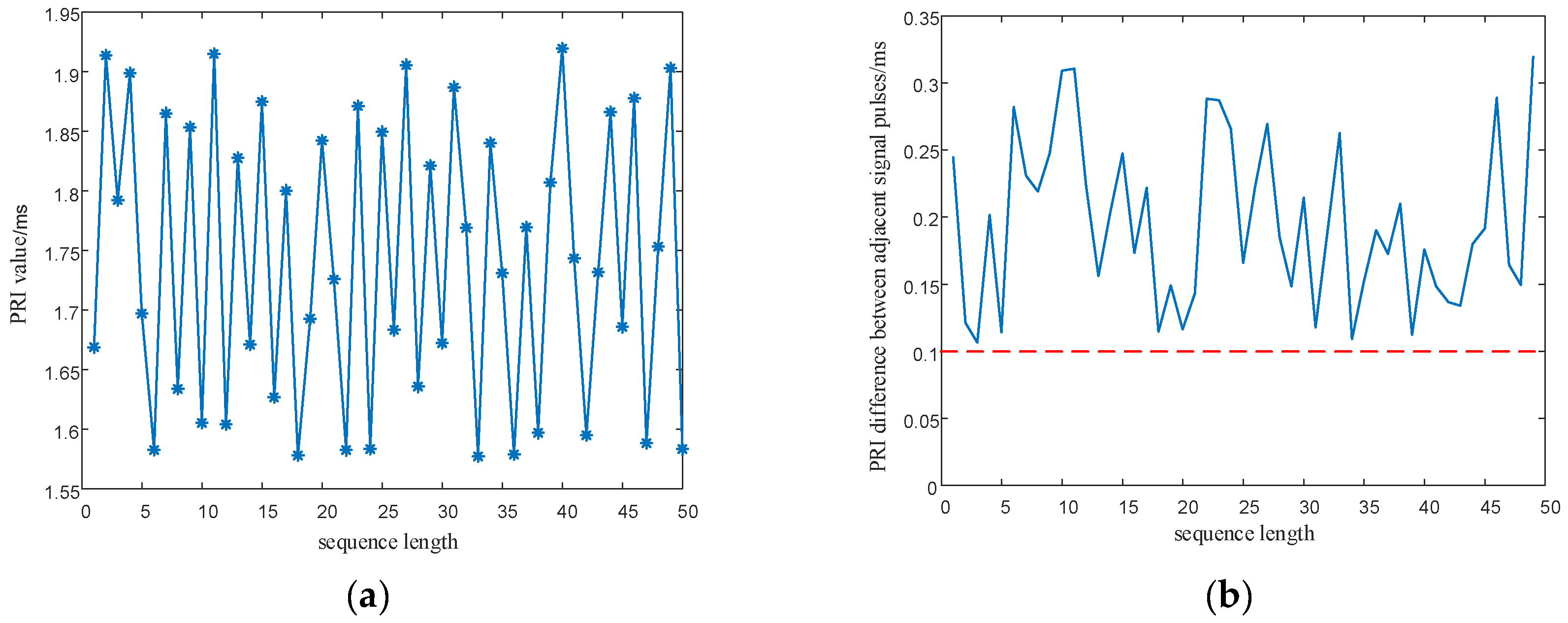
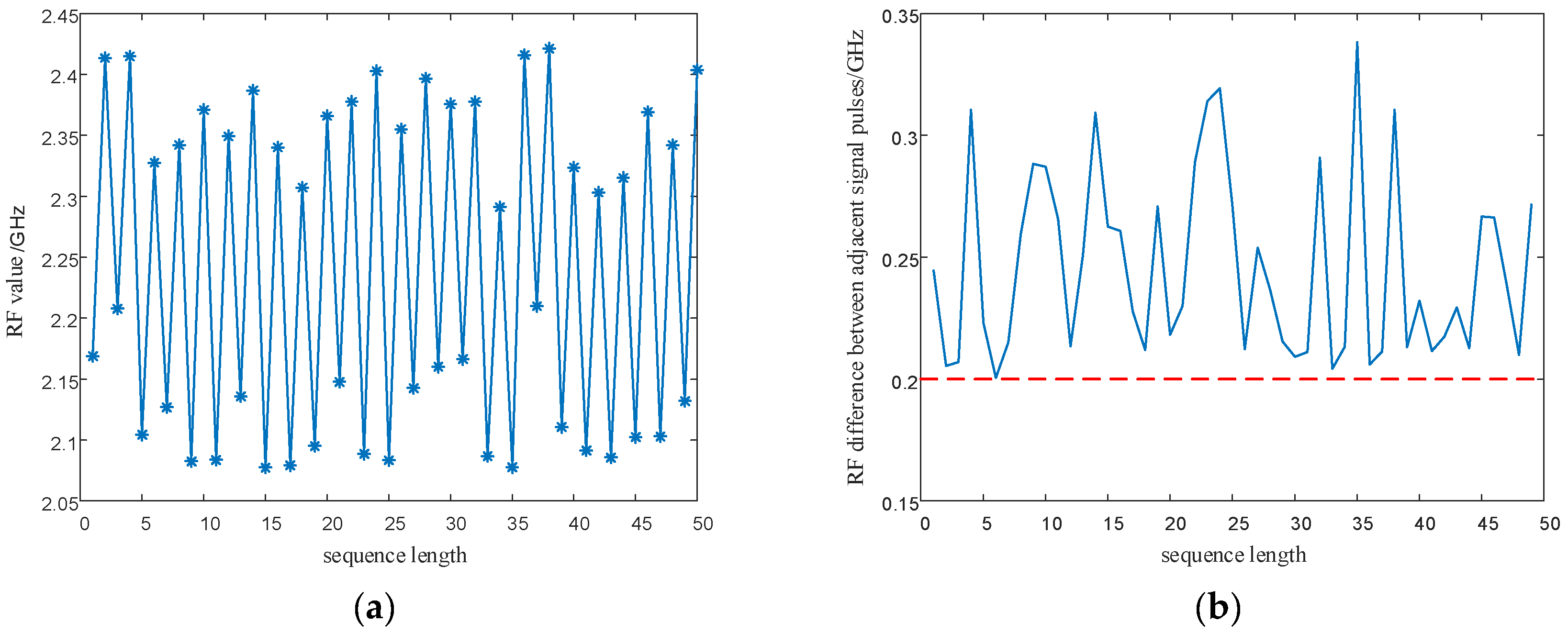
5.2.2. Signal Parameter Sequence Performance Analysis
5.3. Signal Parameter Estimation Based on CS
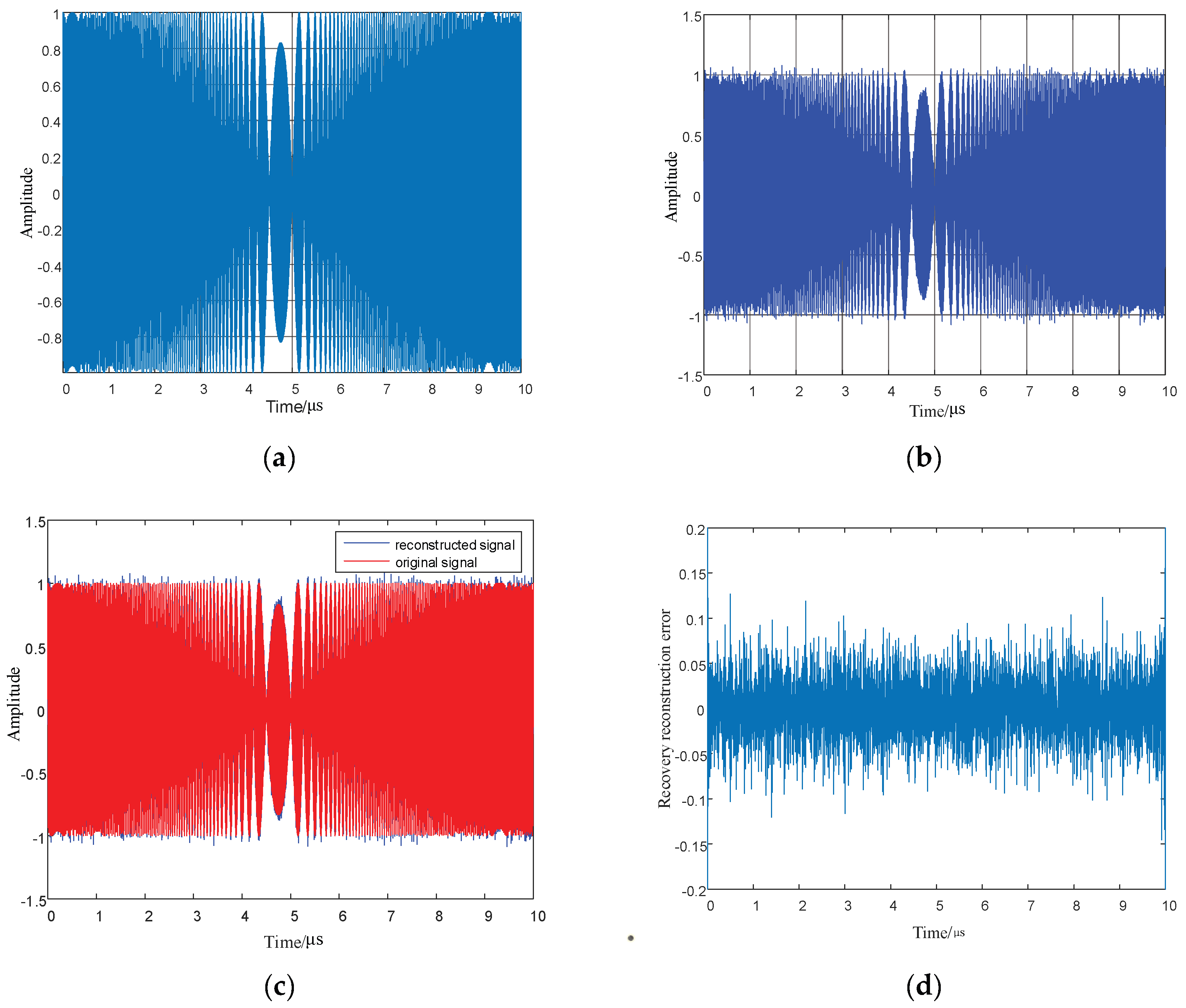
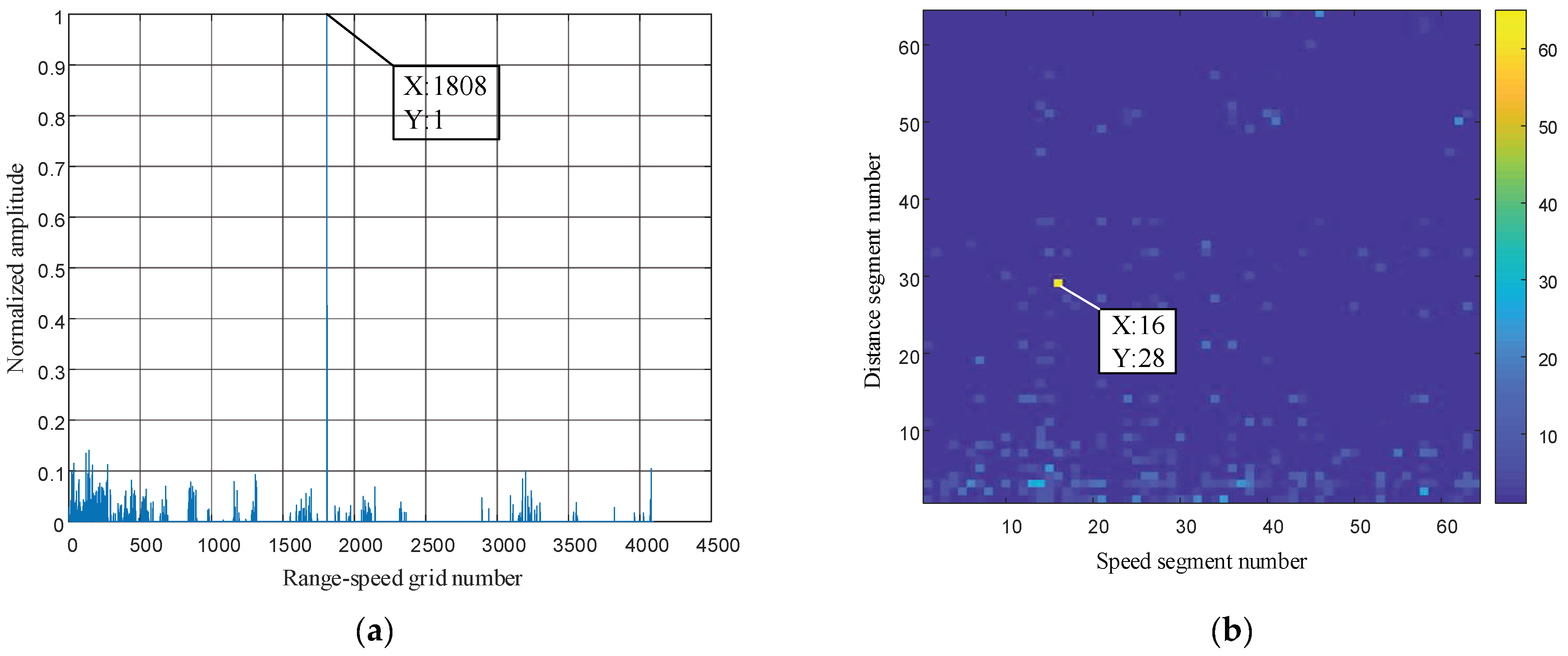
5.3.1. Reconstruction and Recovery of LFM Signals
5.3.2. The Processing of LFM Signals
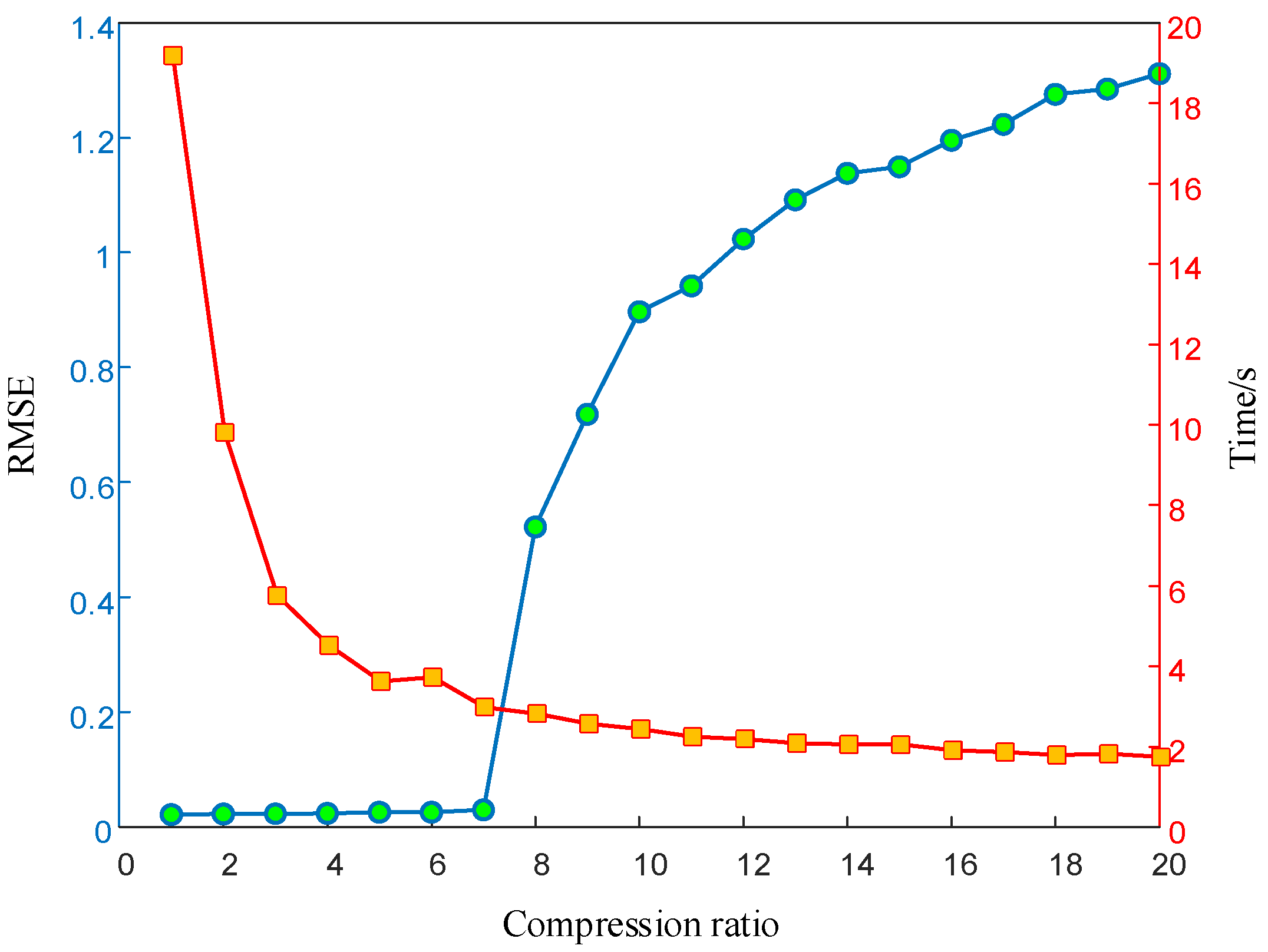
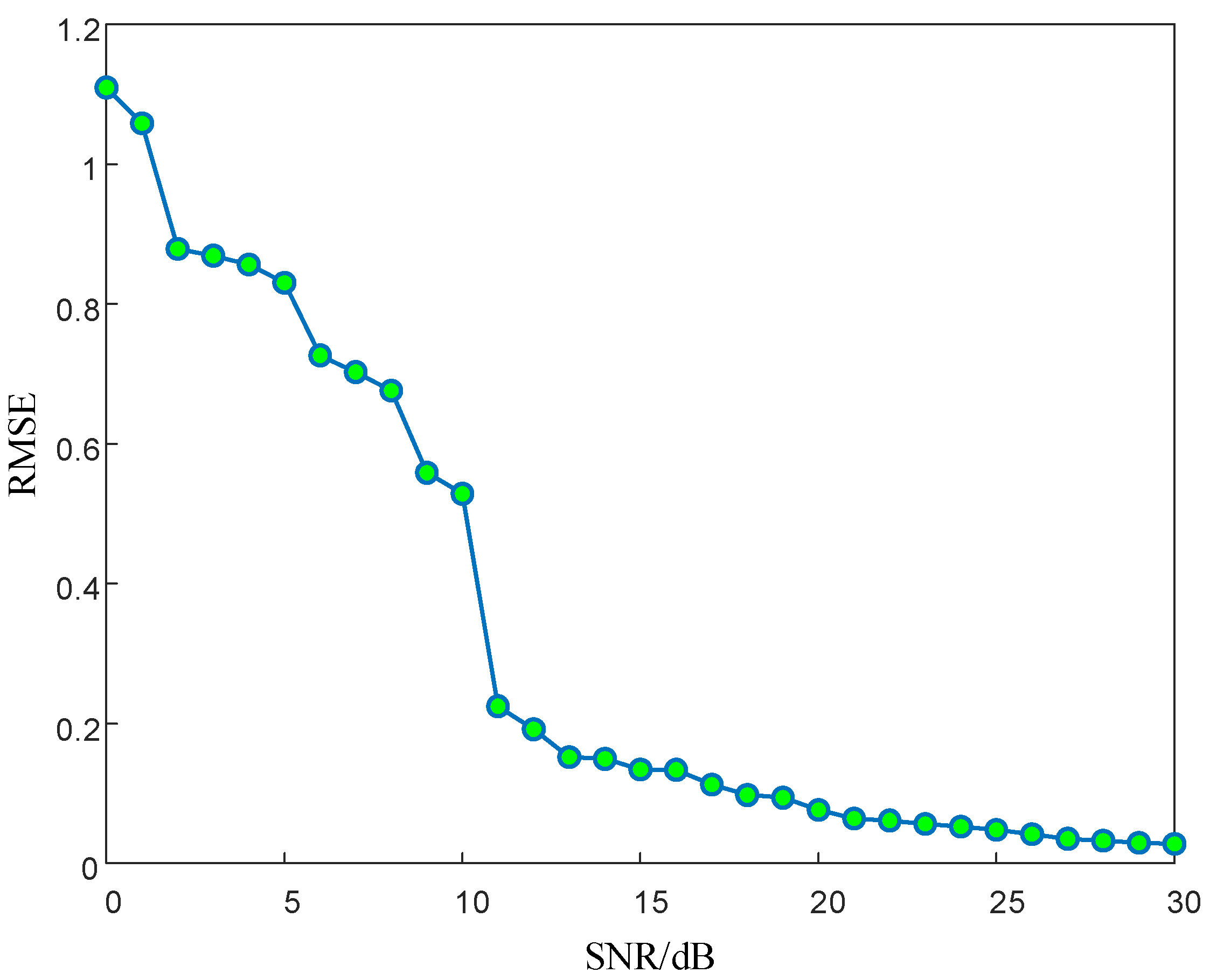
5.3.3. Analysis of Influencing Factors
- (1)
- The compression ratio.
- (2)
- SNR.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| RF | Radio frequency |
| SDIF | Sequential difference histogram |
| CS | Compressed sensing |
| PW | Pulse width |
| DOA | Direction of arrival |
| TOA | Time of arrival |
| PRI | Pulse repetition interval |
| SNP-PLCM | Segment number parameter-piecewise linear chaotic map |
| CDIF | Cumulative difference histogram |
| RR | Recursive rate |
| ENTR | Entropy |
| DET | Determinacy |
| Lmax | Maximum diagonal length |
| OMP | Orthogonal Matching Pursuit |
| LFM | Linear frequency modulation |
| RMSE | Root mean squared error |
| SNR | Signal-to-noise ratio |
References
- Mi, X.; Lv, T.; Tian, Y.; Kang, B. Multi-sensor data fusion based on soft likelihood functions and OWA aggregation and its application in target recognition system. ISA Trans. 2020, 112, 137–149. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Yu, Q. A Dynamic multi-sensor data fusion approach based on evidence theory and WOWA operator. Appl. Intell. 2020, 50, 3837–3851. [Google Scholar] [CrossRef]
- Jia, J.; Han, Z.; Liu, L.; Xie, H.; Lv, M. Research on the Sequential Difference Histogram Failure Principle Applied to the Signal Design of Radio Frequency Stealth Radar. Electronics 2022, 11, 2192. [Google Scholar] [CrossRef]
- Shi, C.; Wang, Y.; Wang, F.; Salous, S.; Zhou, J. Power resource allocation scheme for distributed MIMO dual-function radar-communication system based on low probability of intercept. Digit. Signal Process. 2020, 106, 102850. [Google Scholar] [CrossRef]
- Zhao, X.T.; Zhou, J.J. Improved MUSIC algorithm for MIMO radar with low intercept. Syst. Eng. Electron. 2022, 44, 490–497. [Google Scholar]
- Jia, J.; Han, Z.; Liu, L.; Xie, H.; Lv, M. Research on the SDIF Failure Principle for RF Stealth Radar Signal Design. Electronics 2022, 11, 1777. [Google Scholar] [CrossRef]
- Chang, W. Design of synthetic aperture radar low-intercept radio frequency stealth. J. Syst. Eng. Electron. 2020, 31, 64–72. [Google Scholar] [CrossRef]
- Jia, J.; Liu, L.; Liang, Y.; Han, Z. Anti-sorting signal design for radio frequency stealth radar based on cosine-exponential nonlinear chaotic mapping. J. Wireless Networks. 2022. [Google Scholar] [CrossRef]
- Yang, S.; Hou, C.; Si, W. Extract pulse clustering in radar signal sorting. In Proceedings of the2017 International Applied Computational Electromagnetics Society Symposium (ACES), Firenze, Italy, 26–30 March 2017. [Google Scholar]
- Sui, J.P.; Liu, Z.; Liu, L.; Xiang, L.I. Progress in radar emitter signal deinterleaving. J. Radars 2022, 11, 418–433. (In Chinese) [Google Scholar]
- Jiang, Z.Y.; Sun, S.Y.; Li, H.W.; Guang, L.I.A.N.G. A method for deinterleaving based on JANET. J. Univ. Chin. Acad. Sci. 2021, 38, 825–831. [Google Scholar]
- Yu, Q.; Bi, D.P.; Chen, L. Jamming technology of research based on pri parameter separation of signal to ELINT system. Fire Control Command Control 2016, 41, 143–147. (In Chinese) [Google Scholar]
- Dai, S.B.; Lei, W.H.; Cheng, Y.Z. Electronic anti-reconnaissance based on TOA analysis. Electron. Inf. Warf. Technol. 2014, 29, 45–48. [Google Scholar]
- Wang, F.; Liu, J.F. LPS design of pulse repetition interval for formation radars. Inf. Technol. 2019, 3, 14–18+23. [Google Scholar]
- Zhang, B.Q.; Wang, W.S. Anti-clustering analysis of anti-reconnaissance based on full pulse information extraction. Electron. Inf. Warf. Technol. 2017, 32, 19–25. [Google Scholar]
- Nan, H.; Peng, S.; Yu, J.; Wang, X. Pulse interference method against PRI sorting. J. Eng. 2019, 2019, 5732–5735. [Google Scholar] [CrossRef]
- Sun, Z.Y.; Jiang, Q.X.; Bi, D.P. A Technology for Anti-reconnaissance Based on Factional Quasi Orthogonal Waveform. Mod. Radar 2015, 37, 43–48+77. [Google Scholar]
- Zhang, B.Q. A design method of PRI stagger countering the SDIF sorting algorithm. J. Ordnance Equip. Eng. 2016, 37, 87–91. [Google Scholar]
- Wang, H. Anti-Reconnaissance Performance Analysis of MIMO Radar Configured with OFDM Signal. J. Ordnance Equip. Eng. 2021, 42, 177–182. [Google Scholar]
- Liu, C.Y. Research on Chaotic Series Complexity Algorithm and Its Application in Image Encryption; Heilongjiang University: Harbin, China, 2021. [Google Scholar]
- Zhang, Z.-F.; Huang, L.-L.; Xiang, J.-H.; Liu, S. Dynamic study of a new five-dimensional conservative hyperchaotic system with wide parameter range. Acta Phys. Sin. 2021, 70, 230501. [Google Scholar] [CrossRef]
- Liu, X.; Tong, X.; Wang, Z.; Zhang, M. A new n-dimensional conservative chaos based on Generalized Hamiltonian System and its’ applications in image encryption. Chaos Solitons Fractals 2021, 154, 111693. [Google Scholar] [CrossRef]
- Signing, V.R.F.; Fonzin, T.F.; Kountchou, M.; Kengne, J.; Njitacke, Z.T. Chaotic Jerk System with Hump Structure for Text and Image Encryption Using DNA Coding. Circuits Syst. Signal Process. 2021, 40, 4370–4406. [Google Scholar] [CrossRef]
- Zhou, S.; He, P.; Kasabov, N. A Dynamic DNA Color Image Encryption Method Based on SHA-512. Entropy 2020, 22, 1091. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.X.; Wang, D.X.; Huang, Q. Design Method of Radio Frequency Stealth Frequency Hopping Communications Based on Four-Dimensional Hyperchaotic System. J. Astronaut. 2020, 41, 1341–1349. (In Chinese) [Google Scholar]
- Çavuşoğlu, U.; Kaçar, S.; Pehlivan, I.; Zengin, A. Secure image encryption algorithm design using a novel chaos based S-Box. Chaos Solitons Fractals 2017, 95, 92–101. [Google Scholar] [CrossRef]
- Hua, Z.; Jin, F.; Xu, B.; Huang, H. 2D Logistic-Sine-coupling map for image encryption. Signal Process. 2018, 149, 148–161. [Google Scholar] [CrossRef]
- Tong, X.; Cui, M. Image encryption scheme based on 3D baker with dynamical compound chaotic sequence cipher generator. Signal Process. 2009, 89, 480–491. [Google Scholar] [CrossRef]
- Peng, Z.P.; Wang, C.H.; Lin, Y.; Xiao-Wen, L. A novel four-dimensional multi-wing hyper-chaotic attractor and its application in image encryption. Acta Phys. Sin. 2014, 63, 101–110. [Google Scholar]
- Liu, Y. Study on Chaos Based Pseudorandom Sequence Algorithm and Image Encryption Technique; Harbin Institute of Technology: Harbin, China, 2015. [Google Scholar]
- Jia, J.; Han, Z.; Liang, Y.; Liu, L.; Wang, X. Design of Multi-Parameter Compound Modulated RF Stealth Anti-Sorting Signals Based on Hyperchaotic Interleaving Feedback. Entropy 2022, 24, 1283. [Google Scholar] [CrossRef]
- Dao, X.; Gao, M.; Zhang, Z.; Li, C.; Wang, Y. Design of multi-parameter composite modulated signal for anti-deceptive jamming. AEU—Int. J. Electron. Commun. 2021, 132, 153646. [Google Scholar] [CrossRef]
- Jia, J.W.; Han, Z.Z.; Liu, L.M. Research on Design Technology of Radio Frequency Stealth Anti-sorting Signal Based on Cosine-exponential Nonlinear Chaotic Mapping. Acta Armen. 2022. Available online: http://kns.cnki.net/kcms/detail/11.2176.TJ.20220715.1606.002.html (accessed on 1 October 2022).
- Liu, L.D. Chaotic Signal Processing and Its Application in Radar; University of Electronic Science and Technology of China: Chengdu, China, 2012. [Google Scholar]
- Zhang, X.Y. Research on Key Techniques of Random Noise Ultra-Wideband SAR; Nanjing University of Science and Technology: Nanjing, China, 2008. [Google Scholar]
- Yao, H.B. Research on the Anti-Interference Performance of Multiple Parameter-Agility Radar; Xidian University: Xi’an, China, 2019. [Google Scholar]
- Liu, Z.X.; Quan, Y.H.; Xiao, G.Y. Signal design method for integrated radar and communication based on PRI agility. Syst. Eng. Electron. 2021, 43, 2836–2842. [Google Scholar]
- Candès, E.J. Compressive sampling. Proc. Int. Congress Math. 2006, 3, 1433–1452. [Google Scholar]
- Zhang, Q.H.; Yu, S.Q.; Shi, L.P.; Zhang, S.H. Microwave Imaging by Multitask Bayesian Compressed Sensing Within Contrast Source Framework. Acta Electron. Sin. 2020, 48, 2208–2214. [Google Scholar]
- Li, J.Q.; Guo, G.X.; Chen, J.L.; Zhu, Y. Two-dimensional Underwent Synthetic Aperture Radar Imaging Based on Iterative Proximal Projection. J. Electron. Inf. Technol. 2022, 44, 2127–2134. [Google Scholar]
- Du, S.Y.; Liu, Z.X.; Wu, Y.J.; Minghui, S.H.A.; Yinghui, Q.U.A.N. Dense-repeated Jamming Suppression Algorithm Based on the Support Vector Machine for Frequency Agility Radar. J. Radars 2022. Available online: http://kns.cnki.net/kcms/detail/10.1030.TN.20220608.1059.002.html (accessed on 1 October 2022).
- Sui, J.P.; Liu, Z.; Wei, X.Z.; Li, X. Velocity False Target Identification Based on Random Pulse Repetition Interval Compressed Sensing Radar. Acta Electron. Sin. 2017, 45, 98–103. [Google Scholar]
- Li, H.; Wang, C.; Wang, K.; He, Y.; Zhu, X. High resolution range profile of compressive sensing radar with low computational complexity. IET Radar Sonar Navig. 2015, 9, 984–990. [Google Scholar] [CrossRef]
- Liu, Z.; Wei, X.; Li, X. Aliasing-Free Moving Target Detection in Random Pulse Repetition Interval Radar Based on Compressed Sensing. IEEE Sens. J. 2013, 13, 2523–2534. [Google Scholar] [CrossRef]
- Anitori, L.; Maleki, A.; Otten, M.; Baraniuk, R.G.; Hoogeboom, P. Design and Analysis of Compressed Sensing Radar Detectors. IEEE Trans. Signal Process. 2012, 61, 813–827. [Google Scholar] [CrossRef]
- Jia, Q.H. Application and Analysis of Recurrence Plot in Non-Stationary Signals; Hefei University of Technology: Hefei, China, 2019. [Google Scholar]











| r | Logistic | Cubic | Chebyshev | Proposed |
|---|---|---|---|---|
| 0.5 | 7.2584 × 10−7 | 8.2199 × 10−7 | 2.7641 × 10−5 | 1.9331 |
| 1 | 2.0764 × 10−5 | 2.9270 × 10−5 | 0 | 1.5572 |
| 1.5 | 7.1890 × 10−7 | 0 | 0.6103 | 1.6901 |
| 2 | 1.8422 × 10−7 | 0.0107 | 0.7113 | 1.6842 |
| 2.5 | 8.2893 × 10−7 | 0.60 | 0.8543 | 1.2943 |
| 3 | 0.0111 | 1.1301 | 1.0146 | 1.0305 |
| 3.5 | 0.0016 | 0 | 1.0976 | 1.0002 |
| 4 | 0.70 | 0 | 1.2311 | 0.9862 |
| Sequence Types | RR | DET | ENTR | |
|---|---|---|---|---|
| 0.0820 | 0.7787 | 3079 | 0.2284 | |
| White Gaussian noise | 0.0561 | 0.1088 | 5 | 2.3611 |
| Logistic | 0.0770 | 0.7003 | 23 | 0.3611 |
| Cubic | 0.0822 | 0.6703 | 12 | 0.4356 |
| Tent | 0.0799 | 0.6059 | 16 | 0.4123 |
| SNP-PLCM (L = 3) | 0.0648 | 0.3758 | 11 | 1.2515 |
| SNP-PLCM (L = 6) | 0.0564 | 0.2737 | 7 | 1.5422 |
| Serial Number | Parameter Type | Center Value | Parameter Variation | Tolerance | Minimum Parameter Interval between Adjacent Pulses |
|---|---|---|---|---|---|
| 1 | PRI | 1.5 ms | |||
| 2 | RF | 2000 MHz | 1000 MHz | 100 MHz | 200 MHz |
| Simulation Parameter | Value | Simulation Parameter | Value |
|---|---|---|---|
| Center carrier frequency/GHz | 3 | Pulse repetition period/ms | 1 |
| Maximum variation of carrier frequency/GHz | 0.3 | The maximum change in pulse repetition period/ms | 0.1 |
| Bandwidth/MHz | 50 | Pulse width/ | 200 |
| Number of pulses in a CPI | 64 | Signal-to-noise ratio (SNR)/dB | 30 |
| Mean segment number of unambiguous distance | 64 | Mean segment number of unambiguous speed | 64 |
| Simulation time/ms | 64 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, J.; Liu, L.; Liang, Y.; Han, Z.; Wang, X. Chaotic Mapping-Based Anti-Sorting Radio Frequency Stealth Signals and Compressed Sensing-Based Echo Signal Processing Technology. Entropy 2022, 24, 1559. https://doi.org/10.3390/e24111559
Jia J, Liu L, Liang Y, Han Z, Wang X. Chaotic Mapping-Based Anti-Sorting Radio Frequency Stealth Signals and Compressed Sensing-Based Echo Signal Processing Technology. Entropy. 2022; 24(11):1559. https://doi.org/10.3390/e24111559
Chicago/Turabian StyleJia, Jinwei, Limin Liu, Yuying Liang, Zhuangzhi Han, and Xuetian Wang. 2022. "Chaotic Mapping-Based Anti-Sorting Radio Frequency Stealth Signals and Compressed Sensing-Based Echo Signal Processing Technology" Entropy 24, no. 11: 1559. https://doi.org/10.3390/e24111559
APA StyleJia, J., Liu, L., Liang, Y., Han, Z., & Wang, X. (2022). Chaotic Mapping-Based Anti-Sorting Radio Frequency Stealth Signals and Compressed Sensing-Based Echo Signal Processing Technology. Entropy, 24(11), 1559. https://doi.org/10.3390/e24111559





