Novel Simulation and Analysis of Mie-Scattering Lidar for Detecting Atmospheric Turbulence Based on Non-Kolmogorov Turbulence Power Spectrum Model
Abstract
:1. Introduction
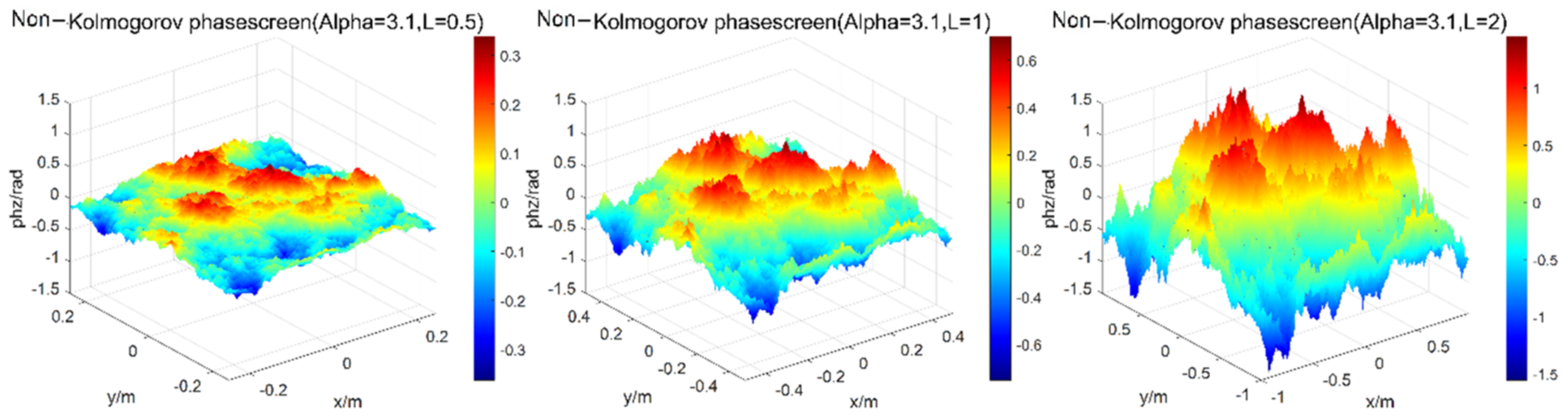
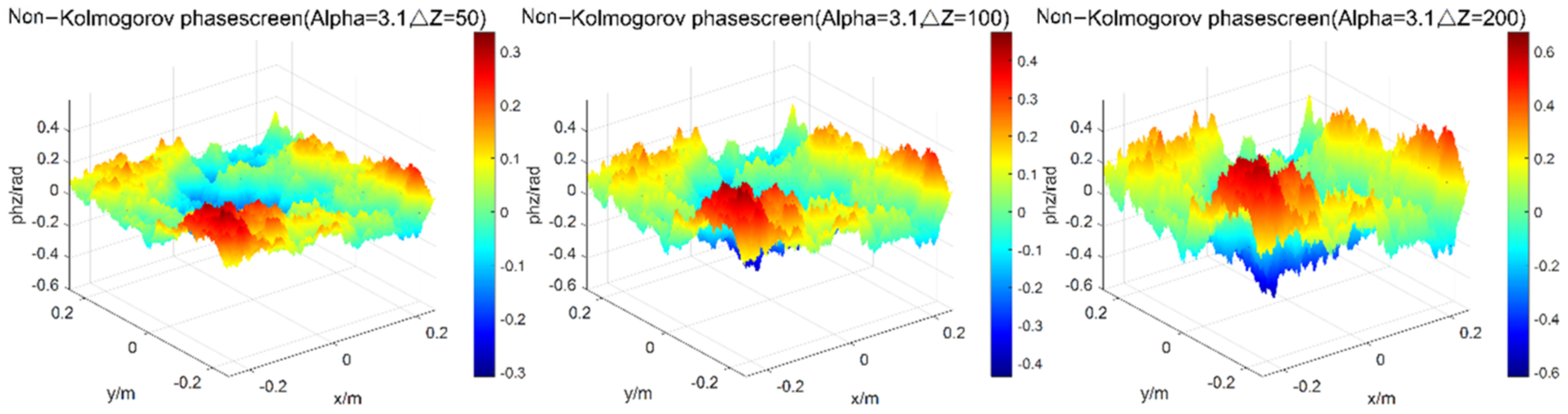
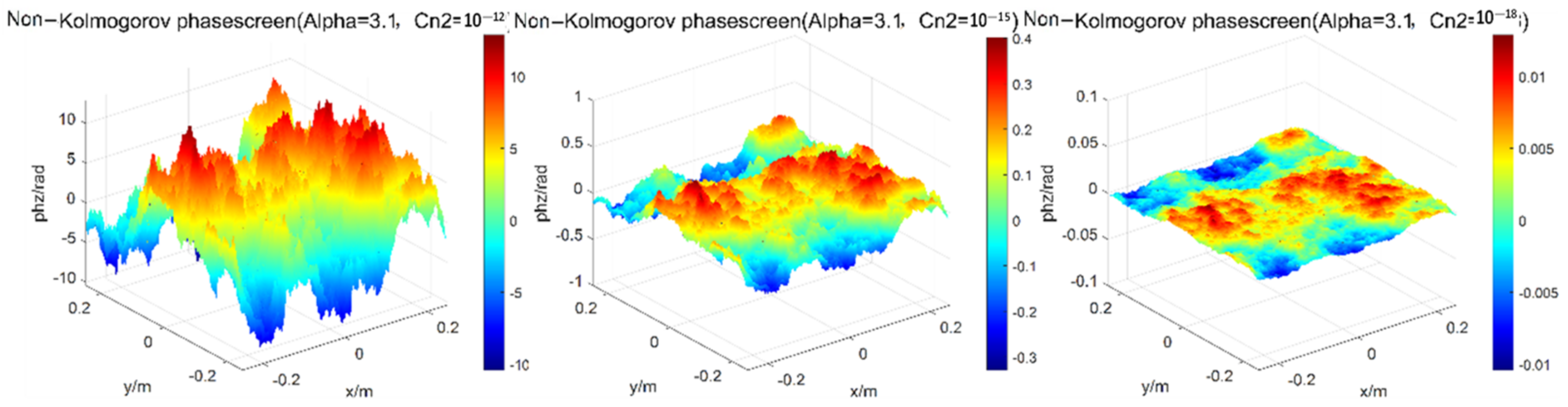
2. Construction of Non-Kolmogorov Turbulent Phase Screen
2.1. Power Spectrum Method
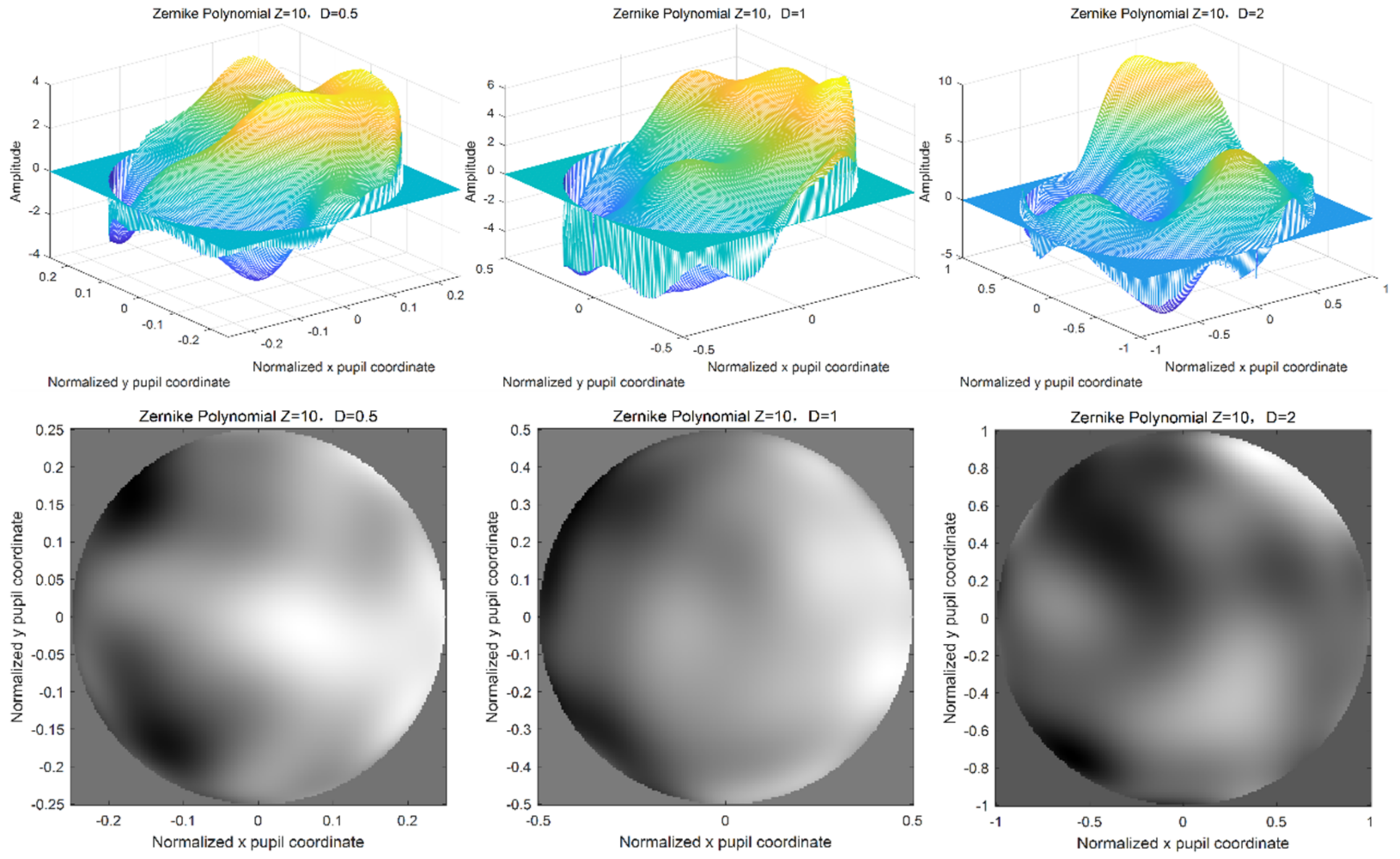
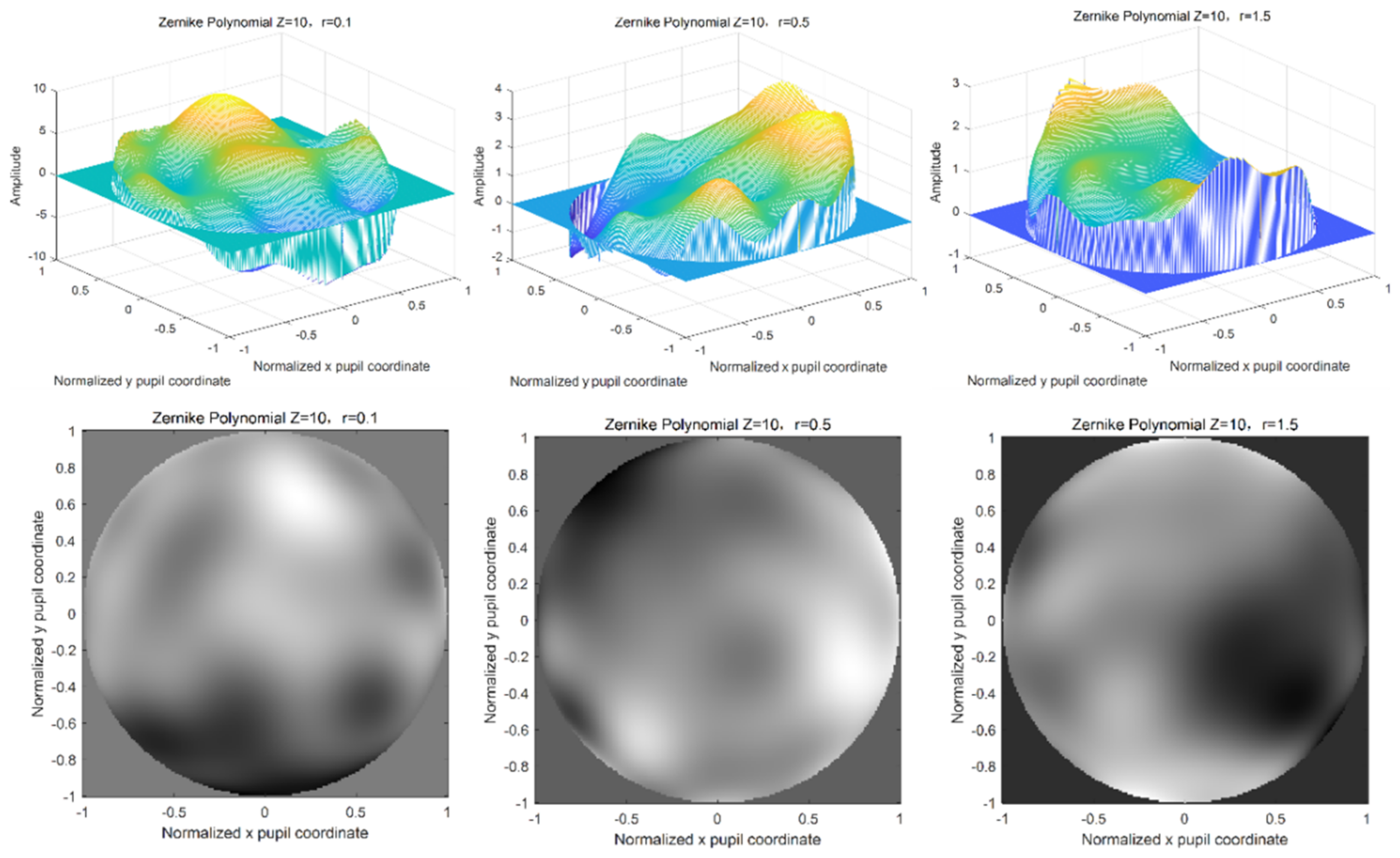
2.2. Zernike Polynomial Method
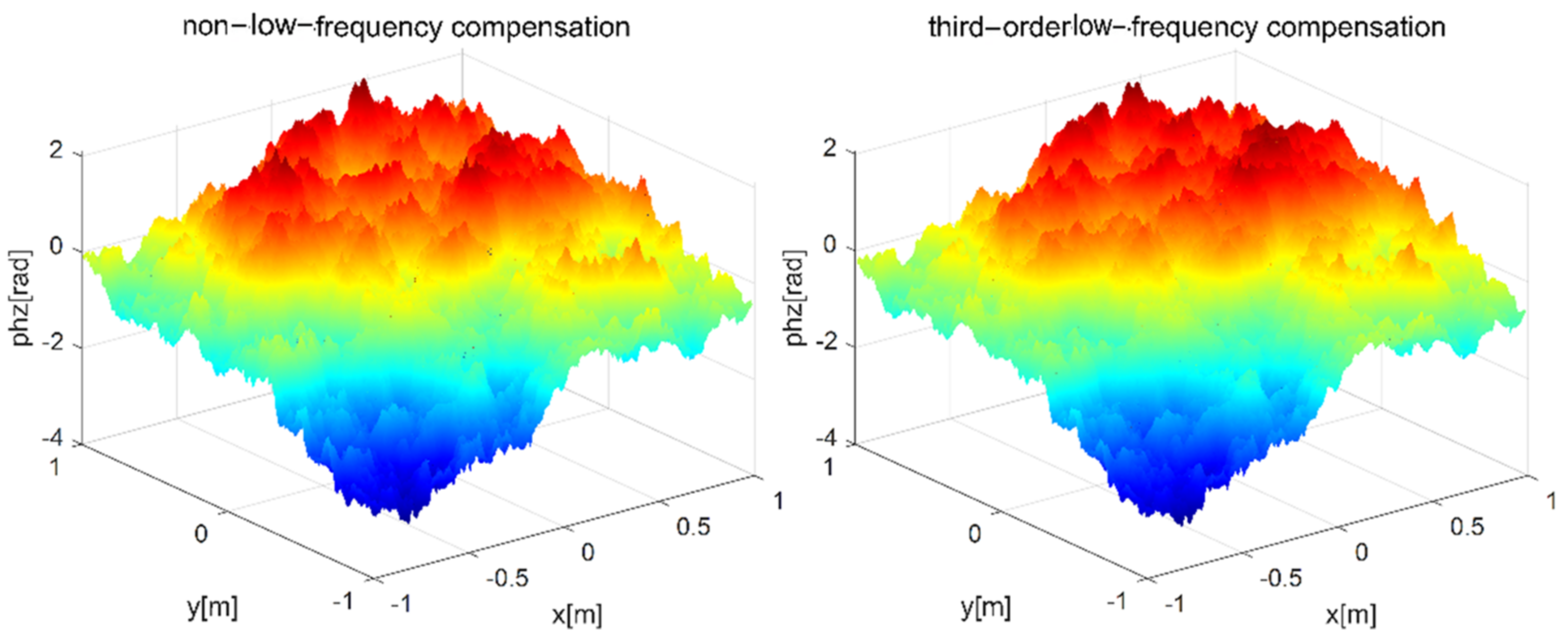
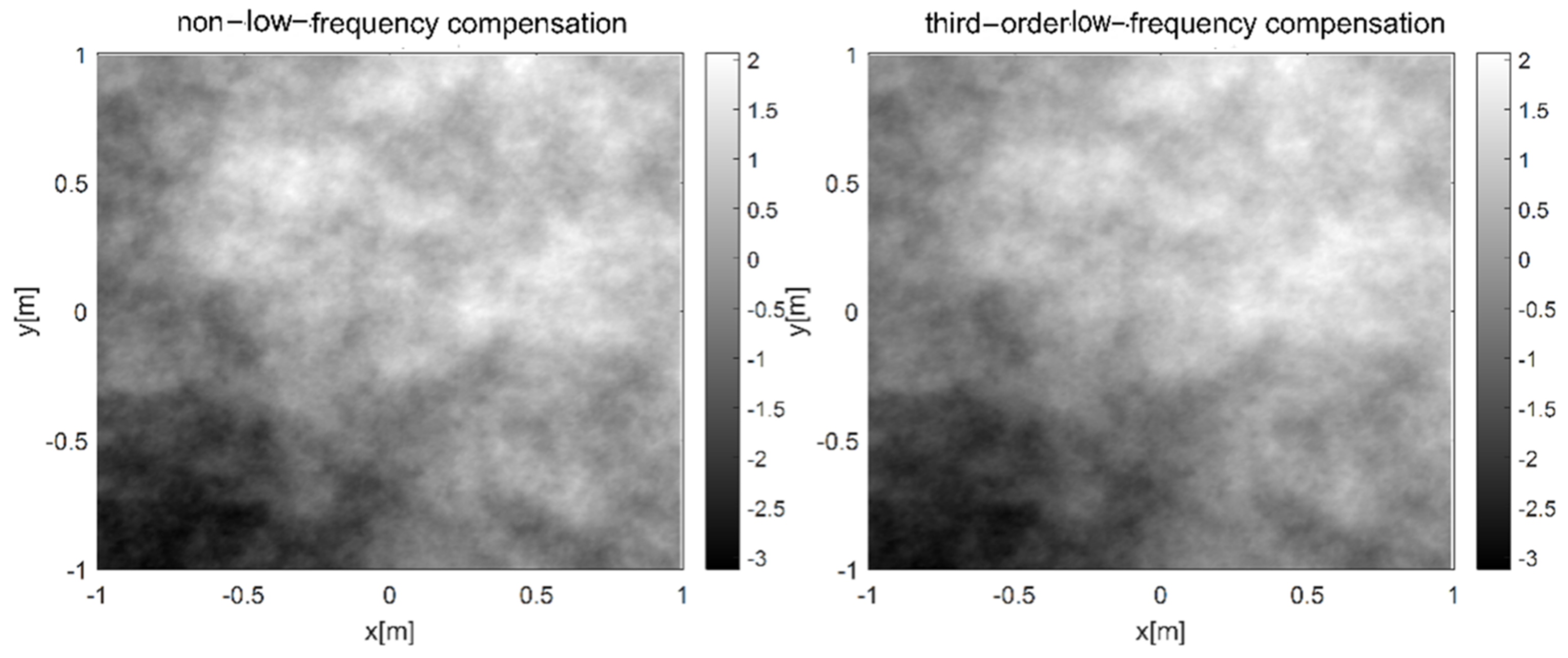
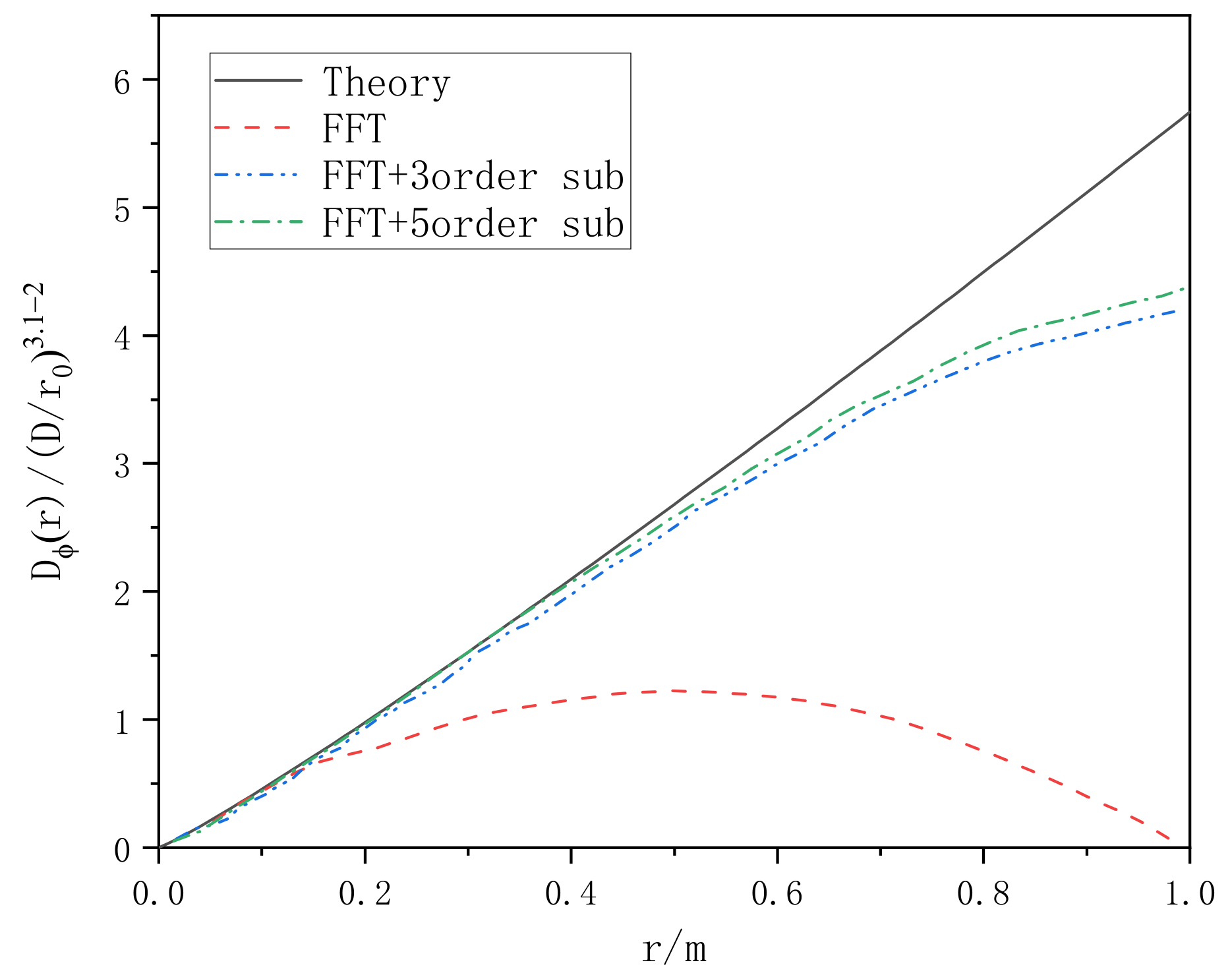
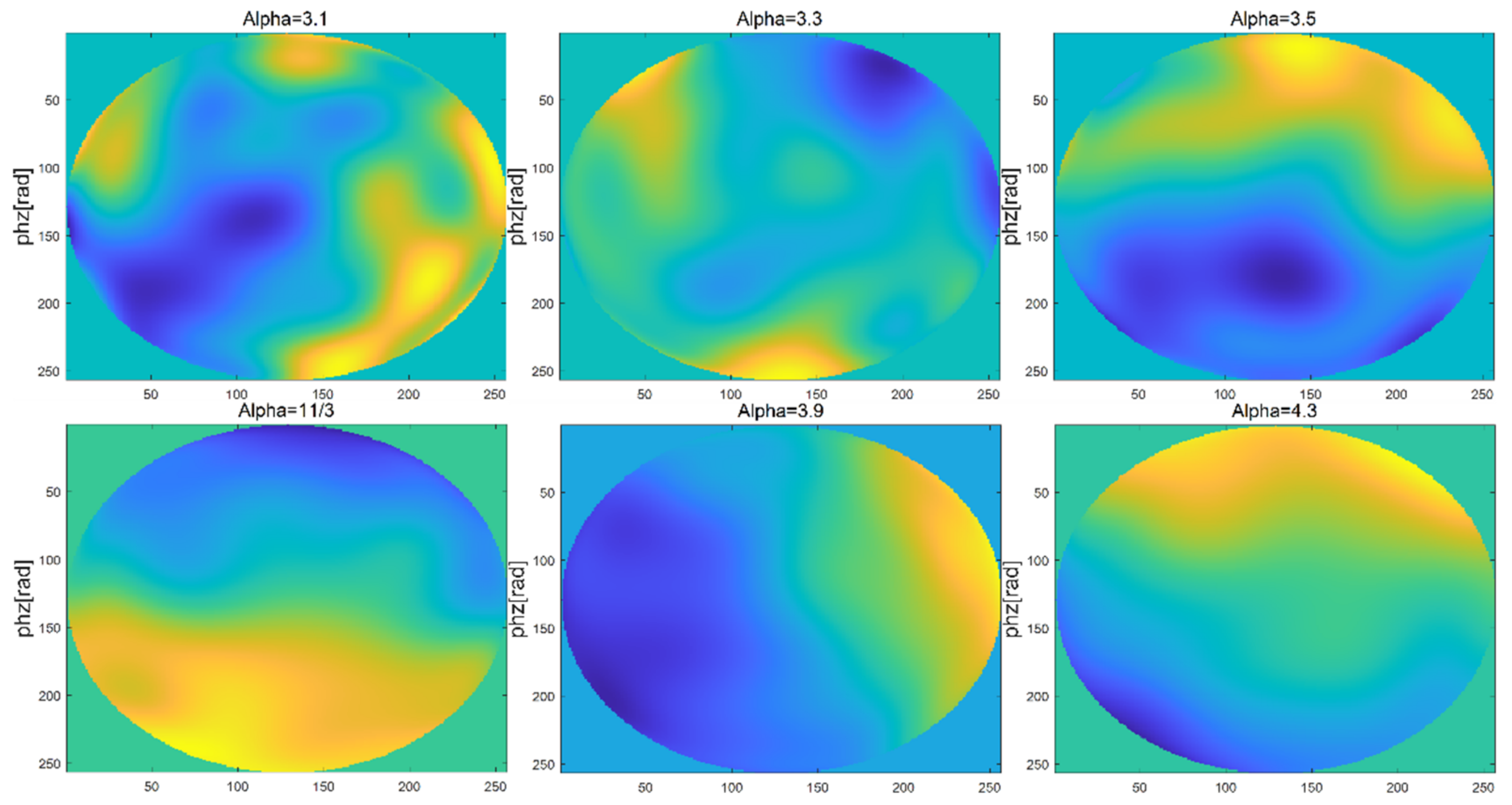
2.3. Verification of Phase Screen Simulation
2.3.1. Verification of Turbulent Phase Screen Simulated by the Power Spectrum Method
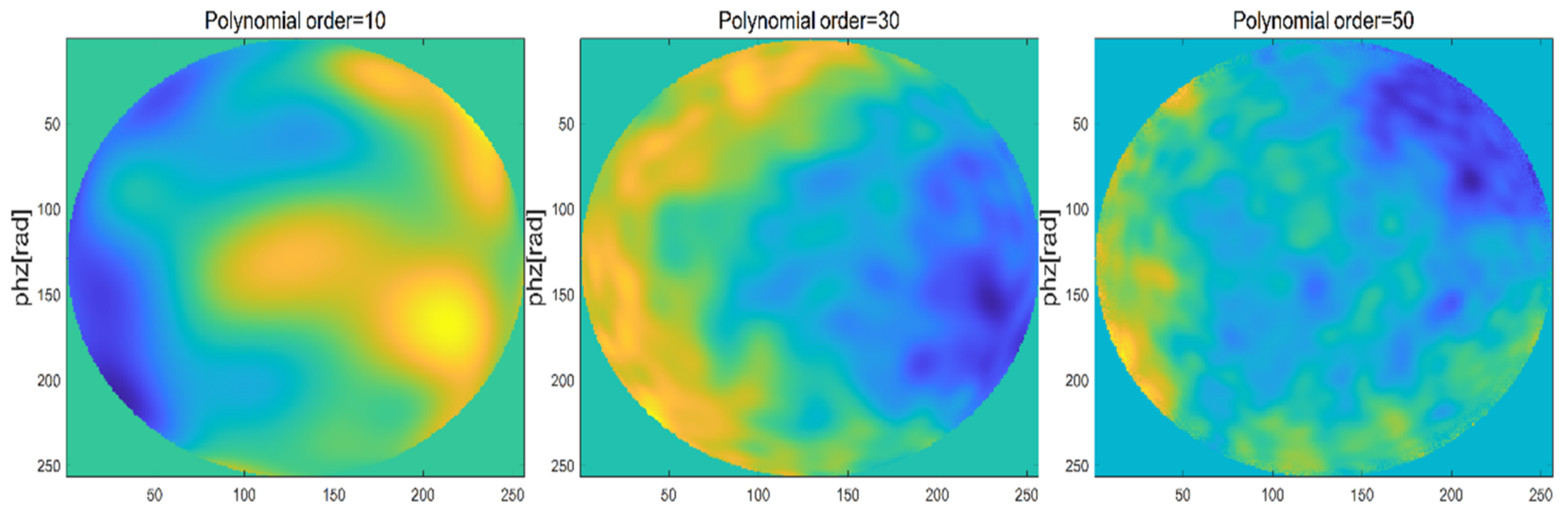
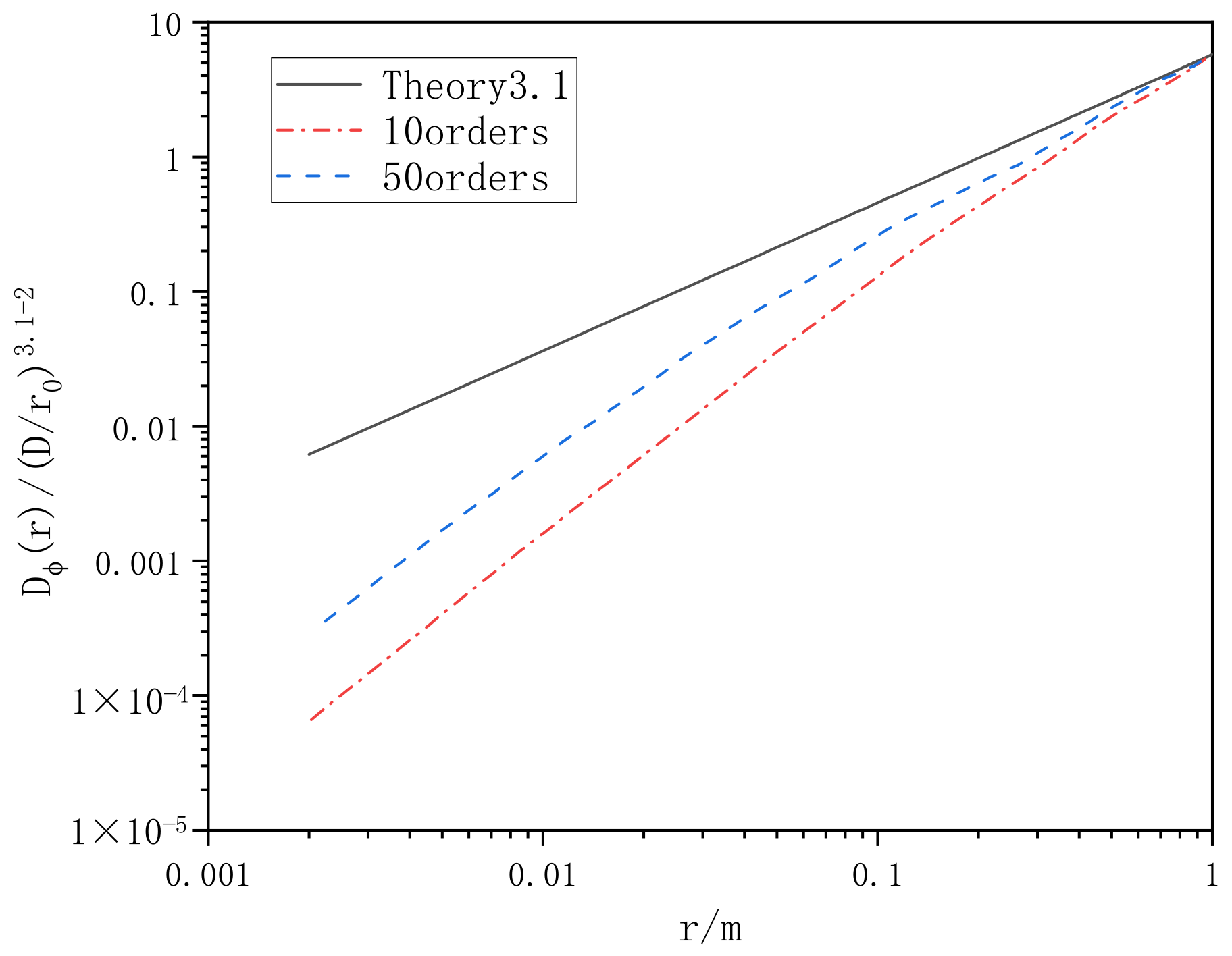
2.3.2. Verification of Turbulent Phase Screen Simulated by Zernike Polynomial Method
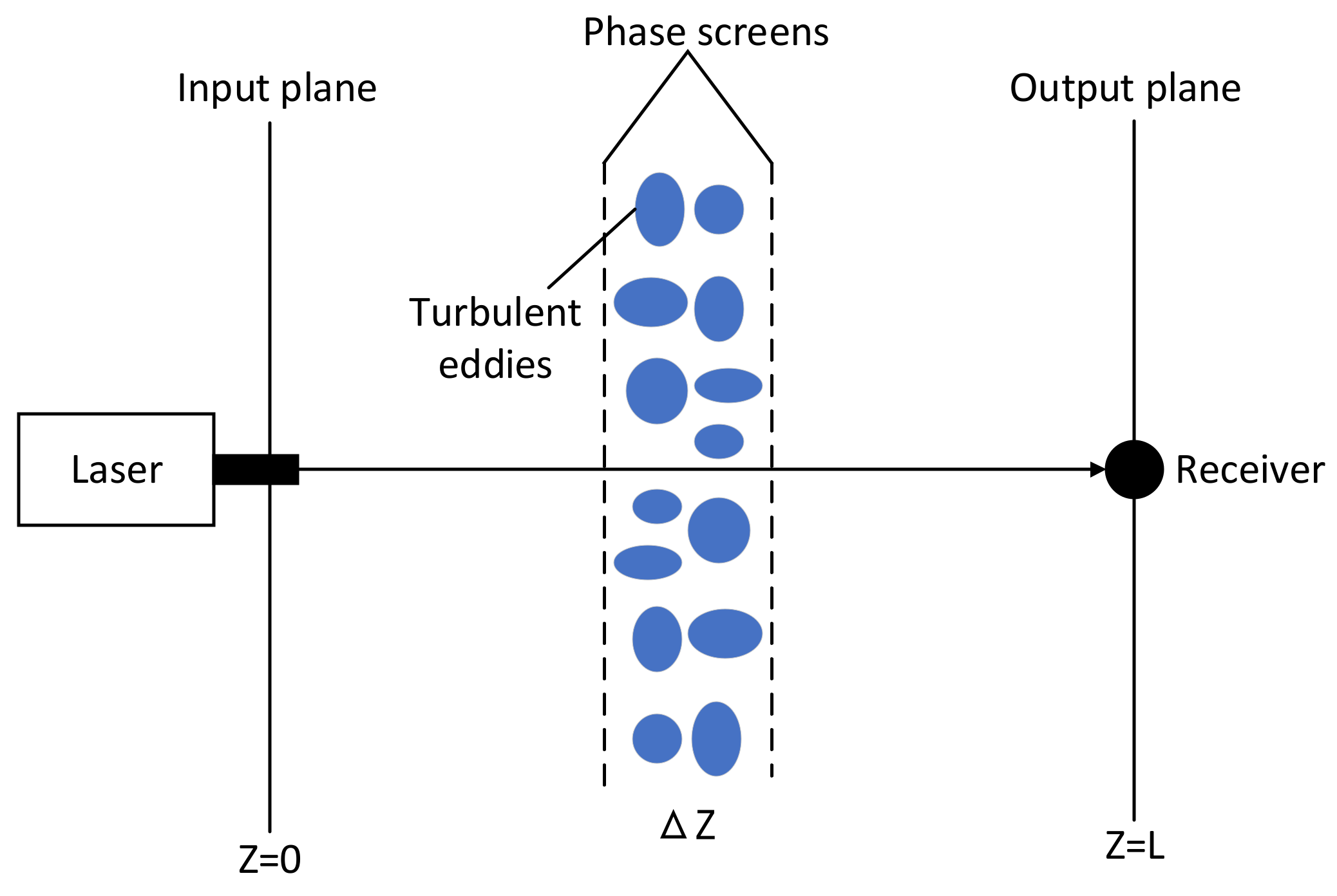
3. Simulation of Atmospheric Turbulence Detection by Mie-Scattering Lidar Using Non-Kolmogorov Turbulence Power Spectrum
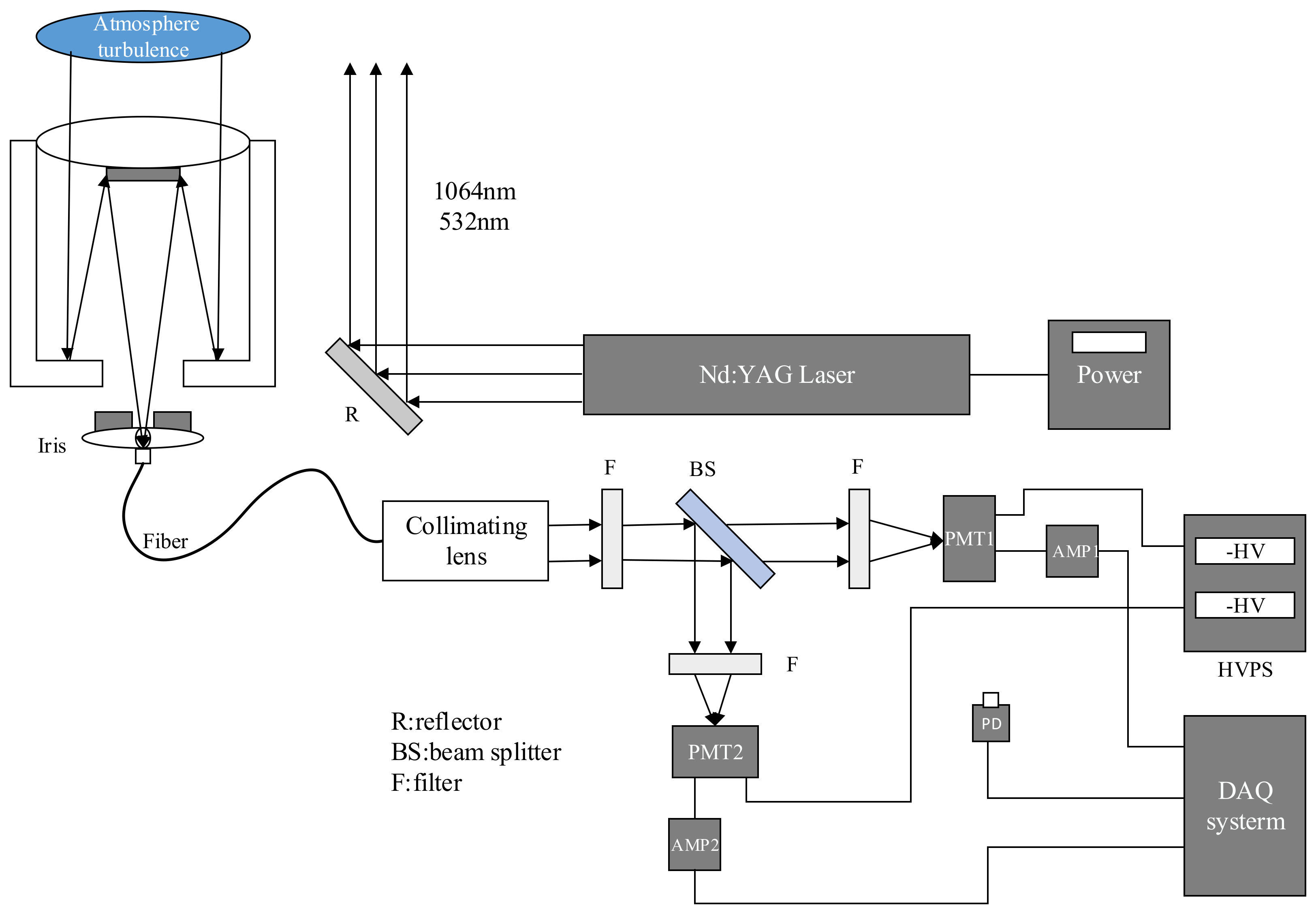
3.1. Mie-Scattering Lidar System
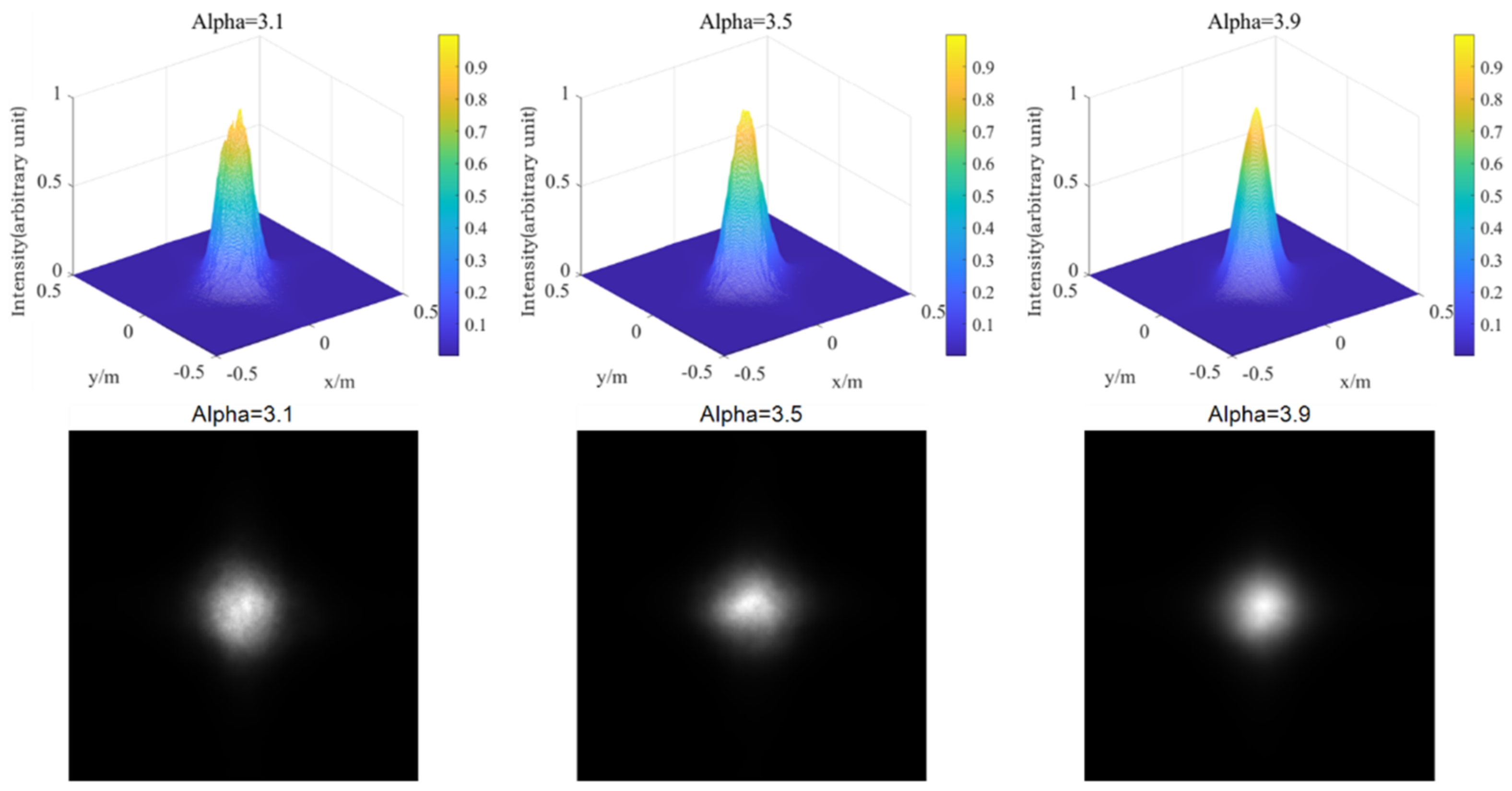
3.2. Light Intensity Simulation of Gaussian Beam Propagation for Non-Kolmogorov Turbulence
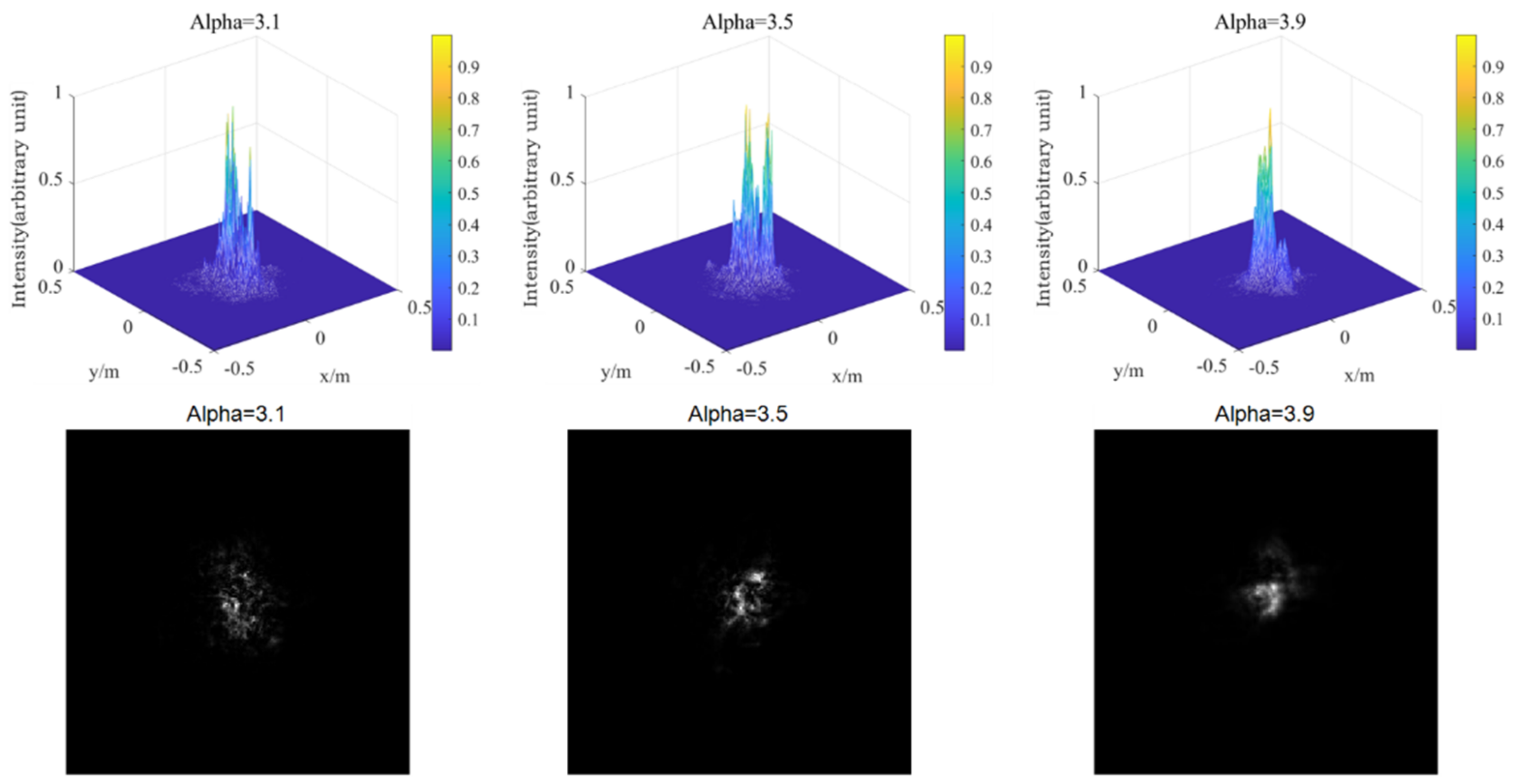
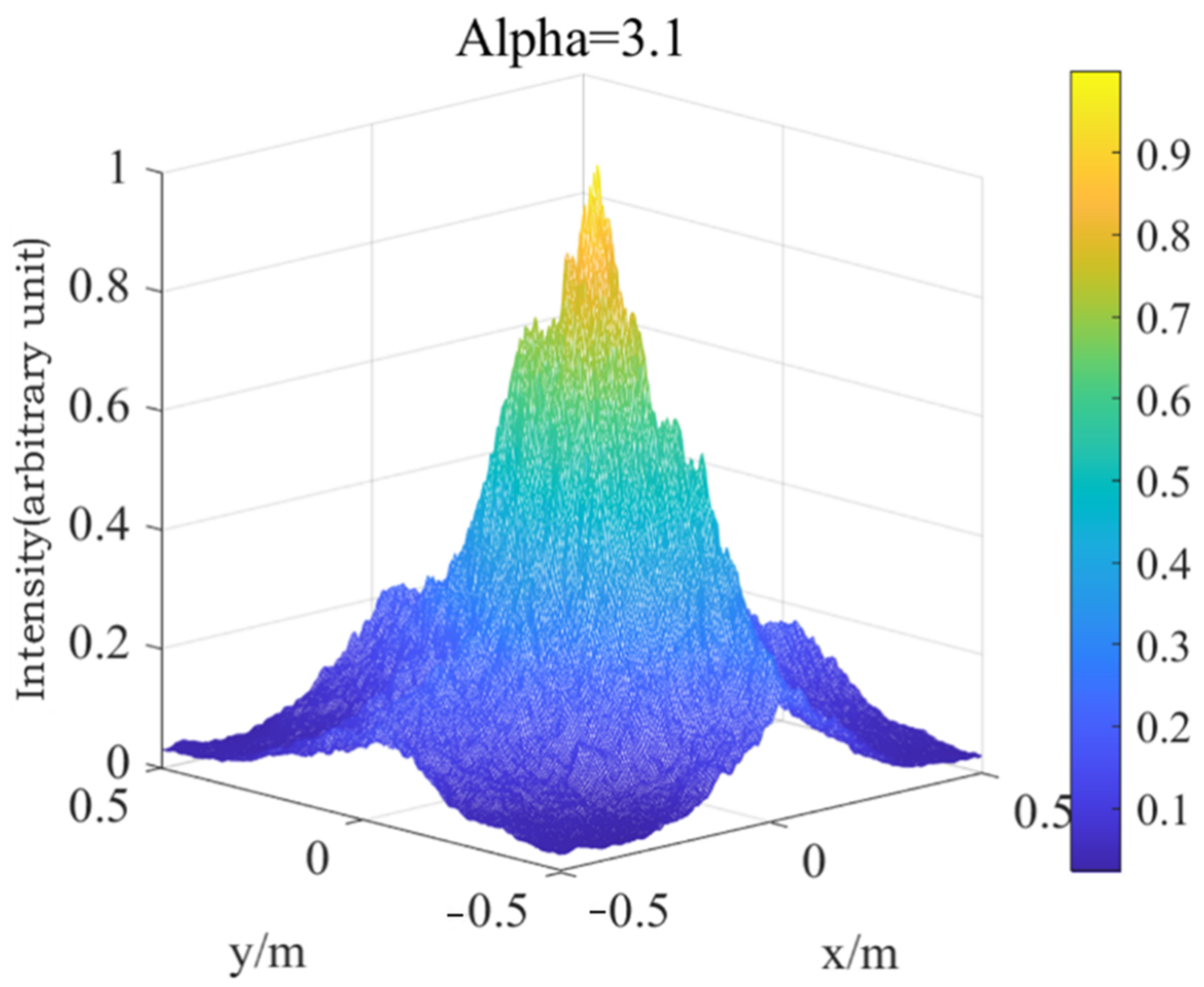
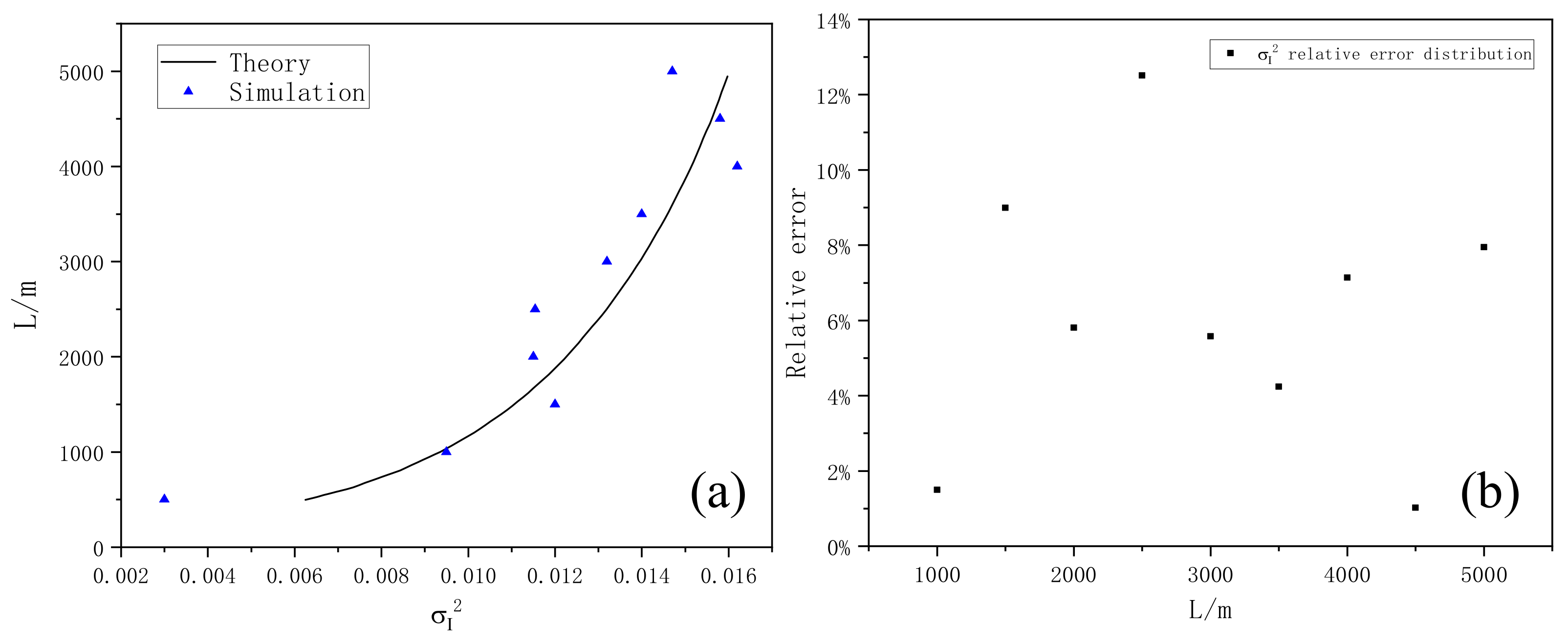
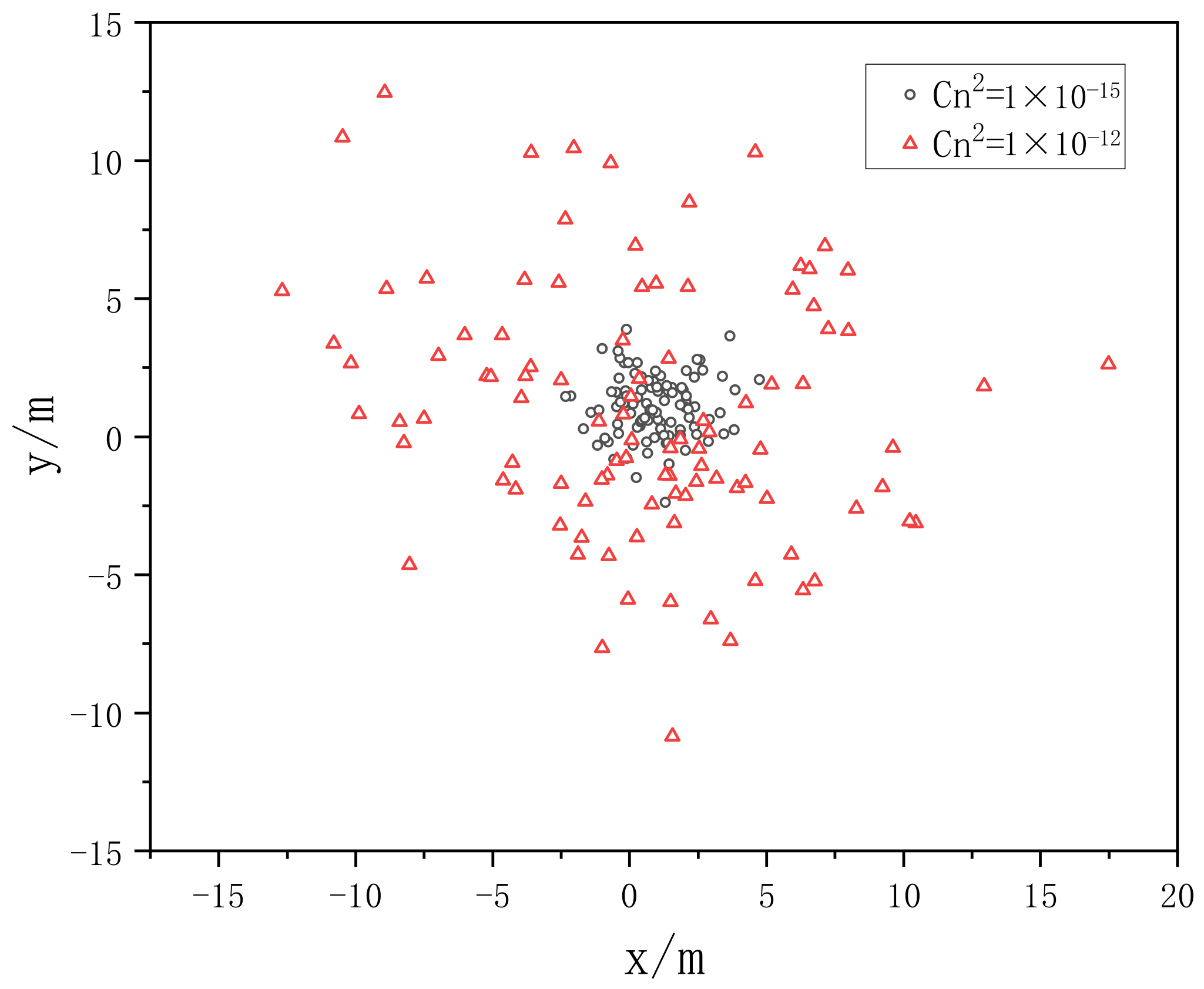
3.3. Spot Drift Effect of Gaussian Beam Propagation in Non-Kolmogorov Turbulence
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rao, R. Light Propagation in the Turbulent Atmosphere; Anhui Science and Technology Press: Hefei, China, 2005; pp. 4–5, 26, 99. [Google Scholar]
- Beland, R.R. Some aspects of propagation through weak isotropic non-Kolmogorov turbulence. In Proceedings of the SPIE—The International Society for Optical Engineering, San Jose, CA, USA, 6–7 February 1995; Volume 2375, pp. 6–16. [Google Scholar]
- Chen, M.; Gao, T.; Hu, S.; Zeng, Q.; Liu, L.; Li, G. Simulating Non-Kolmogorov turbulence phase screens based on equivalent structure constant and its influence on simulations of beam propagation. Results Phys. 2017, 7, 3596–3602. [Google Scholar] [CrossRef]
- Paulson, D.; Wu, C.; Davis, C. A detailed comparison of non-Kolmogorov and anisotropic optical turbulence theories using wave optics simulations. Laser Commun. Propag. Atmos. Ocean. VII 2018, 10770, 234–246. [Google Scholar]
- Stephen, G.; Jeremy, P. Limits on wave optics simulations in non-Kolmogorov turbulence. Laser Commun. Propag. Atmos. Ocean. VII 2018, 10770, 225–233. [Google Scholar]
- Wang, K.; Su, X.; Li, Z.; Wu, S.; Zhou, W.; Wang, R.; Chen, S.; Wang, X. Generation of non-Kolmogorov atmospheric turbulence phase screen using intrinsic embedding fractional Brownian motion method. Opt. Int. J. Light Electron Opt. 2020, 207, 164444. [Google Scholar] [CrossRef]
- Guan, B.; Yu, H.; Song, W.; Choi, J. Spatial Property of Optical Wave Propagation through Anisotropic Atmospheric Turbulence. Wirel. Commun. Mob. Comput. 2021, 2021, 5519786. [Google Scholar] [CrossRef]
- Cui, C.; Huang, H.; Mei, H.; Zhu, W.; Rao, R. Turbulent scintillation lidar for acquiring atmospheric turbulence information. High Power Laser Part. Beams 2013, 25, 1091–1096. [Google Scholar]
- Tang, H.; Yang, W.; Li, H. Detection Performance of Heterodyne Lidar in Non-Kolmogorov Turbulence. Acta Photonica Sin. 2015, 44, 74–79. [Google Scholar]
- Zhou, Y.; Zhou, A.; Sun, D.; Qiang, X. Development of differential image motion LiDAR for profiling optical turbulence. Infrared Laser Eng. 2016, 45, 257–261. [Google Scholar]
- Tatarski, V. Wave Propagation in a Turbulent Medium; Science Press: Beijing, China, 1978. [Google Scholar]
- Mcaulay, A. Generating Kolmogorov phase screens for modeling optical turbulence. In Proceedings of the SPIE—The International Society for Optical Engineering, San Diego, CA, USA, 31 July–2 August 2000; Volume 4034, pp. 50–57. [Google Scholar]
- Wang, S.; Chen, J.; Gu, G. Numerical Simulation of Laguerre-Gaussian Beam Propagation in non-Kolmogorov Turbulence. Opto-Electron. Eng. 2016, 43, 20–24. [Google Scholar]
- Li, Y.; Zhu, W.; Rao, R. Simulation of random phase screen of non-Kolmogorov atmospheric turbulence. Infrared Laser Eng. 2016, 45, 169–176. [Google Scholar]
- Stribling, B.; Welsh, B.; Roggemann, M. Optical Propagation in Non-Kolmogorov Atmospheric Turbulence. In Proceedings of the SPIE—The International Society for Optical Engineering, Orlando, FL, USA, 13–16 April 1998; Volume 2471, pp. 181–196. [Google Scholar]
- Lane, R.; Glindemann, A.; Dainty, J. Simulation of a Kolmogorov phase screen. Waves Random Media 1992, 2, 209–224. [Google Scholar] [CrossRef]
- Roggemann, M.; Welsh, B. Imaging Through Turbulence. Opt. Eng. 1996, 35, 1025–1034. [Google Scholar] [CrossRef]
- Nicolas, A. Atmospheric wavefront simulation using Zernike polynomials. Opt. Eng. 1990, 29, 1174–1179. [Google Scholar]
- Chiba, T. Spot dancing of the laser beam propagated through the turbulent atmosphere. Appl. Opt. 1971, 10, 2456–2461. [Google Scholar] [CrossRef] [PubMed]
- Young, C.; Andrews, L. Optical scintillation of a Gaussian beam in moderate-to-strong irradiance fluctuations. Airborne Laser Adv. Technol. II 1999, 3706, 142–150. [Google Scholar]
- Ma, X.S.; Zhu, W.Y.; Rao, R.Z. Large Aperture Laser Scintillometer for Measuring the Refractive Index Structure Constant of Atmospheric Turbulence. Chin. J. Lasers 2008, 35, 898–902. [Google Scholar]
- Miller, W.; Ricklin, J.; Andrews, L. Effects of the refractive index spectral model on the irradiance variance of a Gaussian beam. Josa A 1994, 11, 2719–2726. [Google Scholar] [CrossRef]
- Wang, L.; Duan, J.; Jing, W.; Dan, Z.; Jiang, H. Laser spot detection and characteristic analysis in space optical communication. Infrared Laser Eng. 2007, 36, 434–438. [Google Scholar]




| Group Number | Subharmonics | Mean Gray Scale | Variance of Gray Scale | Compensated Variance Relative Error |
|---|---|---|---|---|
| 1 | 0 | 163.4397 | 5681.5 | 3.92% |
| 3 | 163.4473 | 5462.3 | ||
| 2 | 0 | 177.8483 | 5531.5 | 2.06% |
| 6 | 177.8651 | 5417.8 | ||
| 3 | 0 | 159.8466 | 6116.3 | 1.42% |
| 10 | 159.8518 | 6029.4 | ||
| 4 | 0 | 181.1989 | 4540.2 | 0.72% |
| 15 | 181.2009 | 4507.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Mao, J.; Li, J.; Gong, X. Novel Simulation and Analysis of Mie-Scattering Lidar for Detecting Atmospheric Turbulence Based on Non-Kolmogorov Turbulence Power Spectrum Model. Entropy 2022, 24, 1764. https://doi.org/10.3390/e24121764
Zhang Y, Mao J, Li J, Gong X. Novel Simulation and Analysis of Mie-Scattering Lidar for Detecting Atmospheric Turbulence Based on Non-Kolmogorov Turbulence Power Spectrum Model. Entropy. 2022; 24(12):1764. https://doi.org/10.3390/e24121764
Chicago/Turabian StyleZhang, Yingnan, Jiandong Mao, Juan Li, and Xin Gong. 2022. "Novel Simulation and Analysis of Mie-Scattering Lidar for Detecting Atmospheric Turbulence Based on Non-Kolmogorov Turbulence Power Spectrum Model" Entropy 24, no. 12: 1764. https://doi.org/10.3390/e24121764







