Exploring the Origin of Maximum Entropy States Relevant to Resonant Modes in Modern Chladni Plates
Abstract
:1. Introduction
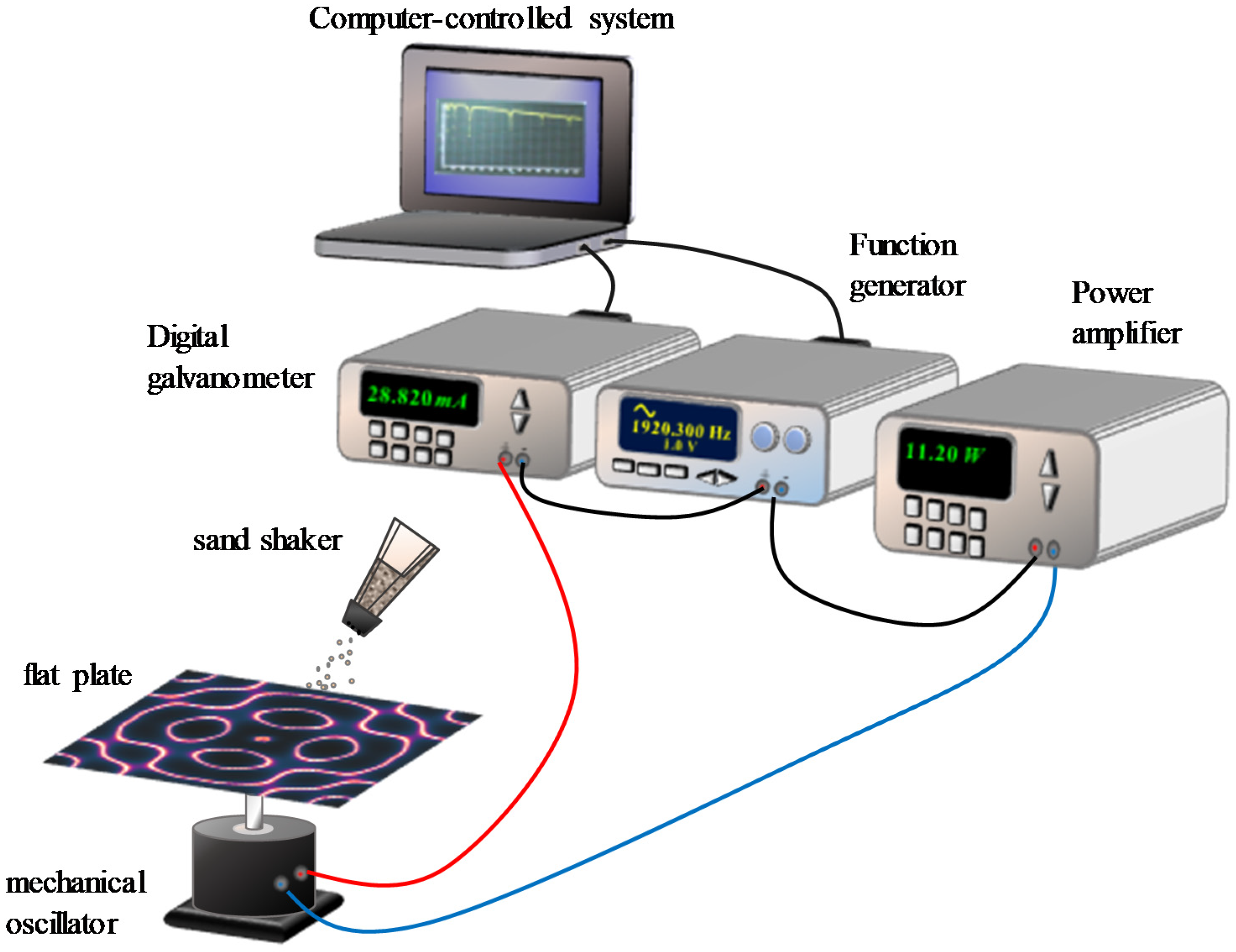
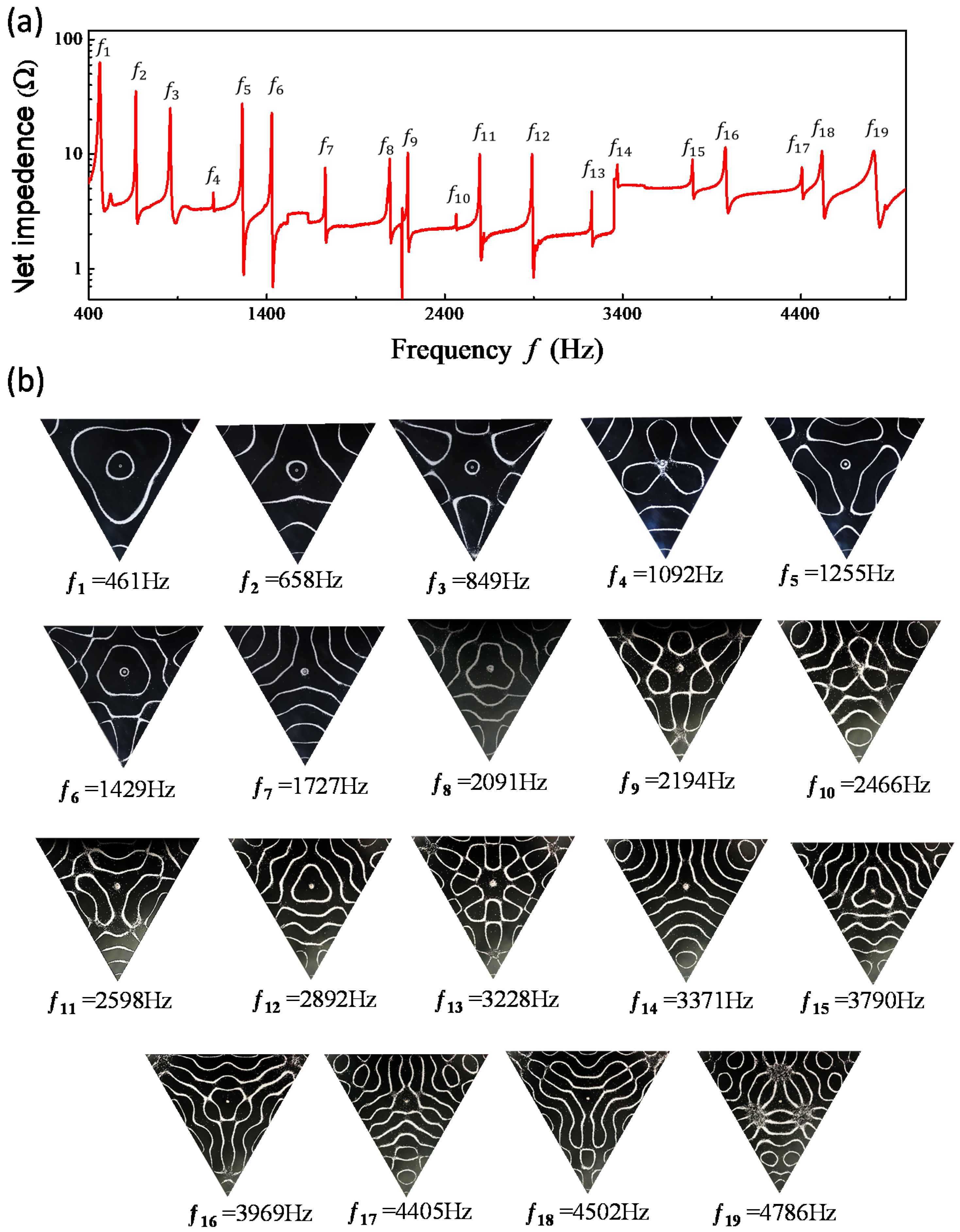
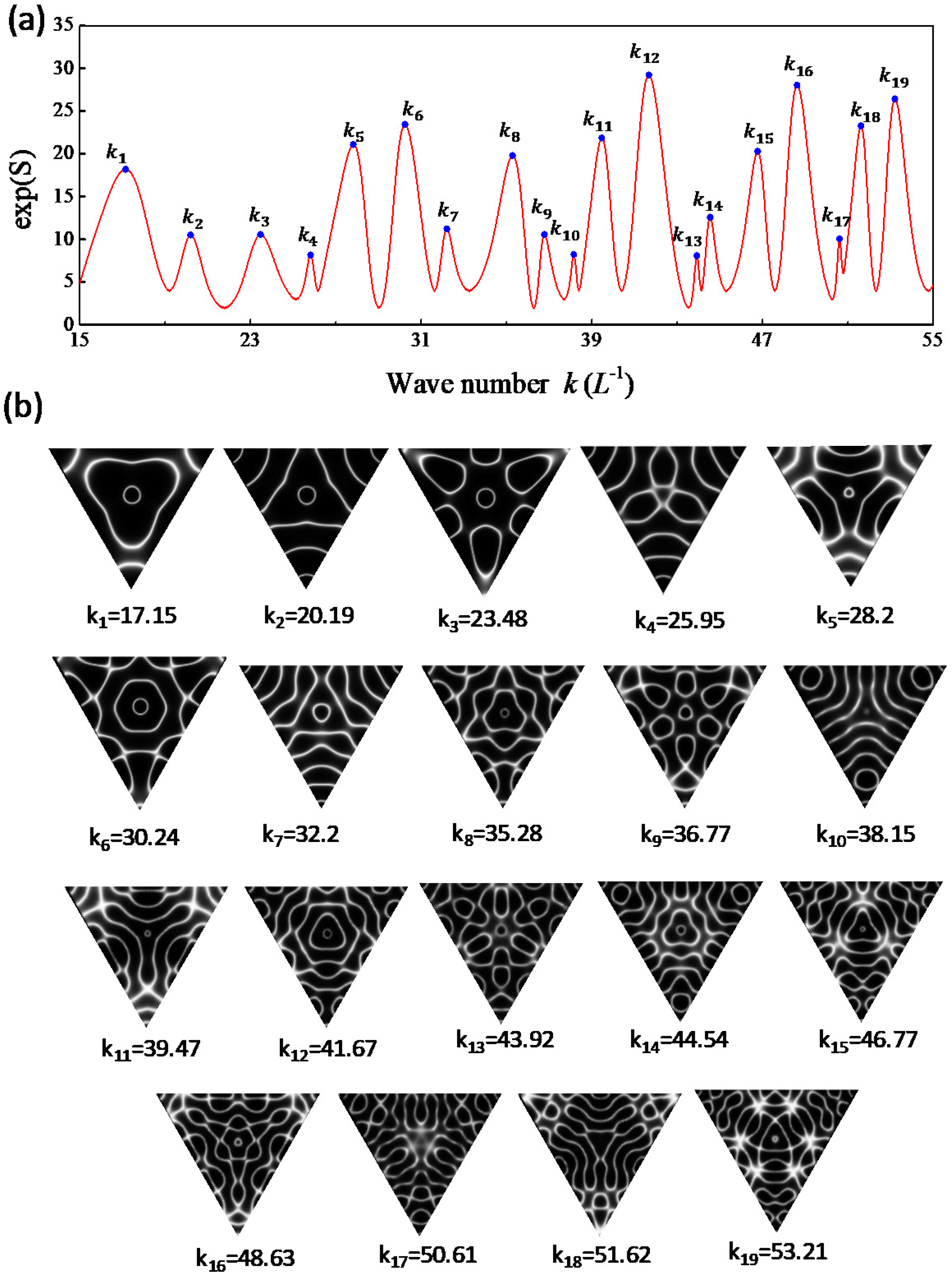
2. Frequency Spectrum and Resonant Modes
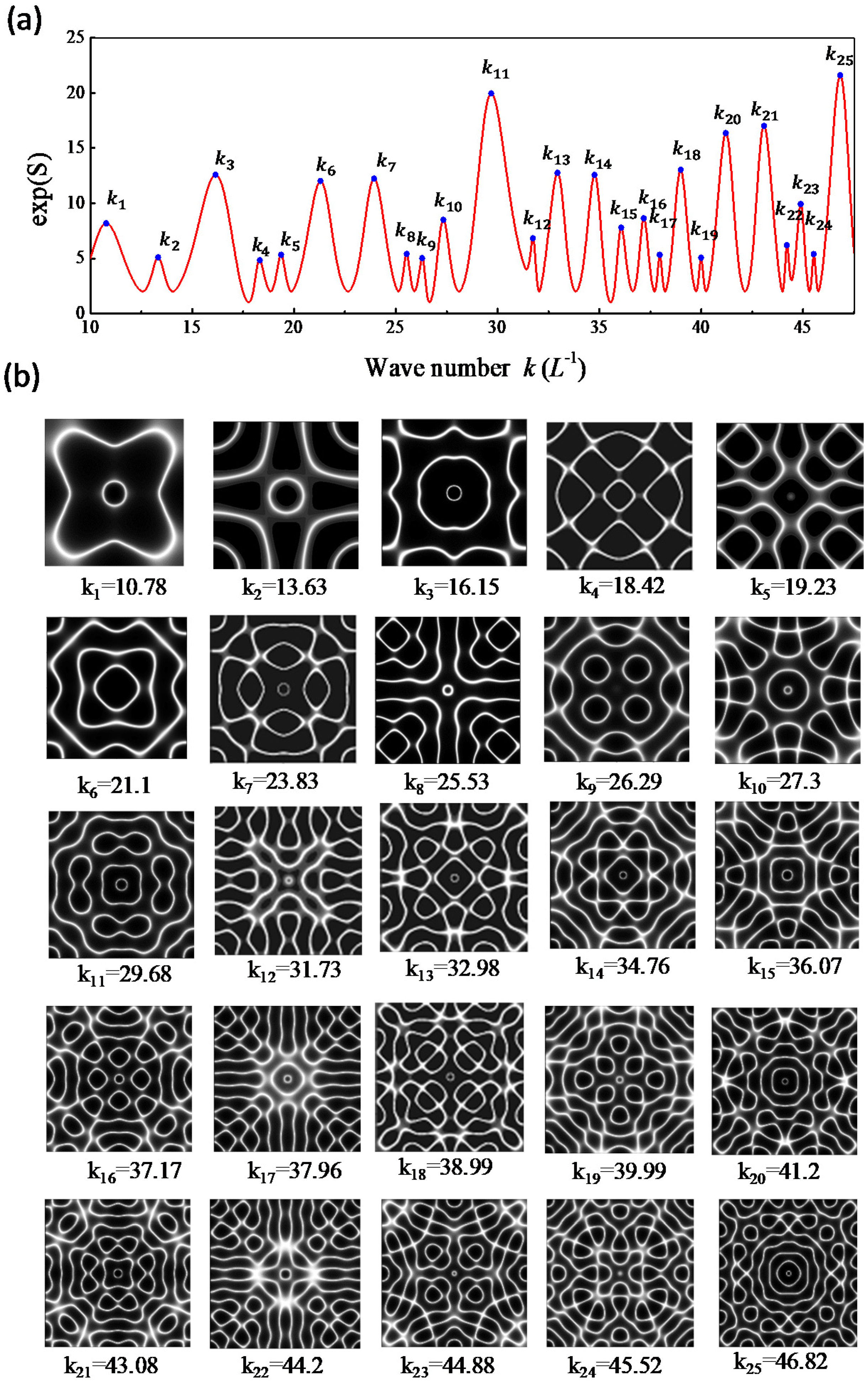
3. Maximum Entropy States of the Vibrating Plate
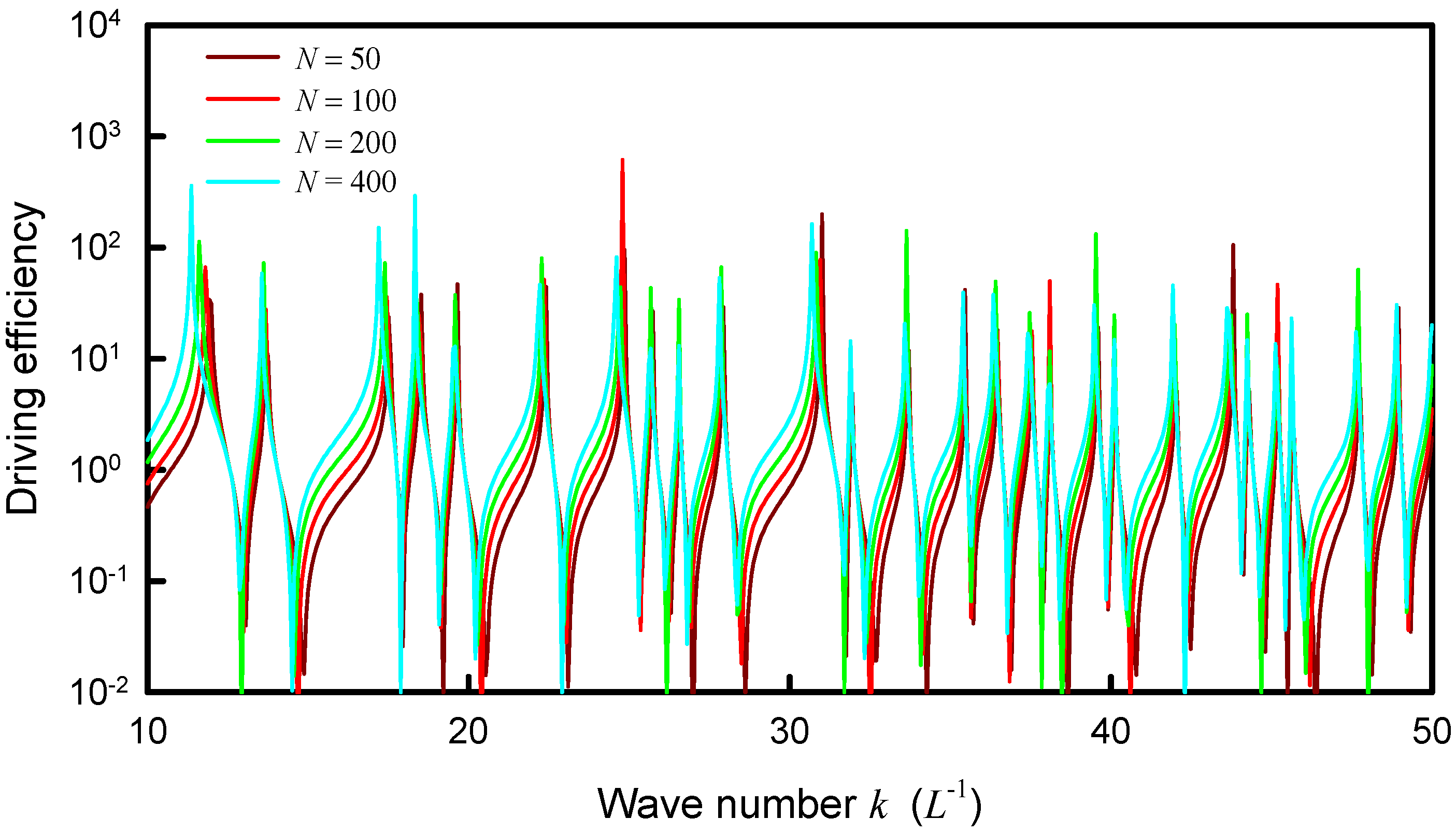
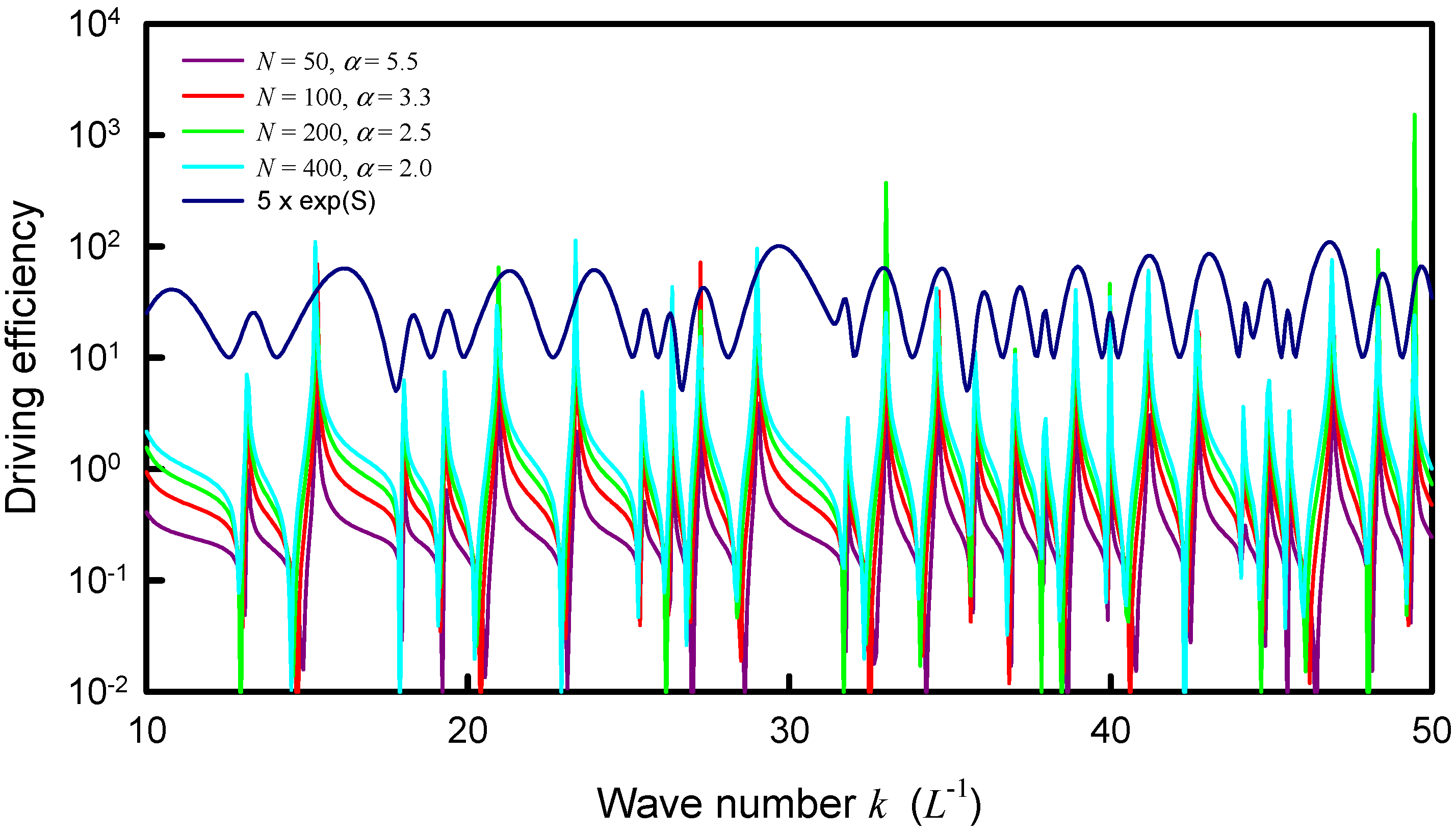
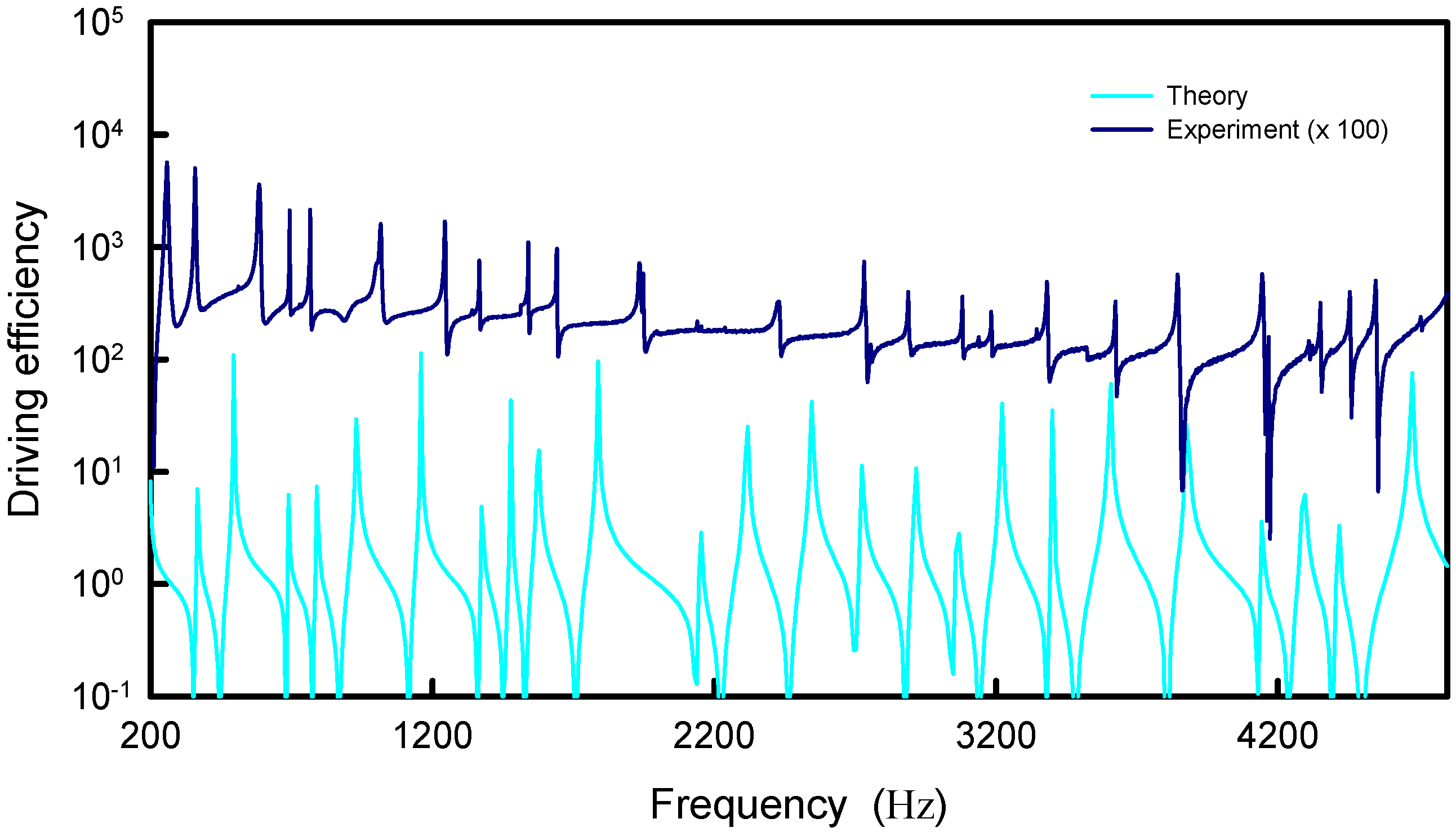
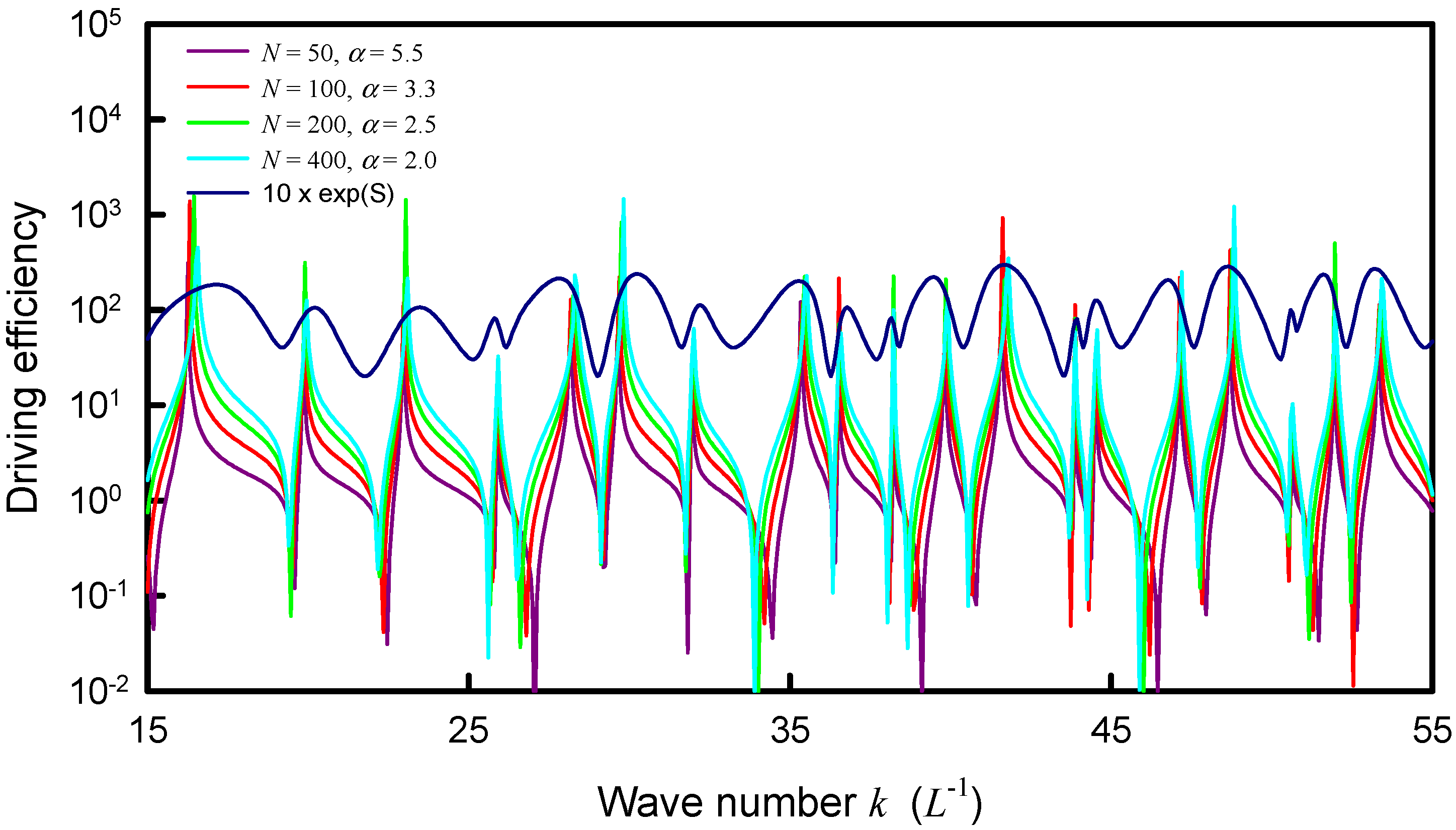
4. Coupling Interaction between Source and Plate
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chladni, E.F.F. Entdeckungen über die Theorie des Klanges; Breitkopf und Härtel: Leipzig, Germany, 1787. [Google Scholar]
- Chladni, E.F.F. Die Akustik; Breitkopf und Härtel: Leipzig, Germany, 1802. [Google Scholar]
- Jain, S.R.; Samajdar, R. Nodal portraits of quantum billiards: Domains, lines, and statistics. Rev. Mod. Phys. 2017, 89, 045005. [Google Scholar] [CrossRef] [Green Version]
- Dorrestijn, M.; Bietsch, A.; Açıkalın, T.; Raman, A.; Hegner, M.; Meyer, E.; Gerber, C. Chladni figures revisited based on nanomechanics. Phys. Rev. Lett. 2007, 98, 026102. [Google Scholar] [CrossRef] [Green Version]
- Taillan, C.; Combe, N.; Morillo, J. Nanoscale self-organization using standing surface acoustic waves. Phys. Rev. Lett. 2011, 106, 076102. [Google Scholar] [CrossRef]
- Friend, J.; Yeo, L.Y. Microscale acoustofluidics: Microfluidics driven via acoustics and ultrasonics. Rev. Mod. Phys. 2011, 83, 647. [Google Scholar] [CrossRef] [Green Version]
- Mak, S.Y.; Li, Z.; Frere, A.; Chan, T.C.; Shum, H.C. Musical interfaces: Visualization and reconstruction of music with a microfluidic two-phase flow. Sci. Rep. 2014, 4, 6675. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ohlin, K.; Berggren, K.F. Patterns beyond Faraday waves: Observation of parametric crossover from Faraday instabilities to the formation of vortex lattices in open dual fluid strata. Eur. J. Phys. 2016, 37, 045803. [Google Scholar] [CrossRef] [Green Version]
- Misseroni, D.; Colquitt, D.J.; Movchan, A.B.; Movchan, N.V.; Jones, I.S. Cymatics for the cloaking of flexural vibrations in a structured plate. Sci. Rep. 2016, 6, 23929. [Google Scholar] [CrossRef] [Green Version]
- Scholz, C.; Engel, M.; Pöschel, T. Rotating robots move collectively and self-organize. Nat. Commun. 2018, 9, 931. [Google Scholar] [CrossRef]
- Scholz, C.; Pöschel, T. Velocity distribution of a homogeneously driven two-dimensional granular gas. Phys. Rev. Lett. 2017, 118, 198003. [Google Scholar] [CrossRef] [Green Version]
- Collins, D.J.; Morahan, B.; Garcia-Bustos, J.; Doerig, C.; Plebanski, M.; Neild, A. Two-dimensional single-cell patterning with once cell per well driven by surface acoustic waves. Nat. Commun. 2015, 6, 8686. [Google Scholar] [CrossRef] [Green Version]
- Ding, X.; Lin, S.; Kiraly, B.; Yue, H.; Li, S.; Chiang, I.K.; Shi, J.; Benkovic, S.; Huang, T. On-chip manipulation of single microparticles, cells, and organisms using surface acoustic waves. Proc. Natl Acad. Sci. USA 2012, 109, 11105–11109. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, Q.; Sariola, V.; Latifi, K.; Liimatainen, V. Controlling the motion of multiple objects on a Chladni plate. Nat. Commun. 2016, 7, 12764. [Google Scholar] [CrossRef] [PubMed]
- Whitehill, J.; Neild, A.; Ng, T.W.; Strokes, M. Collection of suspended particles in a drop using low frequency vibration. Appl. Phys. Lett. 2010, 96, 053501. [Google Scholar] [CrossRef]
- Tuan, P.H.; Wen, C.P.; Chiang, P.Y.; Yu, Y.T.; Liang, H.C.; Huang, K.F.; Chen, Y.F. Exploring the resonant vibration of thin plates: Reconstruction of Chladni patterns and determination of resonant wave numbers. J. Acoust. Soc. Am. 2015, 137, 2113. [Google Scholar] [CrossRef] [PubMed]
- Tuan, P.H.; Liang, H.C.; Tung, J.C.; Chiang, P.Y.; Huang, K.F.; Chen, Y.F. Manifesting the evolution of eigenstates from quantum billiards to singular billiards in the strongly coupled limit with a truncated basis by using RLC networks. Phys. Rev. E 2015, 92, 062906. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tuan, P.H.; Tung, J.C.; Liang, H.C.; Chiang, P.Y.; Huang, K.F.; Chen, Y.F. Resolving the formation of modern Chladni figures. Europhys. Lett. 2015, 111, 64004. [Google Scholar] [CrossRef] [Green Version]
- Tuan, P.H.; Lai, Y.H.; Wen, C.P.; Huang, K.F.; Chen, Y.F. Point-driven modern Chladni figures with symmetry breaking. Sci. Rep. 2018, 8, 10844. [Google Scholar] [CrossRef] [PubMed]
- Tuan, P.H.; Wen, C.P.; Yu, Y.T.; Liang, H.C.; Huang, K.F.; Chen, Y.F. Exploring the distinction between experimental resonant modes and theoretical eigenmodes: From vibrating plates to laser cavities. Phys. Rev. E 2014, 89, 022911. [Google Scholar] [CrossRef] [Green Version]
- Chakraverty, S. Vibration of Plates; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Ventsel, E.; Krauthammer, T. Thin Plates and Shells; Marcel Dekker: New York, NY, USA, 2004; pp. 1–14. [Google Scholar]
- Rayleigh, J.W.S. Theory of Sound; Dover: New York, NY, USA, 1945; pp. 367–380. [Google Scholar]
- Waller, M.D. Vibrations of free square plates: Part I. Normal vibrating modes. Proc. Phys. Soc. 1939, 51, 831–844. [Google Scholar] [CrossRef]
- Shannon, C.E. Prediction and entropy of printed English. Bell Syst. Tech. J. 1951, 30, 50–60. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information theory and statistical mechanics. Phys. Rev. 1957, 106, 602–630. [Google Scholar] [CrossRef]
- Ekert, A.; Knight, P.L. Entangled quantum systems and the Schmidt decomposition. Am. J. Phys. 1995, 63, 415. [Google Scholar] [CrossRef]
- Law, C.K.; Eberly, J.H. Analysis and interpretation of high transverse entanglement in optical parametric down conversion. Phys. Rev. Lett. 2004, 92, 127903. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Law, C.K.; Walmsley, I.A.; Eberly, J.H. Continuous frequency entanglement: Effective finite Hilbert space and entropy control. Phys. Rev. Lett. 2000, 84, 5304. [Google Scholar] [CrossRef] [PubMed]
- Fedorov, M.V.; Miklin, N.I. Schmidt modes and entanglement. Contemp. Phys. 2014, 55, 94–109. [Google Scholar] [CrossRef]
- Práger, M. Eigenvalues and eigenfunctions of the Laplace operator on an equilateral triangle. Appl. Math. 1998, 43, 311–320. [Google Scholar] [CrossRef] [Green Version]
- Leissa, A.W. Vibration of Plates; Acoustical Society of America: New York, NY, USA, 1993; pp. 1–345. [Google Scholar]
- Van Vlack, L.H. Elements of Material Science and Engineering; Addison-Wesley: Boston, MA, USA, 1980. [Google Scholar]
- Tang, C.L.; Statz, H. Maximum-emission principle and phase locking in multimode lasers. J. Appl. Phys. 1967, 38, 2963–2968. [Google Scholar] [CrossRef]
- Haken, H. Information and Self-Organization: A Macroscopic Approach to Complex Systems; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Heller, E.J. Quantum localization and the rate of exploration of phase space. Phys. Rev. A 1987, 35, 1360–1370. [Google Scholar] [CrossRef]
- Jung, C.; Müller, M.; Rotter, I. Phase transitions in open quantum systems. Phys. Rev. E 1999, 60, 114–131. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Albeverio, S.; Gesztesy, F.; Høegh-Krohn, R.; Holden, H. Solvable Models in Quantum Mechanics; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Schmidt, A.G.M.; Cheng, B.K.; da Luz, M.G.E. Green functions for generalized point interactions in one dimension: A scattering approach. Phys. Rev. A 2002, 66, 062712. [Google Scholar] [CrossRef] [Green Version]
- Arnbak, H.; Christiansen, P.L.; Gaididei, Y.B. Non-relativistic and relativistic scattering by short-range potentials. Philos. Trans. R. Soc. A 2011, 369, 1228. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kruppa, A.T.; Varga, K.; Révai, J. Local realizations of contact interactions in two-and three-body problems. Phys. Rev. C 2001, 63, 064301. [Google Scholar] [CrossRef] [Green Version]
- Demkov, Y.; Ostrovskii, V.N. Zero-Range Potentials and Their Applications in Atomic Physics; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Doniach, S.; Sondheimer, E. Green’s Functions for Solid State Physicists; World Scientific: Singapore, 1998. [Google Scholar]
- Thorn, C. Quark confinement in the infinite-momentum frame. Phys. Rev. D 1979, 19, 639. [Google Scholar] [CrossRef]
- Šeba, P. Wave chaos in singular quantum billiard. Phys. Rev. Lett. 1990, 64, 1855. [Google Scholar] [CrossRef]
- Shigehara, T. Conditions for the appearance of wave chaos in quantum singular systems with a pointlike scatterer. Phys. Rev. E 1994, 50, 4357. [Google Scholar] [CrossRef]
- Šeba, P.; Exner, P. Point interactions in two and three dimensions as models of small scatterers. Phys. Lett. A 1996, 222, 1–4. [Google Scholar]
- Bogomolny, E.; Gerland, U.; Schmit, C. Singular statistics. Phys. Rev. E 2001, 63, 036206. [Google Scholar] [CrossRef] [Green Version]
- Berkolaiko, G.; Keating, J.P.; Winn, B. Intermediate wave function statistics. Phys. Rev. Lett. 2003, 91, 134013. [Google Scholar] [CrossRef] [Green Version]
- Tudorovskiy, T.; Kuhl, U.; Stöckmann, H.J. Singular statistics revised. New J. Phys. 2010, 12, 123021. [Google Scholar] [CrossRef] [Green Version]
- Rudnick, Z.; Ueberschär, H. Statistics of wave functions for a point scatterer on the torus. Commun. Math. Phys. 2012, 316, 763–782. [Google Scholar] [CrossRef] [Green Version]
- Weaver, R.L.; Sornette, D. Range of spectral correlations in pseudointegrable systems: Gaussian-orthogonal-ensemble statistics in a rectangular membrane with a point scatterer. Phys. Rev. E 1995, 52, 3341. [Google Scholar] [CrossRef] [PubMed]
- Shigehara, T.; Cheon, T. Wave chaos in quantum billiards with a small but finite-size scatterer. Phys. Rev. E 1996, 54, 1321. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grica, T.; Eldlioa, M.; Cada, M.; Pistor, J. Analytic solution to field distribution in two-dimensional inhomogeneous waveguides. J. Electromagn. Waves Appl. 2015, 8, 29. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shu, Y.-H.; Tseng, Y.-C.; Lai, Y.-H.; Yu, Y.-T.; Huang, K.-F.; Chen, Y.-F. Exploring the Origin of Maximum Entropy States Relevant to Resonant Modes in Modern Chladni Plates. Entropy 2022, 24, 215. https://doi.org/10.3390/e24020215
Shu Y-H, Tseng Y-C, Lai Y-H, Yu Y-T, Huang K-F, Chen Y-F. Exploring the Origin of Maximum Entropy States Relevant to Resonant Modes in Modern Chladni Plates. Entropy. 2022; 24(2):215. https://doi.org/10.3390/e24020215
Chicago/Turabian StyleShu, Yu-Hsin, Yu-Chen Tseng, Yu-Hsiang Lai, Yan-Ting Yu, Kai-Feng Huang, and Yung-Fu Chen. 2022. "Exploring the Origin of Maximum Entropy States Relevant to Resonant Modes in Modern Chladni Plates" Entropy 24, no. 2: 215. https://doi.org/10.3390/e24020215
APA StyleShu, Y.-H., Tseng, Y.-C., Lai, Y.-H., Yu, Y.-T., Huang, K.-F., & Chen, Y.-F. (2022). Exploring the Origin of Maximum Entropy States Relevant to Resonant Modes in Modern Chladni Plates. Entropy, 24(2), 215. https://doi.org/10.3390/e24020215






