Energy Efficiency of User-Centric, Cell-Free Massive MIMO-OFDM with Instantaneous CSI
Abstract
:1. Introduction
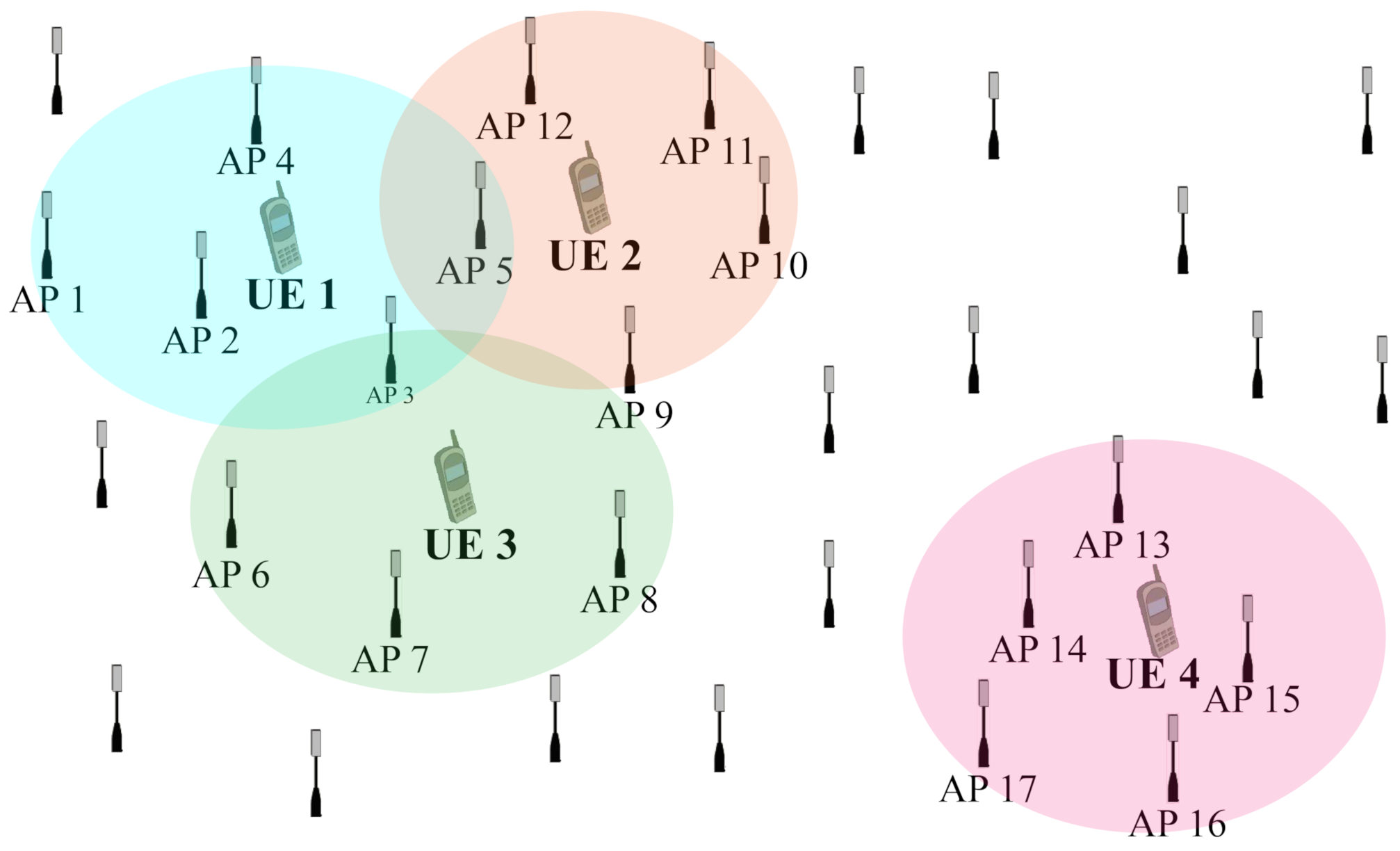
2. System Model
2.1. Channel Model
2.2. Downlink Transmission
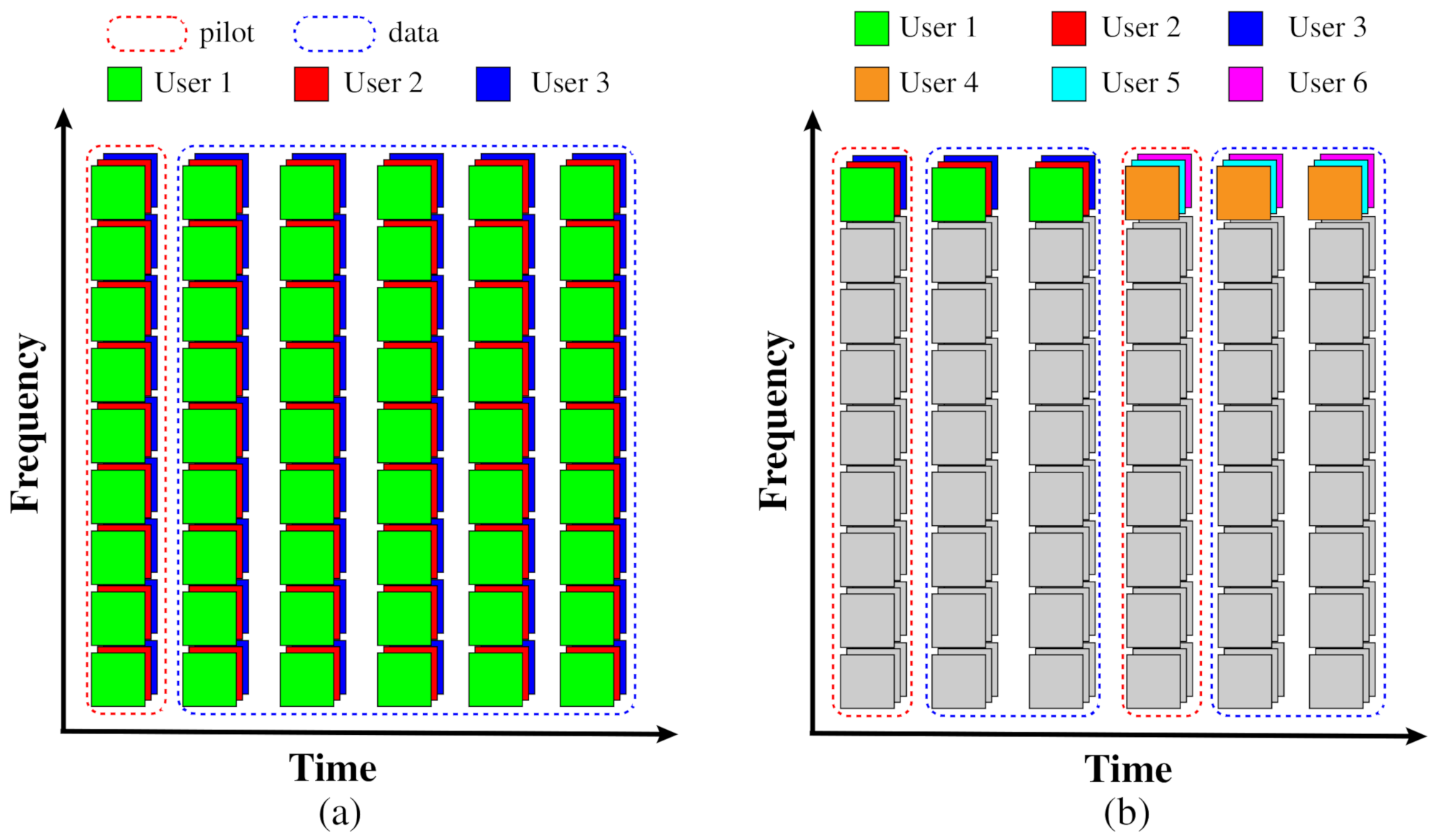
3. Resouce Block Allocation and Downlink Transmitting Rate
3.1. eMBB Case
3.2. mMTC Case
4. Power Consumption Model and Energy Efficiency
5. Energy Efficiency Optimization
6. Results
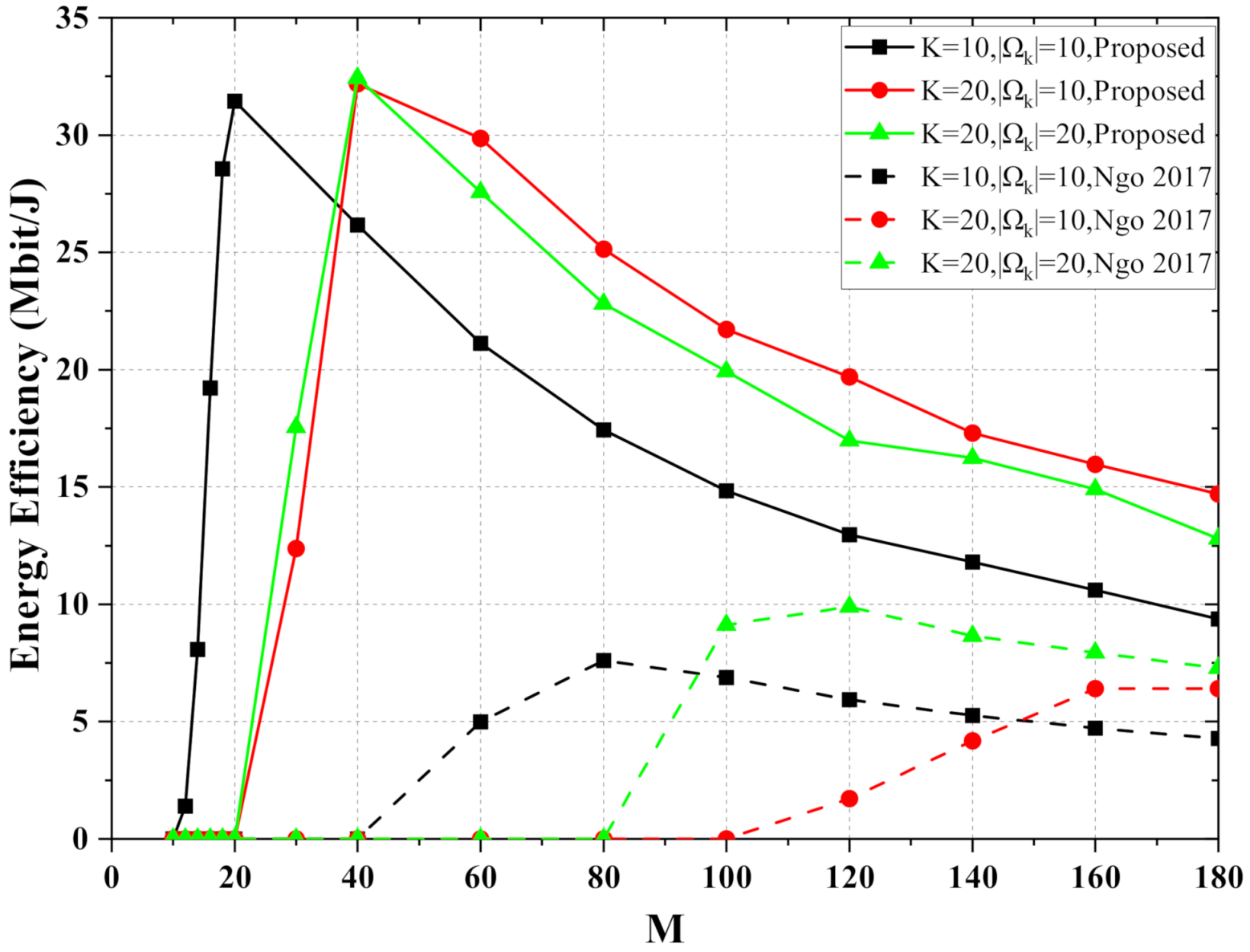
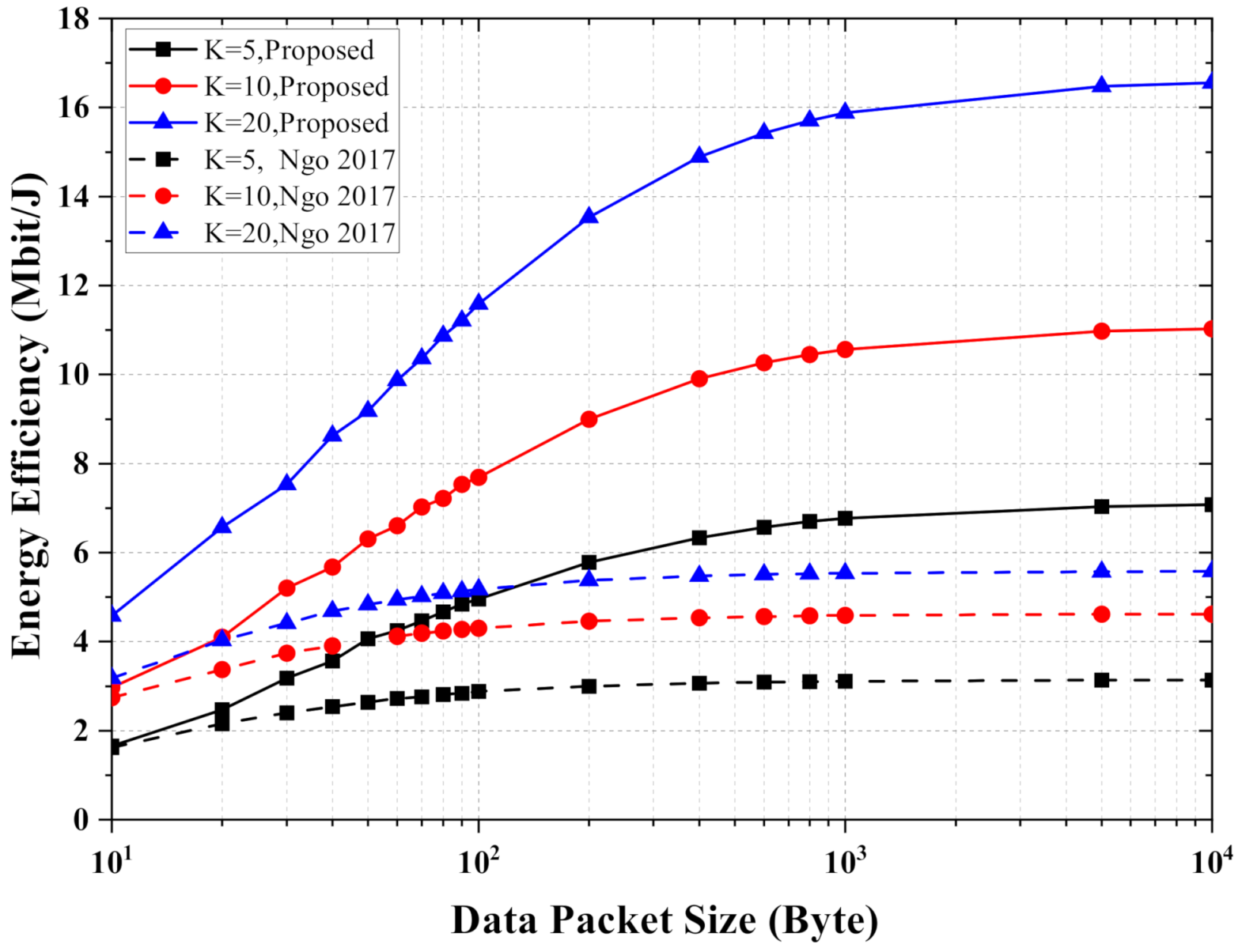
6.1. Simulation for eMBB
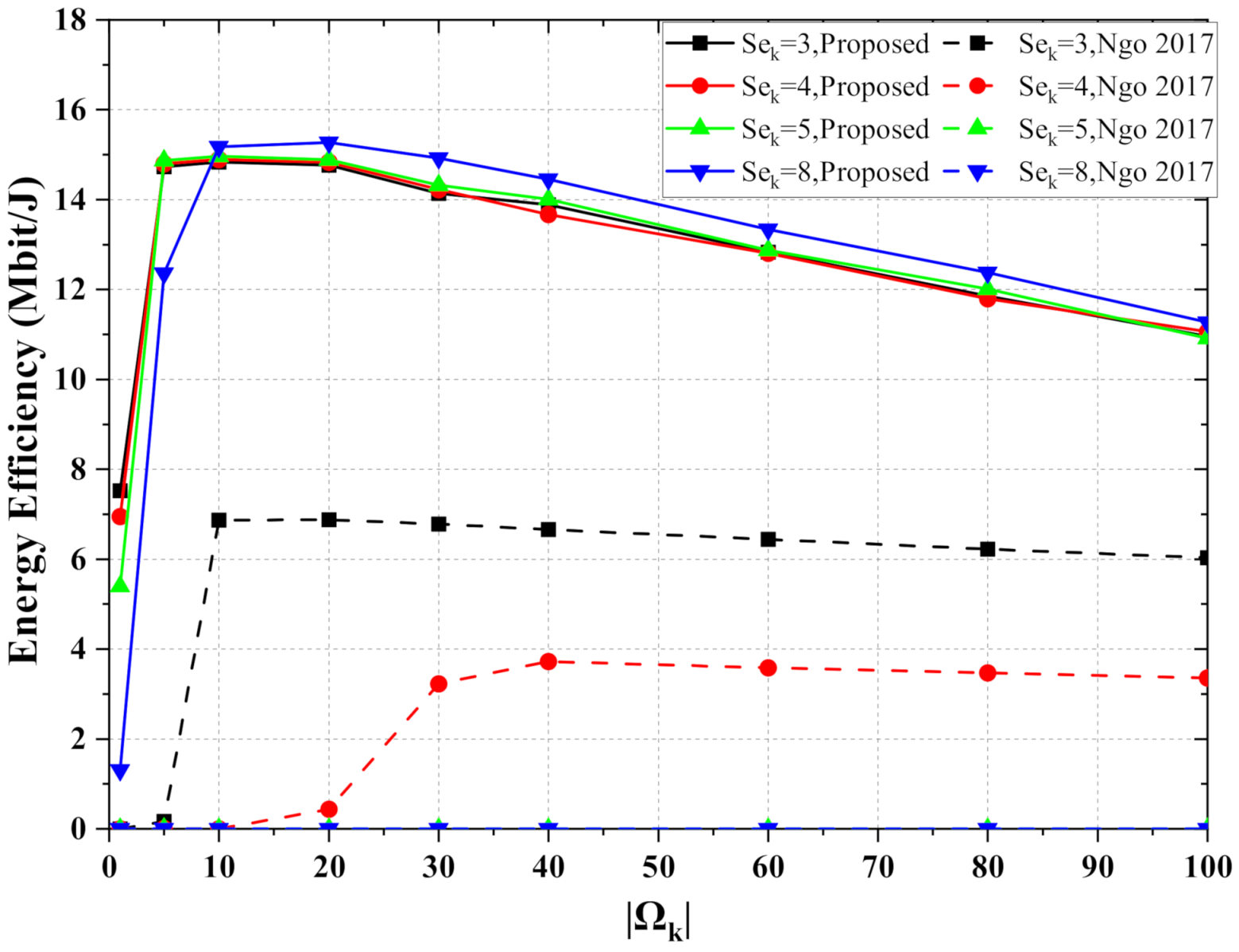
6.2. Simulation for mMTC
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Saad, W.; Bennis, M.; Chen, M. A vision of 6G wireless systems: Applications, trends, technologies, and open research problems. IEEE Netw. 2019, 34, 134–142. [Google Scholar] [CrossRef] [Green Version]
- Cisco. Cisco Visual Networking Index: Forecast and Trends, 2018–2022; White Paper; Cisco: San Jose, CA, USA, 2020. [Google Scholar]
- Marzetta, T.L.; Ngo, H.Q. Fundamentals of massive MIMO; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Ngo, H.Q.; Ashikhmin, A.; Yang, H.; Larsson, E.G.; Marzetta, T.L. Cell-free massive MIMO: Uniformly great service for everyone. In Proceedings of the 2015 IEEE 16th international workshop on signal processing advances in wireless communications (SPAWC), Stockholm, Sweden, 28 June–1 July 2015. [Google Scholar]
- Nayebi, E.; Ashikhmin, A.; Marzetta, T.L.; Yang, H. Cell-free massive MIMO systems. In Proceedings of the 2015 IEEE 49th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 8–11 November 2015. [Google Scholar]
- Ngo, H.Q.; Ashikhmin, A.; Yang, H.; Larsson, E.G.; Marzetta, T.L. Cell-free massive MIMO versus small cells. IEEE Trans. Wirel. Commun. 2017, 16, 1834–1850. [Google Scholar] [CrossRef] [Green Version]
- Buzzi, S.; D’Andrea, C. Cell-free massive MIMO: User-centric approach. IEEE Wirel. Commun. Lett. 2017, 6, 706–709. [Google Scholar] [CrossRef]
- Nayebi, E.; Ashikhmin, A.; Marzetta, T.L.; Yang, H.; Rao, B.D. Precoding and power optimization in cell-free massive MIMO systems. IEEE Trans. Wirel. Commun. 2017, 16, 4445–4459. [Google Scholar] [CrossRef]
- Alsharif, M.H.; Kelechi, A.H.; Kim, J.; Kim, J.H. Energy efficiency and coverage trade-off in 5G for eco-friendly and sustainable cellular networks. Symmetry 2019, 11, 408. [Google Scholar] [CrossRef] [Green Version]
- Fehske, A.; Fettweis, G.; Malmodin, J.; Biczok, G. The global footprint of mobile communications: The ecological and economic perspective. IEEE Commun. Mag. 2011, 49, 55–62. [Google Scholar] [CrossRef]
- Yang, H.; Marzetta, T.L. Energy efficiency of massive MIMO: Cell-free vs. cellular. In Proceedings of the 2018 IEEE 87th Vehicular Technology Conference (VTC Spring), Porto, Portugal, 3–6 June 2018. [Google Scholar]
- Ngo, H.Q.; Tran, L.-N.; Duong, T.Q.; Matthaiou, M.; Larsson, E.G. Energy efficiency optimization for cell-free massive MIMO. In Proceedings of the 2017 IEEE 18th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Sapporo, Japan, 3–6 July 2017. [Google Scholar]
- Ngo, H.Q.; Tran, L.-N.; Duong, T.Q.; Matthaiou, M.; Larsson, E.G. On the total energy efficiency of cell-free massive MIMO. IEEE Trans. Green Commun. Netw. 2018, 2, 25–39. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, L.D.; Duong, T.Q.; Ngo, H.Q.; Tourki, K. Energy efficiency in cell-free massive MIMO with zero-forcing precoding design. IEEE Commun. Lett. 2017, 21, 1871–1874. [Google Scholar] [CrossRef] [Green Version]
- Tran, L.-N.; Ngo, H.Q. First-order methods for energy-efficient power control in cell-free massive mimo. In Proceedings of the 2019 IEEE 53rd Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 3–6 November 2019. [Google Scholar]
- Mai, T.C.; Ngo, H.Q.; Tran, L.-N. APG Method for Energy-Efficient Power Control in Cell-Free Massive MIMO with Zero-Forcing. In Proceedings of the 2020 IEEE Eighth International Conference on Communications and Electronics (ICCE), Phu Quoc Island, Vietnam, 13–15 January 2021. [Google Scholar]
- Mai, T.C.; Ngo, H.Q.; Tran, L.-N. Energy-efficient power allocation in cell-free massive MIMO with zero-forcing: First order methods. Phys. Commun. 2021, 51, 101540. [Google Scholar] [CrossRef]
- Papazafeiropoulos, A.; Ngo, H.Q.; Kourtessis, P.; Chatzinotas, S.; Senior, J.M. Towards optimal energy efficiency in cell-free massive MIMO systems. IEEE Trans. Green Commun. Netw. 2021, 5, 816–831. [Google Scholar] [CrossRef]
- García-Morales, J.; Femenias, G.; Riera-Palou, F. Energy-efficient access-point sleep-mode techniques for cell-free mmWave massive MIMO networks with non-uniform spatial traffic density. IEEE Access 2020, 8, 137587–137605. [Google Scholar] [CrossRef]
- Alonzo, M.; Buzzi, S.; Zappone, A.; D’Elia, C. Energy-efficient power control in cell-free and user-centric massive MIMO at millimeter wave. IEEE Trans. Green Commun. Netw. 2019, 3, 651–663. [Google Scholar] [CrossRef] [Green Version]
- Gapeyenko, M.; Petrov, V.; Moltchanov, D.; Akdeniz, M.R.; Andreev, S.; Himayat, N.; Koucheryavy, Y. On the degree of multi-connectivity in 5G millimeter-wave cellular urban deployments. IEEE Trans. Veh. Technol. 2018, 68, 1973–1978. [Google Scholar] [CrossRef]
- Rangan, S.; Rappaport, T.S.; Erkip, E. Millimeter-wave cellular wireless networks: Potentials and challenges. Proc. IEEE 2014, 102, 366–385. [Google Scholar] [CrossRef] [Green Version]
- Jiang, W.; Schotten, H.D. Cell-Free Massive MIMO-OFDM Transmission over Frequency-Selective Fading Channels. IEEE Commun. Lett. 2021, 25, 2718–2722. [Google Scholar] [CrossRef]
- Björnson, E.; Larsson, E.G.; Marzetta, T.L. Massive MIMO: Ten myths and one critical question. IEEE Commun. Mag. 2016, 54, 114–123. [Google Scholar] [CrossRef] [Green Version]
- Lu, L.; Li, G.Y.; Swindlehurst, A.L.; Ashikhmin, A.; Zhang, R. An overview of massive MIMO: Benefits and challenges. IEEE J. Sel. Top. Signal Process. 2014, 8, 742–758. [Google Scholar] [CrossRef]
- Chen, Z.; Björnson, E. Channel hardening and favorable propagation in cell-free massive MIMO with stochastic geometry. IEEE Trans. Commun. 2018, 66, 5205–5219. [Google Scholar] [CrossRef] [Green Version]
- Han, T.; Zhao, D. The Downlink Performance for Cell-Free Massive MIMO with Instantaneous CSI in Slowly Time-Varying Channels. Entropy 2021, 23, 1552. [Google Scholar] [CrossRef] [PubMed]
- Tse, D.; Viswanath, P. Fundamentals of Wireless Communication; Cambridge Univ. Press: Cambridge, UK, 2005; Chapter 2. [Google Scholar]
- Hochwald, B.M.; Marzetta, T.L.; Tarokh, V. Multiple-antenna channel hardening and its implications for rate feedback and scheduling. IEEE Trans. Inf. Theory 2004, 50, 1893–1909. [Google Scholar] [CrossRef]
- Ammar, H.A.; Adve, R.; Shahbazpanahi, S.; Boudreau, G.; Srinivas, K.V. user-centric, cell-free massive MIMO networks: A survey of opportunities, challenges and solutions. arXiv 2021, arXiv:2104.14589. [Google Scholar] [CrossRef]
- Campos, J. Understanding the 5G NR Physical Layer; 9921-03326.EN; Keysight Technologies Release: Santa Rosa, CA, USA, 2017. [Google Scholar]
- Tombaz, S.; Vastberg, A.; Zander, J. Energy-and cost-efficient ultra-high-capacity wireless access. IEEE Wirel. Commun. 2011, 18, 18–24. [Google Scholar] [CrossRef]
- Zuo, J.; Zhang, J.; Yuen, C.; Jiang, W.; Luo, W. Energy-efficient downlink transmission for multicell massive DAS with pilot contamination. IEEE Trans. Veh. Technol. 2016, 66, 1209–1221. [Google Scholar] [CrossRef] [Green Version]
- Dai, B.; Yu, W. Energy efficiency of downlink transmission strategies for cloud radio access networks. IEEE J. Sel. Areas Commun. 2016, 34, 1037–1050. [Google Scholar] [CrossRef] [Green Version]
- Zhou, J.; Qiao, Y.; Yang, Z.; Cheng, Q.; Wang, Q.; Guo, M.; Tang, X. Capacity limit for faster-than-Nyquist non-orthogonal frequency-division multiplexing signaling. Sci. Rep. 2017, 7, 3380. [Google Scholar] [CrossRef] [Green Version]
- Xu, T.; Xu, T.; Darwazeh, I. Deep intelligent spectral labelling and receiver signal distribution for optical links. Opt. Express 2021, 29, 39611–39632. [Google Scholar] [CrossRef] [PubMed]
- Beck, A.; Ben-Tal, A.; Tetruashvili, L. A sequential parametric convex approximation method with applications to nonconvex truss topology design problems. J. Glob. Optim. 2010, 47, 29–51. [Google Scholar] [CrossRef]
- 3GPP. Study on channel model for frequencies from 0.5 to 100 GHz. In 3rd Generation Partnership Project (3GPP); Report TR 38.901; 3GPP: Sophia, France, 2018. [Google Scholar]
| Parameter | Value |
|---|---|
| Area | 1000 × 1000 m2 |
| Transmit Power of APs and terminals | 1 W |
| Number of APs | 10–180 |
| Number of UEs in eMBB | 10–20 |
| Number of UEs in mMTC | 1000–4000 |
| System bandwidth B | 18 MHz |
| Number of subcarriers | 2400 |
| Subcarrier bandwidth | 7.5 kHz |
| Subcarriers in an RB | 12 |
| Cyclic prefix length | 100 |
| Centering frequency | 2.0 GHz |
| Height of AP and UE antenna | 10 m and 1.5 m |
| Noise figure (NF) | 9 dB |
| 1.381 × 10−23 J/K | |
| 290 K |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, T.; Zhao, D. Energy Efficiency of User-Centric, Cell-Free Massive MIMO-OFDM with Instantaneous CSI. Entropy 2022, 24, 234. https://doi.org/10.3390/e24020234
Han T, Zhao D. Energy Efficiency of User-Centric, Cell-Free Massive MIMO-OFDM with Instantaneous CSI. Entropy. 2022; 24(2):234. https://doi.org/10.3390/e24020234
Chicago/Turabian StyleHan, Tongzhou, and Danfeng Zhao. 2022. "Energy Efficiency of User-Centric, Cell-Free Massive MIMO-OFDM with Instantaneous CSI" Entropy 24, no. 2: 234. https://doi.org/10.3390/e24020234
APA StyleHan, T., & Zhao, D. (2022). Energy Efficiency of User-Centric, Cell-Free Massive MIMO-OFDM with Instantaneous CSI. Entropy, 24(2), 234. https://doi.org/10.3390/e24020234






