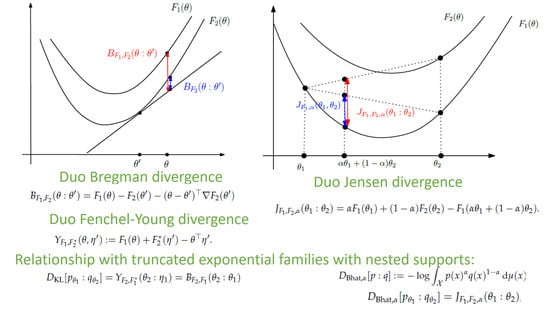
Statistical Divergences between Densities of Truncated Exponential Families with Nested Supports: Duo Bregman and Duo Jensen Divergences
Abstract
:1. Introduction
1.1. Exponential Families
1.2. Truncated Exponential Families with Nested Supports
1.3. Kullback–Leibler Divergence between Exponential Family Distributions
1.4. Kullback–Leibler Divergence between Exponential Family Densities
- if then for all , and
- if then for all ,

1.5. Contributions and Paper Outline
2. Kullback–Leibler Divergence between Different Exponential Families
3. The Duo Fenchel–Young Divergence and Its Corresponding Duo Bregman Divergence

4. Kullback–Leibler Divergence between Distributions of Truncated Exponential Families
5. Bhattacharyya Skewed Divergence between Truncated Densities of an Exponential Family
6. Concluding Remarks
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sundberg, R. Statistical Modelling by Exponential Families; Cambridge University Press: Cambridge, UK, 2019; Volume 12. [Google Scholar]
- Pitman, E.J.G. Sufficient Statistics and Intrinsic Accuracy; Mathematical Proceedings of the cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 1936; Volume 32, pp. 567–579. [Google Scholar]
- Darmois, G. Sur les lois de probabilitéa estimation exhaustive. CR Acad. Sci. Paris 1935, 260, 85. [Google Scholar]
- Koopman, B.O. On distributions admitting a sufficient statistic. Trans. Am. Math. Soc. 1936, 39, 399–409. [Google Scholar] [CrossRef]
- Hiejima, Y. Interpretation of the quasi-likelihood via the tilted exponential family. J. Jpn. Stat. Soc. 1997, 27, 157–164. [Google Scholar] [CrossRef]
- Efron, B.; Hastie, T. Computer Age Statistical Inference: Algorithms, Evidence, and Data Science; Cambridge University Press: Cambridge, UK, 2021; Volume 6. [Google Scholar]
- Akahira, M. Statistical Estimation for Truncated Exponential Families; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Bar-Lev, S.K. Large sample properties of the MLE and MCLE for the natural parameter of a truncated exponential family. Ann. Inst. Stat. Math. 1984, 36, 217–222. [Google Scholar] [CrossRef]
- Shah, A.; Shah, D.; Wornell, G. A Computationally Efficient Method for Learning Exponential Family Distributions. Adv. Neural Inf. Process. Syst. 2021, 34. Available online: https://proceedings.neurips.cc/paper/2021/hash/84f7e69969dea92a925508f7c1f9579a-Abstract.html (accessed on 15 March 2022).
- Keener, R.W. Theoretical Statistics: Topics for a Core Course; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Cover, T.M. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 1999. [Google Scholar]
- Csiszár, I. Eine informationstheoretische Ungleichung und ihre Anwendung auf Beweis der Ergodizitaet von Markoffschen Ketten. Magyer Tud. Akad. Mat. Kutato Int. Koezl. 1964, 8, 85–108. [Google Scholar]
- Azoury, K.S.; Warmuth, M.K. Relative loss bounds for on-line density estimation with the exponential family of distributions. Mach. Learn. 2001, 43, 211–246. [Google Scholar] [CrossRef] [Green Version]
- Rockafellar, R.T. Convex Analysis; Princeton University Press: Princeton, NJ, USA, 2015. [Google Scholar]
- Amari, S.I. Differential-geometrical methods in statistics. Lect. Notes Stat. 1985, 28, 1. [Google Scholar]
- Bregman, L.M. The relaxation method of finding the common point of convex sets and its application to the solution of problems in convex programming. Ussr Comput. Math. Math. Phys. 1967, 7, 200–217. [Google Scholar] [CrossRef]
- Acharyya, S. Learning to Rank in Supervised and Unsupervised Settings Using Convexity and Monotonicity. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 2013. [Google Scholar]
- Blondel, M.; Martins, A.F.; Niculae, V. Learning with Fenchel-Young losses. J. Mach. Learn. Res. 2020, 21, 1–69. [Google Scholar]
- Nielsen, F. An elementary introduction to information geometry. Entropy 2020, 22, 1100. [Google Scholar] [CrossRef] [PubMed]
- Mitroi, F.C.; Niculescu, C.P. An Extension of Young’s Inequality; Abstract and Applied Analysis; Hindawi: London, UK, 2011; Volume 2011. [Google Scholar]
- Jeffreys, H. The Theory of Probability; OUP Oxford: Oxford, UK, 1998. [Google Scholar]
- Nielsen, F.; Nock, R. Sided and symmetrized Bregman centroids. IEEE Trans. Inf. Theory 2009, 55, 2882–2904. [Google Scholar] [CrossRef] [Green Version]
- Nielsen, F. On a variational definition for the Jensen-Shannon symmetrization of distances based on the information radius. Entropy 2021, 23, 464. [Google Scholar] [CrossRef]
- Itakura, F.; Saito, S. Analysis synthesis telephony based on the maximum likelihood method. In Proceedings of the 6th International Congress on Acoustics, Tokyo, Japan, 21–28 August 1968; pp. 280–292. [Google Scholar]
- Del Castillo, J. The singly truncated normal distribution: A non-steep exponential family. Ann. Inst. Stat. Math. 1994, 46, 57–66. [Google Scholar] [CrossRef] [Green Version]
- Burkardt, J. The Truncated Normal Distribution; Technical Report; Department of Scientific Computing Website, Florida State University: Tallahassee, FL, USA, 2014. [Google Scholar]
- Kotz, J.; Balakrishan. Continuous Univariate Distributions, Volumes I and II; John Wiley and Sons: Hoboken, NJ, USA, 1994. [Google Scholar]
- Nielsen, F.; Nock, R. Entropies and cross-entropies of exponential families. In Proceedings of the 2010 IEEE International Conference on Image Processing, Hong Kong, China, 26–29 September 2010; pp. 3621–3624. [Google Scholar]
- Bhattacharyya, A. On a measure of divergence between two statistical populations defined by their probability distributions. Bull. Calcutta Math. Soc. 1943, 35, 99–109. [Google Scholar]
- Nielsen, F.; Boltz, S. The Burbea-Rao and Bhattacharyya centroids. IEEE Trans. Inf. Theory 2011, 57, 5455–5466. [Google Scholar] [CrossRef] [Green Version]
- Hellinger, E. Neue Begründung der Theorie Quadratischer Formen von unendlichvielen Veränderlichen. J. Reine Angew. Math. 1909, 1909, 210–271. [Google Scholar] [CrossRef]
- Rao, C.R. Diversity and dissimilarity coefficients: A unified approach. Theor. Popul. Biol. 1982, 21, 24–43. [Google Scholar] [CrossRef]
- Zhang, J. Divergence function, duality, and convex analysis. Neural Comput. 2004, 16, 159–195. [Google Scholar] [CrossRef] [PubMed]
- Grünwald, P.D. The Minimum Description Length Principle; MIT Press: Cambridge, MA, USA, 2007. [Google Scholar]
- Nielsen, F. The Many Faces of Information Geometry. Not. Am. Math. Soc. 2022, 69. [Google Scholar] [CrossRef]
- Nielsen, F.; Hadjeres, G. Quasiconvex Jensen Divergences and Quasiconvex Bregman Divergences; Workshop on Joint Structures and Common Foundations of Statistical Physics, Information Geometry and Inference for Learning; Springer: Berlin/Heidelberg, Germany, 2020; pp. 196–218. [Google Scholar]
- Emtiyaz Khan, M.; Swaroop, S. Knowledge-Adaptation Priors. arXiv 2021, arXiv:2106.08769. [Google Scholar]





| Quantity | Poisson Family | Geometric Family |
|---|---|---|
| support | ||
| base measure | counting measure | counting measure |
| ordinary parameter | rate | success probability |
| pmf | ||
| sufficient statistic | ||
| natural parameter | ||
| cumulant function | ||
| auxiliary term | ||
| moment | ||
| negentropy | ||
| () |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nielsen, F. Statistical Divergences between Densities of Truncated Exponential Families with Nested Supports: Duo Bregman and Duo Jensen Divergences. Entropy 2022, 24, 421. https://doi.org/10.3390/e24030421
Nielsen F. Statistical Divergences between Densities of Truncated Exponential Families with Nested Supports: Duo Bregman and Duo Jensen Divergences. Entropy. 2022; 24(3):421. https://doi.org/10.3390/e24030421
Chicago/Turabian StyleNielsen, Frank. 2022. "Statistical Divergences between Densities of Truncated Exponential Families with Nested Supports: Duo Bregman and Duo Jensen Divergences" Entropy 24, no. 3: 421. https://doi.org/10.3390/e24030421
APA StyleNielsen, F. (2022). Statistical Divergences between Densities of Truncated Exponential Families with Nested Supports: Duo Bregman and Duo Jensen Divergences. Entropy, 24(3), 421. https://doi.org/10.3390/e24030421