Dissolved Oxygen Concentration Prediction Model Based on WT-MIC-GRU—A Case Study in Dish-Shaped Lakes of Poyang Lake
Abstract
:1. Introduction
2. Modelling
2.1. Wavelet Transform-Based Data Denoising
- The optimal wavelet functions for different feature variables are selected to decompose the signals. In this study, the Daubechies (db), Symlet (sym), Coiflet (coif) wavelet functions were selected.
- The threshold is selected. Thresholds should be set to the high-frequency coefficients for quantification. A proper threshold should be set for each layer, and soft-thresholding is performed on high-frequency coefficients on each layer to smooth the signals.
- The wavelets are restructured. The wavelets of the signals are restructured based on the high-frequency coefficient of each layer and the low-frequency coefficient of the last layer.
- The denoising effect is evaluated. Two indicators, i.e., the signal-noise ratio (SNR) and the root-mean-square error (RMSE), are selected to evaluate the denoising effect. The wavelet function with a larger SNR and a smaller RMSE is considered to have better denoising performance.
2.2. Maximum Information Coefficient-Based Feature Selection
2.3. Construction of the WT-MIC-GRU Prediction Model
2.3.1. Gated Recurrent Unit
2.3.2. WT-MIC-GRU Prediction Model
3. Acquisition of Sample Data
4. Results and Analysis
4.1. Data Pretreatment
4.2. Feature Selection
- The i and j were given, and scatter diagram composed by X and Y were partitioned into i columns and j lines, and the maximal mutual information was obtained;
- The maximal mutual information was normalized;
- The maximal mutual information under different scales was considered as the MIC value.
4.3. GRU Model Training and Evaluation
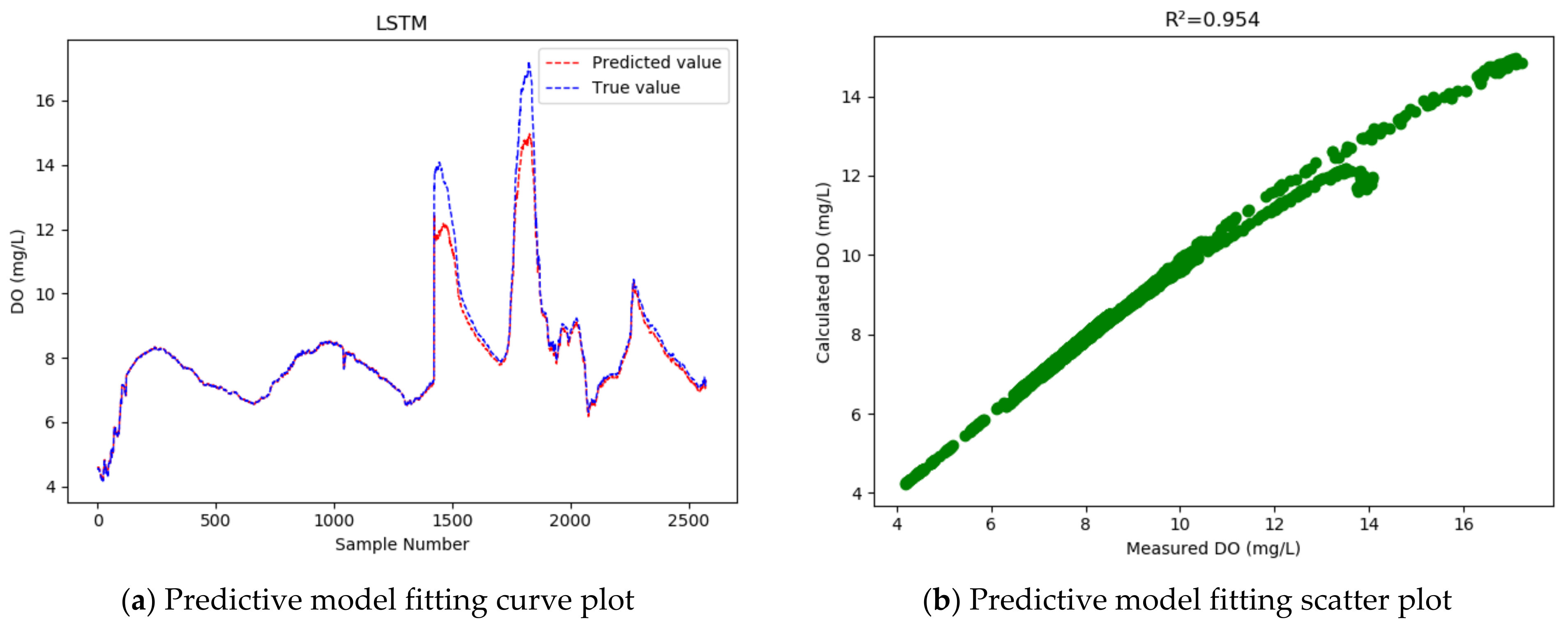
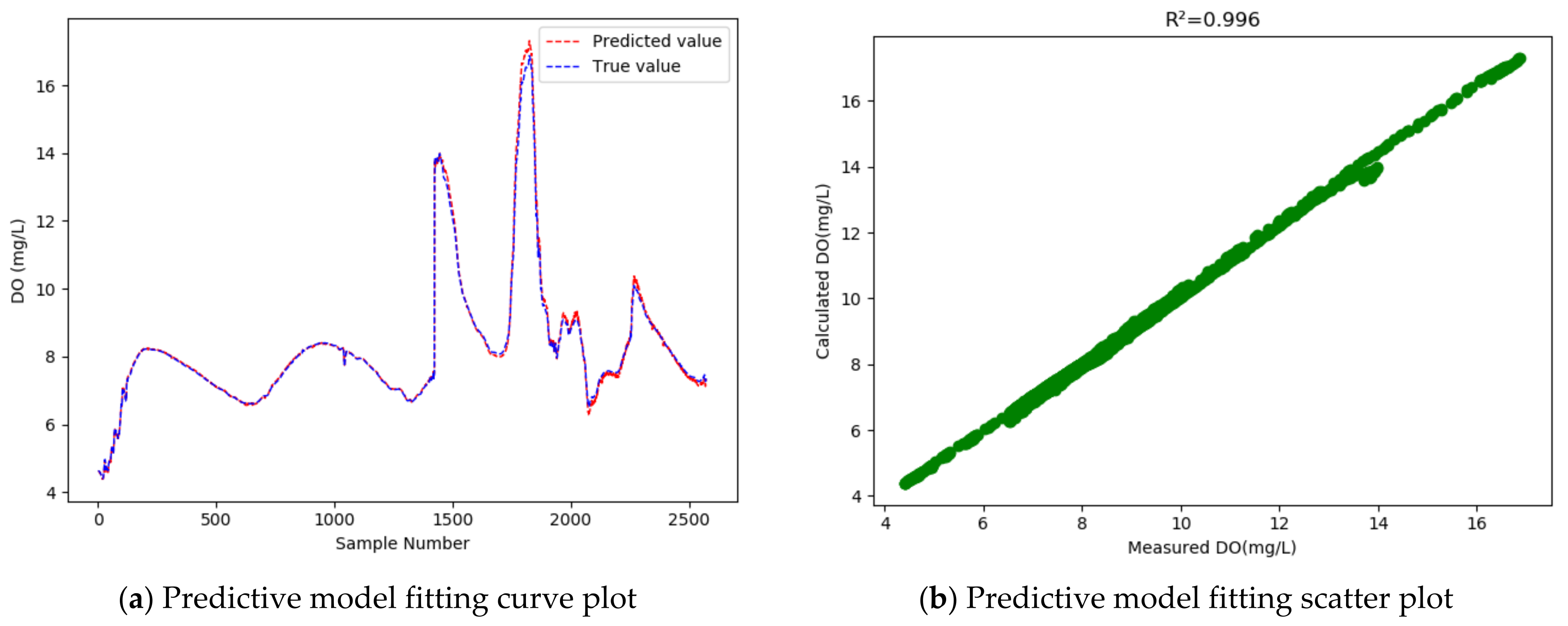
4.4. Comparative Experiments
5. Conclusions
- Compared with the LSTM model, the GRU model achieved higher accuracy in the prediction of the dissolved oxygen concentration in the dish-shaped Poyang Lake, with the coefficient of determination increased from 0.954 to 0.996; meanwhile, the RMSE was reduced by 0.343, and the MAPE dropped from 1.495% to 0.712%, indicating that the GRU model achieves a better fitting effect than LSTM.
- The GRU model, after introducing WT method for data denoising and the MIC method for feature selection, increased the R2 of the conventional GRU model from 0.996 to 0.998, and reduced the RMSE by 0.041, indicating improved prediction accuracy. It also indicates that data denoising and feature selection could considerably improve the model’s performance.
- The GRU model that incorporated the WT for data denoising, but not feature selection, achieved an MAPE of 0.666%, and when the feature selection method was introduced, the MAPE rose to 0.723%, which means that feature selection had a positive impact on the fitting effect. Judging by all the evaluation indicators, our proposed model achieved the best performance among all models that were compared.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, Y.C.; Tie-Song, H.U.; Chen, J.; Ji-Jun, X.U.; Zhou, Y.L. Application of neural network model coupled with dynamic equation in water quality prediction. J. Yangtze River Sci. Res. Inst. 2017, 34, 1–5. [Google Scholar]
- Khan, A.U.; Rahman, H.U.; Ali, L.; Khan, M.I.; Ahmad, I. Complex linkage between watershed attributes and surface water quality: Gaining insight via path analysis. Civ. Eng. J. 2021, 7, 701–712. [Google Scholar] [CrossRef]
- Zhou, Z.Q.; Zou, G.F.; Wang, L. A water quality prediction model based on time series using ARIMA/RBF-NN. Bull. Sci. Technol. 2017, 33, 236–240. [Google Scholar]
- Correa-González, J.C.; Chávez-Parga, M.D.C.; Cortés, J.A.; Pérez-Munguía, R.M. Photosynthesis, respiration and reaeration in a stream with complex dissolved oxygen pattern and temperature dependence. Ecol. Model. 2014, 273, 220–227. [Google Scholar] [CrossRef]
- Terzhevik, A.; Golosov, S.; Palshin, N.; Mitrokhov, A.; Zdorovennov, R.; Zdorovennova, G.; Kirillin, G.; Shipunova, E.; Zverev, I. Some features of the thermal and dissolved oxygen structure in boreal, shallow ice-covered lake vendyurskoe, Russia. Aquat. Ecol. 2009, 43, 617–627. [Google Scholar] [CrossRef]
- Abba, S.I.; Linh, N.; Abdullahi, J.; Ali, S.; Anh, D.T. Hybrid machine learning ensemble techniques for modeling dissolved oxygen concentration. IEEE Access 2020, 8, 157218–157237. [Google Scholar] [CrossRef]
- Heddam, S.; Kisi, O. Modelling daily dissolved oxygen concentration using least square support vector machine, multivariate adaptive regression splines and m5 model tree. J. Hydrol. 2018, 559, 499–509. [Google Scholar] [CrossRef]
- Ji, X.; Xu, S.; Dahlgren, R.A.; Zhang, M. Prediction of dissolved oxygen concentration in hypoxic river systems using support vector machine: A case study of wen-rui tang river, china. Environ. Sci. Pollut. Res. 2017, 24, 16062–16076. [Google Scholar] [CrossRef]
- Keshtegar, B.; Heddam, S.; Hosseinabadi, H. The employment of polynomial chaos expansion approach for modeling dissolved oxygen concentration in river. Environ. Earth Sci. 2019, 78, 1–18. [Google Scholar] [CrossRef]
- Li, W.; Fang, H.; Qin, G.; Tan, X.; Li, S. Concentration estimation of dissolved oxygen in pearl river basin using input variable selection and machine learning techniques. Sci. Total Environ. 2020, 731, 139099. [Google Scholar] [CrossRef]
- Nacar, S.; Bayram, A.; Baki, O.T.; Kankal, M.; Aras, E. Spatial forecasting of dissolved oxygen concentration in the eastern black sea basin, turkey. Water 2020, 12, 1041. [Google Scholar] [CrossRef] [Green Version]
- Nacar, S.; Mete, B.; Bayram, A. Estimation of daily dissolved oxygen concentration for river water quality using conventional regression analysis, multivariate adaptive regression splines, and treenet techniques. Environ. Monit. Assess. 2020, 192, 752. [Google Scholar] [CrossRef] [PubMed]
- Antanasijević, D.; Pocajt, V.; Povrenović, D.; Perić-Grujić, A.; Ristić, M. Modelling of dissolved oxygen content using artificial neural networks: Danube river, north serbia, case study. Environ. Sci. Pollut. Res. 2013, 20, 9006–9013. [Google Scholar] [CrossRef] [PubMed]
- Luo, X.K.; He, Y.X.; Liu, P.; Li, W. Application of the hybrid ARIMA-SVR method in water quality prediction. J. Yangtze River Sci. Res. Inst. 2020, 264, 25–31. [Google Scholar]
- Zhu, N.Y.; Wu, H.; Yin, D.H.; Wang, Z.Q.; Jiang, Y.N.; Guo, Y. Optimization of DO estimation in crab ponds using LSTM. Smart Agric. 2019, 3, 74–83. [Google Scholar]
- Olyaie, E.; Abyaneh, H.Z.; Mehr, A.D. A comparative analysis among computational intelligence techniques for dissolved oxygen prediction in delaware river. Geosci. Front. 2017, 8, 517–527. [Google Scholar] [CrossRef] [Green Version]
- Ai, J.Y.; Zheng, J.W.; Liu, G.X. DO content prediction based on small sample set using GF-LSTM and GAN models. J. Saf. Environ. 2021, 21, 426–434. [Google Scholar]
- Wang, Y.Y. Research on LSTM-Based Water Quality Prediction Methods. Doctoral Dissertation, Nanjing University of Posts and Telecommunications, Nanjing, China, 2019. [Google Scholar]
- Ahmed, A.A.M.; Chowdhury, M.A.I.; Ahmed, O.; Sutradhar, A. Development of Dissolved Oxygen Forecast Model Using Hybrid Machine Learning Algorithm with Hydro-Meteorological Variables. Res. Sq. 2021, in press. [Google Scholar]
- Ahmed, A.A.M. Prediction of dissolved oxygen in surma river by biochemical oxygen demand and chemical oxygen demand using the artificial neural networks (anns)-sciencedirect. J. King Saud Univ.-Eng. Sci. 2017, 29, 151–158. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, A.; Shah, S. Application of adaptive neuro-fuzzy inference system (anfis) to estimate the biochemical oxygen demand (bod) of surma river. J. King Saud Univ.-Eng. Sci. 2017, 29, 237–243. [Google Scholar] [CrossRef] [Green Version]
- Zhu, N.; Xu, L.; Liu, Z.; Kai, H.; Guo, Y. Deep learning for smart agriculture: Concepts, tools, applications, and opportunities. Int. J. Agric. Biol. Eng. 2018, 11, 21–28. [Google Scholar] [CrossRef]
- Fischer, T.; Krauss, C. Deep learning with long short-term memory networks for financial market predictions. Eur. J. Oper. Res. 2017, 270, 654–669. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Peng, L.; Yao, X.; Cui, S.; Hu, Y.; You, C.; Chi, T. Long short-term memory neural network for air pollutant concentration predictions: Method development and evaluation. Environ. Pollut. 2017, 231, 997–1004. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.Y.; Fang, X.M.; Mei, S.Y.; Yu, H.H.; Yang, L. A WT-CNN-LSTM model for DO content prediction. Trans. Chin. Soc. Agric. Mach. 2020, 51, 291–298. [Google Scholar]
- Liu, J.J.; Zhuang, H.; Tie, Z.X.; Cheng, X.N.; Ding, C.F. A multi-factor water quality prediction LSTM model using K-similarity denoising. Comput. Syst. Appl. 2019, 28, 228–234. [Google Scholar]
- Xie, M.L. Short-term prediction of power loads of residential buildings based on the LSTM model. Guangdong Electr. Power 2019, 32, 108–114. [Google Scholar]
- Zheng, X.D.; Chen, T.W.; Wang, L.; Duan, Q.D.; Gan, R. Dam deformation prediction based on the EEMD-PCA-ARIMA model. J. Yangtze River Sci. Res. Inst. 2020, 37, 57–63. [Google Scholar]
- Hu, Z.P.; Zhang, Z.F.; Liu, Y.Z.; Ji, W.T.; Ge, G. The role and significance of the disk-shaped lake in the Poyang Lake wetland ecosystem. Jiangxi Water Conserv. Sci. Technol. 2015, 41, 317–323. [Google Scholar]
- Einstein, A.; Henao, R.G.; Delicado, P.; Mateu, J.; Pearson, I.F.; Henao, R.G.; Styan, G.P.H.; Ashcraft, C.; Grimes, R.G.; Lewis, J.G. An Introduction to Wavelets. IEEE Comput. Sci. Eng. 2015, 2, 50–61. [Google Scholar]
- Zhu, H.; Kwok, T.Y.; Qu, L. Improving de-noising by coefficient de-noising and dyadic wavelet transform. In Proceedings of the 2002 International Conference on Pattern Recognition, Quebec City, QC, Canada, 11–15 August 2002. [Google Scholar]
- Li, L.R. Generation, development and application of wavelet analysis methods. China Water Transp. (Theory Ed.) 2007, 5, 96–98. [Google Scholar]
- Huang, R.; Jiang, W.; Sun, G. Manifold-based constraint laplacian score for multi-label feature selection. Pattern Recognit. Lett. 2018, 112, 346–352. [Google Scholar] [CrossRef]
- Mursalin, M.; Zhang, Y.; Chen, Y.; Chawla, N.V. Automated epileptic seizure detection using improved correlation-based feature selection with random forest classifier. Neurocomputing 2017, 241, 204–214. [Google Scholar] [CrossRef]
- Reshef, D.N.; Reshef, Y.A.; Finucane, H.K.; Grossman, S.R.; Mcvean, G.; Turnbaugh, P.J.; Lander, E.S.; Mitzenmacher, M.; Sabeti, P.C. Detecting Novel Associations in Large Data Sets. Science 2011, 334, 1518–1524. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Reshef, Y.A.; Reshef, D.N.; Finucane, H.K.; Sabeti, P.C.; Mitzenmacher, M.D. Measuring dependence powerfully and equitably. J. Mach. Learn. Res. 2016, 17, 7406–7468. [Google Scholar]
- Jin, R.X.; Lou, D.S.; Huang, H.D.; Mao, H.L. Data cleaning method for condition monitoring of hydropower units. China Rural. Water Conserv. Hydropower 2022. Available online: https://kns.cnki.net/kcms/detail/42.1419.TV.20220119.1056.015.html (accessed on 19 January 2022).
- Kingma, D.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Chi, D.W.; Huang, Q.; Liu, L.Z.; Fang, C.Y. Research on Prediction of Dissolved Oxygen Content in Dish-shaped Lake Based on PCA-MIC-LSTM. Yangtze River 2021. Available online: https://kns.cnki.net/kcms/detail/42.1202.TV.20211119.1643.002.html (accessed on 22 November 2021).
- Sun, L.Q.; Wu, Y.H.; Sun, X.B.; Zhang, S. Prediction of dissolved oxygen content in pond water based on IBAS and LSTM network. Chin. J. Agric. Mach. (S1) 2021, 61, 252–260. [Google Scholar]
- Chen, Y.Y.; Fang, X.M.; Mei, S.Y.; Yu, H.H.; Yang, L. Dissolved oxygen content prediction model based on wt-cnn-lstm. J. Agric. Mach. 2020, 51, 8. [Google Scholar]
- Huang, H.L. Analysis of Dissolved Oxygen Distribution Characteristics and Related Factors in Shitang Lake. J. Anhui Jianzhu Univ. 2015, 23, 5. [Google Scholar]
- Hu, S.J. Discussion on the stability of dissolved oxygen value in deep-water lakes. China Environ. Monit. 2001, 15, 62. [Google Scholar]






| Atmospheric Temperature (°C) | Wind Direction (Degree) | Wind Speed (m/s) | Atmospheric Pressure (KPa) | Relative Humidity (%) | Water Temperature (°C) | pH (/) | Conductivity (µS/cm) | Measured Water Depth (m) | Redox Potential (mv) | Dissolved Oxygen Concentration (mg/L) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | 23.11 | 144.42 | 3.37 | 1009.9 | 81 | 23.46 | 6.87 | 107.14 | 0.36 | 0.27 | 7.48 |
| Maximum | 36.89 | 359 | 13.2 | 1029 | 96 | 31.56 | 9.18 | 151.9 | 0.63 | −0.1 | 17.23 |
| Minimum | 12.28 | 0 | 0.03 | 1001.7 | 49 | 16.4 | 5.79 | 93.2 | 0.25 | −0.4 | 4.17 |
| Standard deviation | 4.55 | 92.7 | 2.10 | 5.75 | 9.37 | 3.01 | 0.38 | 15.72 | 0.07 | 0.04 | 1.53 |
| Coefficient of variation | 19.69% | 64.19% | 62.31% | 0.57% | 11.57% | 12.83% | 5.53% | 14.67% | 19.44% | 14.81% | 20.45% |
| Feature Variables | Evaluation Indicators | Coif5 | Sym10 | Db8 |
|---|---|---|---|---|
| Atmospheric temperature | SNR/db | 25.976 | 27.162 | 23.85 |
| RMSE | 0.225 | 0.196 | 0.282 | |
| Wind direction | SNR/db | 19.354 | 19.295 | 18.383 |
| RMSE | 9.623 | 9.693 | 10.655 | |
| Wind speed | SNR/db | 21.667 | 20.58 | 20.79 |
| RMSE | 0.169 | 0.191 | 0.184 | |
| Atmospheric pressure | SNR/db | 36.214 | 36.936 | 35.494 |
| RMSE | 0.089 | 0.082 | 0.096 | |
| Relative humidity | SNR/db | 24.052 | 23.956 | 22.325 |
| RMSE | 0.577 | 0.583 | 0.683 | |
| Water temperature | SNR/db | 29.468 | 30.894 | 27.133 |
| RMSE | 0.101 | 0.085 | 0.13 | |
| pH scale | SNR/db | 19.413 | 22.115 | 19.162 |
| RMSE | 0.039 | 0.029 | 0.039 | |
| Conductivity | SNR/db | 28.376 | 28.56 | 26.704 |
| RMSE | 0.597 | 0.585 | 0.722 | |
| Measured water depth | SNR/db | 33.009 | 32.887 | 31.849 |
| RMSE | 0.002 | 0.002 | 0.002 | |
| Redox potential | SNR/db | 18.102 | 18.271 | 17.947 |
| RMSE | 0.005 | 0.005 | 0.005 | |
| Dissolved oxygen | SNR/db | 20.926 | 22.161 | 19.233 |
| RMSE | 0.134 | 0.116 | 0.159 |
| Features | Correlation with Dissolved Oxygen |
|---|---|
| Atmospheric temperature | 0.38 |
| Wind direction | 0.19 |
| Wind speed | 0.12 |
| Atmospheric pressure | 0.27 |
| Relative humidity | 0.49 |
| Water temperature | 0.33 |
| pH scale | 0.53 |
| Conductivity | 0.37 |
| Measured water depth | 0.23 |
| Redox potential | 0.073 |
| Model | RMSE | MAPE% | R2 | WIA |
|---|---|---|---|---|
| LSTM | 0.471 | 1.495% | 0.954 | 0.986 |
| GRU | 0.128 | 0.712% | 0.996 | 0.999 |
| GRU-WT | 0.126 | 0.666% | 0.996 | 0.999 |
| WT-MIC-GRU | 0.087 | 0.723% | 0.998 | 1.000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chi, D.; Huang, Q.; Liu, L. Dissolved Oxygen Concentration Prediction Model Based on WT-MIC-GRU—A Case Study in Dish-Shaped Lakes of Poyang Lake. Entropy 2022, 24, 457. https://doi.org/10.3390/e24040457
Chi D, Huang Q, Liu L. Dissolved Oxygen Concentration Prediction Model Based on WT-MIC-GRU—A Case Study in Dish-Shaped Lakes of Poyang Lake. Entropy. 2022; 24(4):457. https://doi.org/10.3390/e24040457
Chicago/Turabian StyleChi, Dianwei, Qi Huang, and Lizhen Liu. 2022. "Dissolved Oxygen Concentration Prediction Model Based on WT-MIC-GRU—A Case Study in Dish-Shaped Lakes of Poyang Lake" Entropy 24, no. 4: 457. https://doi.org/10.3390/e24040457





