Clarifying How Degree Entropies and Degree-Degree Correlations Relate to Network Robustness
Abstract
:1. Introduction
2. Background
2.1. Network Robustness
2.2. Heterogeneity Measures
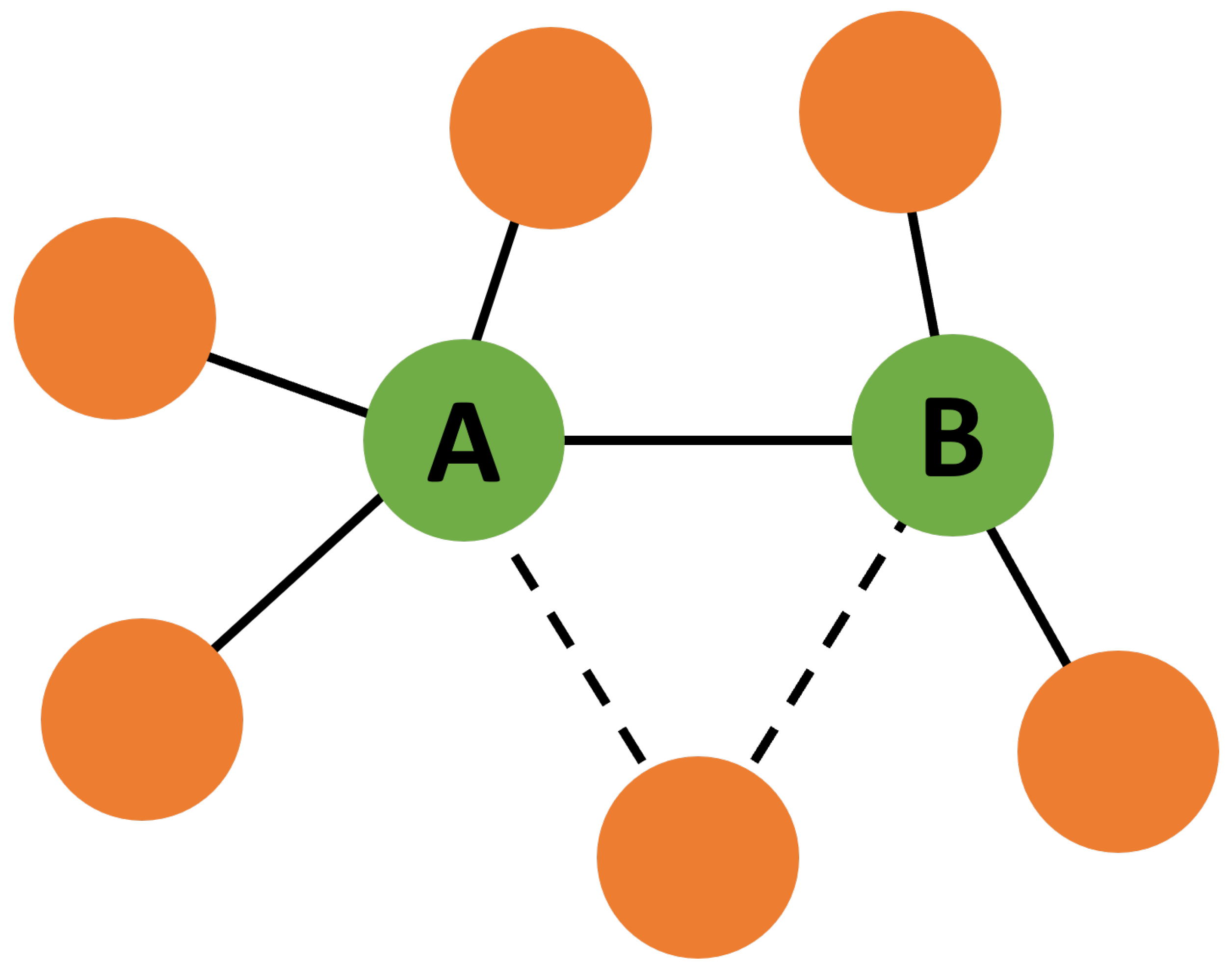
2.3. Mutual Information
2.4. Probability Distributions
3. Results
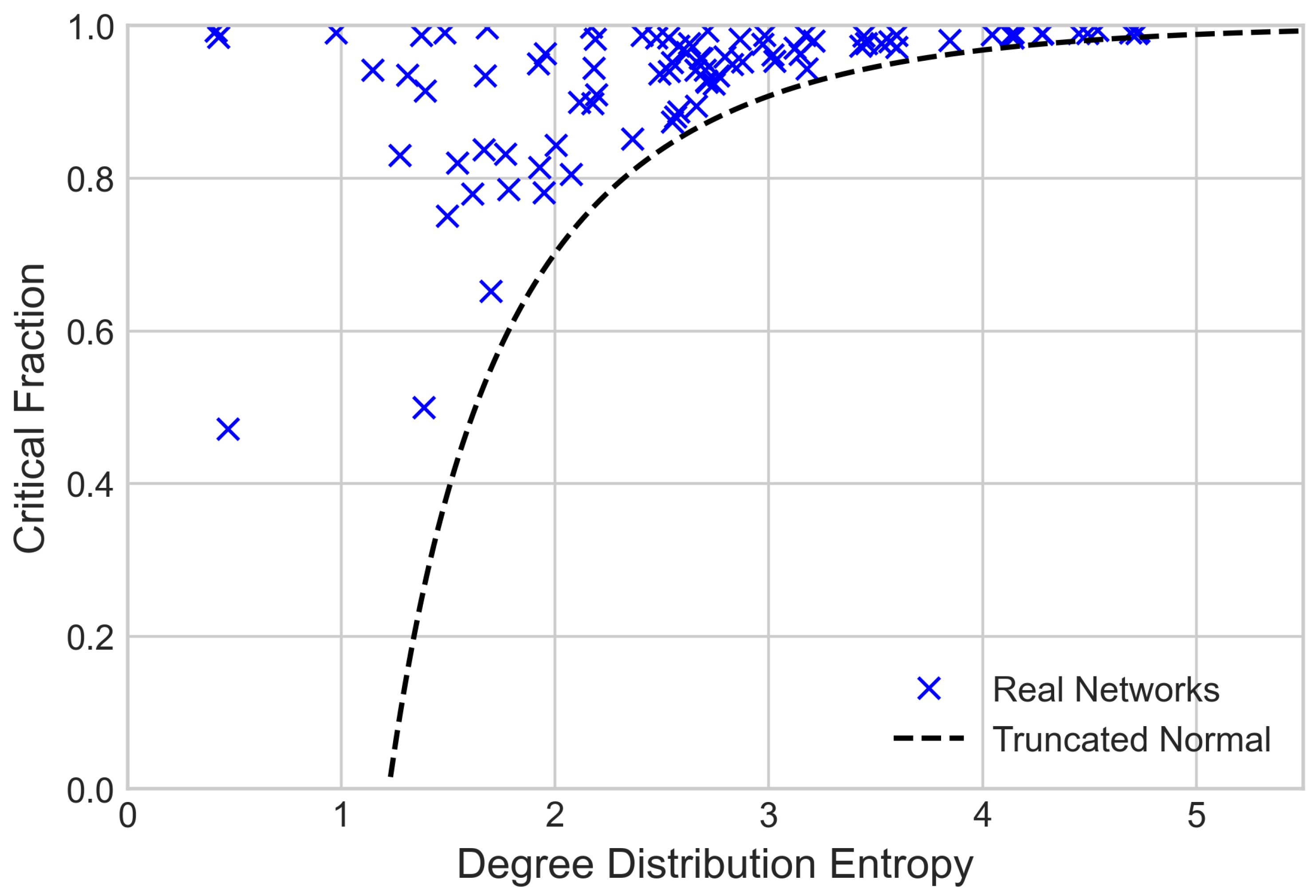
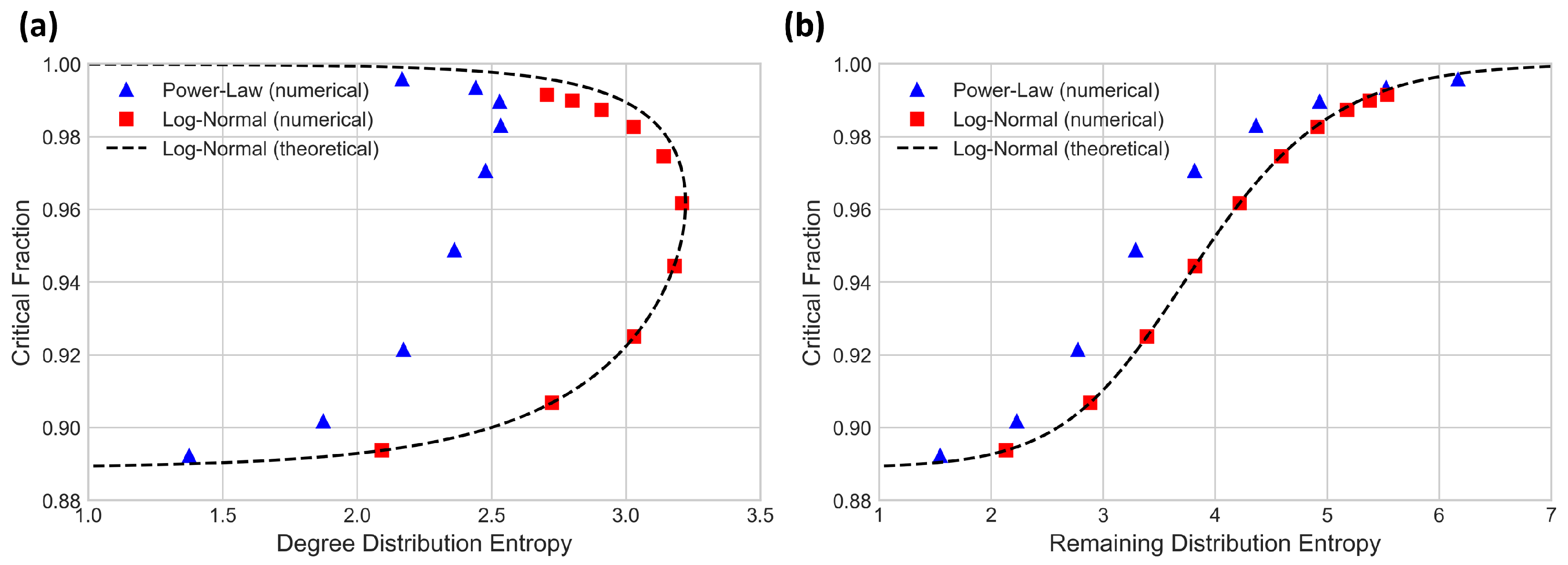
3.1. The Entropy-Robustness Plane
3.2. Distribution Entropies and Robustness
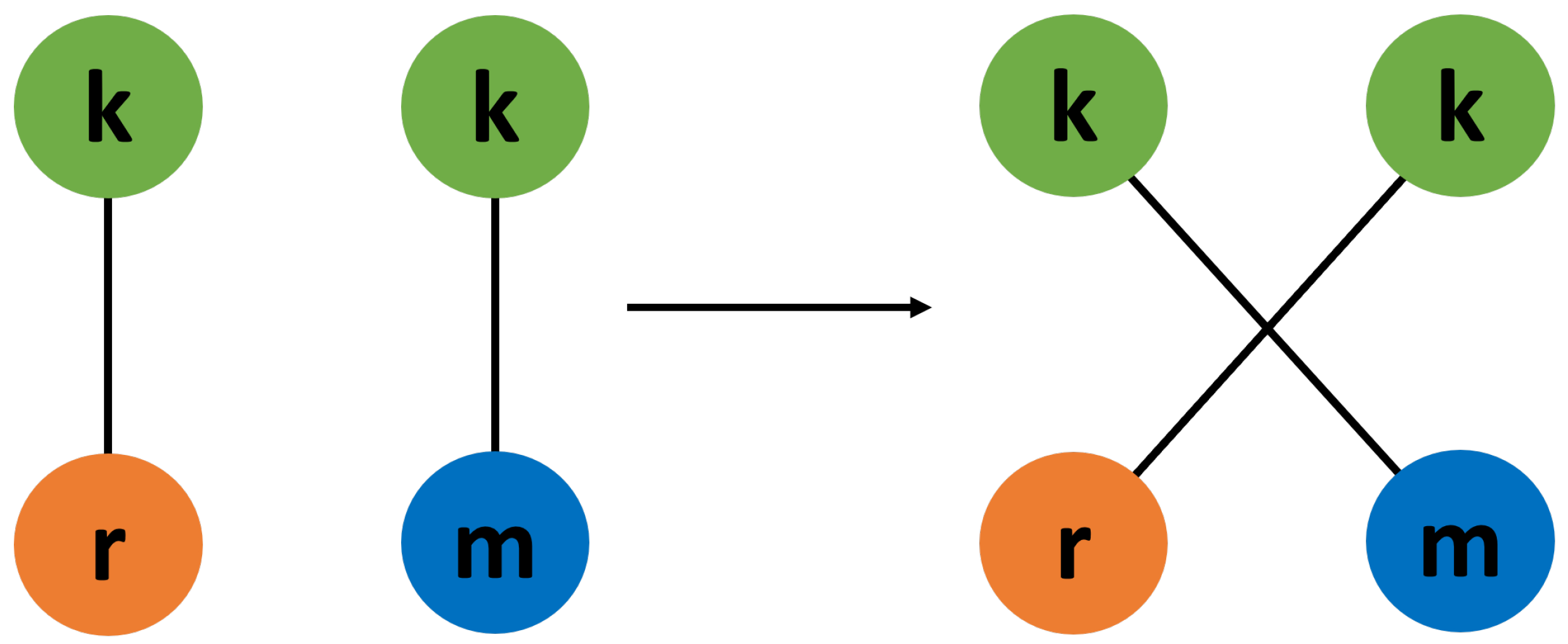
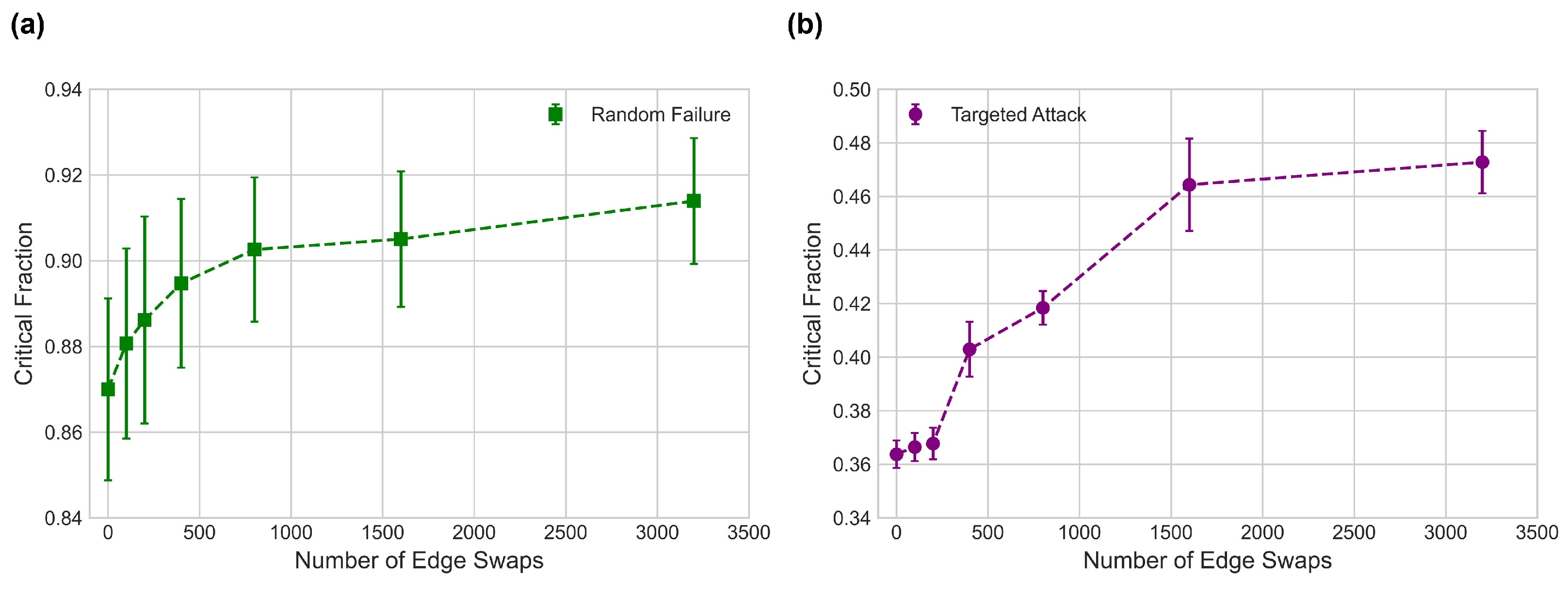
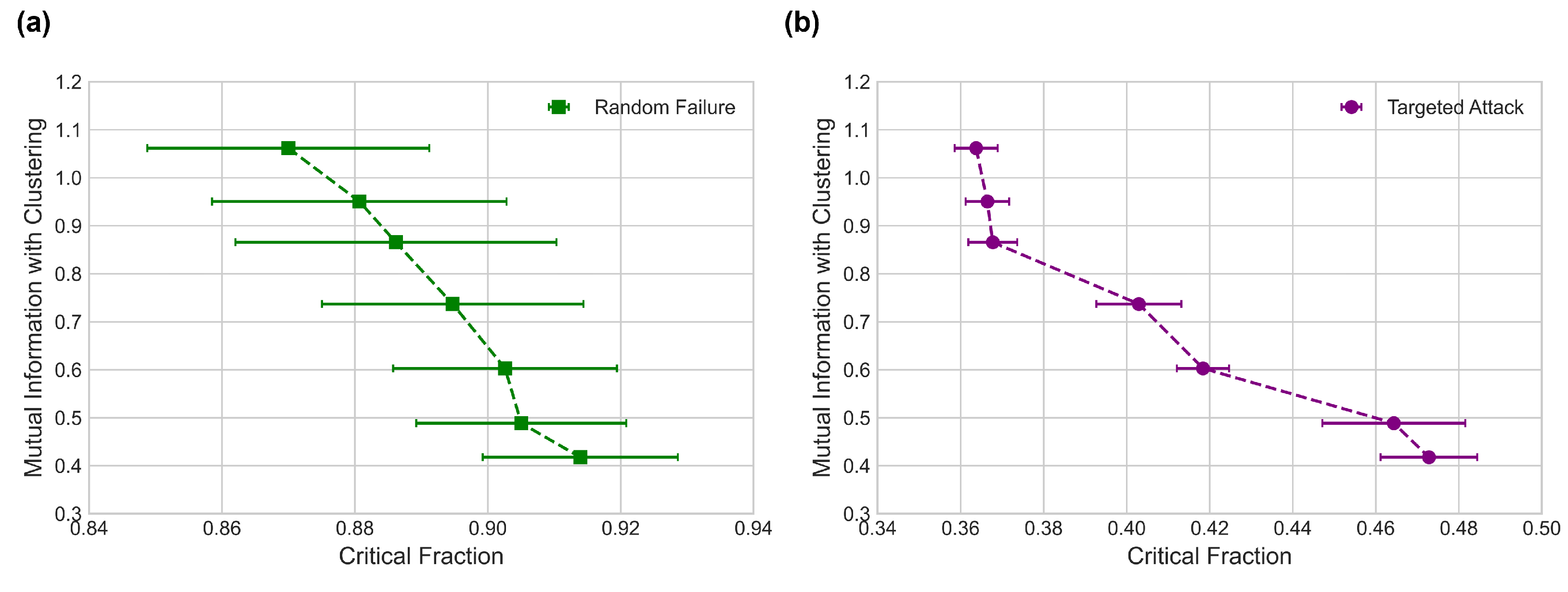
3.3. Mutual Information and Robustness
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mason, O.; Verwoerd, M. Graph theory and networks in biology. IET Syst. Biol. 2007, 1, 89–119. [Google Scholar] [CrossRef]
- Besson, M.; Delmas, E.; Poisot, T.; Gravel, D. Complex ecological networks. Encycl. Ecol. 2019, 1, 536–545. [Google Scholar]
- Freeman, L. The Development of Social Network Analysis: A Study in the Sociology of Science; Empirical Press: New York, NY, USA, 2004. [Google Scholar]
- Souma, W.; Fujiwara, Y.; Aoyama, H. Complex networks and economics. Physica A 2003, 324, 396–401. [Google Scholar] [CrossRef]
- Costa, L.; Rodrigues, F.; Travieso, G.; Boas, P. Characterization of complex networks: A survey of measurements. Adv. Phys. 2007, 56, 167–242. [Google Scholar] [CrossRef]
- Shannon, C. A mathematical theory of communication. Bell Syst. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Jaynes, E. Information theory and statistical mechanics. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Albert, R.; Barabási, A. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47–97. [Google Scholar] [CrossRef]
- Carpi, L.; Rosso, O.; Saco, P.; Ravetti, M. Analyzing complex networks evolution through information theory quantifiers. Phys. Lett. A 2011, 375, 801–804. [Google Scholar] [CrossRef]
- Demetrius, L.; Manke, T. Robustness and network evolution—An entropic principle. Physica A 2005, 346, 682–696. [Google Scholar] [CrossRef]
- Bianconi, G. Entropy of network ensembles. Phys. Rev. E 2009, 79, 036114. [Google Scholar] [CrossRef]
- Anand, K.; Bianconi, G. Entropy measures for networks: Toward an information theory of complex topologies. Phys. Rev. E 2009, 80, 045102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Anand, K.; Bianconi, G. Gibbs entropy of network ensembles by cavity methods. Phys. Rev. E 2010, 82, 011116. [Google Scholar] [CrossRef] [PubMed]
- Radicchi, F.; Krioukov, D.; Hartle, H.; Bianconi, G. Classical information theory of networks. J. Phys. Complex. 2020, 1, 025001. [Google Scholar] [CrossRef]
- Rosvall, M.; Bergstrom, C. An information-theoretic framework for resolving community structure in complex networks. Proc. Natl. Acad. Sci. USA 2007, 104, 7327–7331. [Google Scholar] [CrossRef]
- Oehlers, M.; Fabian, B. Graph metrics for network robustness a survey. Mathematics 2021, 9, 895. [Google Scholar] [CrossRef]
- Albert, R.; Jeong, H.; Barabási, A. Error and attack tolerance of complex networks. Nature 2000, 406, 378–382. [Google Scholar] [CrossRef]
- Cohen, R.; Erez, K.; Avraham, D.b.; Havlin, S. Resilience of the internet to random breakdowns. Phys. Rev. Lett. 2000, 85, 4626–4628. [Google Scholar] [CrossRef] [PubMed]
- Estrada, E. Quantifying network heterogeneity. Phys. Rev. E 2010, 82, 066102. [Google Scholar] [CrossRef] [PubMed]
- Molloy, M.; Reed, B. A Critical Point For Random Graphs with a Given Degree Sequence. Random Struct. Algorithms 1995, 6, 161–180. [Google Scholar] [CrossRef]
- Wang, B.; Tang, H.; Xiu, Z. Entropy Optimization of Scale-Free Networks Robustness to Random Failures. Physica A 2006, 363, 591–596. [Google Scholar] [CrossRef]
- Solé, R.; Valverde, S. Information Theory of Complex Networks: On Evolution and Architectural Constraints. In Complex Networks; Springer: Berlin/Heidelberg, Germany, 2004; pp. 189–207. [Google Scholar]
- Newman, M. Assortative mixing in networks. Phys. Rev. Lett. 2002, 89, 208701. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Noldus, R.; Mieghem, P.V. Assortativity in complex networks. J. Complex Netw. 2015, 3, 507–542. [Google Scholar] [CrossRef]
- Schneider, C.; Moreira, A.; Andrade, J.; Havlin, S.; Herrmann, H. Mitigation of malicious attacks on networks. Proc. Natl. Acad. Sci. USA 2011, 108, 3838–3841. [Google Scholar] [CrossRef] [PubMed]
- Latora, V.; Marchiori, M. Efficient behavior of small-world networks. Phys. Rev. Lett. 2001, 87, 198701. [Google Scholar] [CrossRef] [PubMed]
- Bellingeri, M.; Cassi, D.; Vincenzi, S. Efficiency of attack strategies on complex model and real-world networks. Physica A 2014, 414, 174–180. [Google Scholar] [CrossRef]
- Iyer, S.; Killingback, T.; Sundaram, B.; Wang, Z. Attack robustness and centrality of complex networks. PLoS ONE 2013, 8, e59613. [Google Scholar]
- Newman, M. Chapter 13.2: The configuration model. In Networks: An Introduction; Oxford University Press: Oxford, UK, 2010; pp. 434–445. [Google Scholar]
- Newman, M.; Ziff, R. A fast Monte Carlo algorithm for site or bond percolation. Phys. Rev. E 2001, 64, 016706. [Google Scholar] [CrossRef] [PubMed]
- Cover, T.; Thomas, J. Chapter 2: Entropy, relative entropy and mutual information. In Elements of Information Theory; Wiley-Interscience: New York, NY, USA, 2006; pp. 13–55. [Google Scholar]
- Barabási, A.; Bonabeau, E. Scale-free networks. Sci. Am. 2003, 288, 60–69. [Google Scholar] [CrossRef]
- Goh, K.; Oh, E.; Jeong, H.; Kahng, B.; Kim, D. Classification of scale-free networks. Proc. Natl. Acad. Sci. USA 2002, 99, 12583–12588. [Google Scholar] [CrossRef]
- Albert, R. Scale-free networks in cell biology. J. Cell Sci. 2005, 118, 4947–4957. [Google Scholar] [CrossRef]
- Mitzenmacher, M. A Brief History of Generative Models for Power Law and Lognormal Distributions. Internet Math. 2003, 1, 226–251. [Google Scholar] [CrossRef]
- Broido, A.; Clauset, A. Scale-free networks are rare. Nat. Commun. 2019, 10, 1017. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Holme, P. Rare and everywhere: Perspectives on scale-free networks. Nat. Commun. 2019, 10, 12. [Google Scholar] [CrossRef] [PubMed]
- Clauset, A.; Shalizi, C.; Newman, M. Power-law distributions in empirical data. SIAM Rev. 2009, 51, 661–703. [Google Scholar] [CrossRef]
- Thomopoulos, N. Chapter 9: Lognormal. In Statistical Distributions: Applications and Parameter Estimates; Springer International Publishing: Berlin, Germany, 2017; pp. 77–84. [Google Scholar]
- Johnson, N.; Kotz, S.; Balakrishnan, N. Chapter 13: Normal distributions. In Continuous Univariate Distributions, 2nd ed.; Wiley Series in Probability and Statistics; Wiley: New York, NY, USA, 1994; Volume 1. [Google Scholar]
- Orsini, C.; Dankulov, M.M.; Simon, P.C.; Jamakovic, A.; Mahadevan, P.; Vahdat, A.; Bassler, K.; Toroczkai, Z.; Boguñá, M.; Caldarelli, G.; et al. Quantifying randomness in real networks. Nat. Commun. 2015, 6, 10. [Google Scholar] [CrossRef] [PubMed]
- Freeman, L.C. A set of measures of centrality based on betweenness. Sociometry 1977, 40, 35–41. [Google Scholar] [CrossRef]
- Rozemberczki, B.; Davies, R.; Sarkar, R.; Sutton, C. Gemsec: Graph embedding with self clustering. In Proceedings of the 2019 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining, Vancouver, BC, Canada, 27–30 August 2019; Association for Computing Machinery: New York, NY, USA, 2019; pp. 65–72. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jones, C.; Wiesner, K. Clarifying How Degree Entropies and Degree-Degree Correlations Relate to Network Robustness. Entropy 2022, 24, 1182. https://doi.org/10.3390/e24091182
Jones C, Wiesner K. Clarifying How Degree Entropies and Degree-Degree Correlations Relate to Network Robustness. Entropy. 2022; 24(9):1182. https://doi.org/10.3390/e24091182
Chicago/Turabian StyleJones, Chris, and Karoline Wiesner. 2022. "Clarifying How Degree Entropies and Degree-Degree Correlations Relate to Network Robustness" Entropy 24, no. 9: 1182. https://doi.org/10.3390/e24091182
APA StyleJones, C., & Wiesner, K. (2022). Clarifying How Degree Entropies and Degree-Degree Correlations Relate to Network Robustness. Entropy, 24(9), 1182. https://doi.org/10.3390/e24091182





