Enthalpy-Entropy Compensation Effect in Saturated Solutions on an Example of Polynuclear Aromatics According to Thermodynamics at Melting Temperature
Abstract
:1. Introduction
2. Equations Describing Saturated Solutions in Terms of Temperature
3. Results
3.1. Objective of the Work
- depending on the purpose of the study, ideal solutions are considered, where the activity coefficient is omitted (ln (γ) = 0) [5,27,35,36,37,38,39,40,41,42,43,44] in many works, mainly for pharmacy, the molar fraction x = on the left side of the Equation (11) is referred to as CLFR (Crystal-Liquid Fugacity Ratio) [39,41,43,44],
3.2. The Thermodynamic Aspect of the A&M Equation
3.3. Correlations Using Known Activity Coefficients
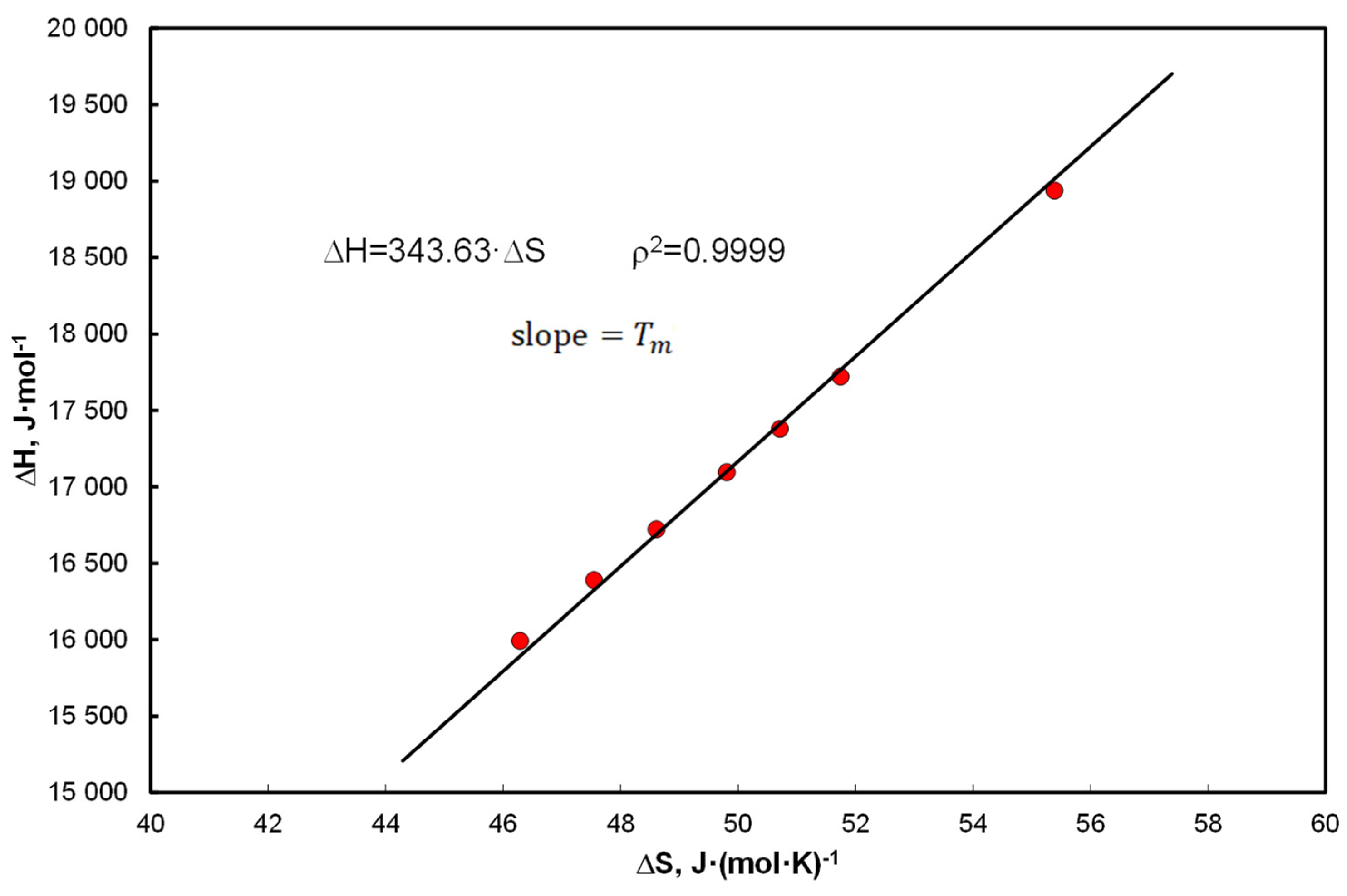
- The thermodynamic aspect of Equation (15) leads to EEC as shown in Figure 1, and at the same time the A&M equation is itself compensated by Equation (27).
- For this reason, the imperfection of Equation (31) for decalin and to a lesser extent for tetralin can be explained by deviations from thermodynamic values at melting temperature.
- It has been theoretically shown that approximating ∆cp with entropy is justified, but it is the average value of the population, understood as a set of only hydrocarbons, without a solvent.
- Linear correlation of the coefficients at the functional terms in Equation (15), A1 vs. determines the mean values of the enthalpy and entropy of the analyzed systems. Equation (40) determines the compensation temperature, except that the thermodynamic quantities refer to the mean values of the population, analogously to Equation (5), which determines melting temperature.
3.4. Forms of Activity Coefficients in This Paper
4. Discussion
5. Conclusions
- On the example of the thermodynamic analysis of the Apelblat & Manzurola equation, included in the Equations (15) and (28)–(33), it has been shown that expressing the absolute temperature through bifunctional () members is an alternative to the simultaneous determination of enthalpy and entropy. The ratio of this determines the melting temperature, in accordance with Equation (5), as where the thermodynamic functions are temperature dependent (Figure 1). Thus, it has been shown that the structure of the A&M equation is itself thermodynamically compensated by EEC. Combined use of bifunctional functional members with respect to temperature is thermodynamically justified and brings new information in this regard.
- It has been shown that the simplest Equations (6) or (8) also allow for the simultaneous determination of enthalpy and entropy. Details of the transformation are included in Equations (59)–(64) but these quantities do not always come down to melting temperature in isoequilibrium state according to (
- It has been shown that approximation by entropy is justified, but it is an average value from the population, understood as a set of hydrocarbons (without solvent). Linear correlation of coefficients with functional terms in Equation (15), vs. determines the average values of enthalpy and entropy of the analyzed systems (Figure 3c).
- Saturated solutions of 12 polynuclear aromatic hydrocarbons, including those containing heteroatoms (N, S, O) in tetralin and decalin, have been described with A&M Equation (15). The end of the dissolution process is recognized by melting point temperature, i.e., for pure solute (without solvent) 1. Equations (28)–(31) contain three or two factors and the dependent variable is in the form of concentrations or activities. A very good linear correlation was found for the equation coefficients Equation (15) at the functional members, expressed by Equation (37). In this way, Equation (40) defines the thermodynamic aspect of the compensation temperature—analogically acc. to Equation (5). It is the ratio of average enthalpy to entropy values in the analyzed population, for the considered population of 12 hydrocarbons in two solvents. As shown in Table A1, Table A2 and Table A3 and these calculations, the total numerical variability of molar enthalpy is 16.5–29.4 kJ*mol−1 (in [21]: 16.8–28.6 kJ*mol−1). The discussion presented for these equations indicates high compatibility of molar enthalpy with literature data [14,17,23].
- It has been proposed to extend the Apelblat & Manzurola equation in the form of Equation (51) after eliminating intercept and inserting in its place a characteristic segment for the coefficient of activity for regular and simple solutions Equation (50). Since in several cases unbelievable values were obtained, it was found that this is the result of too much dilution of the solution (Figure 5), which practically means that this effect occurs when: It should be noted that there are no ideal conditions for this premise ( but this fact does not affect the quality of the correlation.
- On the basis of simplified forms for regular and simple solutions, a significant problem is the variability in binary solutions of excess Gibbs free energy depending on the molar fraction of the solute. This applies to the acceptance of the adoption of such solutions, which are correct in the notation Equation (49), i.e., considerations based on the simplest approach in the Hildebrand theory.
Computational Techniques
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Symbols
| a | activity [-], |
| Ao, A1, A2, B, C | coefficients in Equations (15) and (49)–(51), A1 and C in K, B in J*mol−1, |
| ∆ | difference between its solid and liquid heat capacities—and heat capacities, J*(mol*K)−1, |
| ∆ G, GE | molar Gibbs free energy and excess Gibbs free energy, J*mol−1, |
| ∆ H, HE | molar enthalpy and excess enthalpy, J*mol−1, |
| l12 | extended regular solution model binary parameter in S-H Equation (43) [-], |
| n | number of moles, |
| N | amount of data, |
| P | pressure, Pa, |
| R | 8.315 J*(mol*K)−1, absolute gas constant, |
| R2, r2 andρ2 | determinations coefficient of multiple, linear or without intercept [-], |
| ∆ S, SE | molar entropy and excess entropy, J*(mol*K)−1, |
| T | absolute temperature, K, |
| V | volume, cm3 mol−1, |
| Vm | mixing volume, cm3 mol−1, |
| x | solute mol fraction [-], |
| constant in Equation (34), K and in Equation (26), Jmol−1, | |
| γ | activity coefficient [-], |
| λ | constant in Equation (16) [-], |
| δ | , |
| Subscripts | |
| 1—solvent, 2—solute, c—compensation, h—harmonic mean, m—melting point, i-th component, j-th component, i ≠ j. | |
| Superscripts | |
| α, β—phase, o—pure component, sat—saturation, ∅—standard condition, -—average. | |
Appendix A
| Compound | , kJ*mol−1 | Tetralin | Decalin (Mix Cis and Trans) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Equation (28) | Equation (29) | Equation (30) | Equation (31) | Equation (32) | Equation (33) | Equation (28) | Equation (29) | Equation (30) | Equation (31) | Equation (32) | Equation (33) | ||
| Biphenyl | 16.75–16.80 [18,21,27] | 21.20 | 19.43 | 19.84 | 18.94 | 18.94 | 17.70 | 29.74 | 18.28 | 20.11 | 19.81 | 31.31 | 17.72 |
| Fluorene | 19.60 [21,27] | 23.59 | 20.81 | 21.56 | 19.90 | 21.00 | 20.88 | 33.81 | 24.85 | 14.79 | 16.07 | 21.00 | 19.38 |
| Phenanthrene | 16.50 [21,27] | 17.03 | 17.87 | 14.65 | 16.97 | 19.66 | 16.80 | 44.4 | 19.28 | 13.73 | 13.28 | 36.54 | 16.62 |
| Acenaphthene | 21.50 [21,27] | 23.59 | 22.08 | 22.41 | 21.51 | 22.33 | 21.11 | 31.35 | 25.62 | 18.22 | 19.11 | 30.39 | 21.15 |
| Naphthalene | 18.24–18.98 [21,27] | 18.13 | 19.13 | 16.41 | 18.88 | 19.60 | 18.20 | 27.27 | 22.49 | 14.79 | 17.03 | 27.93 | 18.11 |
| Dibenzofuran | 18.60 [18,21] | 19.33 | 19.01 | 18.13 | 18.58 | 20.95 | 18.43 | 28.43 | 16.37 | 19.07 | 16.05 | 20.10 | 18.24 |
| Dibenzothiophene | 21.00–21.60 [18,21,27] | 27.77 | 24.18 | 21.95 | 21.87 | 23.03 | 20.13 | 61.42 | 34.47 | 20.70 | 20.04 | 38.25 | 20.08 |
| Thioxanthene | 26.10 [18,21] | 29.27 | 28.97 | 24.87 | 26.49 | 26.55 | 25.23 | 56.71 | 44.93 | 32.62 | 24.13 | 34.83 | 25.36 |
| Xanthene | 19.20 [18,21] | 32.45 | 23.45 | 27.29 | 21.58 | 20.76 | 18.72 | 26.59 | 25.62 | 2.95 | 15.66 | 37.58 | 18.60 |
| Carbazole | 27.20 [18,21] | 107.95 | 68.27 | 61.47 | 34.94 | 43.92 | 26.70 | 56.62 | 55.84 | 8.22 | 8.86 | 48.28 | 56.19 |
| Acridine | 19.70 [18,21] | 32.65 | 24.91 | 21.39 | 20.17 | 22.87 | 18.27 | 101.26 | 50.29 | 23.68 | 8.70 | 46.60 | 17.25 |
| Anthracene | 28.60–29.40 [18,21,27] | 20.13 | 33.69 | 17.65 | 30.34 | 26.20 | 28.03 | 41.27 | 48.43 | 28.92 | 27.62 | 28.53 | 28.16 |
| Compound | Tetralin | Decalin (Mix Cis and Trans) | ||||
|---|---|---|---|---|---|---|
| ±Stand. Error | ±Stand. Error | |||||
| Biphenyl | 67.273 | 0.404 | 0.99982 | 265.74 | 1.164 | 0.99992 |
| Fluorene | 52.060 | 0.456 | 0.999539 | 293.355 | 0.965 | 0.99995 |
| Phenantrene | 90.942 | 1.023 | 0.99999 | 351.706 | 0.128 | 1.000 |
| Acetnaphtene | 39.024 | 0.175 | 0.99990 | 209.313 | 1.841 | 0.99961 |
| Naphthalene | 62.601 | 0.537 | 0.99971 | 233.473 | 3.938 | 0.99830 |
| Dibenzofurene | 82.111 | 0.302 | 0.99995 | 289.377 | 1.401 | 0.99991 |
| Dibenzotiophene | 115.099 | 1.225 | 0.99955 | 380.684 | 3.782 | 0.99951 |
| Thioxanthene | 74.174 | 0.726 | 0.99952 | 356.456 | 0.137 | 1.000 |
| Xanthene | 106.751 | 1.073 | 0.99950 | 367.627 | 1.234 | 0.99994 |
| Carbazole | 708.621 | 2.776 | 0.99995 | 921.758 | 2.422 | 0.99992 |
| Acridine | 183.991 | 1.689 | 0.99958 | 660.202 | 1.003 | 0.99999 |
| Anthracene | 88.299 | 0.154 | 0.99999 | 428.099 | 0.095 | 1.000 |
| Compound | , kJ*mol−1 | Tetralin | Decalin (Mix Cis and Trans) | ||
|---|---|---|---|---|---|
| , kJ*mol−1 | , kJ*mol−1 | ||||
| Biphenyl | 16.75–16.80 | 18.12 | 1.000 | 16.61 | 0.99998 |
| Fluorene | 19.60 | 17.82 | 0.99998 | 17.35 | 0.99993 |
| Phenantrene | 16.50 | 18.49 | 1.000 | 13.04 | 0.99999 |
| Acetnaphtene | 21.50 | 20.59 | 0.99999 | 20.34 | 0.99993 |
| Naphthalene | 18.24–18.98 | 19.20 | 0.99997 | 19.34 | 0.99994 |
| Dibenzofurene | 18.60 | 16.92 | 0.99994 | 16.94 | 0.99999 |
| Dibenzotiophene | 21.00–21.60 | 20.68 | 0.99999 | 16.75 * | 0.99999 |
| Thioxanthene | 26.10 | 27.33 | 0.99999 | −10.44 * | 0.99999 |
| Xanthene | 19.20 | 17.48 | 0.99691 | 22.51 | 0.99987 |
| Carbazole | 27.20 | 26.12 | 0.99691 | 28.19 | 0.998832 |
| Acridine | 19.70 | 13.78 * | 0.99997 | −3.58 * | 0.99930 |
| Anthracene | 28.60–29.40 | −7.53 * | 1.000 | 31.64 * | 0.99999 |
| Compound | , K | K | K | Solvent T or D |
|---|---|---|---|---|
| xantene | 373.7 | 376.1 | 374.8 | T (-) |
| carbazole | 519.2 | - | 523.8 | T (-) |
| anthracene | 489.5 | 491.4 | 492.4 | T (-) |
| biphenyl | 342.6 | 342.0 | - | D (+) |
| dibenzofurene | 355.7 | 355.4 | 354.7 | D (+) |
| dibenzotiophene | 371.4 | 371.3 | 370.4 | D (+) |
| acridine | 384.2 | - | 384.2 | D (+) |
References
- Le Fèvre, R.J.W.; Tideman, C.G. Calculation of the Latent Heat of Fusion of Camphor from Vapour Pressure–Temperature Data. Nature 1931, 127, 972–973. [Google Scholar] [CrossRef]
- Romps, D.M. The Rankine-Kirchhoff approximations for moist thermodynamics. Q. J. R. Met. Soc. 2021, 147, 3493–3497. [Google Scholar] [CrossRef]
- Seok, S.-H.; Jung, S.-M.; Lee, Y.-S.; Min, D.-J. Viscosity of Highly Basic Slags. ISIJ Int. 2007, 47, 1090–1096. [Google Scholar] [CrossRef] [Green Version]
- Weymann, H.D. On the Hole Theory of Viscosity, Compressibility, and Expansivity of Liquids. Kolloid-Zeitschrifl Zeitschrifl Für Polym. 1961, 181, 131–137. [Google Scholar] [CrossRef]
- Gong, Y.; Grant, D.J.W.; Brittain, H.G. Principles of Solubility. In Solvent Systems and Their Selection in Pharmaceutics and Biopharmaceutics; Augustijns, P., Brewster, M.E., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 1–27. [Google Scholar]
- Acree, W.E., Jr. Polycyclic Aromatic Hydrocarbons: Binary Non-Aqueous System; Solubility Data Series; Oxford University Press: Oxford, UK, 1995; Volume 58. [Google Scholar]
- Acree, W.E., Jr. IUPAC-NIST Solubility Data Series. 98. Solubility of Polycyclic Aromatic Hydrocarbons in Pure and Organic Solvent Mixtures: Revised and Updated. Part 1. Binary Solvent Mixtures. J. Phys. Chem. Ref. Data 2013, 42, 1–188. [Google Scholar]
- Acree, W.E., Jr. IUPAC-NIST Solubility Data Series. 98. Solubility of Polycyclic Aromatic Hydrocarbons in Pure and Organic Solvent Mixtures: Revised and Updated. Part 2. Ternary Solvent Mixtures. J. Phys. Chem. Ref. Data 2013, 42, 1–84. [Google Scholar]
- Lorimer, J.W.; Cohen-Adad, R. Thermodynamics of Solubility. In The Experimental Determination of Solubilities; Hefter, G.T., Tomkins, R.P.T., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 2003; Chapter 1.1. [Google Scholar]
- Clarke, E.C.W.; Glew, D.N. Evaluation of thermodynamic functions from equilibrium constants. Trans. Faraday Soc. 1966, 62, 539–547. [Google Scholar] [CrossRef]
- Monte, M.J.S.; Pinto, S.P.; Ferreira, A.I.M.C.; Amaral, L.M.P.F.; Freitas, V.L.S. Fluorene: An extended experimental thermodynamic study. J. Chem. Thermodyn. 2012, 45, 53–58. [Google Scholar] [CrossRef]
- Liu, M.; Fu, H.; Yin, D.; Zhang, Y.; Lu, C.; Cao, H.; Zhou, J. Measurement and correlation of the solubility of enrofloxacin in different solvents from (303.15 to 321.05) K. J. Chem. Eng. Data 2014, 59, 2070–2074. [Google Scholar] [CrossRef]
- Štejfa, V.; Fulem, M.; Růžička, K.; Matějka, P. Vapor pressures and thermophysical properties of selected hexenols and recommended vapor for hexan-1-ol. Fluid Phase Equilibria 2015, 402, 18–29. [Google Scholar] [CrossRef]
- Oliveira, J.A.S.A.; Freitas, V.L.S.; Notario, R.; Ribeiro da Silva, M.D.M.C.; Monte, M.J.S. Thermodynamic properties of 2,7-di-tert-butylfluorene—An experimental and computational study. J. Chem. Thermodyn. 2016, 101, 115–122. [Google Scholar] [CrossRef]
- Elliot, J.R.; Lira, C.T. Introductory Chemical Engineering Thermodynamics, Chapter 11, An Introduction to Activity Models, 2nd ed.; Prentice-Hall: Hoboken, NJ, USA, 2012; pp. 226–251. ISBN 978-0-13-606854-9. [Google Scholar]
- Szarawara, J. Termodynamika Chemiczna Stosowana, 3rd ed.; WNT: Warszawa, Poland, 1997. (In Polish) [Google Scholar]
- Wilson, G.M. Vapor-Liquid Equilibrium. XI. A New Expression for the Excess Free Energy of Mixing. J. Am. Chem. Soc. 1964, 86, 127–130. [Google Scholar] [CrossRef]
- Coon, J.E.; Sediawan, W.B.; Auwaerter, J.E.; McLaughlin, E. Solubilities of families of heterocyclic polynuclear aromatics in organic solvents and their mixtures. J. Sol. Chem. 1988, 17, 519–535. [Google Scholar] [CrossRef]
- Hristova, M.; Donchev, T.; Kolev, D.; Baloch, I.; Georgiev, H. Parameter’s estimate in Wilson equation. Int. Electron. J. Pure Appl. Math. 2015, 9, 29–35. [Google Scholar] [CrossRef] [Green Version]
- Farajnezhad, A.; Afshar, O.A.; Khansary, M.A. Correlation of interaction parameters in Wilson, NRTL and UNIQUAC models using theoretical methods. Fluid Phase Equilibria 2016, 417, 181–186. [Google Scholar] [CrossRef]
- Coon, J.E.; Auwaerter, J.E.; McLaughlin, E. A comparison of solid-liquid equilibrium with vapor-liquid equilibrium for prediction of activity coefficients in systems containing polynuclear aromatics. Fluid Phase Equilibria 1989, 44, 305–345. [Google Scholar] [CrossRef]
- Han, K.J.; In, S.J. The measurement and prediction of flash point for binary mixtures {C1~ C3 alcohols + p-xylene} at 101.3 kPa. Open J. Saf. Sci. Technol. 2017, 7, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Abrams, D.S.; Prausnitz, J.M. Statistical thermodynamics of liquid mixtures: A new expression for the excess Gibbs energy of partly or completely miscible systems. AIChE J. 1975, 21, 116–128. [Google Scholar] [CrossRef]
- Santori, G.; Franciolini, M.; Di Nicola, G.; Polonara, F.; Brandani, S.; Stryjek, R. An algorithm for the regression of the UNIQUAC interaction parameters in liquid-liquid equilibrium for single- and multi-temperature experimental data. Fluid Phase Equilibria 2014, 374, 79–85. [Google Scholar] [CrossRef] [Green Version]
- Correa, A.; Tojo, J.; Correa, J.M.; Blanco, A. New analytical solution of group’s method parameters for the prediction of vapor-liquid equilibrium. Ind. Eng. Chem. Res. 1989, 28, 609–611. [Google Scholar] [CrossRef]
- Bronneberg, R.; Pfennig, A. MOQUAC, a new expression for the excess Gibbs free energy based on molecular orientations. Fluid Phase Equilibria 2013, 338, 67–77. [Google Scholar] [CrossRef]
- Mishra, D.S.; Yalkowsky, S.H. Ideal solubility of a solid solute: Effect of heat capacity assumptions. Pharm. Res. 1992, 9, 958–959. [Google Scholar] [CrossRef] [PubMed]
- Apelblat, A.; Manzurola, E. Solubilities of o-acetylsalicylic, 4-aminosalicylic, 3,5-dinitrosalicylic, and p-toluic acid, and magnesium-DL-aspartate in water from T = (278 to 348) K. J. Chem. Thermodyn. 1999, 31, 85–91. [Google Scholar] [CrossRef]
- Heryanto, R.; Hasan, M.; Abdullah, E.C.; Kumoro, A.C. Solubility of stearic acid in various organic solvents and its prediction using non-ideal solution models. Sci. Asia 2007, 33, 469–472. [Google Scholar] [CrossRef]
- Zhang, C.-L.; Zhao, F.; Wang, Y. Thermodynamics of the solubility of sulfamethazine in methanol, ethanol, 1-propanol, acetone, and chloroform from 293.15 to 333.15 K. J. Mol. Liquids 2011, 159, 170–172. [Google Scholar] [CrossRef]
- Yan, F.-Y.; Wang, M.; Wen, J.-Y.; Fu, Y.; Chen, L. Solubility of fudosteine in some pure and mixed solvents from (278.15 to 308.15) K. J. App. Sol. Chem. Mod. 2012, 1, 100–104. [Google Scholar] [CrossRef]
- Noubigh, A.; Oueslati, M.H. Measurement and modeling of the solubility of vanillin constituent of olive mill wastewater in binary water + ethanol solvents mixtures between 278.15 K and 308.15 K. Aust. J. Basic Appl. Sci. 2014, 8, 396–403. [Google Scholar]
- Shakeel, F.; Alanazi, F.K.; Alsarra, I.A.; Haq, N. Solution thermodynamics and solubility of indomethacin in ethanol-water mixtures in the temperature range from 293.15 to 318.15 K. Bulg. Chem. Commun. 2015, 47, 125–130. [Google Scholar]
- Buchowski, H.; Książczak, A.; Pietrzyk, S. Solvent activity along a saturation line and solubility of hydrogen-bonding solids. J. Phys. Chem. 1980, 84, 975–979. [Google Scholar] [CrossRef]
- Opperhulzen, A.; Gobas, F.A.P.C.; Van der Steen, J.M.D. Aqueous solubility of polychlorinated biphenyls related to molecular structure. Environ. Sci. Technol. 1988, 22, 638–646. [Google Scholar] [CrossRef]
- Neau, S.H.; Flynn, G.L. Solid and liquid heat capacities of n-alkyl para-aminobenzoates near the melting point. Pharm. Res. 1990, 7, 1157–1162. [Google Scholar] [CrossRef] [PubMed]
- Neau, S.H.; Bhandarkar, S.V.; Hellmuth, E.W. Differential molar heat capacities to test ideal solubility estimations. Pharm. Res. 1997, 14, 601–605. [Google Scholar] [CrossRef] [PubMed]
- Shilei, L.; Neng, Z.; Guohu, F. Eutectic mixtures of capric acid and lauric acid applied in building wallboards for heat energy storage. Energy Build. 2006, 38, 708–711. [Google Scholar] [CrossRef]
- Yalkowsky, S.H.; Wu, M. Estimation of the ideal solubility (Crystal-Liquid Fugacity Ratio) of organic compounds. Pharm. Sci. 2010, 99, 1100–1106. [Google Scholar] [CrossRef] [PubMed]
- Baluja, S.; Bhesaniya, K.; Bhalodia, R.; Chanda, S. Solubility of butylated hydroxytoluene (BHT) in aqueous and alcohol solutions from 293. 15 to 313.15 K. Int. Lett. Chem. Phys. Astron. 2014, 9, 48–58. [Google Scholar] [CrossRef]
- Zakeri-Milani, P.; Fasihi, Z.; Akbari, J.; Jannatabadi, E.; Barzegar-Jalali, M.; Loebenberg, R.; Valizadeh, H. Crystal-liquid fugacity ration as a surrogate parameter for intestinal permeability. J. Pharm. Pharm. Sci. 2016, 19, 312–324. [Google Scholar] [CrossRef] [Green Version]
- Delgado, D.R.; Peña, M.Á.; Martínez, F. Extended Hildebrand solubility approach applied to some sulphapyrimidines in some {methanol (1) + water (2)} mixtures. Phys. Chem. Liquids 2017, 56, 176–188. [Google Scholar] [CrossRef]
- Fasihi, Z.; Zakeri-Milani, P.; Nokhodchi, A.; Akbari, J.; Barzegar-Jalali, M.; Loebenberg, R.; Valizadeh, H. Thermodynamic approaches for the prediction of oral drug absorption. J. Therm. Anal. Cal. 2017, 130, 1371–1382. [Google Scholar] [CrossRef]
- Yalkowsky, B.S. Unified physicochemical properly estimation relationships (UPPER). J. Pharm. Pharm. Sci. 2014, 103, 2710–2723. [Google Scholar]
- Choi, P.B.; Williams, C.P.; Buehring, K.G.; McLaughlin, E. Solubility of aromatic hydrocarbon solids in mixtures of benzene and cyclohexane. J. Chem. Eng. Data 1985, 30, 403–409. [Google Scholar] [CrossRef]
- Ruelle, P.; Sarraf, E.; Kesselring, U.W. Prediction of carbazole solubility and its dependence upon the solvent nature. Int. J. Pharm. 1994, 104, 125–133. [Google Scholar] [CrossRef]
- Ruelle, P.; Kesselring, U.W. Aqueous solubility prediction of environmentally important chemicals from the mobile order thermodynamics. Chemosphere 1997, 34, 275–298. [Google Scholar] [CrossRef]
- Available online: https://pubchem.ncbi.nlm.nih.gov/compound/8404#section=Kovats-Retention-Index (accessed on 30 October 2022).
- Available online: https://webbook.nist.gov/cgi/cbook.cgi?ID=C493027&Mask=2 (accessed on 30 October 2022).
- Delgado, D.G.; Martínez, F. Solution Thermodynamics and Preferential Solvation of Sulfamerazine in Methanol + Water Mixtures. J. Solut. Chem. 2015, 44, 360–377. [Google Scholar] [CrossRef]
- Starikov, E.B. ‘Entropy is anthropomorphic’: Does this lead to interpretational devalorisation of entropy-enthalpy compensation? Monatsh. Chem. 2013, 144, 97–102. [Google Scholar] [CrossRef]
- Adjei, A.; Newburger, J.; Martin, A. Extended Hildebrand approach: Solubility of caffeine in dioxane-water mixtures. J. Pharm. Sci. 1980, 69, 659–661. [Google Scholar] [CrossRef]
- Siudyga, T.; Mianowski, A. Examination of polyolefins—organic compounds interactions by inverse gas chromatography. J. Therm. Anal. Cal. 2007, 89, 191–196. [Google Scholar] [CrossRef]
- Rathi, P.B.; Mourya, V.K. Extended Hildebrand solubility approach: Satranidazole in mixtures of dioxane and water. Indian J. Pharm. Sci. 2011, 73, 315–319. [Google Scholar]
- Fornari, T.; Ibañez, E.; Reglero, G.; Stateva, R.P. Analysis of predictive thermodynamic models for estimation of polycyclic aromatic solid solubility in hot pressurized water. Open Thermodyn. J. 2011, 5 (Suppl. 1-M4), 40–47. [Google Scholar] [CrossRef] [Green Version]
- Pan, A.; Biswas, T.; Rakshit, A.K.; SPMoulik, S.P. Enthalpy-Entropy compensation (EEC) effect: A revisit. J. Phys. Chem. B 2015, 119, 15876–15884. [Google Scholar] [CrossRef] [PubMed]
- Krug, R.R. Detection of the Compensation Effect (θ Rule). Ind. Eng. Chem. Fundamen. 1980, 19, 50–59. [Google Scholar] [CrossRef]
- Freed, K.F. Entropy-enthalpy compensation in chemical reactions and adsorption: An exactly solvable model. J. Phys. Chem. B 2011, 115, 1689–1692. [Google Scholar] [CrossRef] [PubMed]
- Starikov, E.B. Entropy-Enthalpy Compensation and its Significance—in Particular for Nanoscale Events. J. Appl. Sol. Chem. Model. 2013, 2, 126–135. [Google Scholar] [CrossRef]
- Grant, D.J.W.; Mehdizadeh, M.; Chow, A.H.-L.; Fairbrother, J.E. Non-linear van’t Hoff solubility-temperature plots and their pharmaceutical interpretation. Int. J. Pharm. 1984, 18, 25–38. [Google Scholar] [CrossRef]
- Mianowski, A.; Urbańczyk, W. Isoconversional methods in thermodynamic principles. J. Phys. Chem. A 2018, 122, 6819–6828. [Google Scholar] [CrossRef] [PubMed]
- Krug, R.R.; Hunter, W.G.; Grieger, R.A. Enthalpy-Entropy Compensation. 2. Separation of the Chemical from the Statistical Effect. J. Phys. Chem. 1976, 80, 2341–2351. [Google Scholar] [CrossRef]
- Shakeel, F.; Alshehri, S.; Imran, M.; Haq, N.; Alanazi, A.; Anwer, M.K. Experimental and Computational Approaches for Solubility Measurement of Pyridazinone Derivative in Binary (DMSO + Water) Systems. Molecules 2020, 25, 171. [Google Scholar] [CrossRef]
- Tinjacá, D.A.; Martinez, F.; Almanza, O.A.; Jouyban, A.; Acree, W.E., Jr. Dissolution thermodynamics and preferential solvation of meloxicam in (acetonitrile + water) mixtures. Phys. Chem. Liquids 2021, 59, 733–752. [Google Scholar] [CrossRef]
- Starikov, E.B.; Nordén, B.; Tanaka, S. Entropy-Enthalpy Compensation: An Attempt to Find a Methodological Common Denominator; Jenny Stanford Publishing Pte. Ltd.: Singapore, 2021; ISBN 978-981-4877-30-5/978-1-003-05625-6. Available online: www.jennystanford.com (accessed on 19 December 2022).
- Starikov, E.B.; Nordén, B. Entropy–enthalpy compensation as a fundamental concept and analysis tool for systematical experimental data. Chem. Phys. Let. 2012, 538, 118–120. [Google Scholar] [CrossRef]
- Starikov, E.B. Valid entropy–enthalpy compensation: Fine mechanisms at microscopic level. Chem. Phys. Let. 2013, 564, 88–92. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mianowski, A.; Łabojko, G. Enthalpy-Entropy Compensation Effect in Saturated Solutions on an Example of Polynuclear Aromatics According to Thermodynamics at Melting Temperature. Entropy 2023, 25, 55. https://doi.org/10.3390/e25010055
Mianowski A, Łabojko G. Enthalpy-Entropy Compensation Effect in Saturated Solutions on an Example of Polynuclear Aromatics According to Thermodynamics at Melting Temperature. Entropy. 2023; 25(1):55. https://doi.org/10.3390/e25010055
Chicago/Turabian StyleMianowski, Andrzej, and Grzegorz Łabojko. 2023. "Enthalpy-Entropy Compensation Effect in Saturated Solutions on an Example of Polynuclear Aromatics According to Thermodynamics at Melting Temperature" Entropy 25, no. 1: 55. https://doi.org/10.3390/e25010055
APA StyleMianowski, A., & Łabojko, G. (2023). Enthalpy-Entropy Compensation Effect in Saturated Solutions on an Example of Polynuclear Aromatics According to Thermodynamics at Melting Temperature. Entropy, 25(1), 55. https://doi.org/10.3390/e25010055






