Testing Nonlinearity with Rényi and Tsallis Mutual Information with an Application in the EKC Hypothesis
Abstract
:1. Introduction
2. Relative Entropy, Mutual Information, and Dependence
2.1. Mutual Information
2.2. Testing Linearity by Using Mutual Information
2.3. Method for Bin-Size Selection
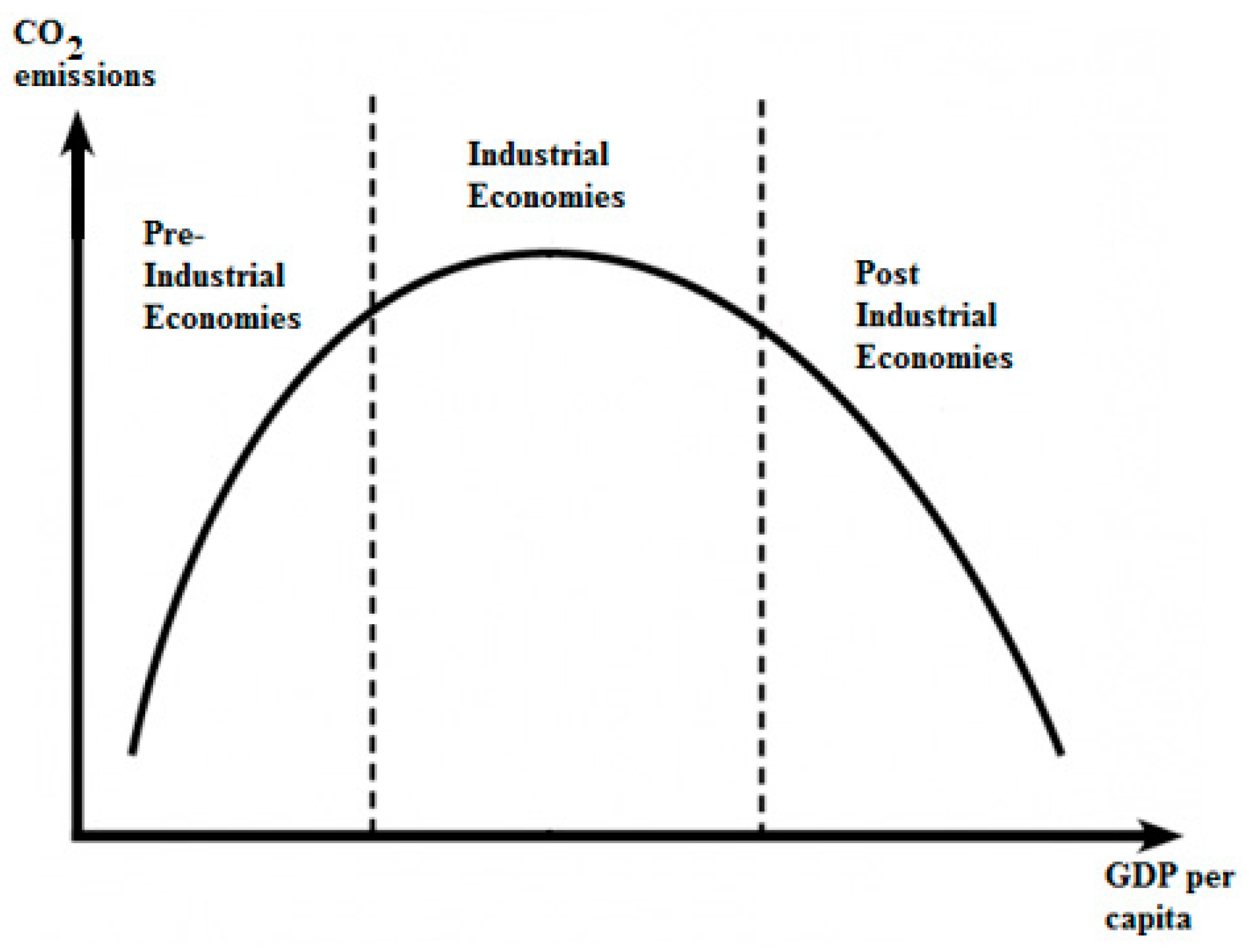
3. Checking the EKC Hypothesis for East Asian and Asia-Pacific Countries (1971–2016)
3.1. Model
3.2. Testing Linearity on the Basis of Shannon, Rényi, and Tsallis Mutual Information Measures
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Smith, R. A Mutual Information Approach to Calculating Nonlinearity. Stat 2015, 4, 291–303. [Google Scholar] [CrossRef] [Green Version]
- Yi, W.; Li, Y.; Cao, H.; Xiong, M.; Shugart, Y.Y.; Jin, L. Efficient Test for Nonlinear Dependence of Two Continuous Variables. BMC Bioinform. 2015, 16, 260. [Google Scholar]
- Weatherburn, C.E. A First Course Mathematical Statistics; Cambridge University Press: Cambridge, UK, 1961. [Google Scholar]
- Pestaña-Melero, F.L.; Haff, G.; Rojas, F.J.; Pérez-Castilla, A.; García-Ramos, A. Reliability of the Load-Velocity Relationship Obtained Through Linear and Polynomial Regression Models to Predict the 1-Repetition Maximum Load. J. Appl. Biomech. 2018, 34, 184–190. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Valent, A.; Amendola, L. H0 from Cosmic Chronometers and Type Ia Supernovae, with Gaussian Processes and the Novel Weighted Polynomial Regression Method. J. Cosmol. Astropart. Phys. 2018, 2018, 51. [Google Scholar] [CrossRef] [Green Version]
- Akhlaghi, Y.G.; Ma, X.; Zhao, X.; Shittu, S.; Li, J. A Statistical Model for Dew Point Air Cooler Based on the Multiple Polynomial Regression Approach. Energy 2019, 181, 868–881. [Google Scholar] [CrossRef] [Green Version]
- Gajewicz-Skretna, A.; Kar, S.; Piotrowska, M.; Leszczynski, J. The Kernel-Weighted Local Polynomial Regression (Kwlpr) Approach: An Efficient, Novel Tool for Development of Qsar/Qsaar Toxicity Extrapolation Models. J. Cheminform. 2021, 13, 9. [Google Scholar] [CrossRef]
- Morris, J.S. Functional Regression. Annu. Rev. Stat. Its Appl. 2015, 2, 321–359. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. ACM SIGMOBILE Mob. Comput. Commun. Rev. 2001, 5, 3–55. [Google Scholar] [CrossRef] [Green Version]
- Darbellay, G.A.; Wuertz, D. The Entropy as a Tool for Analysing Statistical Dependences in Financial Time Series. Phys. A Stat. Mech. Its Appl. 2000, 287, 429–439. [Google Scholar] [CrossRef]
- Dionisio, A.; Menezes, R.; Mendes, D.A. Mutual Information: A Measure of Dependency for Nonlinear Time Series. Phys. A Stat. Mech. Its Appl. 2004, 344, 326–329. [Google Scholar] [CrossRef]
- BBarbi, A.; Prataviera, G. Nonlinear Dependencies on Brazilian Equity Network from Mutual Information Minimum Spanning Trees. Phys. A Stat. Mech. Its Appl. 2019, 523, 876–885. [Google Scholar] [CrossRef]
- Mohti, W.; Dionísio, A.; Ferreira, P.; Vieira, I. Frontier Markets’ Efficiency: Mutual Information and Detrended Fluctuation Analyses. J. Econ. Interact. Coord. 2019, 14, 551–572. [Google Scholar] [CrossRef]
- Wu, X.; Jin, L.; Xiong, M. Mutual Information for Testing Gene-Environment Interaction. PLoS ONE 2009, 4, e4578. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, J.; Dong, W.; Meng, D. Grouped Gene Selection of Cancer Via Adaptive Sparse Group Lasso Based on Conditional Mutual Information. IEEE/ACM Trans. Comput. Biol. Bioinform. 2017, 15, 2028–2038. [Google Scholar] [CrossRef]
- Rosas, F.E.; Mediano, P.A.; Gastpar, M.; Jensen, H.J. Quantifying High-Order Interdependencies Via Multivariate Extensions of the Mutual Information. Phys. Rev. E 2019, 100, 032305. [Google Scholar] [CrossRef] [Green Version]
- Tanaka, N.; Okamoto, H.; Naito, M. Detecting and Evaluating Intrinsic Nonlinearity Present in the Mutual Dependence between Two Variables. Phys. D Nonlinear Phenom. 2000, 147, 1–11. [Google Scholar] [CrossRef]
- Grossman, G.M.; Krueger, A.B. Economic Growth and the Environment, Quarterly Journal of Economics, Cx, May, 353–377. Int. Libr. Crit. Writ. Econ. 2002, 141, 105–129. [Google Scholar]
- Selden, T.M.; Song, D. Neoclassical Growth, the J Curve for Abatement, and the Inverted U Curve for Pollution. J. Environ. Econ. Manag. 1995, 29, 162–168. [Google Scholar] [CrossRef]
- Panayotou, T. Empirical Tests and Policy Analysis of Environmental Degradation at Different Stages of Economic Development; Tech. & Emp. Prog.: Geneva, Switzerland, 1993. [Google Scholar]
- Antle, J.M.; Heidebrink, G. Environment and Development: Theory and International Evidence. Econ. Dev. Cult. Chang. 1995, 43, 603–625. [Google Scholar] [CrossRef]
- Vasilev, A. Is There an Environmental Kuznets Curve: Empirical Evidence in a Cross-Section Country Data; ZBW: Kiel, Germany, 2014. [Google Scholar]
- Thomas, M.T.C.A.J.; Joy, A.T. Elements of Information Theory; Wiley-Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
- Ullah, A. Entropy, Divergence and Distance Measures with Econometric Applications. J. Stat. Plan. Inference 1996, 49, 137–162. [Google Scholar] [CrossRef]
- Freedman, D.; Diaconis, P. On the Histogram as a Density Estimator: L 2 Theory. Z. Für Wahrscheinlichkeitstheorie Und Verwandte Geb. 1981, 57, 453–476. [Google Scholar] [CrossRef]
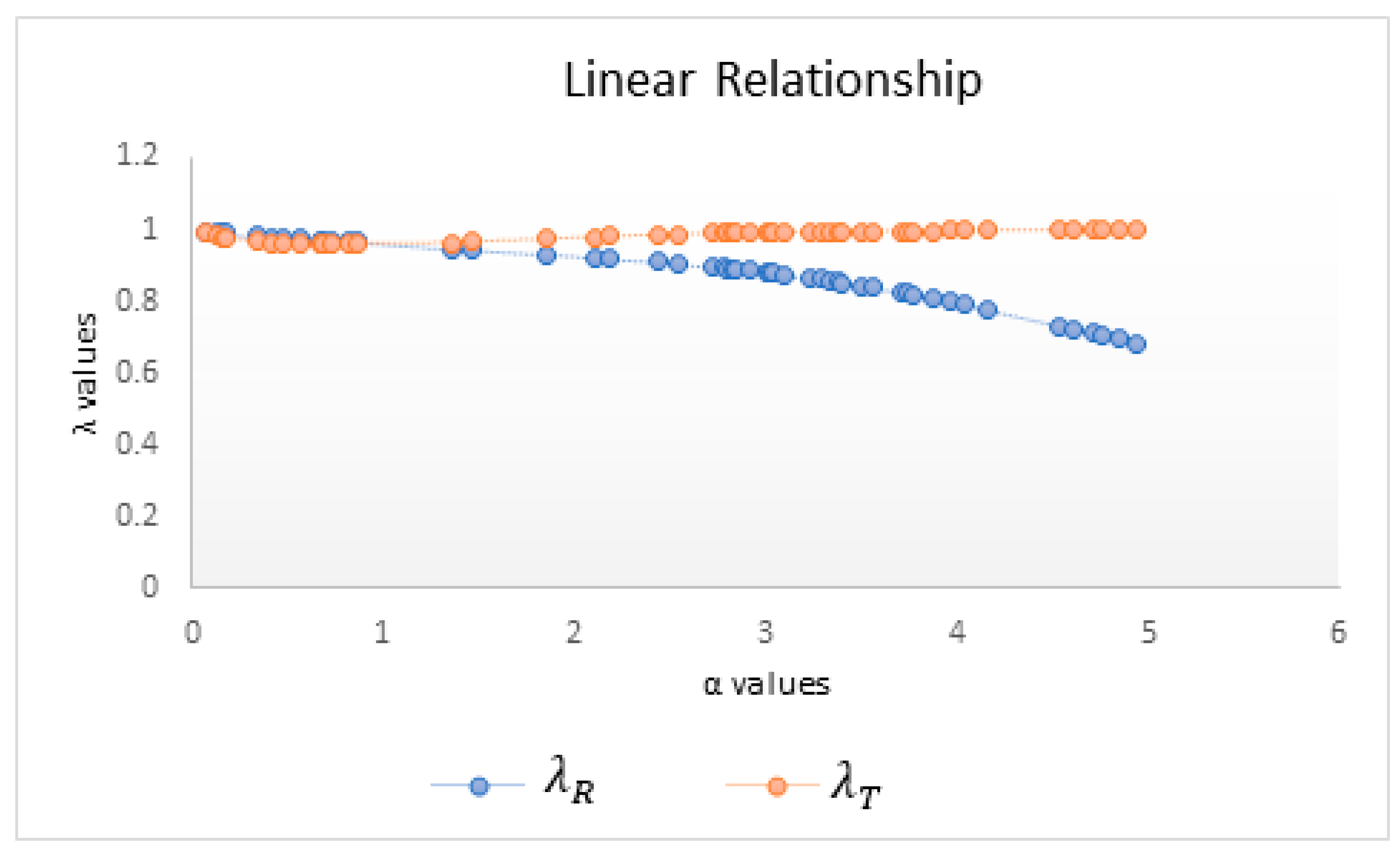
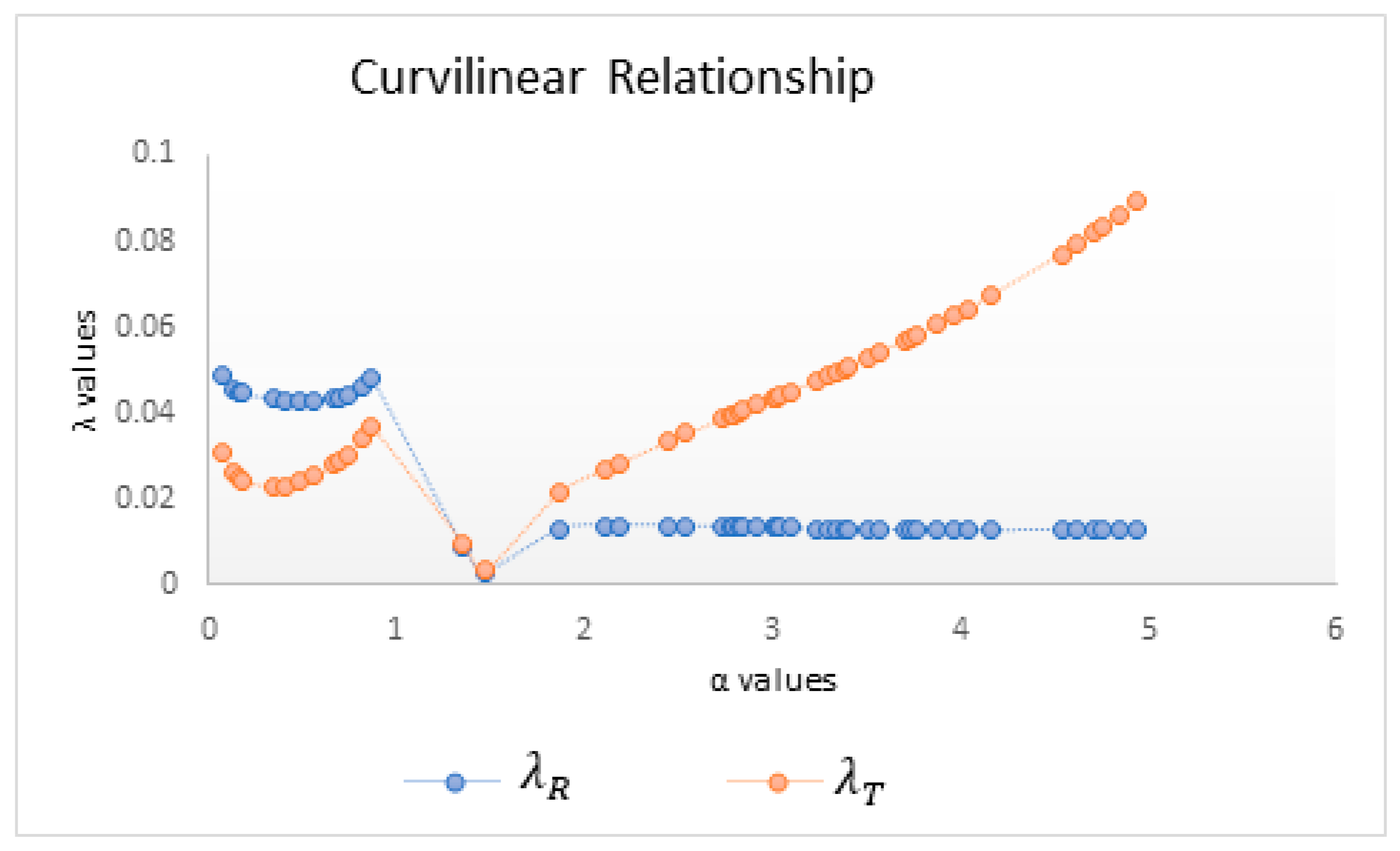
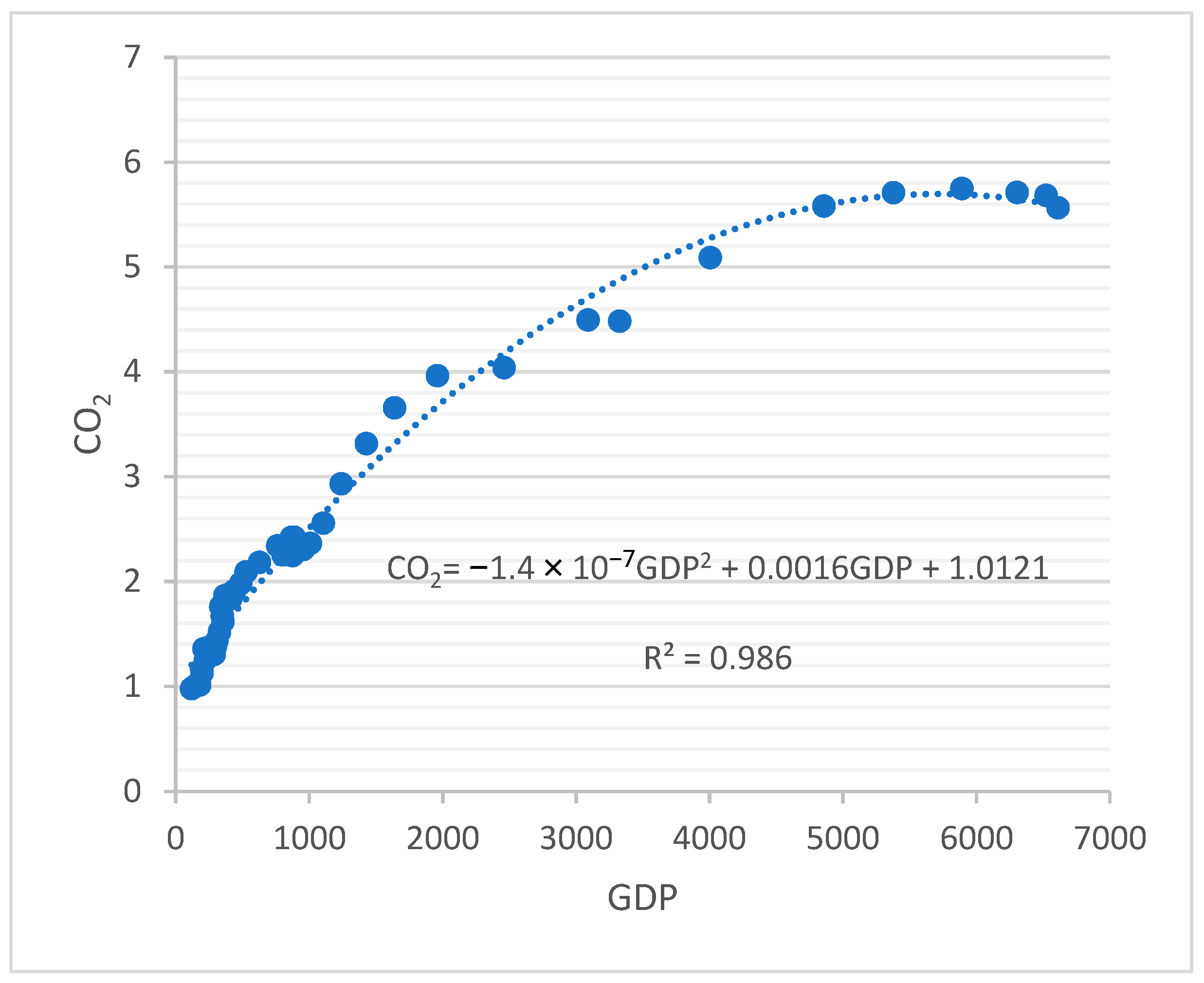
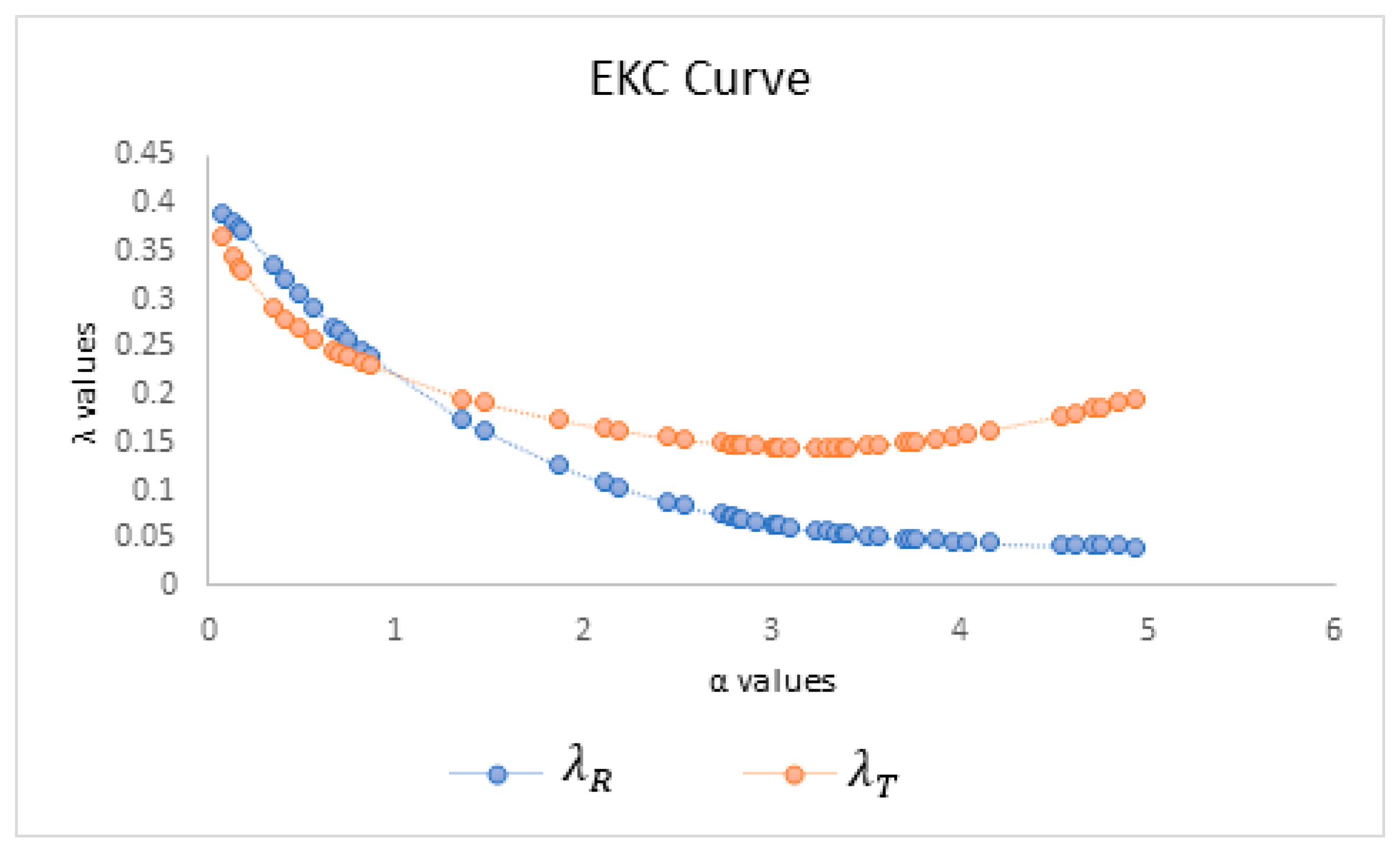
| Linear Relationship | Curvilinear Relationship | |||
|---|---|---|---|---|
| α | λR | λT | λR | λT |
| 0.07 | 0.9956 | 0.9906 | 0.0489 | 0.0308 |
| 0.13 | 0.9917 | 0.983 | 0.0457 | 0.0263 |
| 0.17 | 0.9894 | 0.9788 | 0.0447 | 0.0247 |
| 0.18 | 0.9888 | 0.9778 | 0.0445 | 0.0244 |
| 0.35 | 0.9808 | 0.9664 | 0.0433 | 0.0228 |
| 0.41 | 0.9785 | 0.964 | 0.0431 | 0.0232 |
| 0.48 | 0.976 | 0.9619 | 0.0429 | 0.024 |
| 0.56 | 0.9734 | 0.9604 | 0.0429 | 0.0254 |
| 0.67 | 0.9702 | 0.9595 | 0.0435 | 0.0281 |
| 0.69 | 0.9696 | 0.9595 | 0.0437 | 0.0287 |
| 0.74 | 0.9684 | 0.9596 | 0.0444 | 0.0304 |
| 0.82 | 0.9668 | 0.9605 | 0.0464 | 0.0339 |
| 0.87 | 0.9663 | 0.9618 | 0.0483 | 0.0369 |
| 1.36 | 0.9473 | 0.964 | 0.0087 | 0.0099 |
| 1.46 | 0.9446 | 0.9662 | 0.003 | 0.0037 |
| 1.86 | 0.9323 | 0.9749 | 0.0129 | 0.0214 |
| 2.11 | 0.9236 | 0.9797 | 0.0138 | 0.0271 |
| 2.18 | 0.9209 | 0.981 | 0.0139 | 0.0285 |
| 2.44 | 0.9102 | 0.9851 | 0.0139 | 0.0334 |
| 2.54 | 0.9056 | 0.9865 | 0.0138 | 0.0352 |
| 2.73 | 0.8962 | 0.9888 | 0.0136 | 0.0386 |
| 2.78 | 0.8935 | 0.9893 | 0.0136 | 0.0395 |
| 2.8 | 0.8924 | 0.9895 | 0.0136 | 0.0398 |
| 2.83 | 0.8908 | 0.9898 | 0.0135 | 0.0403 |
| 2.84 | 0.8902 | 0.9899 | 0.0135 | 0.0405 |
| 2.92 | 0.8856 | 0.9907 | 0.0134 | 0.0419 |
| 3.01 | 0.8801 | 0.9914 | 0.0133 | 0.0436 |
| 3.02 | 0.8795 | 0.9915 | 0.0133 | 0.0437 |
| 3.04 | 0.8782 | 0.9917 | 0.0133 | 0.0441 |
| 3.09 | 0.8749 | 0.9921 | 0.0132 | 0.045 |
| 3.23 | 0.8652 | 0.9931 | 0.0131 | 0.0476 |
| 3.29 | 0.8608 | 0.9934 | 0.0131 | 0.0487 |
| 3.34 | 0.857 | 0.9937 | 0.013 | 0.0497 |
| 3.38 | 0.8538 | 0.994 | 0.013 | 0.0504 |
| 3.4 | 0.8522 | 0.9941 | 0.013 | 0.0508 |
| 3.5 | 0.844 | 0.9946 | 0.0129 | 0.0528 |
| 3.57 | 0.8379 | 0.9949 | 0.0128 | 0.0542 |
| 3.71 | 0.8249 | 0.9954 | 0.0128 | 0.057 |
| 3.74 | 0.822 | 0.9956 | 0.0128 | 0.0576 |
| 3.77 | 0.8191 | 0.9957 | 0.0127 | 0.0583 |
| 3.88 | 0.808 | 0.996 | 0.0127 | 0.0607 |
| 3.97 | 0.7985 | 0.9963 | 0.0127 | 0.0627 |
| 4.04 | 0.7908 | 0.9964 | 0.0127 | 0.0643 |
| 4.17 | 0.7762 | 0.9967 | 0.0127 | 0.0673 |
| 4.54 | 0.7318 | 0.9974 | 0.0128 | 0.0769 |
| 4.62 | 0.7219 | 0.9975 | 0.0128 | 0.0792 |
| 4.71 | 0.7108 | 0.9976 | 0.0129 | 0.0818 |
| 4.76 | 0.7046 | 0.9976 | 0.0129 | 0.0833 |
| 4.85 | 0.6934 | 0.9977 | 0.013 | 0.0861 |
| 4.94 | 0.6822 | 0.9978 | 0.0131 | 0.089 |
| 0.9589 | 0.0121 | |||
| Mean | 0.8783 | 0.9848 | 0.0211 | 0.0443 |
| Std. Dev. | 0.0869 | 0.0134 | 0.0143 | 0.0199 |
| a | b | c | F | ||
|---|---|---|---|---|---|
| Parameter Estimates | 1.0121 | 0.0016 | 1.4 × 10−7 | 1581.224 | 0.986 |
| Standard Error | 0.04599 | 5.9 × 10−5 | 9.35 × 10−9 | ||
| p-Value | 4.99 × 10−25 | 4.39 × 10−29 | 5.08 × 10−19 | ||
| Model | |||||
| Source of Variation | Df | Sum of Squares | Mean Squares |
|---|---|---|---|
| Explained variation by linear regression | 1 | SSR = 98.658 | 98.658 |
| Explained variation by nonlinear regression | 3 | SSLF = 4.925 | 1.641 |
| Unexplained variation | 41 | SSPE = 4.425 | 0.107 |
| Total | 45 | SST = 108.01 |
| Variables | |
|---|---|
| 7 | |
| GDP | 14 |
| Residuals | 9 |
| α | λR | λT | α | λR | λT |
|---|---|---|---|---|---|
| 0.07 | 0.3892 | 0.3655 | 3.01 | 0.0649 | 0.1460 |
| 0.13 | 0.3809 | 0.3444 | 3.02 | 0.0646 | 0.1459 |
| 0.17 | 0.3741 | 0.3323 | 3.04 | 0.0640 | 0.1458 |
| 0.18 | 0.3722 | 0.3295 | 3.09 | 0.0625 | 0.1455 |
| 0.35 | 0.3355 | 0.2902 | 3.23 | 0.0587 | 0.1453 |
| 0.41 | 0.3221 | 0.2797 | 3.29 | 0.0573 | 0.1455 |
| 0.48 | 0.3071 | 0.2690 | 3.34 | 0.0562 | 0.1457 |
| 0.56 | 0.2910 | 0.2586 | 3.38 | 0.0553 | 0.1460 |
| 0.67 | 0.2708 | 0.2466 | 3.4 | 0.0549 | 0.1461 |
| 0.69 | 0.2673 | 0.2447 | 3.5 | 0.0530 | 0.1471 |
| 0.74 | 0.2590 | 0.2402 | 3.57 | 0.0518 | 0.1481 |
| 0.82 | 0.2468 | 0.2339 | 3.71 | 0.0497 | 0.1505 |
| 0.87 | 0.2400 | 0.2307 | 3.74 | 0.0493 | 0.1511 |
| 1.36 | 0.1735 | 0.1961 | 3.77 | 0.0489 | 0.1518 |
| 1.46 | 0.1631 | 0.1913 | 3.88 | 0.0476 | 0.1545 |
| 1.86 | 0.1271 | 0.1743 | 3.97 | 0.0467 | 0.1570 |
| 2.11 | 0.1087 | 0.1653 | 4.04 | 0.0461 | 0.1591 |
| 2.18 | 0.1040 | 0.1630 | 4.17 | 0.0451 | 0.1635 |
| 2.44 | 0.0888 | 0.1556 | 4.54 | 0.0430 | 0.1782 |
| 2.54 | 0.0837 | 0.1532 | 4.62 | 0.0427 | 0.1817 |
| 2.73 | 0.0751 | 0.1494 | 4.71 | 0.0423 | 0.1858 |
| 2.78 | 0.0731 | 0.1486 | 4.76 | 0.0421 | 0.1881 |
| 2.8 | 0.0723 | 0.1483 | 4.85 | 0.0418 | 0.1923 |
| 2.83 | 0.0711 | 0.1479 | 4.94 | 0.0415 | 0.1965 |
| 2.84 | 0.0708 | 0.1477 | λS | 0.2181 | 0.2181 |
| 2.92 | 0.0679 | 0.1468 | Mean | 0.1313 | 0.1914 |
| St. Dev. | 0.1147 | 0.0607 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tuna, E.; Evren, A.; Ustaoğlu, E.; Şahin, B.; Şahinbaşoğlu, Z.Z. Testing Nonlinearity with Rényi and Tsallis Mutual Information with an Application in the EKC Hypothesis. Entropy 2023, 25, 79. https://doi.org/10.3390/e25010079
Tuna E, Evren A, Ustaoğlu E, Şahin B, Şahinbaşoğlu ZZ. Testing Nonlinearity with Rényi and Tsallis Mutual Information with an Application in the EKC Hypothesis. Entropy. 2023; 25(1):79. https://doi.org/10.3390/e25010079
Chicago/Turabian StyleTuna, Elif, Atıf Evren, Erhan Ustaoğlu, Büşra Şahin, and Zehra Zeynep Şahinbaşoğlu. 2023. "Testing Nonlinearity with Rényi and Tsallis Mutual Information with an Application in the EKC Hypothesis" Entropy 25, no. 1: 79. https://doi.org/10.3390/e25010079
APA StyleTuna, E., Evren, A., Ustaoğlu, E., Şahin, B., & Şahinbaşoğlu, Z. Z. (2023). Testing Nonlinearity with Rényi and Tsallis Mutual Information with an Application in the EKC Hypothesis. Entropy, 25(1), 79. https://doi.org/10.3390/e25010079






