Sustainable Optimal Control for Switched Pollution-Control Problem with Random Duration
Abstract
1. Introduction
- A novel model is proposed to address challenges within the context of an n-player cooperative differential game for pollution control with time-driven switches and random duration. The time-driven switches within system are denoted by a periodic piecewise-constant function. Taking into account the randomness of game duration and the players’ equipment warranty period, the finite-horizon optimal control problem is reformulated as an infinite-horizon optimal control problem, in which the game duration is modeled considering two scenarios based on shifted exponential distributions. The proposed model introduces innovative concepts and refines previously established methodologies, aiming to enhance its adaptability to real-world scenarios and yield more practical outcomes.
- In addition, this study proves the sustainability and uniqueness of the environmentally sustainable solution upon the proposed model.
- Solving the optimal pollution-control problem with time-driven switches and random duration: We employed Pontryagin’s maximum principle and thoroughly analyzed the adjoint variable dynamics to derive the shifted equilibrium value, resulting in a unique environmentally sustainable solution in the form of an HLC, which is environmentally friendly and guarantees the profit of all players.
2. The Problem Statement
3. Cooperative Game with Identical Shifted Exponential Distribution
3.1. Second Interval—
3.2. First Interval—
3.3. Numerical Overall Adjoint Variable
4. Cooperative Game with Different Shifted Exponential Distributions
4.1. The Last Interval—
4.2. Former Intervals—
5. Numerical Optimal Solution
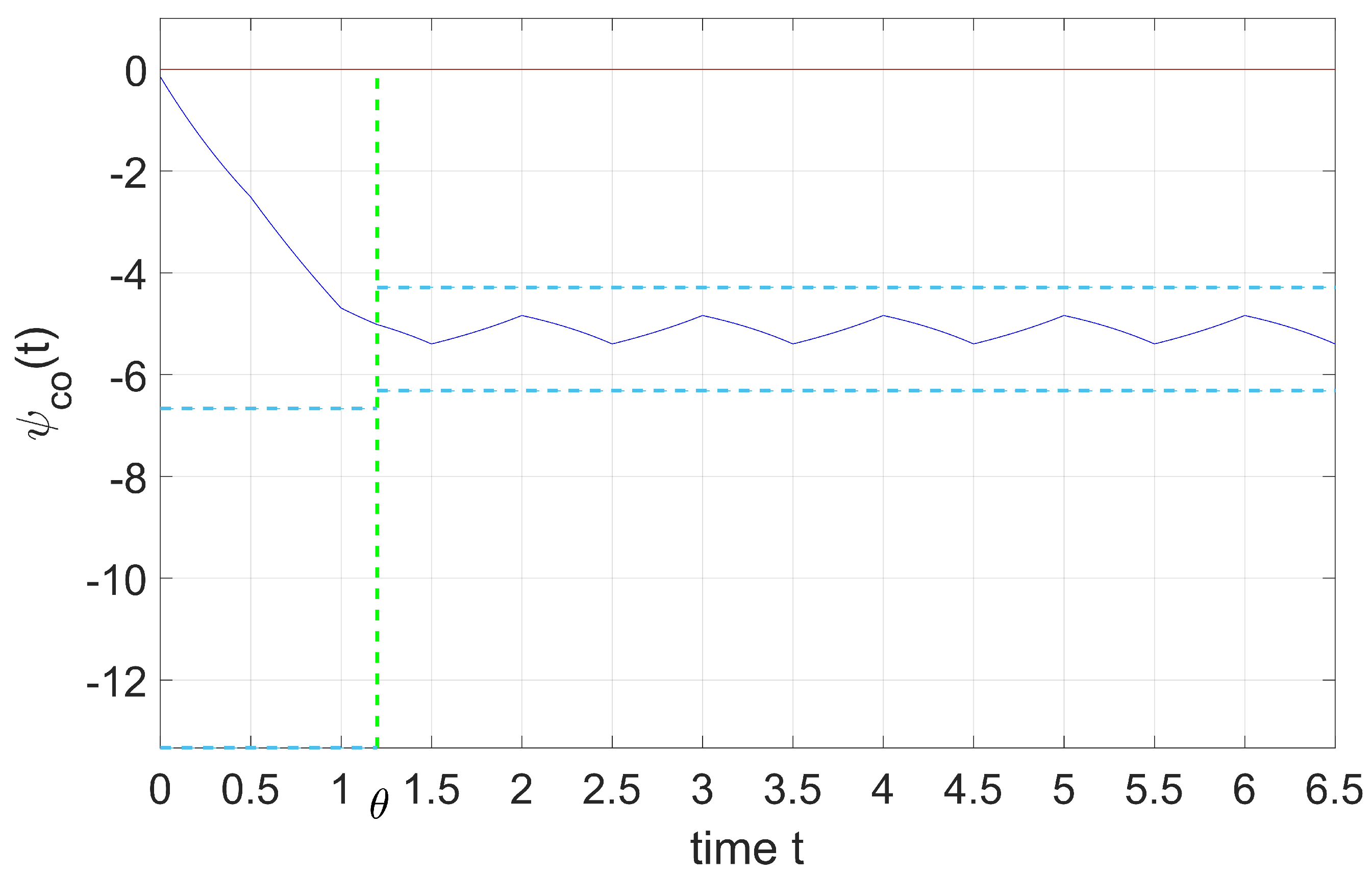
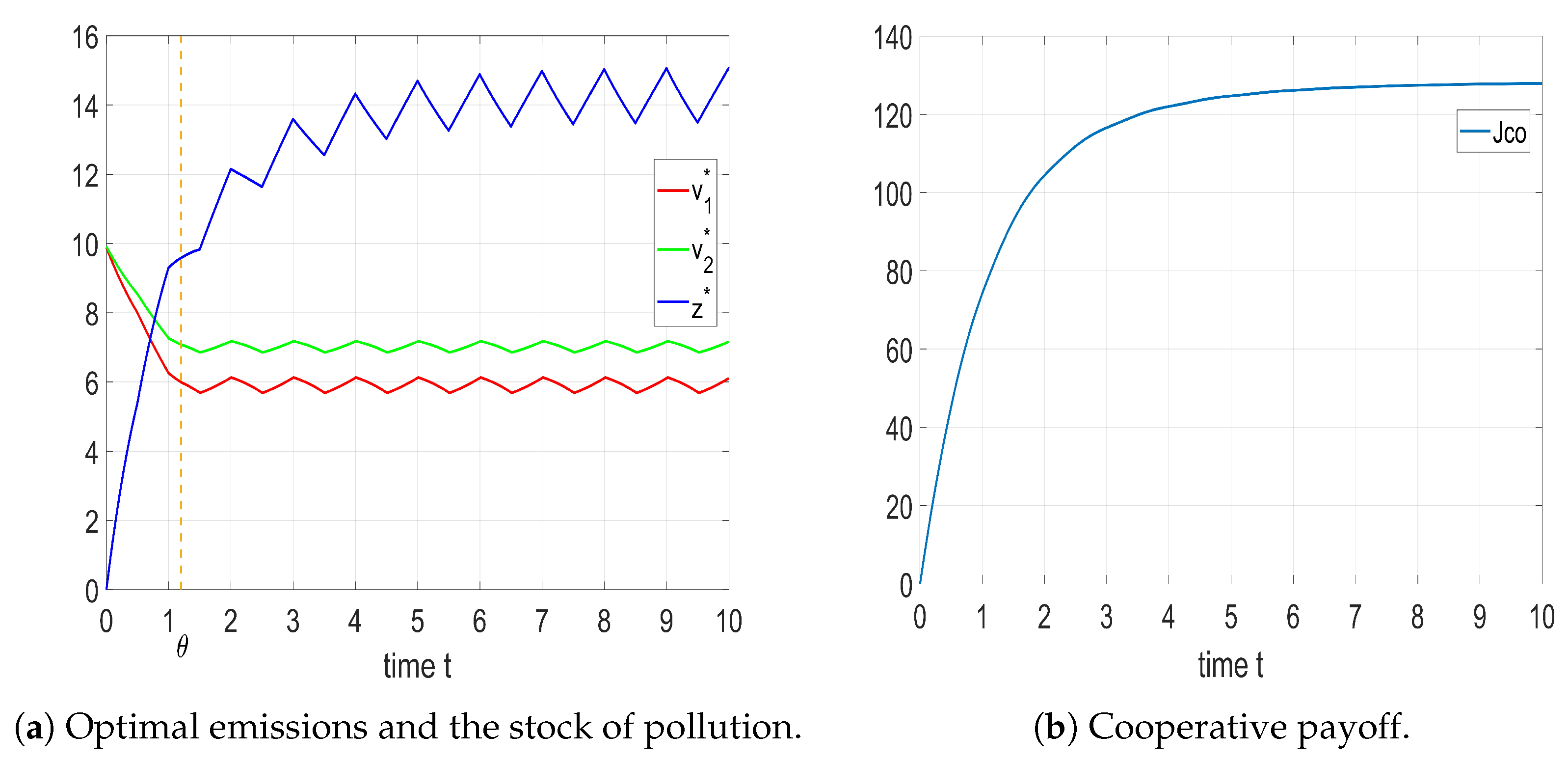
5.1. Solution of Identical Shifted Exponential Distribution
5.2. Solution of Different Shifted Exponential Distributions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Symbols | Descriptions |
|---|---|
| the game duration | |
| the i-th player’s equipment failure time | |
| T | the period time |
| the switching ratio | |
| z | the stock of pollution within a fixed natural reservoir (e.g., a lake) |
| the emissions rate of player i | |
| the maximal admissible emissions rate of player i | |
| the fraction of the emitted pollutants accumulated in the reservoir from each player (e.g., factory) | |
| the self-cleaning rate of the reservoir in time t | |
| the damage cost of player i | |
| the revenue functional of player i | |
| the instantaneous payoff of player i | |
| the positive constant used to transform the player i’s emissions flow to the profit flow | |
| the positive constant, corresponding to the tax that player i must bear | |
| the integral payoff of player i | |
| the joint payoff | |
| the shift parameter of the exponential distribution from the initiation of game | |
| the parameter of distribution | |
| the shifted parameter of player i | |
| the distribution parameter of player i |
References
- Scheffer, M.; Carpenter, S.; Foley, J.A.; Folke, C.; Walker, B. Catastrophic shifts in ecosystems. Nature 2001, 413, 591–596. [Google Scholar] [PubMed]
- Ang, A.; Bekaert, G. Regime switches in interest rates. J. Bus. Econ. Stat. 2002, 20, 163–182. [Google Scholar] [CrossRef]
- Rasmussen, L.V.; Christensen, A.E.; Danielsen, F.; Dawson, N.; Martin, A.; Mertz, O.; Sikor, T.; Thongmanivong, S.; Xaydongvanh, P. From food to pest: Conversion factors determine switches between ecosystem services and disservices. Ambio 2017, 46, 173–183. [Google Scholar] [CrossRef] [PubMed]
- Hiskens, I.A. Stability of hybrid system limit cycles: Application to the compass gait biped robot. In Proceedings of the 40th IEEE Conference on Decision and Control, Orlando, FL, USA, 4–7 December 2001; pp. 774–779. [Google Scholar]
- Lennartson, B.; Tittus, M.; Egardt, B.; Pettersson, S. Hybrid systems in process control. IEEE Control. Syst. Mag. 1996, 16, 44–56. [Google Scholar]
- Hoekstra, J.; Van den Bergh, J.C. Harvesting and conservation in a predator–prey system. J. Econ. Dyn. Control 2005, 29, 1097–1120. [Google Scholar] [CrossRef]
- Zelikin, M.I.I.; Lokutsievskiy, L.V.; Skopincev, S.V. On optimal harvesting of a resource on a circle. Math. Notes 2017, 102, 521–532. [Google Scholar] [CrossRef]
- Moberg, E.A.; Pinsky, M.L.; Fenichel, E.P. Capital investment for optimal exploitation of renewable resource stocks in the age of global change. Ecol. Econ. 2019, 165, 106335. [Google Scholar]
- Gromov, D.; Bondarev, A.; Gromova, E. On periodic solution to control problem with time-driven switching. Optim. Lett. 2022, 16, 2019–2031. [Google Scholar] [CrossRef]
- Xin, B.; Peng, W.; Sun, M. Optimal coordination strategy for international production planning and pollution abating under cap–and–trade regulations. Int. J. Environ. Res. Public Health 2019, 16, 3490. [Google Scholar] [CrossRef]
- Gromov, D.; Shigoka, T.; Bondarev, A. Optimality and sustainability of hybrid limit cycles in the pollution control problem with regime shifts. Environ. Dev. Sustain. 2023, 1–18. [Google Scholar] [CrossRef]
- Su, S.; Tur, A. Estimation of Initial Stock in Pollution Control Problem. Mathematics 2022, 10, 3457. [Google Scholar] [CrossRef]
- Huang, X.; He, P.; Hua, Z. A cooperative differential game of transboundary industrial pollution between two regions. J. Clean. Prod. 2015, 120, 43–52. [Google Scholar] [CrossRef]
- Jørgensen, S.; Martín-Herrán, G.; Zaccour, G. Dynamic games in the economics and management of pollution. Environ. Model. Assess. 2010, 15, 433–467. [Google Scholar]
- Gromova, E.V.; Tur, A.V.; Balandina, L.I. A game-theoretic model of pollution control with asymmetric time horizons. Contrib. Game Theory Manag. 2016, 9, 170–179. [Google Scholar]
- Shevkoplyas, E.V.; Kostyunin, S.Y. Modeling of environmental projects under condition of a random time horizon. Contrib. Game Theory Manag. 2011, 4, 447–459. [Google Scholar]
- Aleksandrov, A.Y.; Andriyanova, N.R. Fixed–time stability of switched systems with application to a problem of formation control. Nonlinear Anal. Hybrid Syst. 2021, 40, 101008. [Google Scholar] [CrossRef]
- Breton, M.; Zaccour, G.; Zahaf, M. A differential game of joint implementation of environmental projects. Automatica 2005, 41, 1737–1749. [Google Scholar] [CrossRef]
- De Zeeuw, A.; Zemel, A. Regime shifts and uncertainty in pollution control. J. Econ. Dyn. Control 2012, 36, 939–950. [Google Scholar] [CrossRef][Green Version]
- Kostyunin, S.; Shevkoplyas, E. On simplification of integral payoff in the dif-ferential games with random duration. Vestn. St. Petersburg Univ. 2011, 10, 47–56. [Google Scholar]
- Goodland, R. The concept of environmental sustainability. Annu. Rev. Ecol. Syst. 1995, 26, 1–24. [Google Scholar] [CrossRef]
- Gromov, D.; Gromova, E. On a class of hybrid differential games. Dyn. Games Appl. 2017, 7, 266–288. [Google Scholar] [CrossRef]
- Balas, T.; Tur, A. The Hamilton–Jacobi–Bellman Equation for Differential Games with Composite Distribution of Random Time Horizon. Mathematics 2023, 11, 462. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Tur, A.; Wang, H. Sustainable Optimal Control for Switched Pollution-Control Problem with Random Duration. Entropy 2023, 25, 1426. https://doi.org/10.3390/e25101426
Wu Y, Tur A, Wang H. Sustainable Optimal Control for Switched Pollution-Control Problem with Random Duration. Entropy. 2023; 25(10):1426. https://doi.org/10.3390/e25101426
Chicago/Turabian StyleWu, Yilun, Anna Tur, and Hongbo Wang. 2023. "Sustainable Optimal Control for Switched Pollution-Control Problem with Random Duration" Entropy 25, no. 10: 1426. https://doi.org/10.3390/e25101426
APA StyleWu, Y., Tur, A., & Wang, H. (2023). Sustainable Optimal Control for Switched Pollution-Control Problem with Random Duration. Entropy, 25(10), 1426. https://doi.org/10.3390/e25101426








