Application of the Esscher Transform to Pricing Forward Contracts on Energy Markets in a Fuzzy Environment
Abstract
1. Introduction
2. Overview of Valuation Methods
2.1. Electricity Crisp Prices Models
2.1.1. Jump-Diffusion Models
2.1.2. Regime Switching Models
2.1.3. ARMA Models
2.1.4. Other Approaches
2.2. Fuzzy Approaches to Pricing Derivatives
3. The Proposed Model Underlying Dynamics of Electricity Spot Prices
4. Pricing Forward Contracts with Crisp Parameters
5. The Adjusted Fuzzy Decision-Making Method
6. Modified Method of Decision Making in a Fuzzy Environment
7. Numerical Examples
7.1. Automatized Investment Decision-Making
7.2. Price’s -Level Sets, Membership Function, Sensitivity Analysis
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cai, N.; Kou, S.G. Option Pricing Under a Mixed-Exponential Jump Diffusion Model. Manag. Sci. 2011, 57, 2067–2081. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, O.E. Processes of normal inverse Gaussian type. Financ. Stoch. 1998, 2, 41–68. [Google Scholar] [CrossRef]
- Madan, D.B.; Seneta, E. The Variance Gamma (V.G.) Model for Share Market Returns. J. Bus. 1990, 63, 511–524. [Google Scholar] [CrossRef]
- Nowak, P. Option Pricing with Levy Process in a Fuzzy Framework; Atanassov, K., Homenda, W., Hryniewicz, O., Kacprzyk, J., Krawczak, M., Nahorski, Z., Szmidt, E., Zadrozny, S., Eds.; Recent Advances in Fuzzy Sets, Intuitionistic Fuzzy Sets, Generalized Nets and Related Topics; Polish Academy of Sciences: Warsaw, Poland, 2011. [Google Scholar]
- Nowak, P.; Romaniuk, M. Application of Levy processes and Esscher transformed martingale measures for option pricing in fuzzy framework. J. Comput. Appl. Math. 2014, 263, 129–151. [Google Scholar] [CrossRef]
- Nowak, P. On Jacod-Grigelionis characteristics for Hilbert space valued semimartingales. Stoch. Anal. Appl. 2002, 20, 963–998. [Google Scholar] [CrossRef]
- Deelstra, G.; Simon, M. Multivariate European option pricing in a Markov-modulated Lévy framework. J. Comput. Appl. Math. 2017, 317, 171–187. [Google Scholar] [CrossRef]
- Bao, J.; Zhao, Y. Option pricing in Markov-modulated exponential Lévy models with stochastic interest rates. J. Comput. Appl. Math. 2019, 357, 146–160. [Google Scholar] [CrossRef]
- Feng, C.; Tan, J.; Jiang, Z.; Chen, S. A generalized European option pricing model with risk management. Phys. A Stat. Mech. Its Appl. 2020, 545, 123797. [Google Scholar] [CrossRef]
- Tan, X.; Li, S.; Wang, S. Pricing European-Style Options in General Lévy Process with Stochastic Interest Rate. Mathematics 2020, 8, 731. [Google Scholar] [CrossRef]
- Nowak, P.; Romaniuk, M. Valuing catastrophe bonds involving correlation and CIR interest rate model. Comput. Appl. Math. 2018, 37, 365–394. [Google Scholar] [CrossRef]
- Pawłowski, M.; Nowak, P. Stochastic approach to model spot price and value forward contracts on energy markets under uncertainty. J. Ambient. Intell. Humaniz. Comput. 2021, 1–15. [Google Scholar] [CrossRef]
- Nowak, P.; Pawłowski, M. Option Pricing With Application of Levy Processes and the Minimal Variance Equivalent Martingale Measure Under Uncertainty. IEEE Trans. Fuzzy Syst. 2017, 25, 402–416. [Google Scholar] [CrossRef]
- Nowak, P.; Pawłowski, M. Pricing European options under uncertainty with application of Levy processes and the minimal Lq equivalent martingale measure. J. Comput. Appl. Math. 2019, 345, 416–433. [Google Scholar] [CrossRef]
- Ma, X.; Fei, Q.; Qin, H.; Li, H.; Chen, W.T. A new efficient decision making algorithm based on interval-valued fuzzy soft set. Appl. Intell. 2021, 51, 3226–3240. [Google Scholar] [CrossRef]
- Ma, X.; Qin, H.; Abawajy, J.H. Interval-Valued Intuitionistic Fuzzy Soft Sets Based Decision-Making and Parameter Reduction. IEEE Trans. Fuzzy Syst. 2022, 30, 357–369. [Google Scholar] [CrossRef]
- Nomikos, N.; Soldatos, O.A. Analysis of model implied volatility for jump diffusion models: Empirical evidence from the Nordpool market. Energy Econ. 2010, 32, 302–312. [Google Scholar] [CrossRef]
- Miyahara, Y. A Note on Esscher Transformed Martingale Measures for Geometric Levy Processes; Discussion Papers in Economics; Nagoya City University: Nagoya, Japan, 2004; Volume 379, pp. 1–14. [Google Scholar]
- Lucia, J.; Schwartz, E. Electricity prices and power derivatives: Evidence from the Nordic Power Exchange. Rev. Deriv. Res. 2002, 5, 5–50. [Google Scholar] [CrossRef]
- Cartea, A.; Figueroa, M. Pricing in Electricity Markets: A mean reverting jump diffusion model with seasonality. Appl. Math. Financ. 2005, 12, 313–335. [Google Scholar] [CrossRef]
- Bodea, A.; Mare, B. Valuation of Swing Options in Electricity Commodity Markets; University of Heidelberg: Heidelberg, Germany, 2012. [Google Scholar]
- Geman, H.; Roncoroni, A. Understanding the Fine Structure of Electricity Prices. J. Bus. 2006, 79, 1225–1261. [Google Scholar] [CrossRef]
- Janczura, J.; Weron, R. An empirical comparison of alternate regime-switching models for electricity spot prices. Energy Econ. 2010, 32, 1059–1073. [Google Scholar] [CrossRef]
- de Jong, C.; Huisman, R. Option Formulas for Mean-Reverting Power Prices with Spikes; Energy Global Research Paper; Department of Finance: Sacramento, CA, USA, 2002.
- Lindstrom, E.; Regland, F. Modelling extreme dependence between European electricity markets. Energy Econ. 2012, 34, 899–904. [Google Scholar] [CrossRef]
- Seifert, J.; Uhrig-Homburg, M. Modelling jumps in electricity prices: Theory and empirical evidence. Rev. Deriv. Res. 2007, 10, 59–85. [Google Scholar] [CrossRef]
- Benth, F.; Šaltytė-Benth, J. The normal inverse Gaussian distribution and spot price modelling in energy markets. Int. J. Theor. Appl. Financ. 2004, 7, 177–192. [Google Scholar] [CrossRef]
- Benth, F.; Kallsen, J.; Meyer-Brandis, T. A Non-Gaussian Ornstein-Uhlenbeck Process for Electricity Spot Price Modeling and Derivatives Pricing. Appl. Math. Financ. 2007, 14, 153–169. [Google Scholar] [CrossRef]
- Benth, F.; Kiesel, R.; Nazarova, A. A critical empirical study of three electricity price models. Energy Econ. 2011, 34, 1589–1616. [Google Scholar] [CrossRef]
- Kluppelberg, C.; Meyer-Brandis, T.; Schmidt, A. Electricity spot price modelling with a view towards extreme spike risk. Quant. Financ. 2010, 10, 963–974. [Google Scholar] [CrossRef]
- Wu, H.C. Pricing European options based on the fuzzy pattern of Black-Scholes formula. Comput. Oper. Res. 2004, 31, 1069–1081. [Google Scholar] [CrossRef]
- Chrysafis, K.A.; Papadopoulos, B.K. On theoretical pricing of options with fuzzy estimators. J. Comput. Appl. Math. 2009, 223, 552–566. [Google Scholar] [CrossRef]
- Thiagarajah, K.; Appadoo, S.S.; Thavaneswaran, A. Option valuation model with adaptive fuzzy numbers. Comput. Math. Appl. 2007, 53, 831–841. [Google Scholar] [CrossRef]
- Xian-Dong, W.; Jian-Min, H. Reload option pricing in fuzzy framework. In Proceedings of the 2014 International Conference on Management Science Engineering 21th Annual Conference Proceedings, Helsinki, Finland, 17–19 August 2014; pp. 147–152. [Google Scholar]
- Zhang, W.G.; Xiao, W.L.; Kong, W.T.; Zhang, Y. Fuzzy pricing of geometric Asian options and its algorithm. Appl. Soft Comput. 2015, 28, 360–367. [Google Scholar] [CrossRef]
- Yoshida, Y. The valuation of European options in uncertain environment. Eur. J. Oper. Res. 2003, 145, 221–229. [Google Scholar] [CrossRef]
- De Andres-Sanchez, J. Pricing European Options with Triangular Fuzzy Parameters: Assessing Alternative Triangular Approximations in the Spanish Stock Option Market. Int. J. Fuzzy Syst. 2018, 20, 1624–1643. [Google Scholar] [CrossRef]
- Nowak, P.; Romaniuk, M. Computing option price for Levy process with fuzzy parameters. Eur. J. Oper. Res. 2010, 201, 206–210. [Google Scholar] [CrossRef]
- Nowak, P.; Romaniuk, M. A fuzzy approach to option pricing in a Levy process setting. Int. J. Appl. Math. Comput. Sci. 2013, 23, 613–622. [Google Scholar] [CrossRef]
- Liu, W.Q.; Li, S.H. European option pricing model in a stochastic and fuzzy environment. Appl.-Math. J. Chin. Univ. 2013, 28, 321–334. [Google Scholar] [CrossRef]
- Zhang, H.; Watada, J. A European Call Options Pricing Model Using the Infinite Pure Jump Levy Process in a Fuzzy Environment. IEEJ Trans. Electr. Electron. Eng. 2018, 13, 1468–1482. [Google Scholar] [CrossRef]
- Wang, X.; Hea, J. A geometric Levy model for n-fold compound option pricing in a fuzzy framework. J. Comput. Appl. Math. 2016, 306, 248–264. [Google Scholar] [CrossRef]
- Wu, L.; Wang, J.t.; Liu, J.f.; Zhuang, Y.m. The Total Return Swap Pricing Model under Fuzzy Random Environments. Discret. Dyn. Nat. Soc. 2017, 2017, 9762841. [Google Scholar] [CrossRef]
- Li, H.; Ware, A.; Di, L.; Yuan, G.; Swishchuk, A.; Yuan, S. The application of nonlinear fuzzy parameters PDE method in pricing and hedging European options. Fuzzy Sets Syst. 2018, 331, 14–25. [Google Scholar] [CrossRef]
- Qin, X.; Lin, X.W.; Shang, Q. Fuzzy pricing of binary option based on the long memory property of financial markets. J. Intell. Fuzzy Syst. 2020, 38, 4889–4900. [Google Scholar] [CrossRef]
- Dash, J.K.; Panda, S.; Panda, G.B. A new method to solve fuzzy stochastic finance problem. J. Econ. Stud. 2021. [Google Scholar] [CrossRef]
- Muzzioli, S.; Torricelli, C. A multiperiod binomial model for pricing options in a vague world. J. Econ. Dyn. Control. 2004, 28, 861–887. [Google Scholar] [CrossRef]
- Tolga, A.C. New Product Development Process Valuation using Compound Options with Type-2 Fuzzy Numbers. In Proceedings of the International Multiconference of Engineers and Computer Scientists, Hong Kong, China, 15–17 March 2017; Volume 2, pp. 1–6. [Google Scholar]
- Zmeskal, Z. Generalised soft binomial American real option pricing model (fuzzy–stochastic approach). Eur. J. Oper. Res. 2010, 207, 1096–1103. [Google Scholar] [CrossRef]
- Anzilli, L.; Facchinetti, G.; Pirotti, T. Pricing of minimum guarantees in life insurance contracts with fuzzy volatility. Inf. Sci. 2018, 460–461, 578–593. [Google Scholar] [CrossRef]
- Botta, R.F.; Harris, C.M. Approximation with generalized hyperexponential distributions: Weak convergence results. Queueing Syst. 1986, 1, 169–190. [Google Scholar] [CrossRef]
- Benth, F.E.; Sgarra, C. The Risk Premium and the Esscher Transform in Power Markets. Stoch. Anal. Appl. 2012, 30, 20–43. [Google Scholar] [CrossRef][Green Version]
- Nowak, P.; Romaniuk, M. Application of the One-Factor Affine Interest Rate Models to Catastrophe Bonds Pricing. J. Autom. Mob. Robot. Intell. Syst. 2014, 8, 19–27. [Google Scholar]
- Puri, M.L.; Ralescu, D.A. Fuzzy random variables. J. Math. Anal. Appl. 1986, 114, 409–422. [Google Scholar] [CrossRef]
- Zadeh, L. The concept of a linguistic variable and its application to approximate reasoning—I. Inf. Sci. 1975, 8, 199–249. [Google Scholar] [CrossRef]
- Zadeh, L. The concept of a linguistic variable and its application to approximate reasoning—II. Inf. Sci. 1975, 8, 301–357. [Google Scholar] [CrossRef]
- Zadeh, L. The concept of a linguistic variable and its application to approximate reasoning—III. Inf. Sci. 1975, 9, 43–80. [Google Scholar] [CrossRef]
- Fullér, R.; Majlender, P. On weighted possibilistic mean and variance of fuzzy numbers. Fuzzy Sets Syst. 2003, 136, 363–374. [Google Scholar] [CrossRef]
- Buckley, J.; Eslami, E. Pricing Stock Options Using Fuzzy Sets. Iran. J. Fuzzy Syst. 2007, 4, 1–14. [Google Scholar]
- Gil-Lafuente, A. Fuzzy Logic in Financial Analysis; Springer: Berlin, Germany, 2005. [Google Scholar]
- Piasecki, K. On Imprecise Investment Recommendations. Stud. Logic Gramm. Rhetor. 2014, 37, 179–194. [Google Scholar] [CrossRef]
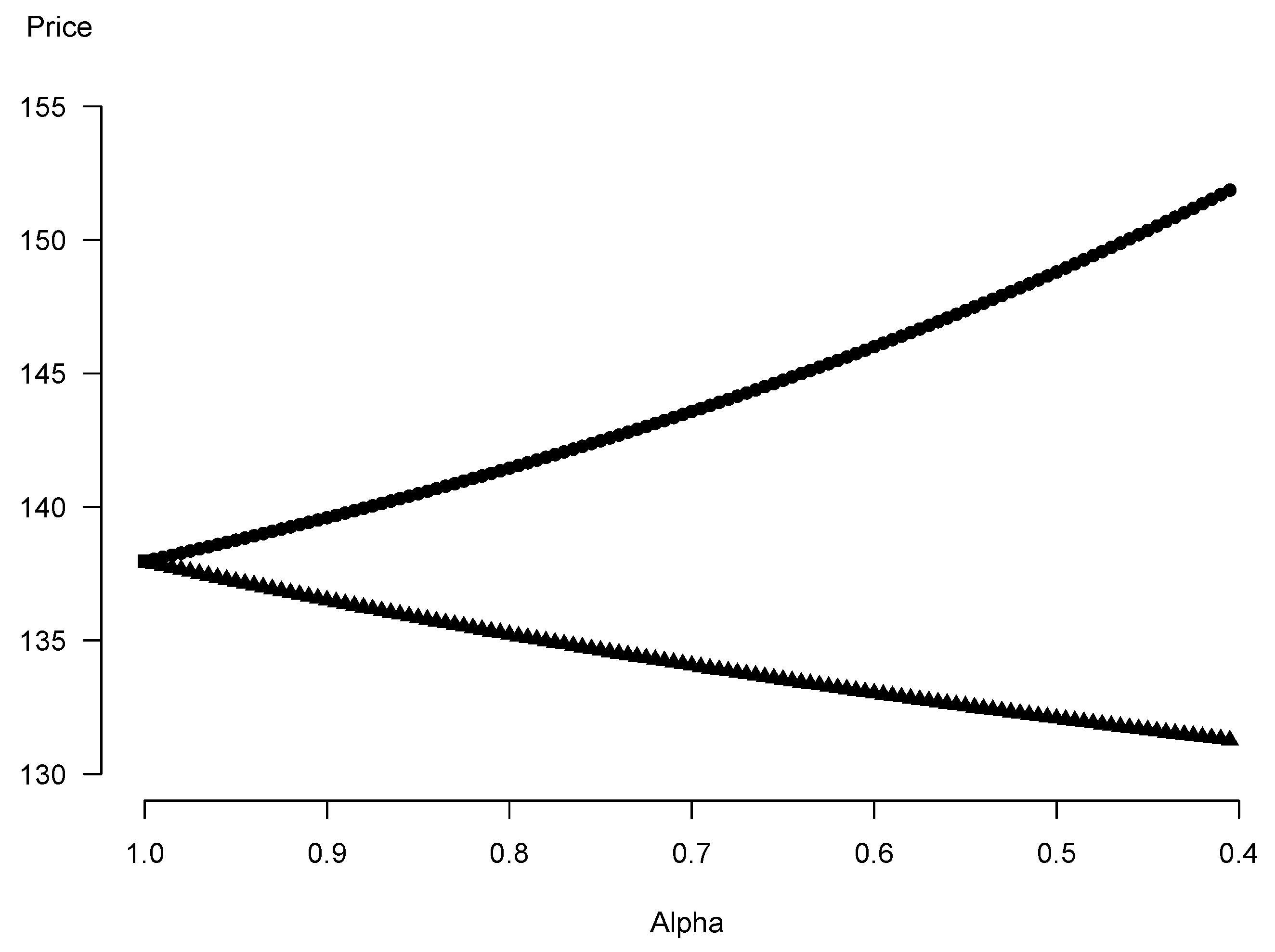
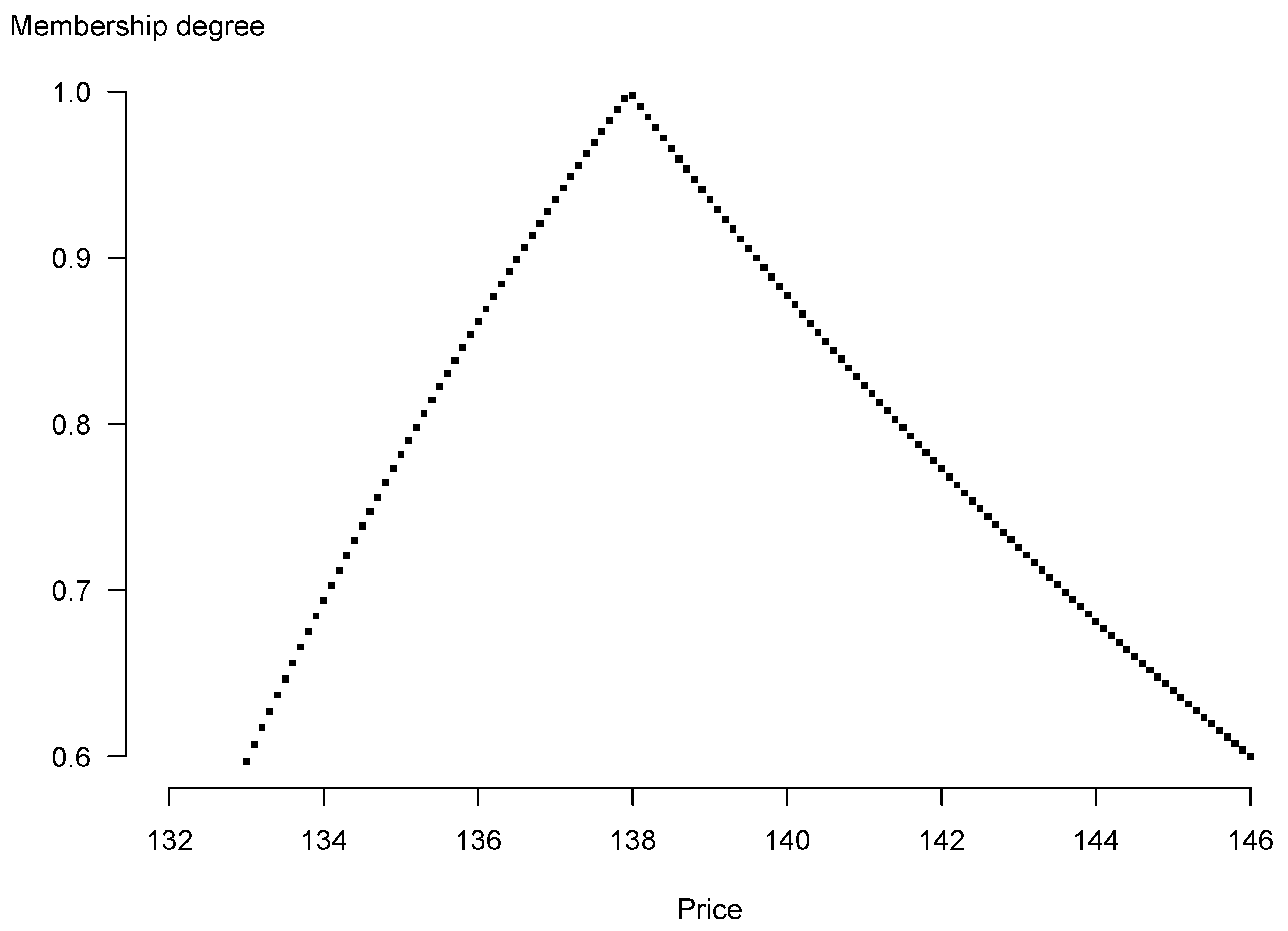
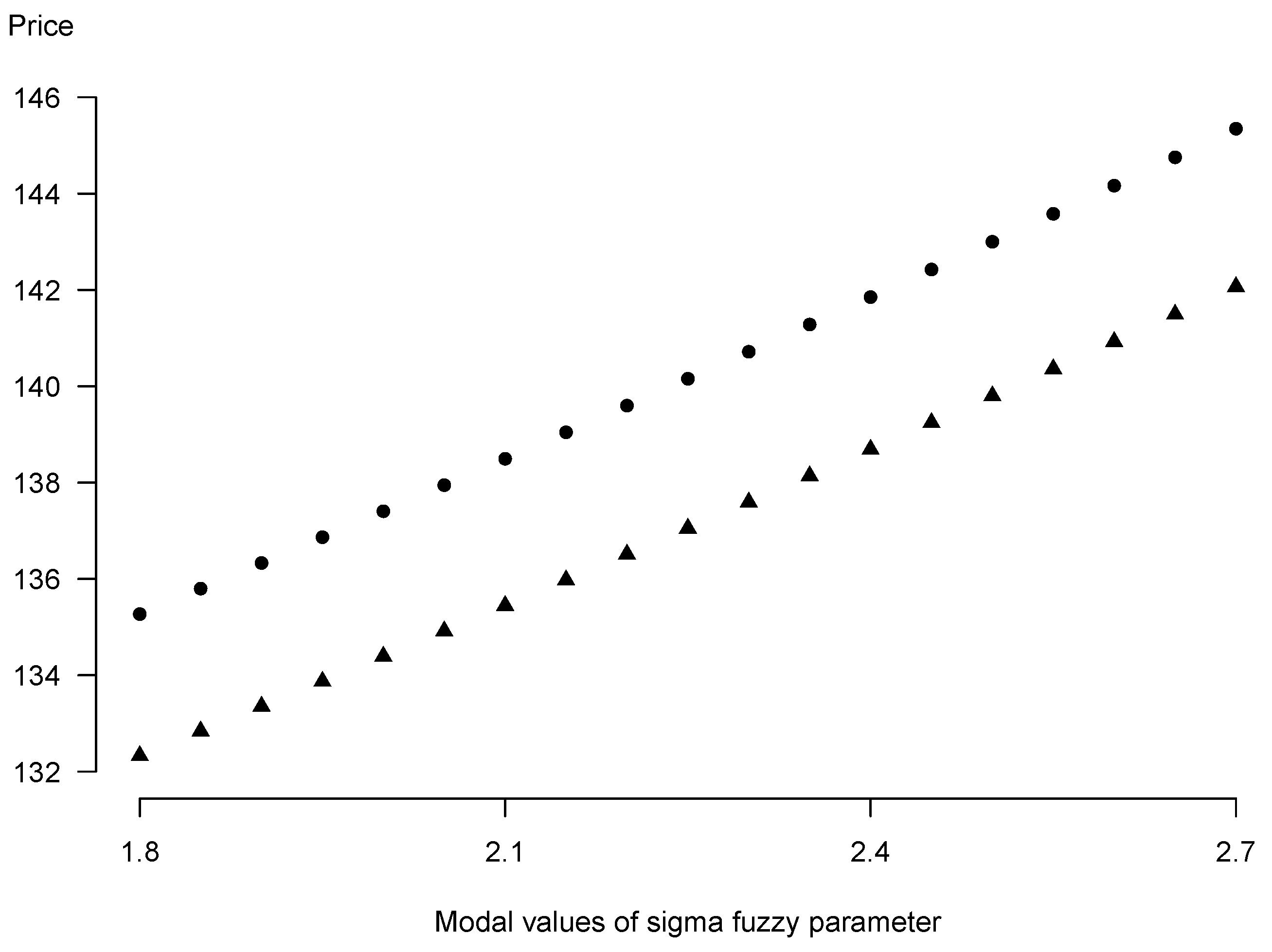
| (95, 100, 105) | |
| (110, 115, 120) | |
| (1.9, 2.2, 2.5) | |
| (20, 22.5, 25) | |
| (10, 10.5, 11) | |
| (14, 14.5, 15) | |
| (8, 8.5, 9) | |
| (48, 48.5, 49) |
| 128.5 | 0.91 | 1 | 0.09 | 0.09 | 0 | |||
| 135 | 0.22 | 1 | 0.78 | 0.78 | 0 | ∅ | ||
| 136.5 | 0.1 | 1 | 0.9 | 0.9 | 0 | |||
| 139 | 0 | 0.94 | 0.94 | 1 | 0.06 | |||
| 140 | 0 | 0.88 | 0.88 | 1 | 0.12 | ∅ | ||
| 141 | 0 | 0.82 | 0.82 | 1 | 0.18 | ∅ | ||
| 166 | 0 | 0.09 | 0.09 | 1 | 0.91 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nowak, P.; Pawłowski, M. Application of the Esscher Transform to Pricing Forward Contracts on Energy Markets in a Fuzzy Environment. Entropy 2023, 25, 527. https://doi.org/10.3390/e25030527
Nowak P, Pawłowski M. Application of the Esscher Transform to Pricing Forward Contracts on Energy Markets in a Fuzzy Environment. Entropy. 2023; 25(3):527. https://doi.org/10.3390/e25030527
Chicago/Turabian StyleNowak, Piotr, and Michał Pawłowski. 2023. "Application of the Esscher Transform to Pricing Forward Contracts on Energy Markets in a Fuzzy Environment" Entropy 25, no. 3: 527. https://doi.org/10.3390/e25030527
APA StyleNowak, P., & Pawłowski, M. (2023). Application of the Esscher Transform to Pricing Forward Contracts on Energy Markets in a Fuzzy Environment. Entropy, 25(3), 527. https://doi.org/10.3390/e25030527







