Remaining Useful Life Prediction of Rolling Bearings Based on Multi-scale Permutation Entropy and ISSA-LSTM
Abstract
:1. Introduction
2. Correlation Methods
2.1. Maximum Correlation Kurtosis Deconvolution
- (1)
- Initialize parameters such as the deconvolution period T, the number of shifts M, and the length of the filter L.
- (2)
- Calculate the and of the input signal x.
- (3)
- Compute the filtered output signal y.
- (4)
- Calculate and based on y.
- (5)
- Update the coefficients of the filter f’.
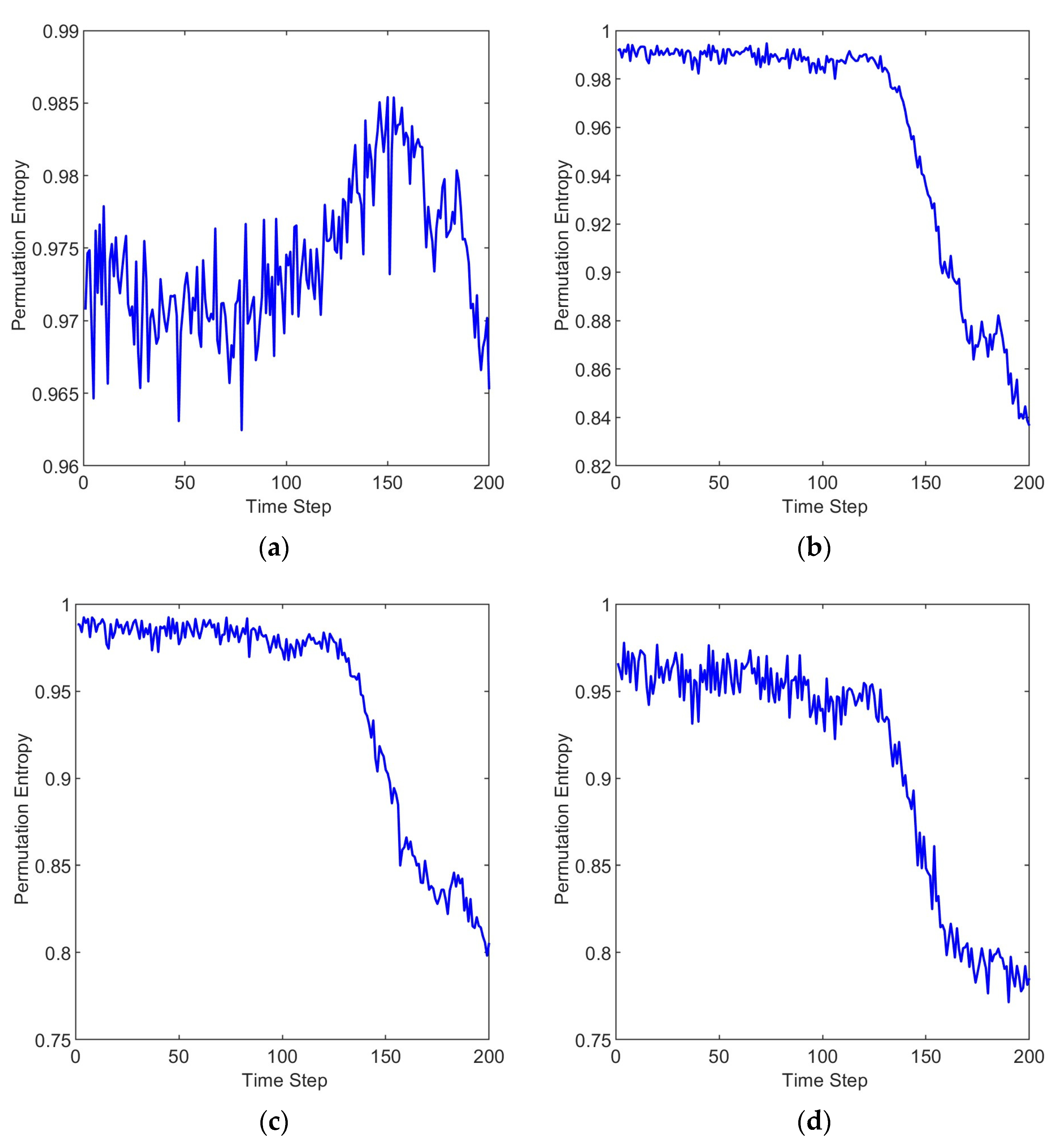
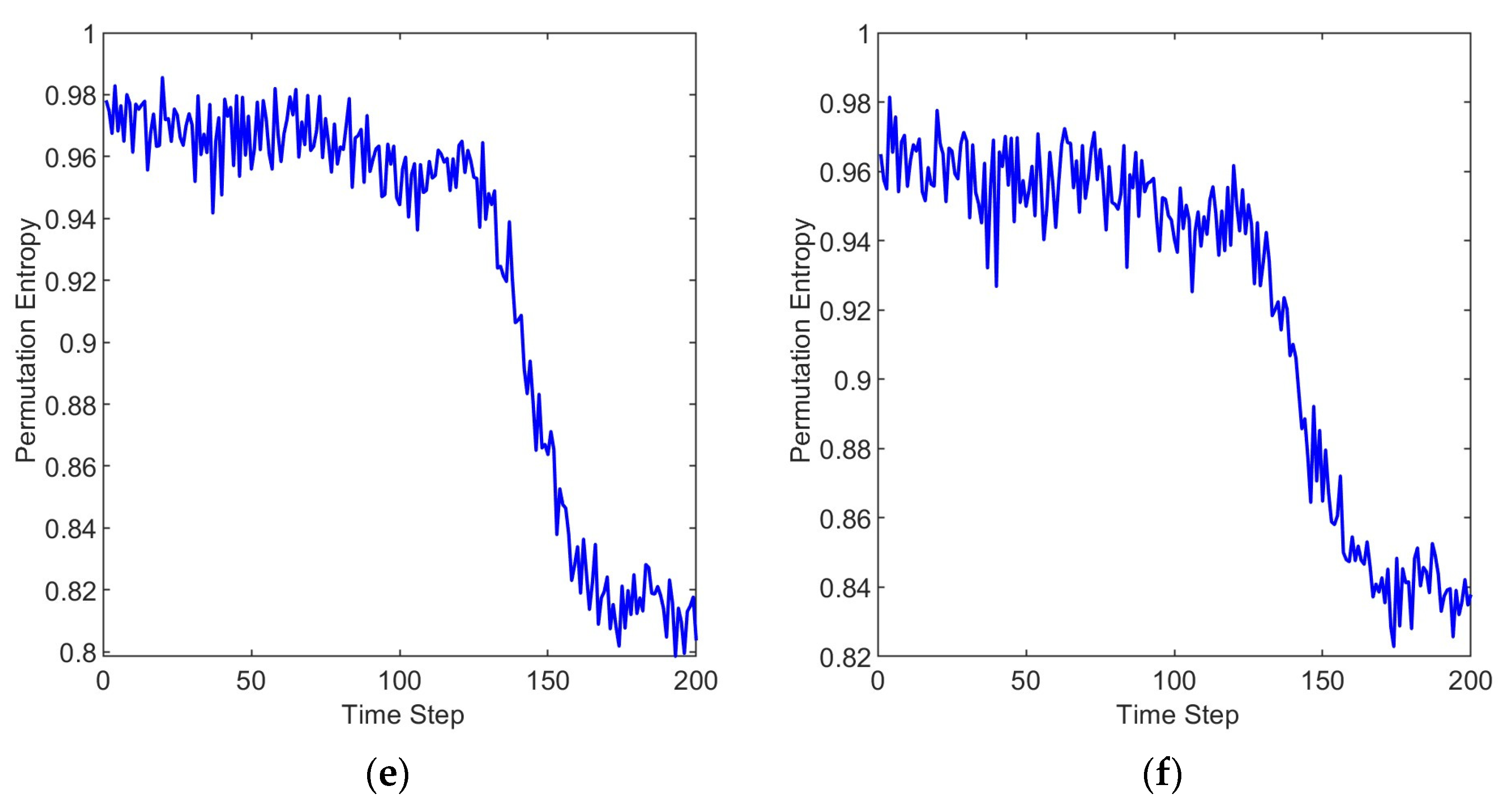
2.2. Multi-Scale Permutation Entropy
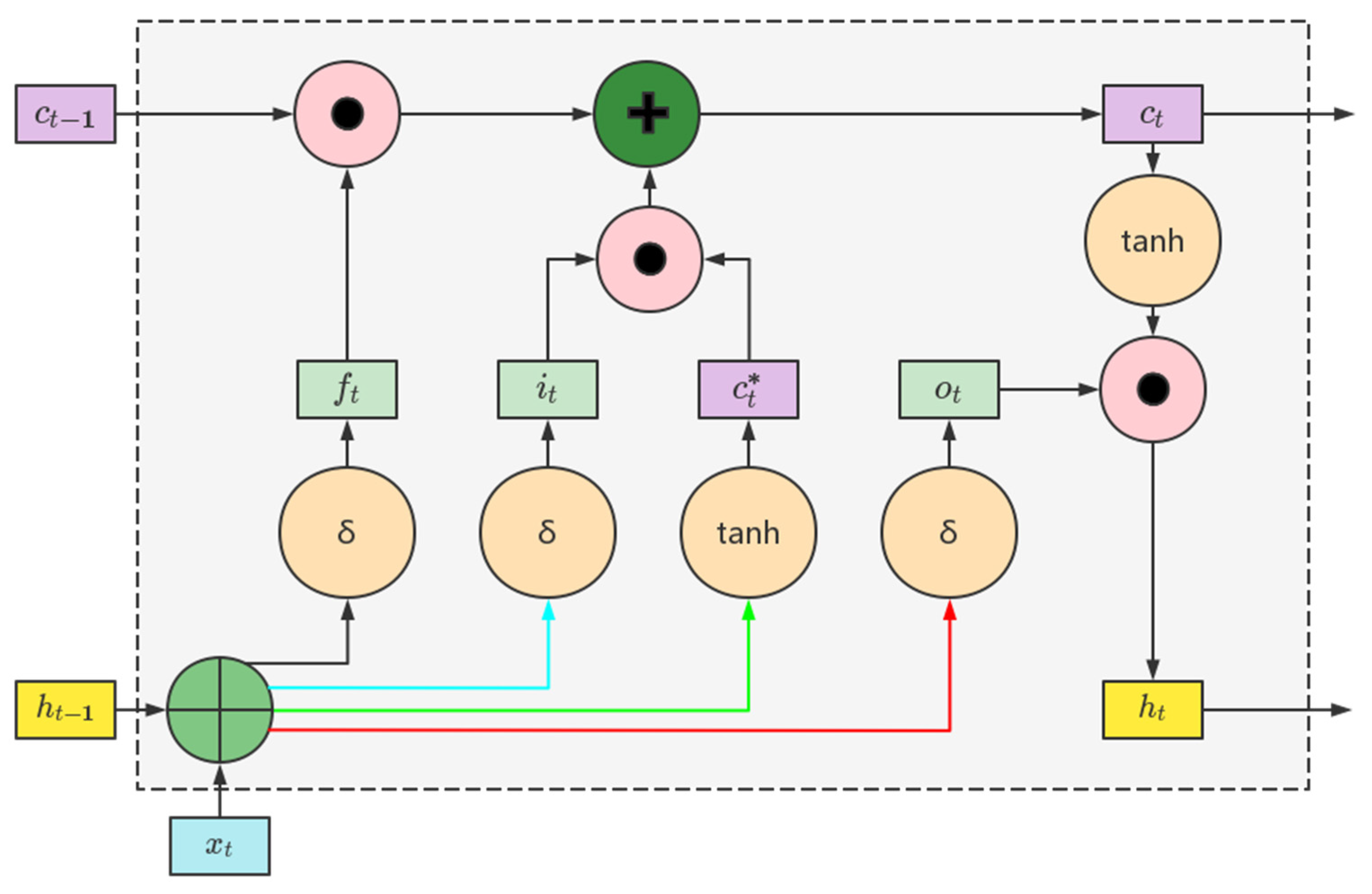
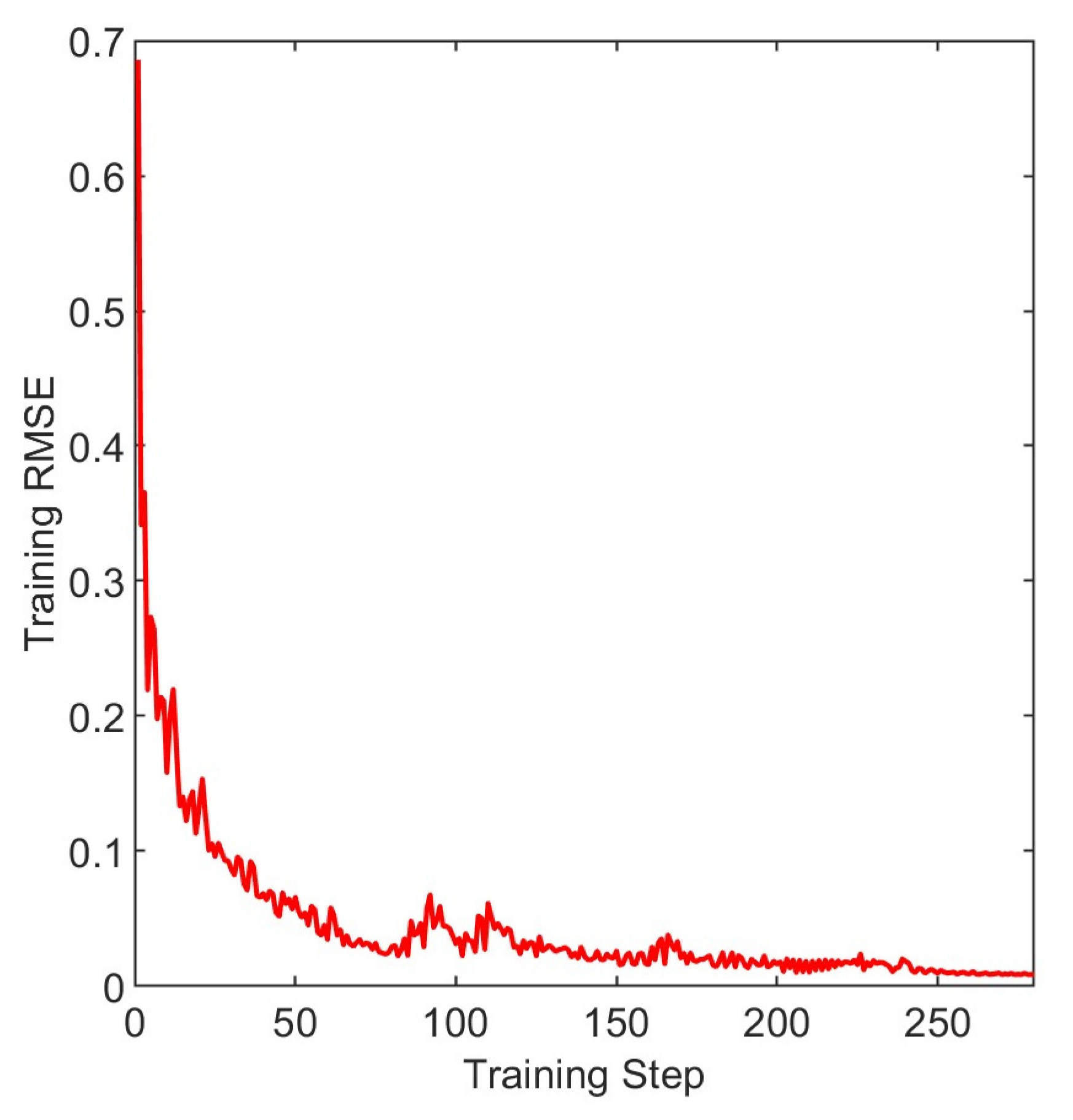
2.3. ISSA-LSTM
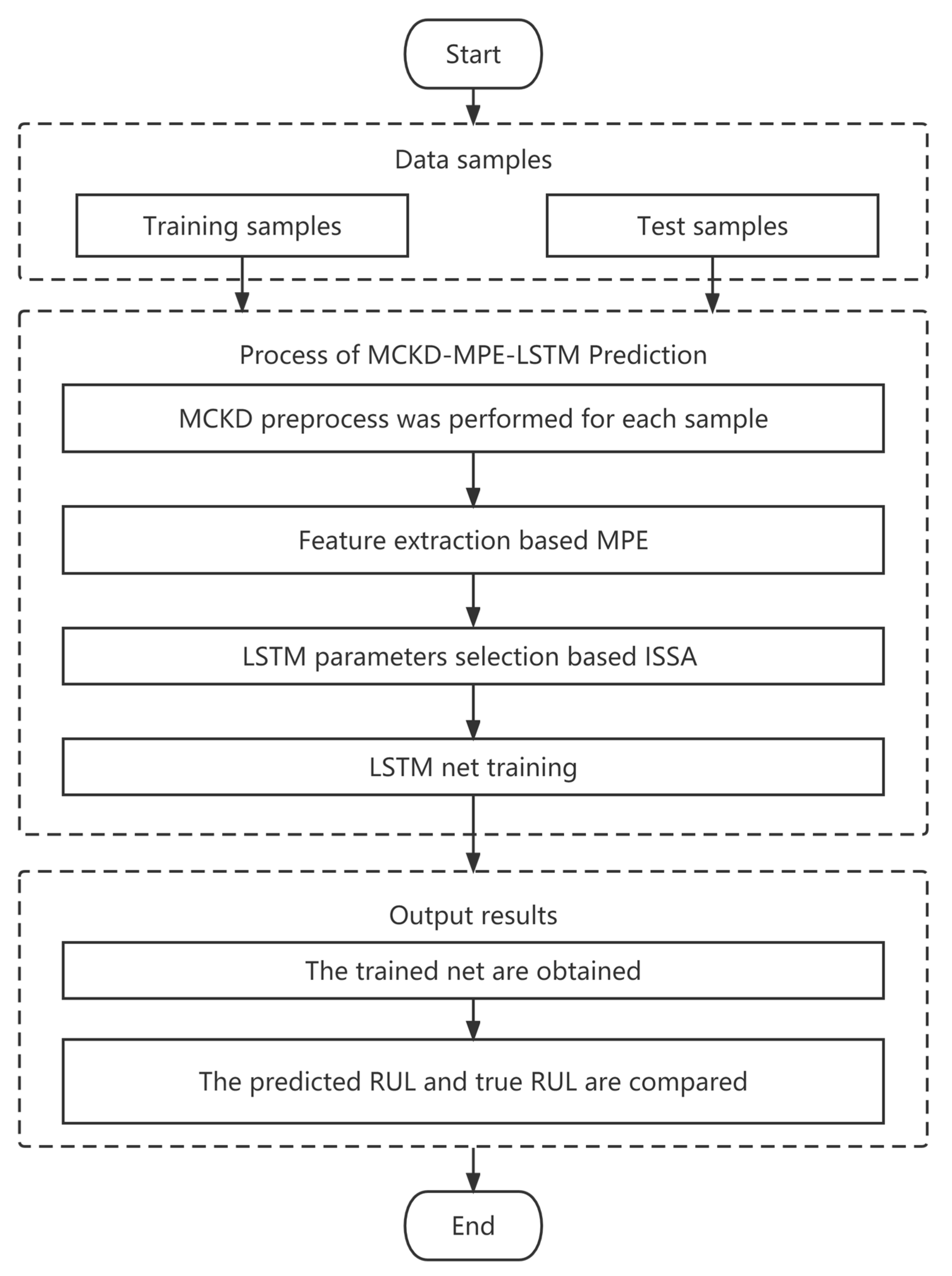
3. Experiments and Results
3.1. Experimental Platform
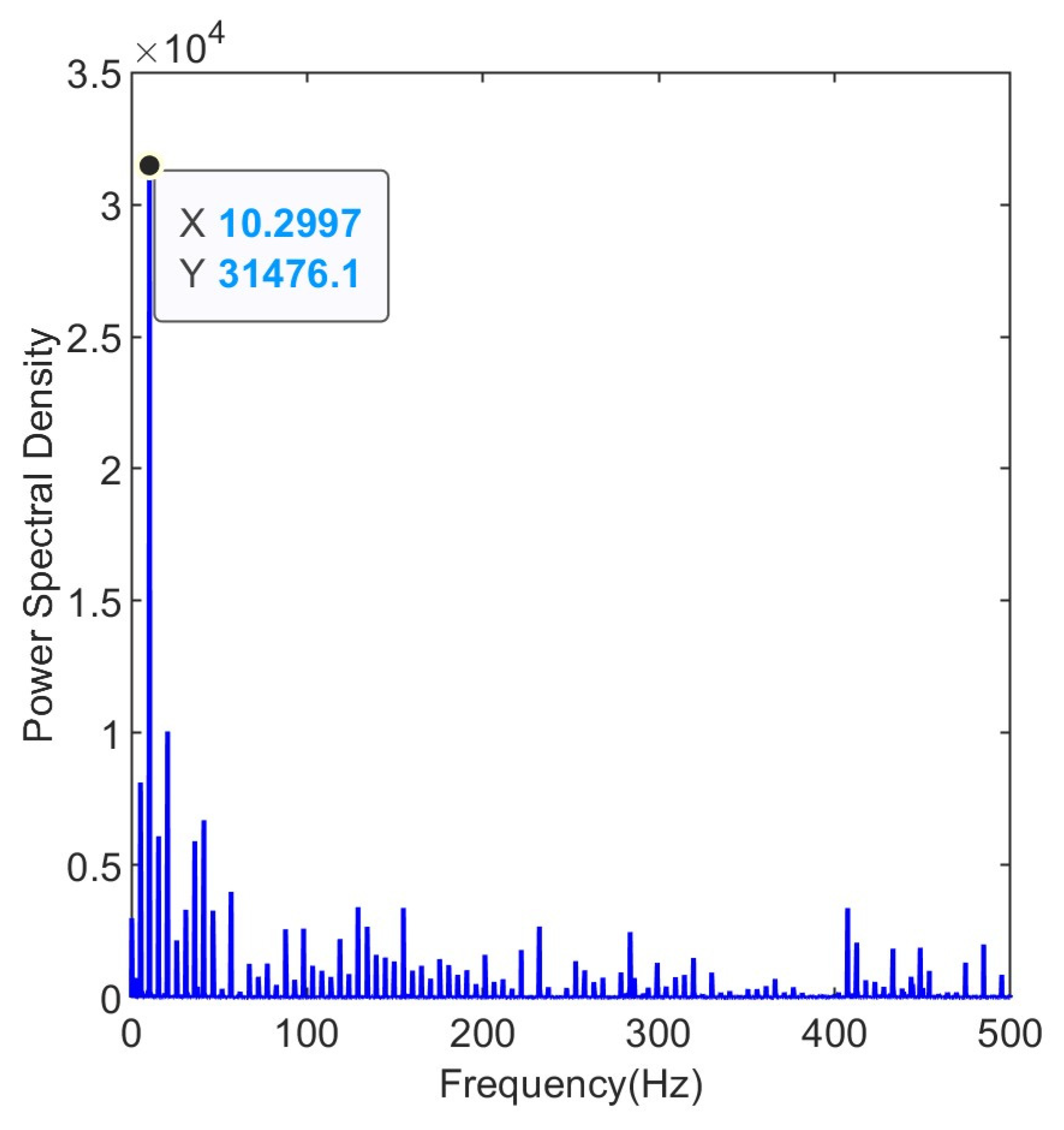
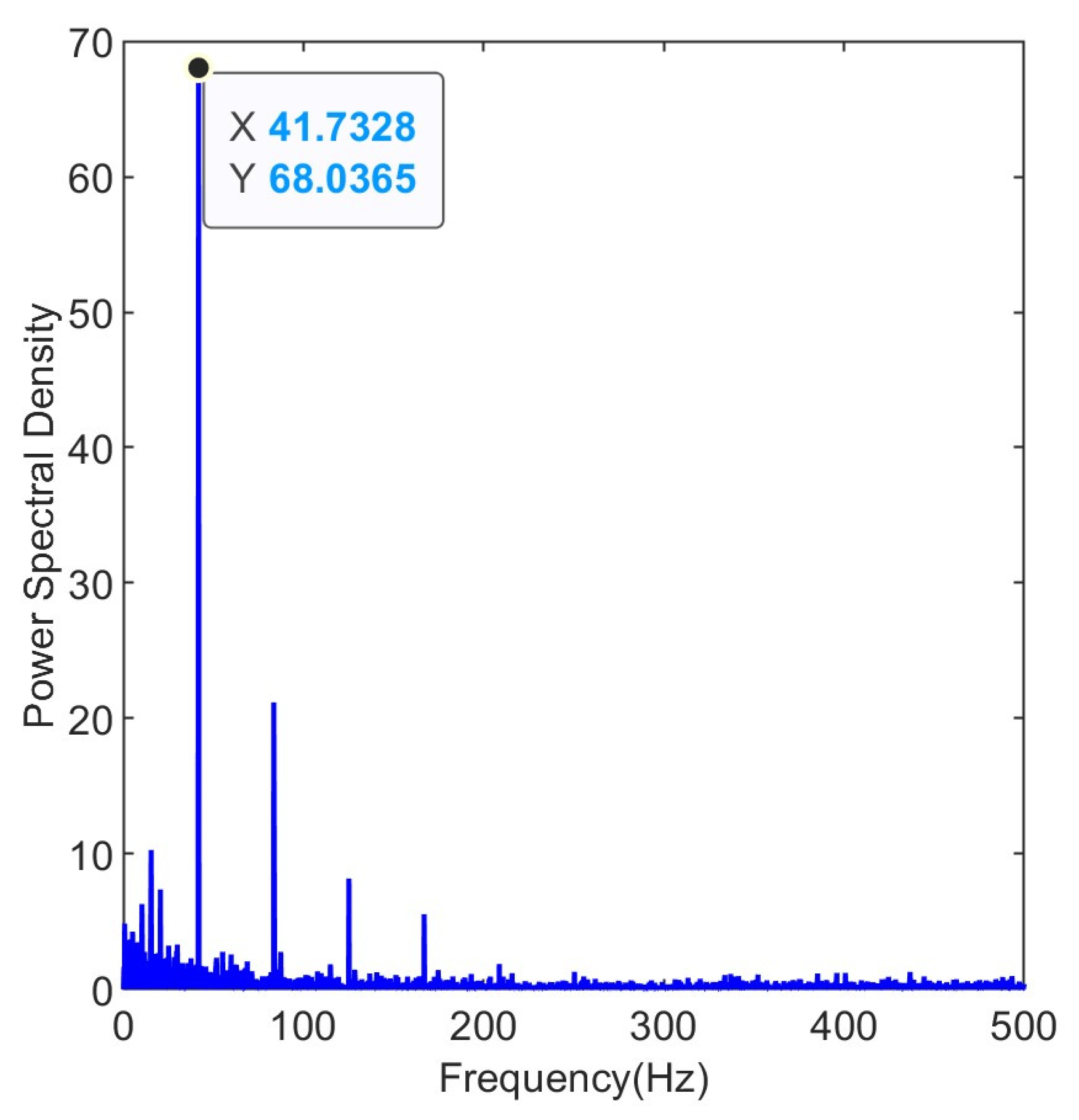
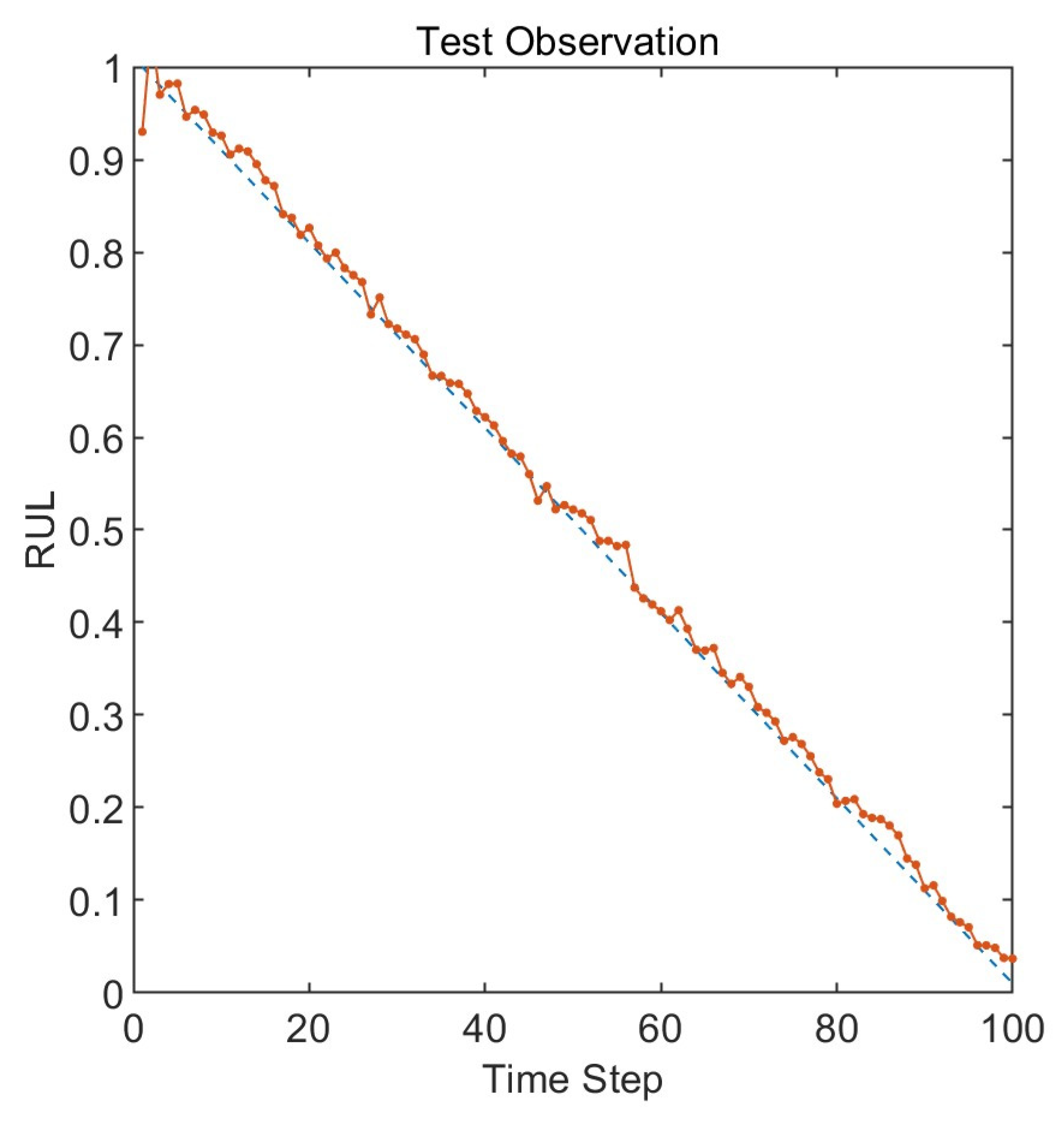
3.2. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shi, R.; Wang, B.; Wang, Z.; Liu, J.; Feng, X.; Dong, L. Research on Fault Diagnosis of Rolling Bearings Based on Variational Mode Decomposition Improved by the Niche Genetic Algorithm. Entropy 2022, 24, 825. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Kang, J.; Hao, L.; Cai, L.; Zhao, J. Bearing fault diagnosis and degradation analysis based on improved empirical mode decomposition and maximum correlated kurtosis deconvolution. J. Vibroeng. 2015, 17, 243–260. [Google Scholar]
- Heng, W.; Guangxian, N.; Jinhai, C.; Jiangming, Q. Research on Rolling Bearing State Health Monitoring and Life Prediction Based on PCA and Internet of Things with Multi-sensor. Measurement 2020, 157, 107657. [Google Scholar]
- Si, X.S.; Zhang, Z.X.; Hu, C.H. Data-Driven Remaining Useful Life Prognosis Techniques. In Springer Series in Reliability Engineering; National Defense Industry Press and Springer-Verlag GmbH: Beijing, China, 2017. [Google Scholar]
- Zhao, Z.; Qiao, B.; Wang, S.; Shen, Z.; Chen, X. A weighted multi-scale dictionary learning model and its applications on bearing fault diagnosis. J. Sound Vib. 2019, 446, 429–452. [Google Scholar] [CrossRef]
- Yan, Z.; Chao, P.; Ma, J.; Cheng, D.; Liu, C. Discrete convolution wavelet transform of signal and its application on BEV accident data analysis. Mech. Syst. Signal Process. 2021, 159, 107823. [Google Scholar] [CrossRef]
- Sharma, V.; Parey, A. Extraction of weak fault transients using variational mode decomposition for fault diagnosis of gearbox under varying speed. Eng. Fail. Anal. 2020, 107, 104204. [Google Scholar] [CrossRef]
- Zhang, Y.; Ren, G.; Wu, D.; Wang, H. Rolling bearing fault diagnosis utilizing variational mode decomposition based fractal dimension estimation method. Measurement 2021, 181, 109614. [Google Scholar] [CrossRef]
- Zhao, X.; Wu, P.; Yin, X. A quadratic penalty item optimal variational mode decomposition method based on single-objective salp swarm algorithm. Mech. Syst. Signal Process. 2020, 138, 106567.1–106567.12. [Google Scholar] [CrossRef]
- Feng, G.; Wei, H.; Qi, T.; Pei, X.; Wang, H. A Transient Electromagnetic Signal Denoising Method Based on An Improved Variational Mode Decomposition Algorithm. Measurement 2021, 184, 109815. [Google Scholar] [CrossRef]
- Mcdonald, G.L.; Zhao, Q.; Zuo, M.J. Maximum correlated Kurtosis deconvolution and application on gear tooth chip fault detection. Mech. Syst. Signal Process. 2012, 33, 237–255. [Google Scholar] [CrossRef]
- Hong, L.; Liu, X.; Zuo, H. Compound faults diagnosis based on customized balanced multiwavelets and adaptive maximum correlated kurtosis deconvolution. Measurement 2019, 146, 87–100. [Google Scholar] [CrossRef]
- Qi, Y.; Liu, F.; Gao, X.; Li, Y.; Liu, L. Composite fault diagnosis of rolling bearing based on MCKD and teager energy operator. J. Dalian Univ. Technol. 2019, 59, 10. [Google Scholar] [CrossRef]
- Lyu, Z.; Haili, Z. Application of improved MCKD method based on QGA in planetary gear compound fault diagnosis. Measurement 2019, 139, 236–248. [Google Scholar] [CrossRef]
- Miao, Y.; Zhao, M.; Lin, J.; Lei, Y. Application of an improved maximum correlated kurtosis deconvolution method for fault diagnosis of rolling element bearings. Mech. Syst. Signal Process. 2017, 92, 173–195. [Google Scholar] [CrossRef]
- Bin, Y.; Jiawei, Z.; Gairong, F.; Jianguo, W. Application of OPMCKD and ELMD in bearing compound fault diagnosis. J. Vib. Shock. 2019, 38, 59–67. [Google Scholar]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436. [Google Scholar] [CrossRef]
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. Neural Netw. IEEE Trans. 1994, 5, 157–166. [Google Scholar] [CrossRef]
- Lecun, Y.; Bottou, L. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Ren, L.; Sun, Y.; Cui, J.; Zhang, L. Bearing remaining useful life prediction based on deep autoencoder and deep neural networks. J. Manuf. Syst. 2018, 48, 71–77. [Google Scholar] [CrossRef]
- Deutsch, J.; He, D. Using Deep Learning-Based Approach to Predict Remaining Useful Life of Rotating Components. IEEE Trans. Syst. Man Cybern. Syst. 2017, 48, 11–20. [Google Scholar] [CrossRef]
- Jun, Z.; Chen, N.; Peng, W. Estimation of Bearing Remaining Useful Life Based on Multiscale Convolutional Neural Network. IEEE Trans. Ind. Electron. 2019, 66, 3208–3216. [Google Scholar]
- Xia, T.; Song, Y.; Zheng, Y.; Pan, E.; Xi, L. An ensemble framework based on convolutional bi-directional LSTM with multiple time windows for remaining useful life estimation. Comput. Ind. 2020, 115, 103182. [Google Scholar] [CrossRef]
- Kang, J.; Zhang, X.; Teng, H.; Zhao, J. Application of maximum correlated Kurtosis deconvolution on bearing fault detection and degradation analysis. Vibroeng. Procedia 2014, 4, 119–124. [Google Scholar]
- Morabito, F.C.; Labate, D.; La Foresta, F.; Bramanti, A.; Morabito, G.; Palamara, I. Multivariate Multi-Scale Permutation Entropy for Complexity Analysis of Alzheimer’s Disease EEG. Entropy 2012, 14, 1186–1202. [Google Scholar] [CrossRef]
- Akandeh, A.; Salem, F.M. Simplified Long Short-term Memory Recurrent Neural Networks: Part III. arXiv 2017, arXiv:1707.04626. [Google Scholar]
- Zhang, Y.; Lv, Y.; Ge, M. Time–frequency analysis via complementary ensemble adaptive local iterative filtering and enhanced maximum correlation kurtosis deconvolution for wind turbine fault diagnosis. Energy Rep. 2021, 7, 2418–2435. [Google Scholar] [CrossRef]
- Zhang, L.; Li, B. Roller Bearing Fault Diagnosis Method Based on Iterative Filtering and Maximum Correlation Kurtosis Deconvolution. Modul. Mach. Tool Autom. Manuf. Tech. 2019, 3, 5. [Google Scholar] [CrossRef]
- Sun, W.; Cao, Y.; Chen, X.; Chen, B.; Feng, W.; Chen, L. A two-stage method for bearing fault detection using graph similarity evaluation. Measurement 2020, 165, 1. [Google Scholar] [CrossRef]
- He, C.; Wu, T.; Gu, R.; Jin, Z.; Ma, R.; Qu, H. Rolling bearing fault diagnosis based on composite multiscale permutation entropy and reverse cognitive fruit fly optimization algorithm—Extreme learning machine—ScienceDirect. Measurement 2020, 173, 108636. [Google Scholar] [CrossRef]
- Tang, G.; Wang, X.; He, Y. A Novel Method of Fault Diagnosis for Rolling Bearing Based on Dual Tree Complex Wavelet Packet Transform and Improved Multiscale Permutation Entropy. Math. Probl. Eng. 2016, 2016, 5432648. [Google Scholar] [CrossRef]
- Zheng, J.; Cheng, J.; Yang, Y. Multiscale Permutation Entropy Based Rolling Bearing Fault Diagnosis. Shock. Vib. 2014, 2014, 1–8. [Google Scholar] [CrossRef]
- Yao, D.; Yang, J.; Pang, Z.; Nie, C.; Wen, F. Railway axle box bearing fault identification using LCD-MPE and ELM-AdaBoost. J. Vibroeng. 2018, 20, 165–174. [Google Scholar] [CrossRef]
- Shenghan, Z.; Silin, Q.; Wenbing, C.; Yiyong, X.; Yang, C. A Novel Bearing Multi-Fault Diagnosis Approach Based on Weighted Permutation Entropy and an Improved SVM Ensemble Classifier. Sensors 2018, 18, 1934. [Google Scholar]
- Zaytar, M.A.; Amrani, C.E. Sequence to Sequence Weather Forecasting with Long Short-Term Memory Recurrent Neural Networks. Int. J. Comput. Appl. 2016, 143, 7–11. [Google Scholar]
- Zhou, X.; Jing, G. Tool remaining useful life prediction method based on LSTM under variable working conditions. Int. J. Adv. Manuf. Technol. 2019, 104, 9a12. [Google Scholar] [CrossRef]
- Song, T.; Liu, C.; Wu, R.; Jin, Y.; Jiang, D. A hierarchical scheme for remaining useful life prediction with long short-term memory networks. Neurocomputing 2022, 28, 487. [Google Scholar] [CrossRef]
- Mao, W.; He, J.; Tang, J.; Li, Y. Predicting remaining useful life of rolling bearings based on deep feature representation and long short-term memory neural network. Adv. Mech. Eng. 2018, 10, 12. [Google Scholar] [CrossRef]
- Elsheikh, A.; Yacout, S.; Ouali, M.S. Bidirectional handshaking LSTM for remaining useful life prediction. Neurocomputing 2019, 323, 148–156. [Google Scholar] [CrossRef]
- Chen, C.; Shi, J.; Lu, N.; Zhu, Z.H.; Jiang, B. Data-driven predictive maintenance strategy considering the uncertainty in remaining useful life prediction. Neurocomputing 2022, 14, 494. [Google Scholar] [CrossRef]
- Liu, Z.H.; Meng, X.D.; Wei, H.L.; Chen, L.; Chen, L. A Regularized LSTM Method for Predicting Remaining Useful Life of Rolling Bearings. Int. J. Autom. Comput. 2021, 18, 581–593. [Google Scholar] [CrossRef]
- Tang, X.; Xu, W.; Tan, J.; Tan, Y. Prediction for remaining useful life of rolling bearings based on Long Short-Term Memory. J. Mach. Des. 2019, 36, 117–119. [Google Scholar]
- Morgenroth, J.; Kalenchuk, K.; Moreau-Verlaan, L.; Perras, M.A.; Khan, U.T. A novel long-short term memory network approach for stress model updating for excavations in high stress environments. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2023, 17, 196–216. [Google Scholar] [CrossRef]
- Xiang, S.; Qin, Y.; Zhu, C.; Wang, Y.; Chen, H. Long short-term memory neural network with weight amplification and its application into gear remaining useful life prediction. Eng. Appl. Artif. Intell. 2020, 91, 103587. [Google Scholar] [CrossRef]
- Wang, B.; Lei, Y.; Li, N. A Hybrid Prognostics Approach for Estimating Remaining Useful Life of Rolling Element Bearings. IEEE Trans. Reliab. 2018, 6, 173–182. [Google Scholar] [CrossRef]
- Wang, B.; Lei, Y.; Li, N.; Yan, T. Deep separable convolutional network for remaining useful life prediction of machinery. Mech. Syst. Signal Process. 2019, 134, 106330. [Google Scholar] [CrossRef]
- Wu, S.-D.; Wu, P.-H.; Wu, C.-W.; Ding, J.-J.; Wang, C.-C. Bearing Fault Diagnosis Based on Multiscale Permutation Entropy and Support Vector Machine. Entropy 2012, 14, 1343–1356. [Google Scholar] [CrossRef]
- Zhang, Y.; Lv, Y.; Ge, M. A Rolling Bearing Fault Classification Scheme Based on k-Optimized Adaptive Local Iterative Filtering and Improved Multiscale Permutation Entropy. Entropy 2021, 23, 191. [Google Scholar] [CrossRef]
- Zhang, W.; Zhou, J. Fault Diagnosis for Rolling Element Bearings Based on Feature Space Reconstruction and Multiscale Permutation Entropy. Entropy 2019, 21, 519. [Google Scholar] [CrossRef]
- Zhu, X.; Zhang, P.; Xie, M. A Joint Long Short-Term Memory and AdaBoost regression approach with application to remaining useful life estimation. Measurement 2021, 170, 108707. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, H.; Li, X.; Gao, S.; Guo, K.; Wei, Y. Fault Diagnosis of Mine Ventilator Bearing Based on Improved Variational Mode Decomposition and Density Peak Clustering. Machines 2022, 11, 27. [Google Scholar] [CrossRef]
- Abdelli, K.; Griesser, H.; Pachnicke, S. A Hybrid CNN-LSTM Approach for Laser Remaining Useful Life Prediction. arXiv 2022, arXiv:2203.12415. [Google Scholar]




| Operating Condition | Radial Force (kN) | Rotating Speed (rpm) | Bearing Dataset |
|---|---|---|---|
| Condition 1 | 12 | 2100 | Bearing 1–1 Bearing 1–2 Bearing 1–3 Bearing 1–4 Bearing 1–5 |
| Condition 2 | 11 | 2250 | Bearing 2–1 Bearing 2–2 Bearing 2–3 Bearing 2–4 Bearing 2–5 |
| Condition 3 | 10 | 2400 | Bearing 3–1 Bearing 3–2 Bearing 3–3 Bearing 3–4 Bearing 3–5 |
| Method | VMD-SVM | MCKD-SVM | VMD-LSTM | MCKD-LSTM |
|---|---|---|---|---|
| RMSE | 0.023 | 0.015 | 0.012 | 0.007 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Zhang, X.; Ren, M.; Xu, T.; Lu, C.; Zhao, Z. Remaining Useful Life Prediction of Rolling Bearings Based on Multi-scale Permutation Entropy and ISSA-LSTM. Entropy 2023, 25, 1477. https://doi.org/10.3390/e25111477
Wang H, Zhang X, Ren M, Xu T, Lu C, Zhao Z. Remaining Useful Life Prediction of Rolling Bearings Based on Multi-scale Permutation Entropy and ISSA-LSTM. Entropy. 2023; 25(11):1477. https://doi.org/10.3390/e25111477
Chicago/Turabian StyleWang, Hongju, Xi Zhang, Mingming Ren, Tianhao Xu, Chengkai Lu, and Zicheng Zhao. 2023. "Remaining Useful Life Prediction of Rolling Bearings Based on Multi-scale Permutation Entropy and ISSA-LSTM" Entropy 25, no. 11: 1477. https://doi.org/10.3390/e25111477
APA StyleWang, H., Zhang, X., Ren, M., Xu, T., Lu, C., & Zhao, Z. (2023). Remaining Useful Life Prediction of Rolling Bearings Based on Multi-scale Permutation Entropy and ISSA-LSTM. Entropy, 25(11), 1477. https://doi.org/10.3390/e25111477






