Security of the Decoy-State BB84 Protocol with Imperfect State Preparation
Abstract
:1. Introduction
2. Intensity Fluctuations
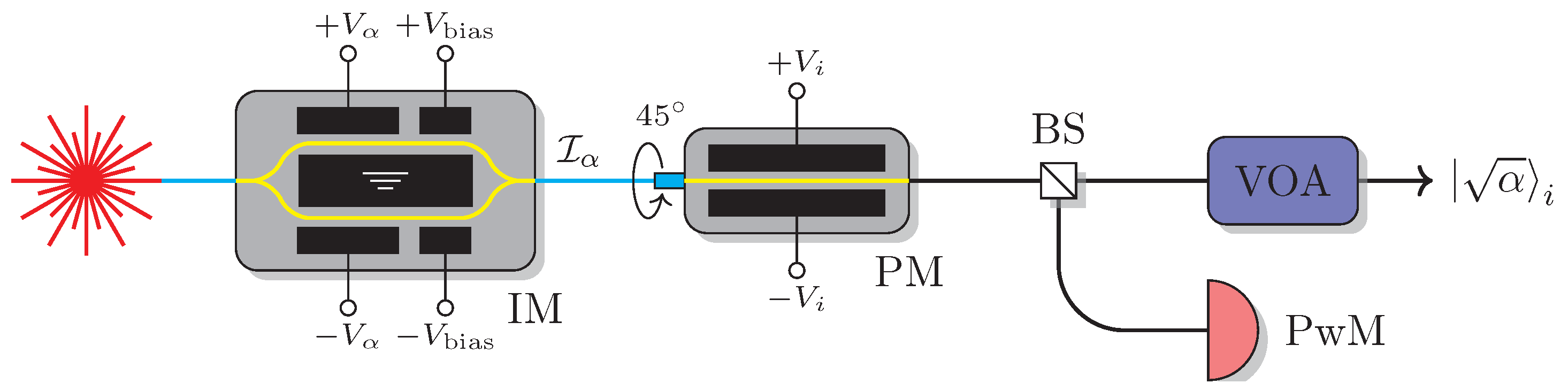
2.1. Experimental Setup
2.2. Non-Poissonian Photon-Number Statistics
3. Phase Fluctuations
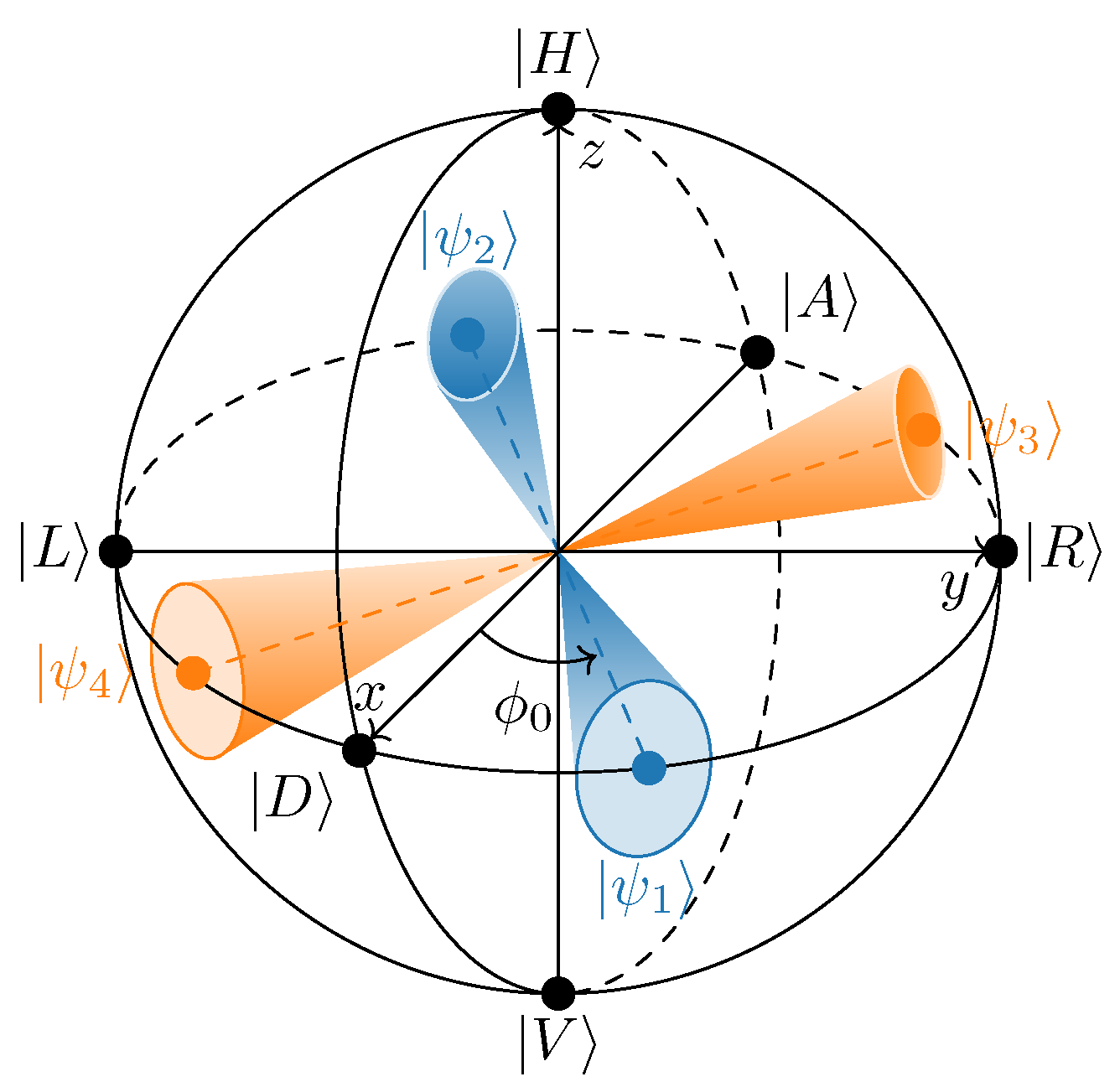
3.1. Polarization State Preparation and Basis-Dependence
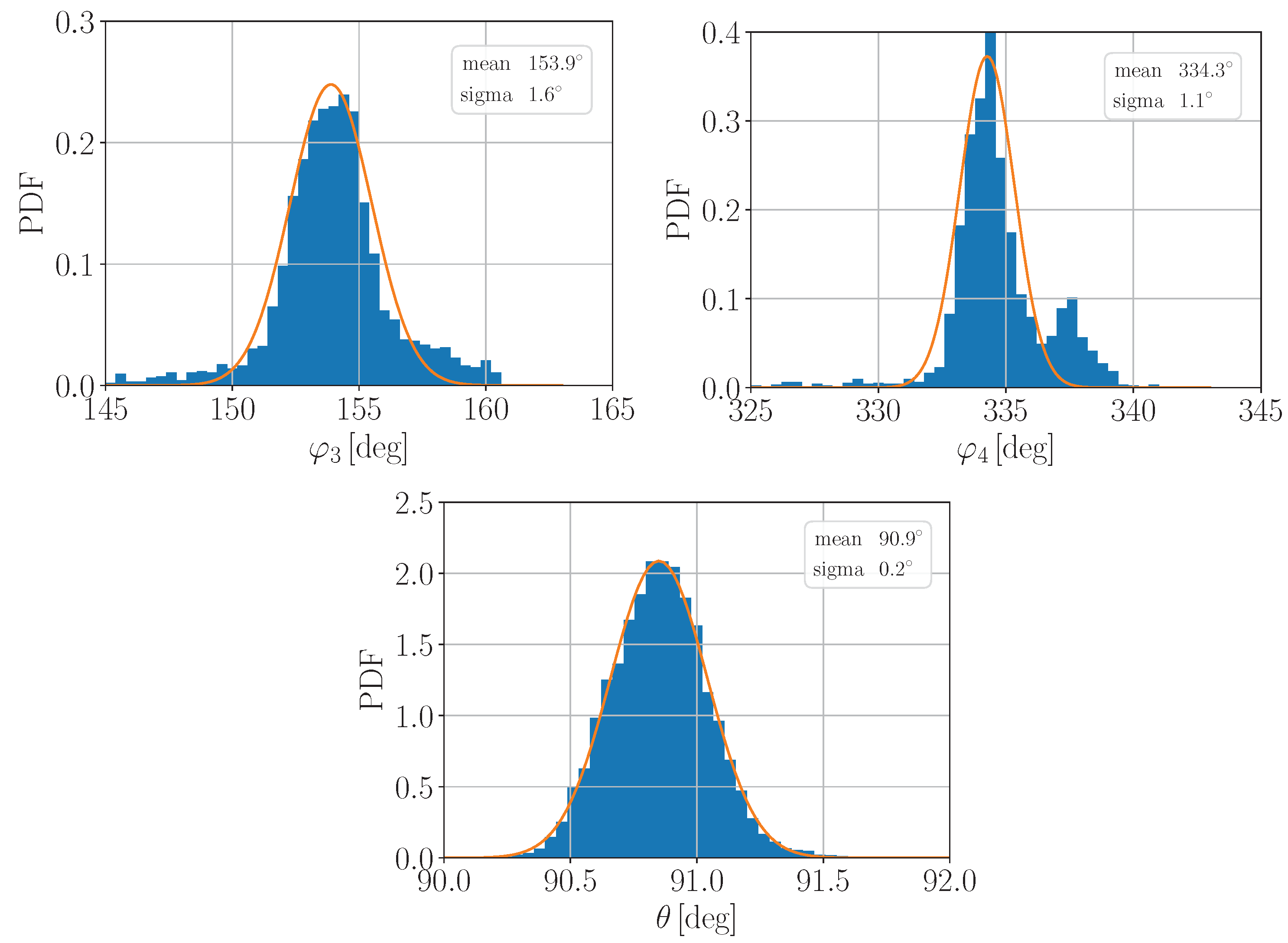
3.2. Experimental Data Analysis
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| QKD | Quantum Key Distribution |
| BB84 | QKD protocol developed by Bennett and Brassard in 1984 |
| GLLP | Gottesman, Lo, Lütkenhaus, Preskill |
| EPR | Einstein, Podolsky, Rosen |
| IM | Intensity Modulator |
| PM | Phase Modulator |
| Probability Density Function |
Appendix A. Generalized Bounds on
Appendix B. Secret Key Length
References
- Bennett, C.H.; Brassard, G. Quantum cryptography: Public-key distribution and coin tossing. In Proceedings of the IEEE International Conference on Computers, Systems, and Signal Processing, Bangalore, India, 9–12 December 1984; IEEE: New York, NY, USA, 1984; pp. 175–179. [Google Scholar] [CrossRef]
- Mayers, D. Quantum key distribution and string oblivious transfer in noisy channels. In Proceedings of the Advances in Cryptology—CRYPTO’96, Santa Barbara, CA, USA, 18–22 August 1996; pp. 343–357. [Google Scholar] [CrossRef]
- Koashi, M.; Preskill, J. Secure Quantum Key Distribution with an Uncharacterized Source. Phys. Rev. Lett. 2003, 90, 057902. [Google Scholar] [CrossRef]
- Lo, H.K.; Chau, H.F. Unconditional Security of Quantum Key Distribution over Arbitrarily Long Distances. Science 1999, 283, 2050–2056. [Google Scholar] [CrossRef] [PubMed]
- Shor, P.W.; Preskill, J. Simple proof of security of the BB84 quantum key distribution protocol. Phys. Rev. Lett. 2000, 85, 441–444. [Google Scholar] [CrossRef] [PubMed]
- Koashi, M. Simple security proof of quantum key distribution based on complementarity. New J. Phys. 2009, 11, 045018. [Google Scholar] [CrossRef]
- Gottesman, D.; Lo, H.K.; Lüttkenhaus, N.; Preskill, J. Security of quantum key distribution with imperfect devices. Quant. Inf. Comput. 2004, 4, 325–360. [Google Scholar] [CrossRef]
- Tamaki, K.; Curty, M.; Kato, G.; Lo, H.K.; Azuma, K. Loss-tolerant quantum cryptography with imperfect sources. Phys. Rev. A 2014, 90, 052314. [Google Scholar] [CrossRef]
- Xu, F.; Wei, K.; Sajeed, S.; Kaiser, S.; Sun, S.; Tang, Z.; Qian, L.; Makarov, V.; Lo, H.K. Experimental quantum key distribution with source flaws. Phys. Rev. A 2015, 92, 032305. [Google Scholar] [CrossRef]
- Tang, Z.; Wei, K.; Bedroya, O.; Qian, L.; Lo, H.K. Experimental measurement-device-independent quantum key distribution with imperfect sources. Phys. Rev. A 2016, 93, 042308. [Google Scholar] [CrossRef]
- Mizutani, A.; Curty, M.; Lim, C.C.W.; Imoto, N.; Tamaki, K. Finite-key security analysis of quantum key distribution with imperfect light sources. New J. Phys. 2015, 17, 093011. [Google Scholar] [CrossRef]
- Mizutani, A.; Kato, G.; Azuma, K.; Curty, M.; Ikuta, R.; Yamamoto, T.; Imoto, N.; Lo, H.K.; Tamaki, K. Quantum key distribution with setting-choice-independently correlated light sources. npj Quantum Inf. 2019, 5, 8. [Google Scholar] [CrossRef]
- Pereira, M.; Curty, M.; Tamaki, K. Quantum key distribution with flawed and leaky sources. npj Quantum Inf. 2019, 5, 62. [Google Scholar] [CrossRef]
- Pereira, M.; Kato, G.; Mizutani, A.; Curty, M.; Tamaki, K. Quantum key distribution with correlated sources. Sci. Adv. 2020, 6, eaaz4487. [Google Scholar] [CrossRef]
- Currás-Lorenzo, G.; Navarrete, A.; Pereira, M.; Tamaki, K. Finite-key analysis of loss-tolerant quantum key distribution based on random sampling theory. Phys. Rev. A 2021, 104, 012406. [Google Scholar] [CrossRef]
- Pereira, M.; Currás-Lorenzo, G.; Navarrete, A.; Mizutani, A.; Kato, G.; Curty, M.; Tamaki, K. Modified BB84 quantum key distribution protocol robust to source imperfections. Phys. Rev. Res. 2023, 5, 023065. [Google Scholar] [CrossRef]
- Currás-Lorenzo, G.; Pereira, M.; Kato, G.; Curty, M.; Tamaki, K. A security framework for quantum key distribution implementations. arXiv 2023, arXiv:2305.05930. [Google Scholar]
- Brassard, G.; Lütkenhaus, N.; Mor, T.; Sanders, B.C. Limitations on Practical Quantum Cryptography. Phys. Rev. Lett. 2000, 85, 1330–1333. [Google Scholar] [CrossRef]
- Lütkenhaus, N. Security against individual attacks for realistic quantum key distribution. Phys. Rev. A 2000, 61, 052304. [Google Scholar] [CrossRef]
- Hwang, W.Y. Quantum Key Distribution with High Loss: Toward Global Secure Communication. Phys. Rev. Lett. 2003, 91, 057901. [Google Scholar] [CrossRef]
- Lo, H.K.; Ma, X.; Chen, K. Decoy State Quantum Key Distribution. Phys. Rev. Lett. 2005, 94, 230504. [Google Scholar] [CrossRef]
- Wang, X.B. Beating the Photon-Number-Splitting Attack in Practical Quantum Cryptography. Phys. Rev. Lett. 2005, 94, 230503. [Google Scholar] [CrossRef]
- Ma, X.; Qi, B.; Zhao, Y.; Lo, H.K. Practical decoy state for quantum key distribution. Phys. Rev. A 2005, 72, 012326. [Google Scholar] [CrossRef]
- Trushechkin, A.; Kiktenko, E.; Kronberg, D.; Fedorov, A. Security of the decoy state method for quantum key distribution. Physics-Uspekhi 2021, 64, 88. [Google Scholar] [CrossRef]
- Lucamarini, M.; Choi, I.; Ward, M.; Dynes, J.; Yuan, Z.; Shields, A. Practical Security Bounds Against the Trojan-Horse Attack in Quantum Key Distribution. Phys. Rev. X 2015, 5, 031030. [Google Scholar] [CrossRef]
- Tamaki, K.; Curty, M.; Lucamarini, M. Decoy-state quantum key distribution with a leaky source. New. J. Phys. 2016, 18, 065008. [Google Scholar] [CrossRef]
- Wang, W.; Tamaki, K.; Curty, M. Finite-key security analysis for quantum key distribution with leaky sources. New. J. Phys. 2018, 20, 083027. [Google Scholar] [CrossRef]
- Molotkov, S. Trojan horse attacks, decoy state method, and side channels of information leakage in quantum cryptography. J. Exp. Theor. Phys. 2020, 130, 809–832. [Google Scholar] [CrossRef]
- Molotkov, S. Side channels of information leakage in quantum cryptography: Nonstrictly single-photon states, different quantum efficiencies of detectors, and finite transmitted sequences. J. Exp. Theor. Phys. 2021, 133, 272–304. [Google Scholar] [CrossRef]
- Wang, X.B.; Peng, C.Z.; Zhang, J.; Yang, L.; Pan, J.W. General theory of decoy-state quantum cryptography with source errors. Phys. Rev. A 2008, 77, 042311. [Google Scholar] [CrossRef]
- Wang, X.B.; Yang, L.; Peng, C.Z.; Pan, J.W. Decoy-state quantum key distribution with both source errors and statistical fluctuations. New. J. Phys. 2009, 11, 075006. [Google Scholar] [CrossRef]
- Foletto, G.; Picciariello, F.; Agnesi, C.; Villoresi, P.; Vallone, G. Security bounds for decoy-state quantum key distribution with arbitrary photon-number statistics. Phys. Rev. A 2022, 105, 012603. [Google Scholar] [CrossRef]
- Wang, W.; Wang, R.; Hu, C.; Zapatero, V.; Qian, L.; Qi, B.; Curty, M.; Lo, H.K. Fully Passive Quantum Key Distribution. Phys. Rev. Lett. 2023, 130, 220801. [Google Scholar] [CrossRef] [PubMed]
- Lo, H.K.; Chau, H.; Ardehali, M. Efficient Quantum Key Distribution Scheme and a Proof of Its Unconditional Security. J. Cryptol. 2005, 18, 133–165. [Google Scholar] [CrossRef]
- Huang, A.; Mizutani, A.; Lo, H.K.; Makarov, V.; Tamaki, K. Characterization of State-Preparation Uncertainty in Quantum Key Distribution. Phys. Rev. Appl. 2023, 19, 014048. [Google Scholar] [CrossRef]
- Huang, A.; Sun, S.H.; Liu, Z.; Makarov, V. Quantum key distribution with distinguishable decoy states. Phys. Rev. A 2018, 98, 012330. [Google Scholar] [CrossRef]
- Duplinskiy, A.; Ustimchik, V.; Kanapin, A.; Kurochkin, V.; Kurochkin, Y. Low loss QKD optical scheme for fast polarization encoding. Opt. Express 2017, 25, 28886–28897. [Google Scholar] [CrossRef]
- Zapatero, V.; Wang, W.; Curty, M. A fully passive transmitter for decoy-state quantum key distribution. Quantum Sci. Technol. 2023, 8, 025014. [Google Scholar] [CrossRef]
- Tamaki, K.; Koashi, M.; Imoto, N. Unconditionally Secure Key Distribution Based on Two Nonorthogonal States. Phys. Rev. Lett. 2003, 90, 167904. [Google Scholar] [CrossRef]
- Lo, H.K.; Preskill, J. Security of Quantum Key Distribution Using Weak Coherent States with Nonrandom Phases. Quantum Info. Comput. 2007, 7, 431–458. [Google Scholar] [CrossRef]
- Jozsa, R. Fidelity for Mixed Quantum States. J. Mod. Opt. 1994, 41, 2315–2323. [Google Scholar] [CrossRef]
- Trushechkin, A.; Kiktenko, E.; Fedorov, A. Practical issues in decoy-state quantum key distribution based on the central limit theorem. Phys. Rev. A 2017, 96, 022316. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhao, Q.; Razavi, M.; Ma, X. Improved key-rate bounds for practical decoy-state quantum-key-distribution systems. Phys. Rev. A 2017, 95, 012333. [Google Scholar] [CrossRef]
- Borisov, N.; Petrov, I.; Tayduganov, A. Asymmetric Adaptive LDPC-Based Information Reconciliation for Industrial Quantum Key Distribution. Entropy 2023, 25, 31. [Google Scholar] [CrossRef] [PubMed]



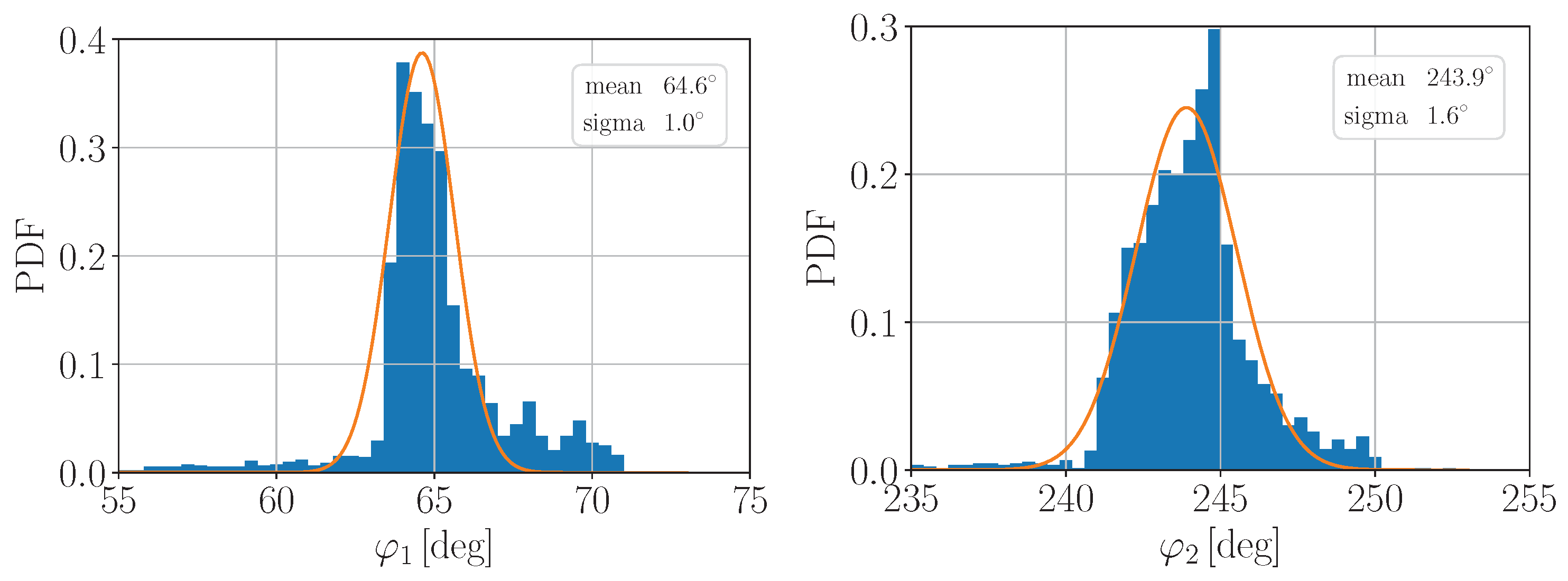
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reutov, A.; Tayduganov, A.; Mayboroda, V.; Fat’yanov, O. Security of the Decoy-State BB84 Protocol with Imperfect State Preparation. Entropy 2023, 25, 1556. https://doi.org/10.3390/e25111556
Reutov A, Tayduganov A, Mayboroda V, Fat’yanov O. Security of the Decoy-State BB84 Protocol with Imperfect State Preparation. Entropy. 2023; 25(11):1556. https://doi.org/10.3390/e25111556
Chicago/Turabian StyleReutov, Aleksei, Andrey Tayduganov, Vladimir Mayboroda, and Oleg Fat’yanov. 2023. "Security of the Decoy-State BB84 Protocol with Imperfect State Preparation" Entropy 25, no. 11: 1556. https://doi.org/10.3390/e25111556
APA StyleReutov, A., Tayduganov, A., Mayboroda, V., & Fat’yanov, O. (2023). Security of the Decoy-State BB84 Protocol with Imperfect State Preparation. Entropy, 25(11), 1556. https://doi.org/10.3390/e25111556




