Research on the Threshold Determination Method of the Duffing Chaotic System Based on Improved Permutation Entropy and Poincaré Mapping
Abstract
:1. Introduction
2. Duffing Chaotic Oscillator Detection System
2.1. Duffing Oscillator System
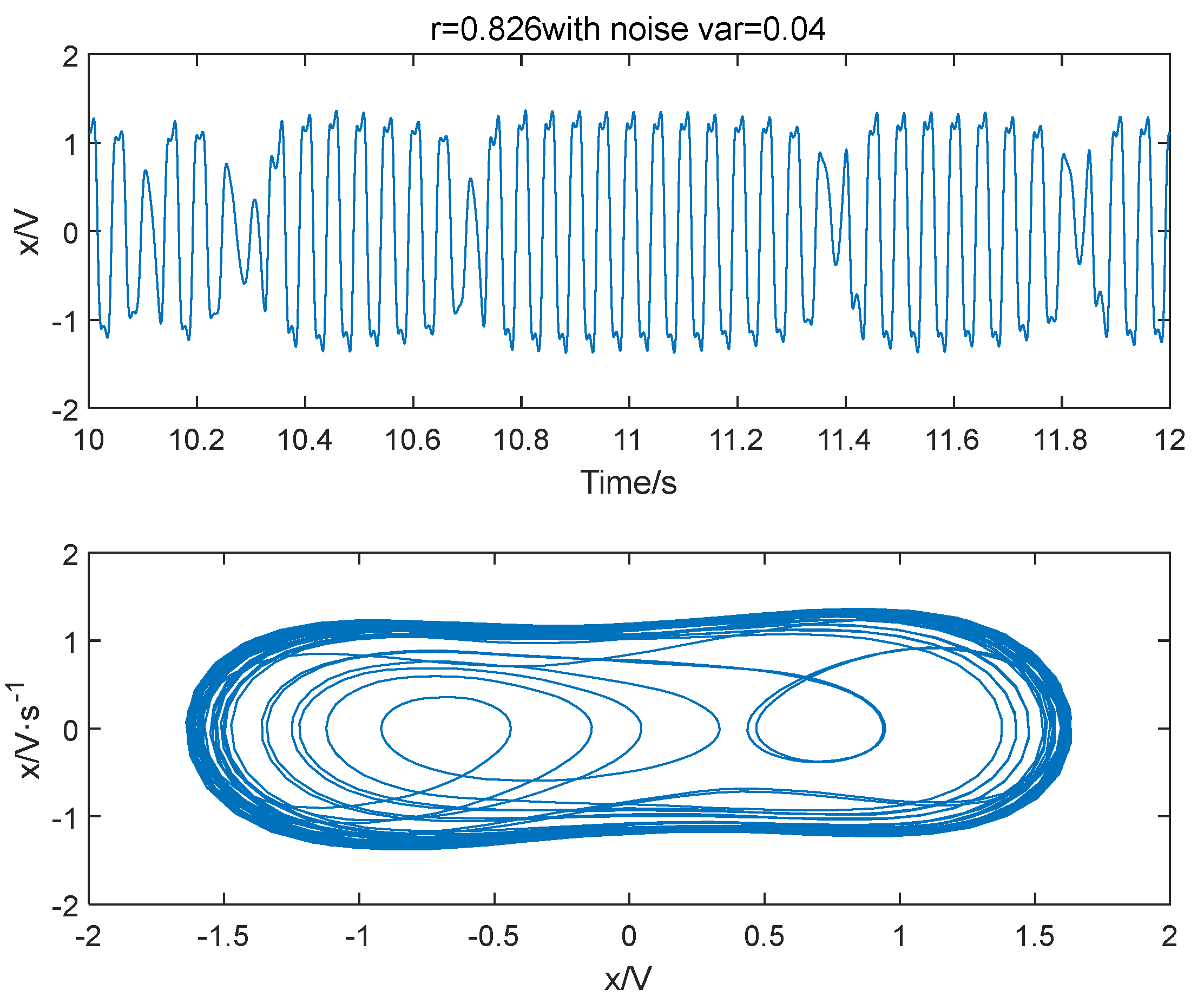
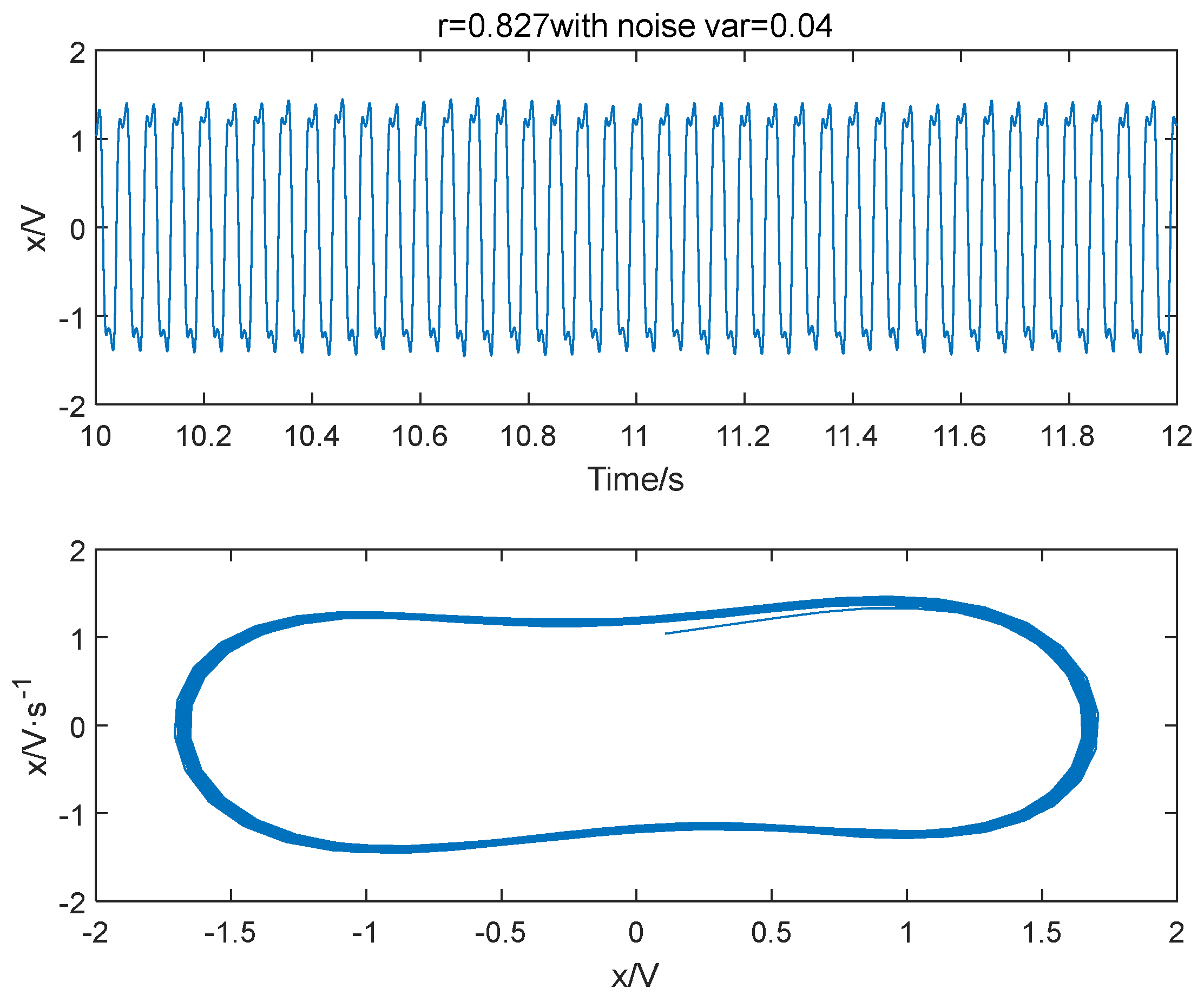
2.2. Impact of Noise on Duffing Oscillator System
3. Poincaré Mapping Improved Permutation Entropy
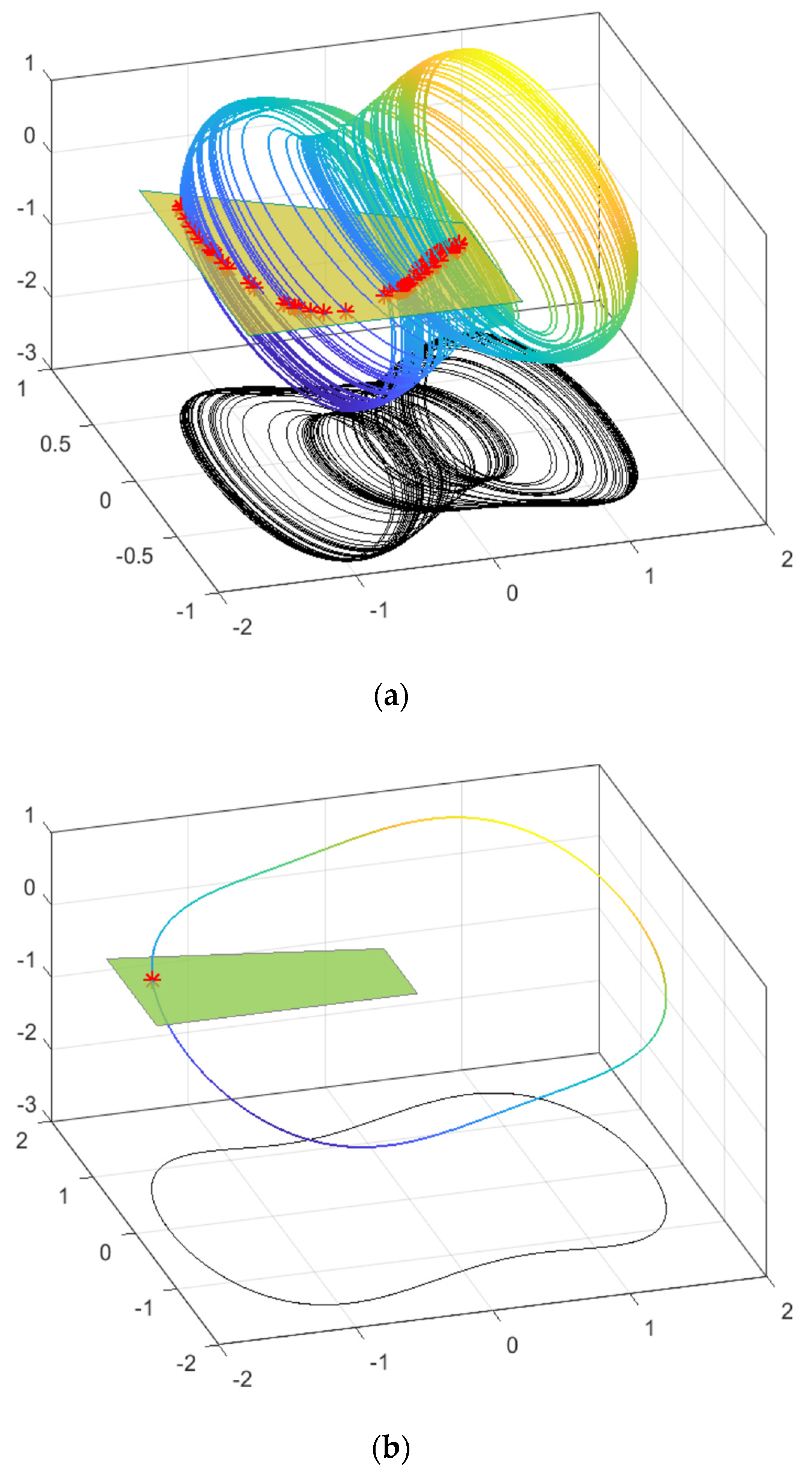
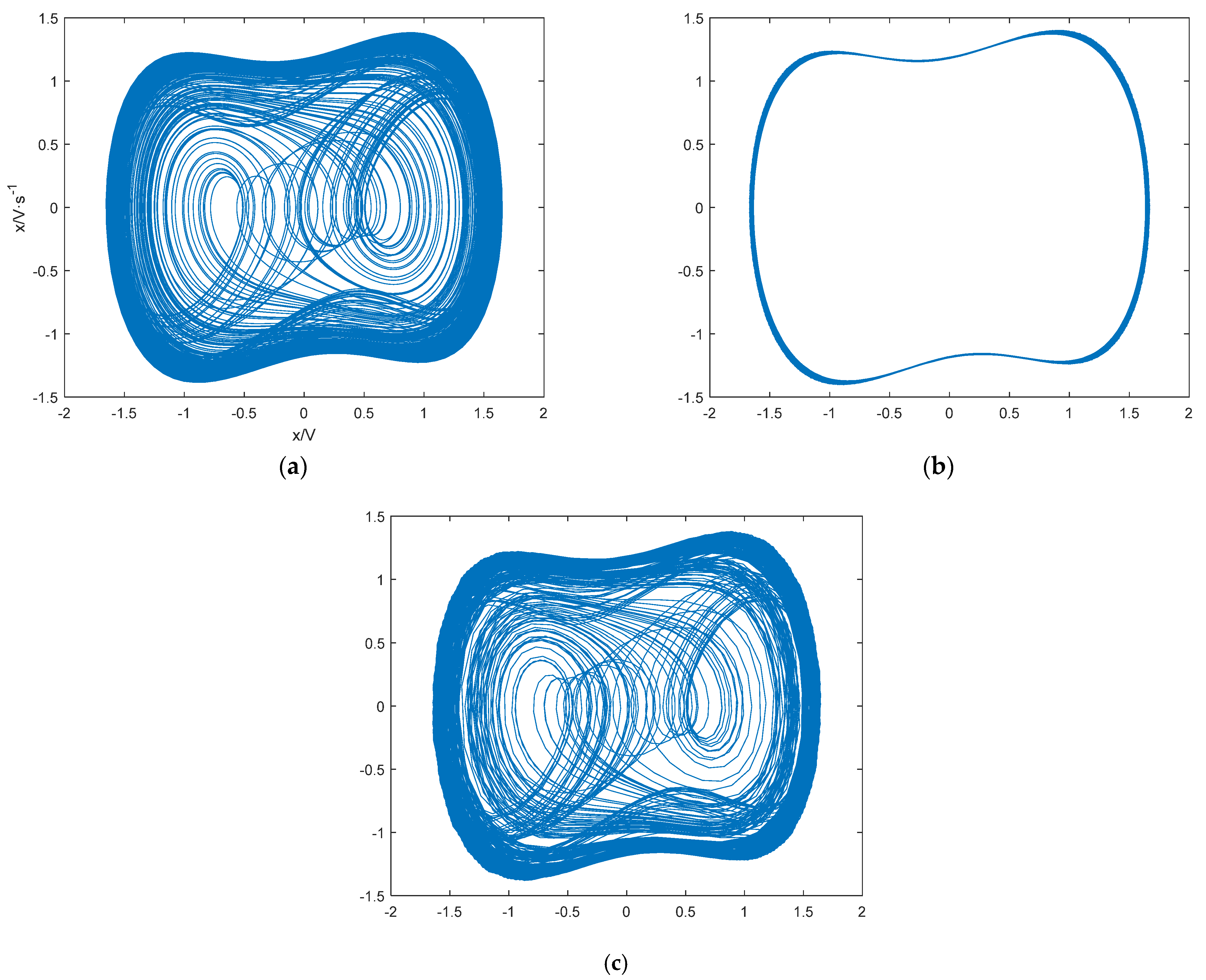
3.1. Poincaré Mapping
- (1)
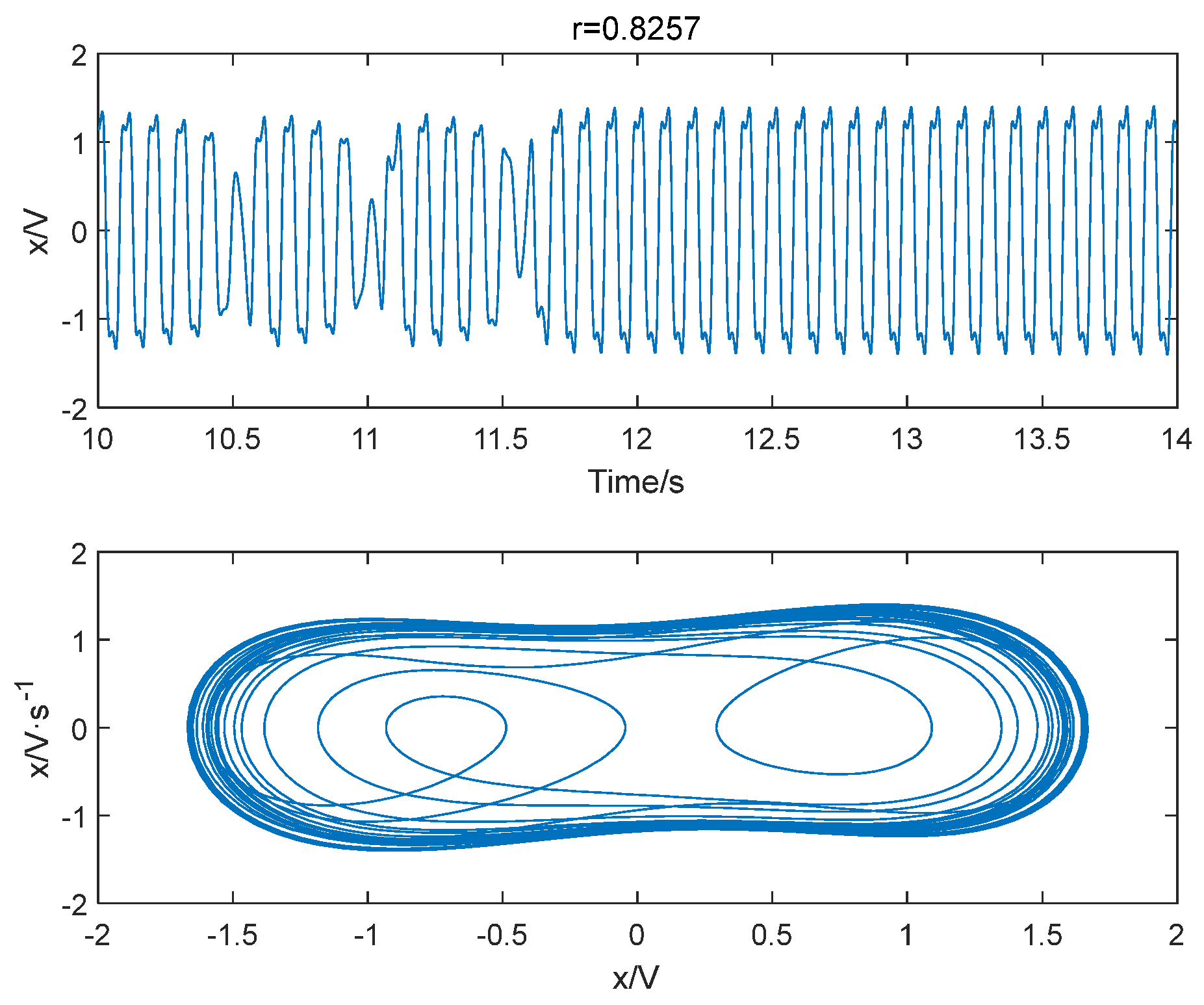
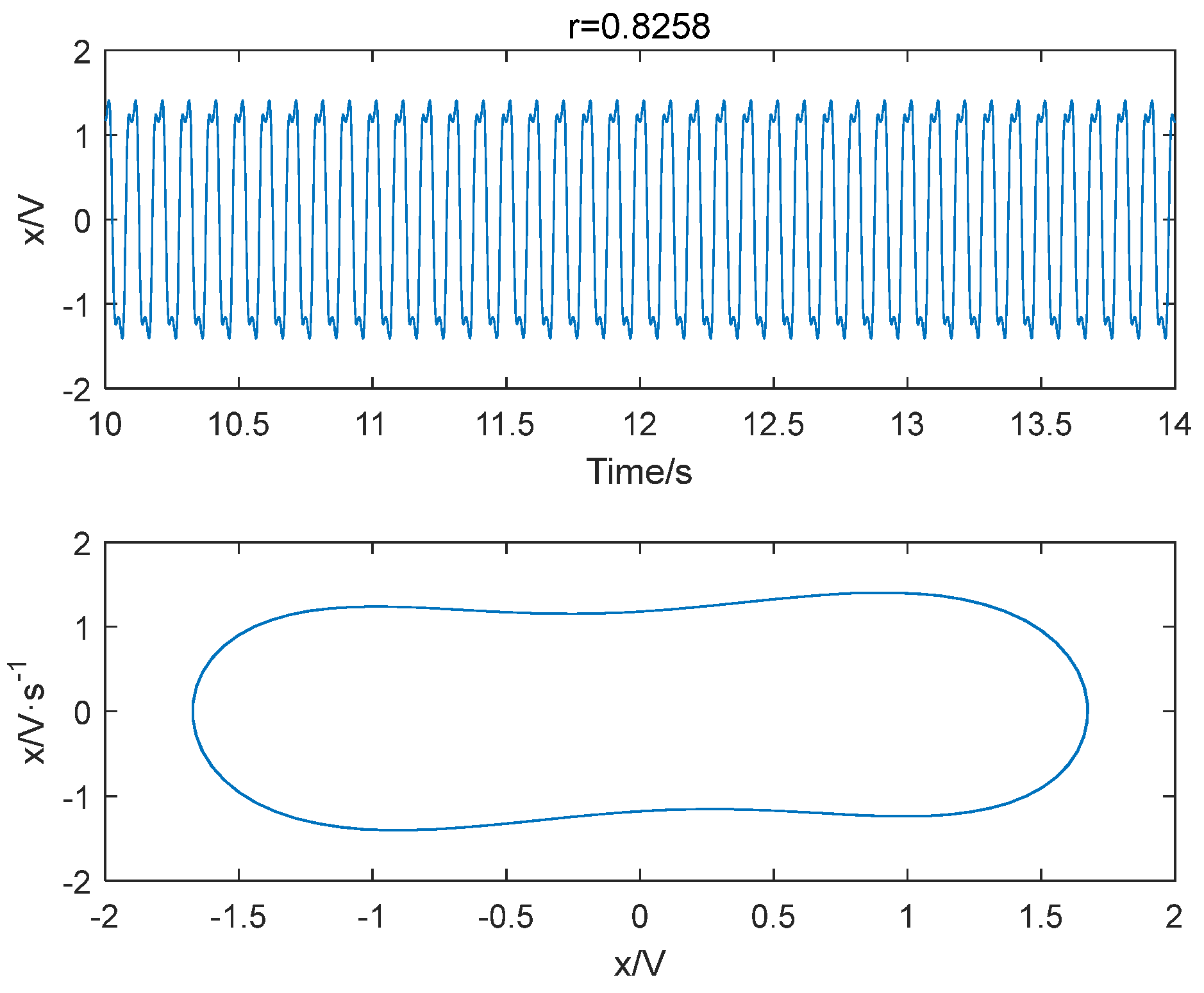
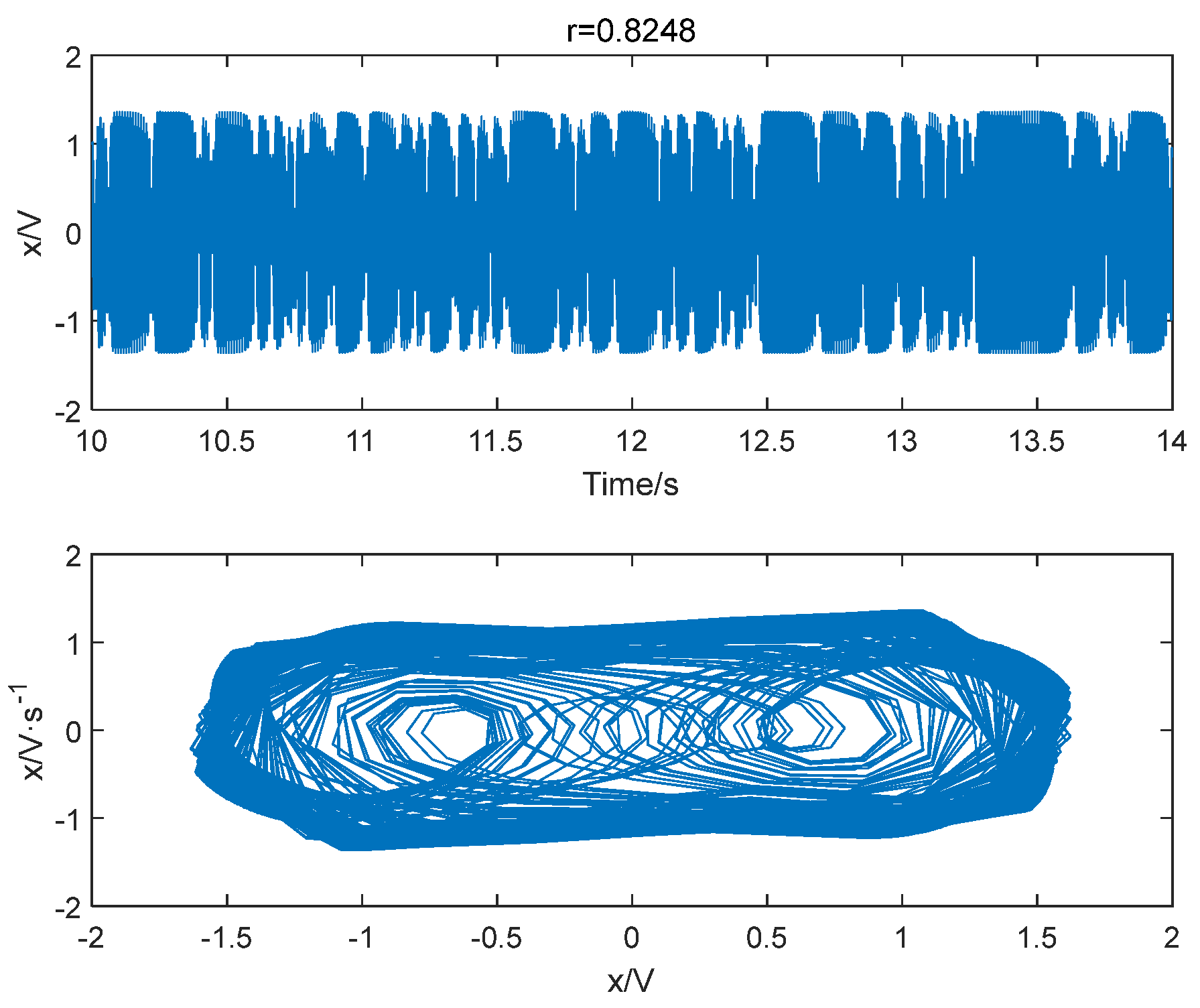
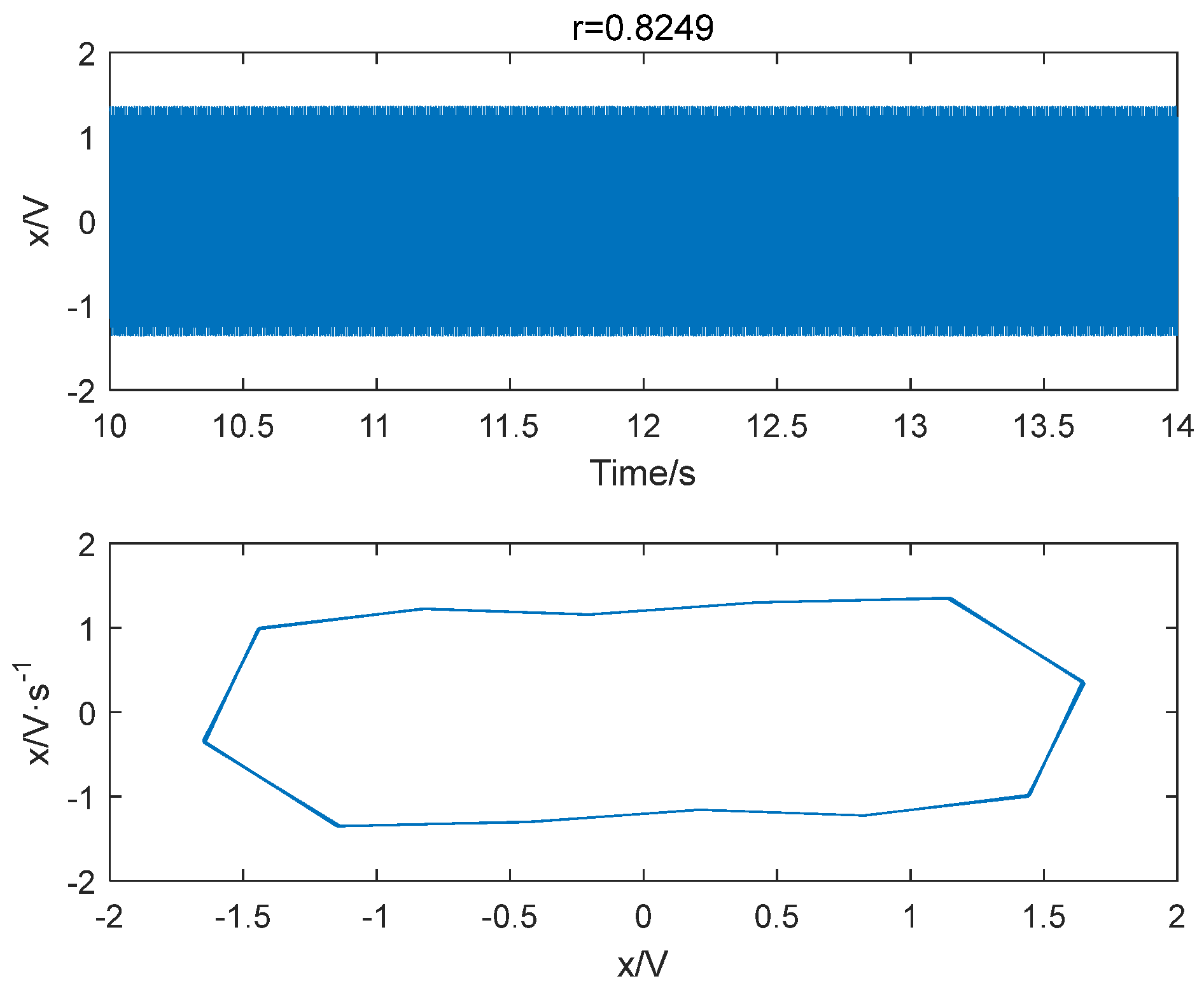
- When there is a fixed point or a few discrete points on the Poincaré section, the motion trajectory is periodic;
- (2)
- When the Poincaré section consists of dense points with self-similar structures, the motion trajectory is chaotic.
3.2. Improved Permutation Entropy Algorithm
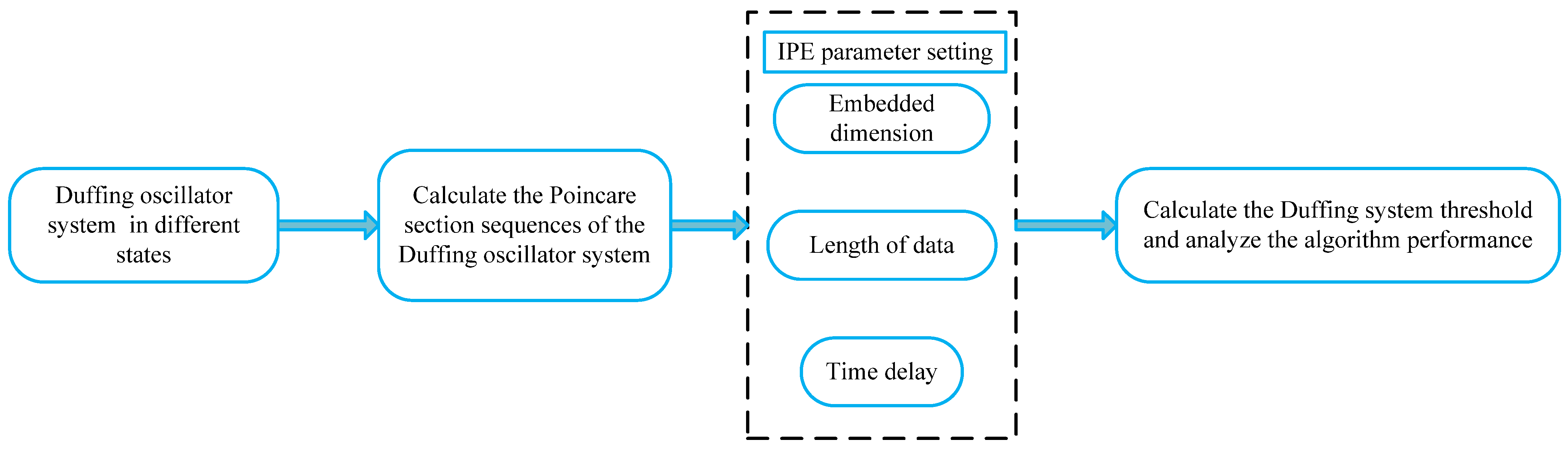
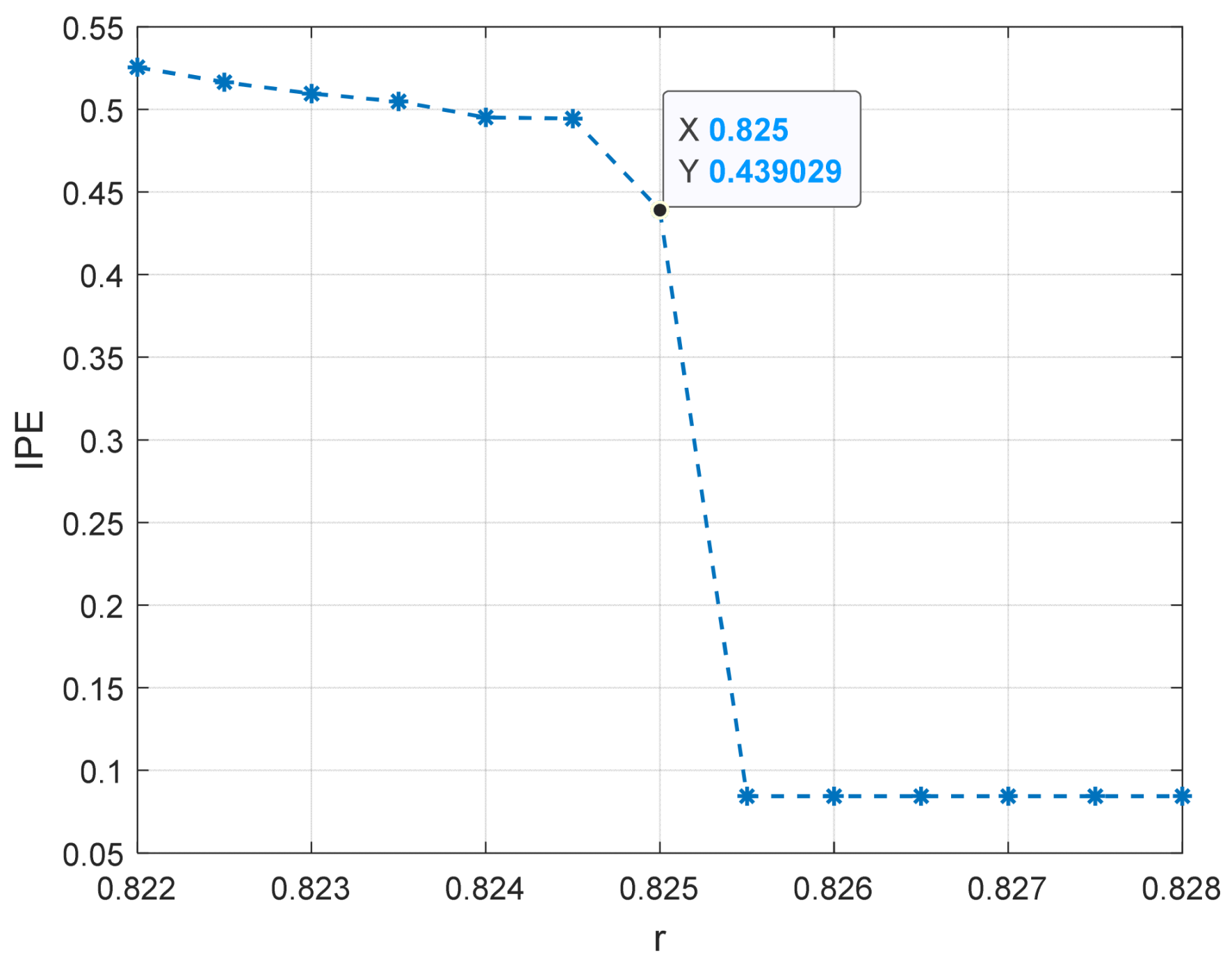
3.3. Threshold Determination Method for Duffing System Based on PMIPE
- (1)
- Determine the frequency and other parameters of the Duffing oscillator system based on the signal to be detected by the weak signal detection system.
- (2)
- Impose distinct driving forces on the Duffing oscillator system to induce periodic and chaotic states, respectively.
- (3)
- Calculate the Poincaré section sequences of the Duffing oscillator system, in chaotic and periodic states, correspondingly, to obtain a set of Poincaré section sequences in varied states.
- (4)
- Use the IPE algorithm to calculate the complexity of this set of Poincaré section sequences and obtain the curve of complexity as a function of driving force.
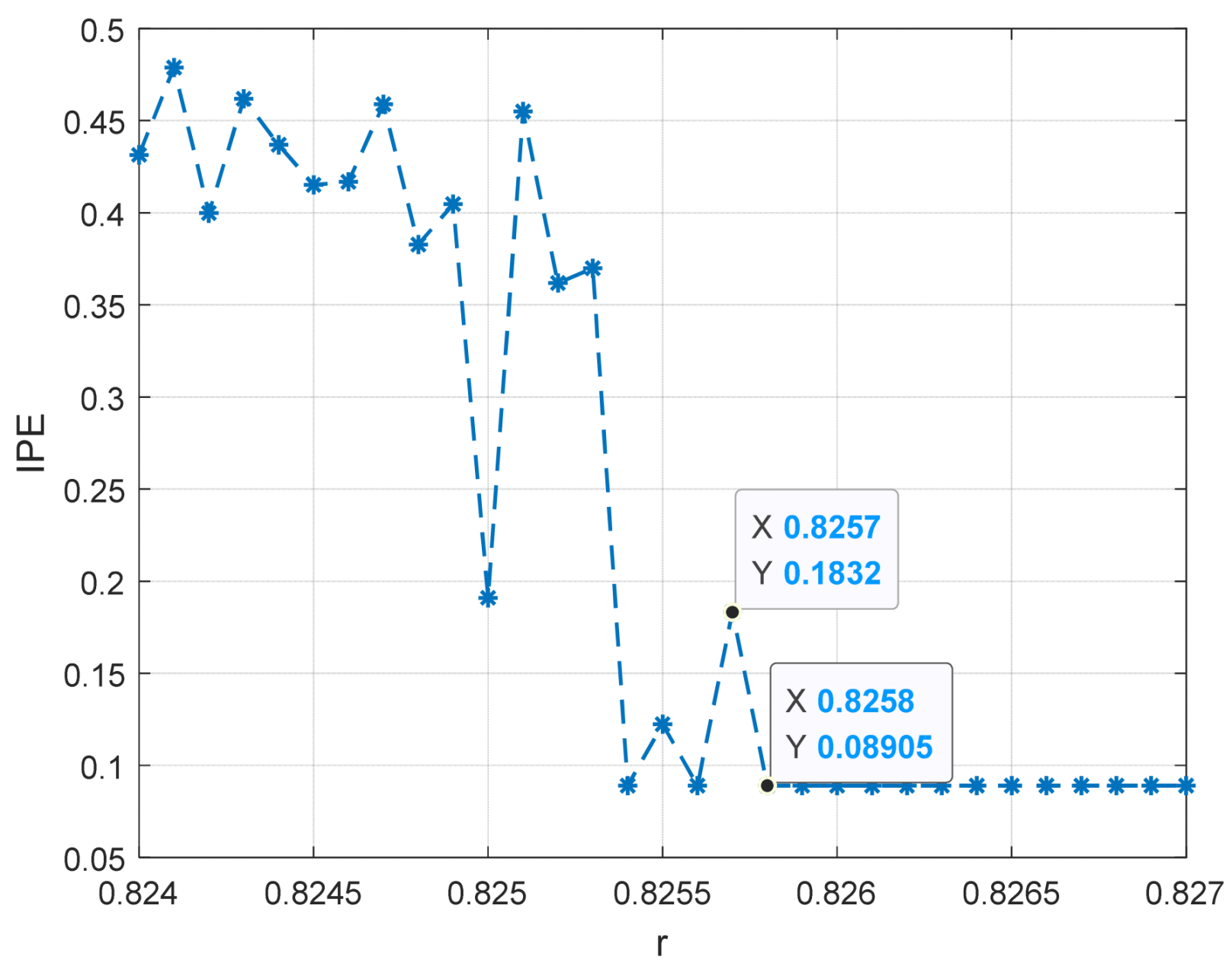
- (5)
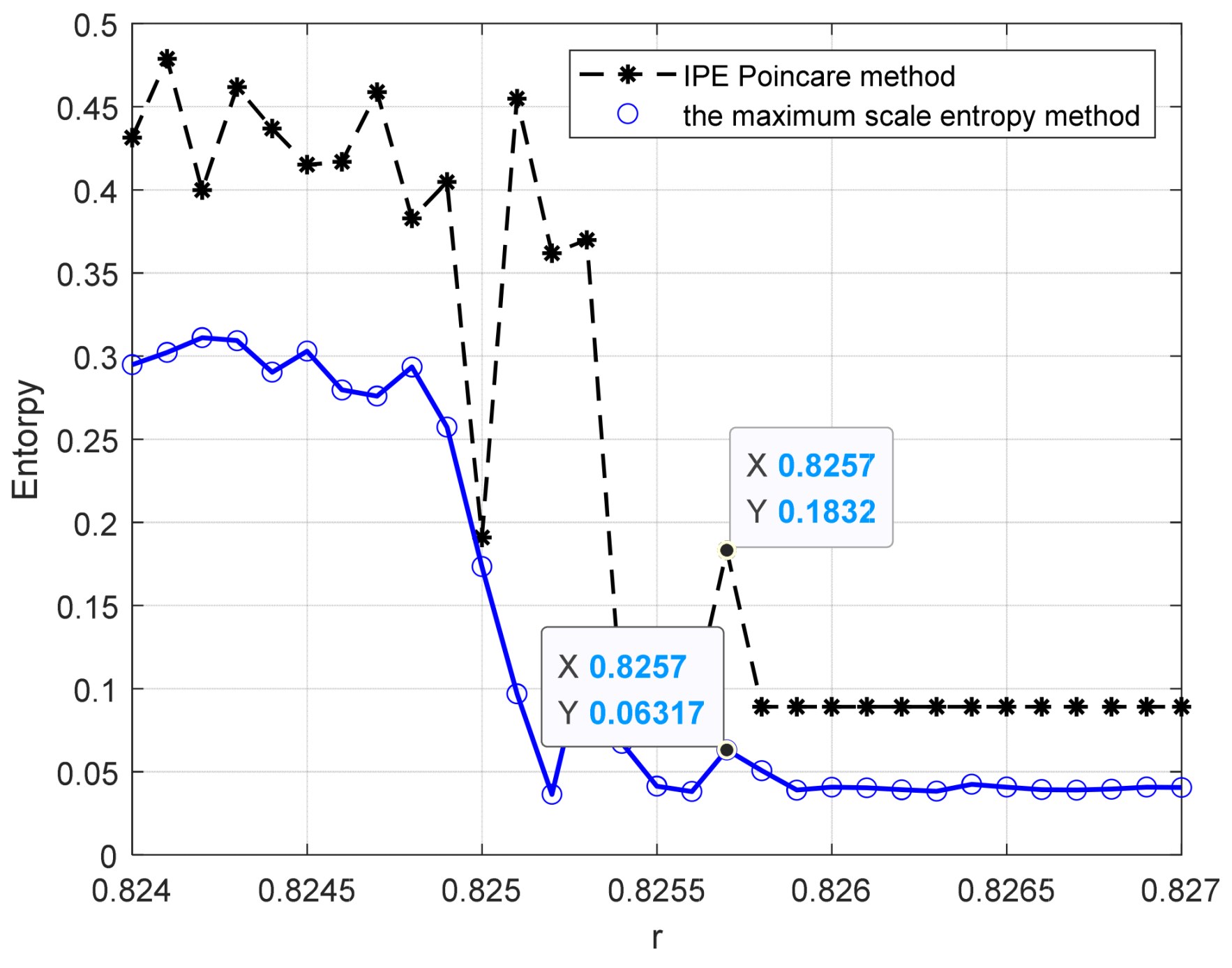
- Using entropy = 0.15 as a critical standard, if entropy < 0.15, it is considered that the system is in a stable periodic state, with entropy values exceeding 0.15 defined as non-periodic entropy.
- (6)
- Determine the threshold of the duffing detection system as the maximum driving force that has a non-periodic entropy.
4. Results and Discussion
4.1. Influence of Different Parameters on Improved Permutation Entropy
- (1)
- Influence of Embedding Dimension on IPE
- (2)
- Influence of Data Length on IPE
- (3)
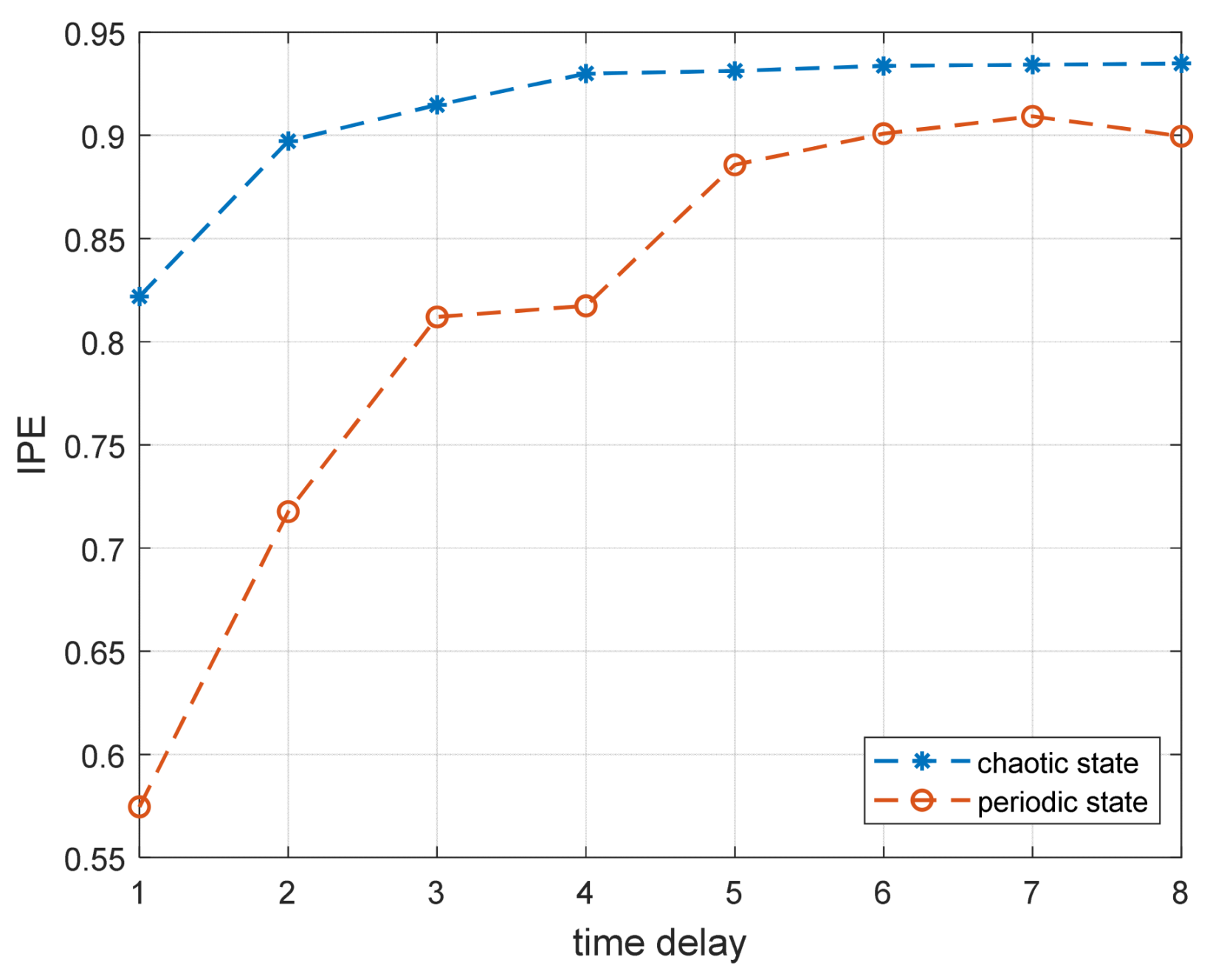
- Influence of time delay on IPE
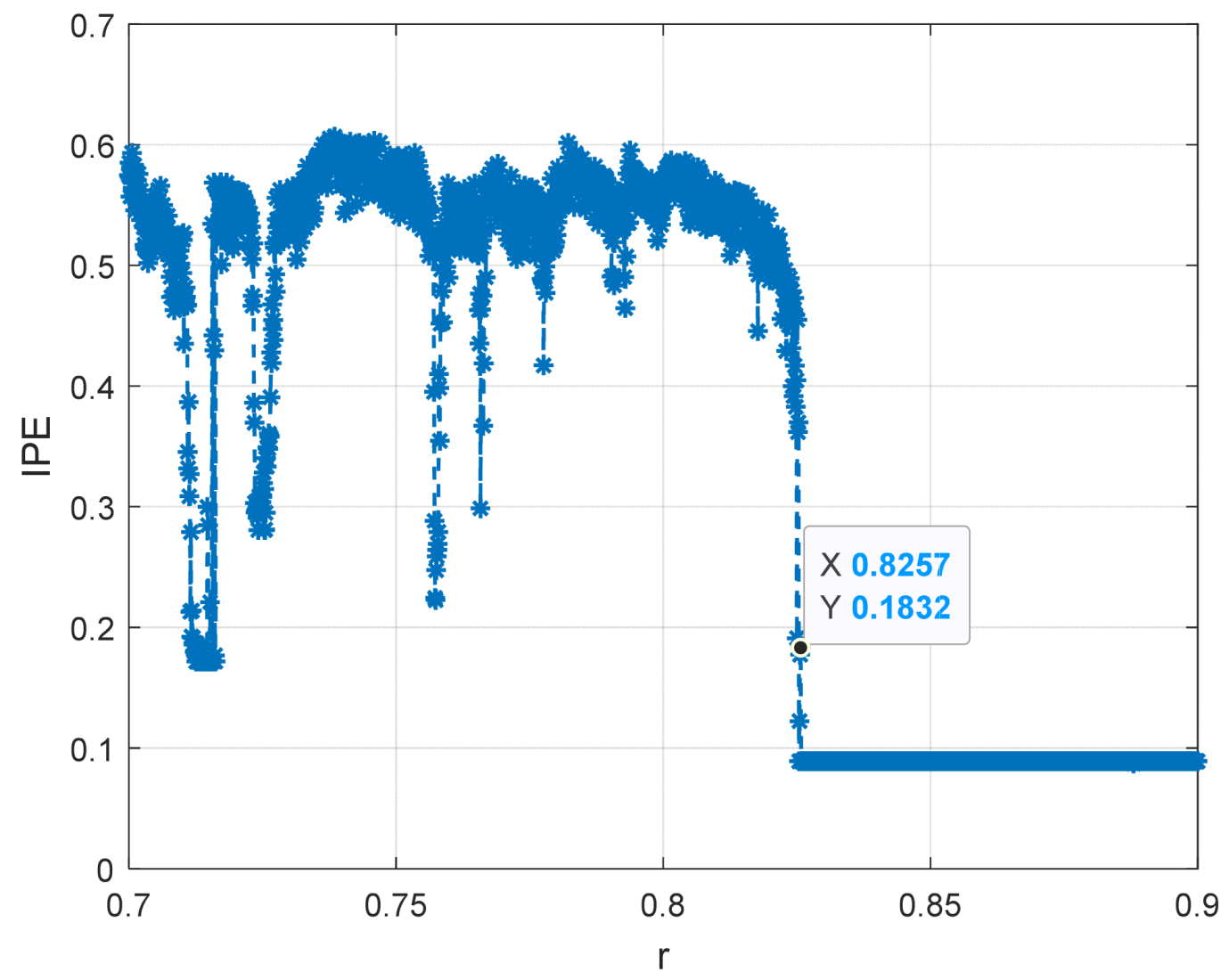
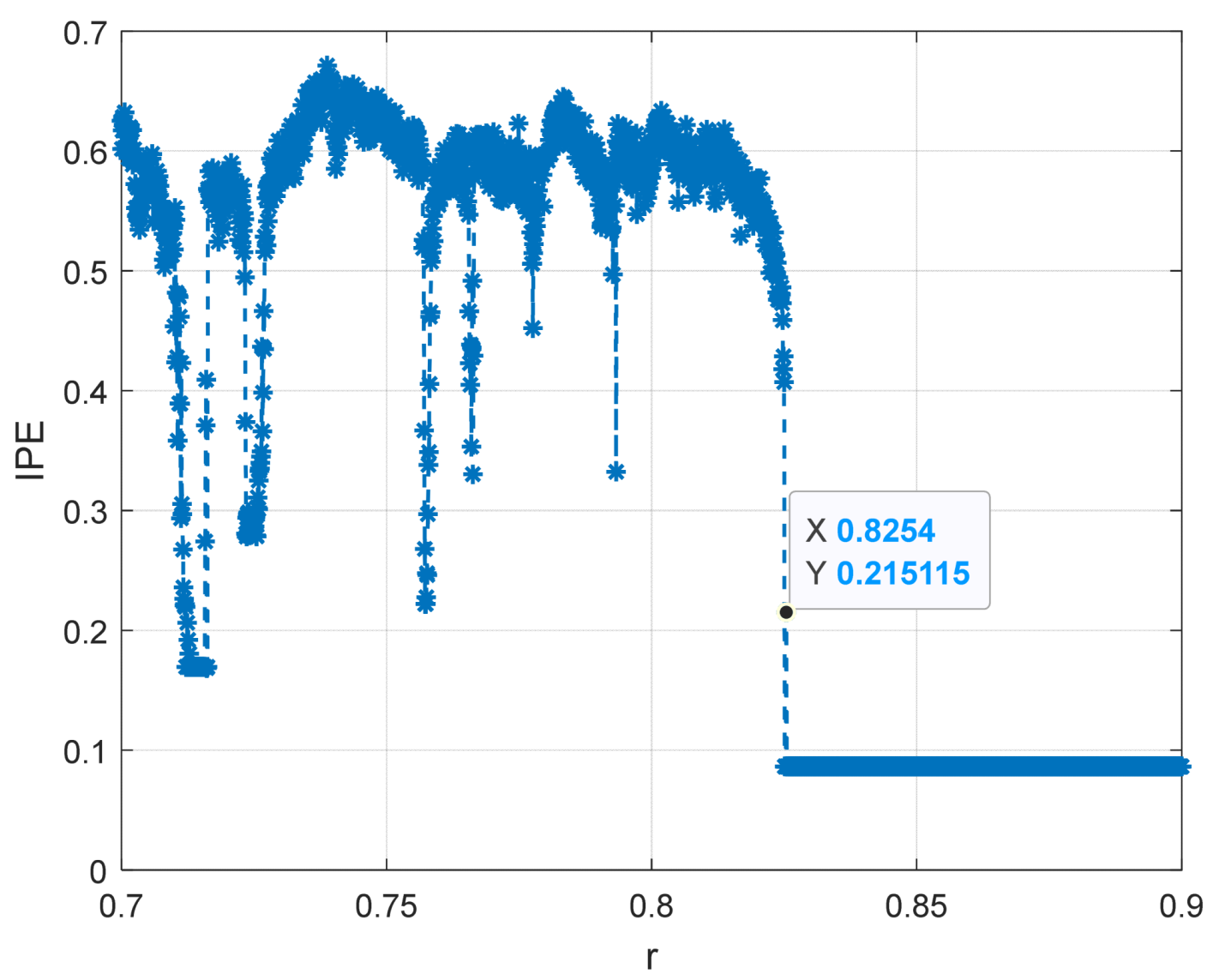
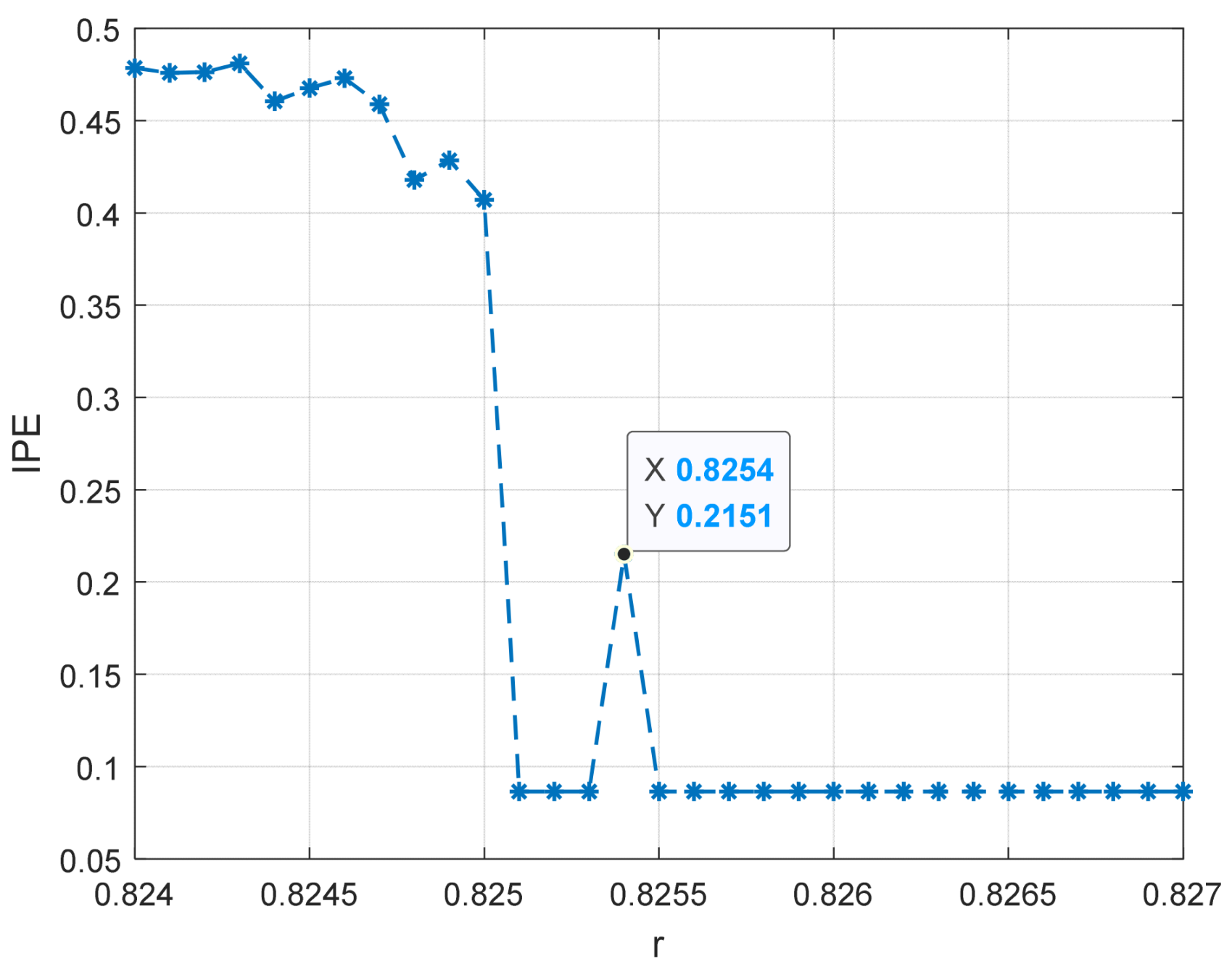
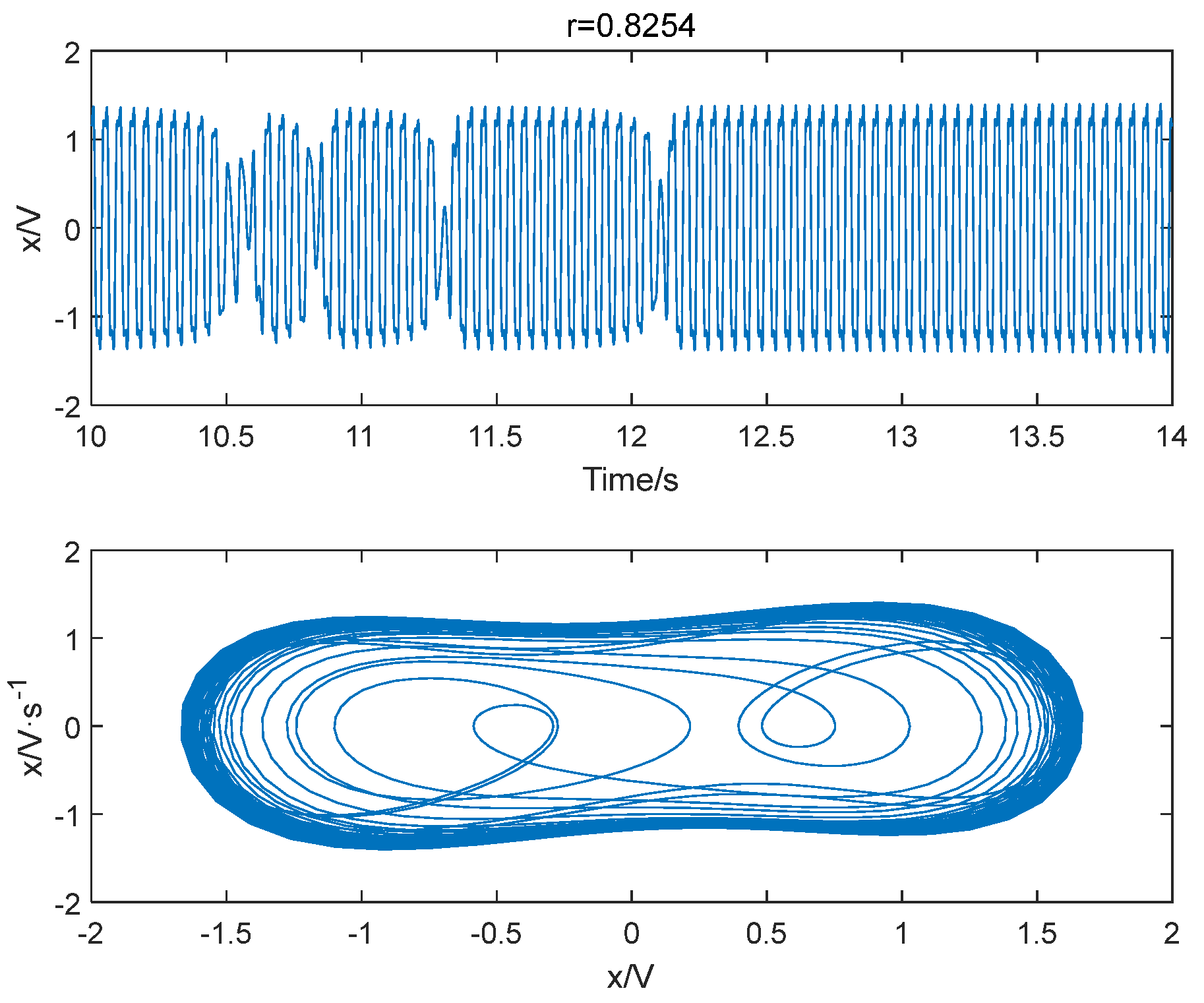
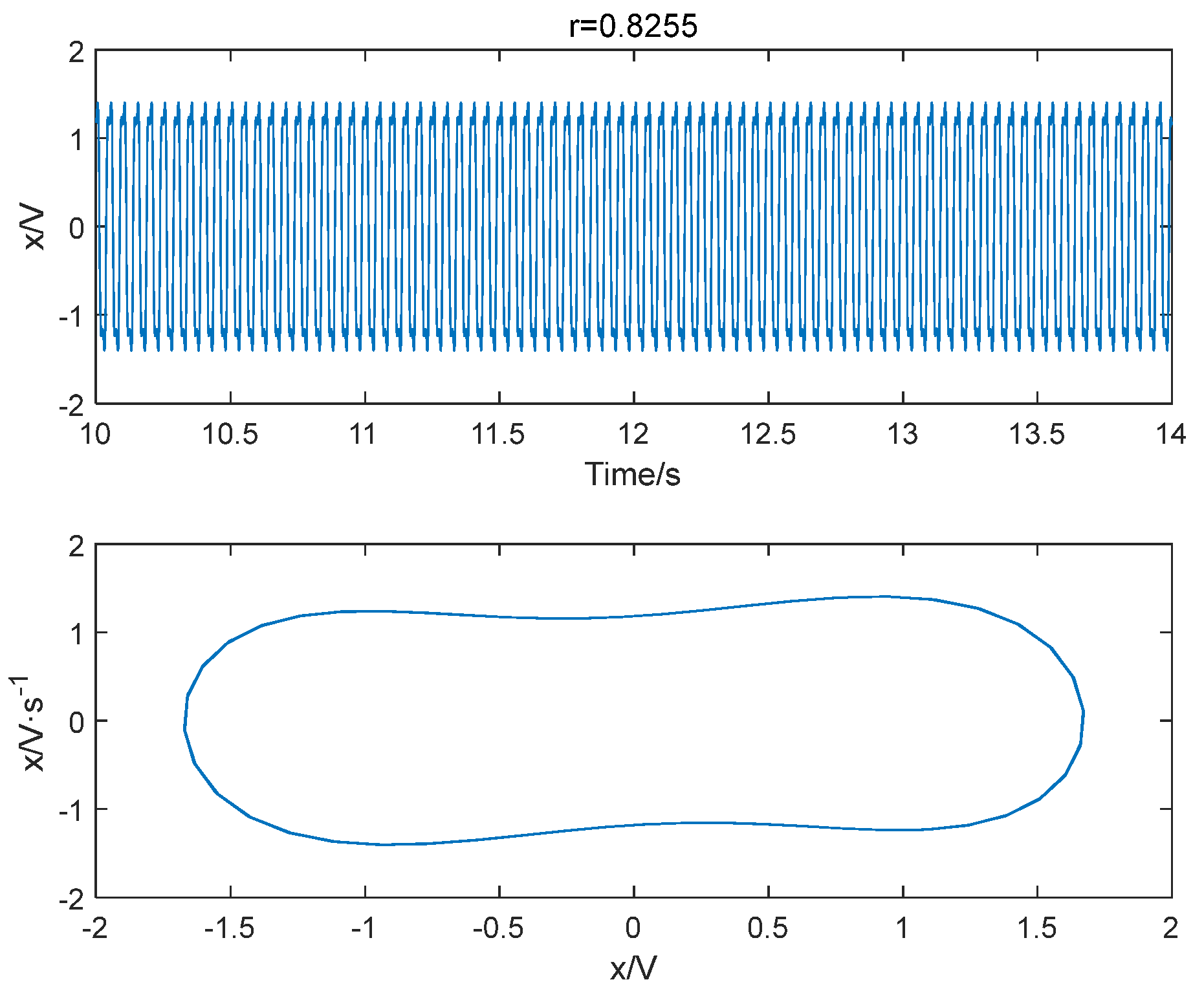
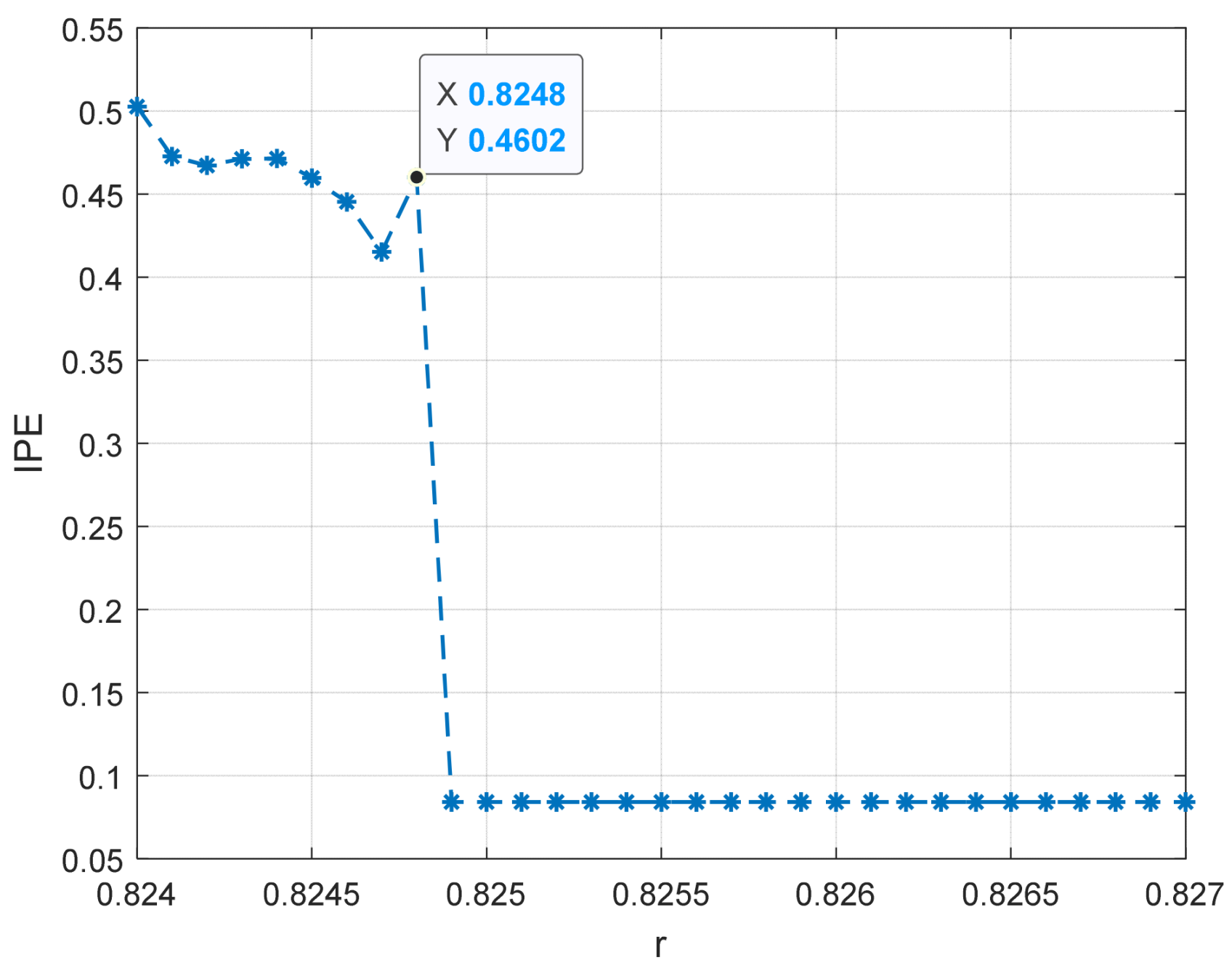
4.2. Simulation of Threshold Determination for Duffing Oscillator System with Different Frequency and Driving Forces
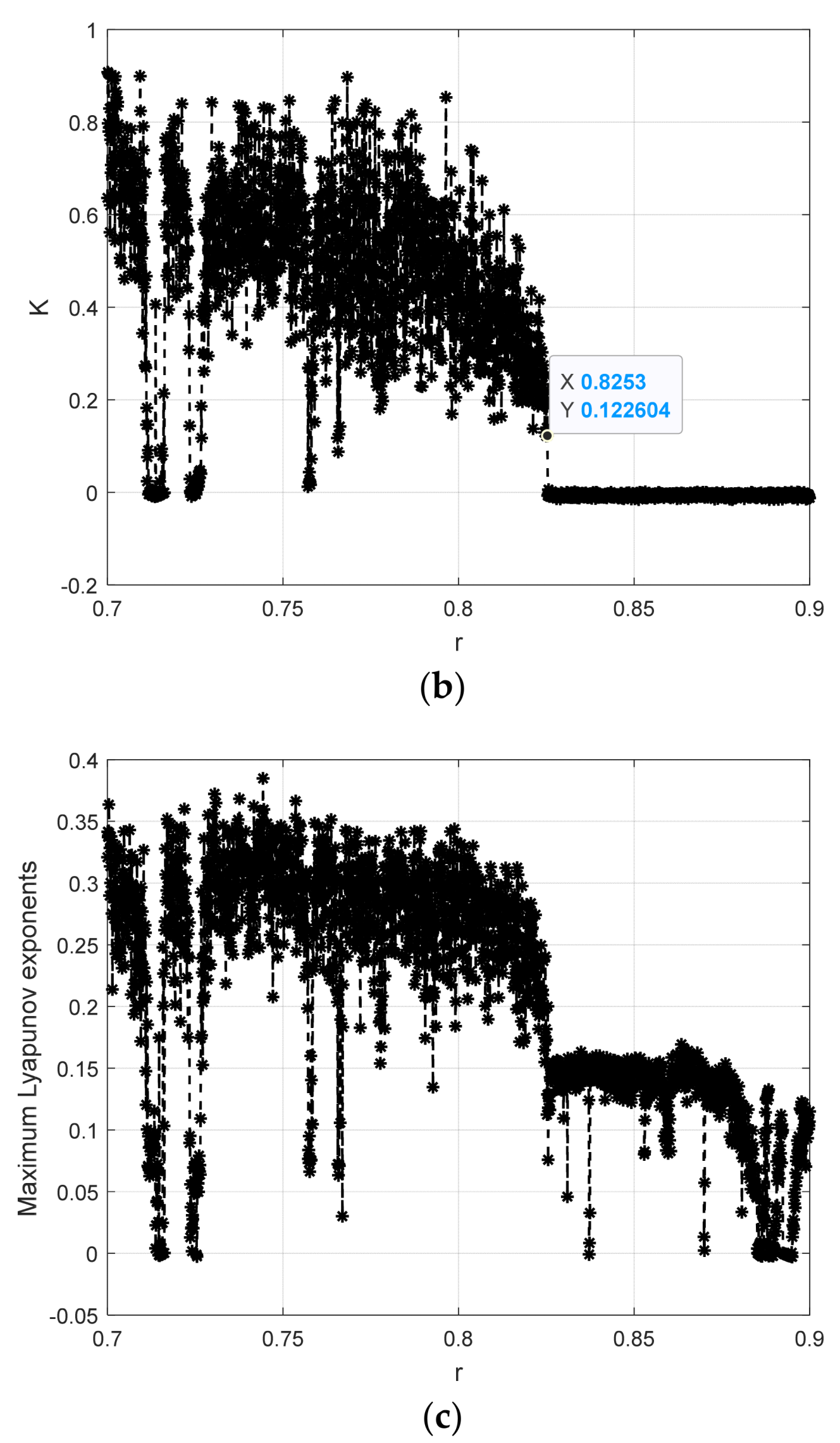
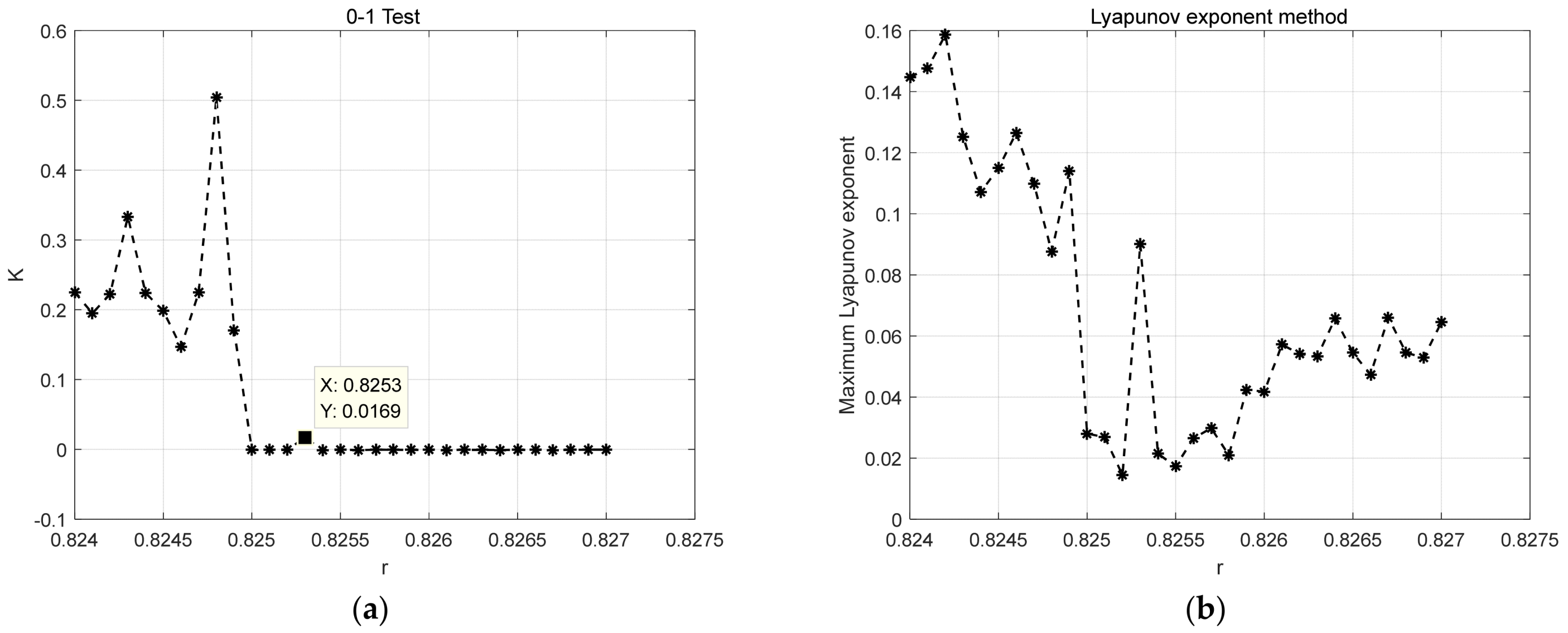
4.3. Comparison and Analysis of Different Methods
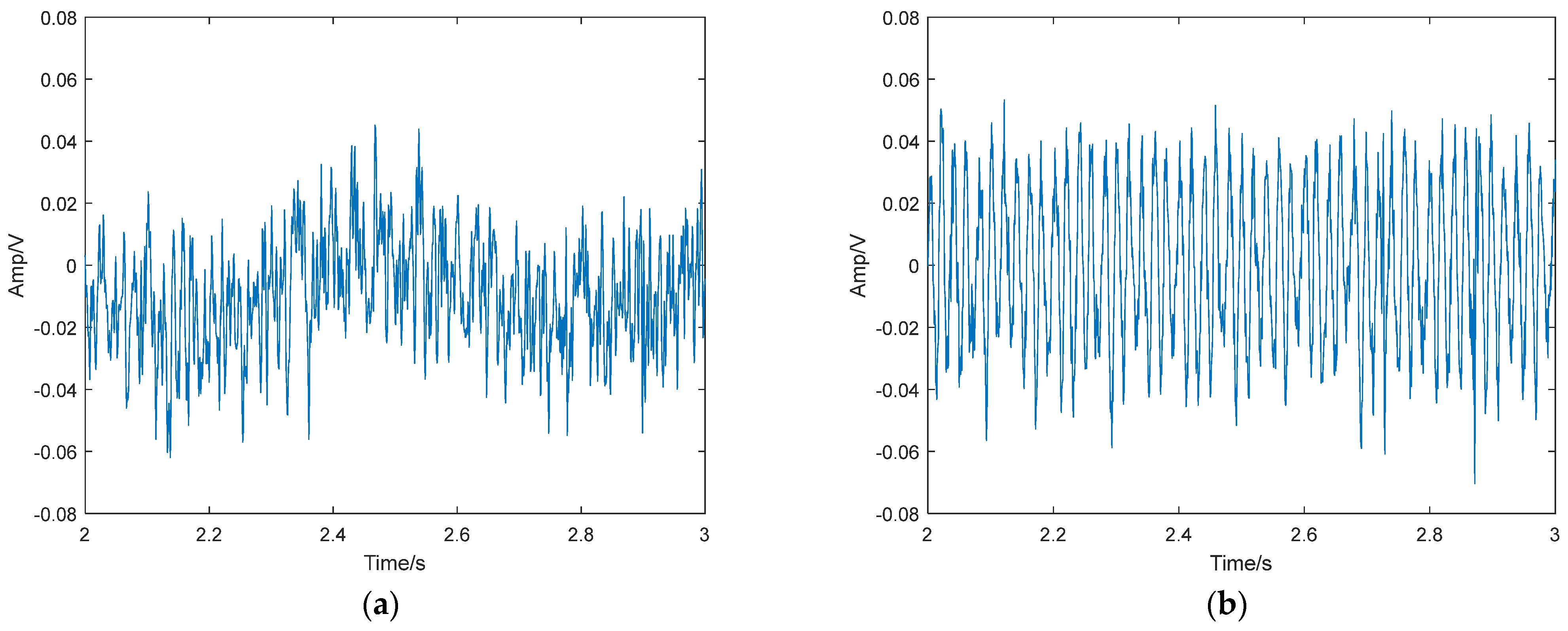
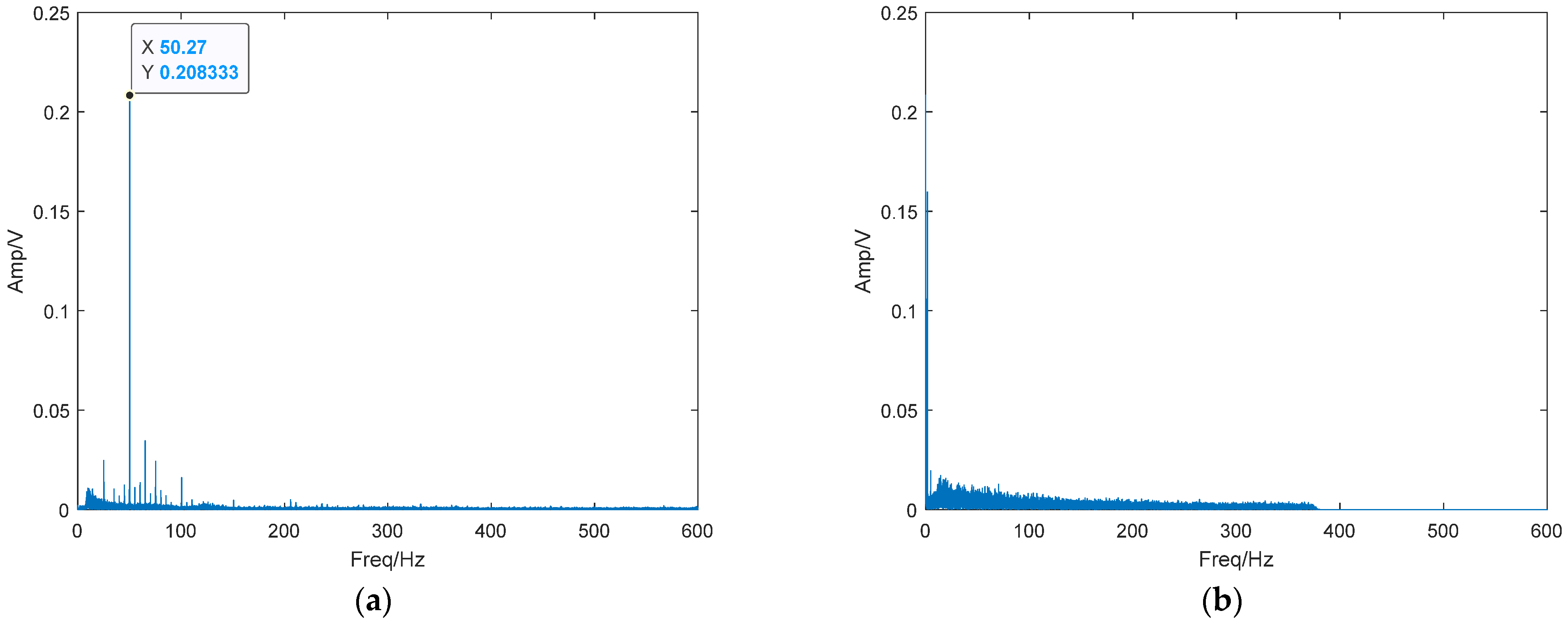
4.4. Verification of the Real Underwater Acoustic Signal
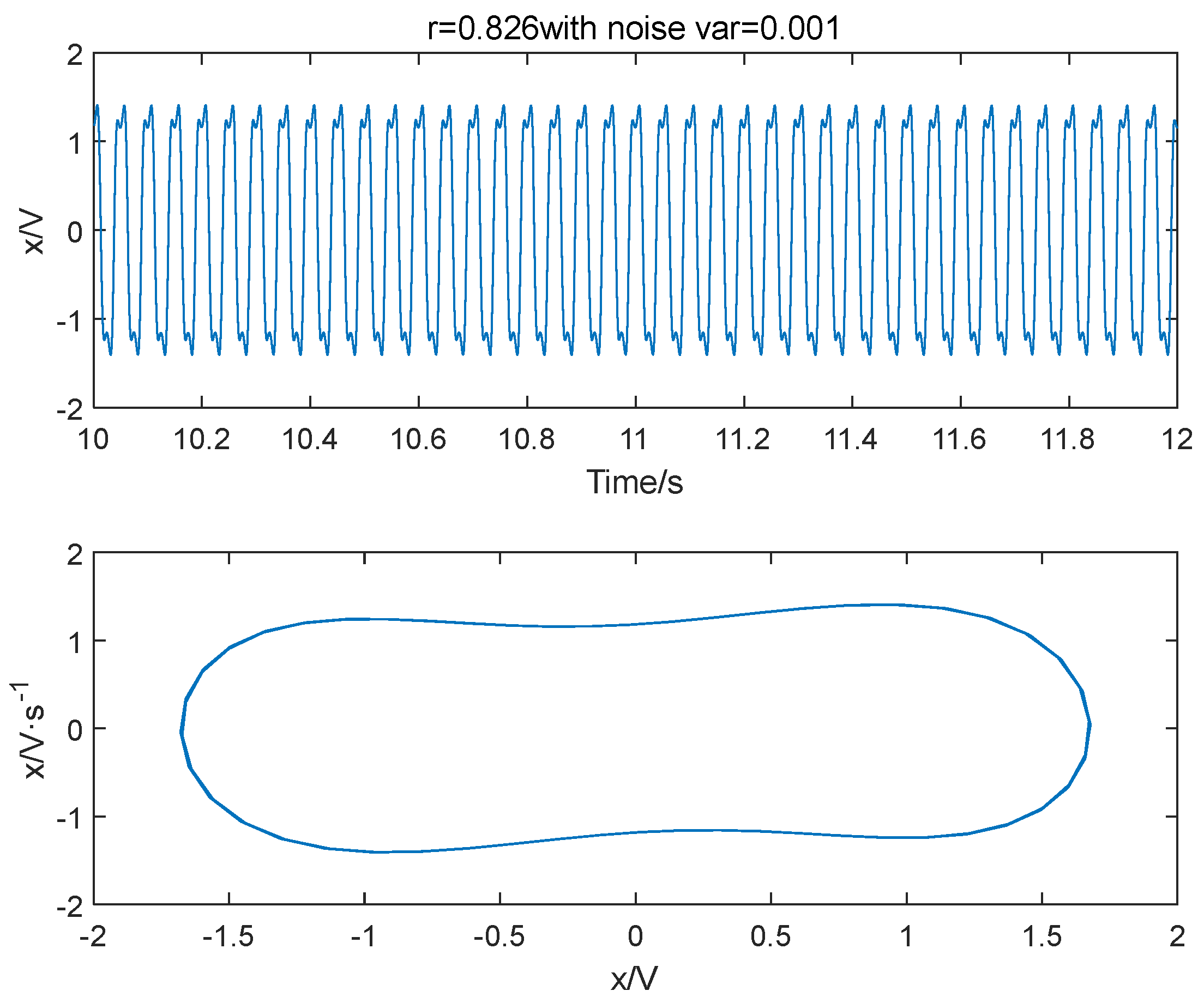
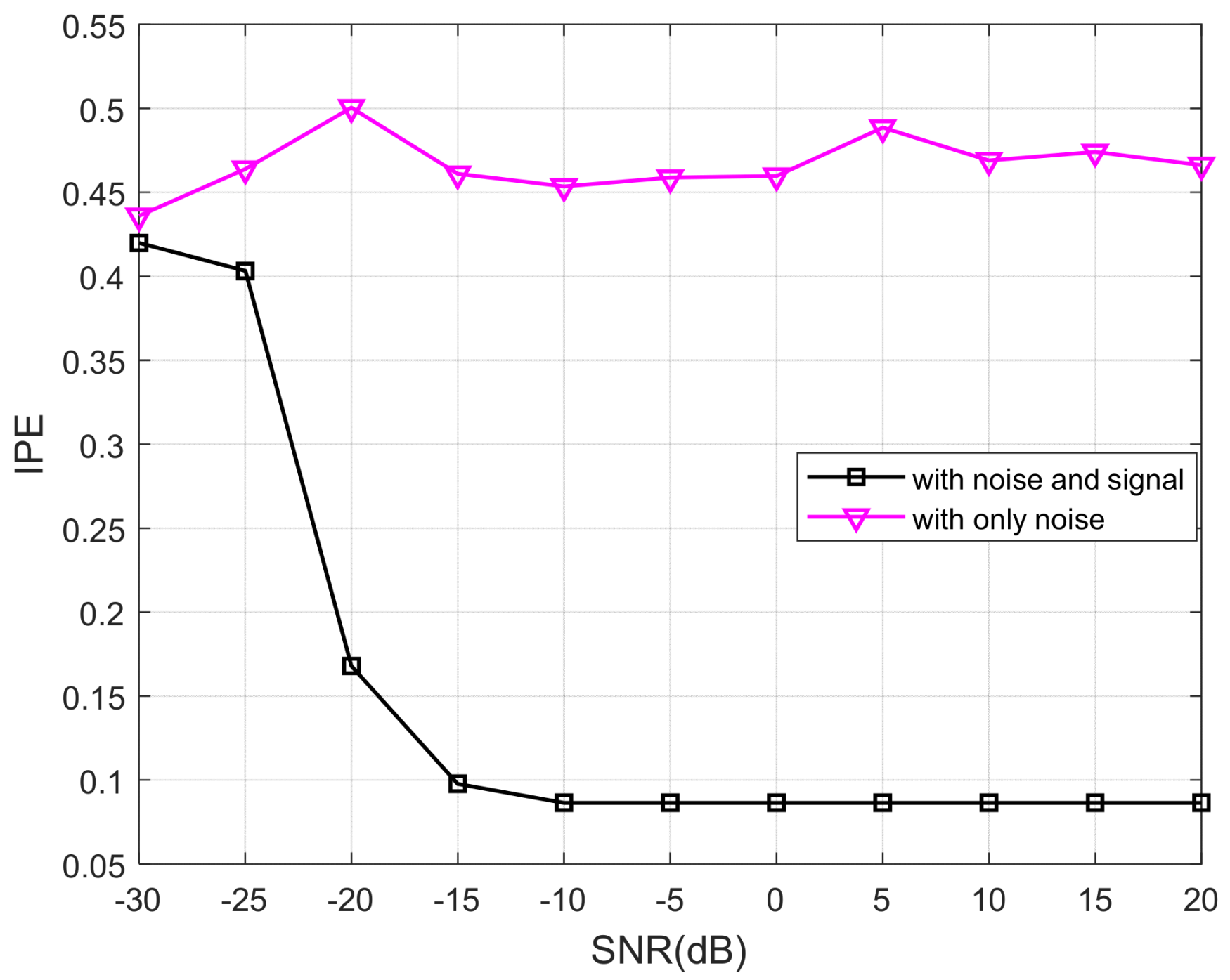
4.5. Analysis of Anti-Noise Performance of Threshold Determination Methods
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A


References
- Chen, J.; Min, F.; Jin, Q.; Ye, B. Coexistence, bifurcation and chaos of a periodically forced duffing system with absolute nonlinearity. Springer J. 2019, 228, 1405–1419. [Google Scholar] [CrossRef]
- Liu, H.; Wu, D.; Jin, W.; Wang, Y. Study on weak signal detection method with Duffing oscillators. Acta Phys. Sin. 2013, 62, 42–47. [Google Scholar]
- Chen, T.; Xiang, Y.; Niu, D. Model modification and feature study of Duffing oscillator. J. Low Freq. Noise Vib. Act. 2022, 41, 230–243. [Google Scholar] [CrossRef]
- Wen, S.; Qin, H.; Shen, Y.; Niu, J. Chaos threshold analysis of Duffing oscillator with fractional-order delayed. Eur. Phys. J. Spec. 2022, 231, 2183–2197. [Google Scholar] [CrossRef]
- Shi, S.; Yuan, Y.; Wang, H.; Luo, M. Weak signal frequency detection method based on generalized Duffing oscillator. Chin. Phys. Lett. 2011, 28, 040502. [Google Scholar] [CrossRef]
- Cong, C.; Li, X.; Song, Y. A method of detecting line spectrum of ship-radiated noise using a new intermittent chaotic oscillator. Acta Phys. Sin. 2014, 63, 168–179. [Google Scholar] [CrossRef]
- Chen, Z.; Li, Y.; Chen, X. Underwater acoustic weak signal detection based on Hilbert transform and intermittent chaos. Acta Phys. Sin. 2015, 64, 73–80. [Google Scholar]
- Guohui, L.; Yongming, H.; Hong, Y. A new Duffing detection method for underwater weak target signal. J. Intell. Manuf. 2022, 61, 2859–2876. [Google Scholar]
- Pedro, P.; Rogerio, A.; Antonio, H.; José, F. Lienard chaotic system based on Duffing and the Sinc function for weak signals detection. IEEE Lat. Am. Trans. 2022, 20, 2114–2121. [Google Scholar]
- Glendininng, P.; Perry, L. Melnikov Analysis of Chaos in a Simple Epidemiological Model. Math. Biol. 1997, 34, 359–373. [Google Scholar] [CrossRef]
- Gottwald, G.; Melbourne, I. On the Implementation of the 0–1 Test for chaos. Siam J. Appl. Dyn. Syst. 2009, 8, 129–145. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Minowa, H. Power spectrum of chaotic motion near a crisis of a one-dimensional map. Phys. Rev. A 1985, 32, 3758–3761. [Google Scholar] [CrossRef]
- Xie, T.; Wei, X.; Yu, R.; Wang, Y. A Method of Intermittent Chaotic Signal Identification Based on the Difference Poincaré Mapping. J. Beijing Jiaotong Univ. 2009, 33, 20–24. [Google Scholar]
- Daniel, C.; Serletis Esteban, T.; Luis-Gerardo, F.; Rangel-Magdaleno, J.; Munoz-Pacheco, J. Poincaré maps for detecting chaos in fractional-order systems with hidden attractors for its Kaplan-Yorke dimension optimization. AIMS Math. 2022, 7, 5871–5894. [Google Scholar]
- Rubén, M.; Qin, H.; Jean, C.; Pablo, L.; Diego, C. Gear and bearing fault classification under different load and speed by using Poincaré plot features and SVM. J. Intell. Manuf. 2022, 33, 1031–1055. [Google Scholar]
- Yan, S.; Sun, X.; Wang, E.; Song, J.; Cui, Y. Application of Weak Signal Detection Based on Improved Duffing Chaotic System. J. Vib. Eng. Technol. 2022, 11, 3057–3068. [Google Scholar] [CrossRef]
- Serletis, S.; Shahmoradi, A.; Serletis, D. Effect of Noise on the Bifurcation Behavior of Nonlinear Dynamical Systems. Chaos Solitons Fractals 2007, 33, 914–921. [Google Scholar] [CrossRef]
- Shannon, C. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Renyi, A. On measures of information and entropy. In Proceedings of the 4th Berkeley Symposium on Mathematics, Statistics and Probability, Berkeley, CA, USA, 30 June–30 July 1960; Volume 1961, pp. 547–561. [Google Scholar]
- Pincus, S.; Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef]
- Richman, J.; Moorman, J. Physiological Time-Series Analysis Using Approximate Entropy and Sample Entropy. Acad. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, 39–49. [Google Scholar] [CrossRef]
- George, M.; Md, A.; Roberto, S. Low Computational Cost for Sample Entropy. Entropy 2018, 20, 20010061. [Google Scholar]
- Bandt, C.; Pompe, B. Permutation Entropy: A Natural Complexity Measure for Time Series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Aziz, W.; Arif, M. Multiscale Permutation Entropy of Physiological Time Series. In Proceedings of the 9th International Multitopic Conference, IEEE INMIC. Karachi, Pakistan, 23–24 December 2005; pp. 1–6. [Google Scholar]
- Fadlallah, B.; Chen, B.; Keil, A. Weighted-permutation entropy: A complexity measure for time series incorporating amplitude information. Phys. Rev. E 2013, 87, 022911. [Google Scholar] [CrossRef] [PubMed]
- Bian, C.; Qin, C.; Ma, Q. Modified permutation-entropy analysis of heartbeat dynamics. Phys. Rev. E 2012, 85, 021906. [Google Scholar] [CrossRef] [PubMed]
- Shaobo, H.; Kehui, S.; Huihai, W. Modified multiscale permutation entropy algorithm and its application for multiscroll chaotic systems. Complexity 2016, 21, 52–58. [Google Scholar] [CrossRef]
- Chen, Z.; Li, Y.; Liang, H.; Yu, J. Improved Permutation Entropy For Measuring Complexity Of Time Series Under Noisy Condition. Complexity 2019, 2019, 1403829. [Google Scholar] [CrossRef]
- Huang, Z.; Li, Y.; Chen, Z.; Liu, L. Threshold determination method of Duffing chaotic system based on multi-scale entropy. Acta Phys. Sin. 2020, 16, 17–25. [Google Scholar] [CrossRef]


| Methods | Weakness |
|---|---|
| Melnikov analysis | High implementation difficulty |
| Phase diagram method | Poor computational accuracy |
| Power spectrum method | Unable to distinguish between periodic and chaotic dynamics |
| Poincaré section method | Subjective |
| 0–1 test | Poor computational accuracy |
| Frequency | True Threshold | Evaluated Threshold by Our Method |
|---|---|---|
| 10 Hz | 0.8257 | 0.8257 |
| 20 Hz | 0.8254 | 0.8254 |
| 100 Hz | 0.8248 | 0.8248 |
| Methods | Frequency | True Threshold | Evaluated Threshold | Computation Time (s) |
|---|---|---|---|---|
| MSE | 10 Hz | 0.8257 | 0.8257 | 573.95 |
| 0–1 test | 10 Hz | 0.8257 | 0.8253 | 598.38 |
| Lyapunov | 10 Hz | 0.8257 | \ | 561.57 |
| Our method | 10 Hz | 0.8257 | 0.8257 | 30.69 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, J.; Li, Y.; Wang, M. Research on the Threshold Determination Method of the Duffing Chaotic System Based on Improved Permutation Entropy and Poincaré Mapping. Entropy 2023, 25, 1654. https://doi.org/10.3390/e25121654
Zhou J, Li Y, Wang M. Research on the Threshold Determination Method of the Duffing Chaotic System Based on Improved Permutation Entropy and Poincaré Mapping. Entropy. 2023; 25(12):1654. https://doi.org/10.3390/e25121654
Chicago/Turabian StyleZhou, Jing, Yaan Li, and Mingzhou Wang. 2023. "Research on the Threshold Determination Method of the Duffing Chaotic System Based on Improved Permutation Entropy and Poincaré Mapping" Entropy 25, no. 12: 1654. https://doi.org/10.3390/e25121654
APA StyleZhou, J., Li, Y., & Wang, M. (2023). Research on the Threshold Determination Method of the Duffing Chaotic System Based on Improved Permutation Entropy and Poincaré Mapping. Entropy, 25(12), 1654. https://doi.org/10.3390/e25121654






