Quantum Control by Few-Cycles Pulses: The Two-Level Problem
Abstract
1. Introduction
2. The Model with a Few-Cycle Pulse
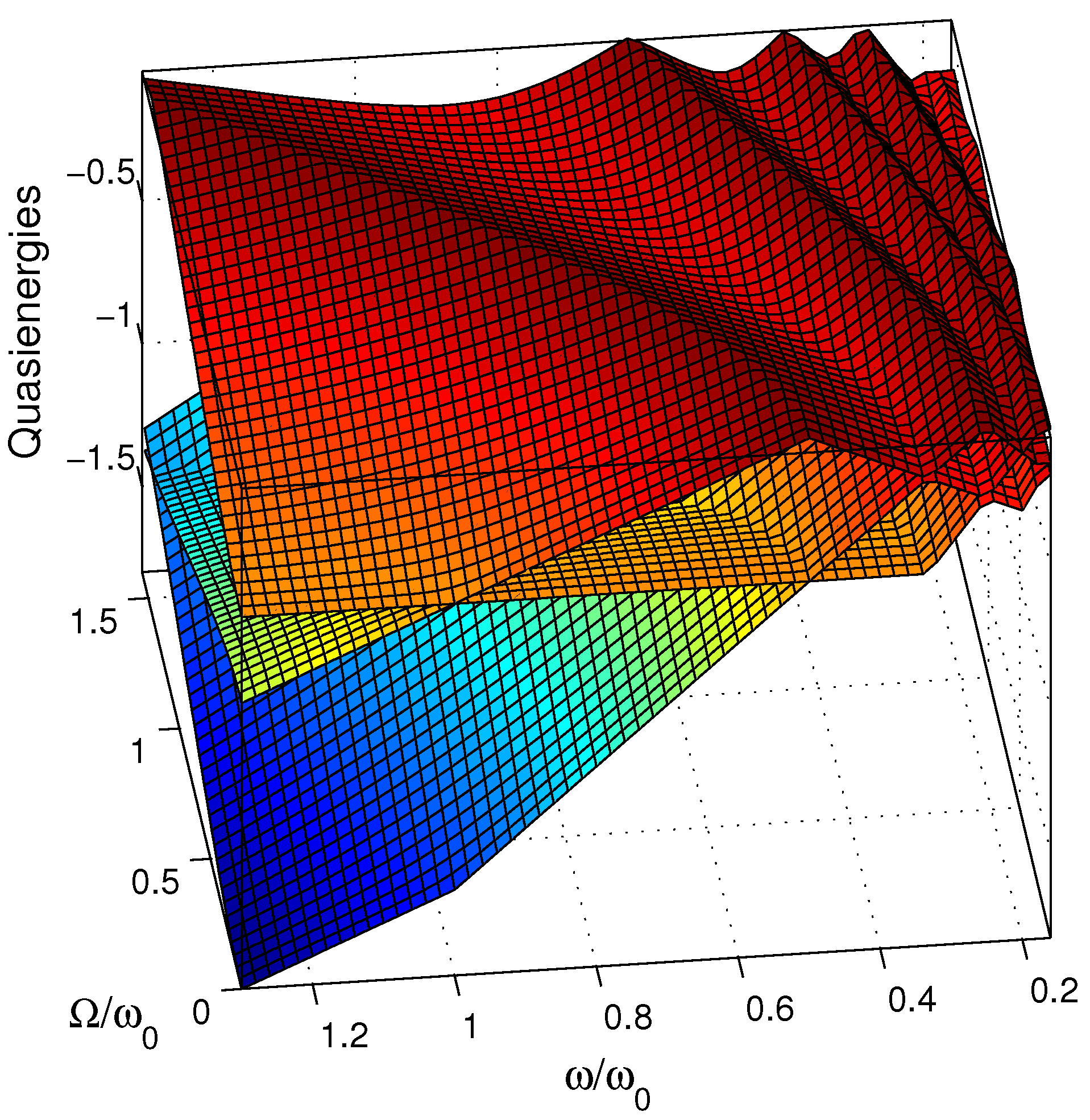
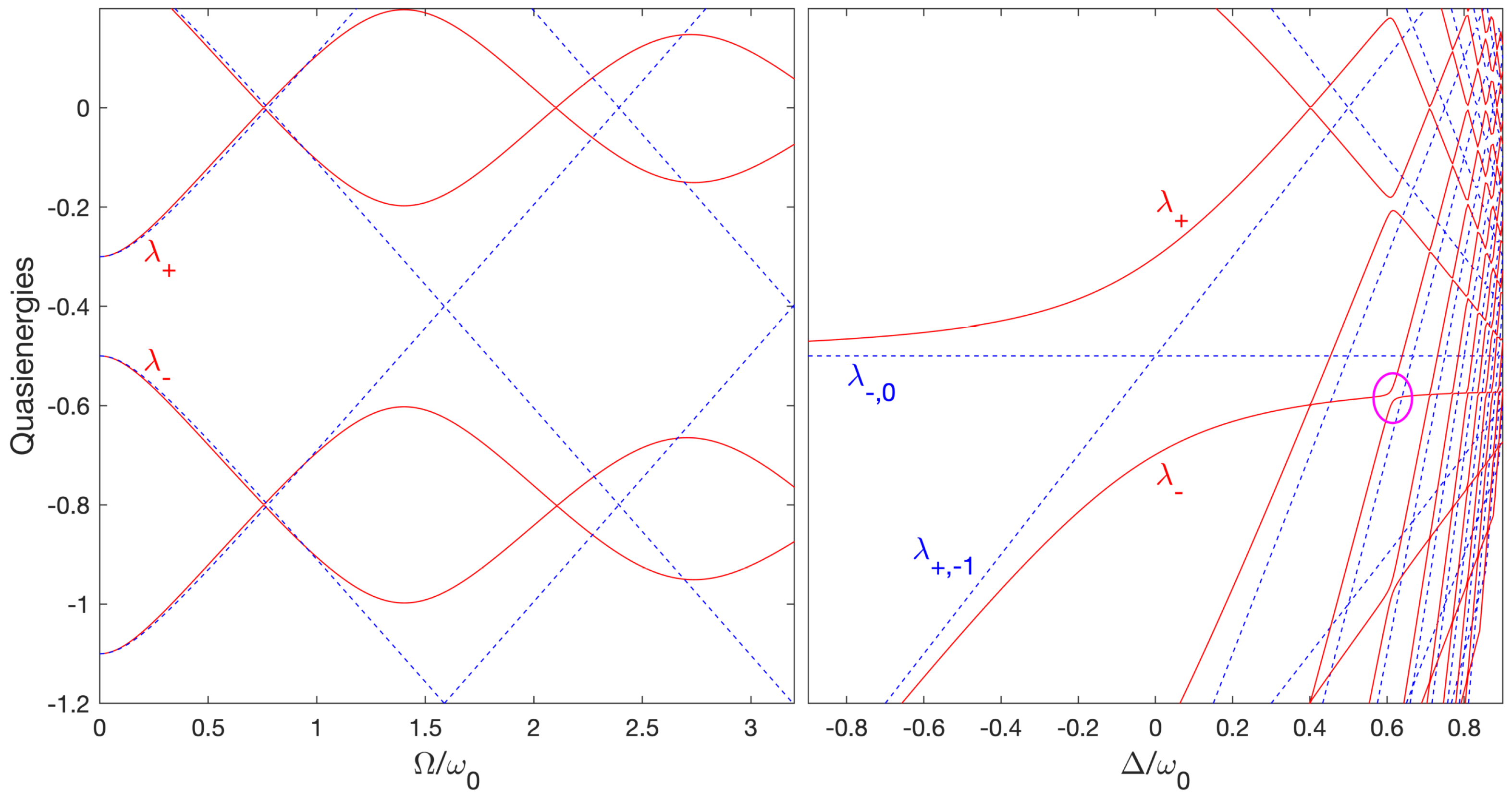
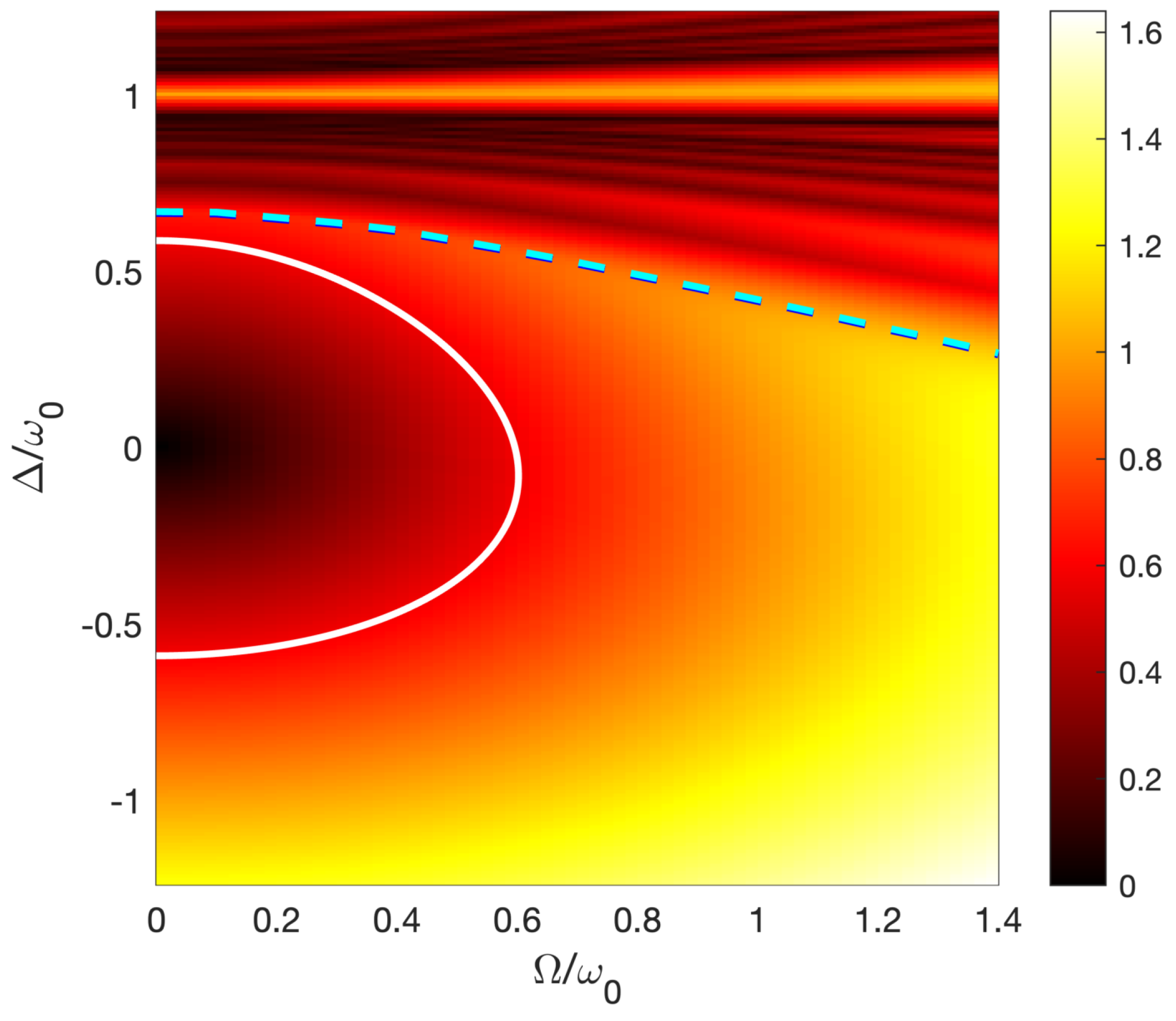
3. Few-Cycle-Pulse Adiabatic Floquet Theory
4. Few-Cycle Generalized -Pulse and Non-Adiabatic Regimes
4.1. Definition
4.2. Few-Cycle Resonant Rabi Oscillations
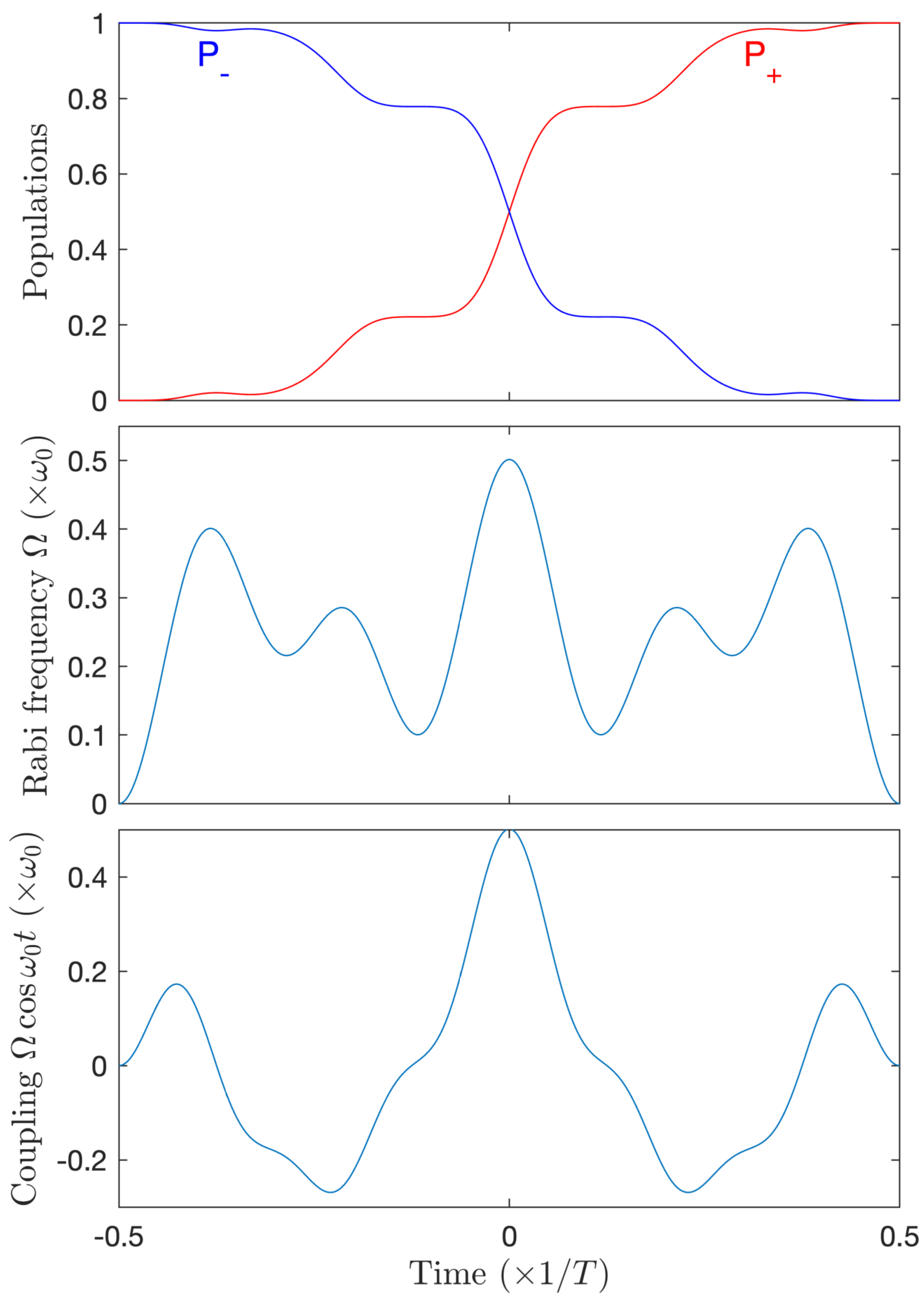
4.3. -Resonance Strategy
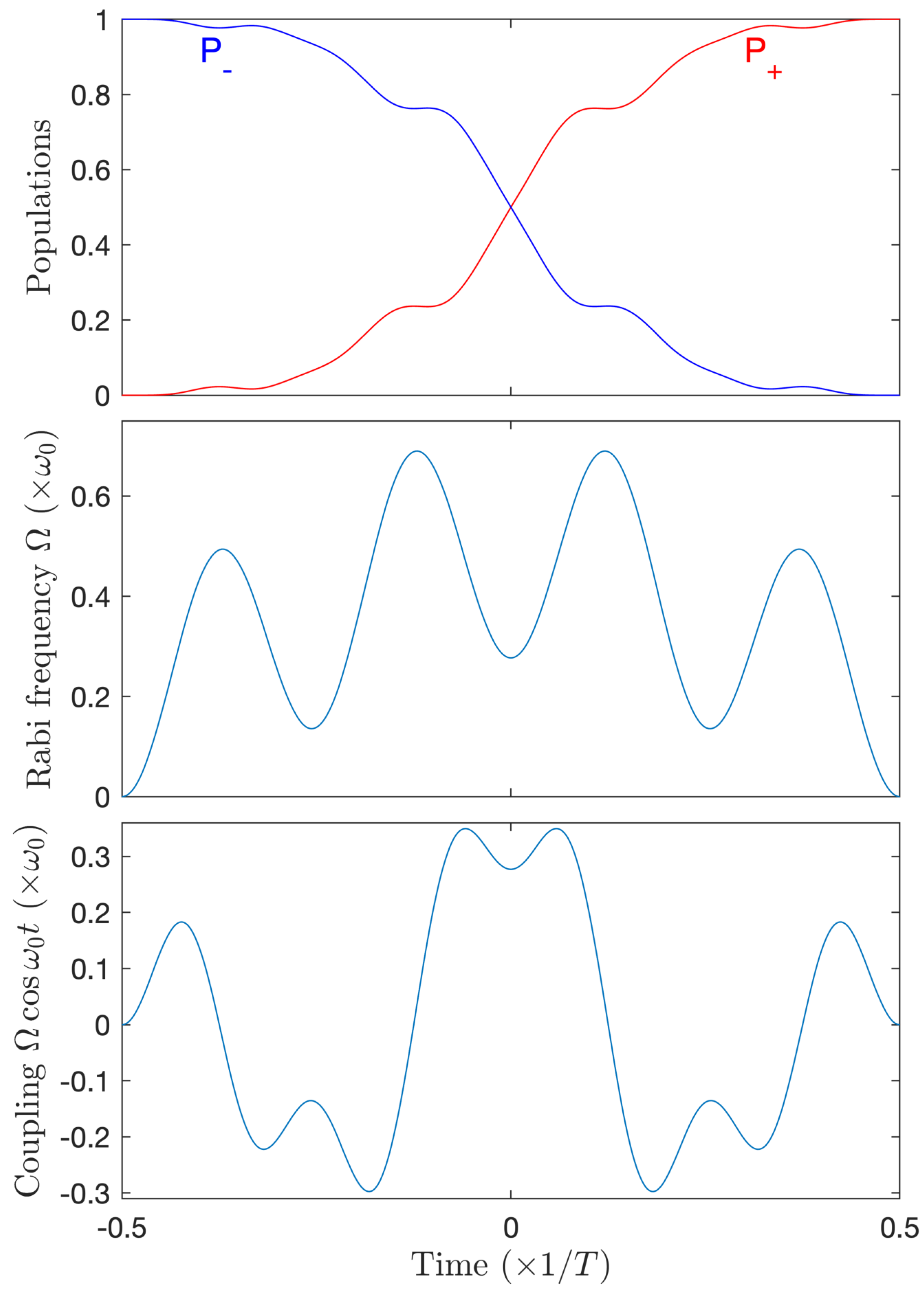
4.4. Two-Modes-Resonance Strategy
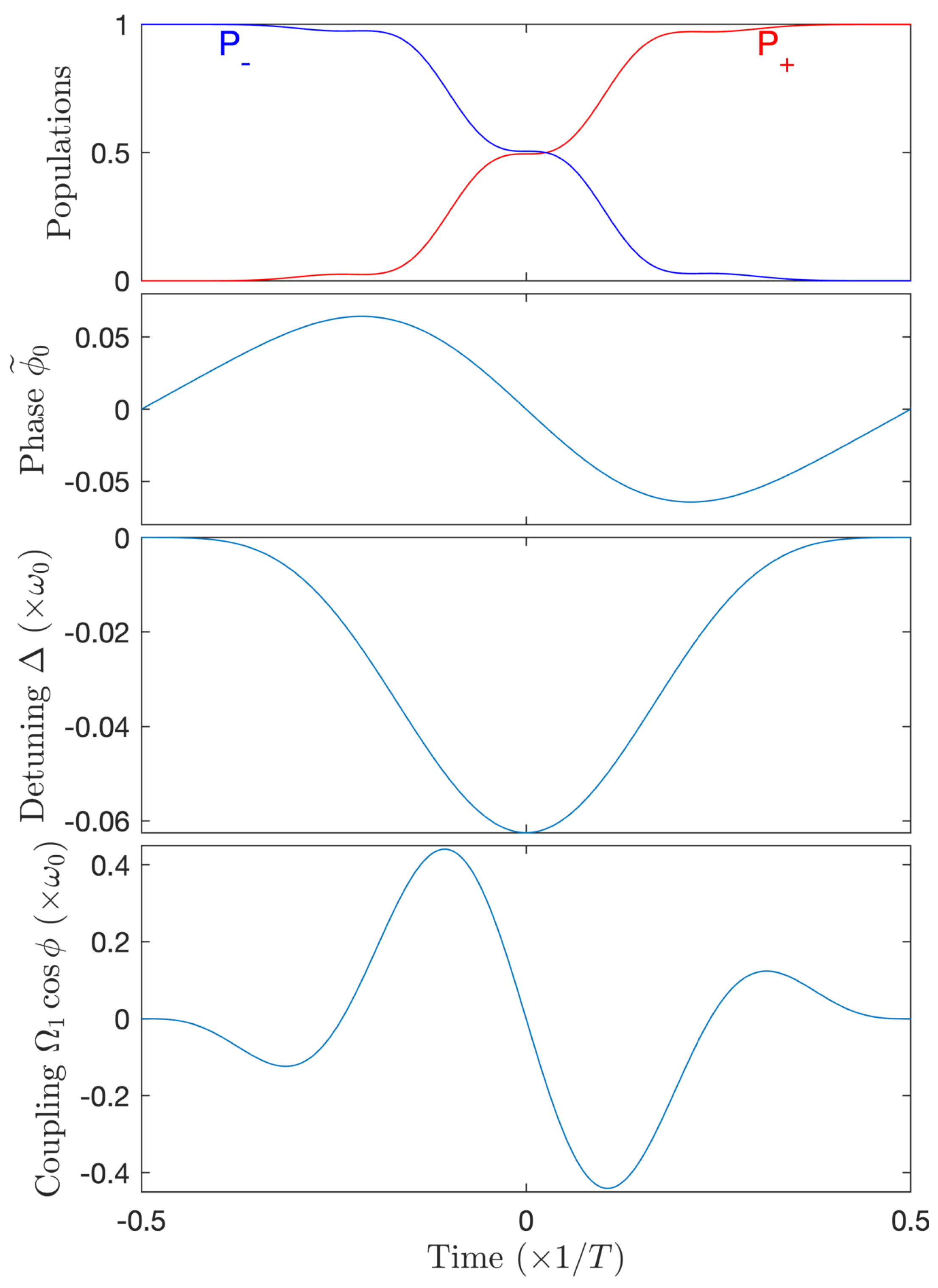
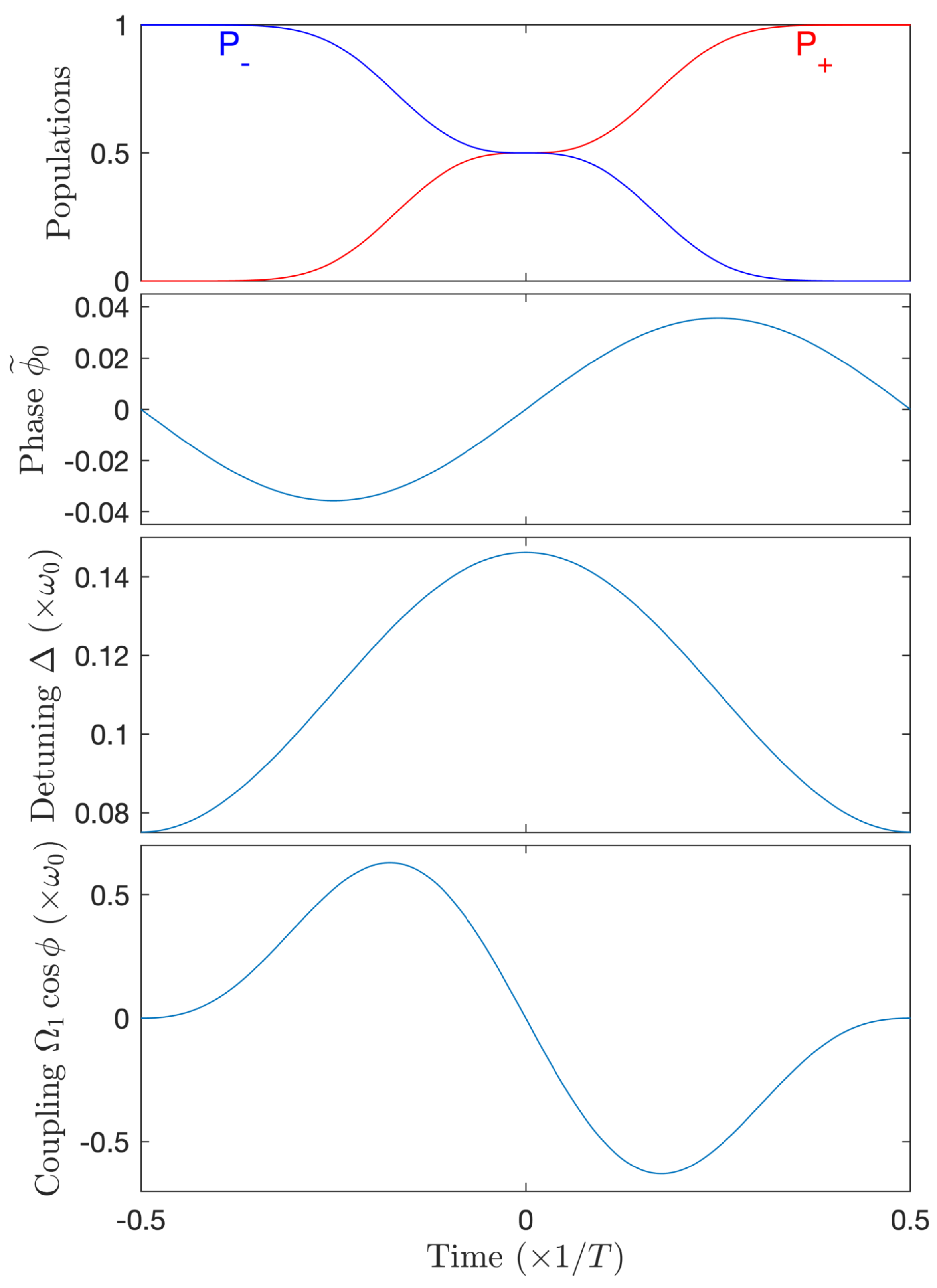
5. Chirped Few-Cycle Pulses: Stark-Shift Compensation Strategy
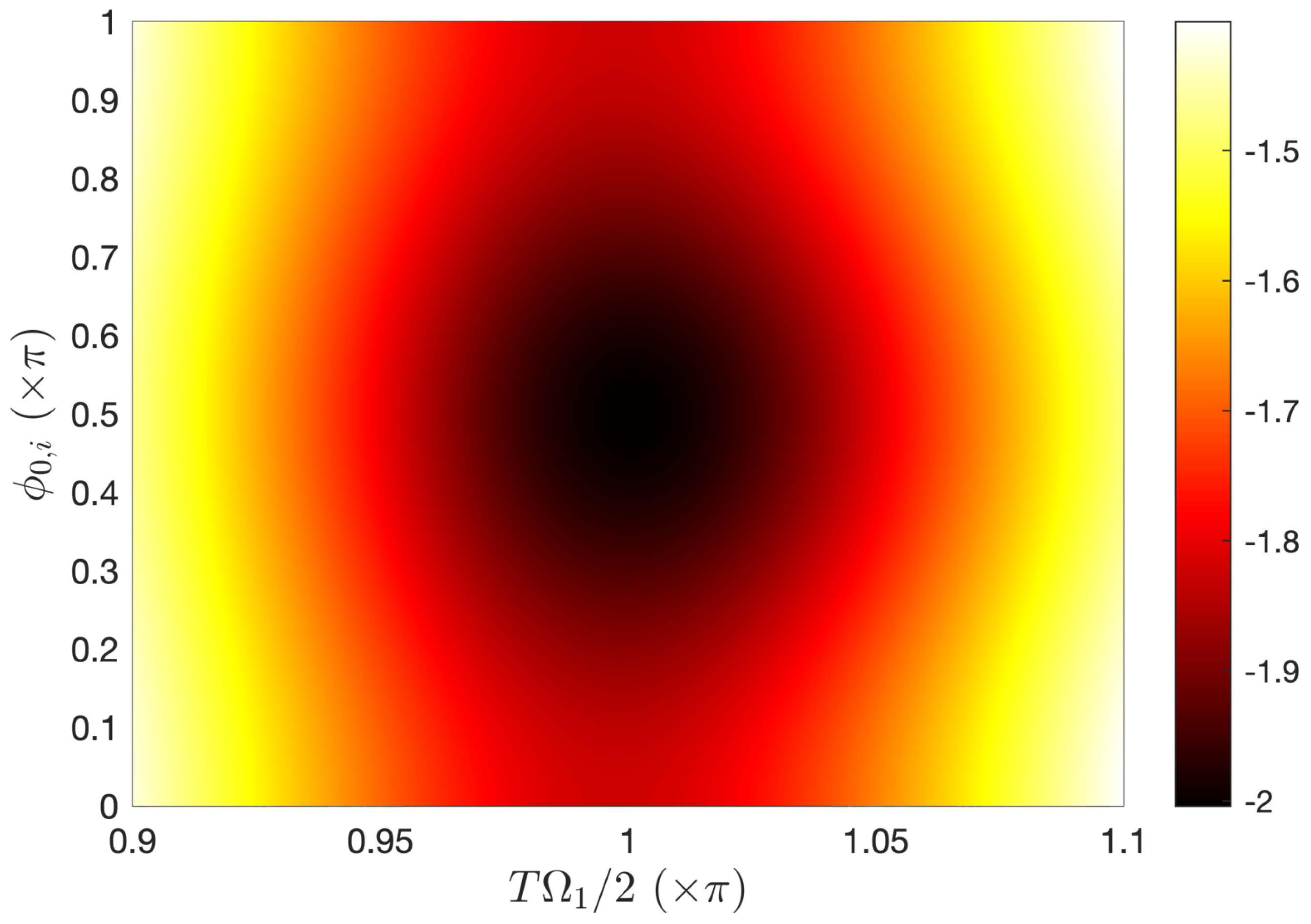
6. Numerical Optimization
6.1. -Resonance Strategy
6.2. Two-Modes-Resonance Strategy
6.3. Stark-Shift Compensation Strategy
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Adiabatic Floquet Theory
Appendix A.1. Floquet Theory for Periodic Systems
Appendix A.2. Adiabatic Floquet Theory
Appendix B. Algorithms

Appendix C. Perturbation Theory Formulated with KAM Techniques
Appendix D. High-Frequency Perturbation Theory
References
- Shapiro, M.; Brumer, P. Quantum Control of Molecular Processes; Wiley-VCH: Weinheim, Germany, 2012. [Google Scholar]
- Shore, B.W. Manipulating Quantum Structure Using Laser Pulses; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Bergmann, K.; Theuer, H.; Shore, B.W. Coherent population transfer among quantum states of atoms and molecules. Rev. Mod. Phys. 1998, 70, 1003. [Google Scholar] [CrossRef]
- Nisbet-Jones, P.B.R.; Dilley, J.; Ljunggren, D.; Kuhn, A. Highly efficient source for indistinguishable single photons of controlled shape. New J. Phys. 2011, 13, 103036. [Google Scholar] [CrossRef]
- Rousseaux, B.; Dzsotjan, D.; Francs, G.C.d.; Jauslin, H.R.; Couteau, C.; Guérin, S. Adiabatic passage mediated by plasmons: A route towards a decoherence-free quantum plasmonic platform. Phys. Rev. B 2016, 93, 045422, Erratum in: Phys. Rev. B 2016, 94, 199902. [Google Scholar] [CrossRef]
- Dorier, V.; Gevorgyan, M.; Ishkhanyan, A.; Leroy, C.; Jauslin, H.R.; Guérin, S. Non-linear stimulated Raman exact passage by resonance-locked inverse engineering. Phys. Rev. Lett. 2017, 119, 243902. [Google Scholar] [CrossRef]
- Dupont, N.; Chatelain, G.; Gabardos, L.; Arnal, M.; Billy, J.; Peaudecerf, B.; Sugny, D.; Guéry- Odelin, D. Quantum State Control of a Bose-Einstein Condensate in Optical Lattice. PRX Quantum 2021, 2, 040303. [Google Scholar] [CrossRef]
- Motzoi, F.; Gambetta, J.; Rebentrost, P.; Wilhelm, F.K. Simple pulses for elimination of leakage in weakly nonlinear qubits. Phys. Rev. Lett. 2009, 103, 110501. [Google Scholar] [CrossRef] [PubMed]
- Vepsäläinen, A.; Danilin, S.; Paraoanu, G.S. Superadiabatic population transfer in a three-level superconducting circuit. Sci. Adv. 2019, 5, eaau5999. [Google Scholar] [CrossRef]
- Nielson, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Sangouard, N.; Lacour, X.; Guérin, S.; Jauslin, H.R. Fast SWAP gate by adiabatic passage. Phys. Rev. A 2005, 72, 062309. [Google Scholar] [CrossRef]
- Jones, J.A. Designing short robust NOT gates for quantum computation. Phys. Rev. A 2013, 87, 052317. [Google Scholar] [CrossRef]
- Rousseaux, B.; Guérin, S.; Vitanov, N.V. Arbitrary qudit gates by adiabatic passage. Phys. Rev. A 2013, 87, 032328. [Google Scholar] [CrossRef]
- Koch, C.P.; Lemeshko, M.; Sugny, D. Quantum control of molecular rotation. Rev. Mod. Phys. 2019, 91, 035005. [Google Scholar] [CrossRef]
- Lapert, M.; Guérin, S.; Sugny, D. Field-free quantum cogwheel by shaping of rotational wave packets. Phys. Rev. A 2011, 83, 013403. [Google Scholar] [CrossRef]
- Vitanov, N.V.; Rangelov, A.A.; Shore, B.W.; Bergmann, K. Stimulated Raman adiabatic passage in physics, chemistry, and beyond. Rev. Mod. Phys. 2017, 89, 015006. [Google Scholar] [CrossRef]
- Yatsenko, L.P.; Guérin, S.; Jauslin, H.R. Topology of adiabatic passage. Phys. Rev. A 2002, 65, 043407. [Google Scholar] [CrossRef]
- Guérin, S.; Jauslin, H.R. Control of Quantum Dynamics by Laser Pulses: Adiabatic Floquet Theory. Adv. Chem. Phys. 2003, 125, 147. [Google Scholar]
- Levitt, M.H. Spin Dynamics: Basics of Nuclear Magnetic Resonance; John Wiley and Sons: New York, NY, USA, 2008. [Google Scholar]
- Torosov, B.T.; Guérin, S.; Vitanov, N.V. High-fidelity adiabatic passage by composite sequences of chirped pulses. Phys. Rev. Lett. 2011, 106, 233001. [Google Scholar] [CrossRef]
- Genov, G.T.; Schraft, D.; Halfmann, T.; Vitanov, N.V. Correction of Arbitrary Field Errors in Population Inversion of Quantum Systems by Universal Composite Pulses. Phys. Rev. Lett. 2014, 113, 043001. [Google Scholar] [CrossRef]
- Koch, C.P.; Boscain, U.; Calarco, T.; Dirr, G.; Filipp, S.; Glaser, S.J.; Kosloff, R.; Montangero, S.; Schulte-Herbrüggen, T.; Sugny, D.; et al. Quantum optimal control in quantum technologies. Strategic report on current status, visions and goals for research in Europe. EPJ Quantum Technol. 2022, 9, 19. [Google Scholar] [CrossRef]
- Boscain, U.; Sigalotti, M.; Sugny, D. Introduction to the Pontryagin Maximum Principle for Quantum Optimal Control. PRX Quantum 2021, 2, 030203. [Google Scholar] [CrossRef]
- Boscain, U.; Charlot, G.; Gauthier, J.-P.; Guérin, S.; Jauslin, H.R. Optimal control in laser-induced population transfer for two- and three-level quantum systems. J. Math. Phys. 2002, 43, 2107. [Google Scholar] [CrossRef]
- Daems, D.; Ruschhaupt, A.; Sugny, D.; Guérin, S. Robust Quantum Control by a Single-Shot Shaped Pulse. Phys. Rev. Lett. 2013, 111, 050404. [Google Scholar] [CrossRef] [PubMed]
- Dridi, G.; Liu, K.; Guérin, S. Optimal robust quantum control by inverse geometric optimization. Phys. Rev. Lett. 2020, 125, 250403. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Lizuain, I.; Ruschhaupt, A.; Guéry-Odelin, D.; Muga, J.G. Shortcut to Adiabatic Passage in Two- and Three-Level Atoms. Phys. Rev. Lett. 2010, 105, 123003. [Google Scholar] [CrossRef]
- Guéry-Odelin, D.; Ruschhaupt, A.; Kiely, A.; Torrontegui, E.; Martínez-Garaot, S.; Muga, J.G. Shortcuts to adiabaticity: Concepts, methods, and applications. Rev. Mod. Phys. 2019, 91, 045001. [Google Scholar] [CrossRef]
- Ding, Y.-C.; Ban, Y.; Martín-Guerrero, J.D.; Solano, E.; Casanova, J.; Chen, X. Breaking adiabatic quantum control with deep learning. Phys. Rev. A 2021, 103, L040401. [Google Scholar] [CrossRef]
- Giannelli, L.; Sgroi, P.; Brown, J.; Paraoanu, G.S.; Paternostro, M.; Paladino, E.; Falci, G. A tutorial on optimal control and reinforcement learning methods for quantum technologies. Phys. Lett. A 2022, 434, 128054. [Google Scholar] [CrossRef]
- Kärtner, F.X. Few-Cycle Laser Pulse Generation and Its Applications; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Brabec, T.; Krausz, F. Intense few-cycle laser fields: Frontiers of nonlinear optics. Rev. Mod. Phys. 2000, 72, 545. [Google Scholar] [CrossRef]
- Egodapitiya, K.N.; Li, S.; Jones, R.R. Terahertz-Induced Field-Free Orientation of Rotationally Excited Molecules. Phys. Rev. Lett. 2014, 112, 103002. [Google Scholar] [CrossRef]
- Xu, L.; Tutunnikov, I.; Gershnabel, E.; Prior, Y.; Averbukh, I.S. Long-Lasting Molecular Orientation Induced by a Single Terahertz Pulse. Phys. Rev. Lett. 2020, 125, 013201. [Google Scholar] [CrossRef]
- Shu, C.-C.; Hong, Q.-Q.; Guo, Y.; Henriksen, N.E. Orientational quantum revivals induced by a single-cycle terahertz pulse. Phys. Rev. A 2020, 102, 063124. [Google Scholar] [CrossRef]
- Shore, B.W. The Theory of Coherent Atomic Excitation; Wiley: New York, NY, USA, 1990. [Google Scholar]
- Pollock, C.R. Ultrafast optical pulses. In Progress in Optics; Wolf, E., Ed.; Elsevier: Amsterdam, The Netherlands, 2008; pp. 211–249. [Google Scholar]
- Berry, M.V. Quantum phase corrections from adiabatic iteration. Proc. R. Soc. Lond. A 1987, 414, 31. [Google Scholar]
- Guérin, S.; Thomas, S.; Jauslin, H.R. Optimization of population transfer by adiabatic passage. Phys. Rev. A 2002, 65, 023409. [Google Scholar] [CrossRef]
- Dridi, G.; Guérin, S.; Hakobyan, V.; Jauslin, H.R.; Eleuch, H. Ultrafast stimulated Raman parallel adiabatic passage by shaped pulses. Phys. Rev. A 2009, 80, 043408. [Google Scholar] [CrossRef]
- Guérin, S.; Hakobyan, V.; Jauslin, H.R. Optimal adiabatic passage by shaped pulses: Efficiency and robustness. Phys. Rev. A 2011, 84, 01343. [Google Scholar] [CrossRef]
- Vasilev, G.S.; Vitanov, N.V. Complete population transfer by a zero-area pulse. Phys. Rev. A 2006, 73, 023416. [Google Scholar] [CrossRef]
- Thomas, S.; Guérin, S.; Jauslin, H.R. State-selective chirped adiabatic passage on dynamically laser-aligned molecules. Phys. Rev. A 2005, 71, 013402. [Google Scholar] [CrossRef]
- Hong, J.; Liu, Y.; Munthe-Kaas, H.; Zanna, A. Globally conservative properties and error estimation of a multi-symplectic scheme for Schrödinger equations with variable coefficients. Appl. Numer. Math. 2006, 56, 814–843. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peyraut, F.; Holweck, F.; Guérin, S. Quantum Control by Few-Cycles Pulses: The Two-Level Problem. Entropy 2023, 25, 212. https://doi.org/10.3390/e25020212
Peyraut F, Holweck F, Guérin S. Quantum Control by Few-Cycles Pulses: The Two-Level Problem. Entropy. 2023; 25(2):212. https://doi.org/10.3390/e25020212
Chicago/Turabian StylePeyraut, François, Frédéric Holweck, and Stéphane Guérin. 2023. "Quantum Control by Few-Cycles Pulses: The Two-Level Problem" Entropy 25, no. 2: 212. https://doi.org/10.3390/e25020212
APA StylePeyraut, F., Holweck, F., & Guérin, S. (2023). Quantum Control by Few-Cycles Pulses: The Two-Level Problem. Entropy, 25(2), 212. https://doi.org/10.3390/e25020212





