Emergent Criticality in Coupled Boolean Networks
Abstract
:1. Introduction
2. Models and Methods
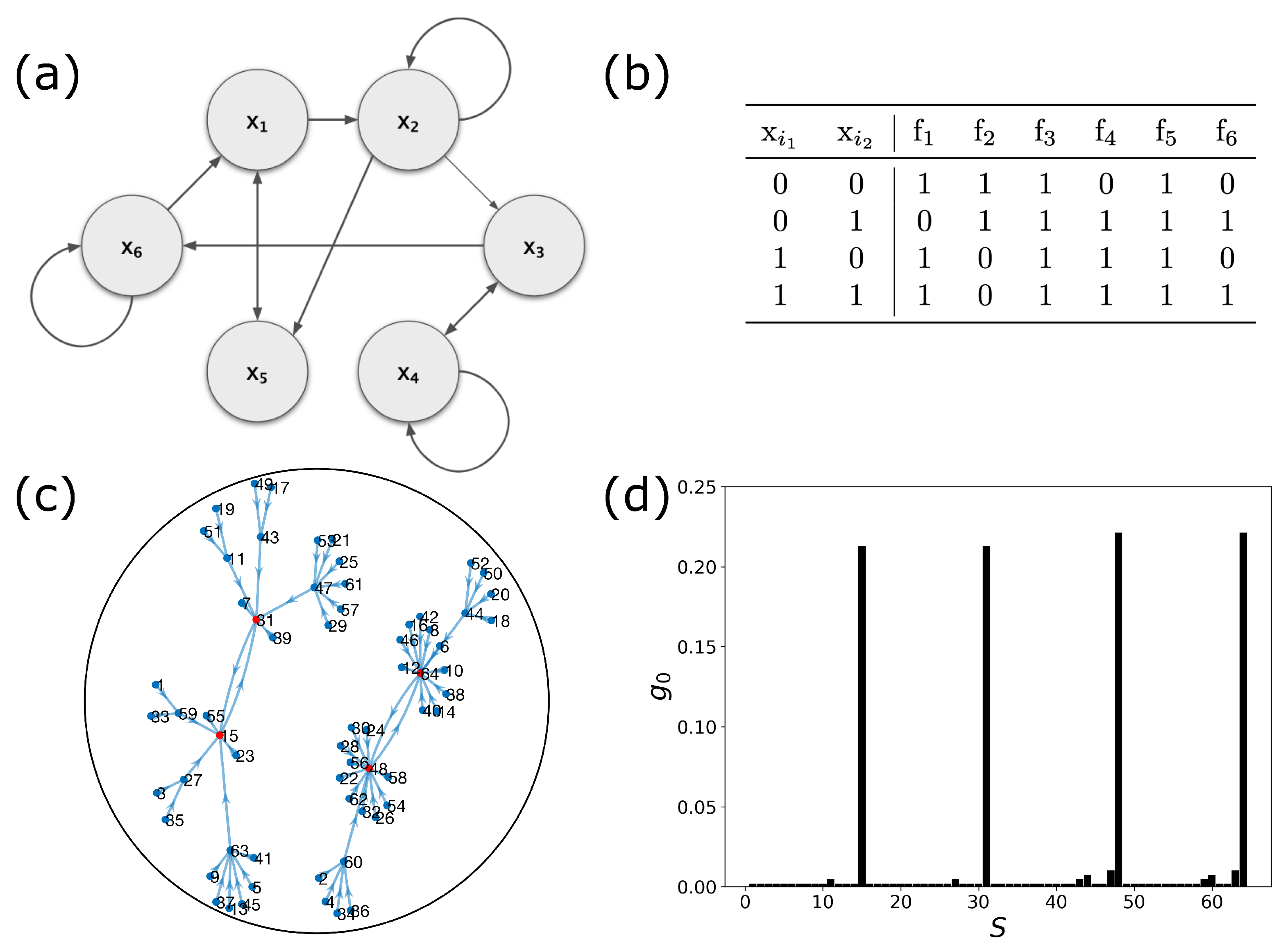
2.1. Boolean Networks
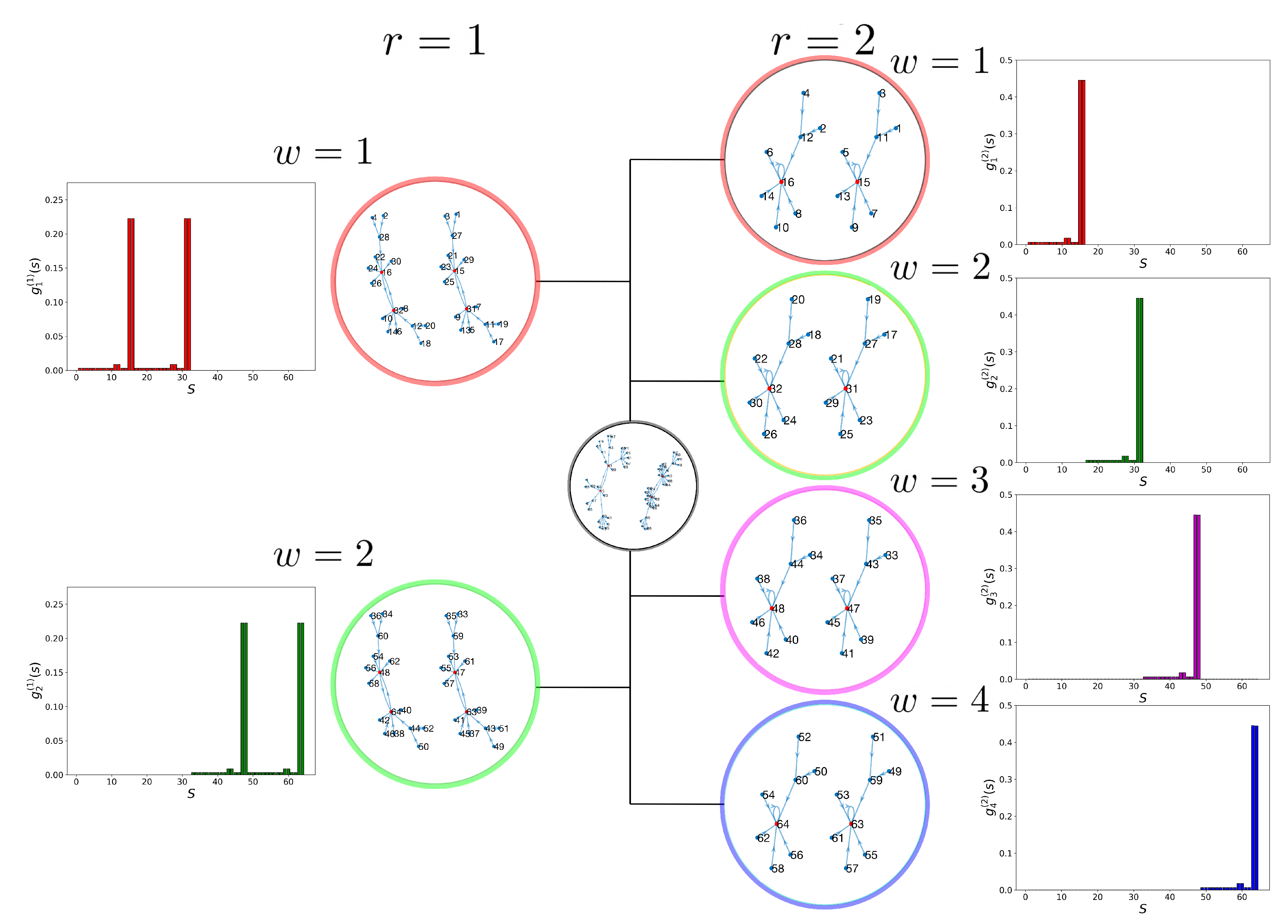
2.2. Dynamic Control Kernel
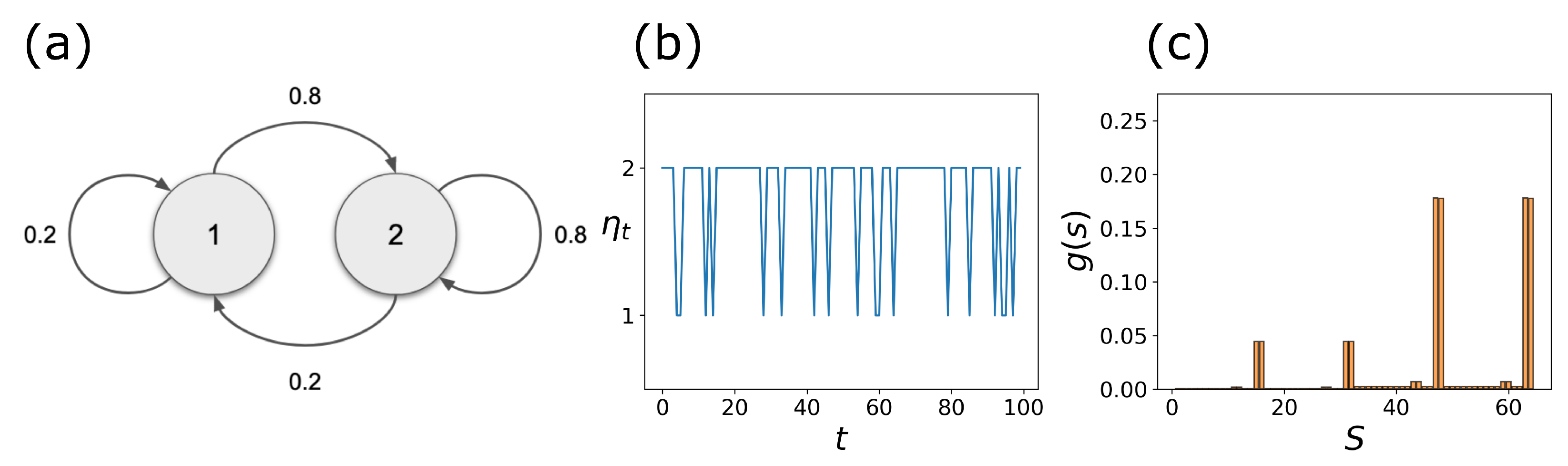
2.3. Coupled Boolean Networks
2.4. Detecting Cell Types
3. Results
- Case 1.
- If , the CK is not affected by unpinned dynamics. Thus, the Hamiltonian reduces to the standard r-layer Ising model under the influence of an external field.
- Case 2.
- If and , then Equation (5) describes L-uncoupled BNs (non-interacting cells).
- Case 3.
- For , the r Ising layers are coupled through the dynamics of each BN. This is a nontrivial, bidirectional, and time-dependent nonlinear coupling.
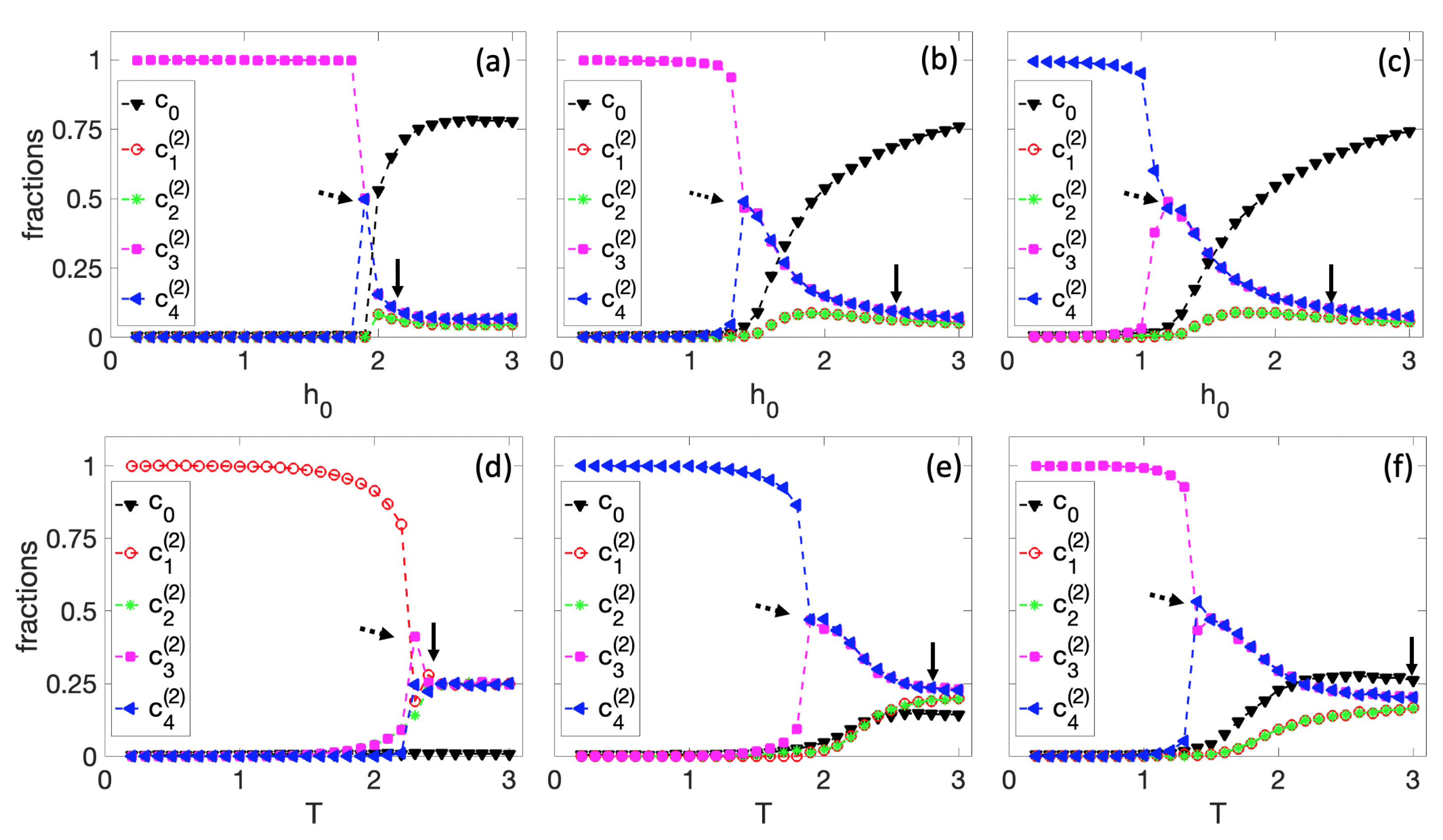
3.1. Spontaneous Cell Differentiation
3.2. Self-Tuned Cell Differentiation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Parameter Notation | Definition | Parameter Values |
|---|---|---|
| k | BN connectivity | 2 |
| p | Boolean function bias | |
| q | perturbation probability | |
| r | control kernel size | |
| J | interaction strength/energy unit | 1 |
| h | external field constant | 0 |
| relaxation coefficient | ||
| simulation time (MC steps) | ||
| equilibration time (MC steps) |
References
- Kærn, M.; Elston, T.C.; Blake, W.J.; Collins, J.J. Stochasticity in gene expression: From theories to phenotypes. Nat. Rev. Genet. 2005, 6, 451–464. [Google Scholar] [CrossRef]
- Huang, S. Reprogramming cell fates: Reconciling rarity with robustness. BioEssays 2009, 31, 546–560. [Google Scholar] [CrossRef]
- Hu, M.; Krause, D.; Greaves, M.; Sharkis, S.; Dexter, M.; Heyworth, C.; Enver, T. Multilineage gene expression precedes commitment in the hemopoietic system. Genes Dev. 1997, 11, 774–785. [Google Scholar] [CrossRef] [Green Version]
- Garcia-Ojalvo, J.; Martinez Arias, A. Towards a statistical mechanics of cell fate decisions. Curr. Opin. Genet. Dev. 2012, 22, 619–626. [Google Scholar] [CrossRef]
- Macarthur, B.D.; Lemischka, I.R. Statistical Mechanics of Pluripotency. Cell 2013, 154, 484–489. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Silva, J.; Smith, A. Capturing Pluripotency. Cell 2008, 132, 532–536. [Google Scholar] [CrossRef] [Green Version]
- Goldenfeld, N. Lectures on Phase Transitions and the Renormalization Group; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Ehrenfest, P. Phasenumwandlungen im ueblichen und erweiterten Sinn, classifiziert nach den entsprechenden Singularitaeten des thermodynamischen Potentiales; NV Noord-Hollandsche Uitgevers Maatschappij: Amsterdam, The Netherlands, 1933. [Google Scholar]
- Jaeger, G. The Ehrenfest classification of phase transitions: Introduction and evolution. Arch. Hist. Exact Sci. 1998, 53, 51–81. [Google Scholar] [CrossRef]
- Pujadas, E.; Feinberg, A.P. Regulated Noise in the Epigenetic Landscape of Development and Disease. Cell 2012, 148, 1123–1131. [Google Scholar] [CrossRef] [Green Version]
- MacArthur, B.D.; Ma, A.; Lemischka, I.R. Systems biology of stem cell fate and cellular reprogramming. Nat. Rev. Mol. Cell Biol. 2009, 10, 672–681. [Google Scholar] [CrossRef] [Green Version]
- Okamoto, K.; Germond, A.; Fujita, H.; Furusawa, C.; Okada, Y.; Watanabe, T.M. Single cell analysis reveals a biophysical aspect of collective cell-state transition in embryonic stem cell differentiation. Sci. Rep. 2018, 8, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Shmulevich, I.; Dougherty, E.R.; Kim, S.; Zhang, W. Probabilistic Boolean networks: A rule-based uncertainty model for gene regulatory networks. Bioinformatics 2002, 18, 261–274. [Google Scholar] [CrossRef] [Green Version]
- Kauffman, S.; Peterson, C.; Samuelsson, B.; Troein, C. Random Boolean network models and the yeast transcriptional network. Proc. Natl. Acad. Sci. USA 2003, 100, 14796–14799. [Google Scholar] [CrossRef] [Green Version]
- Serra, R.; Villani, M.; Graudenzi, A.; Kauffman, S.A. Why a simple model of genetic regulatory networks describes the distribution of avalanches in gene expression data. J. Theor. Biol. 2007, 246, 449–460. [Google Scholar] [CrossRef]
- Albert, R.; Othmer, H.G. The topology of the regulatory interactions predicts the expression pattern of the segment polarity genes in Drosophila melanogaster. J. Theor. Biol. 2003, 223, 1–18. [Google Scholar] [CrossRef]
- Huang, S.; Ingber, D.E. Shape-dependent control of cell growth, differentiation, and apoptosis: Switching between attractors in cell regulatory networks. Exp. Cell Res. 2000, 261, 91–103. [Google Scholar] [CrossRef] [Green Version]
- Saez-Rodriguez, J.; Simeoni, L.; Lindquist, J.A.; Hemenway, R.; Bommhardt, U.; Arndt, B.; Haus, U.U.; Weismantel, R.; Gilles, E.D.; Klamt, S.; et al. A logical model provides insights into T cell receptor signaling. PLoS Comput. Biol. 2007, 3, e163. [Google Scholar] [CrossRef]
- Derrida, B.; Pomeau, Y. Random networks of automata: A simple annealed approximation. EPL (Europhys. Lett.) 1986, 1, 45. [Google Scholar] [CrossRef]
- Luque, B.; Solé, R.V. Lyapunov exponents in random Boolean networks. Phys. A Stat. Mech. Its Appl. 2000, 284, 33–45. [Google Scholar] [CrossRef] [Green Version]
- Kauffman, S.A. Metabolic stability and epigenesis in randomly constructed genetic nets. J. Theor. Biol. 1969, 22, 437–467. [Google Scholar] [CrossRef]
- Kauffman, S. The large scale structure and dynamics of gene control circuits: An ensemble approach. J. Theor. Biol. 1974, 44, 167–190. [Google Scholar] [CrossRef]
- Bornholdt, S.; Kauffman, S. Ensembles, dynamics, and cell types: Revisiting the statistical mechanics perspective on cellular regulation. J. Theor. Biol. 2019, 467, 15–22. [Google Scholar] [CrossRef] [Green Version]
- Shmulevich, I.; Gluhovsky, I.; Hashimoto, R.F.; Dougherty, E.R.; Zhang, W. Steady-state analysis of genetic regulatory networks modelled by probabilistic Boolean networks. Comp. Funct. Genom. 2003, 4, 601–608. [Google Scholar] [CrossRef] [Green Version]
- Ching, W.K.; Zhang, S.; Ng, M.K.; Akutsu, T. An approximation method for solving the steady-state probability distribution of probabilistic Boolean networks. Bioinformatics 2007, 23, 1511–1518. [Google Scholar] [CrossRef]
- Kang, C.; Aguilar, B.; Shmulevich, I. Emergence of diversity in homogeneous coupled Boolean networks. Phys. Rev. E 2018, 97, 052415. [Google Scholar] [CrossRef]
- Brun, M.; Dougherty, E.R.; Shmulevich, I. Steady-state probabilities for attractors in probabilistic Boolean networks. Signal Process. 2005, 85, 1993–2013. [Google Scholar] [CrossRef]
- Elowitz, M.B.; Levine, A.J.; Siggia, E.D.; Swain, P.S. Stochastic gene expression in a single cell. Science 2002, 297, 1183–1186. [Google Scholar] [CrossRef] [Green Version]
- Raser, J.M.; O’Shea, E.K. Control of stochasticity in eukaryotic gene expression. Science 2004, 304, 1811–1814. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Golding, I.; Sawai, S.; Guo, L.; Cox, E.C. Population fitness and the regulation of Escherichia coli genes by bacterial viruses. PLoS Biol. 2005, 3, e229. [Google Scholar] [CrossRef]
- Lei, X.; Tian, W.; Zhu, H.; Chen, T.; Ao, P. Biological sources of intrinsic and extrinsic noise in cI expression of lysogenic phage lambda. Sci. Rep. 2015, 5, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Cheng, D.; Qi, H. Controllability and observability of Boolean control networks. Automatica 2009, 45, 1659–1667. [Google Scholar] [CrossRef]
- Serra, R.; Villani, M.; Semeria, A. Genetic network models and statistical properties of gene expression data in knock-out experiments. J. Theor. Biol. 2004, 227, 149–157. [Google Scholar] [CrossRef]
- Kim, J.; Park, S.M.; Cho, K.H. Discovery of a kernel for controlling biomolecular regulatory networks. Sci. Rep. 2013, 3, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Joo, J.I.; Zhou, J.X.; Huang, S.; Cho, K.H. Determining relative dynamic stability of cell states using boolean network model. Sci. Rep. 2018, 8, 1–14. [Google Scholar] [CrossRef]
- Villani, M.; Serra, R.; Ingrami, P.; Kauffman, S.A. Coupled random Boolean network forming an artificial tissue. In Proceedings of the International Conference on Cellular Automata, Springer, Berlin/Heidelberg, Germany; 2006; pp. 548–556. [Google Scholar]
- Serra, R.; Villani, M.; Damiani, C.; Graudenzi, A.; Colacci, A.; Kauffman, S.A. Interacting random boolean networks. In Proceedings of the ECCS07: European Conference on Complex Systems; Citeseer: University Park, PA, USA, 2007; pp. 1–15. [Google Scholar]
- Damiani, C.; Serra, R.; Villani, M.; Kauffman, S.A.; Colacci, A. Cell—Cell interaction and diversity of emergent behaviours. IET Syst. Biol. 2011, 5, 137–144. [Google Scholar] [CrossRef]
- Flann, N.S.; Mohamadlou, H.; Podgorski, G.J. Kolmogorov complexity of epithelial pattern formation: The role of regulatory network configuration. Biosystems 2013, 112, 131–138. [Google Scholar] [CrossRef]
- Kim, H.; Pineda, O.K.; Gershenson, C. A multilayer structure facilitates the production of antifragile systems in boolean network models. Complexity 2019, 2019, 2783217. [Google Scholar] [CrossRef]
- Lee, D.D.; Seung, H.S. Learning the parts of objects by non-negative matrix factorization. Nature 1999, 401, 788–791. [Google Scholar] [CrossRef]
- Liu, L.; Michowski, W.; Kolodziejczyk, A.; Sicinski, P. The cell cycle in stem cell proliferation, pluripotency and differentiation. Nat. Cell Biol. 2019, 21, 1060–1067. [Google Scholar] [CrossRef]
- Waddington, C.H. Organisers and Genes; Cambridge University Press: Cambridge, UK, 1940. [Google Scholar]
- Wang, J.; Xu, L.; Wang, E.; Huang, S. The potential landscape of genetic circuits imposes the arrow of time in stem cell differentiation. Biophys. J. 2010, 99, 29–39. [Google Scholar] [CrossRef] [Green Version]
- Zhou, J.X.; Aliyu, M.; Aurell, E.; Huang, S. Quasi-potential landscape in complex multi-stable systems. J. R. Soc. Interface 2012, 9, 3539–3553. [Google Scholar] [CrossRef]
- McElroy, M.; Voulgarakis, N.K. 2023; in preparation.
- Tsuchiya, M.; Giuliani, A.; Hashimoto, M.; Erenpreisa, J.; Yoshikawa, K. Emergent Self-Organized Criticality in gene expression dynamics: Temporal development of global phase transition revealed in a cancer cell line. PLoS ONE 2015, 10, e0128565. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Martello, G.; Smith, A. The nature of embryonic stem cells. Annu. Rev. Cell Dev. Biol. 2014, 30, 647–675. [Google Scholar] [CrossRef]
- Hackett, J.A.; Surani, M.A. Regulatory principles of pluripotency: From the ground state up. Cell Stem Cell 2014, 15, 416–430. [Google Scholar] [CrossRef] [PubMed] [Green Version]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, C.; McElroy, M.; Voulgarakis, N.K. Emergent Criticality in Coupled Boolean Networks. Entropy 2023, 25, 235. https://doi.org/10.3390/e25020235
Kang C, McElroy M, Voulgarakis NK. Emergent Criticality in Coupled Boolean Networks. Entropy. 2023; 25(2):235. https://doi.org/10.3390/e25020235
Chicago/Turabian StyleKang, Chris, Madelynn McElroy, and Nikolaos K. Voulgarakis. 2023. "Emergent Criticality in Coupled Boolean Networks" Entropy 25, no. 2: 235. https://doi.org/10.3390/e25020235
APA StyleKang, C., McElroy, M., & Voulgarakis, N. K. (2023). Emergent Criticality in Coupled Boolean Networks. Entropy, 25(2), 235. https://doi.org/10.3390/e25020235










