Considerations for Applying Entropy Methods to Temporally Correlated Stochastic Datasets
Abstract
:1. Introduction
1.1. Information Theory and Information
1.2. Entropy and Information
1.3. Entropy Methods for Physiological Data
1.4. Entropy Methods in Biomechanical Applications
1.5. Problem Statement
1.6. Goal Statement and Contributions
2. Materials and Methods
2.1. Simulations
2.2. ARFIMA Modeling
2.3. SampEn(m, r, )
2.4. Outlier Generation
2.5. Parameter Normalization
3. Results
3.1. Estimation of Temporal Correlations Using ARFIMA Modeling
3.2. Classification of Stochastic Data Using ARFIMA Modeling
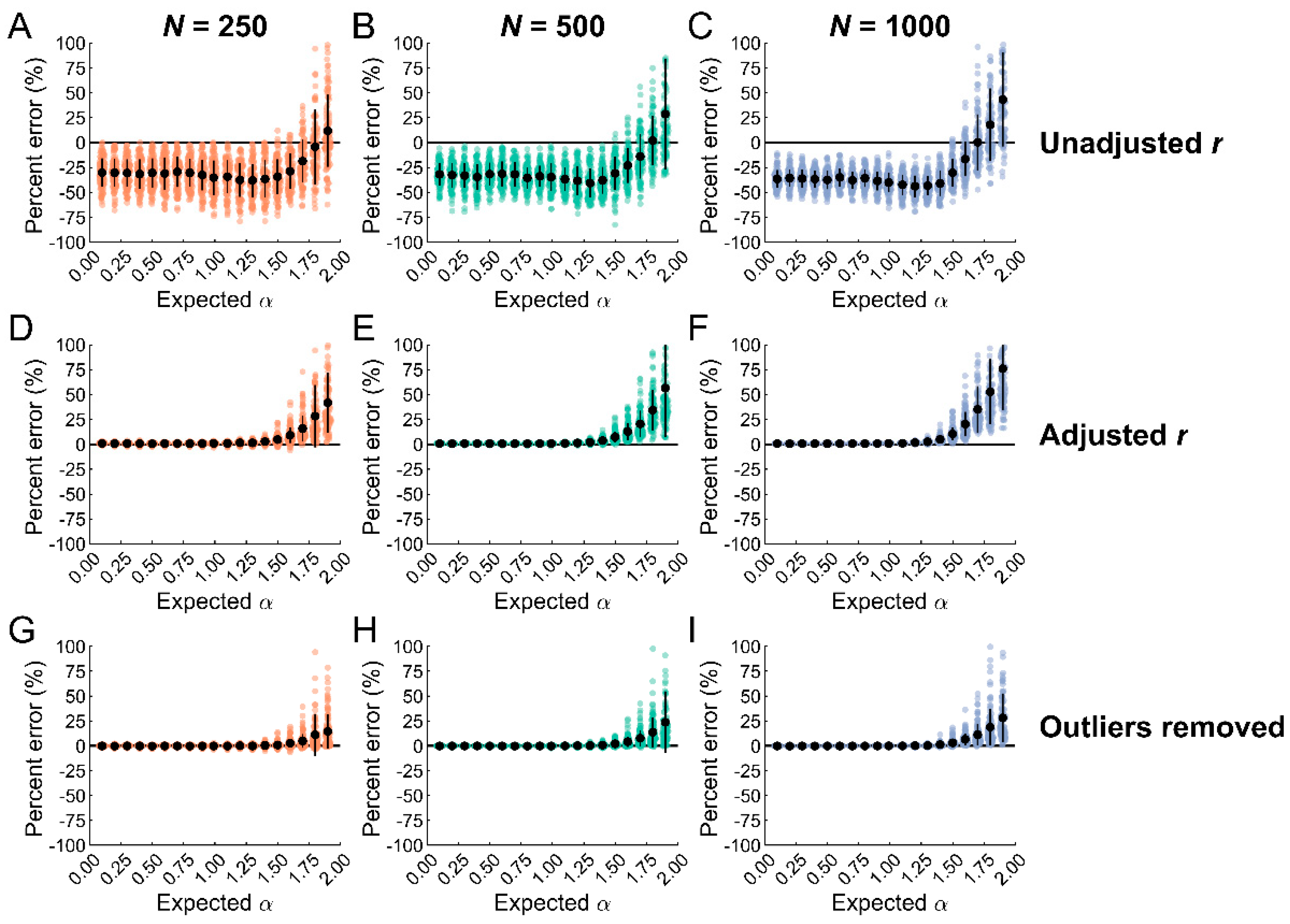
3.3. Outlier Removal with Data Classification Reduces Biases in Entropy Estimates
3.4. Problems with Discriminating Temporally Correlated Stochastic Datasets with SampEn
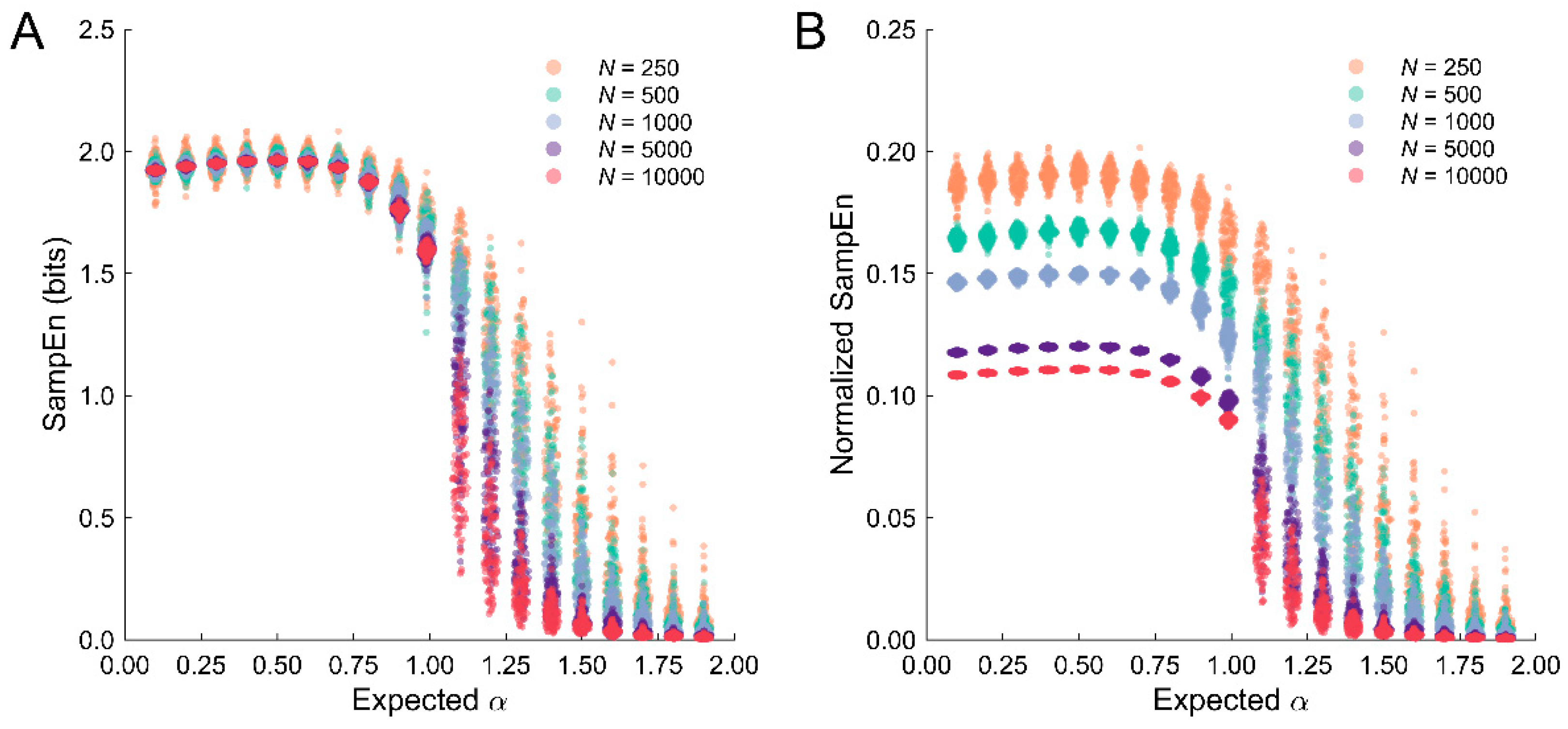
3.5. Normalization of SampEn Estimates across Different Dataset Lengths
4. Discussion
4.1. ARFIMA Modeling for Estimation and Classification of Temporally Correlated Stochastic Datasets
4.2. Outlier Removal Reduces Biases in SampEn Estimates
4.3. Interpreting SampEn Estimates from Temporally Correlated Stochastic Data
4.4. Normalization of SampEn Estimates
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Michalska, J.; Zając, R.; Szydło, K.; Gerasimuk, D.; Słomka, K.J.; Juras, G. Biathletes present repeating patterns of postural control to maintain their balance while shooting. PLoS ONE 2022, 17, e0267105. [Google Scholar] [CrossRef]
- Rhea, C.K.; Diekfuss, J.A.; Fairbrother, J.T.; Raisbeck, L.D. Postural Control Entropy Is Increased When Adopting an External Focus of Attention. Mot. Control 2019, 23, 230–242. [Google Scholar] [CrossRef]
- Diekfuss, J.A.; Rhea, C.K.; Schmitz, R.J.; Grooms, D.R.; Wilkins, R.W.; Slutsky, A.B.; Raisbeck, L.D. The Influence of Attentional Focus on Balance Control over Seven Days of Training. J. Mot. Behav. 2019, 51, 281–292. [Google Scholar] [CrossRef]
- Pantall, A.; Del Din, S.; Rochester, L. Longitudinal changes over thirty-six months in postural control dynamics and cognitive function in people with Parkinson’s disease. Gait Posture 2018, 62, 468–474. [Google Scholar] [CrossRef]
- Riva, F.; Toebes, M.J.P.; Pijnappels, M.A.G.M.; Stagni, R.; Van Dieën, J.H. Estimating fall risk with inertial sensors using gait stability measures that do not require step detection. Gait Posture 2013, 38, 170–174. [Google Scholar] [CrossRef]
- Ihlen, E.A.F.; Weiss, A.; Bourke, A.; Helbostad, J.L.; Hausdorff, J.M. The complexity of daily life walking in older adult community-dwelling fallers and non-fallers. J. Biomech. 2016, 49, 1420–1428. [Google Scholar] [CrossRef]
- Ahmadi, S.; Wu, C.; Sepehri, N.; Kantikar, A.; Nankar, M.; Szturm, T. The Effects of Aging and Dual Tasking on Human Gait Complexity During Treadmill Walking: A Comparative Study Using Quantized Dynamical Entropy and Sample Entropy. J. Biomech. Eng. 2018, 140, 011006. [Google Scholar] [CrossRef]
- Lamoth, C.J.; van Deudekom, F.J.; van Campen, J.P.; Appels, B.A.; de Vries, O.J.; Pijnappels, M. Gait stability and variability measures show effects of impaired cognition and dual tasking in frail people. J. Neuroeng. Rehabil. 2011, 8, 1–9. [Google Scholar] [CrossRef]
- Busa, M.A.; Jones, S.L.; Hamill, J.; van Emmerik, R.E. Multiscale entropy identifies differences in complexity in postural control in women with multiple sclerosis. Gait Posture 2016, 45, 7–11. [Google Scholar] [CrossRef]
- Gruber, A.H.; Busa, M.A.; Gorton Iii, G.E.; Van Emmerik, R.E.; Masso, P.D.; Hamill, J. Time-to-contact and multiscale entropy identify differences in postural control in adolescent idiopathic scoliosis. Gait Posture 2011, 34, 13–18. [Google Scholar] [CrossRef]
- Busa, M.A.; Van Emmerik, R.E.A. Multiscale entropy: A tool for understanding the complexity of postural control. J. Sport Health Sci. 2016, 5, 44–51. [Google Scholar] [CrossRef]
- Manor, B.; Costa, M.D.; Hu, K.; Newton, E.; Starobinets, O.; Kang, H.G.; Peng, C.K.; Novak, V.; Lipsitz, L.A. Physiological complexity and system adaptability: Evidence from postural control dynamics of older adults. J. Appl. Physiol. 2010, 109, 1786–1791. [Google Scholar] [CrossRef]
- Zhou, J.; Lipsitz, L.; Habtemariam, D.; Manor, B. Sub-sensory vibratory noise augments the physiologic complexity of postural control in older adults. J. NeuroEngineering Rehabil. 2016, 13, 44. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, P. Sample entropy analysis of surface EMG for improved muscle activity onset detection against spurious background spikes. J. Electromyogr. Kinesiol. 2012, 22, 901–907. [Google Scholar] [CrossRef]
- Rampichini, S.; Vieira, T.M.; Castiglioni, P.; Merati, G. Complexity Analysis of Surface Electromyography for Assessing the Myoelectric Manifestation of Muscle Fatigue: A Review. Entropy 2020, 22, 529. [Google Scholar]
- Murillo-Escobar, J.; Jaramillo-Munera, Y.E.; Orrego-Metaute, D.A.; Delgado-Trejos, E.; Cuesta-Frau, D. Muscle fatigue analysis during dynamic contractions based on biomechanical features and Permutation Entropy. Math. Biosci. Eng. MBE 2020, 17, 2592–2615. [Google Scholar] [CrossRef]
- Zhao, J.; Xie, Z.; Jiang, L.; Cai, H.; Liu, H.; Hirzinger, G. EMG control for a five-fingered underactuated prosthetic hand based on wavelet transform and sample entropy. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 3215–3220. [Google Scholar]
- Kullback, S. Information Theory and Statistics; John Wiley & Sons: New York, NY, USA, 1959. [Google Scholar]
- Shannon, C.E.; Weaver, W. The Mathematical Theory of Communication; University of Illinois Press: Urbana, IL, USA, 1949. [Google Scholar]
- Sinai, Y.G. On the Notion of Entropy of a Dynamical System. Dokl. Russ. Acad. Sci. 1959, 124, 768–771. [Google Scholar]
- Kolmogorov, A.N. Entropy per unit time as a metric invariant of automorphism. Dokl. Russ. Acad. Sci. 1959, 124, 754–755. [Google Scholar]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov Exponents from a Time-Series. Phys. D 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Delgado-Bonal, A.; Marshak, A. Approximate Entropy and Sample Entropy: A Comprehensive Tutorial. Entropy 2019, 21, 541. [Google Scholar] [CrossRef]
- Pincus, S.M. Approximate Entropy as a Measure of System-Complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef]
- Pincus, S.M.; Gladstone, I.M.; Ehrenkranz, R.A. A regularity statistic for medical data analysis. J. Clin. Monit. Comput. 1991, 7, 335–345. [Google Scholar] [CrossRef]
- Fleisher, L.A.; Pincus, S.M.; Rosenbaum, S.H. Approximate Entropy of Heart-Rate as a Correlate of Postoperative Ventricular Dysfunction. Anesthesiology 1993, 78, 683–692. [Google Scholar] [CrossRef]
- Pincus, S.M.; Viscarello, R.R. Approximate entropy: A regularity measure for fetal heart rate analysis. Obstet. Gynecol. 1992, 79, 249–255. [Google Scholar]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiology. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef]
- Pincus, S.M. Approximate Entropy (ApEn) as a Complexity Measure. Chaos 1995, 5, 110–117. [Google Scholar]
- Pincus, S.M.; Goldberger, A.L. Physiological time-series analysis: What does regularity quantify? Am. J. Physiol. 1994, 266, H1643–H1656. [Google Scholar] [CrossRef]
- Bollt, E.M.; Skufca, J.D.; McGregor, S.J. Control entropy: A complexity measure for nonstationary signals. Math. Biosci. Eng. MBE 2009, 6, 1–25. [Google Scholar]
- McGregor, S.J.; Bollt, E. Control Entropy: What is it and what does it tell us? Clin. Kinesiol. 2012, 66, 7–12. [Google Scholar]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 2002, 89, 068102. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of biological signals. Phys. Rev. 2005, 71, 021906. [Google Scholar] [CrossRef]
- Govindan, R.B.; Wilson, J.D.; Eswaran, H.; Lowery, C.L.; Preissl, H. Revisiting sample entropy analysis. Phys. A 2007, 376, 158–164. [Google Scholar] [CrossRef]
- Caldirola, D.; Bellodi, L.; Caumo, A.; Migliarese, G.; Perna, G. Approximate entropy of respiratory patterns in panic disorder. Am. J. Psychiatry 2004, 161, 79–87. [Google Scholar] [CrossRef] [PubMed]
- Engoren, M. Approximate entropy of respiratory rate and tidal volume during weaning from mechanical ventilation. Crit. Care Med. 1998, 26, 1817–1823. [Google Scholar] [CrossRef]
- Sarlabous, L.; Torres, A.; Fiz, J.A.; Gea, J.; Martinez-Llorene, J.M.; Jane, R. Efficiency of mechanical activation of inspiratory muscles in COPD using sample entropy. Eur. Respir. J. 2015, 46, 1808–1811. [Google Scholar] [CrossRef] [PubMed]
- Tran, Y.; Thuraisingham, R.A.; Wijesuriya, N.; Nguyen, H.T.; Craig, A. Detecting neural changes during stress and fatigue effectively: A comparison of spectral analysis and sample entropy. In Proceedings of the 2007 3rd International IEEE/EMBS Conference on Neural Engineering, Kohala Coast, HI, USA, 2–5 May 2007; pp. 350–353. [Google Scholar]
- Chen, X.; Solomon, I.C.; Chon, K.H. Comparison of the use of approximate entropy and sample entropy: Applications to neural respiratory signal. In Proceedings of the 2005 IEEE Engineering in Medicine and Biology 27th Annual Conference, Shanghai, China, 17–18 January 2006; pp. 4212–4215. [Google Scholar]
- Song, Y.; Zhang, J. Discriminating preictal and interictal brain states in intracranial EEG by sample entropy and extreme learning machine. J. Neurosci. Methods 2016, 257, 45–54. [Google Scholar] [CrossRef] [PubMed]
- McCamley, J.D.; Denton, W.; Arnold, A.; Raffalt, P.C.; Yentes, J.M. On the Calculation of Sample Entropy Using Continuous and Discrete Human Gait Data. Entropy 2018, 20, 764. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Richman, J.S.; Lake, D.E.; Moorman, J.R. Sample Entropy. In Methods in Enzymology; Elsevier: Amsterdam, The Netherlands, 2004; pp. 172–184. [Google Scholar]
- Molina-Picó, A.; Cuesta-Frau, D.; Aboy, M.; Crespo, C.; Miró-Martínez, P.; Oltra-Crespo, S. Comparative study of approximate entropy and sample entropy robustness to spikes. Artif. Intell. Med. 2011, 53, 97–106. [Google Scholar] [CrossRef]
- Lake, D.E.; Richman, J.S.; Griffin, M.P.; Moorman, J.R. Sample entropy analysis of neonatal heart rate variability. Am. J. Physiology Regul. Integr. Comp. Physiol. 2002, 283, R789–R797. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Van Ness, J.W. Fractional Brownian motions, fractional noises and applications. SIAM Rev. 1968, 10, 422–437. [Google Scholar] [CrossRef]
- Yentes, J.M.; Raffalt, P.C. Entropy Analysis in Gait Research: Methodological Considerations and Recommendations. Ann. Biomed. Eng. 2021, 49, 979–990. [Google Scholar] [CrossRef] [PubMed]
- Roume, C.; Ezzina, S.; Blain, H.; Delignieres, D. Biases in the Simulation and Analysis of Fractal Processes. Comput. Math. Methods Med. 2019, 2019, 4025305. [Google Scholar] [CrossRef] [PubMed]
- Davies, R.B.; Harte, D.S. Tests for Hurst effect. Biometrika 1987, 74, 95–101. [Google Scholar] [CrossRef]
- Barnsley, M.F.; Devaney, R.L.; Mandelbrot, B.B.; Peitgen, H.; Saupe, D.; Voss, R.F. The Science of Fractal Images; Springer: New York, NY, USA, 1988. [Google Scholar]
- Box, G.E.P.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Granger, C.W.J.; Joyeux, R. An introduction to long-memory time series models and fractional differencing. J. Time Ser. Anal. 1980, 1, 15–29. [Google Scholar] [CrossRef]
- Fatichi, S. ARFIMA simulations (Version 1.0.0.0). Available online: https://www.mathworks.com/matlabcentral/fileexchange/25611-arfima-simulations (accessed on 28 November 2022).
- Inzelt, G. ARFIMA(p,d,q) Estimator (Version 1.1.0.0). Available online: https://www.mathworks.com/matlabcentral/fileexchange/30238-arfima-p-d-q-estimator (accessed on 28 November 2022).
- Sheppard, K. MFE Toolbox (commit 9622b6c). Available online: https://github.com/bashtage/mfe-toolbox/ (accessed on 28 November 2022).
- Diebolt, C.; Guiraud, V. A note on long memory time series. Qual Quant 2005, 39, 827–836. [Google Scholar] [CrossRef]
- Delignieres, D.; Ramdani, S.; Lemoine, L.; Torre, K.; Fortes, M.; Ninot, G. Fractal analyses for ‘short’ time series: A re-assessment of classical methods. J. Math. Psychol. 2006, 50, 525–544. [Google Scholar] [CrossRef]
- Almurad, Z.M.H.; Delignières, D. Evenly spacing in detrended fluctuation analysis. Phys. A 2016, 451, 63–69. [Google Scholar] [CrossRef]
- Liddy, J.J.; Haddad, J.M. Evenly Spaced Detrended Fluctuation Analysis: Selecting the Number of Points for the Diffusion Plot. Phys. A 2018, 491, 233–248. [Google Scholar] [CrossRef]
- Kaffashi, F.; Foglyano, R.; Wilson, C.G.; Loparo, K.A. The effect of time delay on Approximate & Sample Entropy calculations. Phys. D Nonlinear Phenom. 2008, 237, 3069–3074. [Google Scholar]
- Fraser, A.M.; Swinney, H.L. Independent coordinates for strange attractors from mutual information. Phys. Rev. A Gen. Phys. 1986, 33, 1134–1140. [Google Scholar] [CrossRef]
- Leys, C.; Ley, C.; Klein, O.; Bernard, P.; Licata, L. Detecting outliers: Do not use standard deviation around the mean, use absolute deviation around the median. J. Exp. Soc. Psychol. 2013, 49, 764–766. [Google Scholar] [CrossRef]
- Hausdorff, J.M.; Peng, C.K.; Ladin, Z.V.I.; Wei, J.Y.; Goldberger, A.L. Is walking a random walk? Evidence for long-range correlations in stride interval of human gait. J. Appl. Physiol. 1995, 78, 349–358. [Google Scholar] [CrossRef]
- Delignieres, D.; Torre, K.; Bernard, P.L. Transition from persistent to anti-persistent correlations in postural sway indicates velocity-based control. PLoS Comput. Biol. 2011, 7, e1001089. [Google Scholar] [CrossRef]
- Eke, A.; Herman, P.; Bassingthwaighte, J.B.; Raymond, G.M.; Percival, D.B.; Cannon, M.; Balla, I.; Ikrenyi, C. Physiological time series: Distinguishing fractal noises from motions. Pflügers Arch. Eur. J. Physiol. 2000, 439, 403–415. [Google Scholar]
- Liu, H.; Shah, S.; Jiang, W. On-line outlier detection and data cleaning. Comput. Chem. Eng. 2004, 28, 1635–1647. [Google Scholar]
- Delignieres, D.; Torre, K. Fractal dynamics of human gait: A reassessment of the 1996 data of Hausdorff et al. J. Appl. Physiol. 2009, 106, 1272–1279. [Google Scholar] [CrossRef]
- Hausdorff, J.M.; Purdon, P.L.; Peng, C.K.; Ladin, Z.; Wei, J.Y.; Goldberger, A.L. Fractal dynamics of human gait: Stability of long-range correlations in stride interval fluctuations. J. Appl. Physiol. 1996, 80, 1448–1457. [Google Scholar] [CrossRef]
- Ducharme, S.W.; Liddy, J.J.; Haddad, J.M.; Busa, M.A.; Claxton, L.J.; van Emmerik, R.E.A. Association between stride time fractality and gait adaptability during unperturbed and asymmetric walking. Hum. Mov. Sci. 2018, 58, 248–259. [Google Scholar] [CrossRef] [PubMed]
- Kennel, M.B.; Brown, R.; Abarbanel, H.D. Determining embedding dimension for phase-space reconstruction using a geometrical construction. Phys. Rev. A 1992, 45, 3403–3411. [Google Scholar] [CrossRef] [PubMed] [Green Version]




| Parameter | ||
|---|---|---|
| Difference Order (d) | Scaling Exponent (α) | |
| Stationary (fGn) | −0.4 | 0.1 |
| −0.3 | 0.2 | |
| −0.2 | 0.3 | |
| −0.1 | 0.4 | |
| 0.0 | 0.5 | |
| 0.1 | 0.6 | |
| 0.2 | 0.7 | |
| 0.3 | 0.8 | |
| 0.4 | 0.9 | |
| 0.49 | 0.99 | |
| Nonstationary (fBm) | 0.6 | 1.1 |
| 0.7 | 1.2 | |
| 0.8 | 1.3 | |
| 0.9 | 1.4 | |
| 1.0 | 1.5 | |
| 1.1 | 1.6 | |
| 1.2 | 1.7 | |
| 1.3 | 1.8 | |
| 1.4 | 1.9 | |
| N = 250 | N = 500 | N = 1000 | ||||
|---|---|---|---|---|---|---|
| Expected α | Bias | SD | Bias | SD | Bias | SD |
| 0.1 | −0.015 | 0.058 | −0.004 | 0.036 | −0.005 | 0.028 |
| 0.2 | −0.022 | 0.050 | −0.009 | 0.039 | −0.007 | 0.025 |
| 0.3 | −0.019 | 0.053 | −0.017 | 0.038 | −0.007 | 0.020 |
| 0.4 | −0.022 | 0.053 | −0.005 | 0.038 | −0.006 | 0.026 |
| 0.5 | −0.017 | 0.055 | −0.012 | 0.034 | −0.006 | 0.024 |
| 0.6 | −0.024 | 0.058 | −0.013 | 0.044 | −0.010 | 0.022 |
| 0.7 | −0.021 | 0.059 | −0.010 | 0.041 | −0.004 | 0.023 |
| 0.8 | −0.023 | 0.047 | −0.016 | 0.037 | −0.002 | 0.025 |
| 0.9 | −0.022 | 0.051 | 0.001 | 0.038 | 0.001 | 0.023 |
| 0.99 | −0.001 | 0.055 | 0.001 | 0.038 | 0.008 | 0.026 |
| 1.1 | −0.015 | 0.057 | −0.013 | 0.037 | −0.002 | 0.027 |
| 1.2 | −0.025 | 0.061 | −0.009 | 0.036 | −0.001 | 0.024 |
| 1.3 | −0.019 | 0.058 | −0.010 | 0.036 | −0.009 | 0.027 |
| 1.4 | −0.008 | 0.045 | −0.010 | 0.041 | −0.008 | 0.023 |
| 1.5 | −0.019 | 0.056 | −0.008 | 0.037 | −0.006 | 0.029 |
| 1.6 | −0.019 | 0.058 | −0.006 | 0.050 | −0.007 | 0.028 |
| 1.7 | −0.014 | 0.055 | 0.006 | 0.070 | −0.014 | 0.037 |
| 1.8 | −0.033 | 0.077 | 0.005 | 0.067 | −0.014 | 0.027 |
| 1.9 | −0.012 | 0.075 | −0.032 | 0.066 | −0.032 | 0.030 |
| N = 250 | N = 500 | N = 1000 | ||||
|---|---|---|---|---|---|---|
| Expected α | Mean | SD | Mean | SD | Mean | SD |
| 0.1 | 1.927 | 0.043 | 1.927 | 0.031 | 1.926 | 0.016 |
| 0.2 | 1.947 | 0.053 | 1.939 | 0.030 | 1.937 | 0.018 |
| 0.3 | 1.959 | 0.047 | 1.953 | 0.027 | 1.951 | 0.017 |
| 0.4 | 1.971 | 0.050 | 1.962 | 0.029 | 1.964 | 0.017 |
| 0.5 | 1.969 | 0.043 | 1.965 | 0.024 | 1.968 | 0.015 |
| 0.6 | 1.957 | 0.045 | 1.962 | 0.029 | 1.960 | 0.018 |
| 0.7 | 1.947 | 0.046 | 1.940 | 0.032 | 1.934 | 0.015 |
| 0.8 | 1.906 | 0.052 | 1.893 | 0.039 | 1.881 | 0.026 |
| 0.9 | 1.830 | 0.069 | 1.781 | 0.064 | 1.778 | 0.040 |
| 0.99 | 1.697 | 0.109 | 1.646 | 0.083 | 1.613 | 0.067 |
| 1.1 | 1.512 | 0.161 | 1.442 | 0.141 | 1.315 | 0.159 |
| 1.2 | 1.273 | 0.205 | 1.189 | 0.156 | 0.963 | 0.196 |
| 1.3 | 1.033 | 0.234 | 0.817 | 0.218 | 0.680 | 0.193 |
| 1.4 | 0.744 | 0.216 | 0.539 | 0.204 | 0.431 | 0.177 |
| 1.5 | 0.481 | 0.210 | 0.342 | 0.188 | 0.228 | 0.100 |
| 1.6 | 0.310 | 0.159 | 0.195 | 0.109 | 0.131 | 0.069 |
| 1.7 | 0.211 | 0.137 | 0.126 | 0.068 | 0.074 | 0.035 |
| 1.8 | 0.144 | 0.104 | 0.079 | 0.043 | 0.051 | 0.026 |
| 1.9 | 0.091 | 0.080 | 0.058 | 0.043 | 0.035 | 0.019 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liddy, J.; Busa, M. Considerations for Applying Entropy Methods to Temporally Correlated Stochastic Datasets. Entropy 2023, 25, 306. https://doi.org/10.3390/e25020306
Liddy J, Busa M. Considerations for Applying Entropy Methods to Temporally Correlated Stochastic Datasets. Entropy. 2023; 25(2):306. https://doi.org/10.3390/e25020306
Chicago/Turabian StyleLiddy, Joshua, and Michael Busa. 2023. "Considerations for Applying Entropy Methods to Temporally Correlated Stochastic Datasets" Entropy 25, no. 2: 306. https://doi.org/10.3390/e25020306
APA StyleLiddy, J., & Busa, M. (2023). Considerations for Applying Entropy Methods to Temporally Correlated Stochastic Datasets. Entropy, 25(2), 306. https://doi.org/10.3390/e25020306






