Lightweight Deep Neural Network Embedded with Stochastic Variational Inference Loss Function for Fast Detection of Human Postures
Abstract
:1. Introduction
- Decreasing model sizes while increasing mean average precisions and inference speeds;
- Incorporating the self-attention mechanism for human posture prediction and data point clustering;
- Using a loss function constructed by Bayesian stochastic variational inference with the distributions rather than the coordinates of data points to reduce the computational complexity significantly and raise tolerance to outliers;
- Providing the probabilistic map to predict falling incidents in a timely manner;
- Validating that the types and observing directions of sensors for data acquisition would not affect the accuracy of the probabilistic map exhibition, i.e., highly compatible with various environments.
2. Materials and Methods
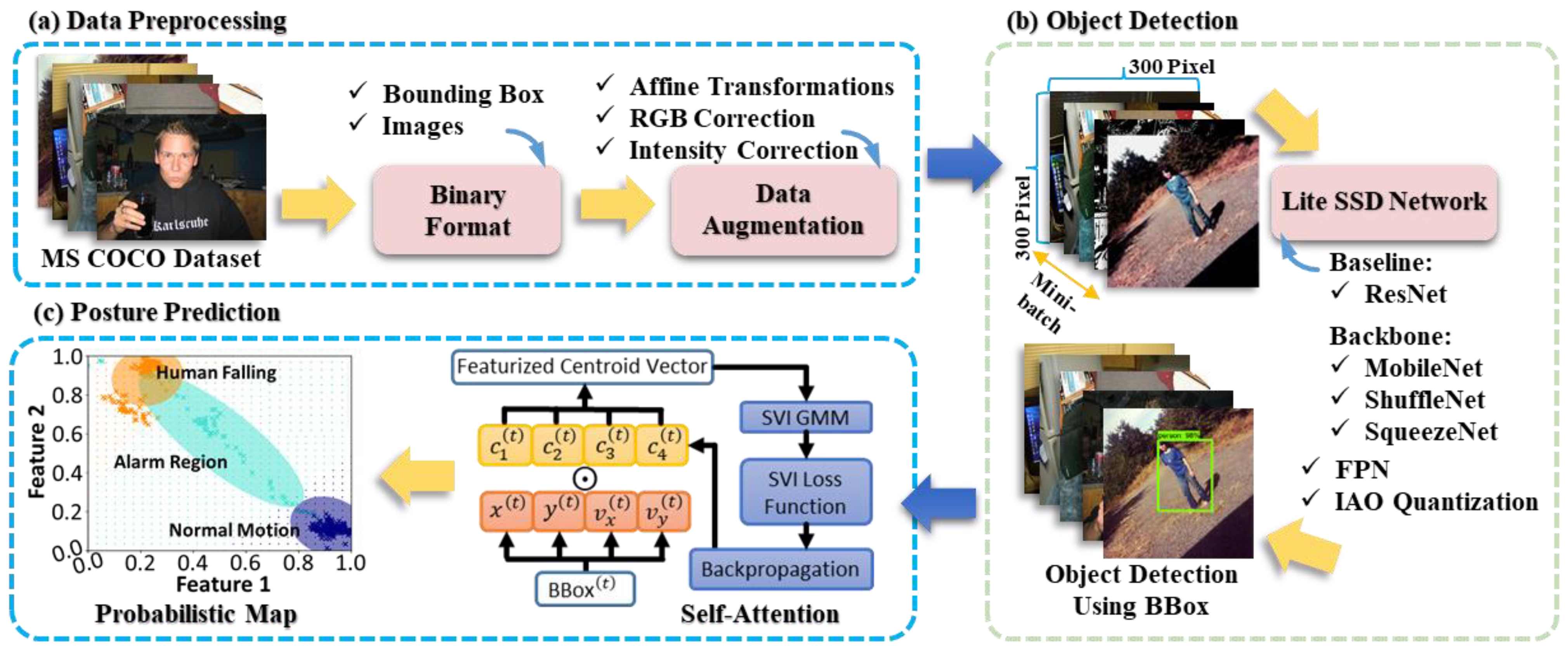
2.1. Establishment of Binary Format and Data Augmentation
2.2. Design of Lite SSD Network and Model Selection
2.3. Theoretical Foundation of Stochastic Variational Inference Gaussian Mixture Model with Self-Attention Mechanism
3. Results and Discussions
3.1. Performance Comparison of the Object Detection Models
3.2. Object Tracking and Human Posture Classification
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chander, H.; Burch, R.F.; Talegaonkar, P.; Saucier, D.; Luczak, T.; Ball, J.E.; Turner, A.; Kodithuwakku Arachchige, S.N.K.; Carroll, W.; Smith, B.K.; et al. Wearable Stretch Sensors for Human Movement Monitoring and Fall Detection in Ergonomics. Int. J. Environ. Res. Public Health 2020, 17, 3554. [Google Scholar] [CrossRef] [PubMed]
- Kerdjidj, O.; Ramzan, N.; Ghanem, K.; Amira, A.; Chouireb, F. Fall detection and human activity classification using wearable sensors and compressed sensing. J. Ambient. Intell. Human Comput. 2020, 11, 349–361. [Google Scholar] [CrossRef]
- Hsu, F.-S.; Chang, T.-C.; Su, Z.-J.; Huang, S.-J.; Chen, C.-C. Smart Fall Detection Framework Using Hybridized Video and Ultrasonic Sensors. Micromachines 2021, 12, 508. [Google Scholar] [CrossRef] [PubMed]
- Shu, F.; Shu, J. An eight-camera fall detection system using human fall pattern recognition via machine learning by a low-cost android box. Sci. Rep. 2021, 11, 2471. [Google Scholar] [CrossRef] [PubMed]
- Rastogi, S.; Singh, J. Human fall detection and activity monitoring: A comparative analysis of vision-based methods for classification and detection techniques. Soft Comput. 2022, 26, 3679–3701. [Google Scholar] [CrossRef]
- Ding, W.; Hu, B.; Liu, H.; Wang, X.; Huang, X. Human posture recognition based on multiple features and rule learning. Int. J. Mach. Learn. Cyber. 2020, 11, 2529–2540. [Google Scholar] [CrossRef]
- Alanazi, T.; Muhammad, G. Human Fall Detection Using 3D Multi-Stream Convolutional Neural Networks with Fusion. Diagnostics 2022, 12, 3060. [Google Scholar] [CrossRef]
- Fei, K.; Wang, C.; Zhang, J.; Liu, Y.; Xie, X.; Tu, Z. Flow-pose Net: An effective two-stream network for fall detection. Vis. Comput. 2022. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Y.; Liu, Y.; Xiang, S.; Pan, C. 3D PostureNet: A unified framework for skeleton-based posture recognition. Pattern Recognit. Lett. 2020, 140, 143–149. [Google Scholar] [CrossRef]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.-Y.; Berg, A.C. SSD: Single Shot MultiBox Detector. In Lecture Notes in Computer Science; Leibe, B., Matas, J., Sebe, N., Welling, M., Eds.; Springer: Cham, Switzerland, 2016; Volume 9905, pp. 21–37. [Google Scholar]
- Araki, R.; Onishi, T.; Hirakawa, T.; Yamashita, T.; Fujiyoshi, H. MT-DSSD: Deconvolutional Single Shot Detector Using Multi Task Learning for Object Detection, Segmentation, and Grasping Detection. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–30 June 2020. [Google Scholar]
- Shen, Z.; Liu, Z.; Li, J.; Jiang, Y.-G.; Xue, X. DSOD: Learning Deeply Supervised Object Detectors from Scratch. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017. [Google Scholar]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You Only Look Once: Unified, Real-Time Object Detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Bochkovskiy, A.; Wang, C.-Y.; Liao, H.-Y.M. YOLOv4: Optimal Speed and Accuracy of Object Detection. arXiv 2020, arXiv:2004.10934. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1137–1149. [Google Scholar] [CrossRef] [Green Version]
- Ansari, M.Y.; Yang, Y.; Balakrishnan, S.; Abinahed, J.; Al-Ansari, A.; Warfa, M.; Almokdad, O.; Barah, A.; Omer, A.; Singh, A.V.; et al. A lightweight neural network with multiscale feature enhancement for liver CT segmentation. Sci. Rep. 2022, 12, 14153. [Google Scholar] [CrossRef]
- Li, W.; Liu, J.; Mei, H. Lightweight convolutional neural network for aircraft small target real-time detection in Airport videos in complex scenes. Sci. Rep. 2022, 12, 14474. [Google Scholar] [CrossRef]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]
- Zhang, X.; Zhou, X.; Lin, M.; Sun, J. ShuffleNet: An Extremely Efficient Convolutional Neural Network for Mobile Devices. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Howard, A.; Sandler, M.; Chu, G.; Chen, L.-C.; Chen, B.; Tan, M.; Wang, W.; Zhu, Y.; Pang, R.; Vasudevan, V.; et al. Searching for MobileNetV3. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar]
- Tan, M.; Le, Q.V. MixConv: Mixed Depthwise Convolutional Kernels. arXiv 2019, arXiv:1907.09595. [Google Scholar]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.-C. MobileNetV2: Inverted Residuals and Linear Bottlenecks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Iandola, F.N.; Han, S.; Moskewicz, M.W.; Ashraf, K.; Dally, W.J.; Keutzer, K. SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and <0.5MB model size. arXiv 2016, arXiv:1602.07360. [Google Scholar]
- Han, S.; Mao, H.; Dally, W.J. Deep Compression: Compressing Deep Neural Networks with Pruning, Trained Quantization and Huffman Coding. arXiv 2015, arXiv:1510.00149. [Google Scholar]
- Ma, N.; Zhang, X.; Zheng, H.-T.; Sun, J. ShuffleNet V2: Practical Guidelines for Efficient CNN Architecture Design. In Proceedings of the 15th European Conference on Computer Vision, Munich, Germany, 8–14 September 2018. [Google Scholar]
- Jacob, B.; Kligys, S.; Chen, B.; Zhu, M.; Tang, M.; Howard, A.; Adam, H.; Kalenichenko, D. Quantization and Training of Neural Networks for Efficient Integer-Arithmetic-Only Inference. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Zhao, H.; Liu, D.; Li, H. Efficient Integer-Arithmetic-Only Convolutional Neural Networks. arXiv 2020, arXiv:2006.11735. [Google Scholar]
- Lin, T.-Y.; Dollar, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature Pyramid Networks for Object Detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Luong, M.-T.; Pham, H.; Manning, C.D. Effective Approaches to Attention-based Neural Machine Translation. arXiv 2015, arXiv:1508.04025. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is All you Need. In Proceedings of the 31st Annual Conference on Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Yao, L.; Ge, Z. Nonlinear Gaussian Mixture Regression for Multimode Quality Prediction With Partially Labeled Data. IEEE Trans. Industr. Inform. 2019, 15, 4044–4053. [Google Scholar] [CrossRef]
- Lin, T.-Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft COCO: Common Objects in Context. In Lecture Notes in Computer Science; Fleet, D., Pajdla, T., Schiele, B., Tuytelaars, T., Eds.; Springer: Cham, Switzerland, 2014; Volume 8693, pp. 740–755. [Google Scholar]
- Jia, D.; Wei, D.; Richard, S.; Li, L.-J.; Li, K.; Li, F.-F. ImageNet: A large-scale hierarchical image database. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Miami, FL, USA, 20–25 June 2009. [Google Scholar]
- Everingham, M.; Eslami, S.M.A.; Gool, L.V.; Williams, C.K.I.; Winn, J.; Zisserman, A. The PASCAL Visual Object Classes Challenge: A Retrospective. Int. J. Comput. Vis. 2015, 111, 98–136. [Google Scholar] [CrossRef]
- Hoffman, M.D.; Blei, D.M.; Wang, C.; Paisley, J. Stochastic Variational Inference. J. Mach. Learn. Res. 2013, 14, 1303–1347. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Blei, D.M.; Kucukelbir, A.; McAuliffe, J.D. Variational Inference: A Review for Statisticians. J. Am. Stat. Assoc. 2017, 112, 859–877. [Google Scholar] [CrossRef]
- Chen, C.-C.; Juan, H.-H.; Tsai, M.-Y.; Lu, H.H.-S. Unsupervised Learning and Pattern Recognition of Biological Data Structures with Density Functional Theory and Machine Learning. Sci. Rep. 2018, 8, 557. [Google Scholar] [CrossRef] [Green Version]





| Backbone | FPN | IAO | mAP | Inference Speed (mSec) | Model Size (MB) |
|---|---|---|---|---|---|
| ResNet | 24.6 | 48 | 227.8 | ||
| MobileNetV1 | 21.2 | 15 | 74.1 | ||
| ✓ a | 33.1 | 28 | 132.9 | ||
| ✓ | 20.6 | 13 | 28.2 | ||
| ✓ | ✓ | 32.5 | 27 | 46.2 | |
| MobileNetV2 | 23.0 | 17 | 174.9 | ||
| ✓ | 35.6 | 29 | 320.1 | ||
| ✓ | 22.7 | 12 | 94.9 | ||
| ✓ | ✓ | 33.6 | 25 | 140.2 | |
| ShuffleNet V1 (Group = 4) | 20.7 | 20 | 77.6 b | ||
| 20.7 | 16 | 77.6 c | |||
| ✓ | 20.3 | -- e | 34.6 d | ||
| ShuffleNet V2 | 21.9 | 18 | 55.1 | ||
| SqueezeNet | 16.5 | 10 | 16.2 |
| True Positive | True Negative | False Position | False Negative |
| 26,857 | 11,472 | 3015 | 1208 |
| Source | Apparatus | Method | Accuracy | Alarm Timing 1 |
|---|---|---|---|---|
| Ref. [3] | Sensor Fusion | Machine Learning | 0.90 | +0.7 s |
| Ref. [4] | Vision-based Method | SpeedyAI, Inc. | 0.89 | +10 s |
| Ref. [6] | Vision-based Method | CNNs | 0.98 | -- 2 |
| Ref. [7] | -- | 3D CNNs | 0.99 | -- |
| This work | Vision-based Method | Lite SSD | 0.90 | −0.66 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hsu, F.-S.; Su, Z.-J.; Kao, Y.; Tsai, S.-W.; Lin, Y.-C.; Tu, P.-H.; Gong, C.-S.A.; Chen, C.-C. Lightweight Deep Neural Network Embedded with Stochastic Variational Inference Loss Function for Fast Detection of Human Postures. Entropy 2023, 25, 336. https://doi.org/10.3390/e25020336
Hsu F-S, Su Z-J, Kao Y, Tsai S-W, Lin Y-C, Tu P-H, Gong C-SA, Chen C-C. Lightweight Deep Neural Network Embedded with Stochastic Variational Inference Loss Function for Fast Detection of Human Postures. Entropy. 2023; 25(2):336. https://doi.org/10.3390/e25020336
Chicago/Turabian StyleHsu, Feng-Shuo, Zi-Jun Su, Yamin Kao, Sen-Wei Tsai, Ying-Chao Lin, Po-Hsun Tu, Cihun-Siyong Alex Gong, and Chien-Chang Chen. 2023. "Lightweight Deep Neural Network Embedded with Stochastic Variational Inference Loss Function for Fast Detection of Human Postures" Entropy 25, no. 2: 336. https://doi.org/10.3390/e25020336
APA StyleHsu, F.-S., Su, Z.-J., Kao, Y., Tsai, S.-W., Lin, Y.-C., Tu, P.-H., Gong, C.-S. A., & Chen, C.-C. (2023). Lightweight Deep Neural Network Embedded with Stochastic Variational Inference Loss Function for Fast Detection of Human Postures. Entropy, 25(2), 336. https://doi.org/10.3390/e25020336









