A Physical Measure for Characterizing Crossover from Integrable to Chaotic Quantum Systems
Abstract
:1. Introduction
2. Preliminary Discussions
2.1. Perturbed and Unperturbed Systems
2.2. Properties of the Perturbation V
2.3. Two Previously Studied Methods
3. as a Crossover Measure
3.1. A Physical Meaning of
3.2. in Systems from Integrable and Chaotic
- In the case that the level is nondegenerate, Equation (19) is valid. Then, clearly, the sparse structure of implies that the distribution should have a high peak at , with .
- In the case of a degenerate level, let us use (with ) to indicate those states that correspond to this unperturbed level. It is straightforward to generalize the perturbative treatment given in the above section and obtain an equation similar to Equation (19), but, for . Then, one reaches a similar conclusion that the distribution should have a high peak at , usually with .
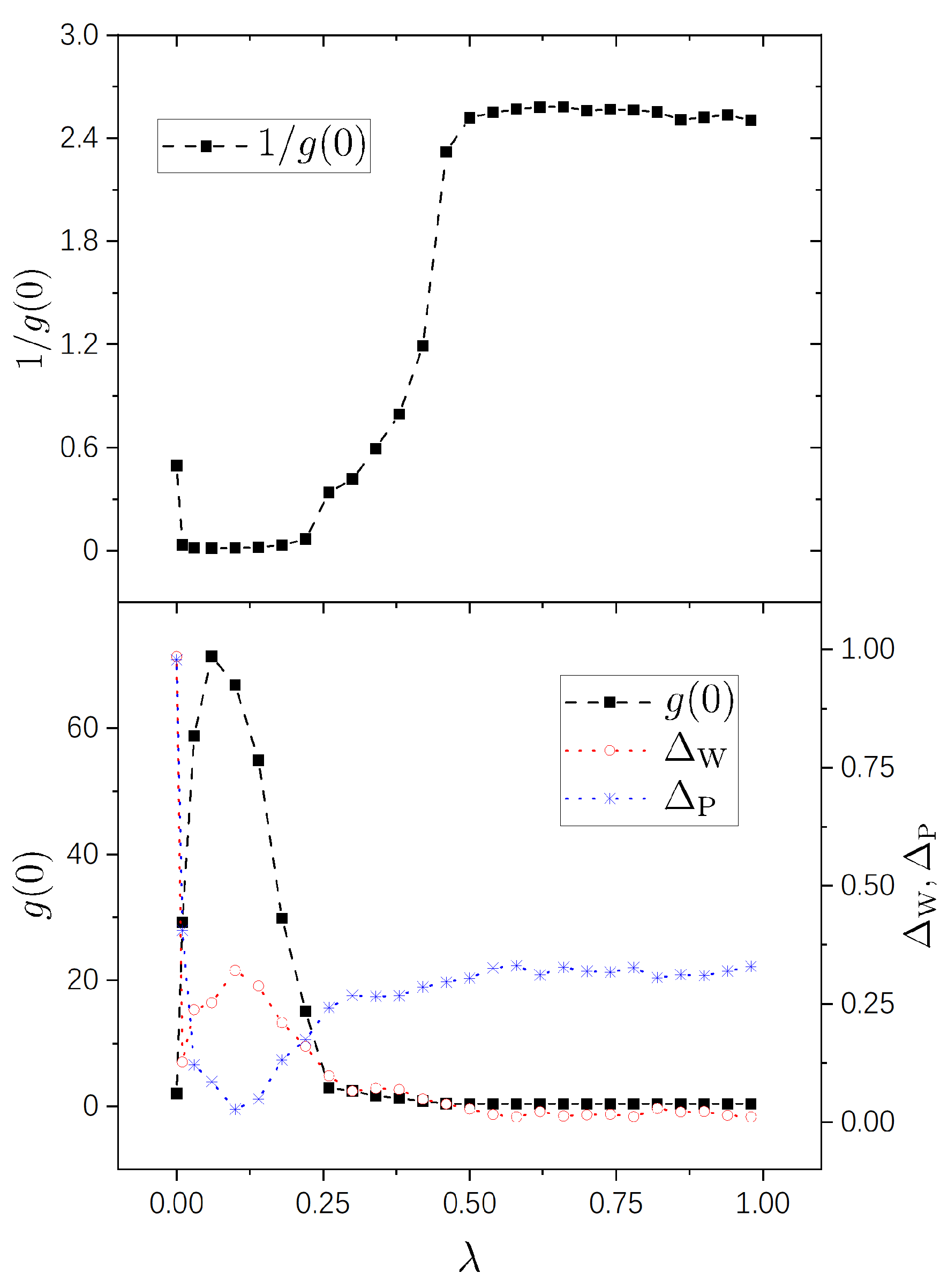
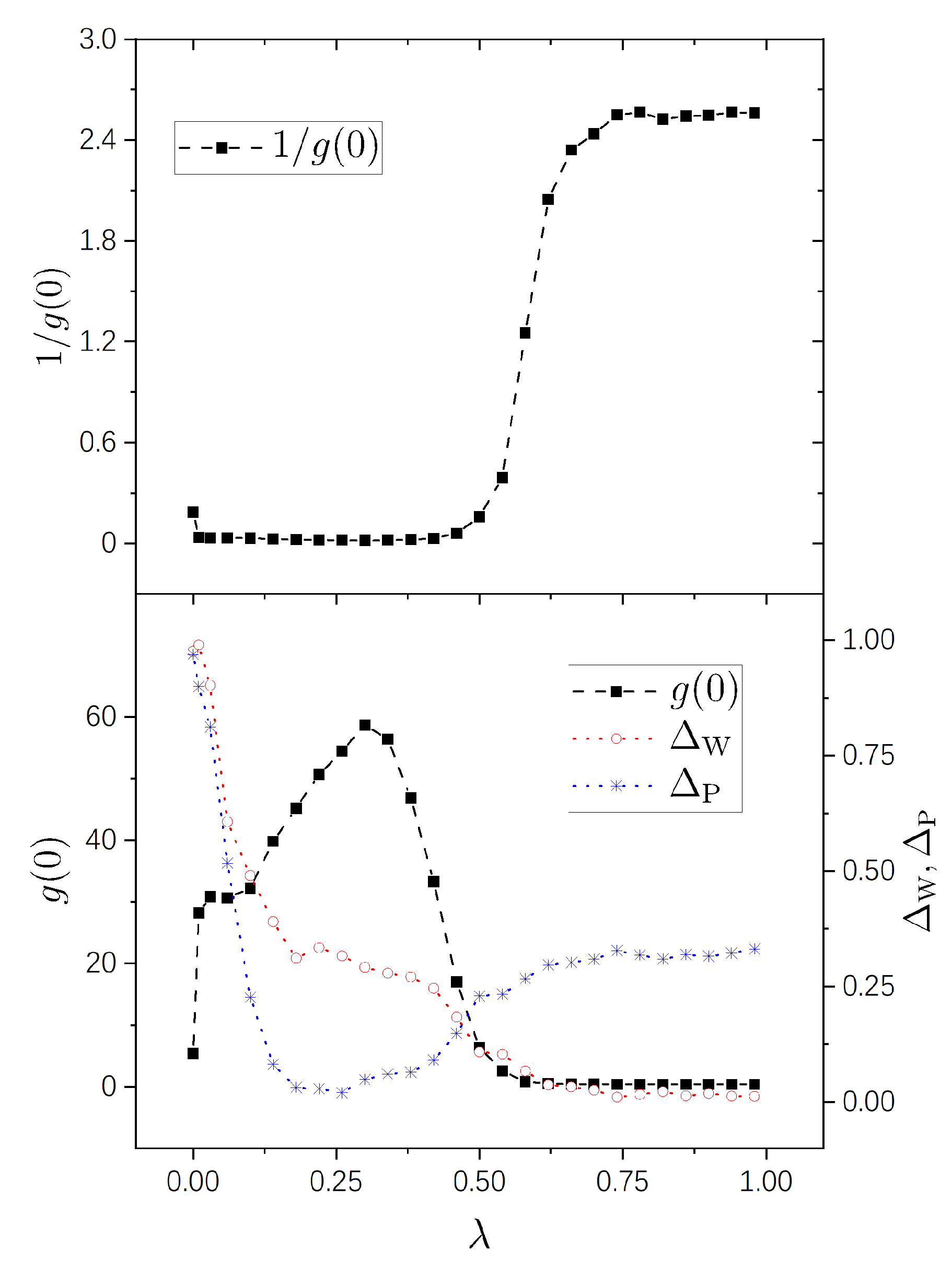
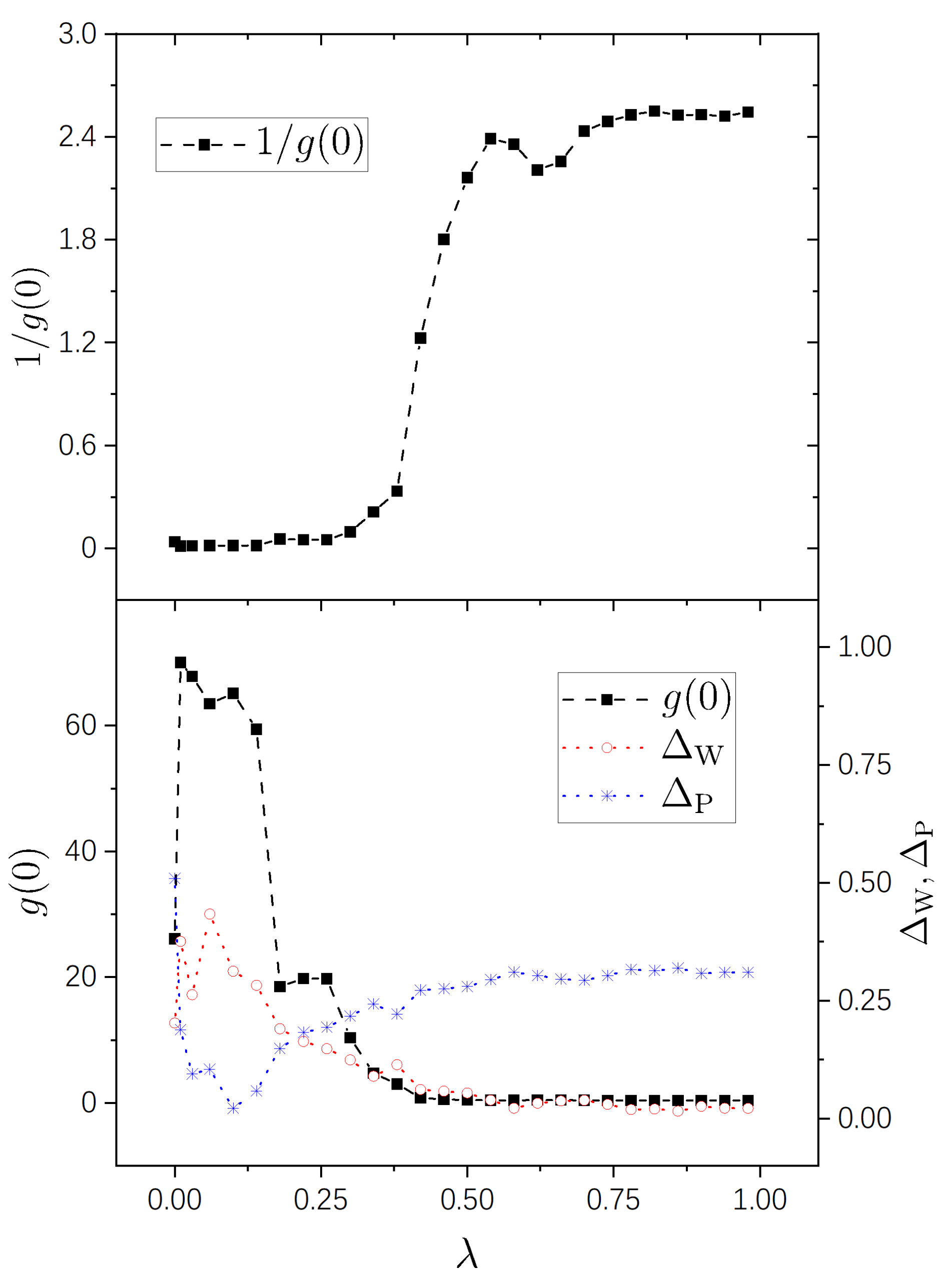
4. Numerical Simulations
4.1. The model
4.2. Numerical Results
- A nearly integrable regime, in which the value of is close to 0. In this regime, the perturbation-induced transition is strongly prohibited between many of the unperturbed states.
- A nearly chaotic regime, in which . In this regime, the perturbation-induced transition is not prohibited in a statistical sense.
- An intermediate (cross-over) regime, in which increases “rapidly”, approximately from 0 to .
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Conflicts of Interest
References
- Casati, G.; Chirikov, B.V.; Guarneri, I.; Izrailev, F.M. Band-random-matrix model for quantum localization in conservative systems. Phys. Rev. E 1993, 48, R1613–R1616. [Google Scholar] [CrossRef] [PubMed]
- Haake, F. Quantum Signatures of Chaos; Springer Series in Synergetics; Springer: Berlin/Heidelberg, Germany, 2010; Volume 54, ISBN 978-3-642-05427-3. [Google Scholar]
- Casati, G.; Valz-Gris, F.; Guarnieri, I. On the Connection between Quantization of Nonintegrable Systems and Statistical Theory of Spectra. Lett. Nuovo C. 1980, 28, 279. [Google Scholar] [CrossRef]
- Bohigas, O.; Giannoni, M.J.; Schmit, C. Characterization of Chaotic Quantum Spectra and Universality of Level Fluctuation Laws. Phys. Rev. Lett. 1984, 52, 1–4. [Google Scholar] [CrossRef]
- Berry, M.V. Semiclassical theory of spectral rigidity. Proc. R. Soc. Lond. Ser. A 1985, 400, 229. [Google Scholar]
- Sieber, M.; Richter, K. Correlations between periodic orbits and their rôle in spectral statistics. Phys. Scr. 2001, T90, 128. [Google Scholar] [CrossRef]
- Sieber, M. Leading off-diagonal approximation for the spectral form factor for uniformly hyperbolic systems. J. Phys. A Math. Gen. 2002, 35, L613. [Google Scholar] [CrossRef]
- Heusler, S.; Müller, S.; Braun, P.; Haake, F. Universal spectral form factor for chaotic dynamics. J. Phys. A Math. Gen. 2004, 37, L31. [Google Scholar] [CrossRef]
- Müller, S.; Heusler, S.; Braun, P.; Haake, F.; Altland, A. Semiclassical Foundation of Universality in Quantum Chaos. Phys. Rev. Lett. 2004, 93, 014103. [Google Scholar] [CrossRef] [Green Version]
- Polkovnikov, A.; Sengupta, K.; Silva, A.; Vengalattore, M. Colloquium: Nonequilibrium dynamics of closed interacting quantum systems. Rev. Mod. Phys. 2011, 83, 863–883. [Google Scholar] [CrossRef] [Green Version]
- Eisert, J.; Friesdorf, M.; Gogolin, C. Quantum many-body systems out of equilibrium. Nat. Phys. 2015, 11, 124–130. [Google Scholar] [CrossRef] [Green Version]
- Gogolin, C.; Eisert, J. Equilibration, thermalisation, and the emergence of statistical mechanics in closed quantum systems. Rep. Prog. Phys. 2016, 79, 056001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- D’Alessio, L.; Kafri, Y.; Polkovnikov, A.; Rigol, M. From quantum chaos and eigenstate thermalization to statistical mechanics and thermodynamics. Adv. Phys. 2016, 65, 239–362. [Google Scholar] [CrossRef] [Green Version]
- Borgonovi, F.; Izrailev, F.M.; Santos, L.F.; Zelevinsky, V.G. Quantum chaos and thermalization in isolated systems of interacting particles. Phys. Rep. 2016, 626, 1–58. [Google Scholar] [CrossRef] [Green Version]
- Mori, T.; Ikeda, T.N.; Kaminishi, E.; Ueda, M. Thermalization and prethermalization in isolated quantum systems: A theoretical overview. J. Phys. B At. Mol. Opt. Phys. 2018, 51, 112001. [Google Scholar] [CrossRef] [Green Version]
- Tasaki, H. Typicality of Thermal Equilibrium and Thermalization in Isolated Macroscopic Quantum Systems. J. Stat. Phys. 2016, 163, 937–997. [Google Scholar] [CrossRef] [Green Version]
- Berry, M.V.; Tabor, M. Level Clustering in the Regular Spectrum. Proc. R. Soc. Lond. 1977, 356, 375–394. [Google Scholar] [CrossRef]
- Brody, T.A.; Flores, J.; French, J.B.; Mello, P.A.; Pandey, A.; Wong, S.S.M. Random-matrix physics: Spectrum and strength fluctuations. Rev. Mod. Phys. 1981, 53, 385–479. [Google Scholar] [CrossRef]
- Berry, M.V.; Robnik, M. Semiclassical level spacings when regular and chaotic orbits coexist. J. Phys. A Math. Gen. 1984, 17, 2413. [Google Scholar] [CrossRef]
- Izrailev, F.M. Chaotic stucture of eigenfunctions in systems with maximal quantum chaos. Phys. Lett. A 1987, 125, 250–252. [Google Scholar] [CrossRef]
- Izrailev, F.M. Quantum localization and statistics of quasienergy spectrum in a classically chaotic system. Phys. Lett. A 1988, 134, 13–18. [Google Scholar] [CrossRef]
- Berry, M.V. Regular and irregular semiclassical wavefunctions. J. Phys. A Math. Gen. 1977, 10, 2083. [Google Scholar] [CrossRef] [Green Version]
- Li, B.; Robnik, M. Sensitivity of the eigenfunctions and the level curvature distribution in quantum billiards. J. Phys. A Math. Gen. 1996, 29, 4387. [Google Scholar] [CrossRef]
- Srednicki, M. Chaos and quantum thermalization. Phys. Rev. E 1994, 50, 888–901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Meredith, D.C.; Koonin, S.E.; Zirnbauer, M.R. Quantum chaos in a schematic shell model. Phys. Rev. A 1988, 37, 3499–3513. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Blümel, R.; Smilansky, U. Suppression of classical stochasticity by quantum-mechanical effects in the dynamics of periodically perturbed surface-state electrons. Phys. Rev. A 1984, 30, 1040–1051. [Google Scholar] [CrossRef]
- Shapiro, M.; Goelman, G. Onset of Chaos in an Isolated Energy Eigenstate. Phys. Rev. Lett. 1984, 53, 1714–1717. [Google Scholar] [CrossRef]
- Benet, L.; Flores, J.; Hernández-Saldaña, H.; Izrailev, F.M.; Leyvraz, F.; Seligman, T.H. Fluctuations of wavefunctions about their classical average. J. Phys. A Math. Gen. 2003, 36, 1289. [Google Scholar] [CrossRef]
- Wang, J.; Wang, W. Correlations in eigenfunctions of quantum chaotic systems with sparse Hamiltonian matrices. Phys. Rev. E 2017, 96, 052221. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Wang, W. Characterization of random features of chaotic eigenfunctions in unperturbed basis. Phys. Rev. E 2018, 97, 062219. [Google Scholar] [CrossRef]
- Wang, Q.; Robnik, M. Statistical properties of the localization measure of chaotic eigenstates in the Dicke model. Phys. Rev. E 2020, 102, 032212. [Google Scholar] [CrossRef]
- Pandey, M.; Claeys, P.W.; Campbell, D.K.; Polkovnikov, A.; Sels, D. Adiabatic Eigenstate Deformations as a Sensitive Probe for Quantum Chaos. Phys. Rev. X 2020, 10, 041017. [Google Scholar] [CrossRef]
- Xu, Z.; Lyu, Y.C.; Wang, J.; Wang, W. Sensitivity of energy eigenstates to perturbation in quantum integrable and chaotic systems. Commun. Theor. Phys. 2021, 73, 15104. [Google Scholar] [CrossRef]
- Peres, A. Stability of quantum motion in chaotic and regular systems. Phys. Rev. A 1984, 30, 1610–1615. [Google Scholar] [CrossRef]
- Jalabert, R.A.; Pastawski, H.M. Environment-Independent Decoherence Rate in Classically Chaotic Systems. Phys. Rev. Lett. 2001, 86, 2490–2493. [Google Scholar] [CrossRef] [Green Version]
- Prosen, T.; Znidaric, M. Stability of quantum motion and correlation decay. J. Phys. A Math. Gen. 2002, 35, 1455. [Google Scholar] [CrossRef]
- Cerruti, N.R.; Tomsovic, S. Sensitivity of Wave Field Evolution and Manifold Stability in Chaotic Systems. Phys. Rev. Lett. 2002, 88, 054103. [Google Scholar] [CrossRef] [Green Version]
- Benenti, G.; Casati, G. Quantum-classical correspondence in perturbed chaotic systems. Phys. Rev. E 2002, 65, 066205. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Li, B. Uniform semiclassical approach to fidelity decay: From weak to strong perturbation. Phys. Rev. E 2005, 71, 066203. [Google Scholar] [CrossRef] [Green Version]
- Gorin, T.; Prosen, T.; Seligman, T.H.; Žnidarič, M. Dynamics of Loschmidt echoes and fidelity decay. Phys. Rep. 2006, 435, 33–156. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Casati, G.; Li, B. Stability of quantum motion in regular systems: A uniform semiclassical approach. Phys. Rev. E 2007, 75, 016201. [Google Scholar] [CrossRef] [Green Version]
- Leviandier, L.; Lombardi, M.; Jost, R.; Pique, J.P. Fourier Transform: A Tool to Measure Statistical Level Properties in Very Complex Spectra. Phys. Rev. Lett. 1986, 56, 2449–2452. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Torres-Herrera, E.J.; Santos, L.F. Dynamics at the many-body localization transition. Phys. Rev. B 2015, 92, 014208. [Google Scholar] [CrossRef] [Green Version]
- Torres-Herrera E., J.; Santos Lea, F. Dynamical manifestations of quantum chaos: Correlation hole and bulgePhil. Phil. Trans. R. Soc. A 2016, 375, 0434. [Google Scholar] [CrossRef] [PubMed]
- Torres-Herrera, E.J.; García-García, A.M.; Santos, L.F. Generic dynamical features of quenched interacting quantum systems: Survival probability, density imbalance, and out-of-time-ordered correlator. Phys. Rev. B 2018, 97, 060303. [Google Scholar] [CrossRef] [Green Version]
- Brenes, M.; Goold, J.; Rigol, M. Low-frequency behavior of off-diagonal matrix elements in the integrable XXZ chain and in a locally perturbed quantum-chaotic XXZ chain. Phys. Rev. B 2020, 102, 075127. [Google Scholar] [CrossRef]
- Gu, S.-J. Fidelity approach to quantum phase transitions. Int. J. Mod. Phys. B 2010, 24, 4371–4458. [Google Scholar] [CrossRef] [Green Version]
- Sierant, P.; Maksymov, A.; Kuś, M.; Zakrzewski, J. Fidelity susceptibility in Gaussian random ensembles. Phys. Rev. E 2019, 99, 050102. [Google Scholar] [CrossRef] [Green Version]
- Lipkin, H.J.; Meshkov, N.; Glick, A.J. Validity of many-body approximation methods for a solvable model: (I). Exact solutions and perturbation theory. Nucl. Phys. 1965, 62, 188–198. [Google Scholar] [CrossRef]
- Kolodrubetz, M.; Sels, D.; Mehta, P.; Polkovnikov, A. Geometry and non-adiabatic response in quantum and classical systems. Phys. Rep. 2017, 697, 1–87. [Google Scholar] [CrossRef] [Green Version]
- Srednicki, M. Thermal fluctuations in quantized chaotic systems. J. Phys. A Math. Gen. 1996, 29, L75. [Google Scholar] [CrossRef] [Green Version]
- Srednicki, M. The approach to thermal equilibrium in quantized chaotic systems. J. Phys. A Math. Gen. 1999, 32, 1163. [Google Scholar] [CrossRef] [Green Version]
- Deutsch, J.M. Quantum statistical mechanics in a closed system. Phys. Rev. A 1991, 43, 2046–2049. [Google Scholar] [CrossRef] [PubMed]
- Rigol, M.; Srednicki, M. Alternatives to Eigenstate Thermalization. Phys. Rev. Lett. 2012, 108, 110601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- De Palma, G.; Serafini, A.; Giovannetti, V.; Cramer, M. Necessity of Eigenstate Thermalization. Phys. Rev. Lett. 2015, 115, 220401. [Google Scholar] [CrossRef] [Green Version]
- Deutsch, J.M. Eigenstate thermalization hypothesis. Rep. Prog. Phys. 2018, 81, 082001. [Google Scholar] [CrossRef] [Green Version]
- Wang, W. Semiclassical proof of the many-body eigenstate thermalization hypothesis. arXiv 2022, arXiv:2210.13183. [Google Scholar]
- Wang, W.; Izrailev, F.M.; Casati, G. Structure of eigenstates and local spectral density of states: A three-orbital schematic shell model. Phys. Rev. E 1998, 57, 323–339. [Google Scholar] [CrossRef] [Green Version]
- Gong-ou, X.; Jiang-bin, G.; Wen-ge, W.; Ya-tian, Y.; De-ji, F. Development of quantum nonintegrability displayed in effective Hamiltonians: A three-level Lipkin model. Phys. Rev. E 1995, 51, 1770–1779. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lyu, C.Y.; Wang, W.-G. A Physical Measure for Characterizing Crossover from Integrable to Chaotic Quantum Systems. Entropy 2023, 25, 366. https://doi.org/10.3390/e25020366
Lyu CY, Wang W-G. A Physical Measure for Characterizing Crossover from Integrable to Chaotic Quantum Systems. Entropy. 2023; 25(2):366. https://doi.org/10.3390/e25020366
Chicago/Turabian StyleLyu, Chenguang Y., and Wen-Ge Wang. 2023. "A Physical Measure for Characterizing Crossover from Integrable to Chaotic Quantum Systems" Entropy 25, no. 2: 366. https://doi.org/10.3390/e25020366
APA StyleLyu, C. Y., & Wang, W.-G. (2023). A Physical Measure for Characterizing Crossover from Integrable to Chaotic Quantum Systems. Entropy, 25(2), 366. https://doi.org/10.3390/e25020366




