Detecting Nonlinear Interactions in Complex Systems: Application in Financial Markets
Abstract
1. Introduction
2. Methods and Data
2.1. The Approach for Detecting Nonlinear Interactions and Structural Change
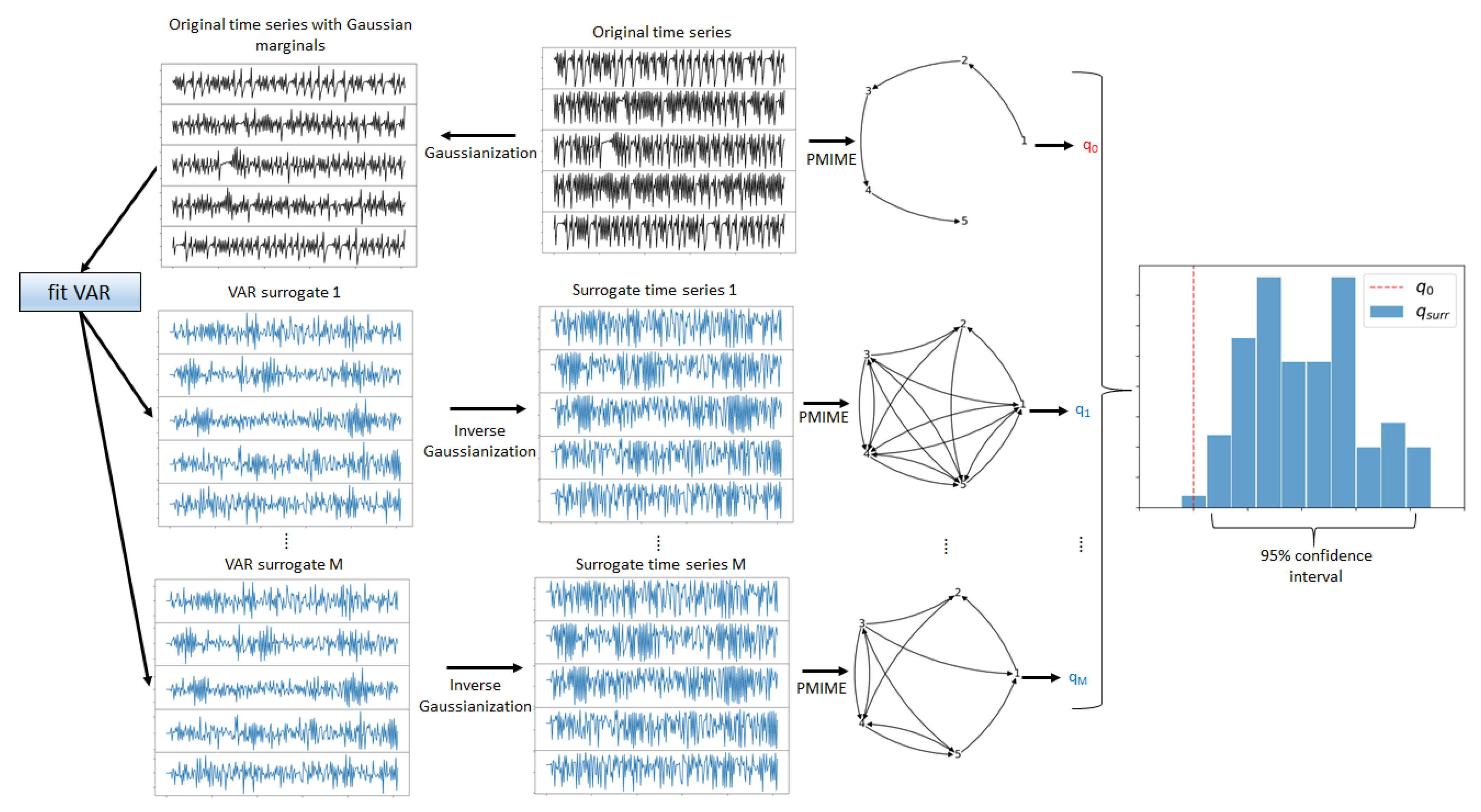
2.2. The Granger Causality Measure PMIME
2.3. Network Indices
2.4. Surrogate Data Generation
2.5. Structural Break Detection Algorithm
| Algorithm 1 Structural break detection |
|
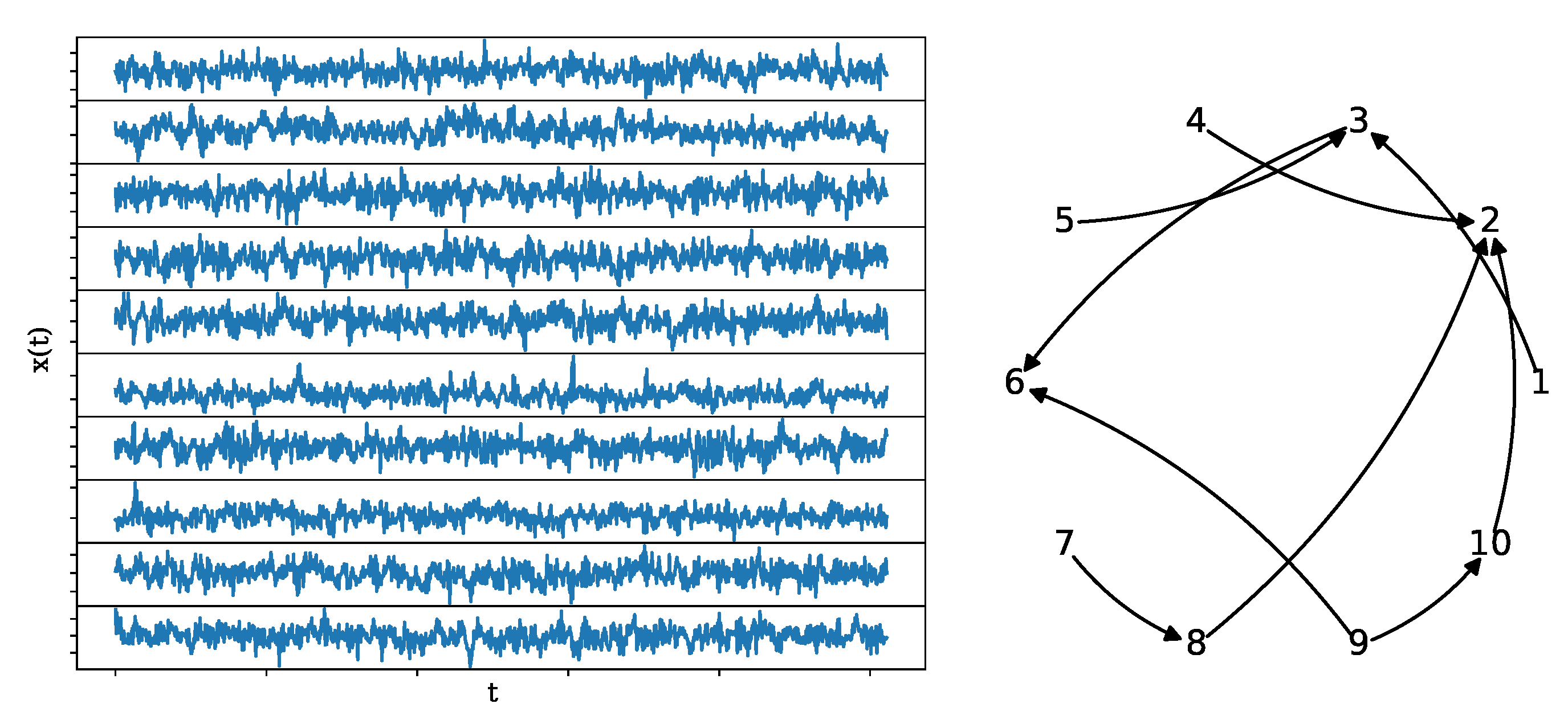
2.6. Data from Synthetic and Financial Systems
2.6.1. Coupled Hénon System
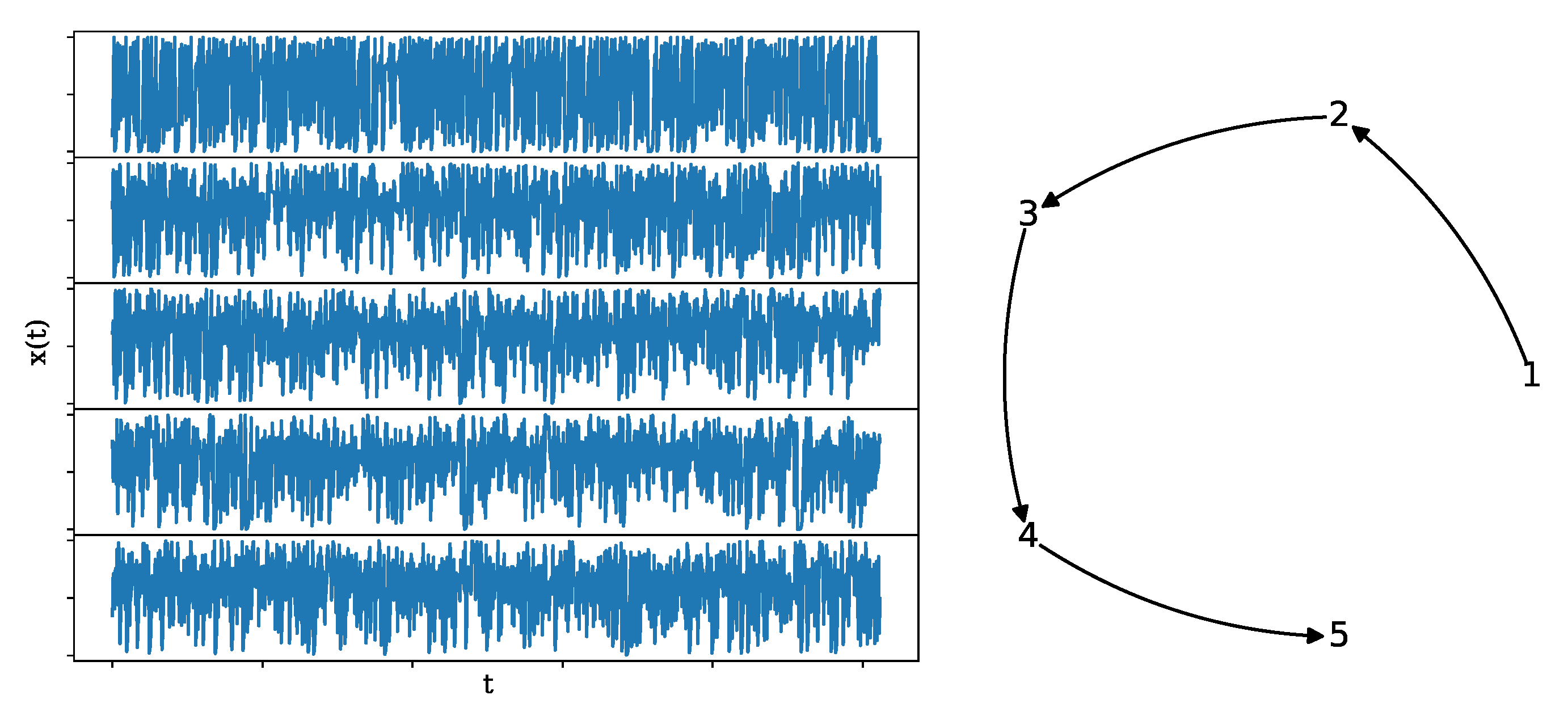
2.6.2. Causal Hénon System
2.6.3. Causal Logistic Map
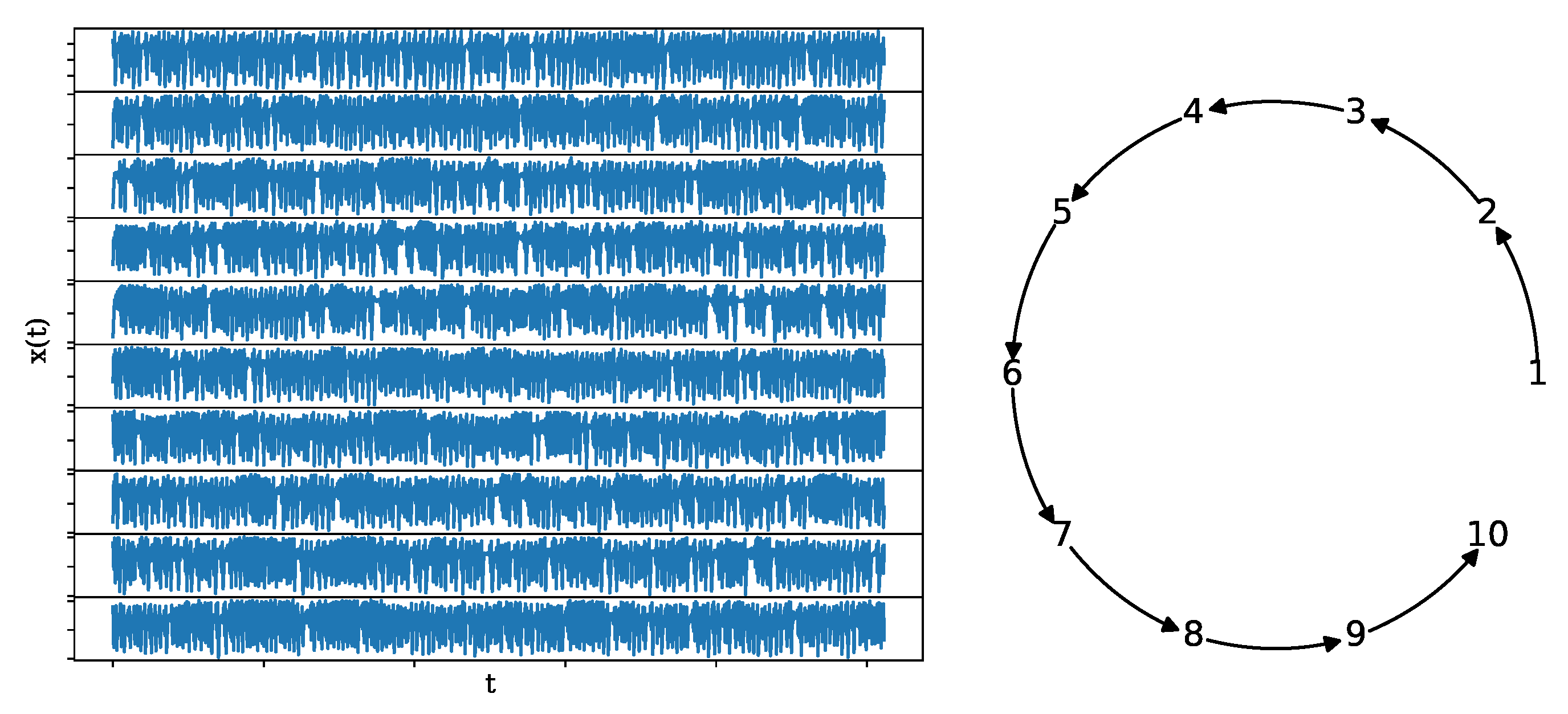
2.6.4. NLVAR(4) System
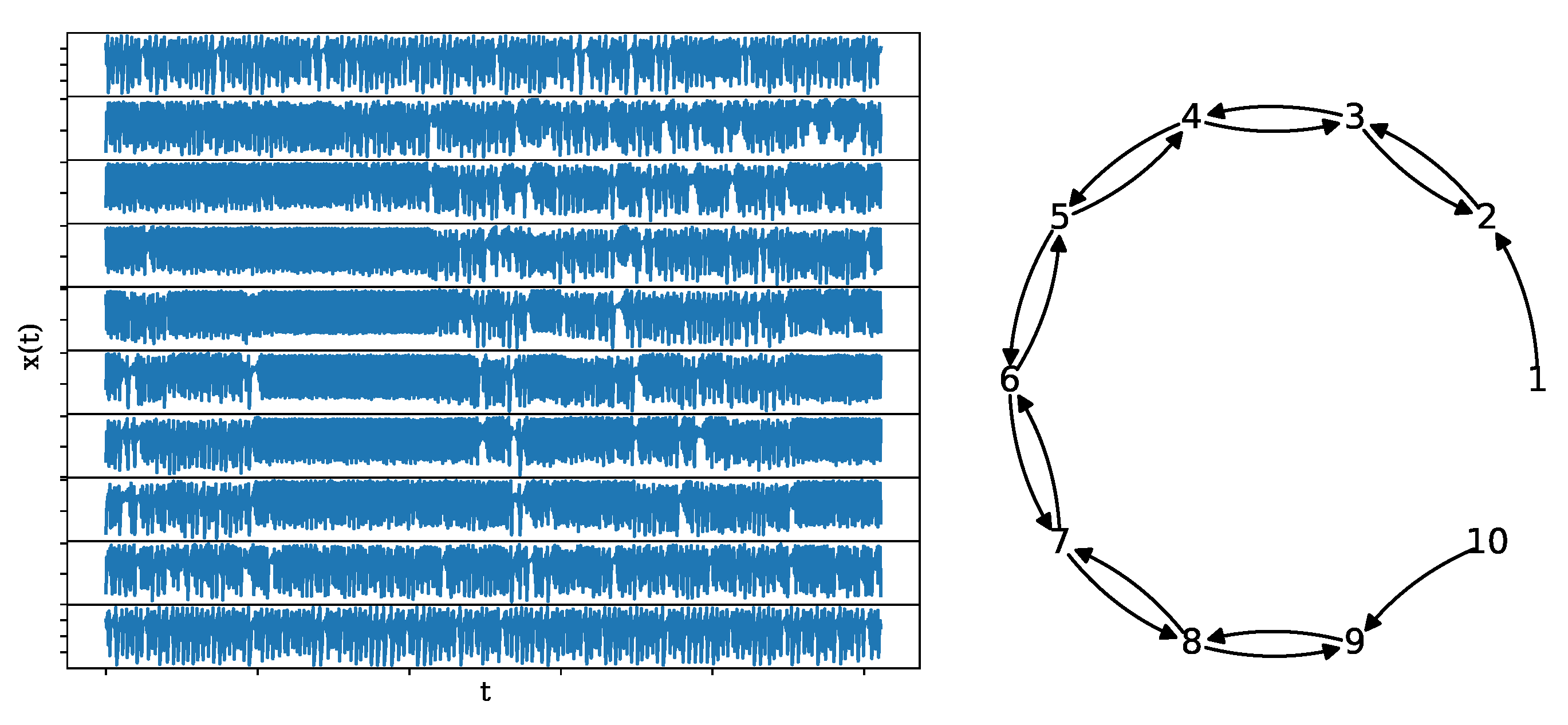
2.6.5. VAR(4) System
2.6.6. Real Data
3. Results
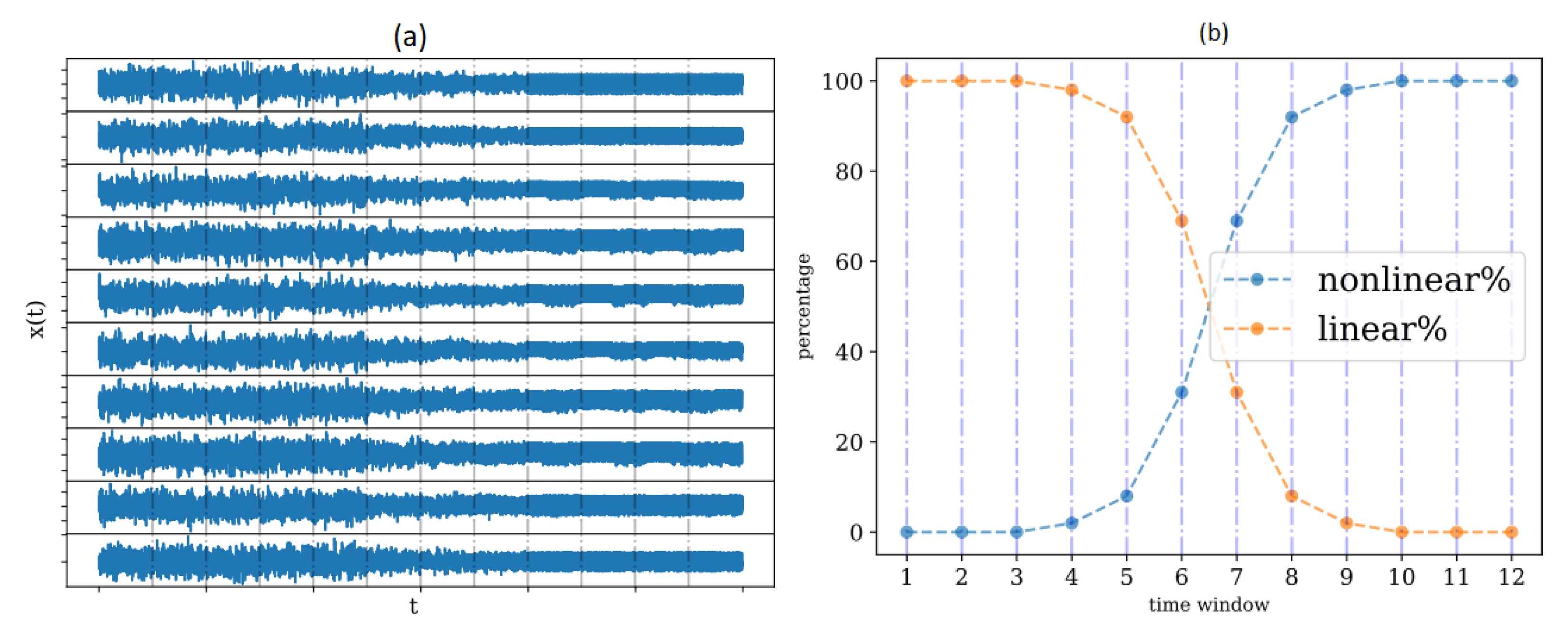
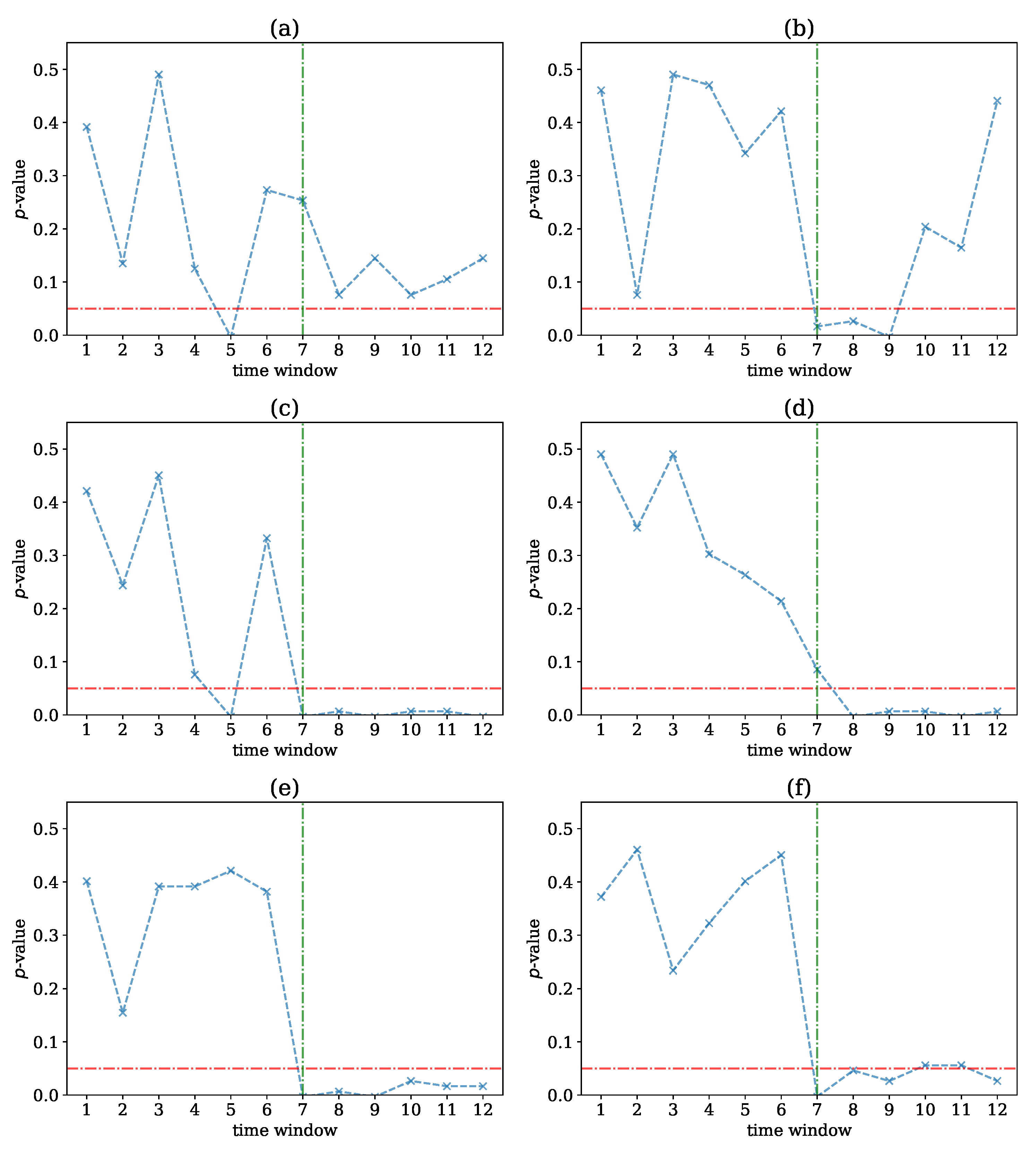
3.1. Structural Change Detection in Simulated Data
3.2. Nonlinearities Detection in Simulated Systems
3.2.1. VAR(4) Model
3.2.2. NLVAR(4)
3.2.3. Causal Hénon Map
3.2.4. Coupled Hénon Map
3.2.5. Causal Logistic Map
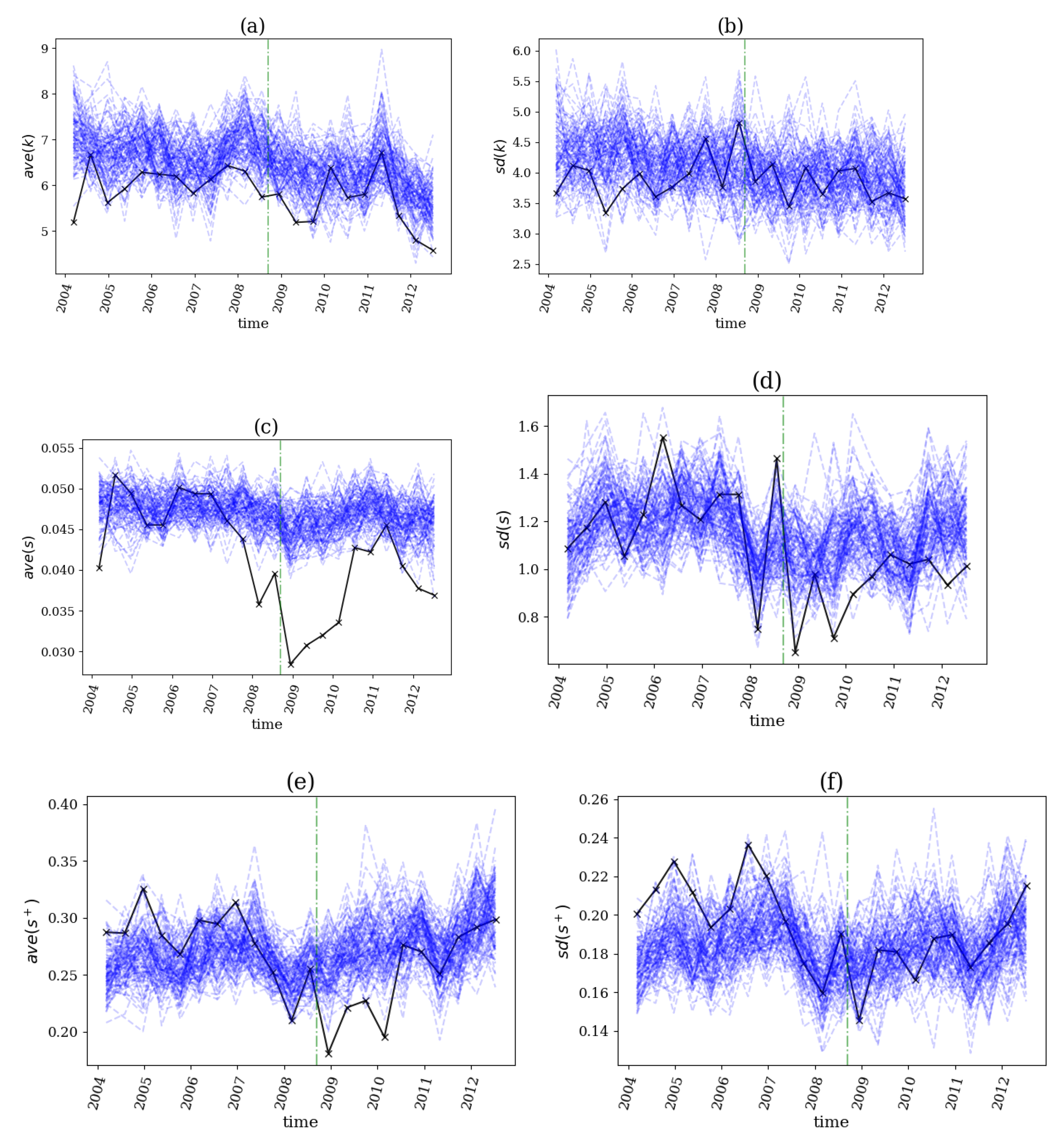
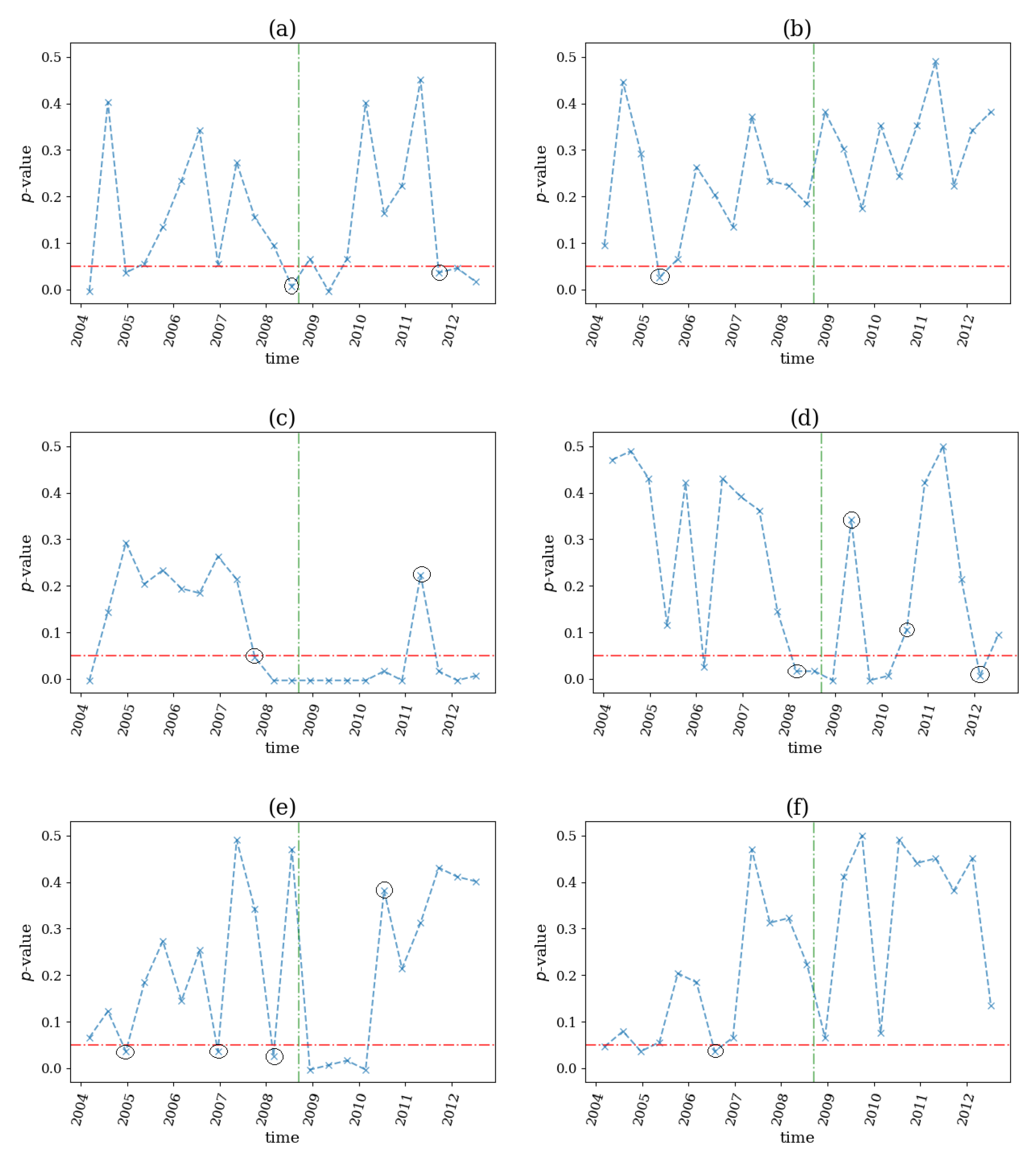
3.3. Structural Break Detection in Real Financial Data
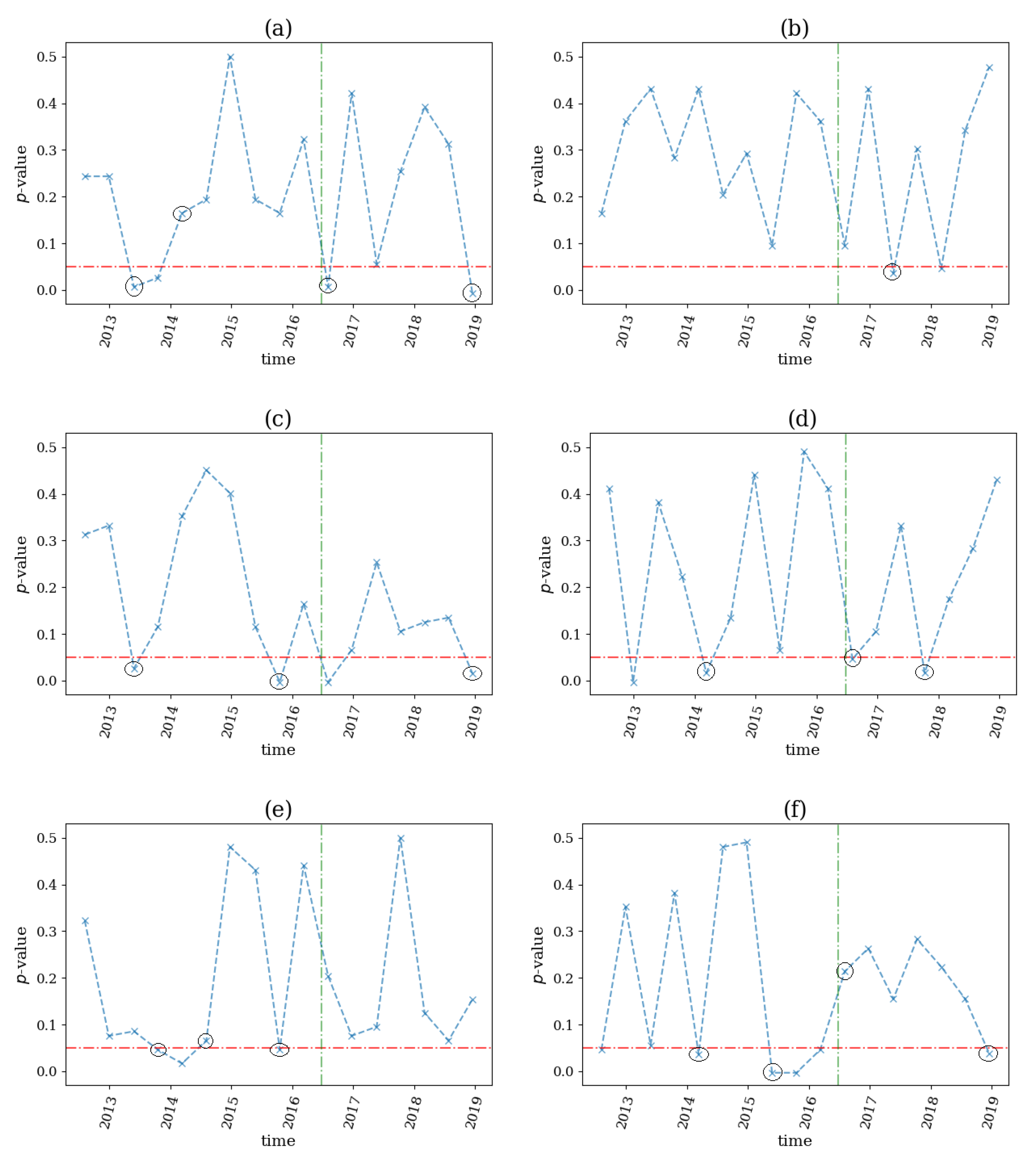
3.3.1. Financial Crisis in 2007–2008
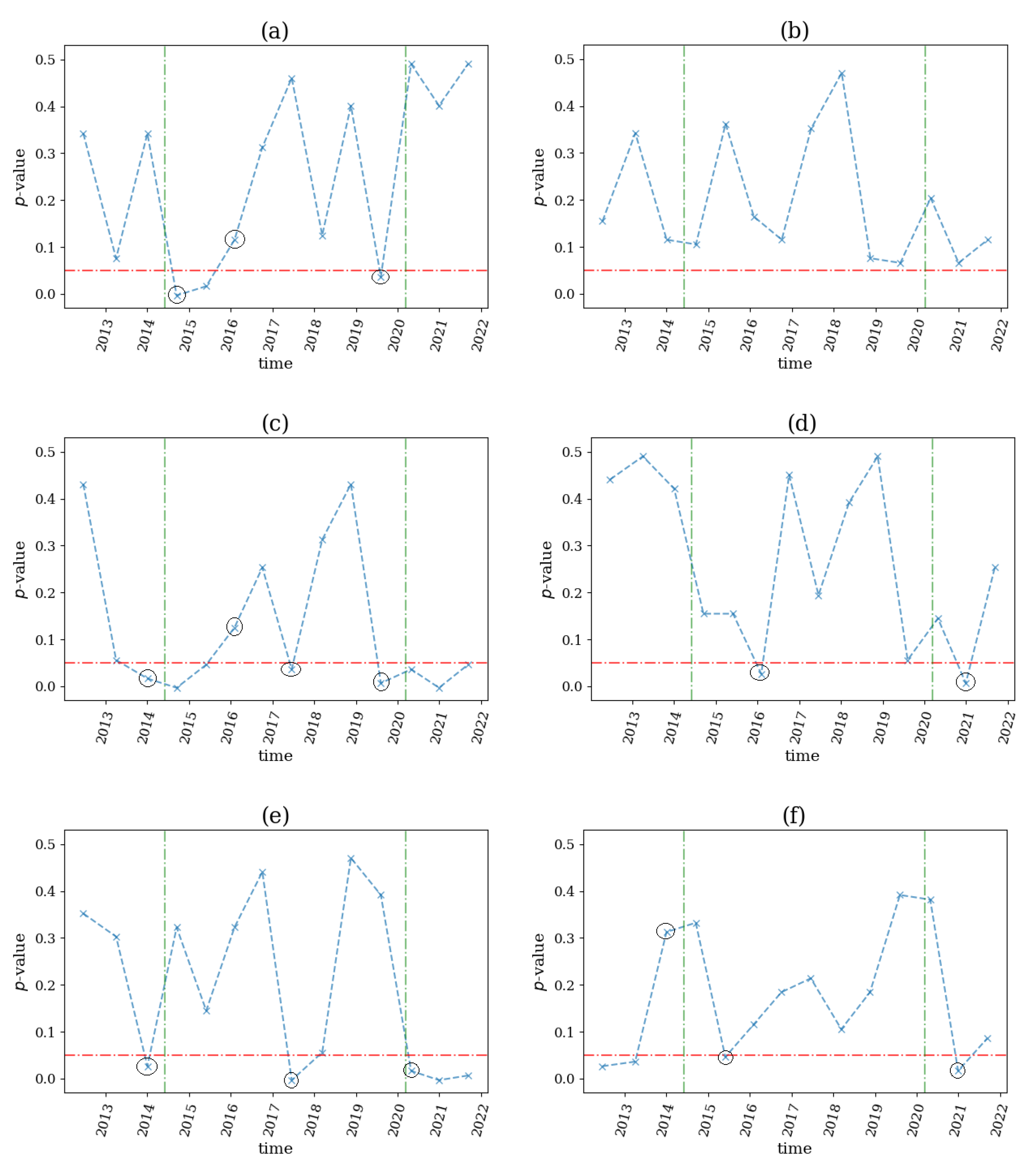
3.3.2. Commodity Crises in the Second Half of 2014 and in April of 2020
3.3.3. Brexit Referendum in 2016
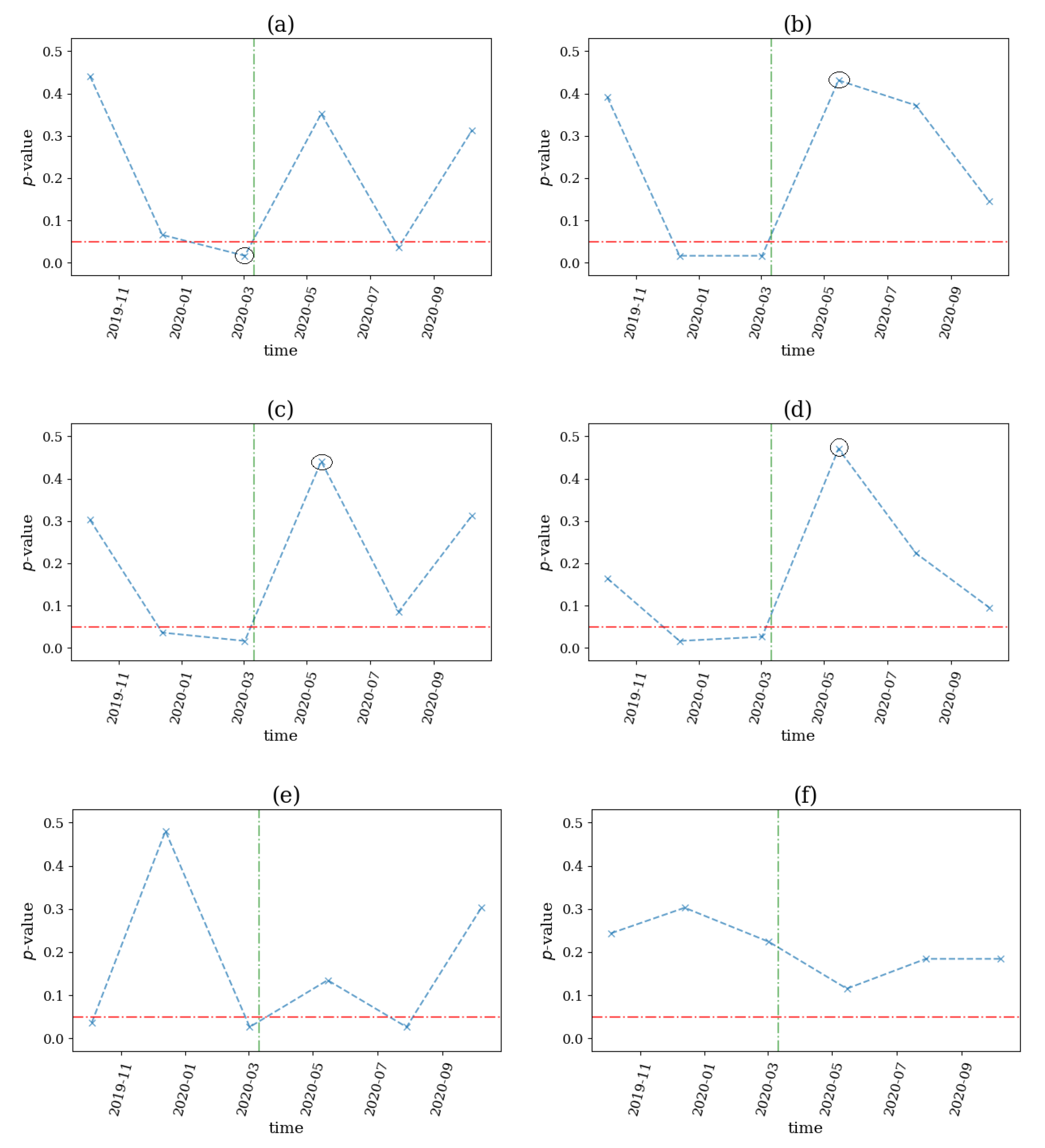
3.3.4. COVID-19 Pandemic
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Bai, J.; Perron, P. Estimating and Testing Linear Models with Multiple Structural changes. Econometrica 1998, 66, 47–78. [Google Scholar] [CrossRef]
- Lavielle, M.; Teyssiere, G. Adaptive Detection of Multiple Change-points in Asset Price Volatility. In Long-Memory in Economics; Springer Science & Business Media: New York, NY, USA, 2007; pp. 129–156. [Google Scholar]
- Frick, K.; Munk, A. Multiscale change point inference. J. R. Stat. Soc. Stat. Methodol. 2014, 76, 495–580. [Google Scholar] [CrossRef]
- van Mierlo, P.; Papadopoulou, M.; Carrette, E.; Boon, P.; Vandenberghe, S.; Vonck, K.; Marinazzo, D. Functional Brain Connectivity from EEG in Epilepsy: Seizure Prediction and Epileptogenic Focus Localization. Prog. Neurobiol. 2014, 121, 19–35. [Google Scholar] [CrossRef] [PubMed]
- Kugiumtzis, D.; Koutlis, C.; Tsimpiris, A.; Kimiskidis, V.K. Dynamics of Epileptiform Discharges Induced by Transcranial Magnetic Stimulation in Genetic Generalized Epilepsy. Int. J. Neural Syst. 2017, 27, 1750037. [Google Scholar] [CrossRef]
- Kalitzin, S.; Petkov, G.; Suffczynski, P.; Grigorovsky, V.; Bardakjian, B.L.; da Silva, F.L.; Carlen, P.L. Epilepsy as a Manifestation of a Multistate Network of Oscillatory Systems. Neurobiol. Dis. 2019, 130, 104488. [Google Scholar] [CrossRef]
- Ragǔz, M.; Predrijevac, N.; Dlaka, D.; Oreskovic, D.; Rotim, A.; Romic, D.; Almahariq, F.; Marcinkovic, P.; Deletis, V.; Kostovic, I.; et al. Structural Changes in Brains of Patients with Disorders of Consciousness Treated with Deep Brain Stimulation. Sci. Rep. 2021, 11, 4401. [Google Scholar] [CrossRef]
- Reeves, J.; Chen, X.; Wang, L. A review and comparison of changepoint detection techniques for climate data. J. Appl. Meteorol. Climatol. 2007, 46, 900–915. [Google Scholar] [CrossRef]
- Killick, R.; Eckley, P.; Jonathan, P. Detection of Changes in the Characteristics of Oceanographic Time Series Using Statistical Change Point Analysis. Ocean Eng. 2010, 37, 1120–1126. [Google Scholar] [CrossRef]
- Vostrikova, L. Detecting disorder in multidimensional random processes. Sov. Math. Dokl. 1981, 24, 55–59. [Google Scholar]
- Killick, R.; Eckley, P. Optimal Detection of Changepoints with a Linear Computational Cost. J. Am. Stat. Assoc. 2012, 107, 1590–1598. [Google Scholar] [CrossRef]
- Smith, S.C.; Bulkley, G.; Leslie, D.S. Equity Premium Forecasts with an Unknown Number of Structural Breaks. J. Financ. Econom. 2020, 18, 59–94. [Google Scholar] [CrossRef]
- Chen, J.; Gupta, A.K. Parametric Statistical Change Point Analysis and Finance with Applications to Genetics, Medicine, 2nd ed.; Birkhäuser: Boston, MA, USA, 2012. [Google Scholar]
- Aue, A.; Horváth, L. Structural breaks in time series. J. Time Ser. Anal. 2013, 34, 1–16. [Google Scholar] [CrossRef]
- Kristensen, D. Non-parametric detection and estimation of structural change. Econom. J. 2012, 15, 420–461. [Google Scholar] [CrossRef]
- Kejriwala, M.; Perron, P. A Sequential Procedure to Determine the Number of Breaks in Trend with an Integrated or Stationary Noise Component. J. Time Ser. Anal. 2010, 31, 305–328. [Google Scholar] [CrossRef]
- Casini, A.; Perron, P. (Eds.) Structural Breaks in Time Series; Oxford University Press: Oxford, UK, 2019. [Google Scholar]
- Acharya, U.R.; Sree, S.V.; Swapna, G.; Martis, R.J.; Suri, J.S. Automated EEG Analysis of Epilepsy: A Review. Knowl.-Based Syst. 2013, 45, 147–165. [Google Scholar] [CrossRef]
- Hussein, A.F.; Arunkumar, N.; Gomes, C.; Alzubaidi, A.K.; Habash, Q.A.; Santamaria-Granados, L.; Francisco Mendoza-Moreno, J.; Ramirez-Gonzalez, G. Focal and Non-Focal Epilepsy Localization: A Review. IEEE Access 2018, 6, 49306–49324. [Google Scholar] [CrossRef]
- Anufriev, M.; Radi, D.; Tramontana, F. Some Reflections on Past and Future of Nonlinear Dynamics in Economics and Finance. Decis. Econ. Financ. 2018, 41, 91–118. [Google Scholar] [CrossRef]
- Kumar, D. Structural Breaks in Volatility Transmission from Developed Markets to Major Asian Emerging Markets. J. Emerg. Mark. Financ. 2019, 18, 172–209. [Google Scholar] [CrossRef]
- Tranquillo, J.V. An Introduction to Complex Systems; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Runge, J.; Nowack, P.; Kretschmer, M.; Flaxman, S.; Sejdinovic, D. Detecting and Quantifying Causal Associations in Large Nonlinear Time Series Datasets. Sci. Adv. 2019, 5, eaau4996. [Google Scholar] [CrossRef]
- Siggiridou, E.; Koutlis, C.; Tsimpiris, A.; Kugiumtzis, D. Evaluation of Granger Causality Measures for Constructing Networks from Multivariate Time Series. Entropy 2019, 21, 1080. [Google Scholar] [CrossRef]
- Seth, A.K.; Barrett, A.B.; Barnett, L. Granger Causality Analysis in Neuroscience and Neuroimaging. J. Neurosci. 2015, 35, 3293–3297. [Google Scholar] [CrossRef]
- Fornito, A.; Zalesky, A.; Bullmore, E.T. Fundamentals of Brain Network Analysis, 1st ed.; Academic Press: New York, NY, USA; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Dijkstra, H.; Hernández-García, E.; Masoller, C.; Barreiro, M. Networks in Climate; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Aste, T.; Di Matteo, T. Sparse Causality Network Retrieval from Short Time Series. Complexity 2017, 2017, 4518429. [Google Scholar] [CrossRef]
- Papana, A.; Kyrtsou, C.; Kugiumtzis, D.; Diks, C. Financial Networks Based on Granger Causality: A Case Study. Phys. A Stat. Mech. Its Appl. 2017, 482, 65–73. [Google Scholar] [CrossRef]
- Lyocsa, S.; Vyrost, T.; Baumohl, E. Return Spillovers around the Globe: A Network Approach. Econ. Model. 2019, 77, 133–146. [Google Scholar] [CrossRef]
- Marti, G.; Nielsen, F.; Binkowski, M.; Donnat, P. Progress in Information Geometry. Signals and Communication Technology; Chapter A Review of Two Decades of Correlations, Hierarchies, Networks and Clustering in Financial Markets; Springer: Cham, Switzerland, 2019; pp. 245–274. [Google Scholar]
- Scagliarini, T.; Faes, L.; Marinazzo, D.; Stramaglia, S.; Mantegna, R.N. Synergistic Information Transfer in the Global System of Financial Markets. Entropy 2020, 22, 1000. [Google Scholar] [CrossRef]
- Salim, L.; Gazi, S.U.; Bekiros, S. Nonlinear Dynamics of Equity, Currency and Commodity Markets in the Aftermath of the Global Financial Crisis. Chaos Solitons Fractals 2017, 103, 342–346. [Google Scholar]
- Salim, L. A Study on Chaos in Crude Oil Markets before and after 2008 International Financial Crisis. Phys. A Stat. Mech. Its Appl. 2017, 466, 389–395. [Google Scholar]
- Purica, I. Nonlinear Dynamics of Financial Crises; Academic Press: New York, NY, USA, 2015. [Google Scholar]
- Vlachos, I.; Kugiumtzis, D. Non-uniform State Space Reconstruction and Coupling Detection. Phys. Rev. E 2010, 82, 016207. [Google Scholar] [CrossRef]
- Kugiumtzis, D. Direct-Coupling Information Measure from Nonuniform Embedding. Phys. Rev. E 2013, 87, 062918. [Google Scholar] [CrossRef]
- Koutlis, C.; Kugiumtzis, D. Discrimination of Coupling Structures Using Causality Networks from Multivariate Time Series. Chaos 2016, 26, 093120. [Google Scholar] [CrossRef]
- Wan, X.; Cruts, B.; Jensen, H.J. The Causal Inference of Cortical Neural Networks during Music Improvisations. PLoS ONE 2014, 9, e112776. [Google Scholar] [CrossRef] [PubMed]
- Kugiumtzis, D.; Kimiskidis, V.K. Direct causal networks for the study of transcranial magnetic stimulation effects on focal epileptiform discharges. Int. J. Neural Syst. 2015, 25, 1550006. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Dai, W.; Sun, D.; Zhao, Y. Risk Evaluation for a Manufacturing Process Based on a Directed Weighted Network. Entropy 2020, 22, 699. [Google Scholar] [CrossRef] [PubMed]
- Heyse, J.; Sheybani, L.; Vulliemoz, S.; Van Mierlo, P. Evaluation of Directed Causality Measures and Lag Estimations in Multivariate Time Series. Front. Syst. Neurosci. 2021, 15, 620338. [Google Scholar] [CrossRef]
- Kraskov, A.; Stögbauer, H.; Grassberger, P. Estimating Mutual Information. Phys. Rev. E 2004, 69, 066138. [Google Scholar] [CrossRef]
- Quian Quiroga, R.; Kraskov, A.; Kreuz, T.; Grassberger, P. Performance of Different Synchronization Measures in Real Data: A Case Study on Electroencephalographic Signals. Phys. Rev. E 2002, 65, 041903. [Google Scholar] [CrossRef]
- Andrzejak, R.G.; Kraskov, A.; Stögbauer, H.; Mormann, F.; Kreuz, T. Bivariate Surrogate Techniques: Necessity, Strengths, and Caveats. Phys. Rev. E 2003, 68, 066202. [Google Scholar] [CrossRef]
- Kugiumtzis, D. Test Your Surrogate Data before You Test for Nonlinearity. Phys. Rev. E 1999, 60, 2808–2816. [Google Scholar] [CrossRef]
- Kugiumtzis, D. Surrogate Data Test for Nonlinearity Including Non-monotonic Transforms. Phys. Rev. E 2000, 62, 25–28. [Google Scholar] [CrossRef]
- Kugiumtzis, D.; Bora-Senta, E. Simulation of Multivariate Non-gaussian Autoregressive Time Series with Given Autocovariance and Marginals. Simul. Model. Pract. Theory 2014, 44, 42–53. [Google Scholar] [CrossRef]
- Yu, G.H.; Huang, C.C. A Distribution Free Plotting Position. Stoch. Environ. Res. Risk Assess. 2001, 15, 462–476. [Google Scholar] [CrossRef]
- Papana, A.; Kugiumtzis, D.; Larsson, P.G. Detection of Direct Causal Effects and Application in the Analysis of Electroencephalograms from Patients with Epilepsy. Int. J. Bifurc. Chaos 2012, 22, 1250222. [Google Scholar] [CrossRef]
- Geweke, J.F. Measures of Conditional Linear Dependence and Feedback between Time Series. J. Am. Stat. Assoc. 1984, 79, 907–915. [Google Scholar] [CrossRef]



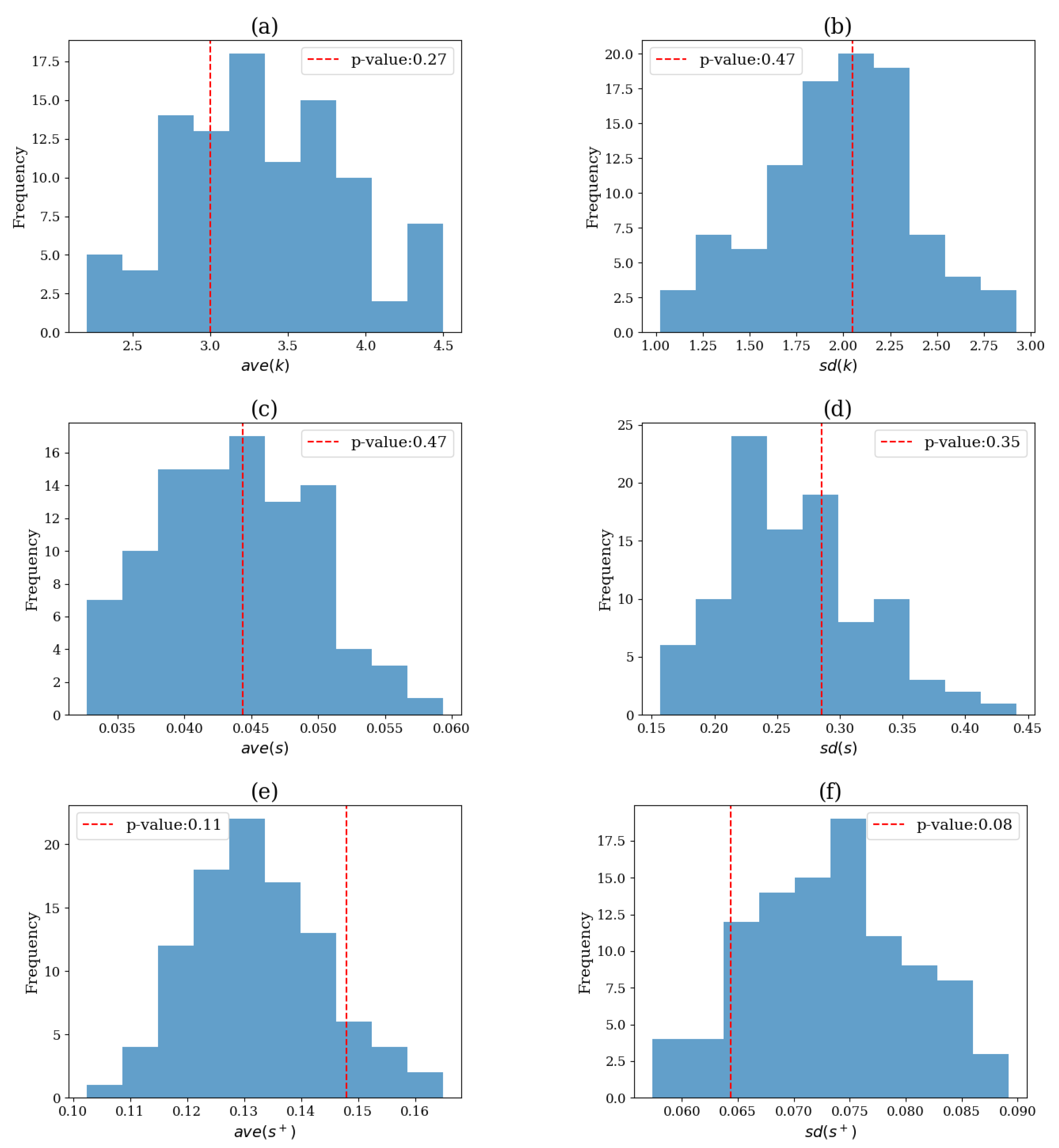

| System | ave(k) | SD(k) | ave(s) | SD(s) | ave(s) | SD(s) |
|---|---|---|---|---|---|---|
| VAR(4) | 0.13 | 0.13 | 0.19 | 0.13 | 0.09 | 0.09 |
| NLVAR(4) | 0.12 | 0.18 | 0.07 | 0.14 | 0.19 | 0.22 |
| CausalHM | 0.35 | 0.47 | 0.28 | 1.00 | 0.26 | 1.00 |
| CoupledHM | 0.27 | 0.24 | 0.45 | 0.52 | 0.41 | 0.08 |
| CausalLM | 0.04 | 0.16 | 1.00 | 1.00 | 1.00 | 0.28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fotiadis, A.; Vlachos, I.; Kugiumtzis, D. Detecting Nonlinear Interactions in Complex Systems: Application in Financial Markets. Entropy 2023, 25, 370. https://doi.org/10.3390/e25020370
Fotiadis A, Vlachos I, Kugiumtzis D. Detecting Nonlinear Interactions in Complex Systems: Application in Financial Markets. Entropy. 2023; 25(2):370. https://doi.org/10.3390/e25020370
Chicago/Turabian StyleFotiadis, Akylas, Ioannis Vlachos, and Dimitris Kugiumtzis. 2023. "Detecting Nonlinear Interactions in Complex Systems: Application in Financial Markets" Entropy 25, no. 2: 370. https://doi.org/10.3390/e25020370
APA StyleFotiadis, A., Vlachos, I., & Kugiumtzis, D. (2023). Detecting Nonlinear Interactions in Complex Systems: Application in Financial Markets. Entropy, 25(2), 370. https://doi.org/10.3390/e25020370







