An Ensemble and Multi-View Clustering Method Based on Kolmogorov Complexity
Abstract
:1. Introduction
- Our main scientific contribution is the proposal of a new heuristic method relying on Kolmogorov complexity to merge partition in an unsupervised ensemble learning context applied to multiview clustering. Compared with earlier methods, we remove the reliance on an arbitrary pivot to choose the merging order. Instead, we reinforce the use of Kolmogorov complexity to make the choice of the merging order, thus rendering our algorithm deterministic, while earlier versions and methods were not. Our method also explores more of the solution space, thus leading to better results.
- We propose a large comparison of unsupervised ensemble learning methods—including four methods from the state of the art—in a context which is not restricted to text corpus analysis, both in terms of state-of-the-art methods but also datasets.
- While not a scientific or technical contribution (because our method relies on known principles), our algorithm brings some novelty in the field of unsupervised ensemble learning, where no other method relies on the same principle. We believe that such diversity is useful to the field of clustering, where a wider choice of methods is a good thing because of the unsupervised context.
2. State of the Art
- Multi-view clustering [2,3,10,11,12,13,14,15,16,17,18,19,20,21] is concerned with any kind of clustering, where the data are split into different views. It does not matter whether the views are physically stored in different places, and if the views are real or artificially created. In multi-view clustering, the goal can either be to build a consensus from all the views, or to produce clustering results specific to each view.
- Distributed data clustering [22] is a sub-case of multi-view clustering that deals with any clustering scenario where the data are physically stored in different sites. In many cases, clustering algorithms used for this kind of task will have to be distributed across the different sites.
- Collaborative clustering [23,24,25,26,27] is a framework in which clustering algorithms work together and exchange information with the goal of mutual improvement. In its horizontal form, it involves clustering algorithms working on different representations of the same data, and it is a sub-case of multi-view clustering with the particularity of never seeking a consensus solution but rather aiming for an improvement in all views. In its vertical form, it involves clustering algorithms working on different data samples with similar distributions and underlying structures. In both forms, these algorithms follow a two-step process: (1) A first clustering is built by local algorithms. (2) These local results are then improved through collaboration. A better name for collaborative clustering could be model collaboration, as one requirement for a framework to qualify as collaborative is that the collaboration process must involve effects at the level of the local models.
- Unsupervised ensemble learning, or cluster ensembles [28,29,30,31,32,33,34,35,36] is the unsupervised equivalent of ensemble methods from supervised learning [37]: It is concerned with either the selection of clustering methods, or the fusion of clustering results from a large pool, with the goal of achieving a single best-quality result. partitions. This pool of multiple algorithms or results may come from a multi-view clustering context [38], or may just be the unsupervised equivalent of boosting methods, where one would attempt to combine the results of several algorithms applied to the same data. Unlike collaborative and multi-view clustering, ensemble clustering does not access the original features, but only the crisp partitions.
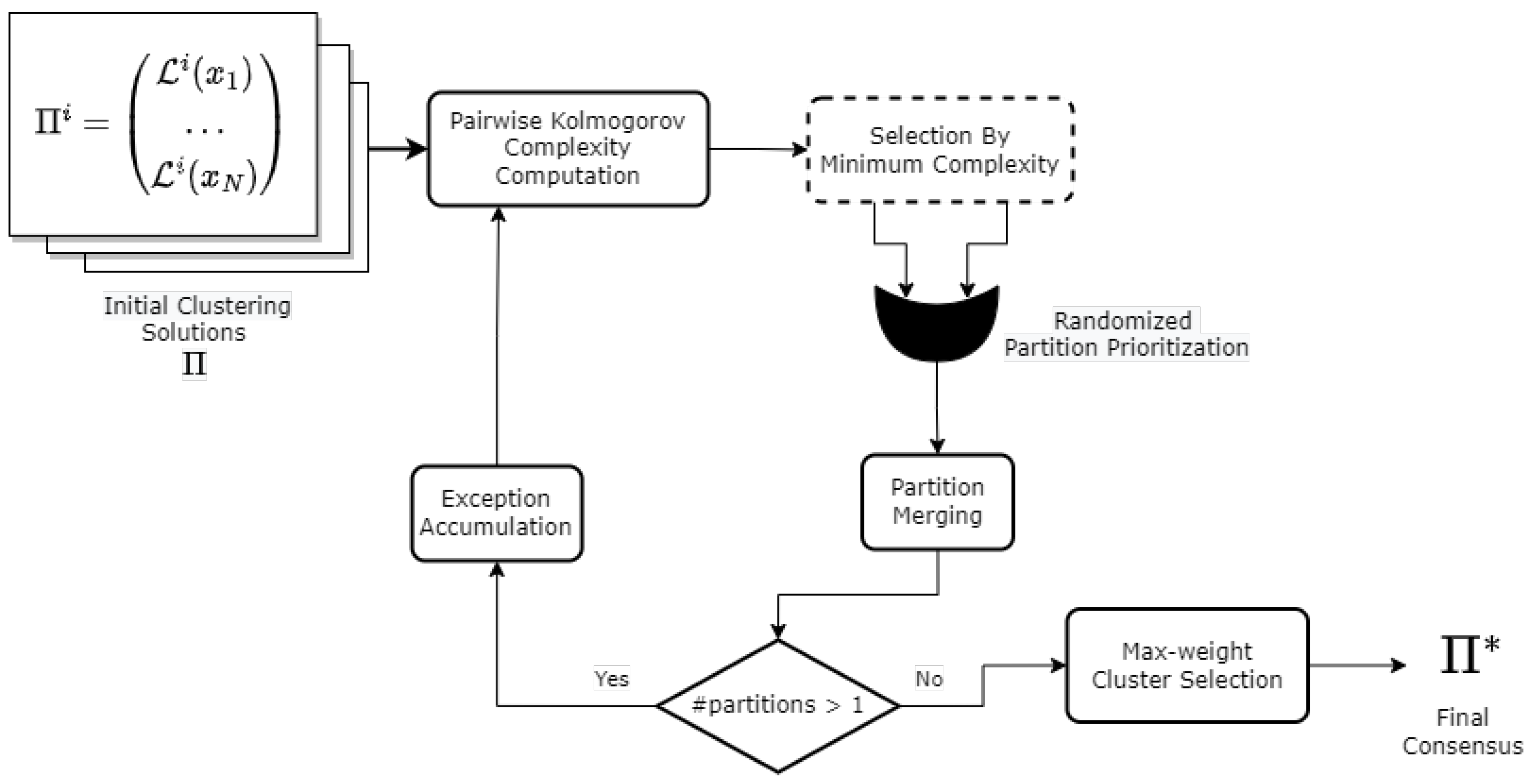
3. The Proposed Method
3.1. Problem Definition and Notations
Table with All Notations
3.2. Merging Partitions Using Kolmogorov Complexity
3.3. The KMC Algorithm
3.3.1. Overall View of the Main Procedure
| Algorithm 1: Main procedure for building the consensus partition. |
 |
3.3.2. Merging Two Views/Partitions
| Algorithm 2: Merge procedure that fuses two partitions into a new one identifying also problematic points as exceptions. |
 |
3.3.3. Handling Mapping Errors through the Merge Process
- First, a data object could be identified as an exception to the majority rule of the current merge operation as formalized in the first case of Equation (7).
- The next two cases show the scenarios in which the data object could come from errors generated in prior merging stages in either of the two former partitions, but not in both.
- The final case defined in Equation (7) is distinguished from previous definitions by denoting the scenario where the data object has been dragged from mapping errors in both input partitions.
3.4. Computational Complexity: Discussion
4. Experimental Analysis
4.1. Clustering Measures
4.2. Analysis on Real Data and Comparison against Other Ensemble Methods
4.2.1. Baseline Methods
4.2.2. Operational Details of the Compared Methods
4.2.3. Discussion of the Experimental Results
4.3. Empirical Analysis of the Stability of the Consensus Solution
Procedure
- Depending on the simulation, we generated multi-view data belonging to k clusters spread across eight views, and the matching ground-truth partitions.
- In m views out of eight, the partitions were altered with a degree of noise that corresponds to random changes in partition assignments to simulate varying qualities of local solutions.
- In the other partitions (not part of the m out of 8 altered partitions), a ration of only 5% alteration was applied.
5. Conclusions and Future Works
- Unlike in [7], which introduced the use of Kolmogorov complexity in a multi-view setting, we aim at a full merging of the clusters, and not just optimizing things locally.
- Unlike in [51], which is multi-view with merging, the optimization process to reduce these conflicts and merge partitions in a effective manner, we propose a new and improved algorithm to choose the merging order of the partitions, thus making our algorithm stable compared with earlier versions of the same technique.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CSPA | Cluster-based Similarity Partitioning |
| ECPCS | Ensemble Clustering via fast Propagation of Cluster-wise Similarities |
| HGPA | Hyper Graph Partitioning |
| KMC | Kolmogorov-based Multi-view Clustering |
| MCLA | Meta Clustering |
| MDEC | Multidiversified Ensemble Clustering |
| NMI | Normalized Mutual Information |
References
- Tagarelli, A.; Karypis, G. A segment-based approach to clustering multi-topic documents. Knowl. Inf. Syst. 2013, 34, 563–595. [Google Scholar] [CrossRef] [Green Version]
- Fraj, M.; HajKacem, M.A.B.; Essoussi, N. Ensemble Method for Multi-view Text Clustering. In Proceedings of the Computational Collective Intelligence—11th International Conference, ICCCI 2019, Hendaye, France, 4–6 September 2019; pp. 219–231. [Google Scholar] [CrossRef]
- Zimek, A.; Vreeken, J. The blind men and the elephant: On meeting the problem of multiple truths in data from clustering and pattern mining perspectives. Mach. Learn. 2015, 98, 121–155. [Google Scholar] [CrossRef]
- Ghosh, J.; Acharya, A. Cluster ensembles. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2011, 1, 305–315. [Google Scholar] [CrossRef]
- Wallace, C.S.; Boulton, D.M. An Information Measure for Classification. Comput. J. 1968, 11, 185–194. [Google Scholar] [CrossRef] [Green Version]
- Rissanen, J. Modeling by shortest data description. Automatica 1978, 14, 465–471. [Google Scholar] [CrossRef]
- Murena, P.; Sublime, J.; Matei, B.; Cornuéjols, A. An Information Theory based Approach to Multisource Clustering. In Proceedings of the IJCAI, Stockholm, Sweden, 13–19 July 2018; pp. 2581–2587. [Google Scholar]
- Zamora, J.; Sublime, J. A New Information Theory Based Clustering Fusion Method for Multi-view Representations of Text Documents. In Proceedings of the Social Computing and Social Media, Design, Ethics, User Behavior, and Social Network Analysis—12th International Conference, SCSM 2020, Held as Part of the 22nd HCI International Conference, HCII 2020, Copenhagen, Denmark, 19–24 July 2020; Meiselwitz, G., Ed.; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2020; Volume 12194, pp. 156–167. [Google Scholar] [CrossRef]
- Murena, P.A.; Sublime, J.; Matei, B. Rethinking Collaborative Clustering: A Practical and Theoretical Study within the Realm of Multi-View Clustering. In Recent Advancements in Multi-View Data Analytics; Studies in Big Data Series; Springer: Berlin/Heidelberg, Germany, 2022; Volume 106. [Google Scholar]
- Bickel, S.; Scheffer, T. Multi-View Clustering. In Proceedings of the 4th IEEE International Conference on Data Mining (ICDM 2004), Brighton, UK, 1–4 November 2004; pp. 19–26. [Google Scholar] [CrossRef]
- Janssens, F.; Glänzel, W.; De Moor, B. Dynamic hybrid clustering of bioinformatics by incorporating text mining and citation analysis. In Proceedings of the 13th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Jose, CA, USA, 12–15 August 2007; pp. 360–369. [Google Scholar]
- Liu, X.; Yu, S.; Moreau, Y.; De Moor, B.; Glänzel, W.; Janssens, F. Hybrid clustering of text mining and bibliometrics applied to journal sets. In Proceedings of the 2009 SIAM International Conference on Data Mining, Sparks, NV, USA, 30 April–2 May 2009; pp. 49–60. [Google Scholar]
- Greene, D.; Cunningham, P. A matrix factorization approach for integrating multiple data views. In Proceedings of the Joint European Conference on Machine Learning and Knowledge Discovery in Databases, Bled, Slovenia, 7–11 September 2009; pp. 423–438. [Google Scholar]
- Yu, S.; Moor, B.; Moreau, Y. Clustering by heterogeneous data fusion: Framework and applications. In Proceedings of the NIPS Workshop, Whistler, BC, Canada, 11 December 2009. [Google Scholar]
- Liu, X.; Glänzel, W.; De Moor, B. Hybrid clustering of multi-view data via Tucker-2 model and its application. Scientometrics 2011, 88, 819–839. [Google Scholar] [CrossRef]
- Liu, X.; Ji, S.; Glänzel, W.; De Moor, B. Multiview partitioning via tensor methods. IEEE Trans. Knowl. Data Eng. 2012, 25, 1056–1069. [Google Scholar]
- Xie, X.; Sun, S. Multi-view clustering ensembles. In Proceedings of the International Conference on Machine Learning and Cybernetics, ICMLC 2013, Tianjin, China, 14–17 July 2013; pp. 51–56. [Google Scholar] [CrossRef]
- Romeo, S.; Tagarelli, A.; Ienco, D. Semantic-based multilingual document clustering via tensor modeling. In Proceedings of the Conference on Empirical Methods in Natural Language Processing EMNLP, Doha, Qatar, 25–29 October 2014; pp. 600–609. [Google Scholar]
- Hussain, S.F.; Mushtaq, M.; Halim, Z. Multi-view document clustering via ensemble method. J. Intell. Inf. Syst. 2014, 43, 81–99. [Google Scholar] [CrossRef]
- Benjamin, J.B.M.; Yang, M.S. Weighted Multiview Possibilistic C-Means Clustering With L2 Regularization. IEEE Trans. Fuzzy Syst. 2022, 30, 1357–1370. [Google Scholar] [CrossRef]
- Xu, Y.M.; Wang, C.D.; Lai, J.H. Weighted Multi-view Clustering with Feature Selection. Pattern Recognit. 2016, 53, 25–35. [Google Scholar] [CrossRef]
- Visalakshi, N.K.; Thangavel, K. Distributed Data Clustering: A Comparative Analysis. In Foundations of Computational, Intelligence Volume 6: Data Mining; Abraham, A., Hassanien, A.E., de Leon, F., de Carvalho, A.P., Snášel, V., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 371–397. [Google Scholar] [CrossRef]
- Cornuéjols, A.; Wemmert, C.; Gançarski, P.; Bennani, Y. Collaborative clustering: Why, when, what and how. Inf. Fusion 2018, 39, 81–95. [Google Scholar] [CrossRef]
- Pedrycz, W. Collaborative fuzzy clustering. Pattern Recognit. Lett. 2002, 23, 1675–1686. [Google Scholar] [CrossRef]
- Grozavu, N.; Bennani, Y. Topological Collaborative Clustering. Aust. J. Intell. Inf. Process. Syst. 2010, 12, 14. [Google Scholar]
- Jiang, Y.; Chung, F.L.; Wang, S.; Deng, Z.; Wang, J.; Qian, P. Collaborative Fuzzy Clustering From Multiple Weighted Views. IEEE Trans. Cybern. 2015, 45, 688–701. [Google Scholar] [CrossRef]
- Yang, M.S.; Sinaga, K.P. Collaborative feature-weighted multi-view fuzzy c-means clustering. Pattern Recognit. 2021, 119, 108064. [Google Scholar] [CrossRef]
- Strehl, A.; Ghosh, J. Cluster ensembles—A knowledge reuse framework for combining multiple partitions. J. Mach. Learn. Res. 2002, 3, 583–617. [Google Scholar]
- Li, T.; Ogihara, M.; Ma, S. On combining multiple clusterings. In Proceedings of the Thirteenth ACM International Conference on INFORMATION and Knowledge Management, Washington, DC, USA, 8–13 November 2004; pp. 294–303. [Google Scholar]
- Fred, A.L.; Jain, A.K. Combining multiple clusterings using evidence accumulation. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 835–850. [Google Scholar] [CrossRef]
- Topchy, A.; Jain, A.K.; Punch, W. Clustering ensembles: Models of consensus and weak partitions. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1866–1881. [Google Scholar] [CrossRef]
- Yi, J.; Yang, T.; Jin, R.; Jain, A.K.; Mahdavi, M. Robust ensemble clustering by matrix completion. In Proceedings of the 2012 IEEE 12th International Conference on Data Mining, Brussels, Belgium, 10–13 December 2012; pp. 1176–1181. [Google Scholar]
- Wu, J.; Liu, H.; Xiong, H.; Cao, J.; Chen, J. K-means-based consensus clustering: A unified view. IEEE Trans. Knowl. Data Eng. 2014, 27, 155–169. [Google Scholar] [CrossRef]
- Liu, H.; Zhao, R.; Fang, H.; Cheng, F.; Fu, Y.; Liu, Y.Y. Entropy-based consensus clustering for patient stratification. Bioinformatics 2017, 33, 2691–2698. [Google Scholar] [CrossRef] [Green Version]
- Rashidi, F.; Nejatian, S.; Parvin, H.; Rezaie, V. Diversity based cluster weighting in cluster ensemble: An information theory approach. Artif. Intell. Rev. 2019, 52, 1341–1368. [Google Scholar] [CrossRef]
- Vega-Pons, S.; Ruiz-Shulcloper, J. A Survey of Clustering Ensemble Algorithms. IJPRAI 2011, 25, 337–372. [Google Scholar] [CrossRef]
- Kuncheva, L.I.; Whitaker, C.J. Measures of Diversity in Classifier Ensembles and Their Relationship with the Ensemble Accuracy. Mach. Learn. 2003, 51, 181–207. [Google Scholar] [CrossRef]
- Wemmert, C.; Gancarski, P. A multi-view voting method to combine unsupervised classifications. In Proceedings of the 2nd IASTED International Conference on Artificial Intelligence and Applications, Málaga, Spain, 9–12 September 2002; pp. 447–452. [Google Scholar]
- Li, Y.; Nie, F.; Huang, H.; Huang, J. Large-Scale Multi-View Spectral Clustering via Bipartite Graph. In Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015; pp. 2750–2756. [Google Scholar]
- Kang, Z.; Guo, Z.; Huang, S.; Wang, S.; Chen, W.; Su, Y.; Xu, Z. Multiple Partitions Aligned Clustering. In Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, IJCAI 2019, Macao, China, 10–16 August 2019; pp. 2701–2707. [Google Scholar]
- Li, S.Y.; Jiang, Y.; Zhou, Z.H. Partial Multi-View Clustering. In Proceedings of the Twenty-Eighth AAAI Conference on Artificial Intelligence, Québec City, QC, Canada, 27–31 July 2014; AAAI Press: Washington, DC, USA, 2014; pp. 1968–1974. [Google Scholar]
- Wang, H.; Yang, Y.; Liu, B. GMC: Graph-Based Multi-View Clustering. IEEE Trans. Knowl. Data Eng. 2020, 32, 1116–1129. [Google Scholar] [CrossRef]
- Kang, Z.; Zhao, X.; Peng, C.; Zhu, H.; Zhou, J.T.; Peng, X.; Chen, W.; Xu, Z. Partition level multiview subspace clustering. Neural Netw. 2020, 122, 279–288. [Google Scholar] [CrossRef]
- Zhong, C.; Hu, L.; Yue, X.; Luo, T.; Fu, Q.; Xu, H. Ensemble clustering based on evidence extracted from the co-association matrix. Pattern Recognit. 2019, 92, 93–106. [Google Scholar] [CrossRef]
- Huang, D.; Wang, C.D.; Lai, J.H.; Kwoh, C.K. Toward Multidiversified Ensemble Clustering of High-Dimensional Data: From Subspaces to Metrics and Beyond. IEEE Trans. Cybern. 2021, 52, 12231–12244. [Google Scholar] [CrossRef]
- Huang, D.; Wang, C.D.; Peng, H.; Lai, J.; Kwoh, C.K. Enhanced Ensemble Clustering via Fast Propagation of Cluster-Wise Similarities. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 508–520. [Google Scholar] [CrossRef] [Green Version]
- Yeh, C.C.; Yang, M.S. Evaluation measures for cluster ensembles based on a fuzzy generalized Rand index. Appl. Soft Comput. 2017, 57, 225–234. [Google Scholar] [CrossRef]
- Sublime, J.; Matei, B.; Cabanes, G.; Grozavu, N.; Bennani, Y.; Cornuéjols, A. Entropy based probabilistic collaborative clustering. Pattern Recognit. 2017, 72, 144–157. [Google Scholar] [CrossRef] [Green Version]
- Ros, F.; Guillaume, S. ProTraS: A probabilistic traversing sampling algorithm. Expert Syst. Appl. 2018, 105, 65–76. [Google Scholar] [CrossRef]
- Karypis, M.; Steinbach, G.; Kumar, V. A comparison of document clustering techniques. In Proceedings of the KDD Workshop on Text Mining, Boston, MA, USA, 20–23 August 2000. [Google Scholar]
- Zamora, J.; Allende-Cid, H.; Mendoza, M. Distributed Clustering of Text Collections. IEEE Access 2019, 7, 155671–155685. [Google Scholar] [CrossRef]


| Notation | Meaning |
|---|---|
| The dataset of N objects split into the M views | |
| M | The number of views |
| Turing machine or a computational clustering method | |
| The partition built by method | |
| The partition in view i | |
| The number of clusters in view i | |
| The a-th cluster in view i | |
| The function mapping any element of view i to a cluster of this view | |
| The mapping matrix from view i to view j | |
| The percentage of elements from in that also belong to | |
| The maximum agreement cluster for in view j | |
| Objects belonging to the same max agreement cluster than x in | |
| Kolmogorov complexity of knowing , see Equation (5) | |
| The error list when mapping to , see Equation (6) | |
| The exception set for any partition (points marked in or ) | |
| Membership weight of point to a cluster , see Equation (7) | |
| W | list of weight for all partitions |
| List of all previous merge exception () | |
| consensus assignments made for each cluster , see Algorithm 2 |
| Dataset | #Doc | #Views |
|---|---|---|
| 3Sources | 169 | 3 |
| BBC-seg2 | 2012 | 2 |
| BBC-seg3 | 1268 | 3 |
| BBC-seg4 | 685 | 4 |
| BBCSports-seg2 | 544 | 2 |
| BBCSports-seg3 | 282 | 3 |
| BBCSports-seg4 | 116 | 4 |
| Handwritten | 2000 | 6 |
| Caltech | 2386 | 6 |
| Dataset | Method | Entropy | Purity | NMI |
|---|---|---|---|---|
| 3Sources | CSPA [28] | |||
| HGPA [28] | ||||
| MCLA [28] | ||||
| ECPCS-MC [46] | ||||
| ECPCS-HC [46] | ||||
| MDEC-BG [45] | ||||
| MDEC-HC [45] | ||||
| MDEC-SC [45] | ||||
| KMC | ||||
| BBC-seg2 | CSPA | |||
| HGPA | ||||
| MCLA | ||||
| ECPCS-MC | ||||
| ECPCS-HC | ||||
| MDEC-BG | ||||
| MDEC-HC | ||||
| MDEC-SC | ||||
| KMC | ||||
| BBC-seg3 | CSPA | |||
| HGPA | ||||
| MCLA | ||||
| ECPCS-MC | ||||
| ECPCS-HC | ||||
| MDEC-BG | ||||
| MDEC-HC | ||||
| MDEC-SC | ||||
| KMC | ||||
| BBC-seg4 | CSPA | |||
| HGPA | ||||
| MCLA | ||||
| ECPCS-MC | ||||
| ECPCS-HC | ||||
| MDEC-BG | ||||
| MDEC-HC | ||||
| MDEC-SC | ||||
| KMC | ||||
| BBCSports-seg2 | CSPA | |||
| HGPA | ||||
| MCLA | ||||
| ECPCS-MC | ||||
| ECPCS-HC | ||||
| MDEC-BG | ||||
| MDEC-HC | ||||
| MDEC-SC | ||||
| KMC | ||||
| BBCSports-seg3 | CSPA | |||
| HGPA | ||||
| MCLA | ||||
| ECPCS-MC | ||||
| ECPCS-HC | ||||
| MDEC-BG | ||||
| MDEC-HC | ||||
| MDEC-SC | ||||
| KMC | ||||
| BBCSports-seg4 | CSPA | |||
| HGPA | ||||
| MCLA | ||||
| ECPCS-MC | ||||
| ECPCS-HC | ||||
| MDEC-BG | ||||
| MDEC-HC | ||||
| MDEC-SC | ||||
| KMC | ||||
| Handwritten | CSPA | |||
| HGPA | ||||
| MCLA | ||||
| ECPCS-MC | ||||
| ECPCS-HC | ||||
| MDEC-BG | ||||
| MDEC-HC | ||||
| MDEC-SC | ||||
| KMC | ||||
| Caltech | CSPA | |||
| HGPA | ||||
| MCLA | ||||
| ECPCS-MC | ||||
| ECPCS-HC | ||||
| MDEC-BG | ||||
| MDEC-HC | ||||
| MDEC-SC | ||||
| KMC |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zamora, J.; Sublime, J. An Ensemble and Multi-View Clustering Method Based on Kolmogorov Complexity. Entropy 2023, 25, 371. https://doi.org/10.3390/e25020371
Zamora J, Sublime J. An Ensemble and Multi-View Clustering Method Based on Kolmogorov Complexity. Entropy. 2023; 25(2):371. https://doi.org/10.3390/e25020371
Chicago/Turabian StyleZamora, Juan, and Jérémie Sublime. 2023. "An Ensemble and Multi-View Clustering Method Based on Kolmogorov Complexity" Entropy 25, no. 2: 371. https://doi.org/10.3390/e25020371






