Here we collect in several appendices the various computational lemmas we used in the proofs that follow and the proofs themselves.
Appendix A.3. Models without Exchange Symmetries
For the computations of this section we add to the energy an external field with a constant
, incorporate the factor of
, and take the positive version of the interaction energy (which merely multiplies
Z by a factor). For example
and
, respectively, for nearest neighbors and mean field. We write:
Here and below “
”, resp. “
”, is shorthand for the sum, resp. product, over all configurations
. We will also write
The starting point is to replace the spherical integral by a Gaussian integral, preserving the definition of the model by projecting
onto the sphere. Hence we can write:
We have introduced a factor of 1/2 before the energy to simplify some calculations below. The basic idea is to note that, although the integrand is singular at
, because the components of
are i.i.d.
, that value is improbable; indeed,
Therefore we define a simpler model by replacing the worrisome sum in the integrand by a constant:
which we will dub the “exactly solvable model” (ESM), as we are reduced to computing a Gaussian integral. We have:
so from the basic Gaussian integral in two dimensions we find:
Next we take two derivatives with respect to
, denoted with primes, divide by
and evaluate at
:
The first term is zero by the spin-flip symmetry (
changes sign but since
is quadratic in
S it does not). Then, observing the prefactors of
, the whole thing tends to zero as
even without a factor of
, so there is no phase transition in the ESM. Finally we must estimate the difference in magnetizations in the two models. We can rewrite
as:
where
By expanding the exponential we can write
Hence, expanding to first order in the small quantities
and
,
Let us treat the third term first. Noting that
Applying Cauchy–Schwarz we can bound the term by:
By standard CLT calculations, the first factor in curly brackets tends to zero, at rate
. Using (
A24) the second factor can be rewritten as
which is easily seen to be bounded (and in fact tends to one). In treating the second term we encounter instead the quantity
This term can also be shown to tend to zero. E.g., writing “
” for the Gaussian integral, factoring the difference of squares and making another Cauchy–Schwarz, we have to estimate:
which is O
. We also have to estimate
, which by the same tricks is seen to be bounded. Recalling that
the other term in (
A28) is even easier to treat. Since moments of Gaussians increase more slowly than a factorial, the sum of the other terms is dominated by a convergent series and of smaller order. QED.
Now consider adding wavefunction energy:
Let us switch to the Gaussian version, divide
by
and replace
by
. Treating the second term in the last line above, define
where “
” means summation over the spin configurations with
held at the fixed value indicated. Then we can write:
Note that, using
for expectation over the Gaussian distribution:
and
Noting the average of i.i.d. mean-zero random variables this last is O
. The last term in (
A32) is a sum of
N terms which are not independent but all of the order just computed. By a simple Jensen inequality, the sum is at most
N times this order. We conclude that the whole term is negligible. The first term is of the form of a mean-field model, still quadratic in
. Hence it can be added to the usual magnetic energy. The bound on
increases to
, but does not affect the argument. For the comparison with the actual model with WFE, we encounter the expression
which can be treated as before.
Thus the argument of the quadratic case goes through and yields that with WFE there is no magnetization at finite temperature.
Appendix A.4. SCW with Wavefunction Energy
We prove here that, assuming the hypotheses of Theorem Two, if
where
is a certain positive function specified in the proof below, then the conclusion of the theorem follows. We will apply the Concentration Lemma (
A3). We can assume by adding a term as usual to render
f positive:
We next define the quantities involved in the lemma. For the sets
U and
V we take, given two positive numbers
and
(
may depend on
N),
Further, define:
We next check the hypotheses of the Concentration Lemma. A quick calculation gives the equivalent description of set
V:
where
and we have defined
Since
, assuming
and
, the condition defining
V implies
. Since
, it follows from (
A40) that
on
. For the lower bound on
, we translate to a model with i.i.d. Gaussians, call them
, replacing:
and the definition of
V becomes:
(Since
has both a real and an imaginary part, we should double the lengths of these sums, but clearly this has no impact on the final result.) We have to find an exponential lower bound on
. Since
, we can get a lower bound by writing:
We will work on the first probability on the last line. (The second one is really the same since, multiplying the inequality through by −1, replacing
by
just reverses the order of its values.) According to Gärtner–Ellis [
38], we have to compute:
where
denotes expectation and
Note that
can take negative and positive values; hence,
must be restricted to ensure that the integral is finite. From the standard Gaussian integral we get:
which, provided the integrand is bounded, we recognize as the Reimann sum converging to:
where
By a change of variable this equals:
The LD approach requires us to compute:
and then the asympotic lower bound is
[
38]. By the definition of the domain where
in the Gärtner–Ellis theorem, the supremum over
in the definition of
can be limited to:
where
is negative but we do not need to know it, while by a simple computation:
(This is the max on the whole line.) We must have positive values of
somewhere in the interval [−1, 1], for otherwise
as
, so
for
. This requires
and that the lower root of
lies in the interval [0, 1] (since
and
). The root is easily computed to be:
Since
, this root is real; letting
the condition
becomes
Since we will eventually identify
with
, the above inequality is identical to (33). Since
, the infimum of the right side is 1/4.
The problem of computing is then well defined. We note that, if the point at which lies in the unit interval, then, as , the integral looks as if it might diverge. However, it remains finite, because logarithmic singularities are integrable. e.g., not . However, the derivative will go to infinity at the boundaries (Ellis calls such a function “steep” and it is an assumption of his theorem).
Assuming that
, it will suffice for Theorem Two to know that for some
:
We can define
to saturate the second inequality above (note that
), which also yields
. The conclusion of the theorem follows.
Can we compute
and
? In fact, the integral defining
is elementary and can be computed as follows. First, integrate by parts:
There are two cases, depending on whether the denominator in the integrand factorizes or not. For positive, it does not; hence, the denominator is an irreducible quadratic. For some negative it does factorize. We can proceed by elementary linear and trig substitutions, yielding either log(linear), log(quadratic), or arctan(quadratic) terms. Clearly, given such formulas with nonalgebraic functions, computing the supremum cannot be expected in closed form, so we would resort to the computer, but do not report detailed results here.
Appendix A.5. SCW without Wavefunction Energy
The idea is to determine whether
or not, where
and similarily with
replaced by
. We can rewrite the integrals as:
where
where as usual we have added a term so that
. To compare these integrals in numerator and denominator, we turn to the UIF, setting
in the numerator and
B equal to the whole sphere in the denominator. Thus, for the numerator we will have to estimate:
which, replacing wavefunctions on the sphere by i.i.d. Gaussians, equivalently:
(since
has two components, the sums are now over 2N + 1 rather than N + 1 indices, with the
repeated; however, as we are taking the limit as
we do not bother with factors of two everywhere) which is the same as writing (introducing factors of
for later purposes):
To motivate the appeal to the Gärtner–Ellis theorem, let
stand for the probability of the set appearing above and
for the probability with the second restriction dropped. We are interested in the ratio:
which has the interpretation of the conditional probability that the magnetization is greater than
, given a bound “
x” on the energy. We expect that
Then, integrating over
x (as in the UIF) we shall arrive at the result. Noting that the events considered have the form of averages of random variables whose means lie outside the indicated bounds, we expect large-deviation asymptotics for both, and so it is natural to consider
and to treat the two terms separately and then compare. We used
with
for the involved sets
S. But what a large deviation principle gives are upper and lower bounds. To have equality
we need
S to be
I-continuous, i.e.,
, see page 30 [
39]. This is the case.
To implement the Gärtner–Ellis procedure, we introduce the random vector with two components:
so we are interested in
To apply G-E we must compute:
where
where
b is a constant depending on the thetas.
We must first determine the region in the
plane in which
. Defining
this region, call it
D, is defined by:
We observe that
D is the domain where
is finite, related to the conditions for the validity of the Gärtner–Ellis theorem, not the domain of the logarithm argument. The geometry of this region is a bit complicated. These are the tests for whether a point lies in
D:
Test1: ;
Test2: ;
Test3: if , the critical point of , lies in [−1, 1], then test whether .
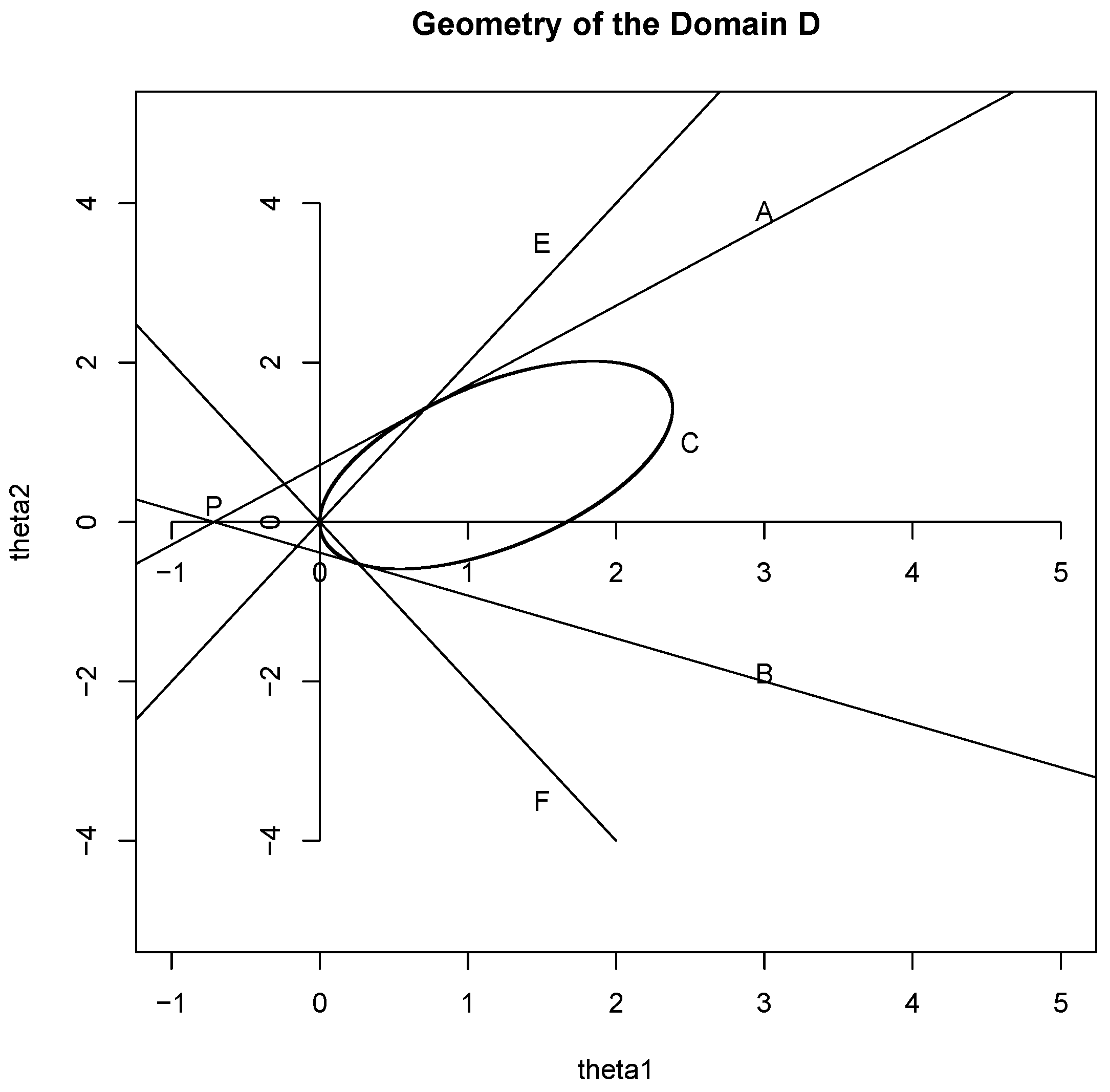
Now see
Figure A1. By tests one and two,
D lies between the lines A and B, and to the left of point P. Test three applies in between lines E and F; to the right of the axis, it is satisfied within the oblique ellipse, curve C; to the left of the axis,
h is negative. Hence we obtain a diamond-shaped compact region of the plane.
Figure A1.
Regions used in describing the domain D where is finite. These lines are obtained by the Tests above. Lines A and B are respectively from and from . To the left of P, Test 1 and 2 can not be satisfied simultaneously. Lines E and F are respectively from and from . The ellipse C is , obtained from of Test 3 to be applied for (for Test 3 is satisfied).
Figure A1.
Regions used in describing the domain D where is finite. These lines are obtained by the Tests above. Lines A and B are respectively from and from . To the left of P, Test 1 and 2 can not be satisfied simultaneously. Lines E and F are respectively from and from . The ellipse C is , obtained from of Test 3 to be applied for (for Test 3 is satisfied).
We note that
is convex (by examination of its Hessian matrix, omitted) and “steep”, meaning its derivatives approach infinity at the boundaries of
D. We have an ellipse as in
Figure A1 if
, otherwise a hyperbola. We restrict the study to the ellipse case, since it is the relevant one: we are primary interested in small
and, from the proof after (
A105), one can see that the small
x are the relevant ones for low temperatures. Therefore, given
, we always restrict to the
x small enough to satisfy
.
The G-E procedure is to compute the dual function:
from which you can compute the I-function as:
By the convexity and steepness of
c, the supremum in (
A63) is attained at a critical point for which
so looking forward to a possible computer search (for which we do not want to solve equations but rather evaluate formulas), we define
Let
G denote the constraint set in the
-plane:
We can express the I-function as
For the proof we have to compare the I-function for the two-variable, two-inequality problem with that of the one-variable, one-inequality problem, given by
where
L is the part of the horizontal axis that lies in
D. A first, critical question to ask is whether necessarily
because the set over which we compute the infimum for
contains the set for which we compute the infimum for
. However, this is not the case. We have:
where
by the restriction that
. The first integral can be done easily by elementary calculus:
Now note that, at
, this integral is zero, and so is the first term in (
A70), while the second term there is negative. Hence
is disjoint from
L.
We need a formula for the first partial of
c:
By long division we can write:
where
Hence:
where we have plugged in (
A71) for one integral.
Note that we have reduced computing these derivatives to computing one integral, of
over the interval
. There are two cases, depending on whether
is irreducible or factorizes. The discriminant is:
If disc.
,
q factorizes as
where the two roots are outside the interval
. The integrals can then be performed by partial fractions, yielding logarithmic terms:
If disc.
, in our case
q can be written:
with
and
, and one makes a trig substitution:
The result contains inverse trig functions:
To check these calculus formulas (and our computer implementation of them) we computed the integral directly (numerically) using the trapezoid rule and compared. We also need a formula for
c, which we can obtain by integrating by parts:
Here
and applying long division again:
with
Combining with previous results yields:
For the function
k we can compute from its definition, but also some simplifications accrue:
For the theorem we have to evaluate the asymptotics of the ratio:
where
B is the set appearing in (
A53) and
We next list some properties of the I-functions that will imply the theorem’s conclusion:
Assumptions on
and
The rate functionals are defined as
Since they are computed from independent Gaussian variables, even if not identically distributed [
40], the corrections to the large deviations are
:
Therefore the approximation
is very good for large
N. If
then it has to be
. The study of their large deviation corrections should prove it.
For (a) we know from the inequality
(for fixed
N) and the Gärtner–Ellis Theorem
, and we showed that these functions result from infimums of the same function over different sets; therefore, it is implausible that they are exactly equal for all
x smaller than a given
x*. (Because of the property (b) and
, if there exists a
such that
, then they have to coincide for all
x smaller than
. We supply some evidence that it is not so, from numerical approximations, see the Computational
Appendix A.6 and
Figure A3.) From the approximation
and
for
one expects strict decreasing monotonicity. This is indeed what we observed from the computer computations. Differentiability and strict decreasing monotonicity can be deduced from the Envelope Theorem in [
41] at pag. 605 applied to (
A63) and (
A64).
is strictly convex and also the Lagrangian
to optimize if the optimizer is on the boundaries. Applying the Envelope Theorem, on the right hand side of (
A93) the derivative coincides with that of
f because the constraint functions do not have dependence on
x. From
, calling
the solution of (
A63) and
the one of (
A64), we have
The smoothness of
and
comes from the implicit function theorem. The right hand side gives
, since
we have that it is negative if and only if
. We know that
is decreasing by definition so it can be only
or
, for
this second case gives
, which it can be only for
by definition; therefore,
when
is not trivial. For
the value
stays in disjoint set from the axis
; therefore, it can be only
since
is decreasing by definition. Second order differentiability needs to develop second order Envelope Theorems; of course it will not be
. Differentiability of the rate functionals can also be deduced from differentiability of the probability functions
; in our case one can apply corollary 4.1 of [
42] and corollary 32 of [
43] because of the quadratic structure of the
’s and other conditions that are verified. These results should be extended to second order differentiability without problem [
44]. We cannot deduce analytically the convexity property (varying
x we are restricting in a continuous way the integration on a regular set of a Gaussian integral) and we observe this property from the numerical computations of the exact formulas of the rate functionals, see
Appendix A.6, within the limits of our computer analysis, that is below
. Here we cannot obtain good numerical estimates since the sampling region shrinks to an infinitesimal volume and we have a vertical asymptote, as proved later for (c). In this vertical asymptote part convexity is natural. Anyway, from the proof after (
A105), if there is some flex from some unexpected reason, the computations can be applied for smaller
x (i.e., lower temperature) where the functionals are convex. From (
A53) we have (d) since the first event for
is the sure event, while the second never contains the average for any
(see also the Computational
Appendix A.6 for a numerical computation).
Furthermore, (e) follows from a computation in a previous section, see (
A14), and the remark that LD results from probabilities of sets that do not contain the mean; otherwise, by the Central Limit Theorem such probabilities go to one.
That leaves (c). It would follow immediately from the observation that
(since
) if we can assume that two limits can be interchanged. As that is not obvious, we supply a proof using previously obtained formulas. Since certainly
it suffices to prove (c) for the latter. Therefore, we set
in the following. From (
A75) we note that
Let us define for a given
x:
We note
, since
there, and
so, if
,
Furthermore:
since by definition of the domain D,
for all
y in [−1, 1]. Hence,
H is convex.
Now consider the left-most point of the domain D on the horizontal axis, labeled “P” in
Figure A1, which has
coordinate
. By definition, as
,
for some
(here, at the endpoints
), so
. Thus
must have a second zero on the line, to the right of
P; let us label it
Q.
The constraint set is
, so from (
A94) we conclude that it lies entirely to the left of
Q (and of course to the right of
P).
Some computer work indicates that
Q is very close to
P for small
x, which explains why we could not locate the constraint set by sampling for
. Hence, suppose that
with
bounded above (or even, as we shall see, tends to zero) as
. From (
A87) we have
Note that, substituting
for
,
Therefore, in the constraint set with the above assumption
, so the second term in
k goes to infinity as
. Hence, since the first term is nonnegative by the constraint,
as
, which yields (c).
In order to prove that
we apply the exact formula for the integral appearing in
, which, with
, lies in the factorizable case, see (
A77). Letting
we find
Next, let
, so that
corresponds to
; i.e.,
. Rewriting the equation for the root
gives:
so exponentiating both sides:
Note that, if
x is small, the right-hand side of (
A104) is very small at
and remains so up to small values of
t, while the left-hand side follows
t. For instance, if
, up to
the RHS is no more than about
which is infinitesimal while the LHS reaches
. Thus, as
, the solution of (
A104) goes to zero, and hence
(in fact exponentially fast), which implies (c).
Granted these assumptions, we now proceed to the proof of Theorem Two. Property (e) implies that we can replace the denominator in (
A88) as follows:
Next, consider whether the
g-functions have critical points in the intervals (0, 1) or (0, 2/3). Using a hat to denote those points, we are asking whether solutions exist for:
First, suppose both exist. If so, since
g is convex, the Laplace approximation applies yielding:
where a hat means evaluate at the critical point.
We are now prepared to argue that the limit of the ratio in (
A105) is always zero. There are four cases, defined by whether the “winner” (largest term asymptotically) in numerator and denominator is the first or second term:
- Case:
numerator, second term; denominator, second term. As the ’s are minimums, and the ratio tends to zero.
- Case:
numerator, first term; denominator, second term. Then
and we are looking essentially at the limit of
which clearly goes to zero.
- Case:
numerator, second term; denominator, first term. Now we are looking at
which goes to zero if
. The reverse is impossible, as the ratio would tend to infinity while we know it is bounded by one from the original definition.
- Case:
numerator, first term; denominator, first term. The ratio tends to zero.
Since we are interested in low temperatures (that is small
x) the presented cases are the relevant ones. However, we can still ask: do these critical points exist? With our assumptions we know that
If in addition we knew that
we can conclude the c.p.’s exist. If not, for sufficiently small
a c.p. might not exist. For instance, let us postulate that
or
. Then in either case
for all
x in the relevant interval. In this case
g is monotonic and we can make a change of variable:
to obtain
Therefore, for the numerator the integral is:
(where we have used assumption (c) to drop a term) and so, if
, the first term in the numerator wins. In the denominator, the order is at most
, so the numerator tends to zero faster whatever term predominates in the denominator.