Energy Stability Property of the CPR Method Based on Subcell Second-Order CNNW Limiting in Solving Conservation Laws
Abstract
1. Introduction
2. Governing Equations and Discretization Methods
2.1. Governing Equations
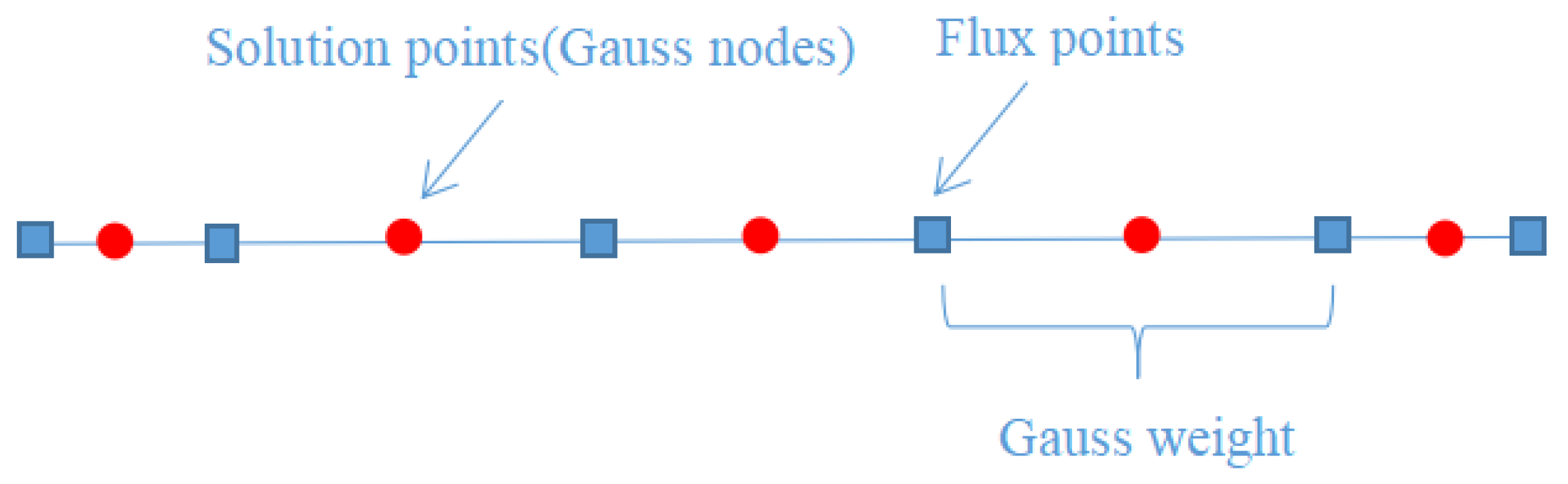
2.2. CPR Method with Staggered Flux Points
3. CPR Method with Subcell CNNW2 Limiting
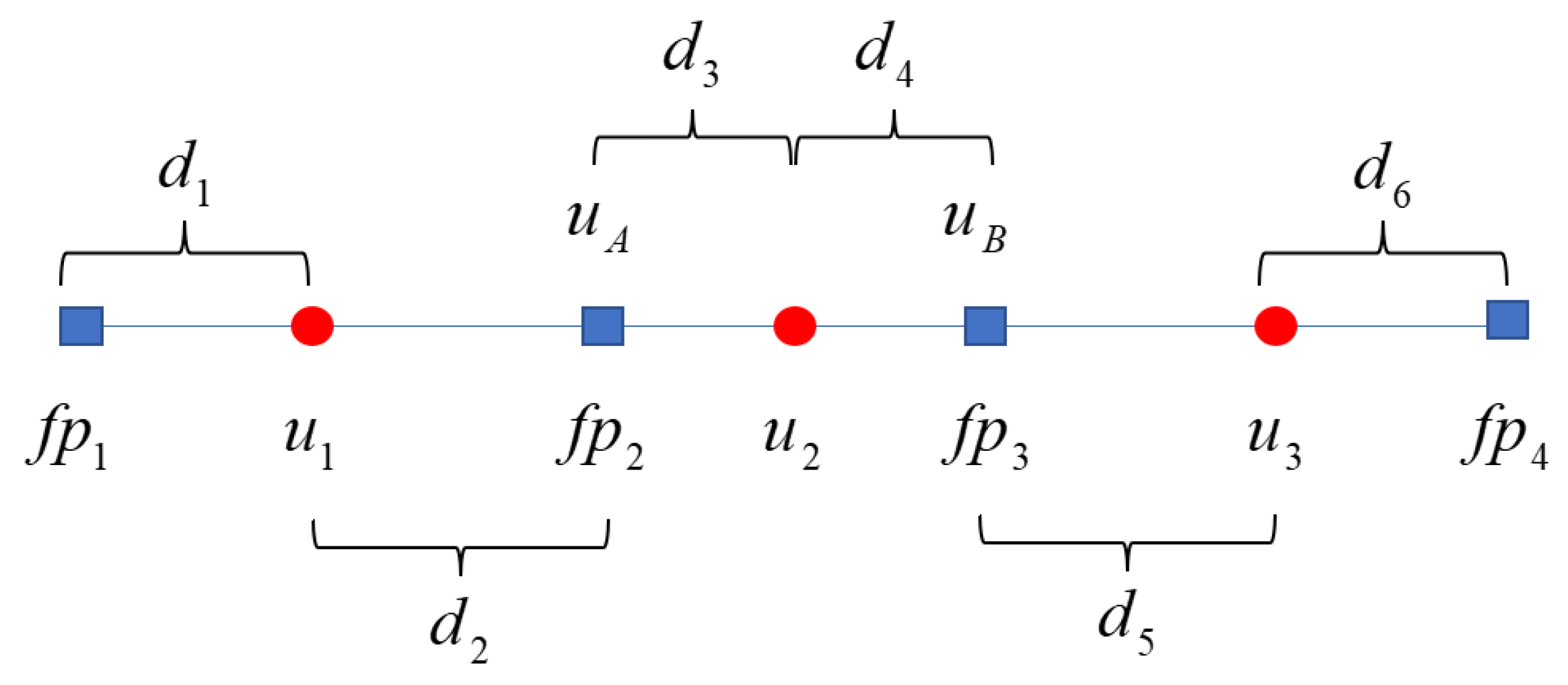
3.1. CNNW2 Scheme
3.2. Proof of the Linear Energy Stability of the CNNW2 Scheme
4. Numerical Experiments
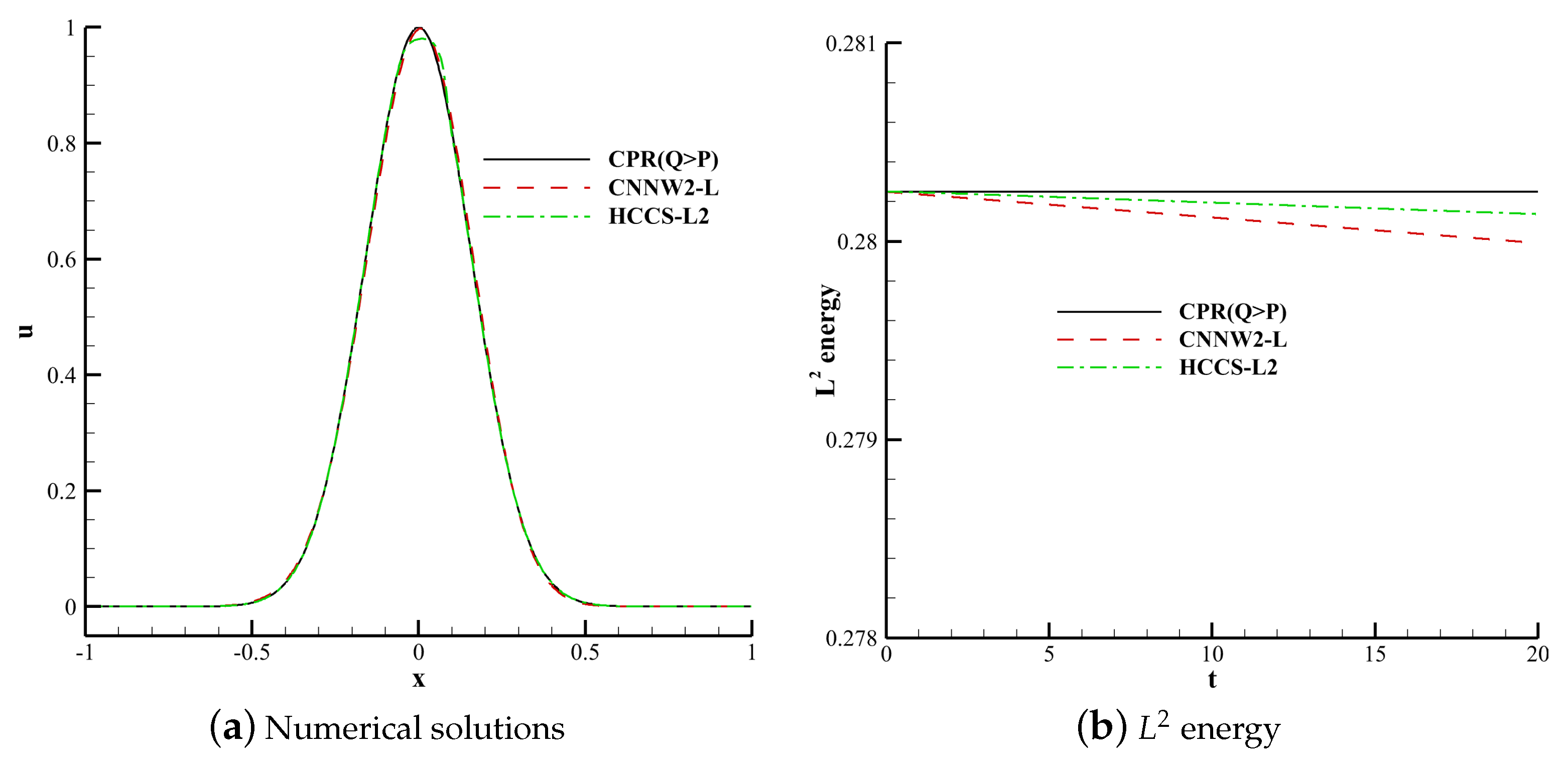
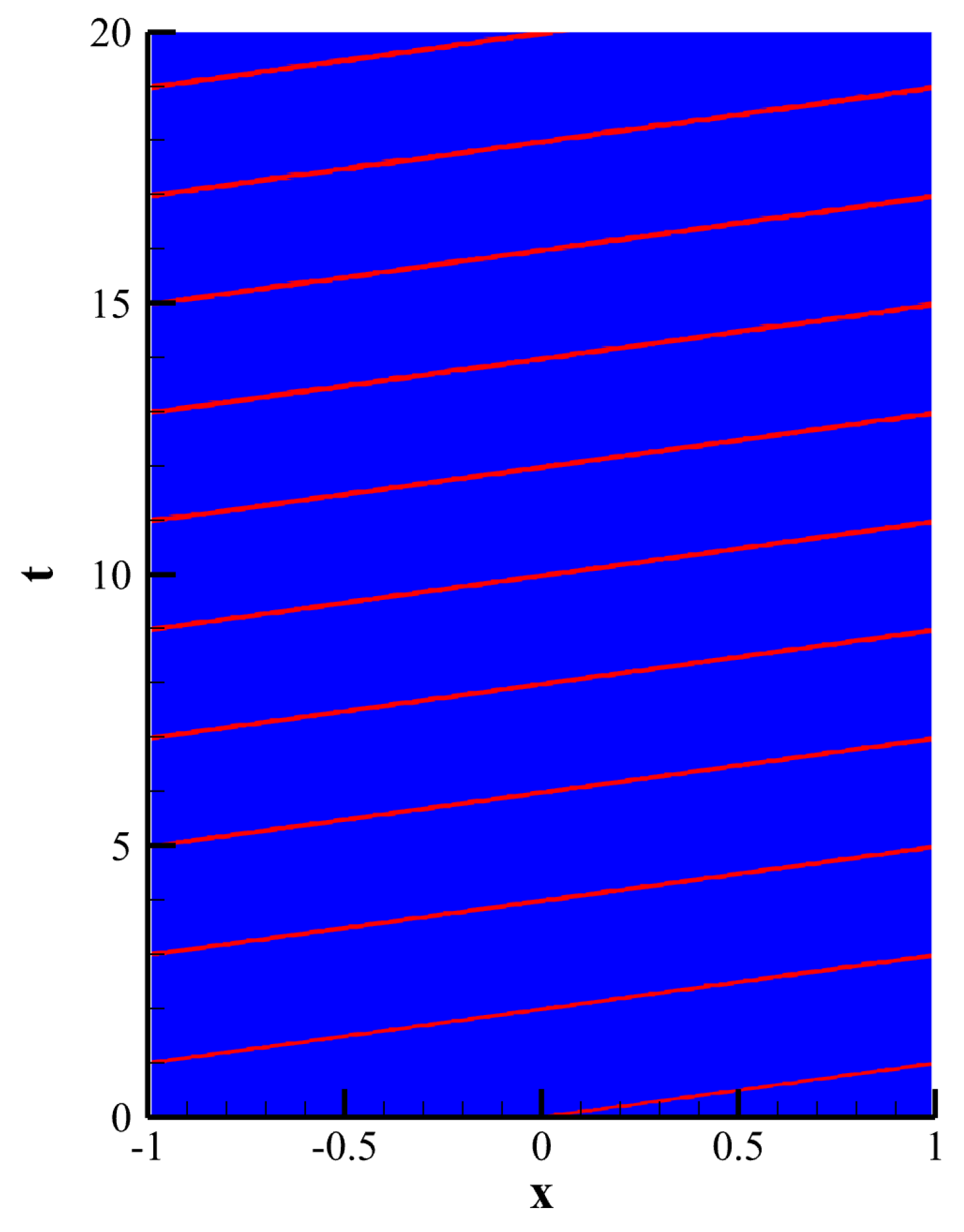
4.1. Linear Energy Stability Test
4.1.1. 1D Linear Convection Equation
4.1.2. 2D Linear Convection Equation
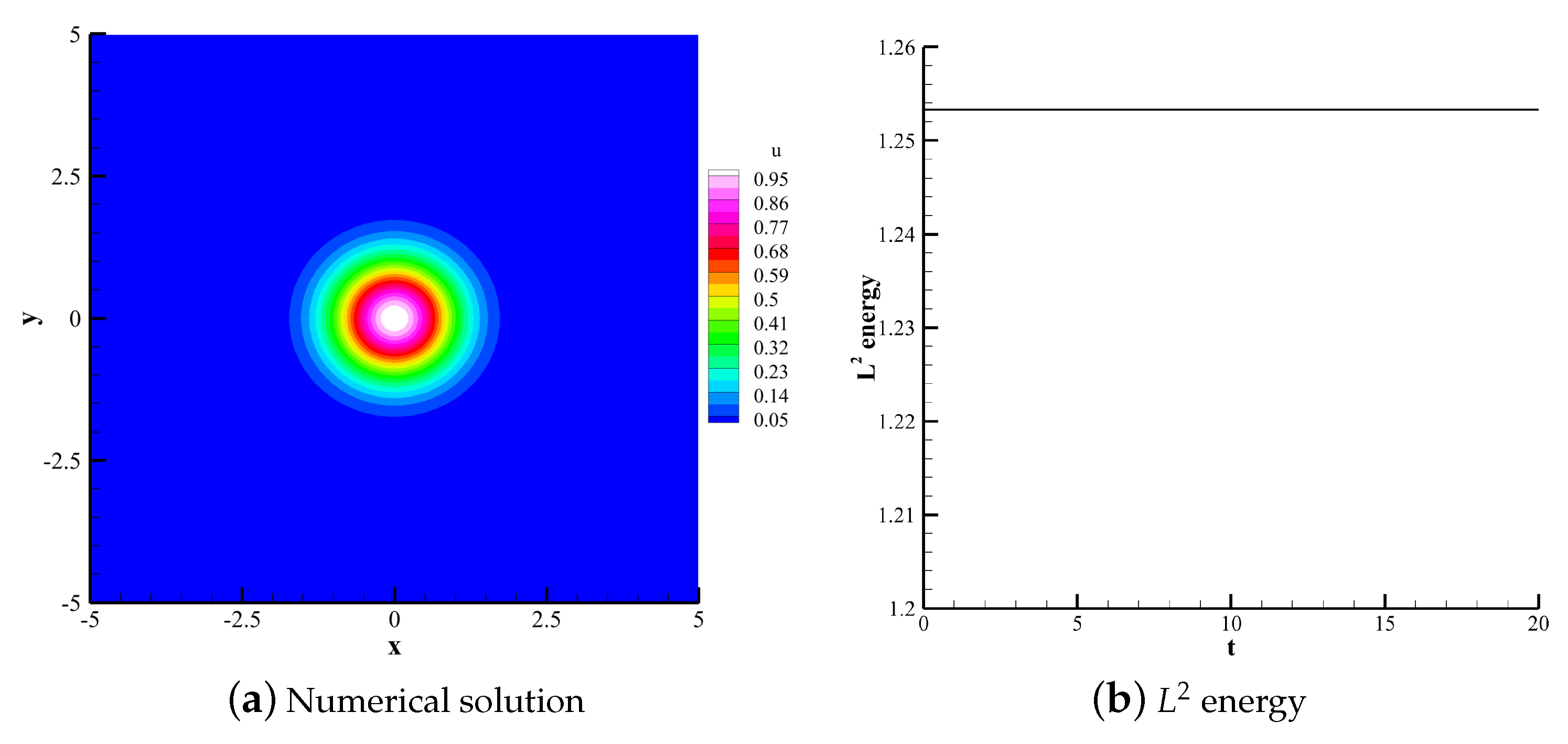
4.2. Nonlinear Stability Test
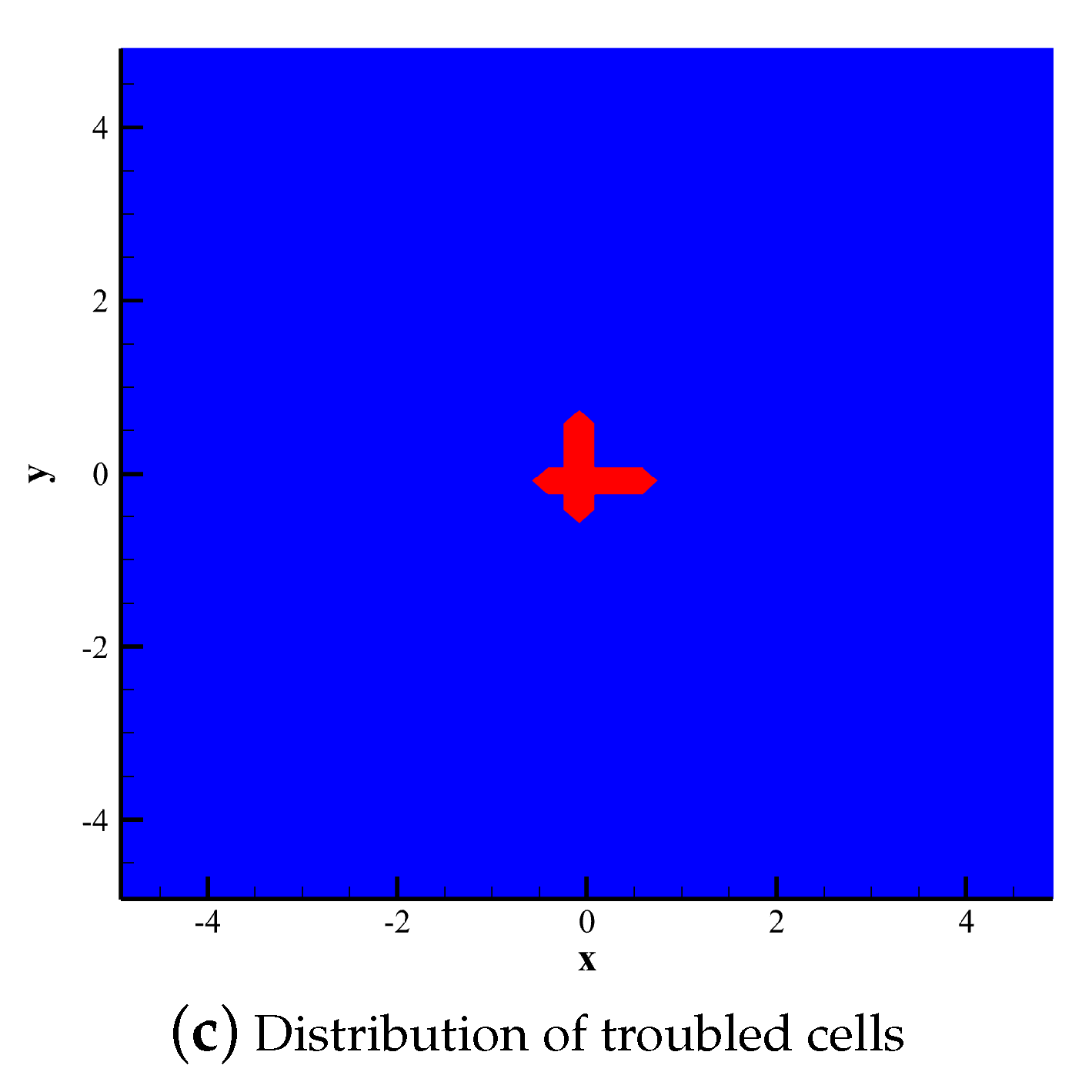
4.2.1. Isentropic Vortex Test
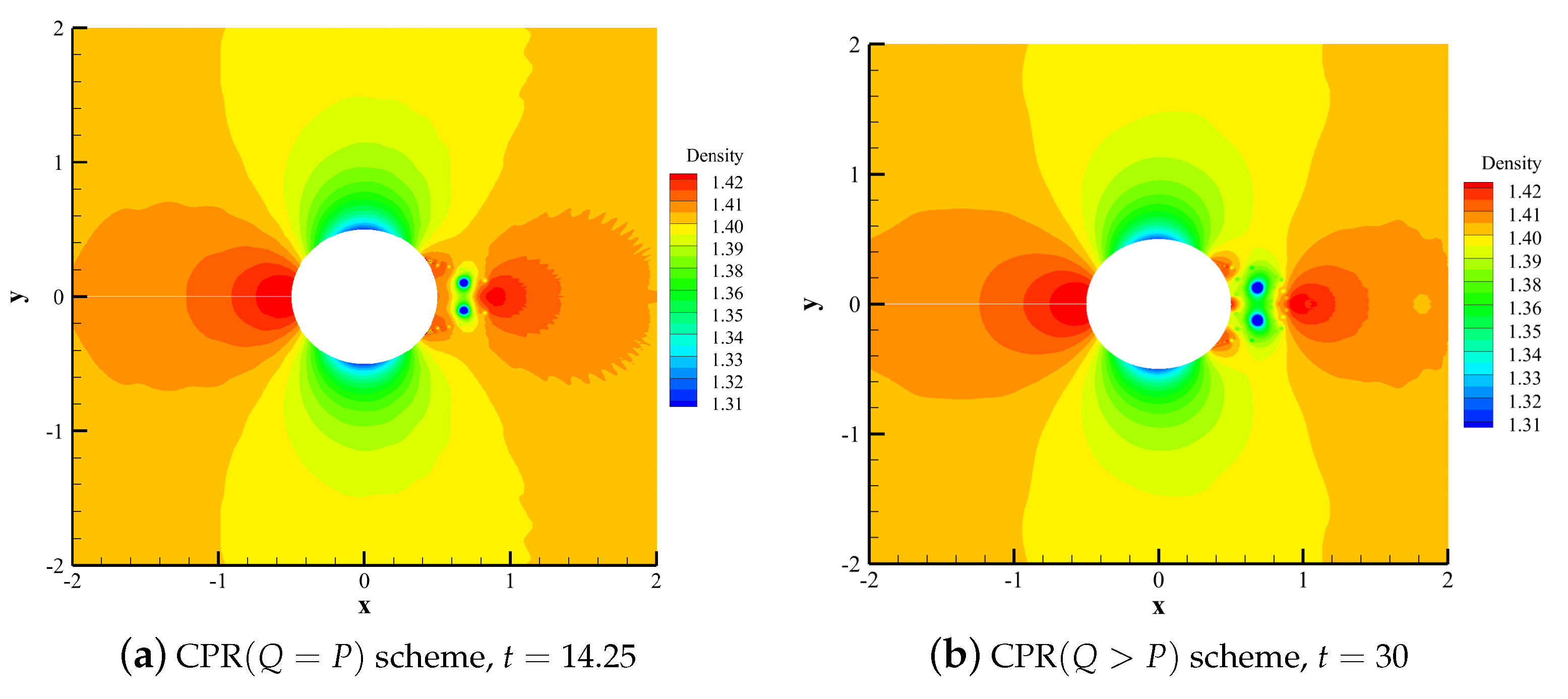
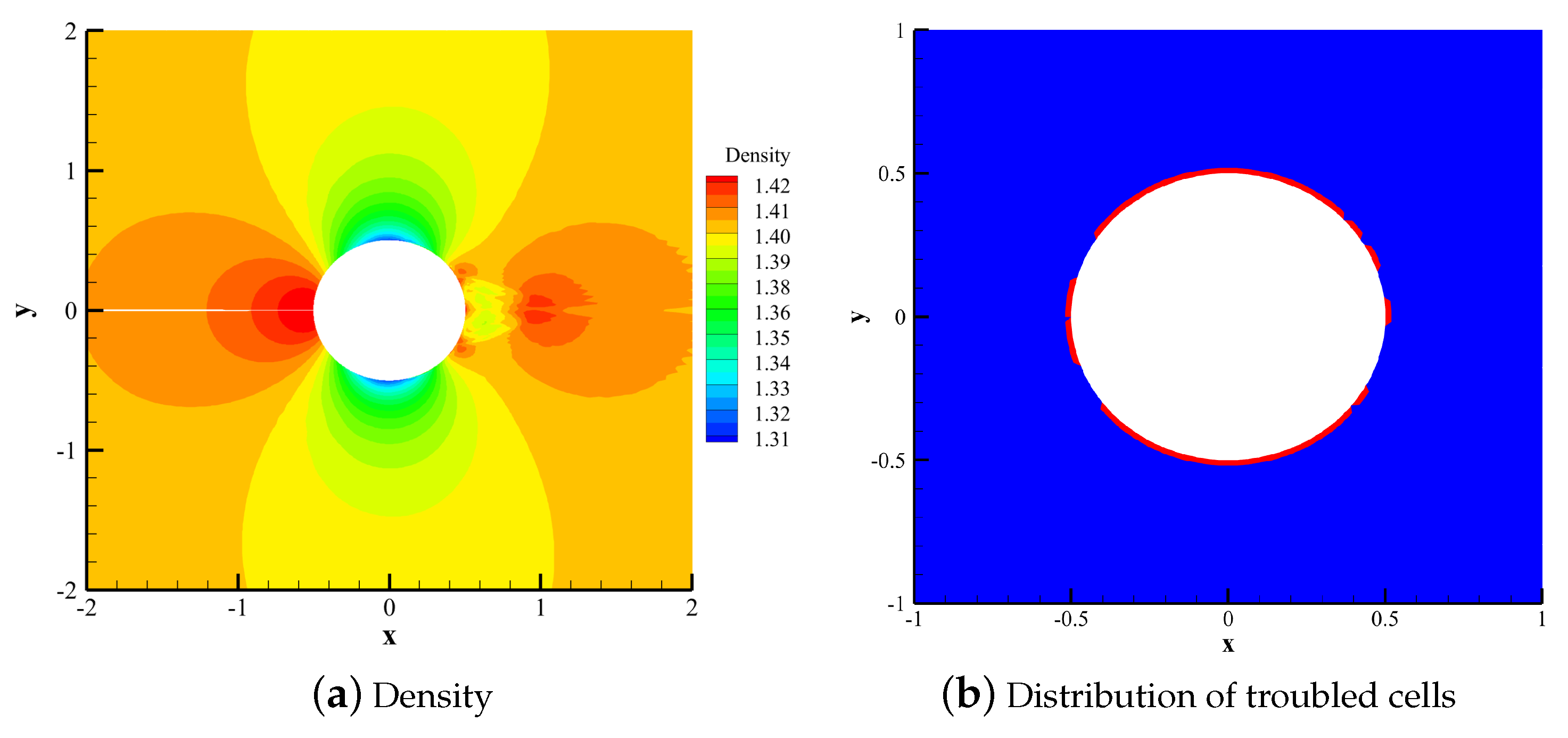
4.2.2. Subsonic Flow over a Cylinder
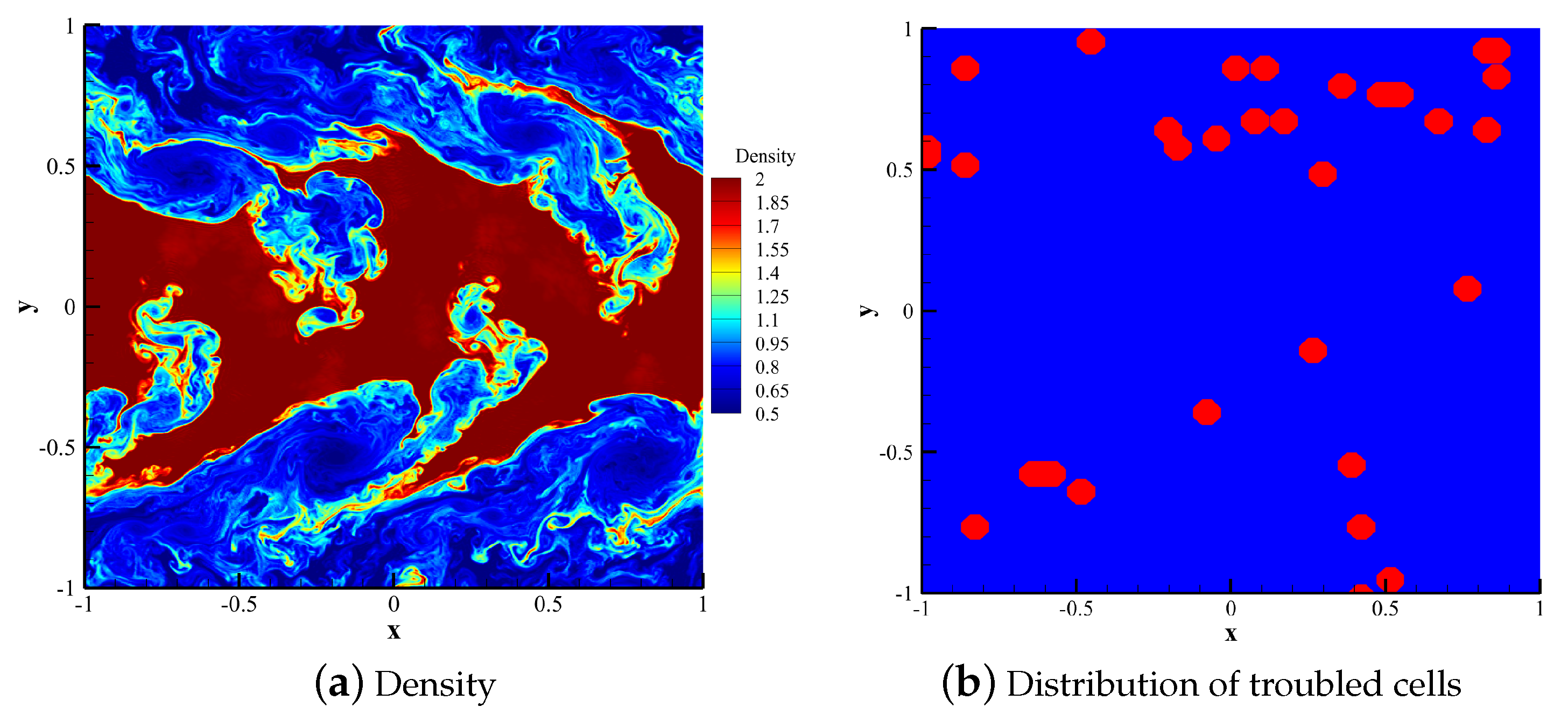
4.2.3. 2D Kelvin-Helmholtz Instability Problem
4.2.4. 2D Transonic Flow around the NACA0012 Airfoil
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Castonguay, P.; Vincent, P.E.; Jameson, A. A new class of high-order energy stable flux reconstruction schemes for triangular elements. J. Sci. Comput. 2012, 51, 224–256. [Google Scholar] [CrossRef]
- Huynh, H.T. A Flux Reconstruction Approach to High-Order Schemes Including Discontinuous Galerkin Methods. In Proceedings of the 18th AIAA Computational Fluid Dynamics Conference, Miami, FL, USA, 25–28 June 2007. [Google Scholar]
- Cockburn, B.; Karniadakis, G.E.; Shu, C.W. The Development of Discontinuous Galerkin Methods; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Cockburn, B.; Shu, C.W. TVB Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws. II. General framework. Math. Comput. 1989, 52, 411–435. [Google Scholar]
- Johnson, C.; Pitkranta, J. An analysis of the discontinuous Galerkin method for a scalar hyperbolic equation. Math. Comput. 1986, 46, 1–26. [Google Scholar] [CrossRef]
- Cockburn, B.; Shu, C.W. The Runge-Kutta local projection-discontinuous-Galerkin finite element method for scalar conservation laws. ESAIM Math. Model. Numer. Anal. 1991, 25, 337–361. [Google Scholar] [CrossRef]
- Liu, Y.; Vinokur, M.; Wang, Z.J. Discontinuous spectral difference method for conservation laws on unstructured grids. In Computational Fluid Dynamics 2004, Proceedings of the Third International Conference on Computational Fluid Dynamics, ICCFD3, Toronto, ON, Canada, 12–16 July 2004; Springer: Berlin/Heidelberg, Germany, 2006; pp. 449–454. [Google Scholar]
- Nakatsu, T.; Ichiyama, S.; Hiratake, J.; Saldanha, A.; Kobashi, N.; Sakata, K.; Kato, H. Structural basis for the spectral difference in luciferase bioluminescence. Nature 2006, 440, 372–376. [Google Scholar] [CrossRef] [PubMed]
- Kopriva, D.A. A Conservative Staggered-Grid Chebyshev Multidomain Method for Compressible Flows. II. A Semi-Structured Method. J. Comput. Phys. 1996, 128, 475–488. [Google Scholar] [CrossRef]
- Kopriva, D.A.; Kolias, J.H. A Conservative Staggered-Grid Chebyshev Multidomain Method for Compressible Flows. J. Comput. Phys. 1996, 125, 244–261. [Google Scholar] [CrossRef]
- Wang, Z.J.; Gao, H. A unifying lifting collocation penalty formulation including the discontinuous Galerkin, spectral volume/difference methods for conservation laws on mixed grids. J. Comput. Phys. 2009, 228, 8161–8186. [Google Scholar] [CrossRef]
- Wang, Z.J.; Gao, H. A unifying lifting collocation penalty formulation for the Euler equations on mixed grids. In Proceedings of the 47th AIAA Aerospace Sciences Meeting Including The New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 5–8 January 2009; p. 401. [Google Scholar]
- Vincent, P.E.; Castonguay, P.; Jameson, A. A New Class of High-Order Energy Stable Flux Reconstruction Schemes. J. Sci. Comput. 2011, 47, 50–72. [Google Scholar] [CrossRef]
- Jameson, A.; Vincent, P.E.; Castonguay, P. On the Non-linear Stability of Flux Reconstruction Schemes. J. Sci. Comput. 2012, 50, 434–445. [Google Scholar] [CrossRef]
- Sheshadri, A.; Jameson, A. On the stability of the flux reconstruction schemes on quadrilateral elements for the linear advection equation. J. Sci. Comput. 2016, 67, 769–790. [Google Scholar] [CrossRef]
- Spiegel, S.C.; Huynh, H.; Debonis, J.R. De-Aliasing through Over-Integration Applied to the Flux Reconstruction and Discontinuous Galerkin Methods. In Proceedings of the 22nd AIAA Computational Fluid Dynamics Conference, Dallas, TX, USA, 22–26 June 2015. [Google Scholar]
- Sonntag, M.; Munz, C.D. Shock capturing for discontinuous Galerkin methods using finite volume subcells. In Proceedings of the Finite Volumes for Complex Applications VII-Elliptic, Parabolic and Hyperbolic Problems: FVCA 7, Berlin, Germany, 15–20 June 2014; Springer International Publishing: Berlin/Heidelberg, Germany, 2014; pp. 945–953. [Google Scholar]
- Dumbser, M.; Zanotti, O.; Loubère, R.; Diot, S. A posteriori subcell limiting of the discontinuous Galerkin finite element method for hyperbolic conservation laws. J. Comput. Phys. 2014, 278, 47–75. [Google Scholar] [CrossRef]
- Dumbser, M.; Loubère, R. A simple robust and accurate a posteriori sub-cell finite volume limiter for the discontinuous Galerkin method on unstructured meshes. J. Comput. Phys. 2016, 319, 163–199. [Google Scholar] [CrossRef]
- Kochi, S.R.S.P.; Ramakrishna, M. A compact subcell WENO limiting strategy using immediate neighbours for Runge-Kutta discontinuous Galerkin methods. Int. J. Comput. Math. 2021, 98, 608–626. [Google Scholar] [CrossRef]
- Zhu, H.; Liu, H.; Yan, Z.-G.; Shi, G.; Deng, X. A priori subcell limiting based on compact nonuniform nonlinear weighted schemes of high-order CPR method for hyperbolic conservation laws. Comput. Fluids 2022, 241, 105456. [Google Scholar] [CrossRef]
- Shi, G.Q.; Yan, Z.G.; Zhu, H.J. Troubled cell detection in subcell limiting for high-order CPR method on unstructured meshes. Acta Aerodyn. Sin. 2023, 41, 38–52. [Google Scholar]
- Liu, R.; Zhu, H.J.; Jia, F.R. An energy stable flux reconstruction method based on over-integration. Math. Numer. Sin. 2023, in press. [Google Scholar]
- Yamaleev, N.K.; Carpenter, M.H. Third-order Energy Stable WENO scheme. J. Comput. Phys. 2009, 228, 3025–3047. [Google Scholar] [CrossRef]
- Cockburn, B.; Shu, C.W. The Runge–Kutta discontinuous Galerkin method for conservation laws V: Multidimensional systems. J. Comput. Phys. 1998, 141, 199–224. [Google Scholar] [CrossRef]
- Shi, G.Q.; Zhu, H.; Yan, Z.G. A priori subcell limiting approach for the FR/CPR method on unstructured meshes. arXiv 2021, arXiv:2108.03446. [Google Scholar] [CrossRef]
- Sheshadri, A.; Jameson, A. An analysis of stability of the flux reconstruction formulation on quadrilateral elements for the linear advection–diffusion equation. J. Sci. Comput. 2018, 74, 1757–1785. [Google Scholar] [CrossRef]
- Cox, C.; Trojak, W.; Dzanic, T.; Witherden, F.D.; Jameson, A. Accuracy, stability, and performance comparison between the spectral difference and flux reconstruction schemes. Comput. Fluids 2021, 221, 104922. [Google Scholar] [CrossRef]
- Rueda-Ramírez, A.M.; Gassner, G.J. A subcell finite volume positivity-preserving limiter for DGSEM discretizations of the Euler equations. arXiv 2021, arXiv:2102.06017. [Google Scholar]
- Park, J.S.; Yoon, S.H.; Kim, C. Multi-dimensional limiting process for hyperbolic conservation laws on unstructured grids. J. Comput. Phys. 2010, 229, 788–812. [Google Scholar] [CrossRef]
- Gottlieb, S.; Shu, C.W.; Tadmor, E. Strong stability-preserving high-order time discretization methods. SIAM Rev. 2001, 43, 89–112. [Google Scholar] [CrossRef]







| Error | Mesh | CPR (Q > P) | HCCS−L2 | HCCS−N2 |
|---|---|---|---|---|
| error | 20 × 20 | 1.01 × 10 | 4.87 × 10 | 6.73 × 10 |
| 40 × 40 | 7.07 × 10 | 1.21 × 10 | 1.54 × 10 | |
| 80 × 80 | 4.05 × 10 | 1.80 × 10 | 2.50 × 10 | |
| error | 20 × 20 | 6.52 × 10 | 5.71 × 10 | 9.07 × 10 |
| 40 × 40 | 7.55 × 10 | 2.10 × 10 | 3.67 × 10 | |
| 80 × 80 | 4.21 × 10 | 6.32 × 10 | 1.44 × 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, R.; Yan, Z.-G.; Zhu, H.; Jia, F.; Feng, X. Energy Stability Property of the CPR Method Based on Subcell Second-Order CNNW Limiting in Solving Conservation Laws. Entropy 2023, 25, 729. https://doi.org/10.3390/e25050729
Liu R, Yan Z-G, Zhu H, Jia F, Feng X. Energy Stability Property of the CPR Method Based on Subcell Second-Order CNNW Limiting in Solving Conservation Laws. Entropy. 2023; 25(5):729. https://doi.org/10.3390/e25050729
Chicago/Turabian StyleLiu, Ran, Zhen-Guo Yan, Huajun Zhu, Feiran Jia, and Xinlong Feng. 2023. "Energy Stability Property of the CPR Method Based on Subcell Second-Order CNNW Limiting in Solving Conservation Laws" Entropy 25, no. 5: 729. https://doi.org/10.3390/e25050729
APA StyleLiu, R., Yan, Z.-G., Zhu, H., Jia, F., & Feng, X. (2023). Energy Stability Property of the CPR Method Based on Subcell Second-Order CNNW Limiting in Solving Conservation Laws. Entropy, 25(5), 729. https://doi.org/10.3390/e25050729





