Effects of Stochastic Noises on Limit-Cycle Oscillations and Power Losses in Fusion Plasmas and Information Geometry
Abstract
:1. Introduction
- How are ELMs affected by stochastic particle and magnetic perturbation?
- Which noise is more effective in reducing the maximum power loss due to ELMs?
- How far from equilibrium is the system driven due to ELMs in the presence of the stochastic noises?
- How are power loss and energy loss due to ELMs affected by the stochastic noises and input power?
- How are power loss and energy loss due to ELMs captured by different statistical measures?
- What are robust diagnostics to identify explosive versus regular small ELMs?
2. Model
- The temperature is constant so that (particle sources) plays a role as the control parameter of the energy flux (input power);
- The input power is much greater than the critical power-threshold so that the electric field is mainly driven by the pressure gradient (diamagnetic velocity);
- There is no ELMy free H-mode gap;
- Time is nondimensionalised by , where is the ion sound speed, , is the ion cyclotron frequency, and k and are the poloidal wave number and radial correlation length of the turbulence (see [12]).
The Fokker–Planck Equation PDF
3. Information Geometry, Entropy Production, and Power Loss
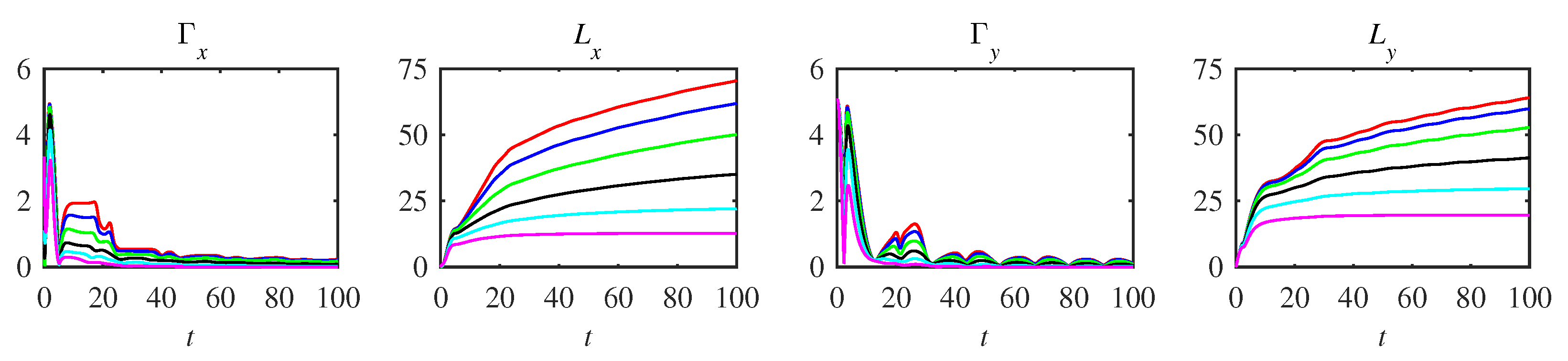
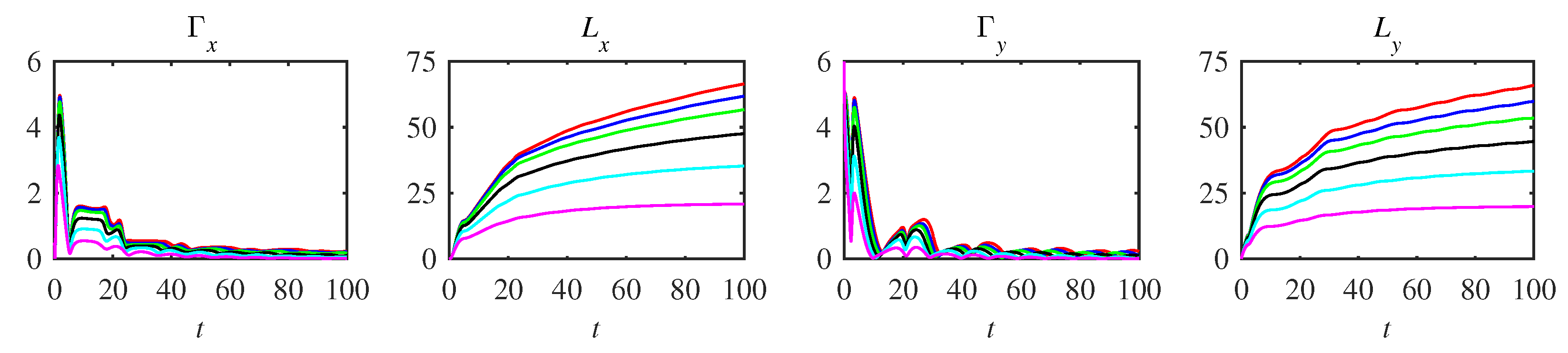
3.1. Information Rate, Length
3.2. Entropy, Entropy Production, and Entropy Flow
3.3. Power Loss
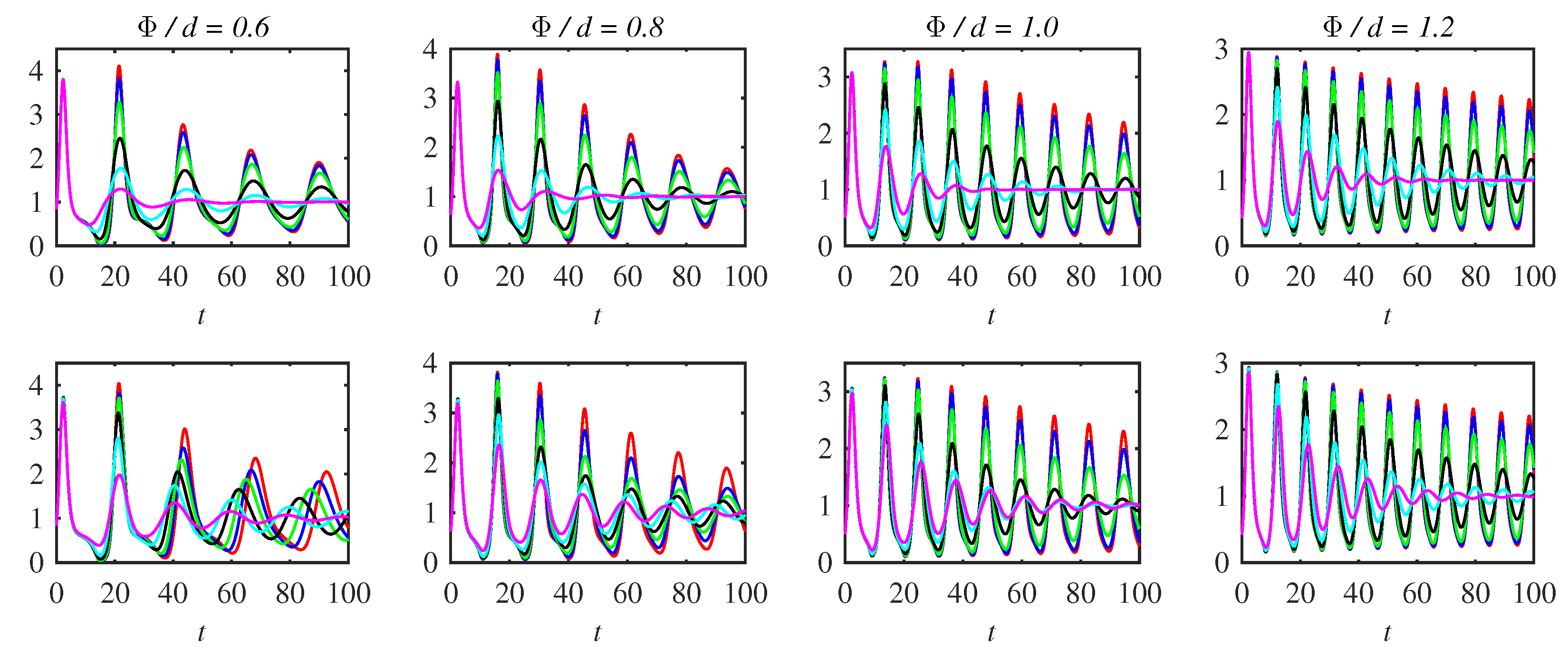
4. Numerical Experiments
5. Results
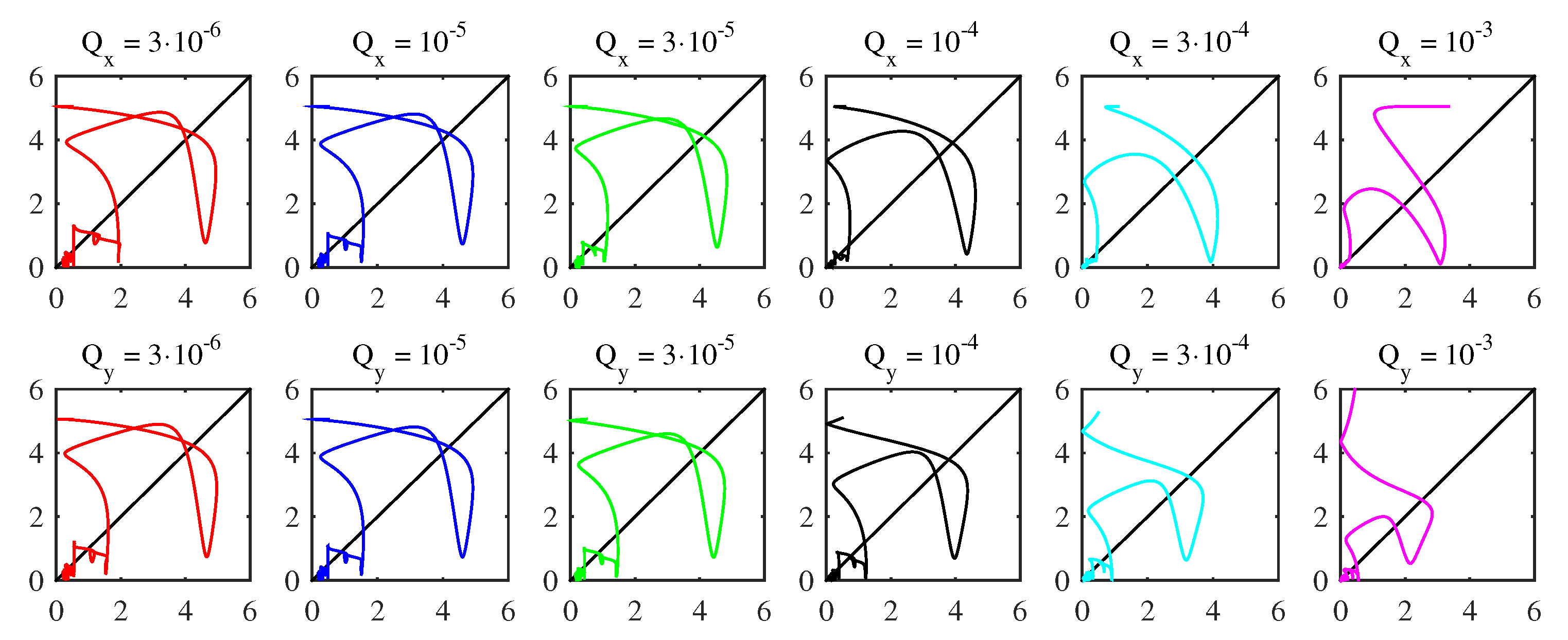
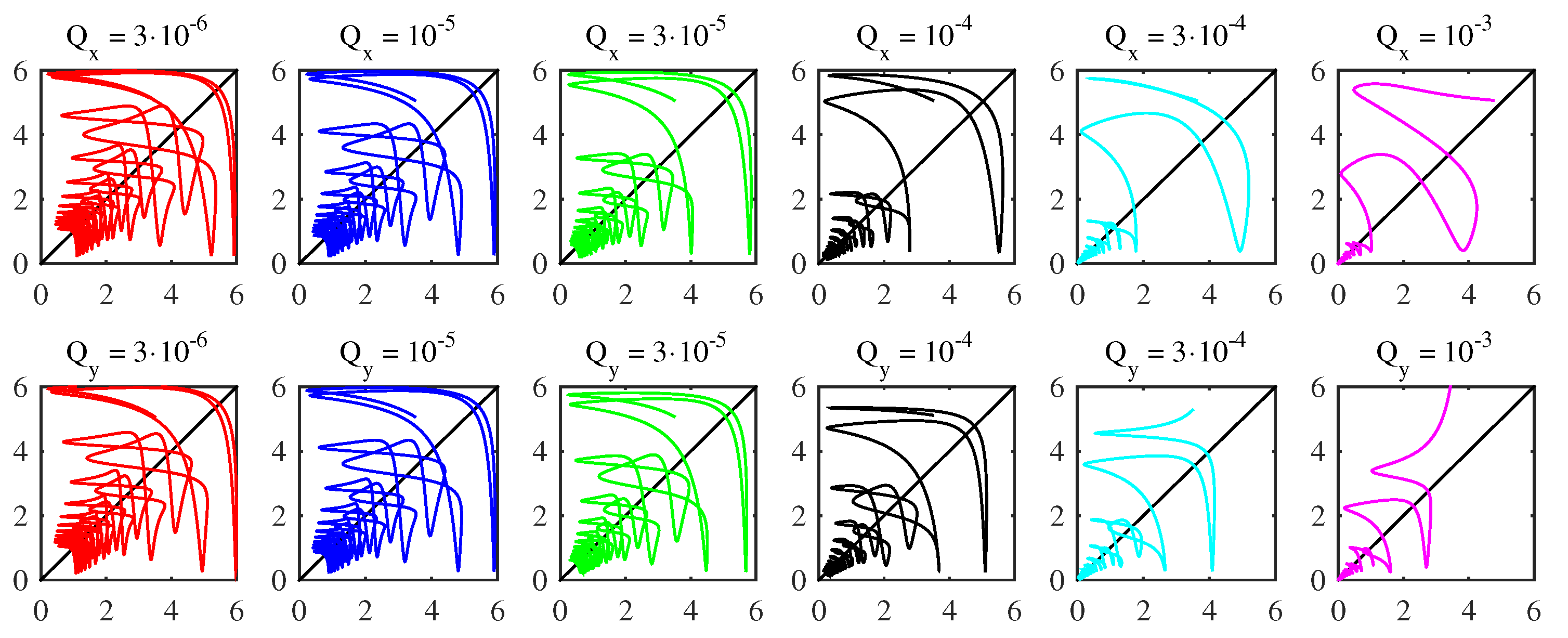
5.1. ODE Solution
5.2. Mean and Standard Deviation
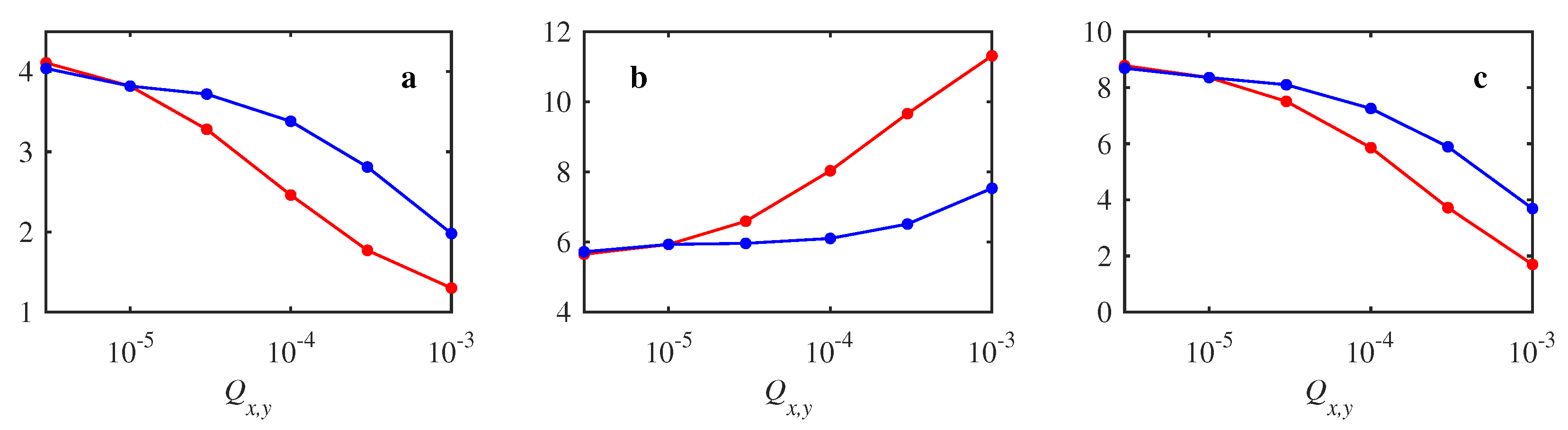
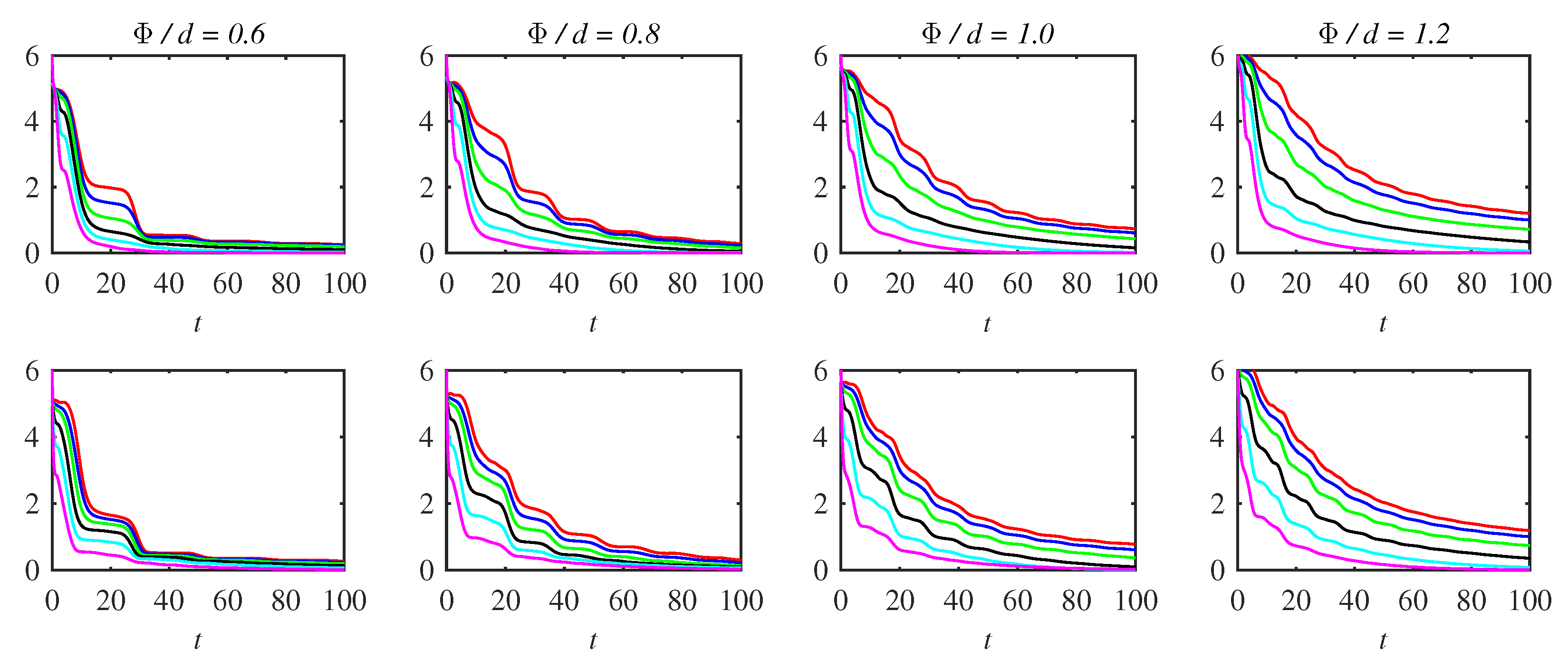
5.3. Power Loss
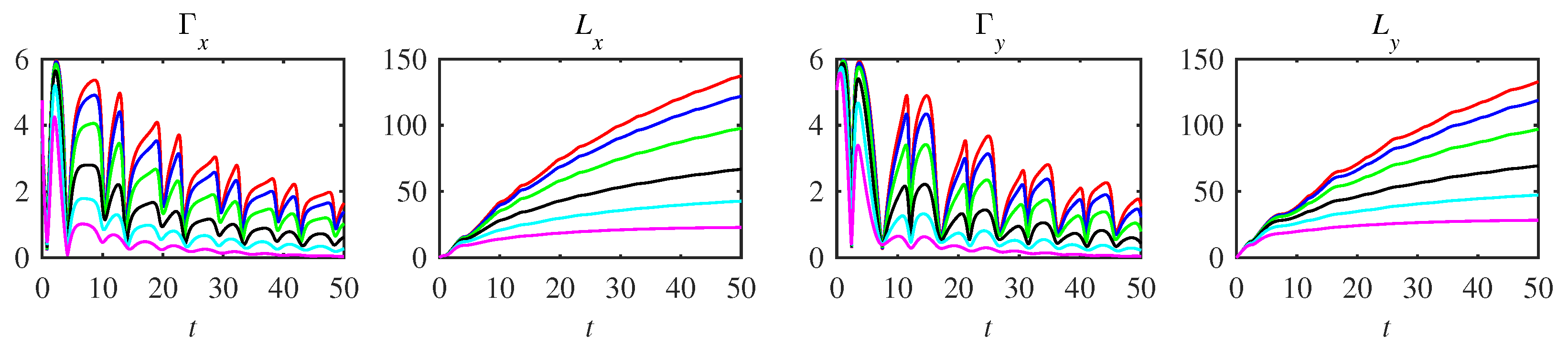
5.4. Information Rate
5.5. Entropy Production
5.6. Comparison among Power Loss, Information Rate, and Entropy Production
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
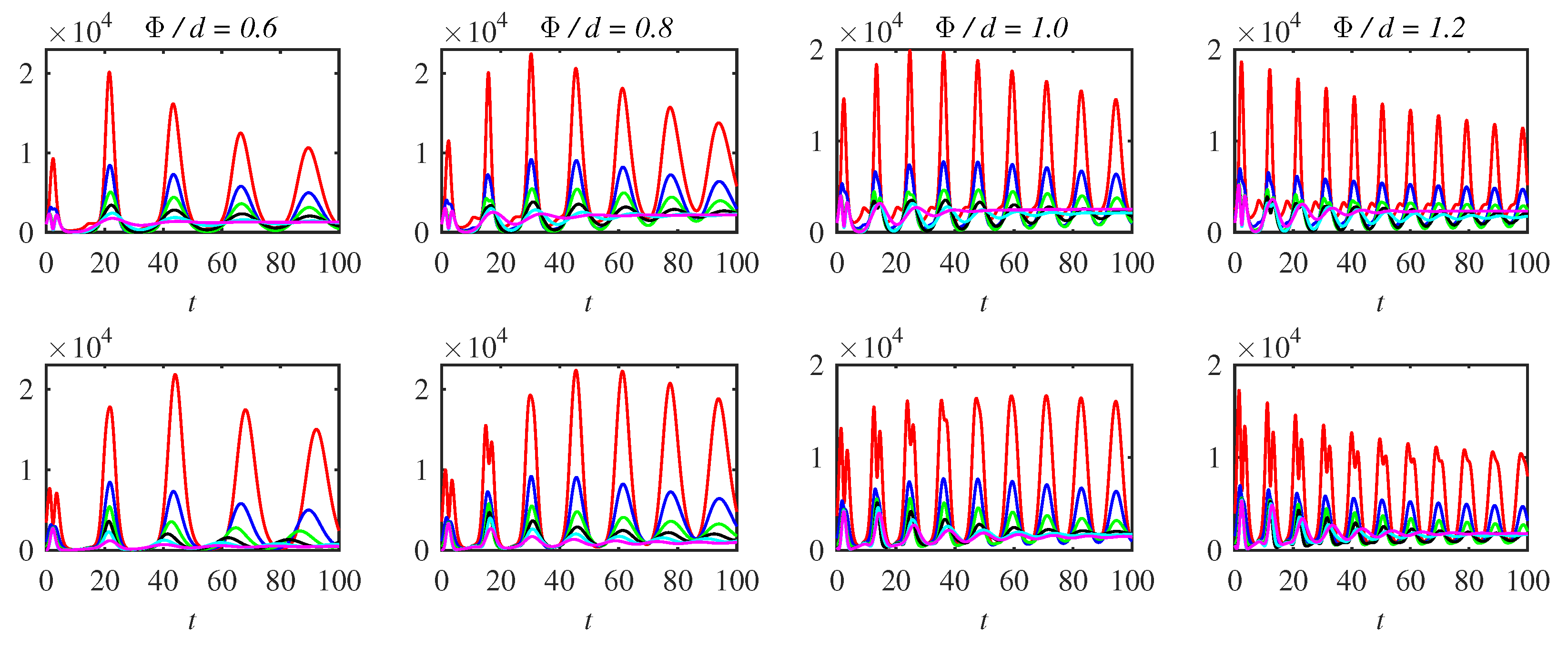
Appendix A. Complementary Figures
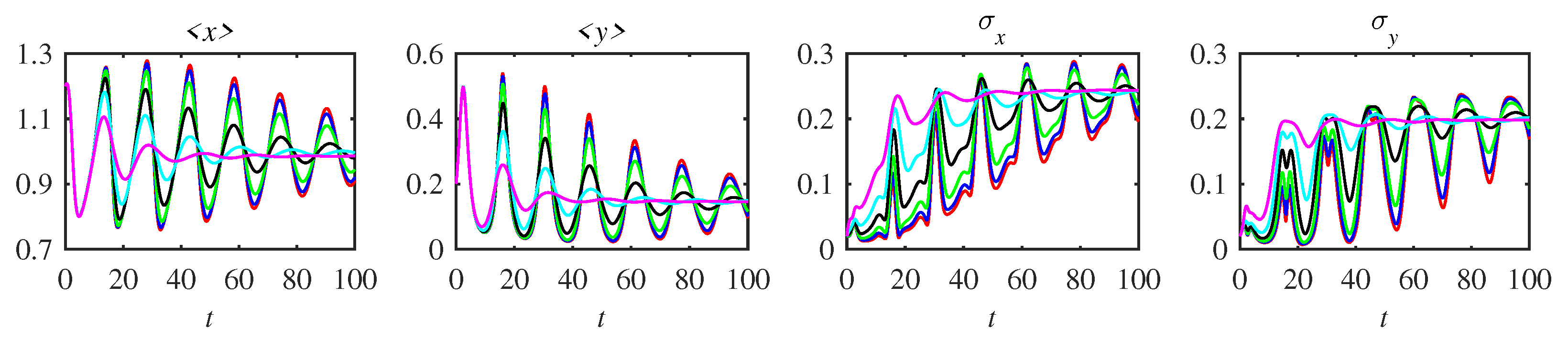
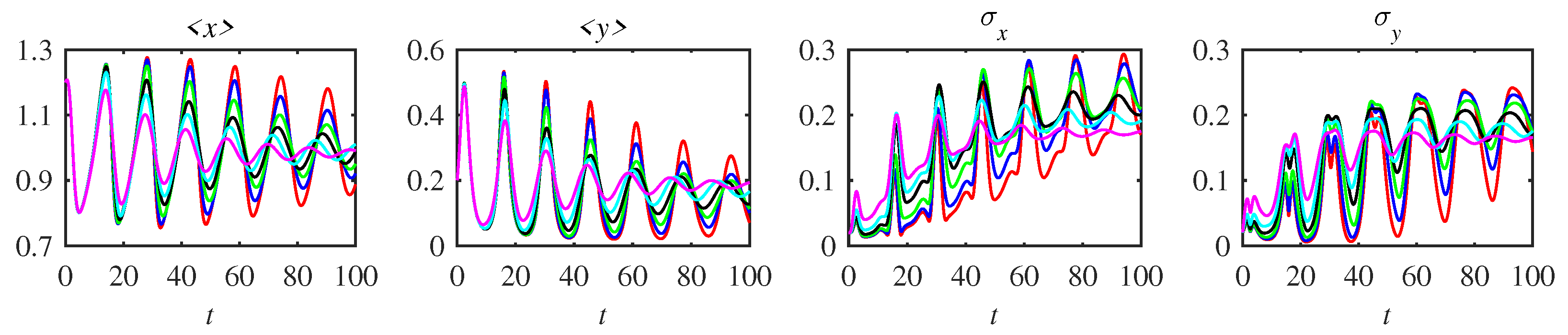
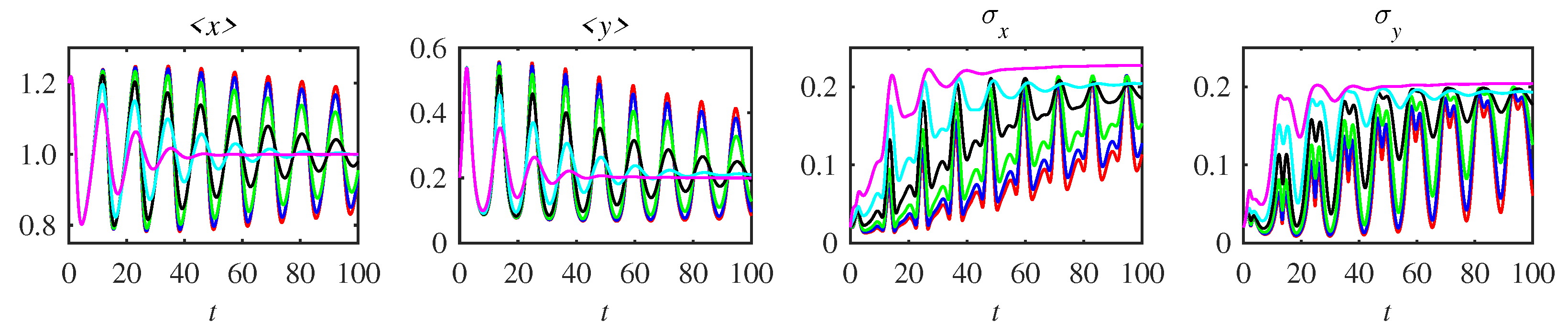
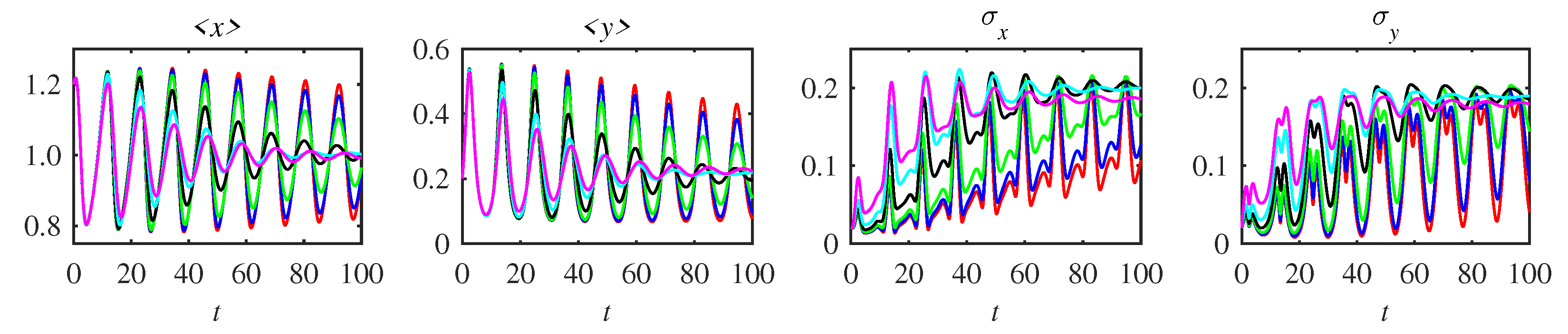
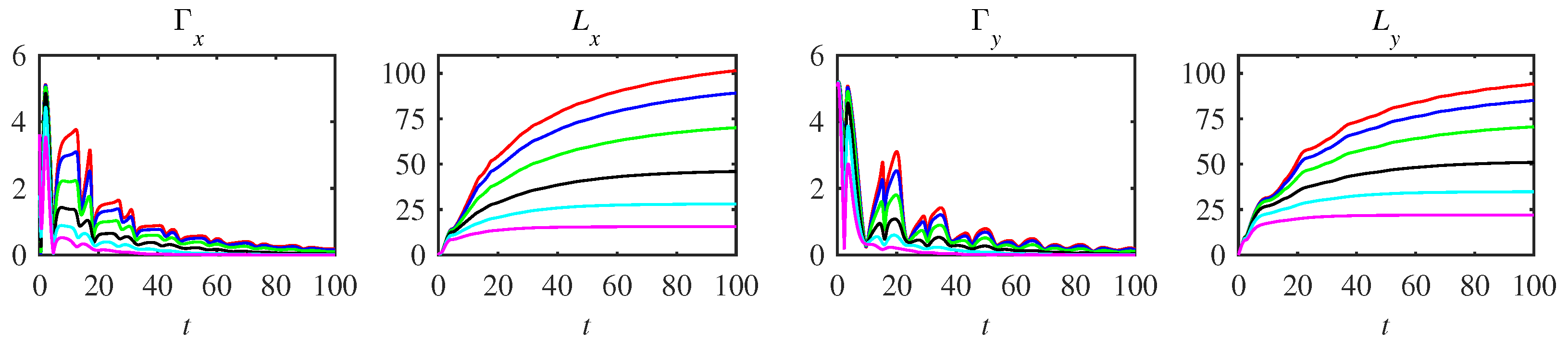
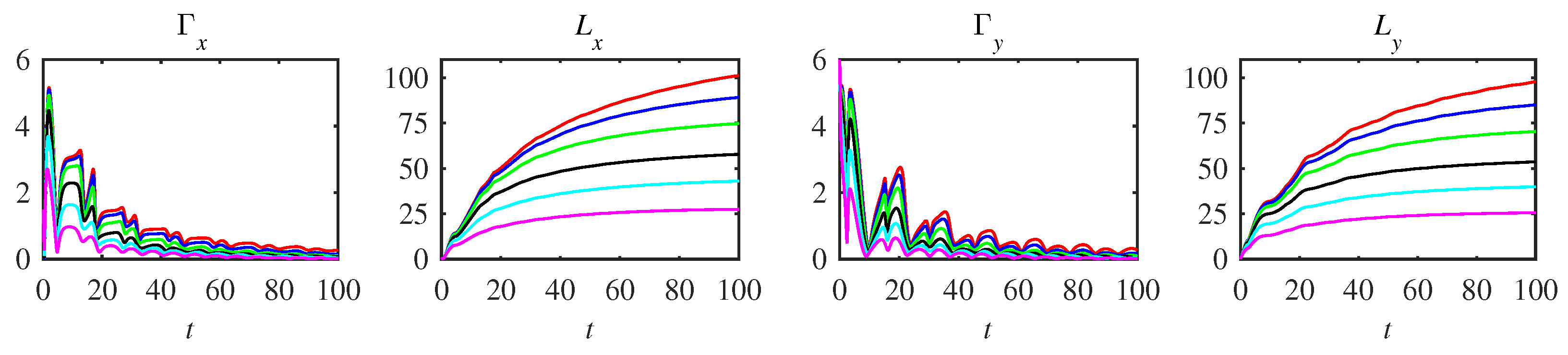
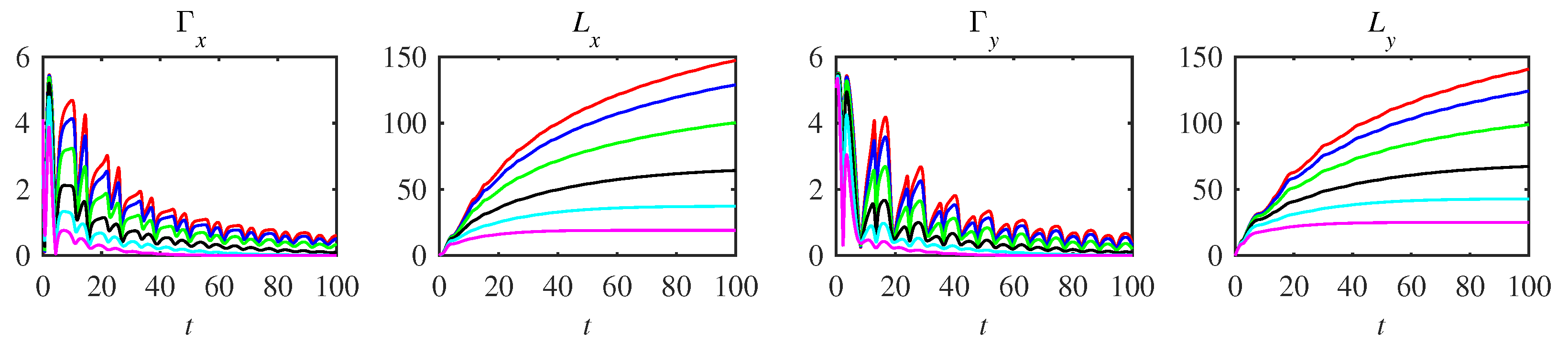
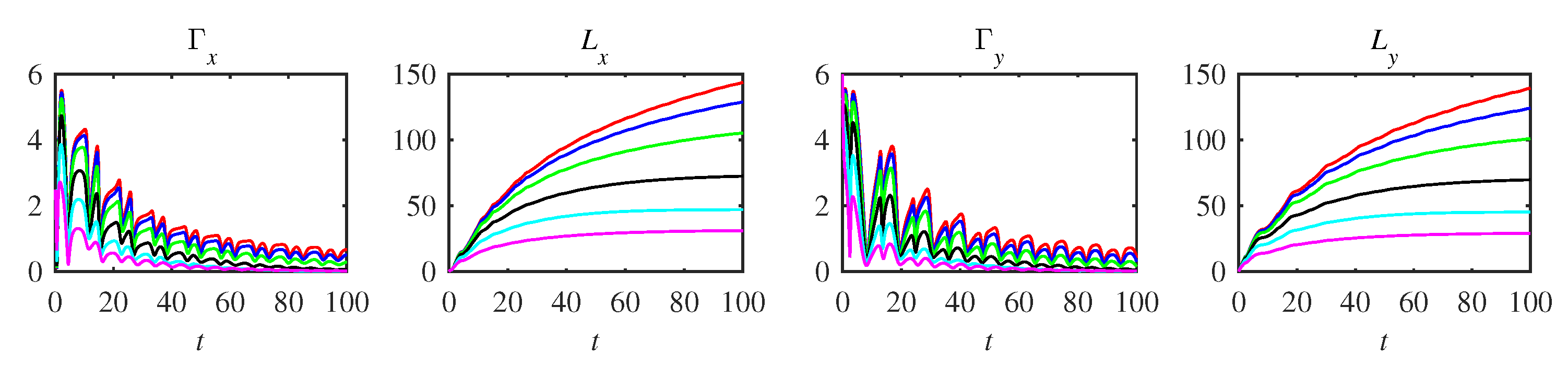
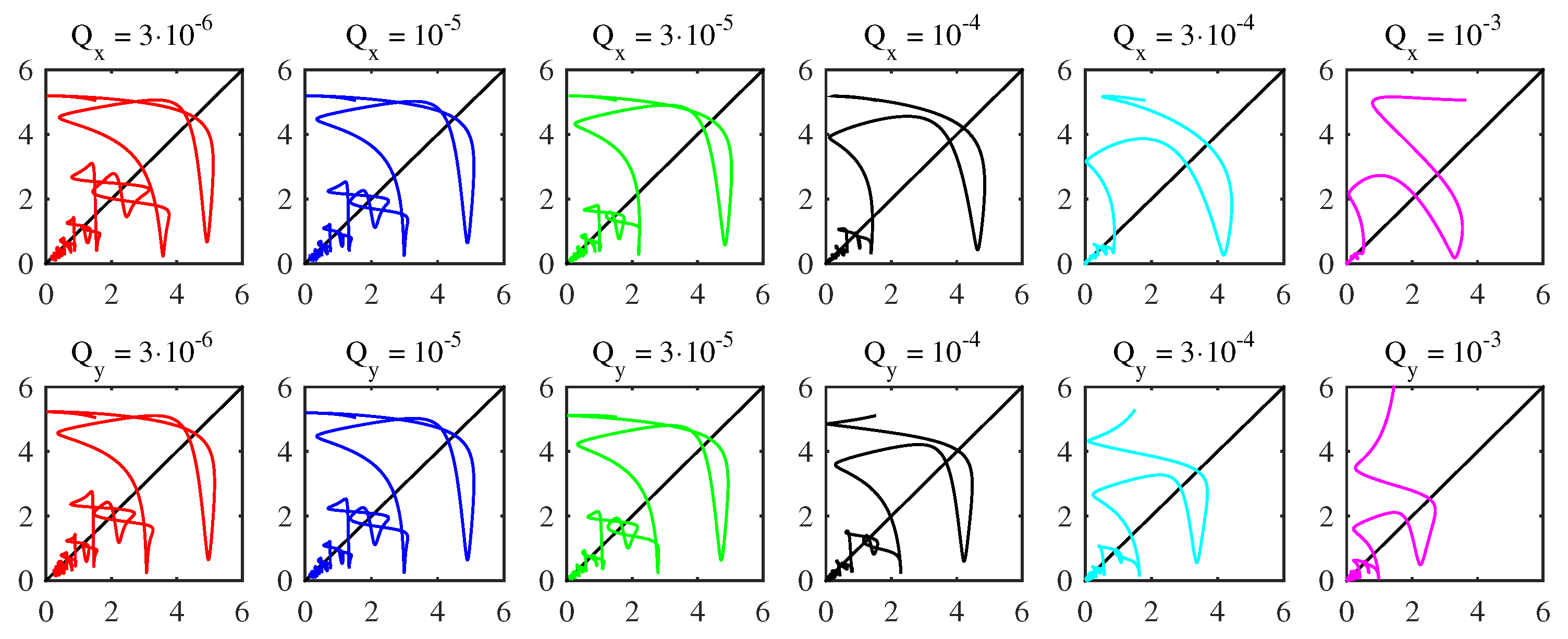
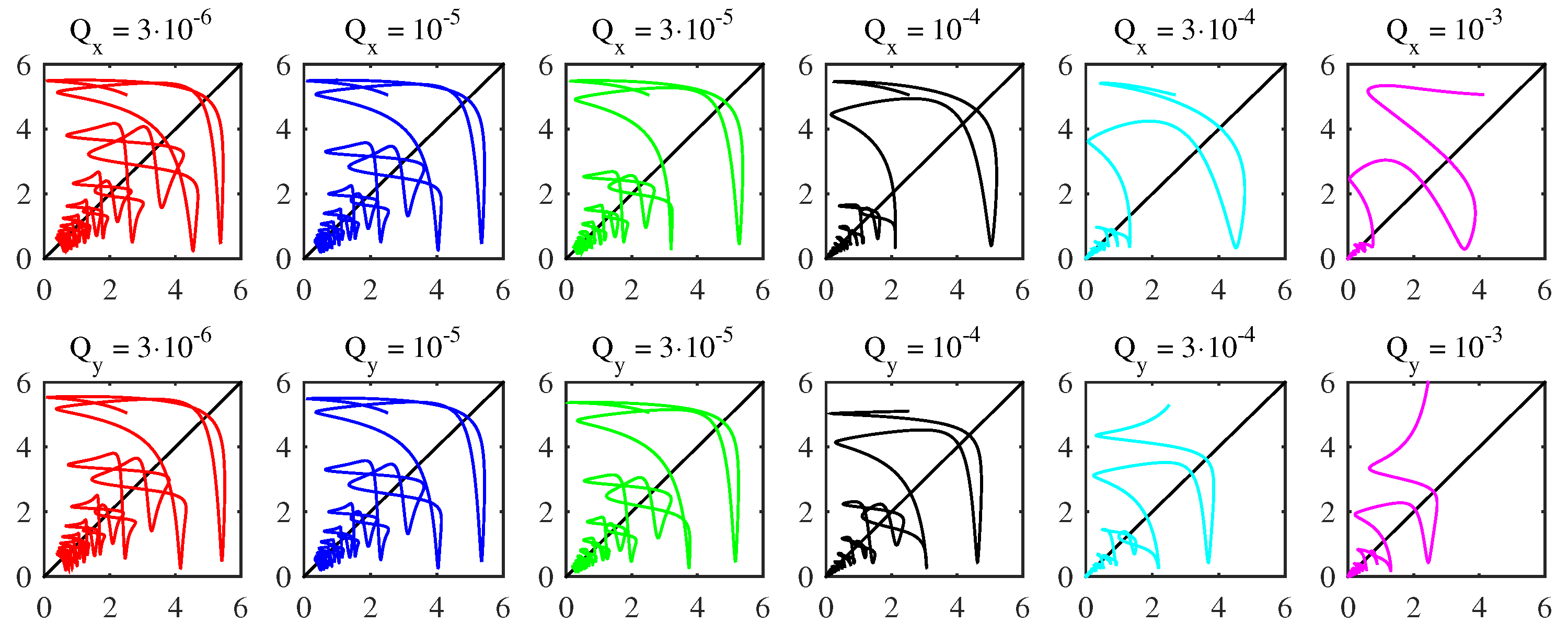

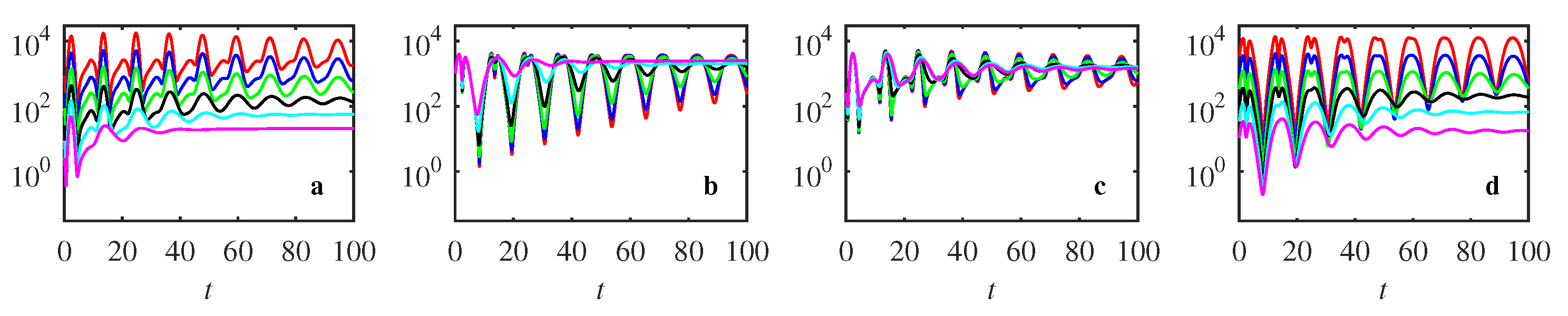
References
- Benzi, R.; Sutera, A.; Vulpiani, A. The mechanism of stochastic resonance. J. Phys. A 1981, 14, L453–L457. [Google Scholar] [CrossRef]
- Gang, H.; Nicolis, G.; Nicolis, C. Periodically forced Fokker-Planck equation and stochastic resonance. Phys. Rev. A 1990, 42, 2030–2041. [Google Scholar] [CrossRef]
- Hollerbach, R.; Kim, E.; Mahi, Y. Information length as a new diagnostic in the periodically modulated double-well model of stochastic resonance. Phys. A 2019, 512, 1313–1322. [Google Scholar] [CrossRef] [Green Version]
- Simakov, D.S.A.; Pérez-Mercader, J. Noise induced oscillations and coherence resonance in a generic model of the nonisothermal chemical oscillator. Sci. Rep. 2013, 3, 2404. [Google Scholar] [CrossRef] [Green Version]
- Jaimes-Reátegui, R.; Magallón-Garcia, D.A.; Gallegos, A.; Huerta-Cuellar, G.; Garcia-López, J.H.; Pisarchik, A.N. Noise-induced intermittent oscillation death in a synergetic mode. Discontinuity Nonlinearity Complex. 2020, 9, 167–172. [Google Scholar] [CrossRef]
- Valenti, D.; Giuffrida, A.; Denaro, G.; Pizzolato, N.; Curcio, L.; Mazzola, S.; Basilone, G.; Bonanno, A.; Spagnolo, B. Noise induced phenomena in the dynamics of two competing species. Math. Model. Nat. Phenom. 2016, 11, 158–174. [Google Scholar] [CrossRef] [Green Version]
- Haken, H. Synergetic Computers and Cognition: A Top-Down Approach to Neural Nets; Springer: Berlin, Germany, 2004. [Google Scholar]
- Franci, A.; Herrera-Valdez, M.A.; Lara-Aparicio, M.; Padilla-Longoria, P. Synchronization, oscillator death, and frequency modulation in a class of biologically inspired coupled oscillators. Front. Appl. Math. Stat. 2018, 4, 51. [Google Scholar] [CrossRef] [Green Version]
- Boccaletti, S.; Pisarchik, A.N.; del Genio, C.I.; Amann, A. Synchronization: From Coupled Systems to Complex Networks; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Koseska, A.; Volkov, E.; Kurths, J. Oscillation quenching mechanisms: Amplitude vs. oscillation death. Phys. Rep. 2013, 531, 173–200. [Google Scholar] [CrossRef]
- Kadomtsev, B.; Laing, E.W. Tokamak Plasma: A Complex Physical System; IOP Publishing: Bristol, UK, 1992. [Google Scholar]
- Lebedev, V.B.; Diamond, P.H.; Gruzinov, I.; Carreras, B.A. A minimal dynamical model of edge localized mode phenomena. Phys. Plasmas 1995, 2, 3345. [Google Scholar] [CrossRef]
- Park, H.K.; Lee, J.; Yun, G.S.; Xu, X.Q.; Bécoulet, M. BOUT++ nonlinear simulation for a comparative study with the measured 2D ELM structures in the KSTAR H-mode plasma. Phys. Plasmas 2019, 26, 052502. [Google Scholar]
- Wang, Y.M.; Zu, X.Q.; Yan, Z.; Mckee, G.R.; Grierson, B.A.; Xia, T.Y.; Gao, X. Simulation of density fluctuations before the L-H transition for hydrogen and deuterium plasmas in the DIII-D tokamak using the BOUT++ code. Nuclear Fusion 2018, 58, 026026. [Google Scholar] [CrossRef]
- Leonard, A.W. Edge-localized-modes in tokamaks. Phys. Plasmas 2014, 21, 090501. [Google Scholar] [CrossRef]
- Lang, P.T.; Alper, P.; Buttery, R.; Gal, K.; Hobirk, J.; Neuhauser, J.; Stamp, M.; JET-EFDA Contributors. ELM triggering by local pellet perturbations in type-I ELMy H-mode plasma at JET. Nucl. Fusion 2007, 47, 754. [Google Scholar] [CrossRef] [Green Version]
- Orain, F.; Hoelzl, M.; Mink, F.; Willensdorfer, M.; Bécoulet, M.; Dunne, M.; Günter, S.; Huijsmans, G.; Lackner, K.; Pamela, S.; et al. Non-linear modeling of the threshold between ELM mitigation and ELM suppression by resonant magnetic perturbations in ASDEX upgrade. Phys. Plasmas 2019, 26, 042503. [Google Scholar] [CrossRef] [Green Version]
- Kirk, A.; Chapman, I.T.; Evans, T.E.; Ham, C.; Harrison, J.R.; Huijsmans, G.; Liang, Y.; Liu, Y.Q.; Loarte, A.; Suttrop, W.; et al. Understanding the effect resonant magnetic perturbations have on ELMs. Plasma Phys. Control. Fusion 2013, 55, 124003. [Google Scholar] [CrossRef] [Green Version]
- Loarte, A.; Becoulet, M.; Saibene, G.; Sartori, R.; Campbell, D.J.; Eich, T.; Herrmann, A.; Laux, M.; Suttrop, W.; Alper, B. Characteristics and scaling of energy and particle losses during Type I ELMs in JET H-modes. Plasma Phys. Control. Fusion 2002, 44, 1815. [Google Scholar] [CrossRef] [Green Version]
- Choi, M.J.; Kwon, J.M.; Kim, J.; Rhee, T.; Bak, J.G.; Shin, G.; Kim, H.-S.; Jhang, H.; Kim, K.; Yun, G.S.; et al. Stochastic fluctuation and transport of tokamak edge plasmas with the resonant magnetic perturbation field. Phys. Plasmas 2022, 29, 122504. [Google Scholar] [CrossRef]
- Sun, Y.; Liang, Y.; Liu, Y.Q.; Gu, S.; Yang, S.; Guo, W.; Shi, T.; Jia, M.; Wang, L.; Lyu, B.; et al. Nonlinear transition from mitigation to suppression of the edge localized mode with resonant magnetic perturbations in the EAST tokamak. Phys. Rev. Lett. 2016, 117, 115001. [Google Scholar] [CrossRef] [Green Version]
- Wagner, T.I. The history of research into improved confinement regimes. Europ. Phys. J. H 2018, 43, 523. [Google Scholar] [CrossRef] [Green Version]
- Diamond, P.H.; Itoh, S.-I.; Itoh, K.; Hahm, T.S. Zonal flows in plasma—A review. Plasma Phys. Control. Fusion 2005, 47, R35. [Google Scholar] [CrossRef]
- Schmitz, L.; Zeng, L.; Rhodes, T.L.; Hillesheim, J.C.; Doyle, E.J.; Groebner, R.J.; Peebles, W.A.; Burrell, K.H.; Wang, G. Role of zonal flow predator-prey oscillations in triggering the transition to H-mode confinement. Phys. Rev. Lett. 2012, 108, 155002. [Google Scholar] [CrossRef] [Green Version]
- Kim, E.; Hollerbach, R. Time-dependent probability density functions and information geometry of the low-to-high confinement transition in fusion plasma. Phys. Rev. Res. 2020, 2, 023077. [Google Scholar] [CrossRef] [Green Version]
- Mlynar, J.; Ficker, O.; Macusova, E.; Markovic, T.; Naydenkova, D.; Papp, G.; Urban, J.; Vlainic, M.; Vondracek, P.; Weinzettl, V.; et al. Runaway electron experiments at COMPASS in support of the EUROfusion ITER physics research. Plasma Phys. Control. Fusion 2018, 61, 014010. [Google Scholar] [CrossRef] [Green Version]
- Svensson, P.; Embreus, O.; Newton, S.L.; Särkimäki, K.; Vallhagen, O.; Fülöp, T. Effects of magnetic perturbations and radiation on the runaway avalanche. J. Plasma Phys. 2021, 87, 905870207. [Google Scholar] [CrossRef]
- Kim, E.; Hollerbach, R. Non-equilibrium statistical properties, path-dependent information geometry, and entropy relations in edge-localized modes in fusion plasmas. Phys. Plasmas 2022, 29, 112302. [Google Scholar] [CrossRef]
- Kowalski, A.M.; Martin, M.T.; Plastino, A.; Rosso, O.A.; Casas, M. Distances in probability space and the statistical complexity setup. Entropy 2011, 13, 1055. [Google Scholar] [CrossRef] [Green Version]
- Oizumi, M.; Tsuchiya, N.; Amari, S. Unified framework for information integration based on information geometry. Proc. Natl. Acad. Sci. USA 2016, 113, 14817. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Frieden, B.R. Science from Fisher Information; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Kim, E. Information geometry, fluctuations, non-equilibrium thermodynamics, and geodesics in complex systems. Entropy 2021, 23, 1393. [Google Scholar] [CrossRef]
- Heseltine, J.; Kim, E. Comparing information metrics for a coupled Ornstein-Uhlenbeck process. Entropy 2019, 21, 775. [Google Scholar] [CrossRef] [Green Version]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Sagawa, T. Thermodynamics of Information Processing in Small Systems; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Roldán, É.; Barral, J.; Martin, P.; Parrondo, J.M.R.; Jülicher, F. Quantifying entropy production in active fluctuations of the hair-cell bundle from time irreversibility and uncertainty relations. New J. Phys. 2021, 23, 083013. [Google Scholar] [CrossRef]
- Sarazin, Y.; Ghendrih, P. Intermittent particle transport in two-dimensional edge turbulence. Phys. Plasmas 1998, 5, 4214. [Google Scholar] [CrossRef]
- Tsui, H.Y.W.; Wootton, A.J.; Bell, J.D.; Bengston, R.D.; Diebold, D.; Harris, J.H.; Hershkowitz, N.; Hidalgo, C.; Ingraham, J.C.; Kilpatrick, S.J.; et al. A comparison of edge turbulence in tokamaks, stellarators, and reversed-field pinches. Phys. Fluids B 1993, 5, 2491. [Google Scholar] [CrossRef]
- Risken, H. The Fokker-Planck Equation: Methods of Solutions and Applications; Springer: Berlin, Germany, 2013. [Google Scholar]
- Thiruthummal, A.A.; Kim, E. Monte Carlo simulation of stochastic differential equation to study information geometry. Entropy 2022, 24, 1113. [Google Scholar] [CrossRef]
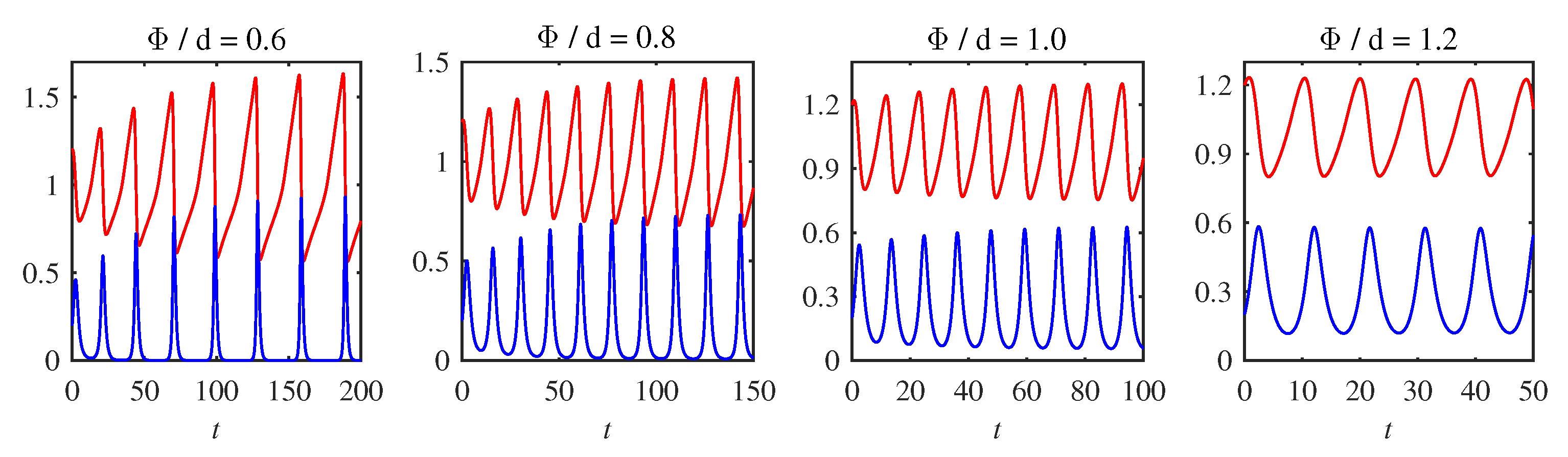
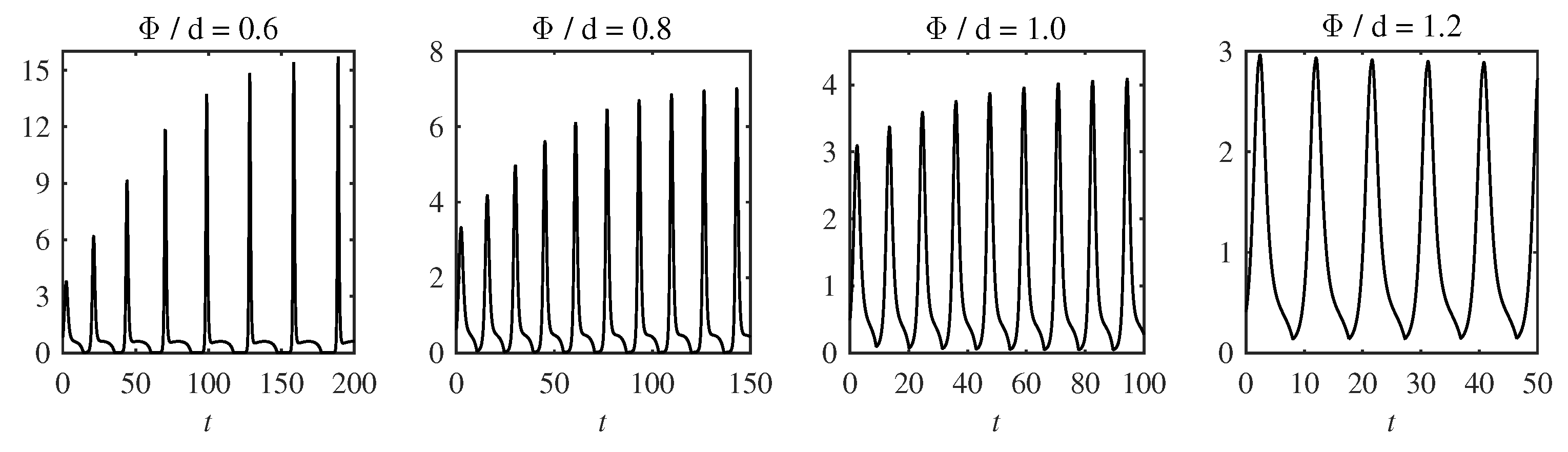
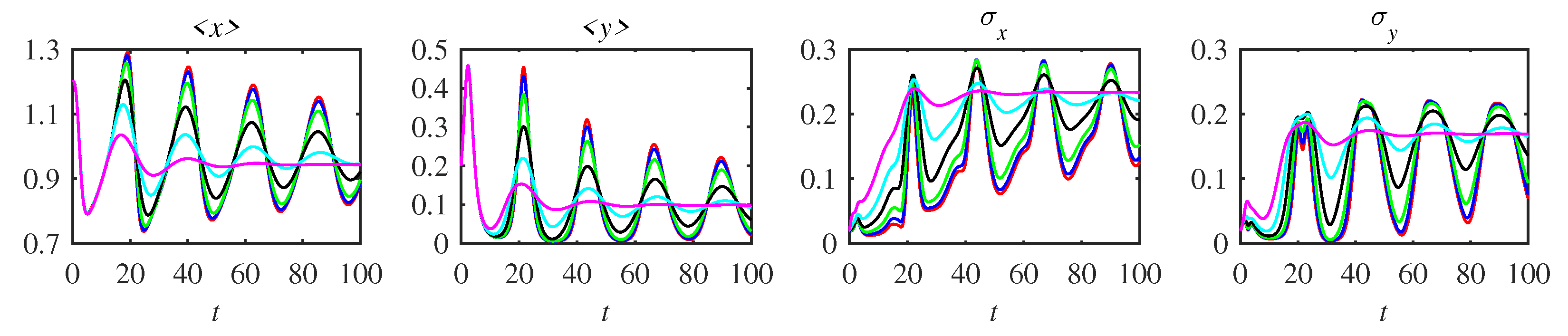
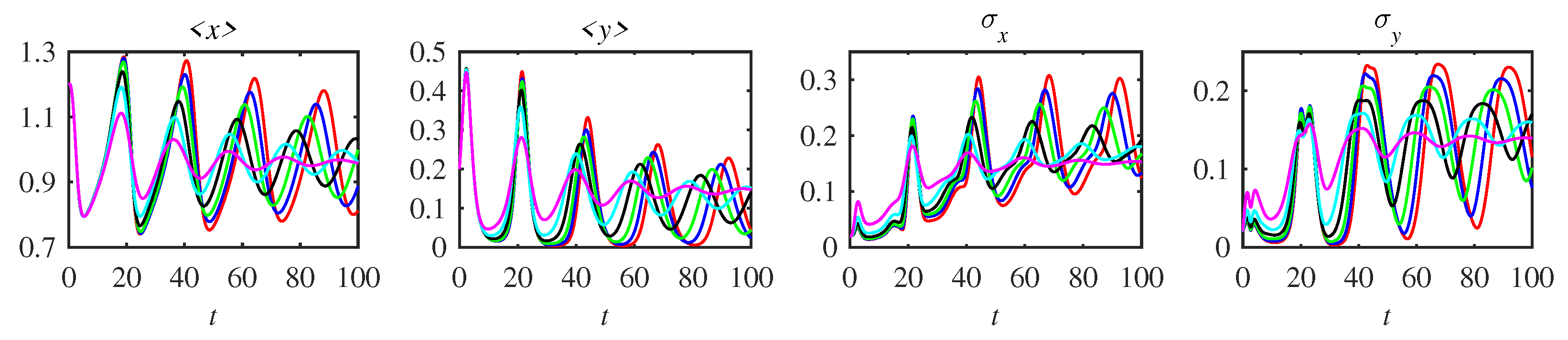
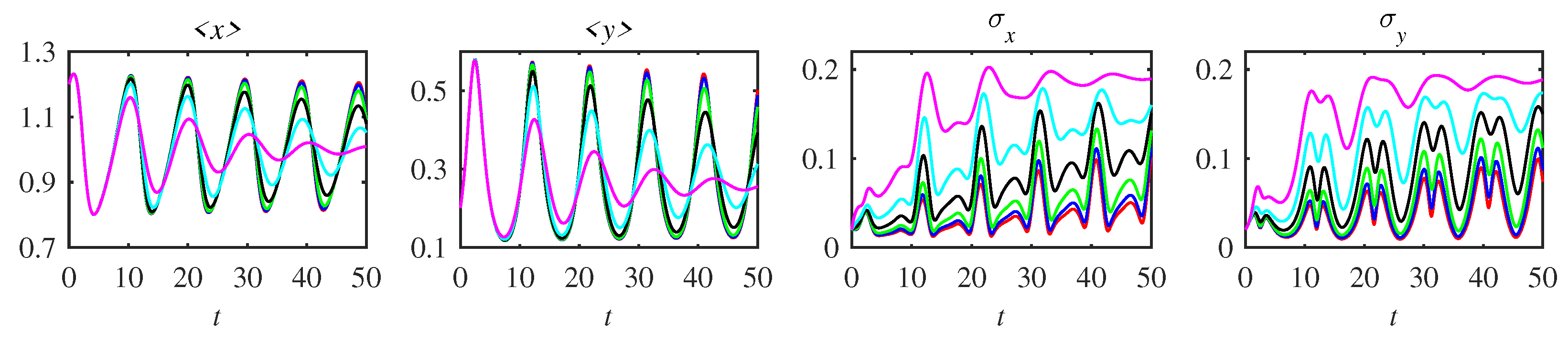




| 0.6 | 4.11 | 5.65 | 8.8 | 22.8 | 0.39 |
| 0.8 | 3.89 | 4.08 | 5.9 | 15.6 | 0.38 |
| 1.0 | 3.27 | 3.69 | 4.2 | 11.6 | 0.36 |
| 1.2 | 2.88 | 3.42 | 3.2 | 9.6 | 0.33 |
| 0.6 | 4.04 | 5.72 | 8.7 | 23.7 | 0.37 |
| 0.8 | 3.82 | 4.13 | 5.8 | 15.6 | 0.37 |
| 1.0 | 3.25 | 3.71 | 4.2 | 11.6 | 0.36 |
| 1.2 | 2.87 | 3.43 | 3.2 | 9.6 | 0.33 |
| 0.6 | 15.71 | 3.07 | 22.6 | 30.3 | 0.75 |
| 0.8 | 7.10 | 3.31 | 10.1 | 16.7 | 0.60 |
| 1.0 | 4.15 | 3.41 | 5.4 | 11.8 | 0.46 |
| 1.2 | 2.87 | 3.40 | 3.2 | 9.6 | 0.33 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hollerbach, R.; Kim, E.-j. Effects of Stochastic Noises on Limit-Cycle Oscillations and Power Losses in Fusion Plasmas and Information Geometry. Entropy 2023, 25, 664. https://doi.org/10.3390/e25040664
Hollerbach R, Kim E-j. Effects of Stochastic Noises on Limit-Cycle Oscillations and Power Losses in Fusion Plasmas and Information Geometry. Entropy. 2023; 25(4):664. https://doi.org/10.3390/e25040664
Chicago/Turabian StyleHollerbach, Rainer, and Eun-jin Kim. 2023. "Effects of Stochastic Noises on Limit-Cycle Oscillations and Power Losses in Fusion Plasmas and Information Geometry" Entropy 25, no. 4: 664. https://doi.org/10.3390/e25040664
APA StyleHollerbach, R., & Kim, E.-j. (2023). Effects of Stochastic Noises on Limit-Cycle Oscillations and Power Losses in Fusion Plasmas and Information Geometry. Entropy, 25(4), 664. https://doi.org/10.3390/e25040664







