Link Prediction with Continuous-Time Classical and Quantum Walks
Abstract
:1. Introduction
2. Materials and Methods
2.1. Continuous-Time Random Walks
2.2. Continuous-Time Quantum Walks
2.3. Datasets and Metrics
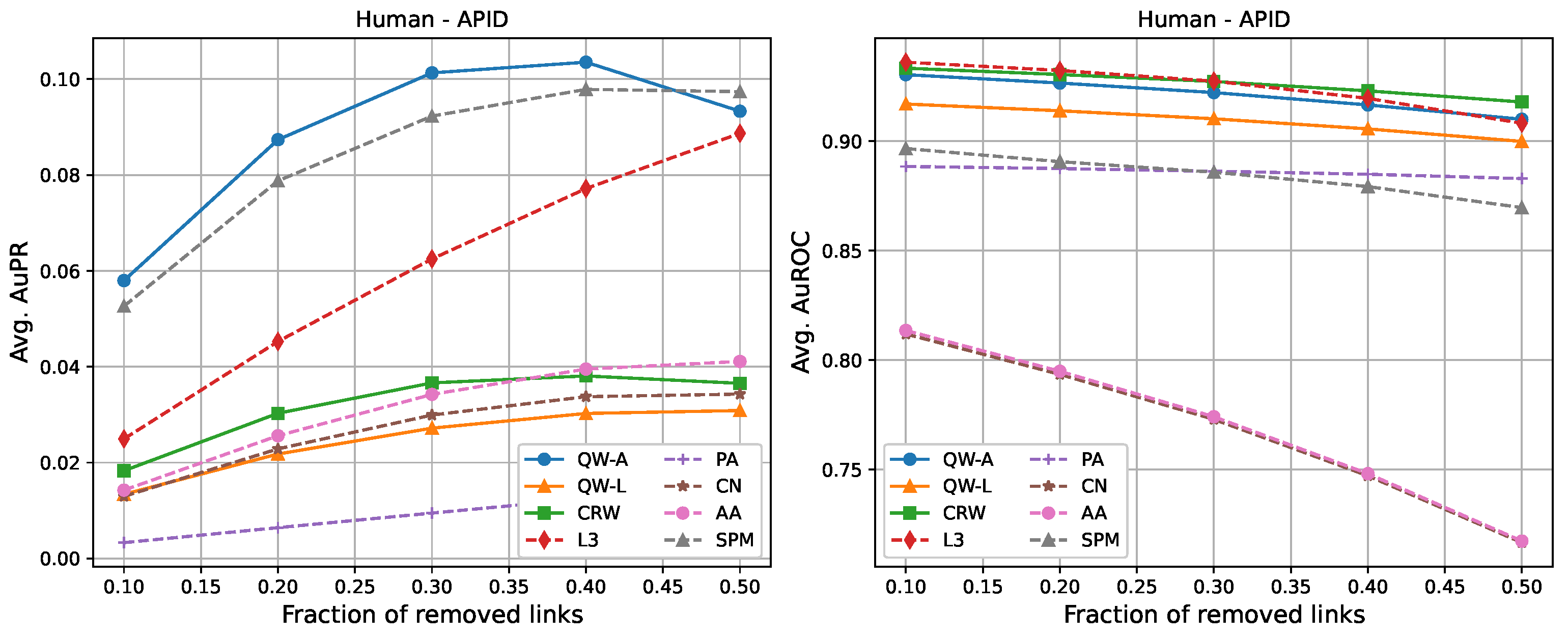
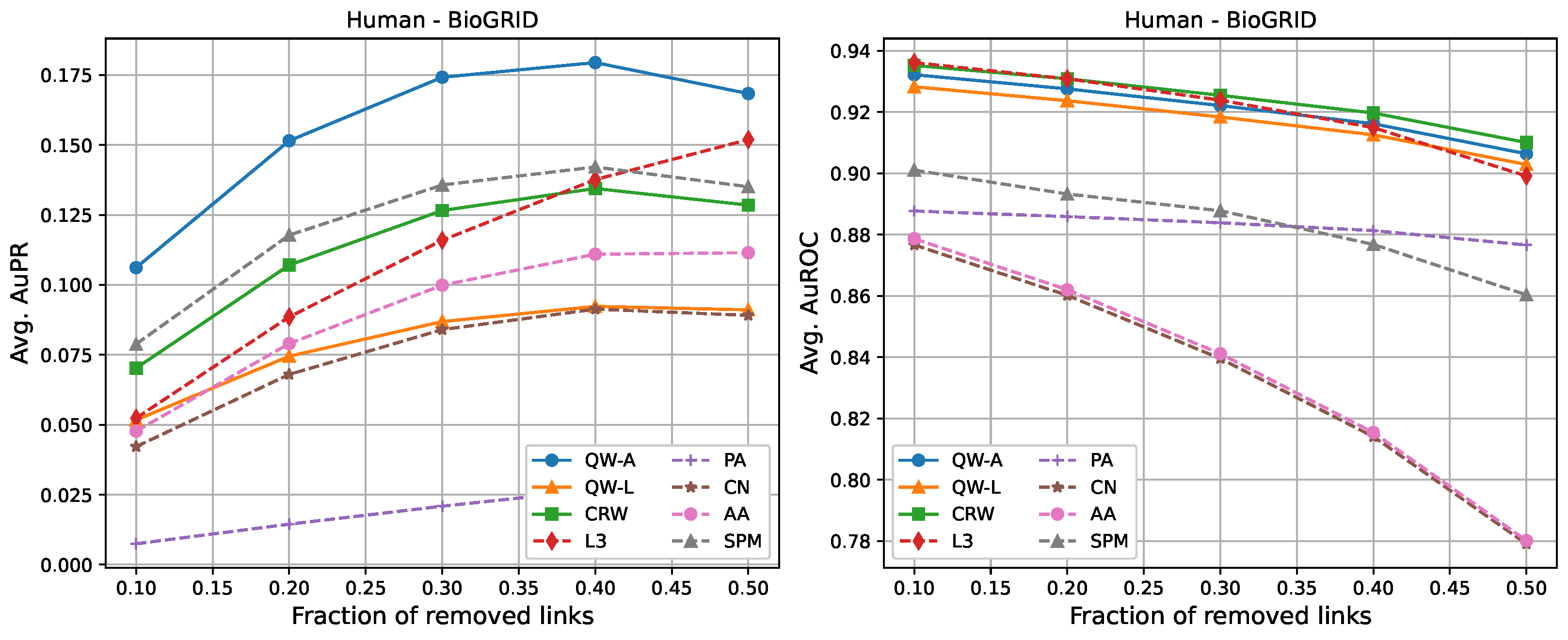
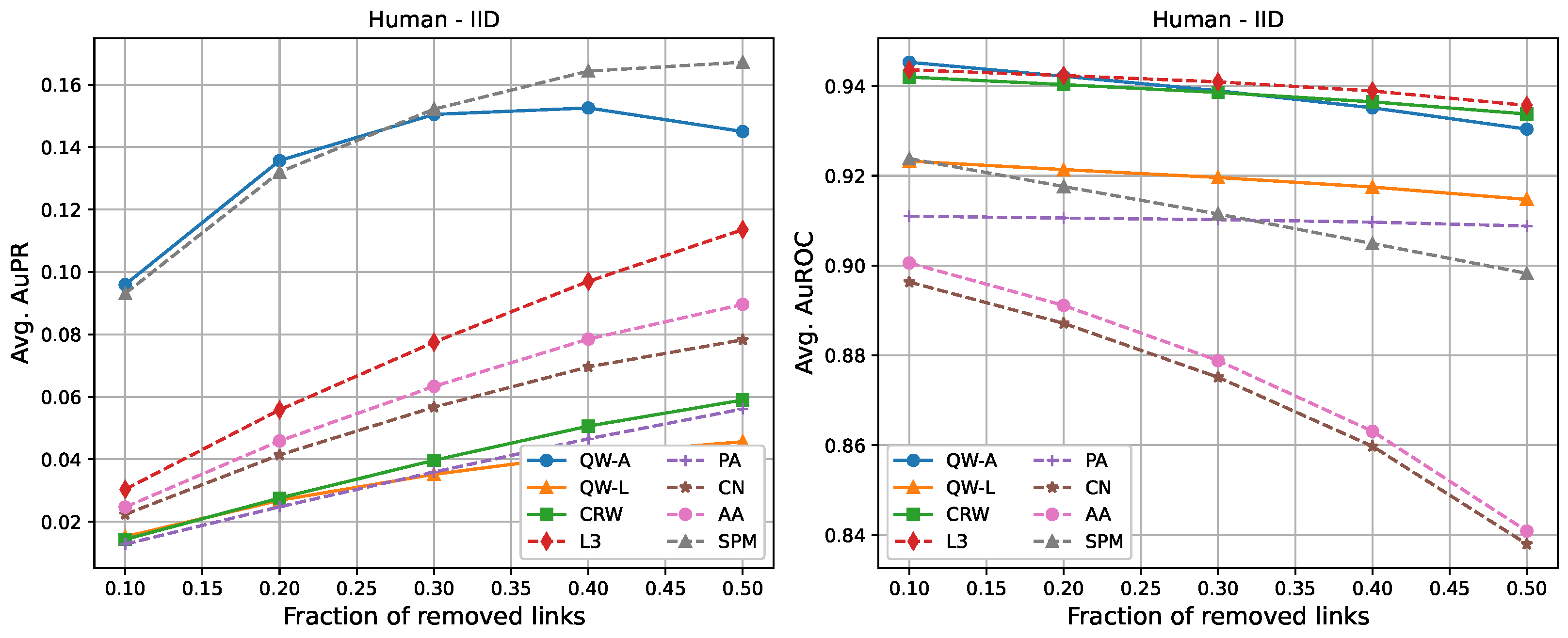
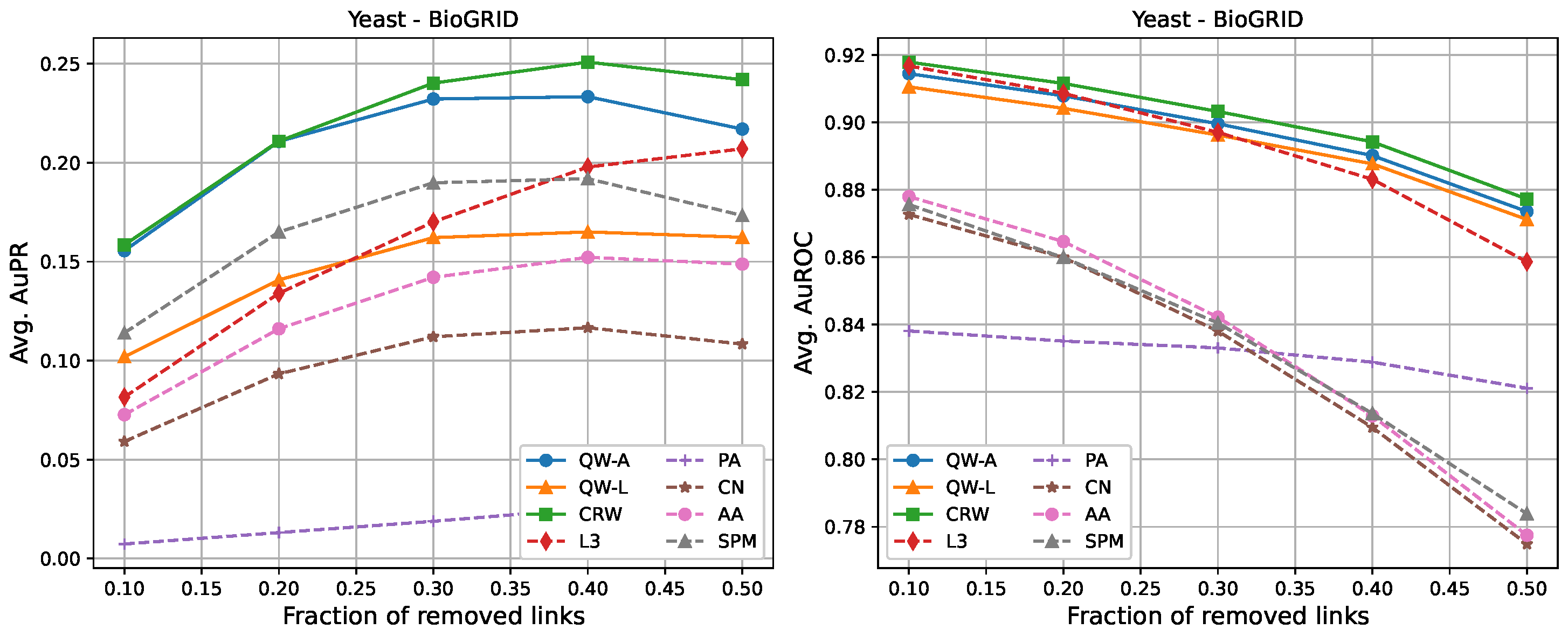
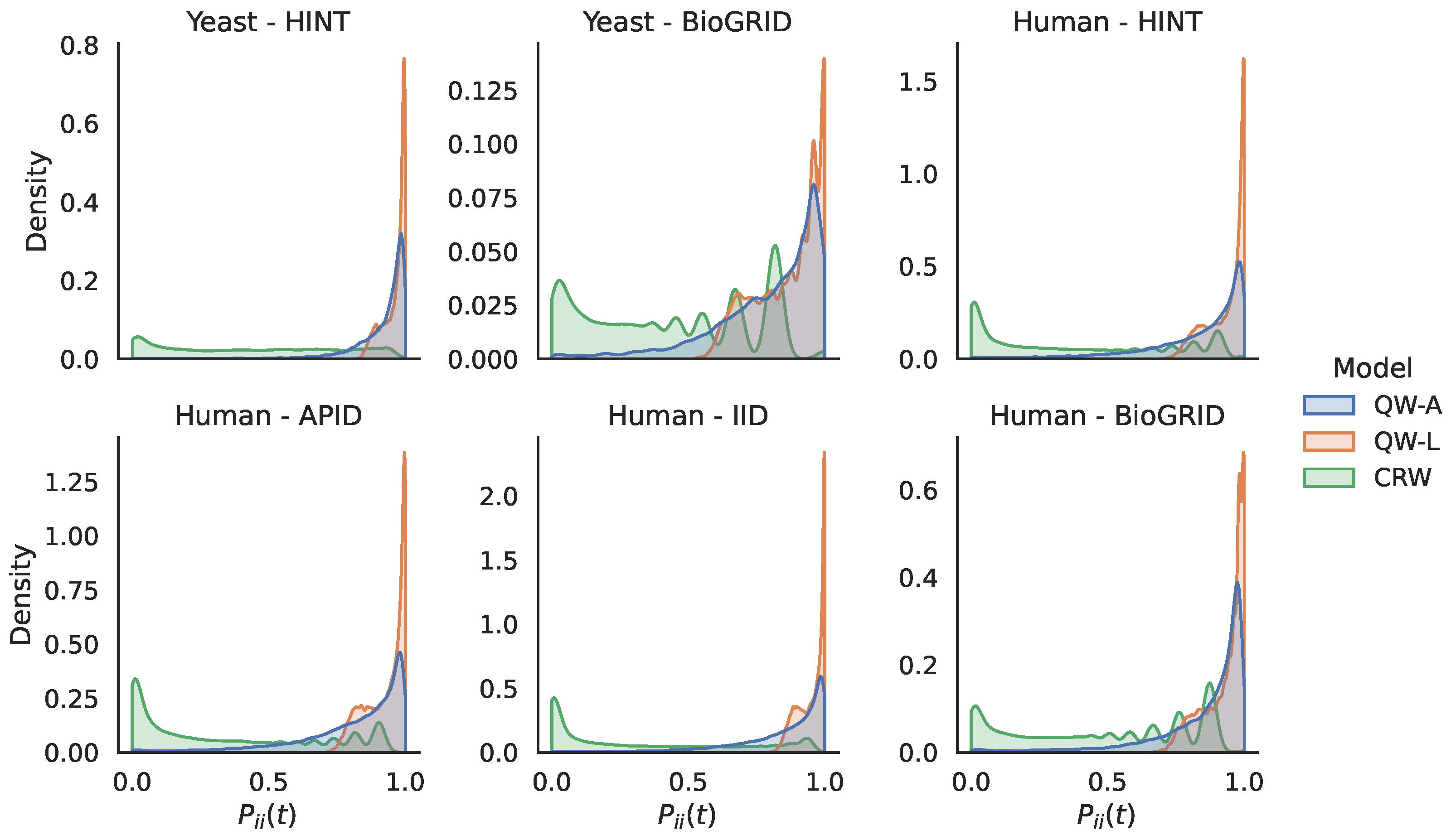
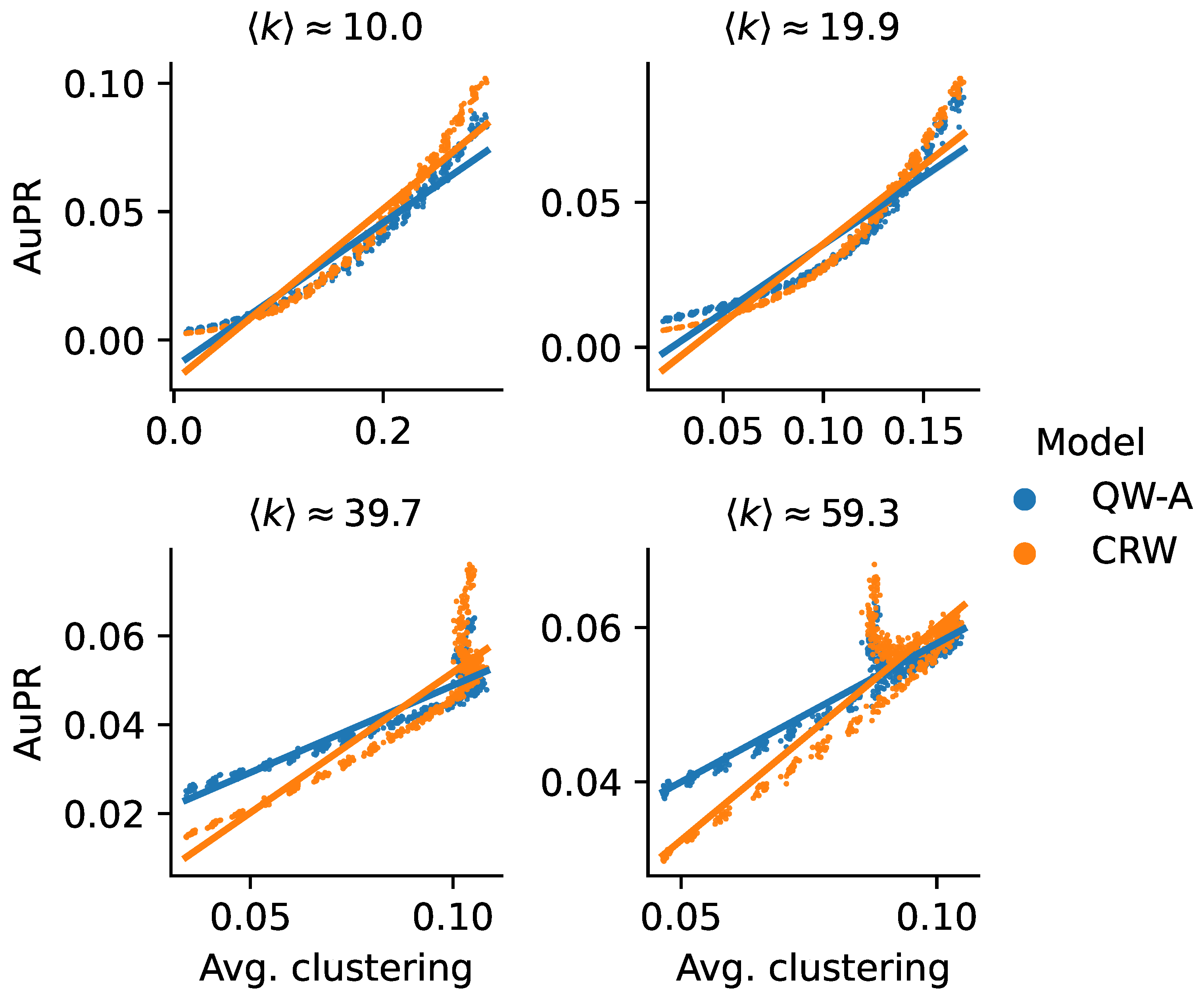
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Adamic, L.A.; Adar, E. Friends and neighbors on the web. Soc. Netw. 2003, 25, 211–230. [Google Scholar] [CrossRef]
- Murata, T.; Moriyasu, S. Link prediction of social networks based on weighted proximity measures. In Proceedings of the IEEE/WIC/ACM International Conference on Web Intelligence (WI’07), Fremont, CA, USA, 2–5 November 2007; pp. 85–88. [Google Scholar]
- Leskovec, J.; Huttenlocher, D.; Kleinberg, J. Predicting positive and negative links in online social networks. In Proceedings of the 19th International Conference on World Wide Web, Raleigh, CA, USA, 26–30 April 2010; pp. 641–650. [Google Scholar]
- Kovács, I.A.; Luck, K.; Spirohn, K.; Wang, Y.; Pollis, C.; Schlabach, S.; Bian, W.; Kim, D.K.; Kishore, N.; Hao, T.; et al. Network-based prediction of protein interactions. Nat. Commun. 2019, 10, 1–8. [Google Scholar]
- Liu, W.; Lü, L. Link prediction based on local random walk. EPL Europhys. Lett. 2010, 89, 58007. [Google Scholar] [CrossRef]
- Kumar, A.; Singh, S.S.; Singh, K.; Biswas, B. Link prediction techniques, applications, and performance: A survey. Phys. Stat. Mech. Its Appl. 2020, 553, 124289. [Google Scholar]
- Martínez, V.; Berzal, F.; Talavera, J.C.C. A Survey of Link Prediction in Complex Networks. ACM Comput. Surv. 2017, 49, 69:1–69:33. [Google Scholar] [CrossRef]
- Zhou, T. Progresses and challenges in link prediction. iScience 2021, 24, 103217. [Google Scholar]
- Che, Y.; Cheng, W.; Wang, Y.; Chen, D. A Random Walk with Restart Model Based on Common Neighbors for Predicting the Clinical Drug Combinations on Coronary Heart Disease. J. Healthc. Eng. 2021, 2021, 4597391. [Google Scholar] [CrossRef]
- Zhou, Y.; Wu, C.; Tan, L. Biased random walk with restart for link prediction with graph embedding method. Phys. A Stat. Mech. Its Appl. 2021, 570, 125783. [Google Scholar] [CrossRef]
- Brin, S.; Page, L. The anatomy of a large-scale hypertextual web search engine. Comput. Netw. Isdn Syst. 1998, 30, 107–117. [Google Scholar]
- Das Sarma, A.; Molla, A.R.; Pandurangan, G.; Upfal, E. Fast distributed pagerank computation. In Proceedings of the International Conference on Distributed Computing and Networking, Mumbai, India, 3–6 January 2013; pp. 11–26. [Google Scholar]
- Fouss, F.; Pirotte, A.; Renders, J.M.; Saerens, M. Random-walk computation of similarities between nodes of a graph with application to collaborative recommendation. IEEE Trans. Knowl. Data Eng. 2007, 19, 355–369. [Google Scholar]
- Pan, J.Y.; Yang, H.J.; Faloutsos, C.; Duygulu, P. Automatic multimedia cross-modal correlation discovery. In Proceedings of the 10th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Seattle, WA, USA, 22–25 August 2004; pp. 653–658. [Google Scholar]
- Tong, H.; Faloutsos, C.; Pan, J.Y. Fast random walk with restart and its applications. In Proceedings of the Sixth International Conference on Data Mining (ICDM’06), Hong Kong, China, 18–22 December 2006; pp. 613–622. [Google Scholar]
- Farhi, E.; Gutmann, S. Quantum computation and decision trees. Phys. Rev. A 1998, 58, 915–928. [Google Scholar] [CrossRef]
- Aharonov, Y.; Davidovich, L.; Zagury, N. Quantum random walks. Phys. Rev. A 1993, 48, 1687–1690. [Google Scholar] [CrossRef] [PubMed]
- Kempe, J. Quantum random walks: An introductory overview. Contemp. Phys. 2003, 44, 307–327. [Google Scholar] [CrossRef]
- Venegas-Andraca, S.E. Quantum walks: A comprehensive review. Quantum Inf. Process. 2012, 11, 1015–1106. [Google Scholar] [CrossRef]
- Childs, A.M. Universal computation by quantum walk. Phys. Rev. Lett. 2009, 102, 180501. [Google Scholar] [CrossRef]
- Mülken, O.; Blumen, A. Continuous-time quantum walks: Models for coherent transport on complex networks. Phys. Rep. 2011, 502, 37–87. [Google Scholar] [CrossRef]
- Qian, J.; Yang, L.; Yu, Z.; Liu, S. Link prediction using discrete-time quantum walk. Teh. Vjesn. 2017, 24, 1329–1334. [Google Scholar] [CrossRef]
- Moutinho, J.A.P.; Melo, A.; Coutinho, B.; Kovács, I.A.; Omar, Y. Quantum link prediction in complex networks. Phys. Rev. A 2023, 107, 032605. [Google Scholar] [CrossRef]
- Manouchehri, K.; Wang, J. Physical Implementation of Quantum Walks; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Young, A.W.; Eckner, W.J.; Schine, N.; Childs, A.M.; Kaufman, A.M. Tweezer-programmable 2D quantum walks in a Hubbard-regime lattice. Science 2022, 377, 885–889. [Google Scholar] [CrossRef]
- Wang, K.; Shi, Y.; Xiao, L.; Wang, J.; Joglekar, Y.N.; Xue, P. Experimental realization of continuous-time quantum walks on directed graphs and their application in PageRank. Optica 2020, 7, 1524–1530. [Google Scholar] [CrossRef]
- Tang, H.; Lin, X.F.; Feng, Z.; Chen, J.Y.; Gao, J.; Sun, K.; Wang, C.Y.; Lai, P.C.; Xu, X.Y.; Wang, Y.; et al. Experimental two-dimensional quantum walk on a photonic chip. Sci. Adv. 2018, 4, eaat3174. [Google Scholar] [CrossRef] [PubMed]
- Peruzzo, A.; Lobino, M.; Matthews, J.C.F.; Matsuda, N.; Politi, A.; Poulios, K.; Zhou, X.Q.; Lahini, Y.; Ismail, N.; Wörhoff, K.; et al. Quantum Walks of Correlated Photons. Science 2010, 329, 1500–1503. [Google Scholar] [CrossRef] [PubMed]
- Preiss, P.; Ma, R.; Tai, E.; Lukin, A.; Rispoli, M.; Zupancic, P.; Lahini, Y.; Islam, R.; Greiner, M. Strongly correlated quantum walks in optical lattices. Science 2015, 347, 1229–1233. [Google Scholar] [CrossRef] [PubMed]
- Gong, M.; Wang, S.; Zha, C.; Chen, M.C.; Huang, H.L.; Wu, Y.; Zhu, Q.; Zhao, Y.; Li, S.; Guo, S.; et al. Quantum walks on a programmable two-dimensional 62-qubit superconducting processor. Science 2021, 372, 948–952. [Google Scholar] [CrossRef] [PubMed]
- Yan, Z.; Zhang, Y.R.; Gong, M.; Wu, Y.; Zheng, Y.; Li, S.; Wang, C.; Liang, F.; Lin, J.; Xu, Y.; et al. Strongly correlated quantum walks with a 12-qubit superconducting processor. Science 2019, 364, 753–756. [Google Scholar] [CrossRef] [PubMed]
- Loke, T.; Wang, J.B. Efficient quantum circuits for continuous-time quantum walks on composite graphs. J. Phys. Math. Theor. 2017, 50, 055303. [Google Scholar] [CrossRef]
- Qiang, X.; Loke, T.; Montanaro, A.; Aungskunsiri, K.; Zhou, X.; O’Brien, J.L.; Wang, J.B.; Matthews, J.C.F. Efficient quantum walk on a quantum processor. Nat. Commun. 2016, 7, 11511. [Google Scholar] [CrossRef]
- Vidal, M.; Cusick, M.E.; Barabási, A.L. Interactome networks and human disease. Cell 2011, 144, 986–998. [Google Scholar] [CrossRef]
- Stelzl, U.; Worm, U.; Lalowski, M.; Haenig, C.; Brembeck, F.H.; Goehler, H.; Stroedicke, M.; Zenkner, M.; Schoenherr, A.; Koeppen, S.; et al. A human protein–protein interaction network: A resource for annotating the proteome. Cell 2005, 122, 957–968. [Google Scholar] [CrossRef]
- Rolland, T.; Taşan, M.; Charloteaux, B.; Pevzner, S.J.; Zhong, Q.; Sahni, N.; Yi, S.; Lemmens, I.; Fontanillo, C.; Mosca, R.; et al. A proteome-scale map of the human interactome network. Cell 2014, 159, 1212–1226. [Google Scholar] [CrossRef]
- Luck, K.; Kim, D.K.; Lambourne, L.; Spirohn, K.; Begg, B.E.; Bian, W.; Brignall, R.; Cafarelli, T.; Campos-Laborie, F.J.; Charloteaux, B.; et al. A reference map of the human binary protein interactome. Nature 2020, 580, 402–408. [Google Scholar] [CrossRef]
- Yuen, H.Y.; Jansson, J. Better Link Prediction for Protein-Protein Interaction Networks. In Proceedings of the 2020 IEEE 20th International Conference on Bioinformatics and Bioengineering (BIBE), Cincinnati, OH, USA, 26–28 October 2020; pp. 53–60. [Google Scholar] [CrossRef]
- Yuen, H.Y.; Jansson, J. Normalized L3-based link prediction in protein protein interaction networks. BMC Bioinform. 2023, 24, 59. [Google Scholar] [CrossRef] [PubMed]
- Liben-Nowell, D.; Kleinberg, J. The link-prediction problem for social networks. J. Am. Soc. Inf. Sci. Technol. 2007, 58, 1019–1031. [Google Scholar] [CrossRef]
- Barabási, A.L.; Jeong, H.; Néda, Z.; Ravasz, E.; Schubert, A.; Vicsek, T. Evolution of the social network of scientific collaborations. Phys. A Stat. Mech. Its Appl. 2002, 311, 590–614. [Google Scholar] [CrossRef]
- Masuda, N.; Porter, M.A.; Lambiotte, R. Random walks and diffusion on networks. Phys. Rep. 2017, 716, 1–58. [Google Scholar] [CrossRef]
- Childs, A.M.; Farhi, E.; Gutmann, S. An Example of the Difference Between Quantum and Classical Random Walks. Quantum Inf. Process. 2002, 1, 35–43. [Google Scholar] [CrossRef]
- Thomas, G. Wong, L.T.; Nahimov, N. Laplacian versus adjacency matrix in quantum walk search. Quantum Inf. Process. 2016, 15, 4029–4048. [Google Scholar] [CrossRef]
- Childs, A.M.; Goldstone, J. Spatial search by quantum walk. Phys. Rev. A 2004, 70, 022314. [Google Scholar] [CrossRef]
- Stark, C.; Breitkreutz, B.J.; Reguly, T.; Boucher, L.; Breitkreutz, A.; Tyers, M. BioGRID: A general repository for interaction datasets. Nucleic Acids Res. 2006, 34, D535–D539. [Google Scholar] [CrossRef]
- Das, J.; Yu, H. HINT: High-quality protein interactomes and their applications in understanding human disease. BMC Syst. Biol. 2012, 6, 1–12. [Google Scholar] [CrossRef]
- Alonso-López, D.; Campos-Laborie, F.J.; Gutiérrez, M.A.; Lambourne, L.; Calderwood, M.A.; Vidal, M.; De Las Rivas, J. APID database: Redefining protein–protein interaction experimental evidences and binary interactomes. Database 2019, 2019, baz005. [Google Scholar] [CrossRef] [PubMed]
- Alonso-Lopez, D.; Gutiérrez, M.A.; Lopes, K.P.; Prieto, C.; Santamaría, R.; De Las Rivas, J. APID interactomes: Providing proteome-based interactomes with controlled quality for multiple species and derived networks. Nucleic Acids Res. 2016, 44, W529–W535. [Google Scholar] [CrossRef]
- Kotlyar, M.; Pastrello, C.; Sheahan, N.; Jurisica, I. Integrated interactions database: Tissue-specific view of the human and model organism interactomes. Nucleic Acids Res. 2016, 44, D536–D541. [Google Scholar] [CrossRef]
- Barabási, A.L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef]
- Hanley, J.A.; McNeil, B.J. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology 1982, 143, 29–36. [Google Scholar] [CrossRef]
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Armengol, E.; Boixader, D.; Grimaldo, F. Evaluating link prediction on large graphs. In Artificial Intelligence Research and Development: Proceedings of the 18th International Conference of the Catalan Association for Artificial Intelligence; IOS Press: Amsterdam, The Netherlands, 2015; Volume 277. [Google Scholar]
- Saito, T.; Rehmsmeier, M. The precision–recall plot is more informative than the ROC plot when evaluating binary classifiers on imbalanced datasets. PLoS ONE 2015, 10, e0118432. [Google Scholar] [CrossRef]
- Lü, L.; Pan, L.; Zhou, T.; Zhang, Y.C.; Stanley, H. Toward link predictability of complex networks. Proc. Natl. Acad. Sci. USA 2015, 112, 201424644. [Google Scholar] [CrossRef]
- Zeng, X.; Liu, L.; Lü, L.; Zou, Q. Prediction of potential disease-associated microRNAs using structural perturbation method. Bioinformatics 2018, 34, 2425–2432. [Google Scholar] [CrossRef]
- Holme, P.; Kim, B.J. Growing scale-free networks with tunable clustering. Phys. Rev. E 2002, 65, 026107. [Google Scholar] [CrossRef]
- Moler, C.; Van Loan, C. Nineteen dubious ways to compute the exponential of a matrix, twenty-five years later. SIAM Rev. 2003, 45, 3–49. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Advances in Neural Information Processing Systems 32; Wallach, H., Larochelle, H., Beygelzimer, A., d’Alché-Buc, F., Fox, E., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2019; pp. 8024–8035. [Google Scholar]
- Bader, P.; Blanes, S.; Casas, F. Computing the matrix exponential with an optimized Taylor polynomial approximation. Mathematics 2019, 7, 1174. [Google Scholar] [CrossRef]
- Strassen, V. Gaussian Elimination is not Optimal. Numer. Math. 1969, 13, 354–356. [Google Scholar] [CrossRef]
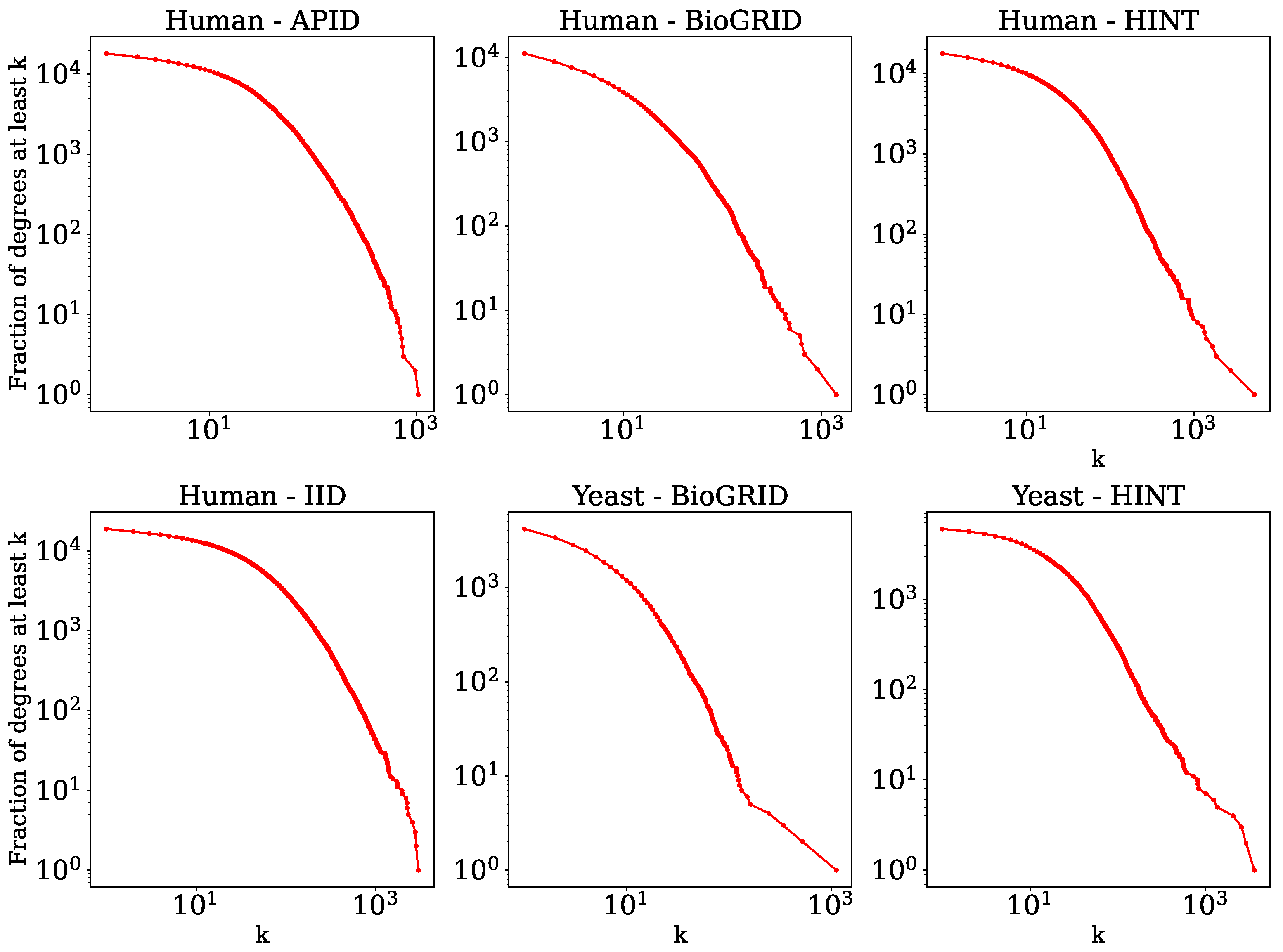



| Network | C | A | SIPs | ||||
|---|---|---|---|---|---|---|---|
| Yeast-BioGRID | 4186 | 20,053 | 9.581 | 0.002 | 0.306 | −0.080 | 826 |
| Yeast-HINT | 6025 | 92,201 | 30.606 | 0.005 | 0.304 | −0.129 | 1837 |
| Human-BioGRID | 11,134 | 79,536 | 14.287 | 0.001 | 0.200 | −0.063 | 1254 |
| Human-HINT | 17,818 | 256,972 | 28.844 | 0.002 | 0.129 | −0.059 | 5223 |
| Human-APID | 18,173 | 265,216 | 29.188 | 0.002 | 0.086 | −0.082 | 2488 |
| Human-IID | 18,925 | 560,628 | 59.247 | 0.003 | 0.126 | −0.085 | 4684 |
| AuPR: 10% Removal | ||||||||
|---|---|---|---|---|---|---|---|---|
| Network | QW-A | QW-L | CRW | L3 | PA | CN | AA | SPM |
| Human-APID | 0.058 | 0.013 | 0.018 | 0.025 | 0.003 | 0.013 | 0.014 | 0.053 |
| Human-BioGRID | 0.106 | 0.052 | 0.070 | 0.052 | 0.007 | 0.042 | 0.048 | 0.079 |
| Human-HINT | 0.081 | 0.026 | 0.023 | 0.037 | 0.008 | 0.019 | 0.023 | 0.078 |
| Human-IID | 0.096 | 0.015 | 0.014 | 0.030 | 0.013 | 0.022 | 0.025 | 0.093 |
| Yeast-BioGRID | 0.156 | 0.102 | 0.158 | 0.082 | 0.007 | 0.059 | 0.073 | 0.114 |
| Yeast-HINT | 0.115 | 0.057 | 0.077 | 0.068 | 0.032 | 0.049 | 0.055 | 0.101 |
| AuPR: 50% Removal | ||||||||
|---|---|---|---|---|---|---|---|---|
| Network | QW-A | QW-L | CRW | L3 | PA | CN | AA | SPM |
| Human-APID | 0.093 | 0.031 | 0.037 | 0.089 | 0.015 | 0.034 | 0.041 | 0.097 |
| Human-BioGRID | 0.168 | 0.091 | 0.129 | 0.152 | 0.032 | 0.089 | 0.111 | 0.135 |
| Human-HINT | 0.141 | 0.055 | 0.072 | 0.125 | 0.033 | 0.055 | 0.072 | 0.136 |
| Human-IID | 0.145 | 0.046 | 0.059 | 0.114 | 0.056 | 0.078 | 0.090 | 0.167 |
| Yeast-BioGRID | 0.217 | 0.162 | 0.242 | 0.207 | 0.030 | 0.108 | 0.149 | 0.173 |
| Yeast-HINT | 0.235 | 0.116 | 0.226 | 0.206 | 0.116 | 0.120 | 0.154 | 0.217 |
| Human | Yeast | |||||
|---|---|---|---|---|---|---|
| Model | APID | BioGRID | IID | HINT | BioGRID | HINT |
| QW-A | 4.15 ± 0.05 | 1.05 ± 0.01 | 5.39 ± 0.14 | 4.52 ± 0.03 | 0.13 ± 0.00 | 0.39 ± 0.00 |
| QW-L | 4.69 ± 0.03 | 1.2 ± 0.01 | 6.03 ± 0.14 | 5.02 ± 0.03 | 0.14 ± 0.00 | 0.44 ± 0.00 |
| CRW | 3.23 ± 0.05 | 0.82 ± 0.02 | 4.43 ± 0.05 | 3.52 ± 0.08 | 0.05 ± 0.00 | 0.17 ± 0.00 |
| L3 | 0.54 ± 0.05 | 0.1 ± 0.01 | 1.15 ± 0.04 | 0.55 ± 0.03 | 0.01 ± 0.00 | 0.1 ± 0.00 |
| PA | 0.23 ± 0.03 | 0.04 ± 0.01 | 0.33 ± 0.03 | 0.18 ± 0.03 | 0.01 ± 0.00 | 0.03 ± 0.00 |
| CN | 0.23 ± 0.04 | 0.04 ± 0.01 | 0.39 ± 0.04 | 0.21 ± 0.03 | 0.01 ± 0.00 | 0.03 ± 0.00 |
| AA | 0.27 ± 0.05 | 0.05 ± 0.01 | 0.41 ± 0.03 | 0.24 ± 0.03 | 0.01 ± 0.00 | 0.04 ± 0.00 |
| SPM | 27.28 ± 1.27 | 6.38 ± 0.03 | 29.68 ± 0.50 | 24.67 ± 0.11 | 0.84 ± 0.01 | 2.67 ± 0.01 |
| AuROC: 10% Removal | ||||||||
|---|---|---|---|---|---|---|---|---|
| Network | QW-A | QW-L | CRW | L3 | PA | CN | AA | SPM |
| Human-APID | 0.930 | 0.917 | 0.933 | 0.936 | 0.888 | 0.812 | 0.814 | 0.897 |
| Human-BioGRID | 0.932 | 0.928 | 0.935 | 0.936 | 0.888 | 0.877 | 0.879 | 0.901 |
| Human-HINT | 0.943 | 0.931 | 0.945 | 0.947 | 0.904 | 0.846 | 0.851 | 0.913 |
| Human-IID | 0.945 | 0.923 | 0.942 | 0.944 | 0.911 | 0.896 | 0.901 | 0.924 |
| Yeast-BioGRID | 0.914 | 0.911 | 0.918 | 0.917 | 0.838 | 0.873 | 0.878 | 0.876 |
| Yeast-HINT | 0.939 | 0.926 | 0.946 | 0.939 | 0.909 | 0.893 | 0.906 | 0.919 |
| AuROC: 50% Removal | ||||||||
|---|---|---|---|---|---|---|---|---|
| Network | QW-A | QW-L | CRW | L3 | PA | CN | AA | SPM |
| Human-APID | 0.910 | 0.900 | 0.918 | 0.908 | 0.883 | 0.717 | 0.717 | 0.870 |
| Human-BioGRID | 0.906 | 0.903 | 0.910 | 0.899 | 0.877 | 0.779 | 0.780 | 0.860 |
| Human-HINT | 0.924 | 0.915 | 0.931 | 0.925 | 0.898 | 0.760 | 0.762 | 0.879 |
| Human-IID | 0.930 | 0.915 | 0.934 | 0.936 | 0.909 | 0.838 | 0.841 | 0.898 |
| Yeast-BioGRID | 0.874 | 0.871 | 0.877 | 0.859 | 0.821 | 0.775 | 0.777 | 0.784 |
| Yeast-HINT | 0.922 | 0.910 | 0.931 | 0.926 | 0.904 | 0.833 | 0.845 | 0.890 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goldsmith, M.; Saarinen, H.; García-Pérez, G.; Malmi, J.; Rossi, M.A.C.; Maniscalco, S. Link Prediction with Continuous-Time Classical and Quantum Walks. Entropy 2023, 25, 730. https://doi.org/10.3390/e25050730
Goldsmith M, Saarinen H, García-Pérez G, Malmi J, Rossi MAC, Maniscalco S. Link Prediction with Continuous-Time Classical and Quantum Walks. Entropy. 2023; 25(5):730. https://doi.org/10.3390/e25050730
Chicago/Turabian StyleGoldsmith, Mark, Harto Saarinen, Guillermo García-Pérez, Joonas Malmi, Matteo A. C. Rossi, and Sabrina Maniscalco. 2023. "Link Prediction with Continuous-Time Classical and Quantum Walks" Entropy 25, no. 5: 730. https://doi.org/10.3390/e25050730
APA StyleGoldsmith, M., Saarinen, H., García-Pérez, G., Malmi, J., Rossi, M. A. C., & Maniscalco, S. (2023). Link Prediction with Continuous-Time Classical and Quantum Walks. Entropy, 25(5), 730. https://doi.org/10.3390/e25050730







