Exponential Consensus of Multi-Agent Systems under Event-Triggered Impulsive Control with Actuation Delays
Abstract
:1. Introduction
- A novel ETIM is proposed, which can exclude Zeno behavior and realize the exponential consensus. With the designed ETIM, some LMI-based sufficient conditions are proposed to achieve the exponential consensus. Moreover, compared with the existing results, the threshold condition is only time-dependent, so the triggered information does not need to be memorized, which makes it easy to implement.
- Different actuation delays are considered in the system model, and it is more general and practical than [32], as delays are not always the same. Compared with [33], restrictions on the decay rate are not required. Since different actuation delays are considered in the impulsive control, the main challenge lies in the estimation of the error state at each triggering instant and the combination of the system dynamics and the designed event-triggered mechanism.
- In comparison to the system with a fixed actuation delay studied in [32], the system proposed in this paper is more versatile as it considers different actuation delays at each impulse instant. Moreover, by utilizing ETIM, our system is capable of achieving exponential consensus.
2. Preliminaries
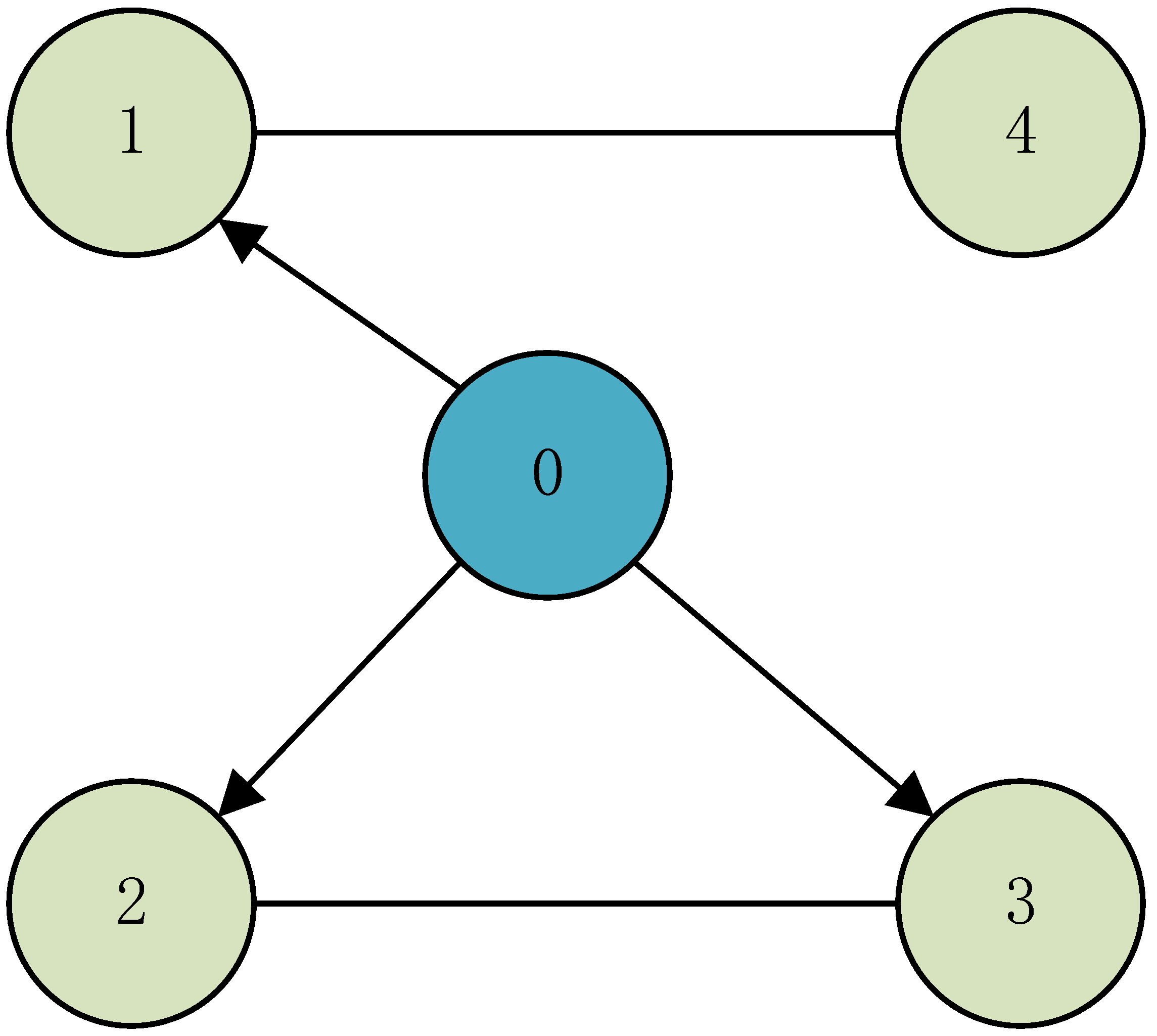
2.1. Graph Notions
2.2. Model Description
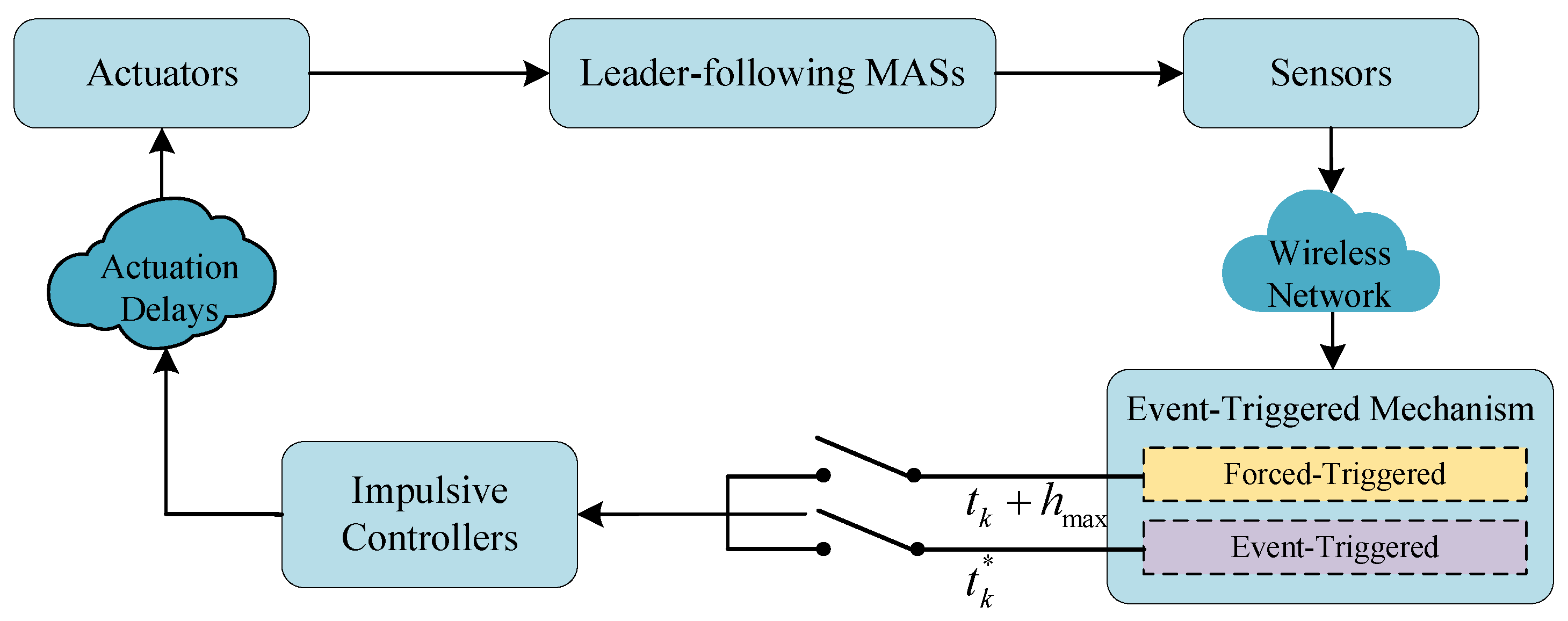
2.3. Event-Triggered Mechanism
2.4. Definitions, Lemmas, and Assumptions
3. Main Results
3.1. Exclusion of Zeno Behavior
3.2. Consensus Analysis
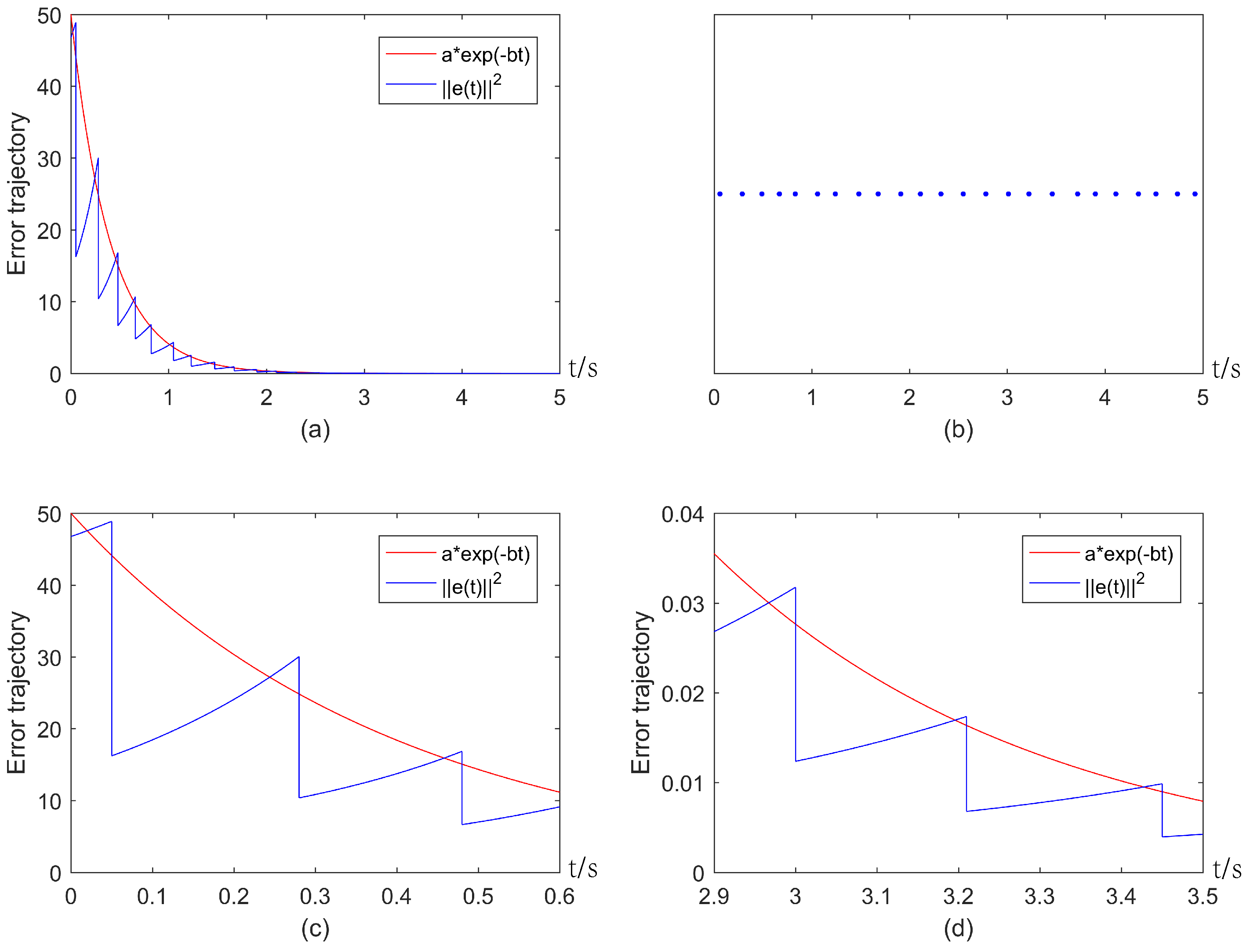
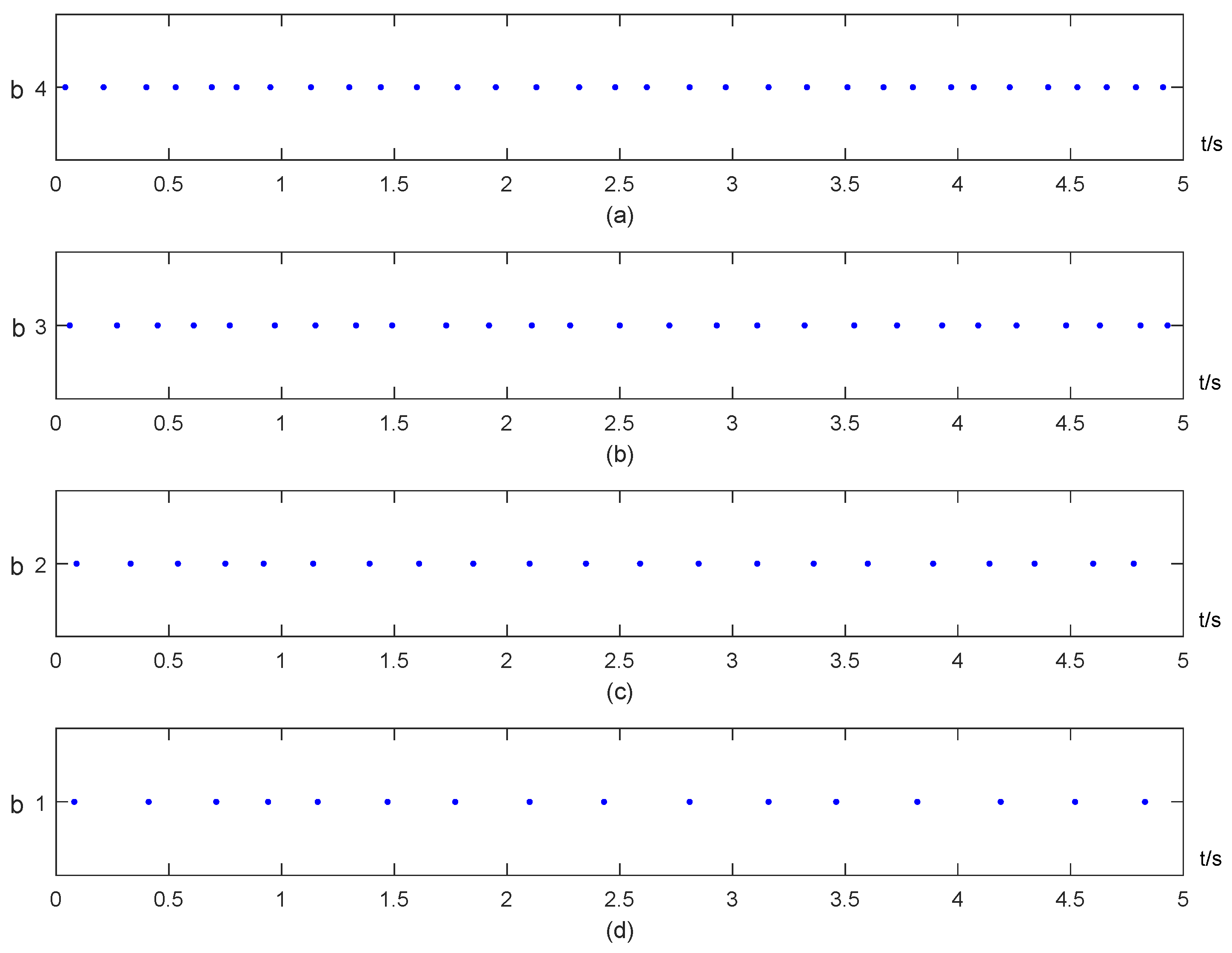
4. Numerical Example
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Zhuang, J.; Peng, S.; Wang, Y. Leader-Following Consensus of Discrete-Time Stochastic Nonlinear Multiagent Systems Under Fixed and Switching Topologies via Impulsive Control. IEEE Syst. J. 2022, 16, 6021–6030. [Google Scholar] [CrossRef]
- Wen, G.; Duan, Z.; Yu, W.; Chen, G. Consensus in multi-agent systems with communication constraints. Int. J. Robust Nonlinear Control 2012, 22, 170–182. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhu, Y.; Wang, L. Consensus of heterogeneous multi-agent systems. IET Control Theory Appl. 2011, 5, 1881–1888. [Google Scholar] [CrossRef]
- Li, Y.; Tan, C. A survey of the consensus for multi-agent systems. Syst. Sci. Control Eng. 2019, 7, 468–482. [Google Scholar] [CrossRef]
- Liang, H.; Chen, L.; Pan, Y.; Lam, H.K. Fuzzy-based robust precision consensus tracking for uncertain networked systems with cooperative-antagonistic interactions. IEEE Trans. Fuzzy Syst. 2022, 31, 1362–1376. [Google Scholar] [CrossRef]
- Cao, L.; Pan, Y.; Liang, H.; Huang, T. Observer-Based Dynamic Event-Triggered Control for Multiagent Systems With Time-Varying Delay. IEEE Trans. Cybern. 2022, 53, 3376–3387. [Google Scholar] [CrossRef]
- Liu, T.; Jiang, Z.P. Distributed formation control of nonholonomic mobile robots without global position measurements. Automatica 2013, 49, 592–600. [Google Scholar] [CrossRef]
- Liu, F.; Dong, X.; Li, Q.; Ren, Z. Robust multi-agent differential games with application to cooperative guidance. Aerosp. Sci. Technol. 2021, 111, 106568. [Google Scholar] [CrossRef]
- Wang, C.; Yan, C.; Liu, Z. Leader-following consensus for second-order nonlinear multi-agent systems under Markovian switching topologies with application to ship course-keeping. Int. J. Control Autom. Syst. 2021, 19, 54–62. [Google Scholar] [CrossRef]
- Olfati-Saber, R.; Fax, J.A.; Murray, R.M. Consensus and cooperation in networked multi-agent systems. Proc. IEEE 2007, 95, 215–233. [Google Scholar] [CrossRef]
- Wang, J.; Yang, C.; Xia, J.; Wu, Z.G.; Shen, H. Observer-based sliding mode control for networked fuzzy singularly perturbed systems under weighted try-once-discard protocol. IEEE Trans. Fuzzy Syst. 2021, 30, 1889–1899. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, H.; Sun, S.; Gao, Z. Leader-follower consensus control for linear multi-agent systems by fully distributed edge-event-triggered adaptive strategies. Inf. Sci. 2021, 555, 314–338. [Google Scholar] [CrossRef]
- Hu, W.; Liu, L.; Feng, G. Consensus of linear multi-agent systems by distributed event-triggered strategy. IEEE Trans. Cybern. 2015, 46, 148–157. [Google Scholar] [CrossRef] [PubMed]
- Yi, X.; Liu, K.; Dimarogonas, D.V.; Johansson, K.H. Dynamic event-triggered and self-triggered control for multi-agent systems. IEEE Trans. Autom. Control 2018, 64, 3300–3307. [Google Scholar] [CrossRef]
- Zou, W.; Xiang, Z. Event-triggered leader–following consensus of non-linear multi-agent systems with switched dynamics. IET Control Theory Appl. 2019, 13, 1222–1228. [Google Scholar] [CrossRef]
- Guan, Z.H.; Wu, Y.; Feng, G. Consensus analysis based on impulsive systems in multiagent networks. IEEE Trans. Circuits Syst. I Regul. Pap. 2011, 59, 170–178. [Google Scholar] [CrossRef]
- Li, X.; Cao, J.; Ho, D.W. Impulsive control of nonlinear systems with time-varying delay and applications. IEEE Trans. Cybern. 2019, 50, 2661–2673. [Google Scholar] [CrossRef]
- He, W.; Chen, G.; Han, Q.L.; Qian, F. Network-based leader-following consensus of nonlinear multi-agent systems via distributed impulsive control. Inf. Sci. 2017, 380, 145–158. [Google Scholar] [CrossRef]
- Yang, T. Impulsive Control Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2001; Volume 272. [Google Scholar]
- Zhuang, J.; Peng, S.; Wang, Y. Exponential consensus of nonlinear stochastic discrete-time multi-agent systems with time-varying delay via impulsive control. Int. J. Syst. Sci. 2022, 53, 3286–3301. [Google Scholar] [CrossRef]
- Dimarogonas, D.V.; Frazzoli, E.; Johansson, K.H. Distributed Event-Triggered Control for Multi-Agent Systems. IEEE Trans. Autom. Control 2012, 57, 1291–1297. [Google Scholar] [CrossRef]
- Xu, Z.; Li, C.; Han, Y. Leader-following fixed-time quantized consensus of multi-agent systems via impulsive control. J. Frankl. Inst. 2019, 356, 441–456. [Google Scholar] [CrossRef]
- Xu, W.; Ho, D.W. Clustered event-triggered consensus analysis: An impulsive framework. IEEE Trans. Ind. Electron. 2016, 63, 7133–7143. [Google Scholar] [CrossRef]
- Tan, X.; Cao, J.; Li, X. Consensus of leader-following multiagent systems: A distributed event-triggered impulsive control strategy. IEEE Trans. Cybern. 2018, 49, 792–801. [Google Scholar] [CrossRef] [PubMed]
- Hu, Z.; Mu, X. Event-Triggered Impulsive Control for Nonlinear Stochastic Systems. IEEE Trans. Cybern. 2022, 52, 7805–7813. [Google Scholar] [CrossRef]
- Li, X.; Song, S.; Wu, J. Exponential stability of nonlinear systems with delayed impulses and applications. IEEE Trans. Autom. Control 2019, 64, 4024–4034. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, K.; Xie, W.C. Consensus of multi-agent systems via hybrid impulsive protocols with time-delay. Nonlinear Anal. Hybrid Syst. 2018, 30, 134–146. [Google Scholar] [CrossRef]
- You, X.; Hua, C.; Peng, D.; Guan, X. Leader–following consensus for multi-agent systems subject to actuator saturation with switching topologies and time-varying delays. IET Control Theory Appl. 2016, 10, 144–150. [Google Scholar] [CrossRef]
- Wang, M.; Wu, S.; Li, X. Event-triggered delayed impulsive control for nonlinear systems with applications. J. Frankl. Inst. 2021, 358, 4277–4291. [Google Scholar] [CrossRef]
- Wang, M.; Li, X.; Duan, P. Event-triggered delayed impulsive control for nonlinear systems with application to complex neural networks. Neural Netw. 2022, 150, 213–221. [Google Scholar] [CrossRef]
- Gu, K.; Chen, J.; Kharitonov, V.L. Stability of Time-Delay Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Zhang, K.; Braverman, E. Event-Triggered Impulsive Control for Nonlinear Systems With Actuation Delays. IEEE Trans. Autom. Control 2023, 68, 540–547. [Google Scholar] [CrossRef]
- Wang, X.; Lemmon, M. On event design in event-triggered feedback systems. Automatica 2011, 47, 2319–2322. [Google Scholar] [CrossRef]
- Ma, Q.; Qin, J.; Yu, X.; Wang, L. On necessary and sufficient conditions for exponential consensus in dynamic networks via uniform complete observability theory. IEEE Trans. Autom. Control 2020, 66, 4975–4981. [Google Scholar] [CrossRef]
- Huang, L.; Mao, X. Robust delayed-state-feedback stabilization of uncertain stochastic systems. Automatica 2009, 45, 1332–1339. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Peng, S. Exponential Consensus of Multi-Agent Systems under Event-Triggered Impulsive Control with Actuation Delays. Entropy 2023, 25, 877. https://doi.org/10.3390/e25060877
Zhang J, Peng S. Exponential Consensus of Multi-Agent Systems under Event-Triggered Impulsive Control with Actuation Delays. Entropy. 2023; 25(6):877. https://doi.org/10.3390/e25060877
Chicago/Turabian StyleZhang, Jian, and Shiguo Peng. 2023. "Exponential Consensus of Multi-Agent Systems under Event-Triggered Impulsive Control with Actuation Delays" Entropy 25, no. 6: 877. https://doi.org/10.3390/e25060877





