Autonomic Nervous System Influences on Cardiovascular Self-Organized Criticality
Abstract
1. Introduction
2. Materials and Methods
2.1. Subjects
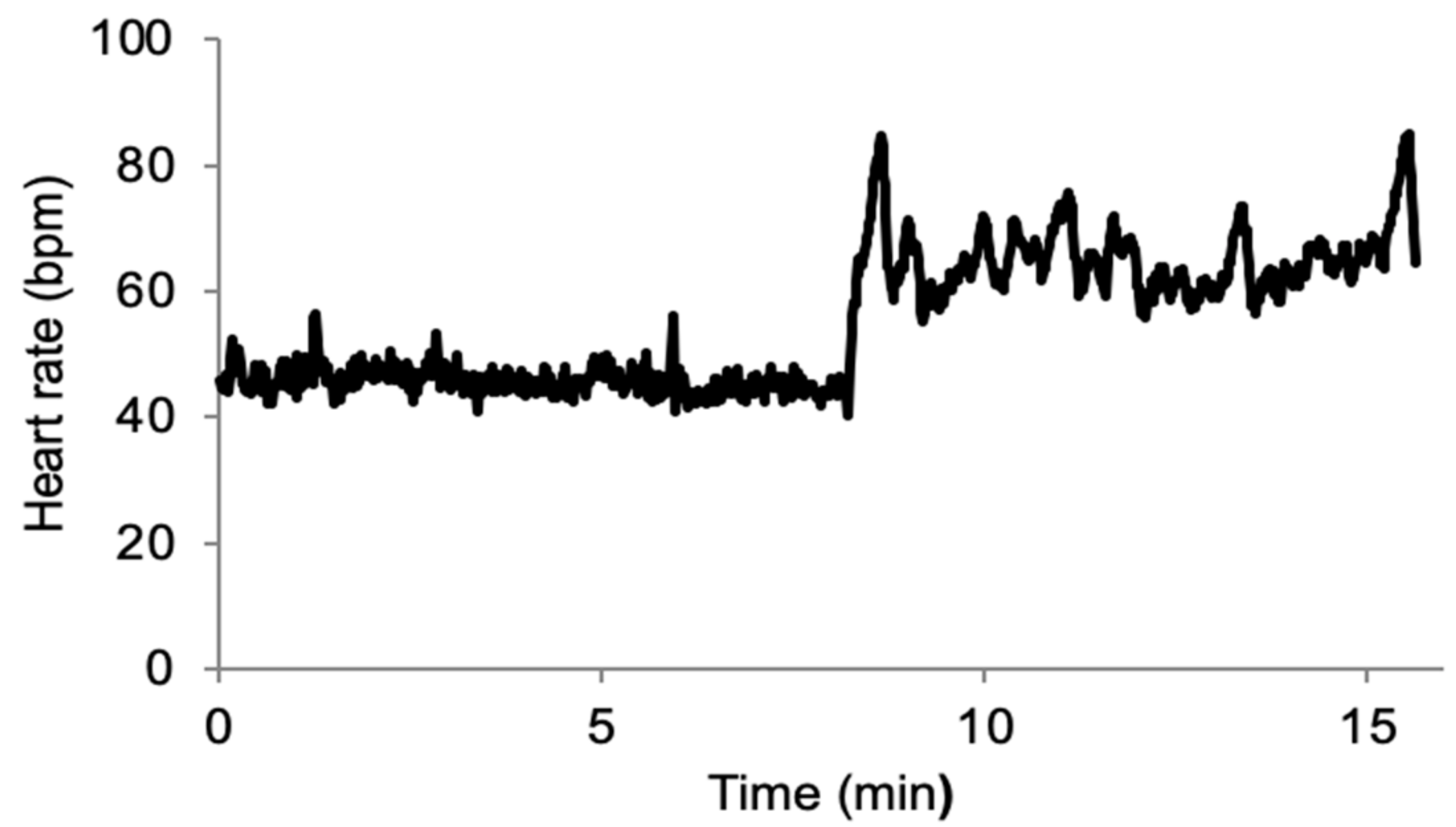
2.2. Experiment
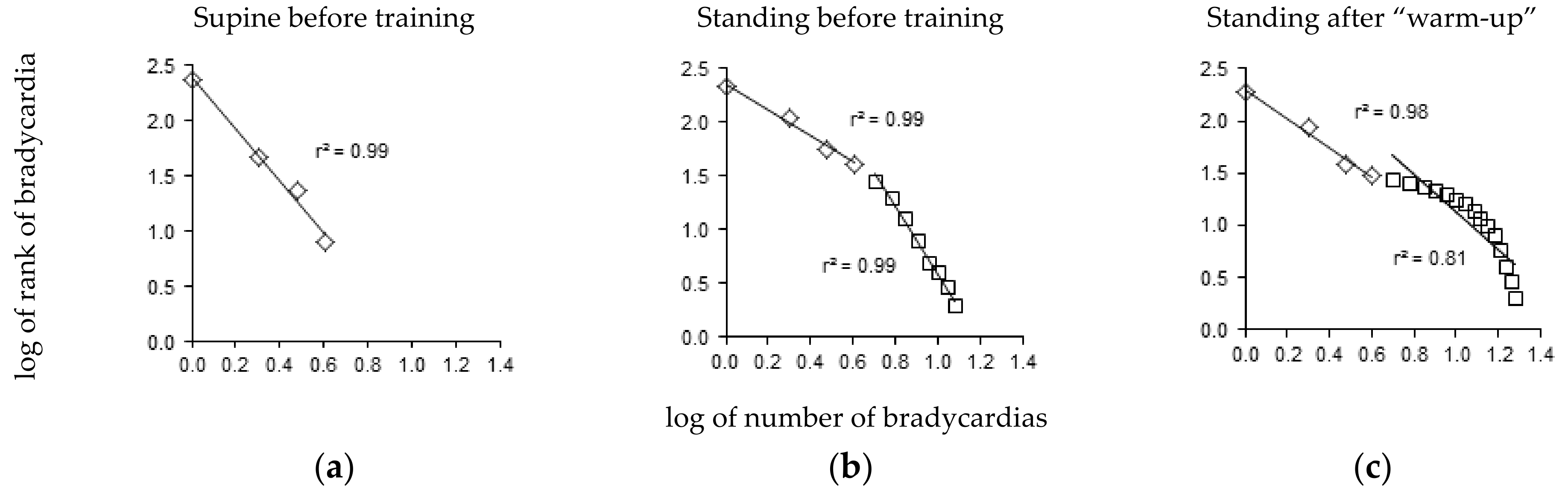
2.3. Data Analysis
2.4. Statistics
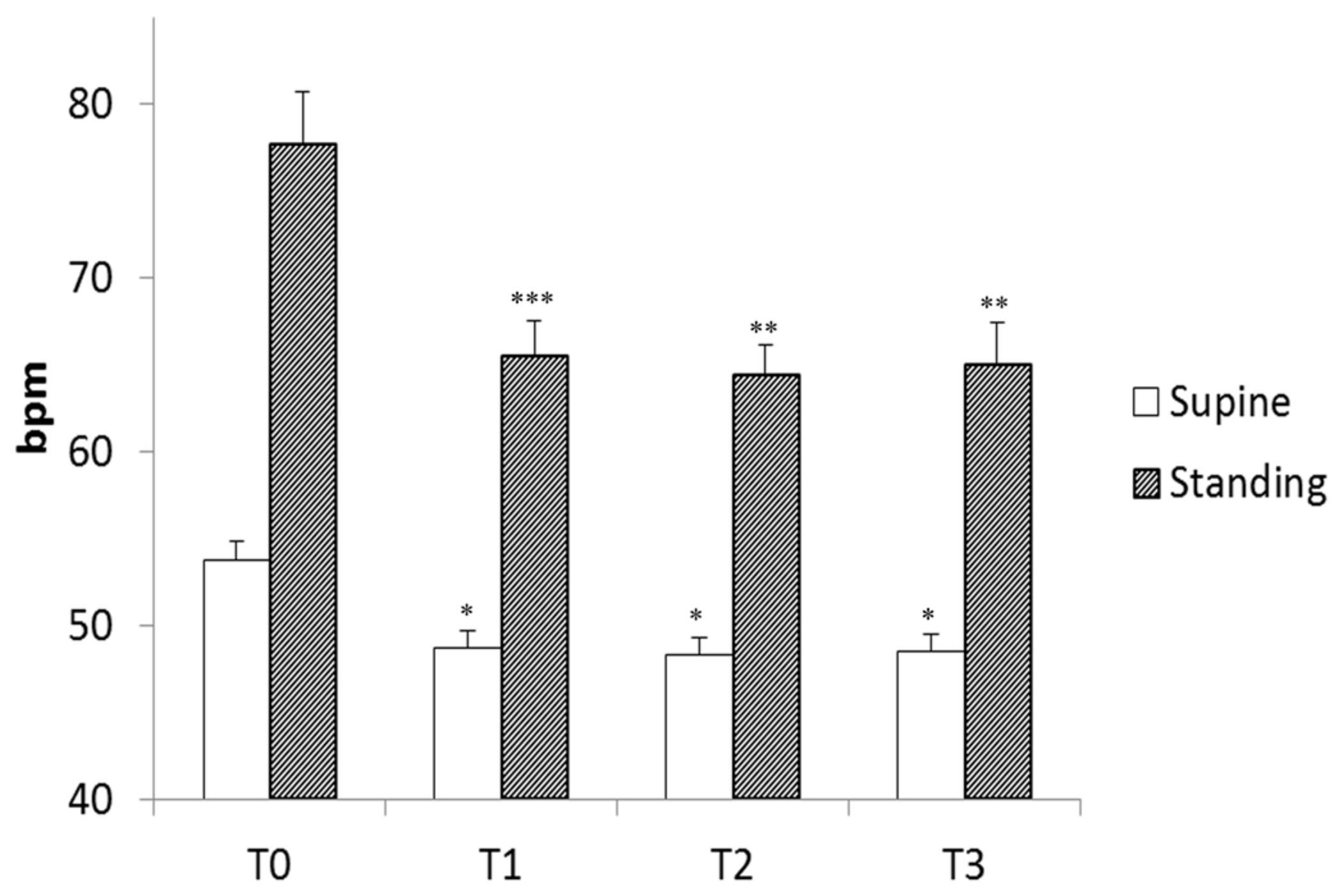
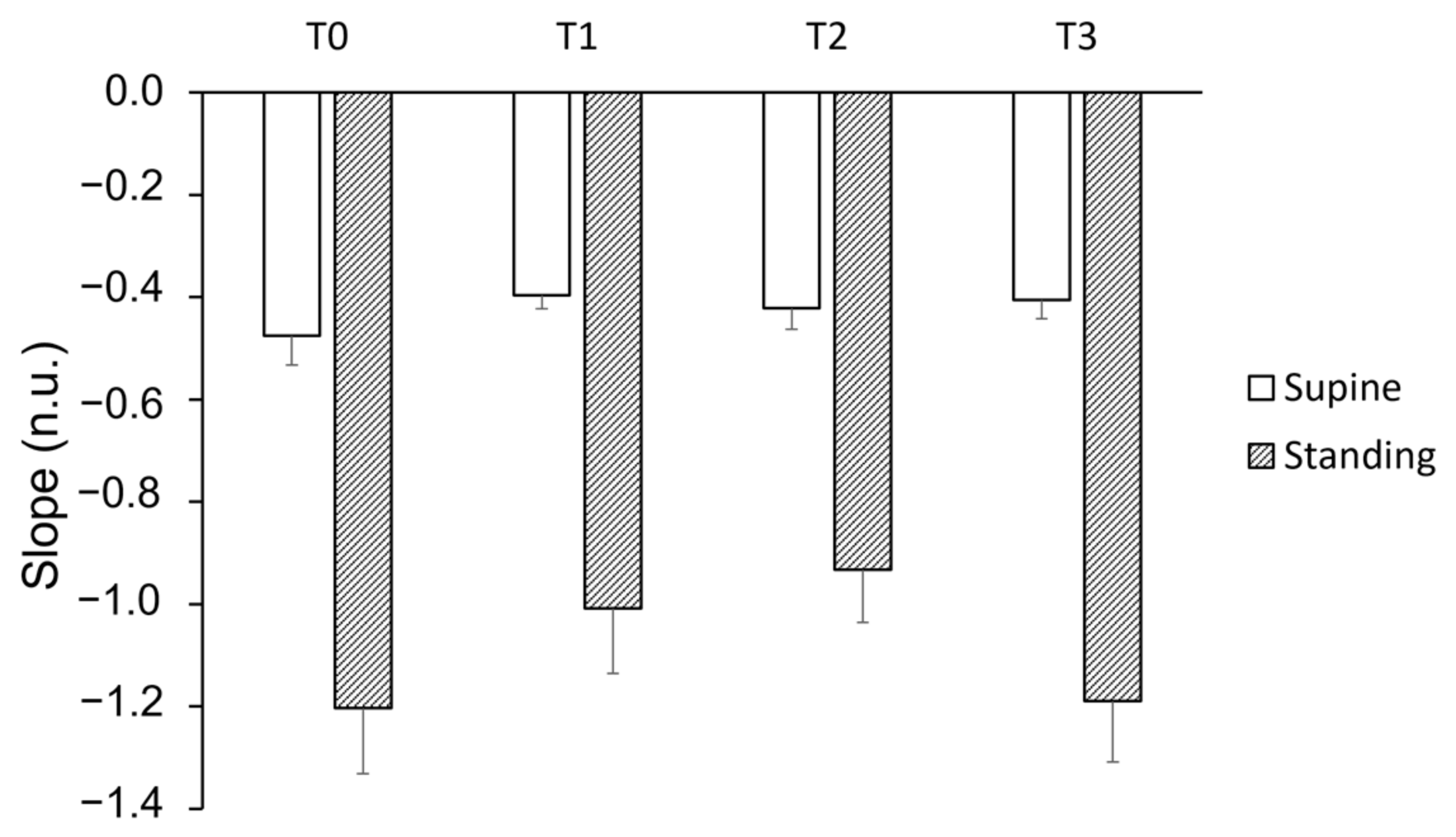
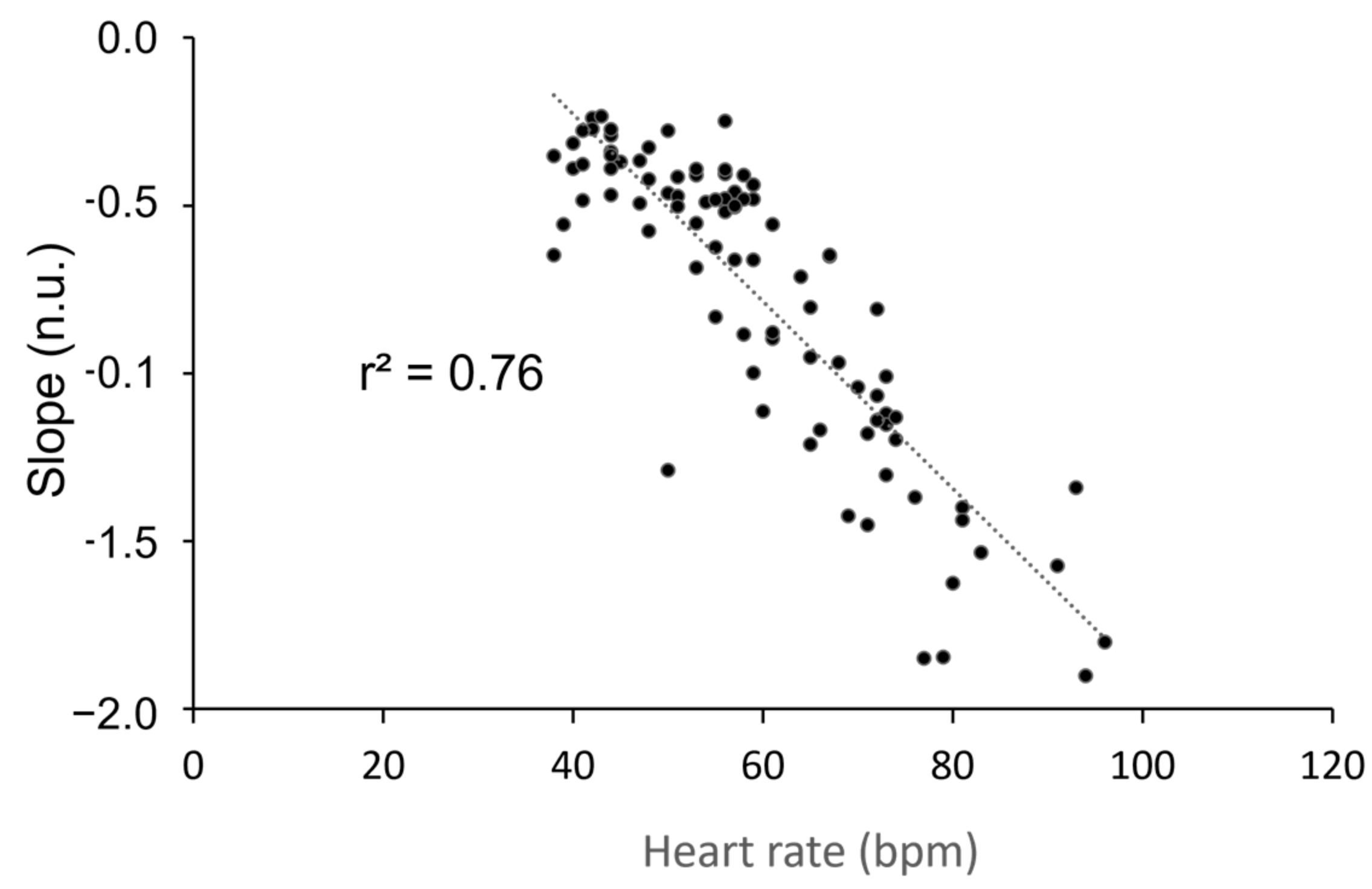
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Goldstein, D.S. How does homeostasis happen? Integrative physiological, systems biological, and evolutionary perspectives. Am. J. Physiol. 2019, 316, R301–R317. [Google Scholar] [CrossRef] [PubMed]
- Billman, G.E. Homeostasis: The underappreciated and far too often ignored central organizing principle of physiology. Front. Physiol. 2020, 11, 200. [Google Scholar] [CrossRef] [PubMed]
- Struzik, Z.R. Is heart rate variability dynamics poised at criticality? In Proceedings of the 8th Conference of the European Study Group on Cardiovascular Oscillations (ESGCO), Trento, Italy, 25–28 May 2014; IEEE: Piscataway, NJ, USA, 2014.
- Muñoz, M.A. Colloquium: Criticality and dynamical scaling in living systems. Rev. Mod. Phys. 2018, 90, 031001. [Google Scholar] [CrossRef]
- Leonor Rivera, A.; Toledo-Roy, J.C.; Frank, A. Symmetry and Signs of Self-Organized Criticality in Living Organisms. J. Phys. Conf. Ser. 2020, 1612, 012024. [Google Scholar] [CrossRef]
- Koushanpour, E. Baroreceptor discharge behavior and resetting. In Baroreceptor Reflexes. Integrative Functions and Clinical Aspect; Persson, P.B., Kirchheim, H.R., Eds.; Springer: Berlin, Germany, 1991; pp. 9–44. [Google Scholar]
- Bak, P. How Nature Works: The Science of Self-Organised Criticality; Copernicus Press: New York, NY, USA, 1996; pp. 1–212. [Google Scholar]
- Crosby, N.B. Introduction. In Self-Organized Criticality Systems; Aschwanden, M.J., Ed.; Open Academic Press: Berlin, Germany; Warsaw, Poland,, 2013; pp. 1–21. [Google Scholar]
- Marković, D.; Gros, C. Power laws and self-organized criticality in theory and nature. Phys. Rep. 2014, 536, 41–74. [Google Scholar] [CrossRef]
- Mora, T.; Bialek, W. Are biological systems poised at criticality? J. Stat. Phys. 2011, 144, 268–302. [Google Scholar] [CrossRef]
- Grubb, B.P. Neurocardiogenic syncope and related disorders of orthostatic intolerance. Circulation 2005, 111, 2997–3006. [Google Scholar] [CrossRef]
- Fortrat, J.O.; Gharib, C. Self-organization of blood pressure regulation: Clinical evidence. Front. Physiol. 2016, 7, 113. [Google Scholar] [CrossRef]
- Fortrat, J.O. Zipf’s law of vasovagal heart rate variability sequences. Entropy 2020, 22, 413. [Google Scholar] [CrossRef]
- Rowell, L.B. Passive effect of gravity. In Human Cardiovascular Control; Oxford University Press: New York, NY, USA, 1993; pp. 3–36. [Google Scholar]
- Ravé, G.; Zouhal, H.; Boullosa, D.; Doyle-Baker, P.K.; Saeidi, A.; Abderrahman, A.B.; Fortrat, J.O. Heart rate variability is correlated with perceived physical fitness in elite soccer players. J. Hum. Kinet. 2020, 72, 141–150. [Google Scholar] [CrossRef]
- Ravé, G.; Fortrat, J.O. Heart rate variability in the standing position reflects training adaptation in professional soccer players. Eur. J. Appl. Physiol. 2016, 116, 1575–1582. [Google Scholar] [CrossRef] [PubMed]
- Ravé, G.; Fortrat, J.O.; Dawson, B.; Carre, F.; Dupont, G.; Saeidi, A.; Boullosa, D.; Zouhal, H. Heart rate recovery and heart rate variability: Use and relevance in European professional soccer. Int. J. Perform. Anal. Sport 2018, 18, 168–183. [Google Scholar] [CrossRef]
- Task Force of the European Society of Cardiology and the North American Society of Pacing and Electrophysiology. Heart rate variability: Standards of measurement, physiological interpretation and clinical use. Circulation 1996, 93, 1043–1065. [Google Scholar] [CrossRef]
- Akselrod, S.; Gordon, D.; Ubel, F.A.; Shannon, D.C.; Berger, A.C.; Cohen, R.J. Power spectrum analysis of heart rate fluctuation: A quantitative probe of beat-to-beat cardiovascular control. Science 1981, 213, 220–222. [Google Scholar] [CrossRef]
- Kobayashi, M.; Musha, T. 1/f fluctuation of heartbeat period. IEEE Trans. Biomed. Eng. 1982, 29, 456–457. [Google Scholar] [CrossRef]
- Racz, F.S.; Mukli, P.; Nagy, Z.; Eke, A. Multifractal dynamics of resting-state functional connectivity in the prefrontal cortex. Physiol. Meas. 2018, 39, 024003. [Google Scholar] [CrossRef] [PubMed]
- Mukli, P.; Nagy, Z.; Racz, F.S.; Portoro, I.; Hartmann, A.; Stylianou, O.; Debreczeni, R.; Bereczki, D.; Eke, A. Two-tiered response of cardiorespiratory-cerebrovascular network to orthostatic challenge. Front. Physiol. 2021, 12, 622569. [Google Scholar] [CrossRef]
- Schöner, G.; Kelso, J.A. Dynamic pattern generation in behavioral and neural systems. Science 1988, 239, 1513–1520. [Google Scholar] [CrossRef]
- Fortrat, J.O.; Levrard, T.; Courcinous, S.; Victor, J. Self-organization of blood pressure regulation: Experimental evidence. Front. Physiol. 2016, 7, 112. [Google Scholar] [CrossRef]
- Bak, P.; Tang, C.; Wiesenfeld, K. Self-organized criticality. Phys. Rev. A 1988, 38, 364–374. [Google Scholar] [CrossRef]
- Kalda, J.; Sakki, M.; Vainu, M.; Laan, M. Zipf’s law in human heart beat dynamics. arXiv 2001, arXiv:physics/0110075v1. [Google Scholar]
- Yang, A.C.; Hseu, S.S.; Yien, H.W.; Goldberger, A.L.; Peng, C.K. Linguistic analysis of the human heartbeat using frequency and rank order statistics. Phys. Rev. Lett. 2003, 90, 108103. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez, J.; Prieto, S.; Correa, C.; Mendoza, F.; Weiz, G.; Soracipa, Y.; Velásquez, N.; Pardo, J.; Martínez, M.; Barrios, F. Physical mathematical evaluation of the cardiac dynamic applying the Zipf-Mandelbrot law. J. Mod. Phys. 2015, 6, 1881–1888. [Google Scholar] [CrossRef]
- Lo, C.C.; Chou, T.; Penzel, T.; Scammell, T.E.; Strecker, R.E.; Stanley, H.E.; Ivanov, P.C. Common scale-invariant patterns of sleep-wake transitions across mammalian species. Proc. Natl. Acad. Sci. USA 2004, 101, 17545–17548. [Google Scholar] [CrossRef]
- Clauset, A.; Shalizi, C.R.; Newman, M.E.J. Power-law distributions in empirical data. SIAM Rev. 2009, 51, 661–703. [Google Scholar] [CrossRef]
- Fortrat, J.O.; Formet, C.; Frutoso, J.; Gharib, C. Even slight movements disturb analysis of cardiovascular dynamics. Am. J. Physiol. 1999, 277, H261–H267. [Google Scholar] [CrossRef]
- Nunes Amaral, L.A.; Ivanov, P.C.; Aoyagi, N.; Hidaka, I.; Tomono, S.; Goldberger, A.L.; Stanley, H.E.; Yamamoto, Y. Behavioral-independent features of complex heartbeat dynamics. Phys. Rev. Lett. 2001, 86, 6026–6029. [Google Scholar] [CrossRef]
- Subramanyan, R. Avalanches in cardiology. Ann. Pediatr. Cardiol. 2021, 14, 401–407. [Google Scholar] [CrossRef]
| T0 | T1 | T2 | T3 | |
|---|---|---|---|---|
| Supine | 0.76 ± 0.04 | 0.71 ± 0.06 | 0.71 ± 0.06 | 0.71 ± 0.04 |
| Standing | 0.61 ± 0.03 | 0.63 ± 0.02 | 0.64 ± 0.03 | 0.68 ± 0.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fortrat, J.-O.; Ravé, G. Autonomic Nervous System Influences on Cardiovascular Self-Organized Criticality. Entropy 2023, 25, 880. https://doi.org/10.3390/e25060880
Fortrat J-O, Ravé G. Autonomic Nervous System Influences on Cardiovascular Self-Organized Criticality. Entropy. 2023; 25(6):880. https://doi.org/10.3390/e25060880
Chicago/Turabian StyleFortrat, Jacques-Olivier, and Guillaume Ravé. 2023. "Autonomic Nervous System Influences on Cardiovascular Self-Organized Criticality" Entropy 25, no. 6: 880. https://doi.org/10.3390/e25060880
APA StyleFortrat, J.-O., & Ravé, G. (2023). Autonomic Nervous System Influences on Cardiovascular Self-Organized Criticality. Entropy, 25(6), 880. https://doi.org/10.3390/e25060880







