Improvement of Error Correction in Nonequilibrium Information Dynamics
Abstract
1. Introduction
2. Memoryless Channel Model and Error Correction
2.1. Memoryless Channel Model and Block Encoding
2.2. Error Correction Decoding
2.3. Random Encoding and Decoding Strategy
2.4. Performance of Error Correction
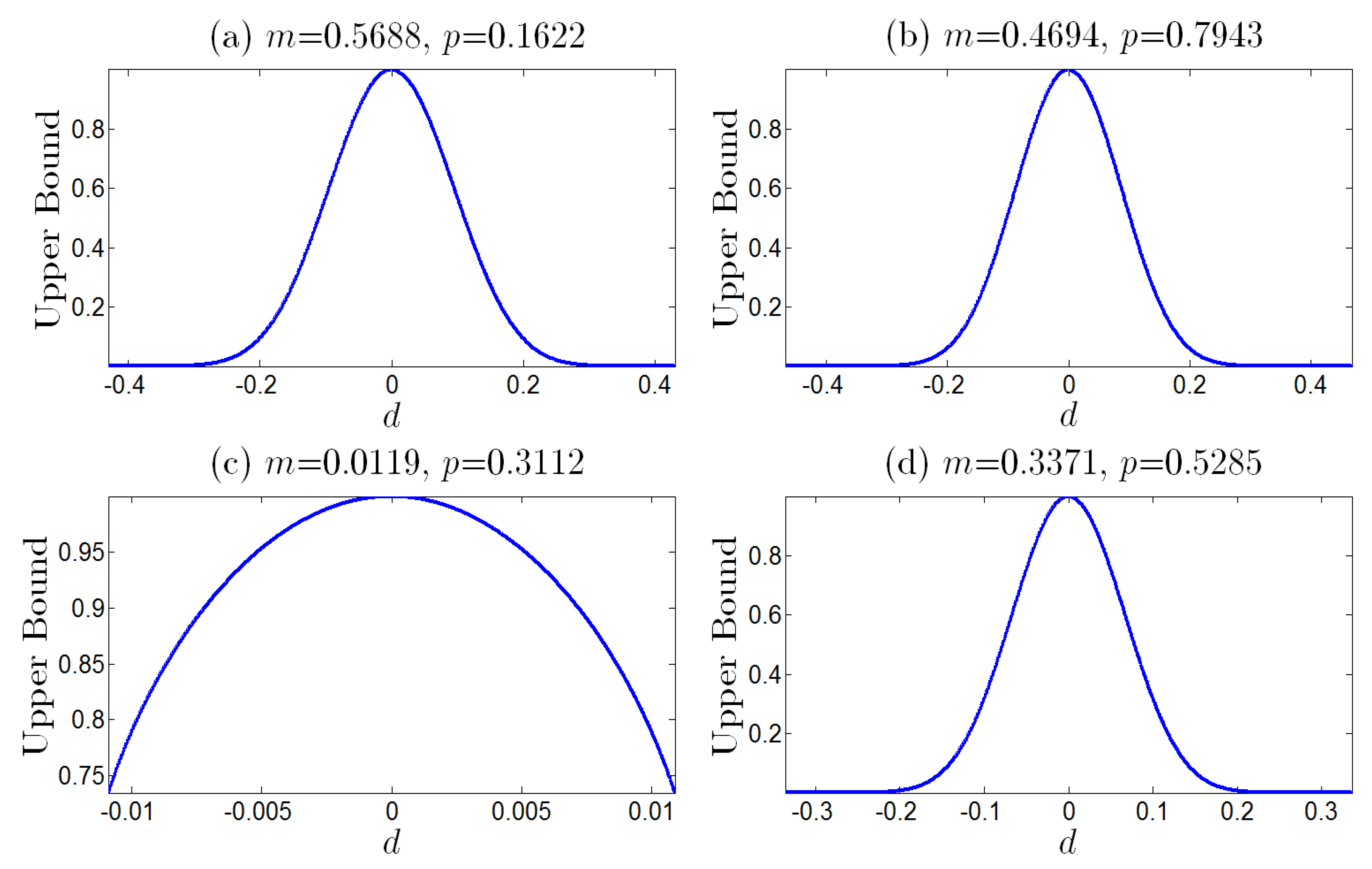
2.5. Concavity of Upper Bound of Error Correction
3. Nonequilibrium Information Dynamics
3.1. Information Dynamics of Memoryless Channel
3.2. Characterization of Nonequilibrium
3.3. Nonequilibrium Decomposition for Transmission Probability
3.4. Nonequilibrium Decomposition for Transmission Probability
4. Nonequilibrium Information Thermodynamics and Performance of Error Correction
Entropy Production Rate Guarantees Reliability of Information Transmission
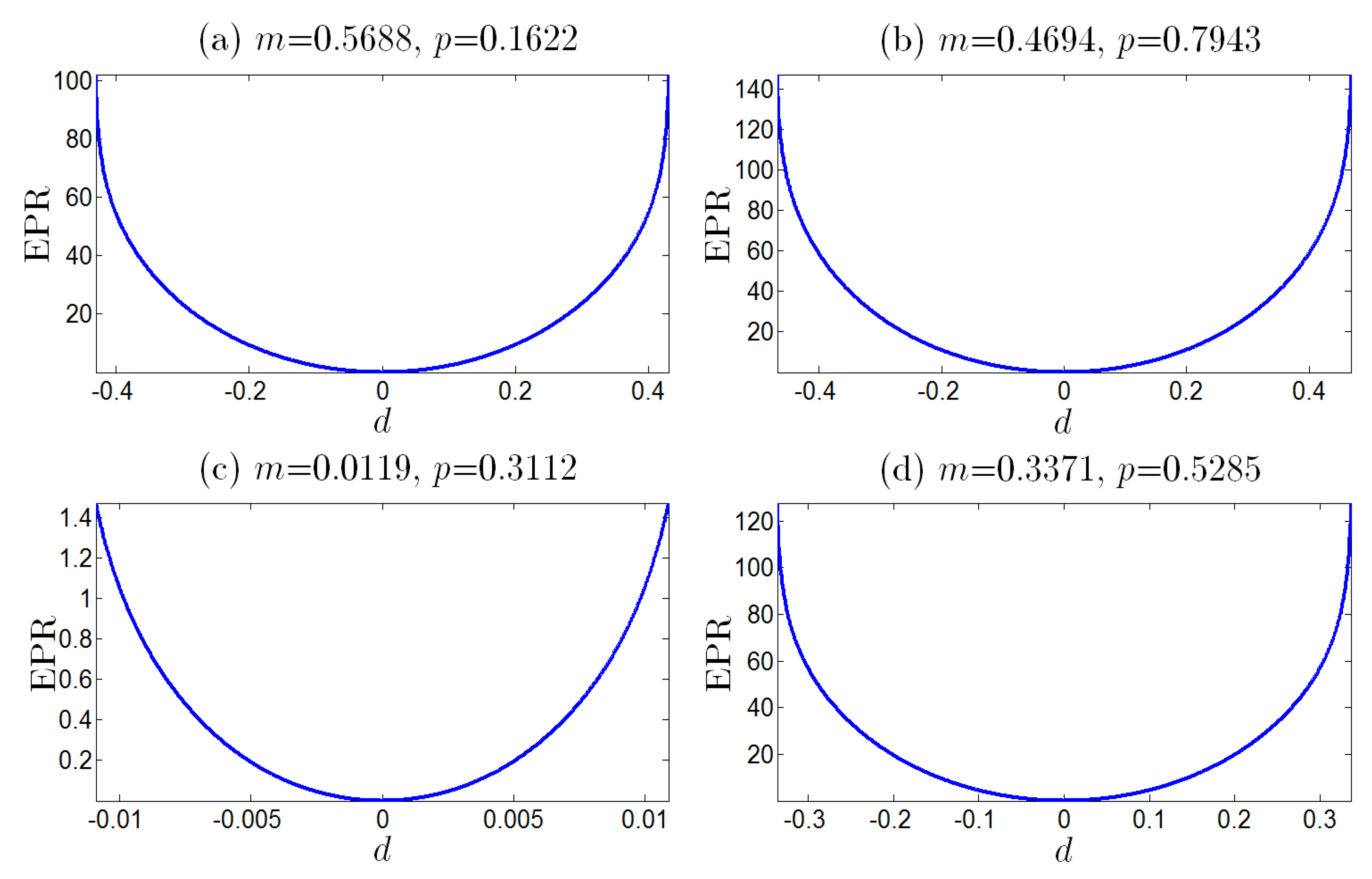
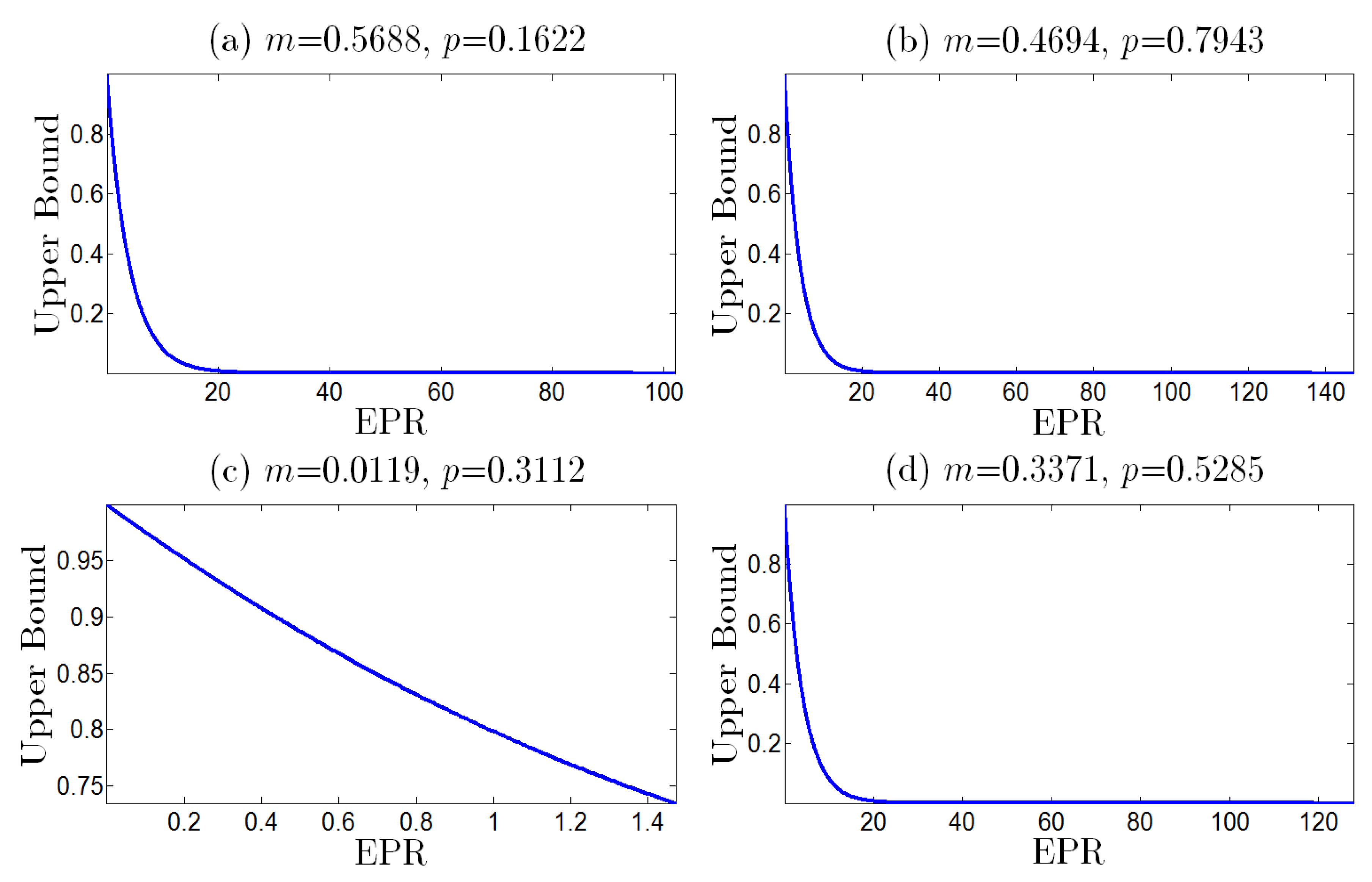
5. Nonequilibrium Dissipation Cost Improves Performance of Error Correction
6. An Illustrative Case of Binary Memoryless Channel
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Hamming, R.W. Error Detecting and Error Correcting Codes. Bell Syst. Tech. J. 1950, 29, 147. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379. [Google Scholar] [CrossRef]
- Gallager, R.G. Low-density parity-check codes. Ire Trans. Inf. Theory 1962, 8, 21. [Google Scholar] [CrossRef]
- Viterbi, A. Approaching the Shannon limit: Theorist’s dream and practitioner’s challenge. In Mobile and Personal Satellite Communications 2; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Crick, F. Central Dogma of Molecular Biology. Nature 1970, 227, 561–563. [Google Scholar] [CrossRef]
- Hopfield, J.J. Kinetic proofreading: A new mechanism for reducing errors in biosynthetic processes requiring high specificity. Proc. Natl. Acad. Sci. USA 1974, 71, 4135–4139. [Google Scholar] [CrossRef] [PubMed]
- Djordjevic, I.B. Classical and quantum error-correction coding in genetics. In Quantum Biological Information Theory; Springer: Berlin/Heidelberg, Germany, 2016; pp. 237–269. [Google Scholar]
- Barbieri, M. Introduction to Biosemiotics: The New Biological Synthesis; Springer: Dordrecht, The Netherlands, 2008. [Google Scholar]
- Faria, L.C.B.; Rocha, A.S.L.; Kleinschmidt, J.H.; Silva-Filho, M.C.; Bim, E.; Herai, R.H.; Yamagishi, M.E.B.; Palazzo, R., Jr. Is a Genome a Codeword of an Error-Correcting Code? PLoS ONE 2012, 7, e36644. [Google Scholar] [CrossRef] [PubMed]
- Hopfield, J.J. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. USA 1974, 71, 4135. [Google Scholar] [CrossRef]
- Kunkel, T.A.; Bebenek, R. DNA replication fidelity. Annu. Rev. Biochem. 2000, 69, 497. [Google Scholar] [CrossRef]
- Kunkel, T.A.; Erie, D.A. DNA mismatch repair. Annu. Rev. Biochem. 2005, 74, 681. [Google Scholar] [CrossRef]
- Liebovitch, L.S.; Tao, Y.; Todorov, A.T.; Levine, L. Is There an Error Correcting Code in the Base Sequence in DNA? Biophys. J. 1996, 71, 1539. [Google Scholar] [CrossRef]
- McKeithan, T.W. Kinetic proofreading in T-cell receptor signal transduction. Proc. Natl. Acad. Sci. USA 1995, 92, 5042. [Google Scholar] [CrossRef] [PubMed]
- Murugan, A.; Vaikuntanathan, S. Biological implications of dynamical phases in non-equilibrium networks. J. Stat. Phys. 2016, 162, 1183. [Google Scholar] [CrossRef]
- Calderbank, A.R.; Rains, E.M.; Shor, P.W.; Sloane, N.J.A. Quantum Error Correction Via Codes Over GF(4). Phys. Rev. Lett. 1997, 78, 405. [Google Scholar] [CrossRef]
- Kitaev, A.Y. Quantum computations: Algorithms and error correction. Russ. Math. Surv. 1997, 52, 1191. [Google Scholar] [CrossRef]
- Knill, E.; Laflamme, R.; Viola, L. Theory of Quantum Error Correction for General Noise. Phys. Rev. Lett. 2000, 84, 2525. [Google Scholar] [CrossRef]
- Moon, T.K. Error Correction Coding: Mathematical Methods and Algorithms; Wiley-Interscience: Hoboken, NJ, USA, 2005. [Google Scholar]
- Sarovar, M.; Young, K.C. Error suppression and error correction in adiabatic quantum computation: Non-equilibrium dynamics. New J. Phys. 2013, 15, 125032. [Google Scholar] [CrossRef]
- Schumacher, B.; Nielsen, M.A. Quantum data processing and error correction. Phys. Rev. A 1996, 54, 2629. [Google Scholar] [CrossRef]
- Gallager, R.G. Information Theory and Reliable Communication; Wiley: New York, NY, USA, 1968. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; Wiley-Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
- Fang, X.N.; Kruse, K.; Lu, T.; Wang, J. Nonequilibrium physics in biology. Rev. Mod. Phys. 2019, 91, 045004. [Google Scholar] [CrossRef]
- Zeng, Q.; Wang, J. Information Landscape and Flux, Mutual Information Rate Decomposition and Connections to Entropy Production. Entropy 2017, 19, 678. [Google Scholar] [CrossRef]
- Zeng, Q.; Wang, J. Non-Markovian nonequilibrium information dynamics. Phys. Rev. E 2018, 98, 032123. [Google Scholar] [CrossRef]
- Andrieux, D.; Gaspard, P.; Ciliberto, S.; Garnier, N.; Joubaud, S.; Petrosyan, A. Entropy production and time asymmetry in nonequilibrium fluctuations. Phys. Rev. Lett. 2007, 98, 150601. [Google Scholar] [CrossRef] [PubMed]
- Crooks, G.E. Entropy production fluctuation theorem and the nonequilibrium work relation for free energy differences. Phys. Rev. E 1999, 60, 2721. [Google Scholar] [CrossRef]
- Crooks, G.E.; Still, S. Marginal and conditional second laws of thermodynamics. Europhys. Lett. 2019, 125, 40005. [Google Scholar] [CrossRef]
- Derrida, B. Non-equilibrium steady states: Fluctuations and large deviations of the density and of the current. J. Stat.-Mech.-Theory Exp. 2007, 45, P07023. [Google Scholar] [CrossRef]
- Dewar, R. Information theory explanation of the fluctuation theorem, maximum entropy production and self-organized criticality in non-equilibrium stationary states. J. Phys. A-Math. Gen. 2003, 36, 631. [Google Scholar] [CrossRef]
- Dewar, R.C. Maximum entropy production and the fluctuation theorem. J. Phys. A-Math. Gen. 2005, 38, L371. [Google Scholar] [CrossRef]
- Evans, D.J.; Searles, D.J. The Fluctuation Theorem. Adv. Phys. 2010, 51, 1529. [Google Scholar] [CrossRef]
- Horowitz, J.M.; Parrondo, J.M.R. Entropy production along nonequilibrium quantum jump trajectories. New J. Phys. 2013, 15, 085028. [Google Scholar] [CrossRef]
- Jarzynski, C. Nonequilibrium Equality for Free Energy Differences. Phys. Rev. Lett. 1997, 78, 2690. [Google Scholar] [CrossRef]
- Ruelle, D. Positivity of entropy production in nonequilibrium statistical mechanics. J. Stat. Phys. 1996, 85, 1. [Google Scholar] [CrossRef]
- Seifert, U. Entropy Production along a Stochastic Trajectory and an Integral Fluctuation Theorem. Phys. Rev. Lett. 2005, 95, 040602. [Google Scholar] [CrossRef] [PubMed]
- Wang, J. Landscape and flux theory of non-equilibrium dynamical systems with application to biology. Adv. Phys. 2015, 64, 1. [Google Scholar] [CrossRef]
- Wang, J.; Li, C.H.; Wang, E.K. Potential and flux landscapes quantify the stability and robustness of budding yeast cell cycle network. Proc. Natl. Acad. Sci. USA 2010, 107, 8195. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Xu, L.; Wang, E.K. Potential landscape and flux framework of nonequilibrium networks: Robustness, dissipation, and coherence of biochemical oscillations. Proc. Natl. Acad. Sci. USA 2008, 105, 12271. [Google Scholar] [CrossRef]
- Boyd, S.P.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2004. [Google Scholar]
- Zeng, Q.; Wang, J. Nonequilibrium Enhanced Classical Measurement and Estimation. J. Stat. Phys. 2022, 189, 10. [Google Scholar] [CrossRef]
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | |
| 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | |
| 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | |
| 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 |
| Set (a) | Set (b) | Set (c) | Set (d) | |
|---|---|---|---|---|
| m | ||||
| p |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, Q.; Li, R.; Wang, J. Improvement of Error Correction in Nonequilibrium Information Dynamics. Entropy 2023, 25, 881. https://doi.org/10.3390/e25060881
Zeng Q, Li R, Wang J. Improvement of Error Correction in Nonequilibrium Information Dynamics. Entropy. 2023; 25(6):881. https://doi.org/10.3390/e25060881
Chicago/Turabian StyleZeng, Qian, Ran Li, and Jin Wang. 2023. "Improvement of Error Correction in Nonequilibrium Information Dynamics" Entropy 25, no. 6: 881. https://doi.org/10.3390/e25060881
APA StyleZeng, Q., Li, R., & Wang, J. (2023). Improvement of Error Correction in Nonequilibrium Information Dynamics. Entropy, 25(6), 881. https://doi.org/10.3390/e25060881






