An Image Encryption Transmission Scheme Based on a Polynomial Chaotic Map
Abstract
1. Introduction
2. Construction of 3D Polynomial Chaotic System Model
2.1. Numerical Example
2.2. Sample Entropy Analysis
2.3. Pseudo-Randomness Analysis
3. A 3D Polynomial Chaotic Image Encryption Transmission Scheme
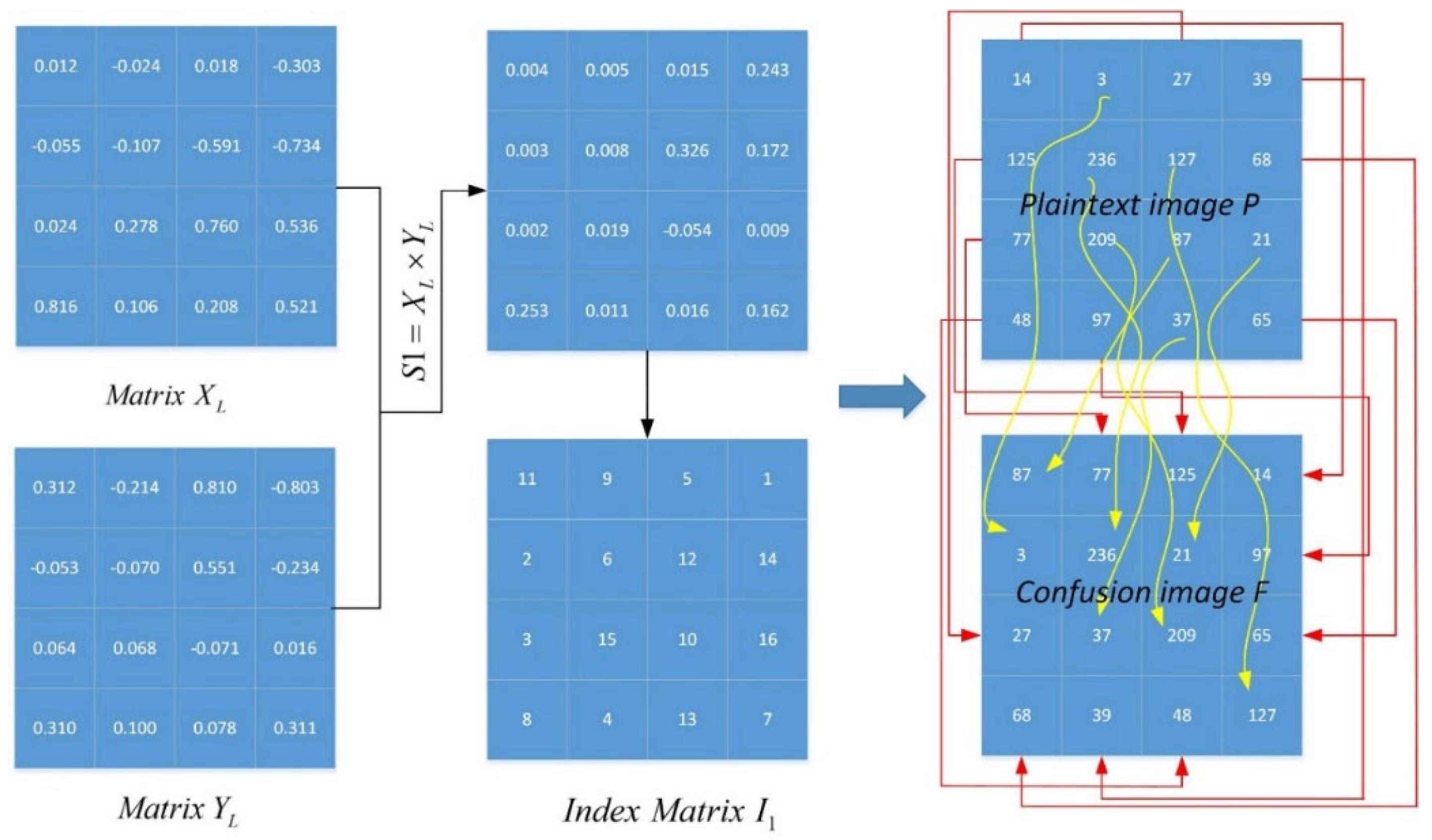
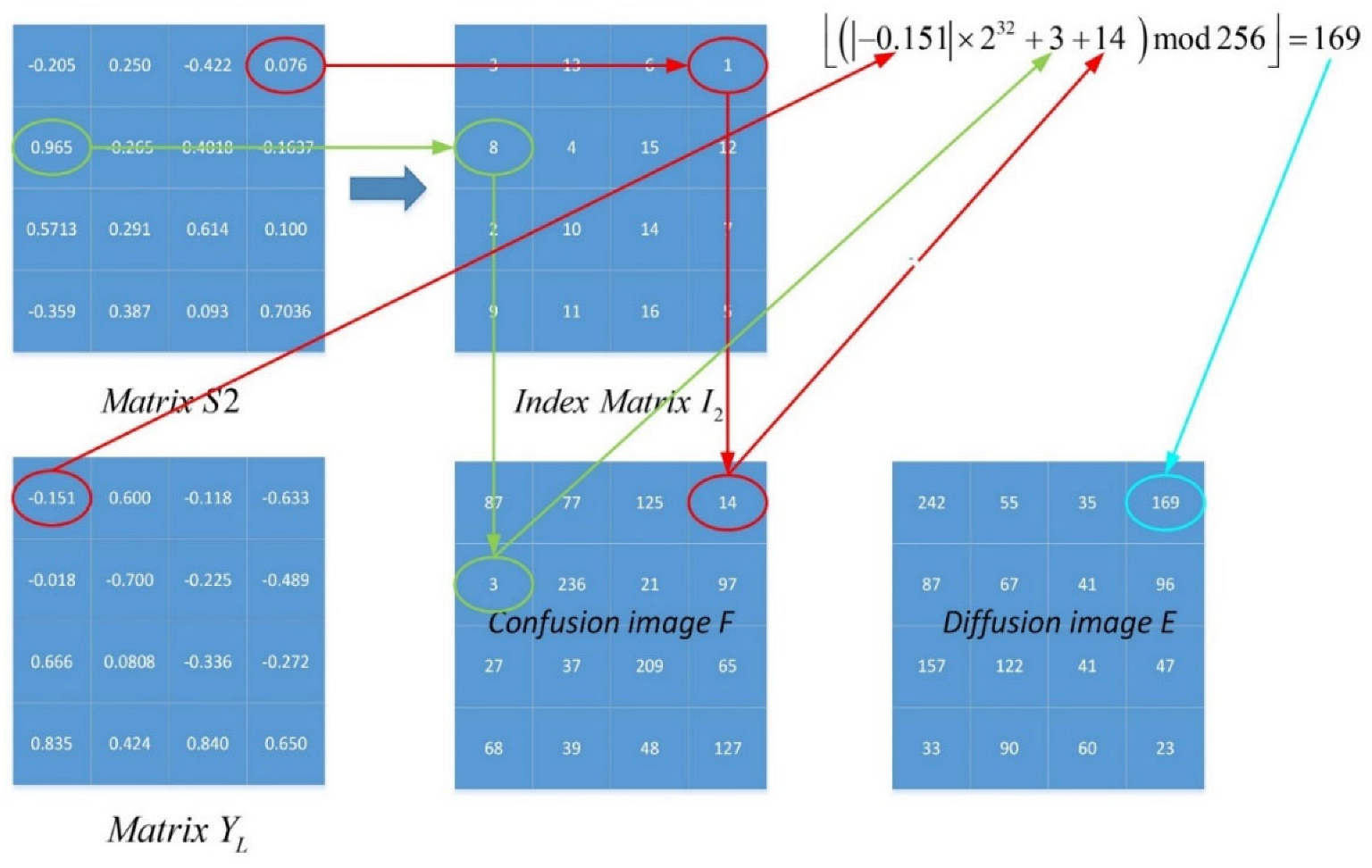
3.1. Image Encryption Scheme
| Algorithm 1: The procedure of the confusion part of the proposed image encryption scheme. |
| Input: Plaintext image and initial values , , . |
| Output: Confusion image |
|
3.2. Image Decryption Scheme
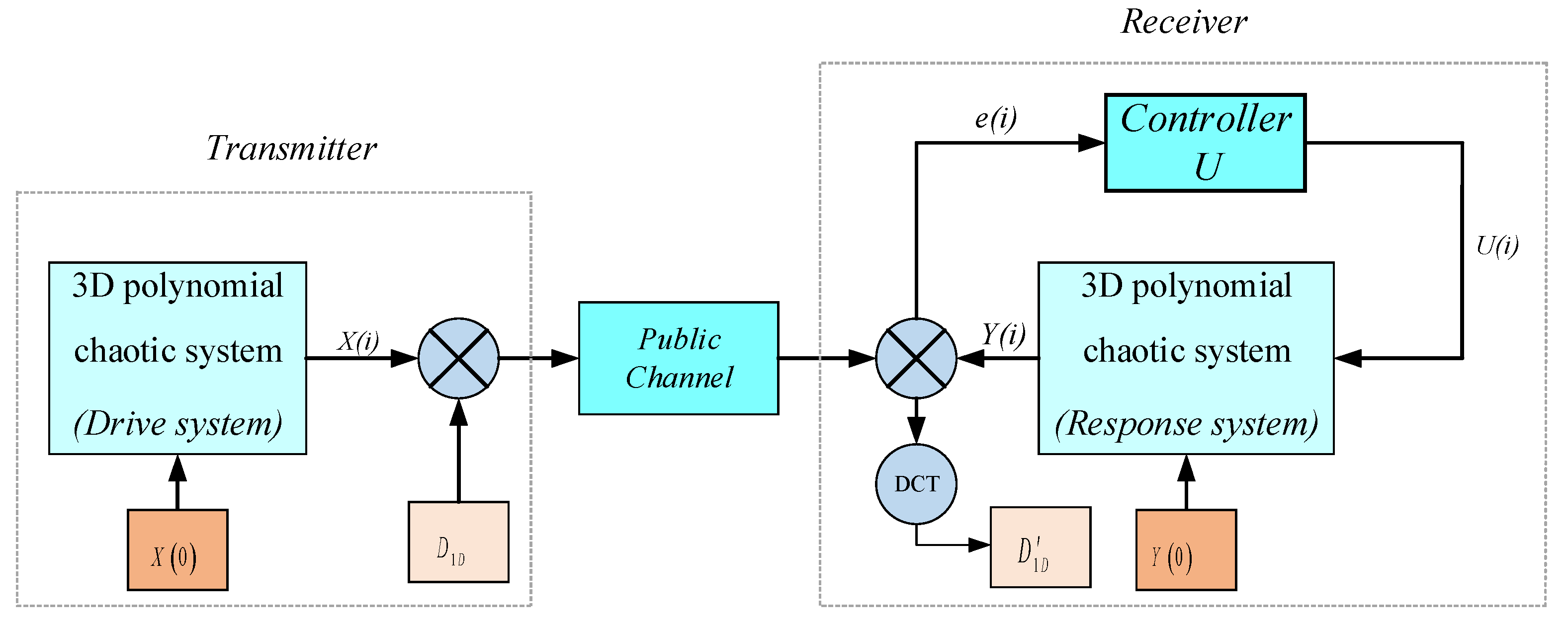
3.3. Nonlinear Feedback Synchronization Control Scheme
3.4. Transmission Scheme
3.5. Simulation Results
4. Security Analysis
4.1. Key Sensitivity Analysis
4.2. Histogram Analysis
4.3. The Shannon Entropy
4.4. Correlation Analysis
4.5. Differential Attack
| Schemes | Horizontal | Vertical | Diagonal |
|---|---|---|---|
| “Lena” image | 0.94010 | 0.97689 | 0.95667 |
| Ref. [23] | 0.00030 | 0.00140 | 0.00220 |
| Ref. [28] | −0.00150 | −0.00210 | 0.00190 |
| Ref. [29] | 0.00283 | 0.00183 | 0.00330 |
| Ref. [30] | 0.00340 | 0.00580 | 0.00450 |
| Ref. [31] | −0.00150 | 0.00410 | 0.00690 |
| Proposed method | −0.00091 | −0.00110 | 0.00100 |
| Images | NPCR (%) | UACI (%) | ||||
|---|---|---|---|---|---|---|
| R | G | B | R | G | B | |
| 4.1.01.tiff | 99.60 | 99.61 | 99.62 | 33.14 | 33.17 | 33.47 |
| 4.1.03.tiff | 99.61 | 99.62 | 99.63 | 33.34 | 33.67 | 33.42 |
| 4.1.04.tiff | 99.64 | 99.60 | 99.64 | 33.25 | 33.36 | 33.43 |
| 4.2.03.tiff | 99.62 | 99.59 | 99.62 | 33.15 | 33.46 | 33.42 |
| 4.2.07.tiff | 99.58 | 99.61 | 99.61 | 33.24 | 33.53 | 33.43 |
| Lena | 99.60 | 99.58 | 99.63 | 33.41 | 33.32 | 33.45 |
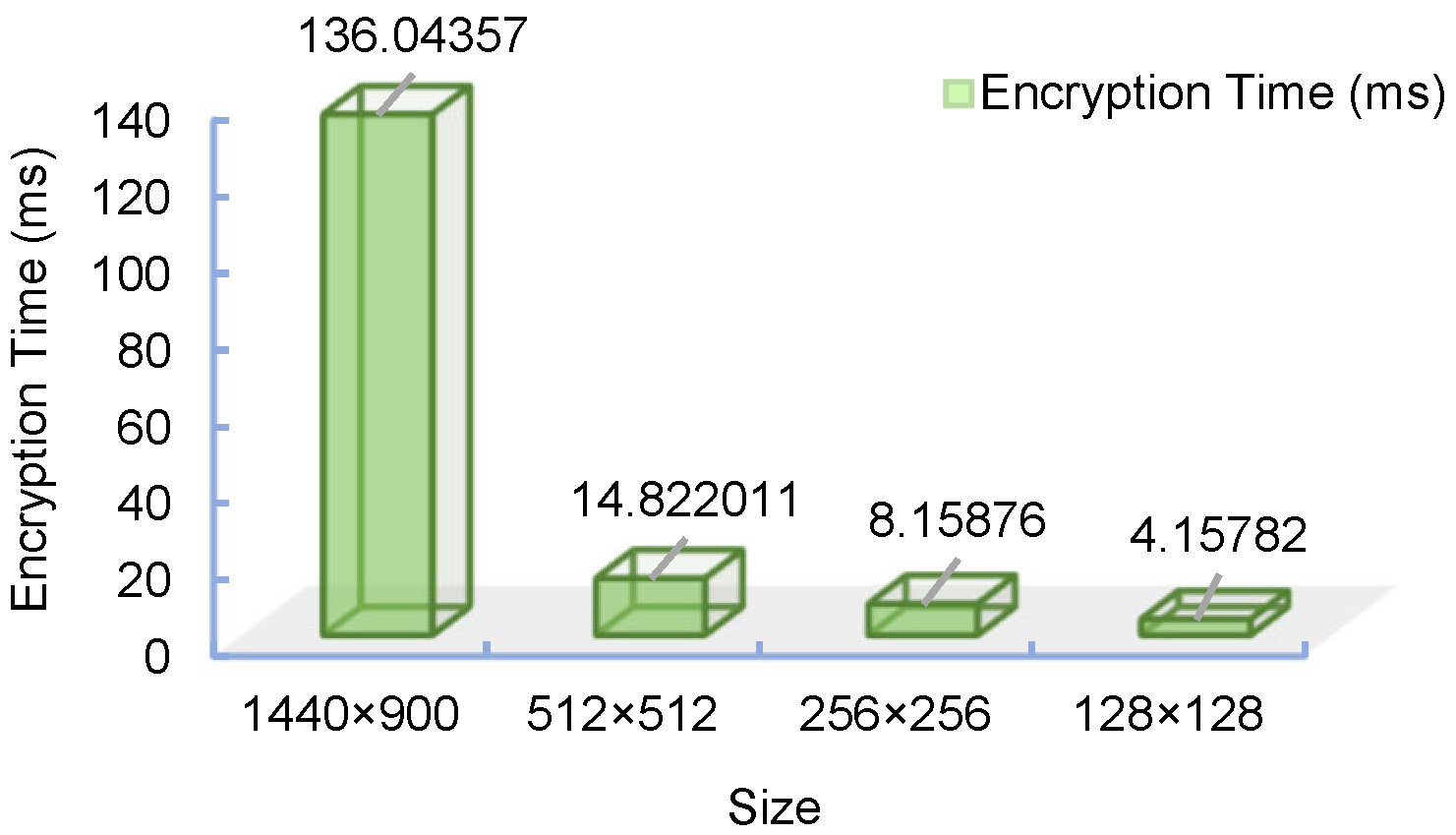
4.6. Complexity Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Dragoi, A.V.; Colutc, D. On local prediction based reversible watermarking. IEEE Trans. Image Process. 2015, 24, 1244–1246. [Google Scholar] [CrossRef]
- Lin, Y.T.; Wang, C.M.; Chen, W.S.; Lin, F.P.; Lin, W. A novel data hiding algorithm for high dynamical range images. IEEE Trans. Multimed. 2017, 19, 196–211. [Google Scholar] [CrossRef]
- Teh, J.S.; Alawida, M.; Sii, Y.C. Implementation and practical problems of chaos-based cryptography revisited. J. Inf. Secur. Appl. 2020, 50, 102421. [Google Scholar] [CrossRef]
- Belazi, A.; Abd El-Latif, A.A.; Diaconu, A.; Rhouma, R.; Belghith, S. Chaos-based partial image encryption scheme based on linear fractional and lifting wavelet transforms. Opt. Lasers Eng. 2017, 88, 37–50. [Google Scholar] [CrossRef]
- Wang, Y.; Wong, K.W.; Liao, X.; Xiang, T. A block cipher with dynamic S-boxes based on tent map. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 3089–3099. [Google Scholar] [CrossRef]
- Lu, X.; Xie, E.Y.; Li, C. Periodicity Analysis of the Logistic Map Over Ring . Int. J. Bifurc. Chaos 2023, 33, 5. [Google Scholar] [CrossRef]
- Yan, W.H.; Ding, Q. A new matrix projective synchronization and its application in secure communication. IEEE Access 2019, 7, 112977–112984. [Google Scholar] [CrossRef]
- Ma, Y.L.; Li, C.Q.; Ou, B. Cryptanalysis of an image block encryption algorithm based on chaotic maps. J. Inf. Secur. Appl. 2020, 50, 102566. [Google Scholar]
- Yan, W.; Dong, W.; Wang, P.; Wang, Y.; Xing, Y.; Ding, Q. Discrete-Time Memristor Model for Enhancing Chaotic Complexity and Application in Secure Communication. Entropy 2022, 24, 864. [Google Scholar] [CrossRef]
- Bao, B.; Rong, K.; Li, H.; Li, K.; Hua, Z.; Zhang, X. Memristor-coupled Logistic hyperchaotic map. IEEE Trans. Circuits Syst. II Exp. Briefs 2021, 68, 2992–2996. [Google Scholar] [CrossRef]
- Pak, C.; Huang, L. A new color image encryption using combination of the 1D chaotic map. Signal Process. 2017, 138, 129–137. [Google Scholar] [CrossRef]
- Zhou, Y.; Bao, L.; Chen, C. Image encryption using a new parametric switching chaotic system. Signal Process. 2013, 93, 3039–3052. [Google Scholar] [CrossRef]
- Hua, Z.; Zhou, Y.; Huang, H. Cosine-transform-based chaotic system for image encryption. Inf. Sci. 2019, 480, 403–419. [Google Scholar] [CrossRef]
- Cao, W.J.; Mao, Y.J.; Zhou, Y.C. Designing a 2D infinite collapse map for image encryption. Signal Process. 2020, 17, 107457. [Google Scholar] [CrossRef]
- Wang, C.F.; Ding, Q. A Class of Quadratic Polynomial Chaotic Maps and Their Fixed Points Analysis. Entropy 2019, 21, 658. [Google Scholar] [CrossRef] [PubMed]
- Li, W.S.; Yan, W.H.; Zhang, R.X.; Ding, Q. A New 3D Discrete Hyperchaotic System and Its Application in Secure Transmission. Int. J. Bifurcat. Chaos 2019, 29, 1950206. [Google Scholar]
- Liu, C.Y.; Ding, Q. A color image encryption scheme based on a novel 3d chaotic mapping. Complexity 2020, 2020, 3837209. [Google Scholar] [CrossRef]
- Wang, C.F.; Ding, Q. Constructing Discrete Chaotic systems with Positive Lyapunov Exponents. Int. J. Bifurcat. Chaos. 2017, 29, 1950206. [Google Scholar] [CrossRef]
- Hua, Z.Y.; Zhang, Y.X.; Zhou, Y.C. Two-dimensional parametric polynomial chaotic system. IEEE Trans. Cybern. 2022, 52, 4402–4414. [Google Scholar] [CrossRef]
- Hua, Z.Y.; Zhang, Y.X.; Zhou, Y.C. Two-dimensional modular chaotification system for improving chaos complexity. IEEE Trans. Singal Process. 2018, 68, 1937–1949. [Google Scholar] [CrossRef]
- Shen, C.W.; Yu, S.M.; Lu, J.H.; Chen, G.R. A systematic methodology for constructing hyperchaotic systems with multiple positive Lyapunov exponents and circuit implementation. IEEE Trans. Circuits Syst. I Reg. Papers 2014, 61, 854–864. [Google Scholar] [CrossRef]
- Chen, G.R.; Lai, D.J. Making a Dynamical System Chaotic: Feedback control of Lyapunov exponents for discrete-time dynamical systems. IEEE Trans. Circuits Syst. I Fund. Theory Appl. 1997, 44, 250–253. [Google Scholar] [CrossRef]
- Richman, J.; Moorman, J. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, 2039–2049. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Zhuang, J.; Yu, W.; Wang, Z. Measuring complexity using fuzzyen, apen, and sampen. Med. Eng. Phys. 2009, 31, 61–68. [Google Scholar] [CrossRef]
- Alvarez, G.; Li, S. Some basic cryptographic requirements for chaos-based cryptosystems. Int. J. Bifurcat. Chaos 2006, 16, 2129–2151. [Google Scholar]
- Lu, L.; Li, Y.; Sun, A. Parameter identification and chaos synchronization for uncertain coupled map lattices. Nonlinear Dyn. 2013, 73, 2111–2117. [Google Scholar] [CrossRef]
- Alawida, M.; Samsudin, A.J.; Teh, S. A new hybrid digital chaotic system with applications in image encryption. Signal Process. 2019, 160, 45–58. [Google Scholar]
- Hua, Z.Y.; Zhou, Y.C. Design of image cipher using block-based scrambling and image filtering. Inf. Sci. 2017, 396, 97–113. [Google Scholar] [CrossRef]
- Liu, X.; Tong, X.; Wang, Z.; Zhang, M. A novel hyperchaotic encryption algorithm for color image utilizing DNA dynamic encoding and self-adapting permutation. Multimed. Tools Appl. 2022, 81, 21779–21810. [Google Scholar] [CrossRef]
- Chai, X.; Fu, X.; Gan, Z.; Lu, Y.; Chen, Y. A color image cryptosystem based on dynamic DNA encryption and chaos. Signal Process. 2018, 155, 44–62. [Google Scholar] [CrossRef]
- Wang, X.; Guan, N.; Zhao, H.; Wang, S. A new image encryption scheme based on coupling map lattices with mixed multi-chaos. Sci. Rep. 2020, 10, 9784. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Cai, S.; Xiong, X.; Xiao, M. On symmetric color image encryption system with permutation-diffusion simultaneous operation. Opt. Laser. Eng. 2019, 115, 7–20. [Google Scholar] [CrossRef]
- Wang, T.; Wang, M. Hyperchaotic image encryption algorithm based on bit-level permutation and DNA encoding. Opt. Laser. Technol. 2020, 132, 106355. [Google Scholar] [CrossRef]
- Zhou, N.R.; Tong, L.J.; Zou, W.P. Multi-image encryption scheme with quaternion discrete fractional Tchebyshev moment transform and cross-coupling operation. Signal Process. 2023, 211, 109107. [Google Scholar] [CrossRef]
- Huang, X.L.; Dong, Y.X.; Ye, G.D.; Shi, Y. Meaningful image encryption algorithm based on compressive sensing and integer wavelet transform. Front. Comput. Sci. 2023, 17, 173804. [Google Scholar] [CrossRef]
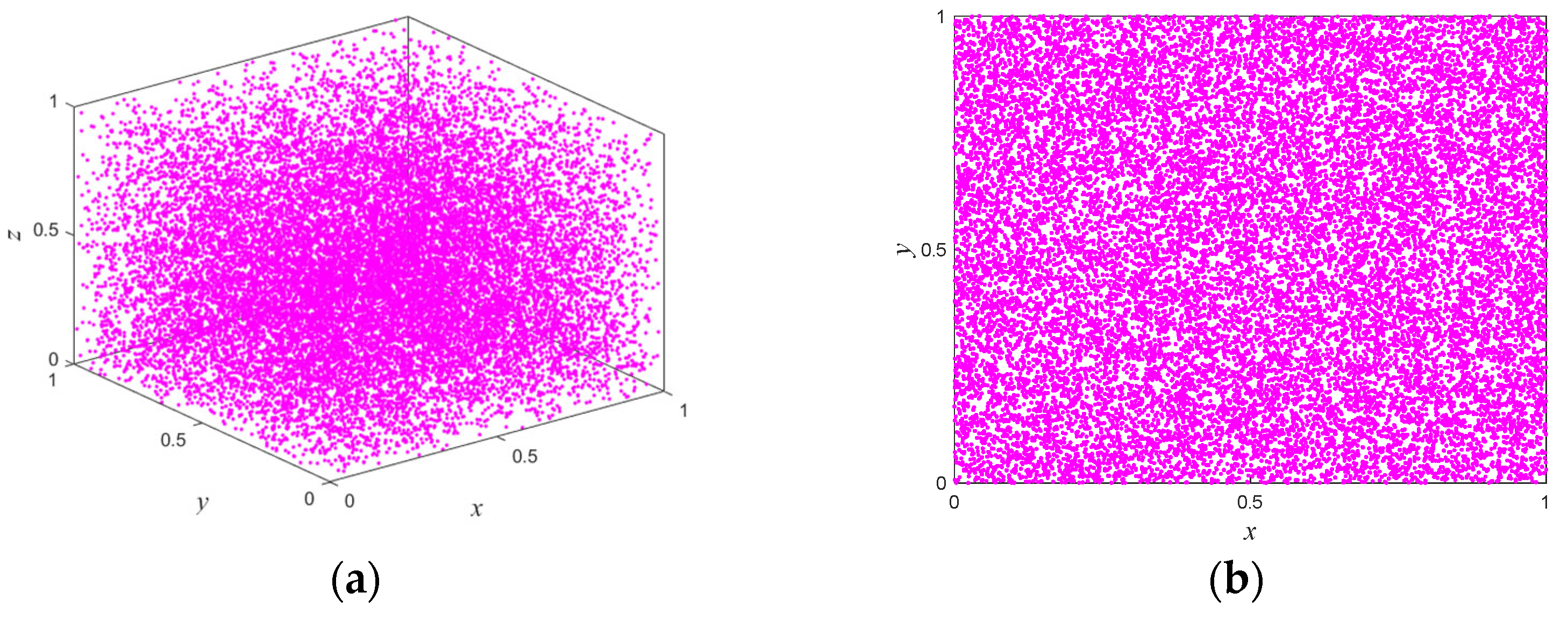
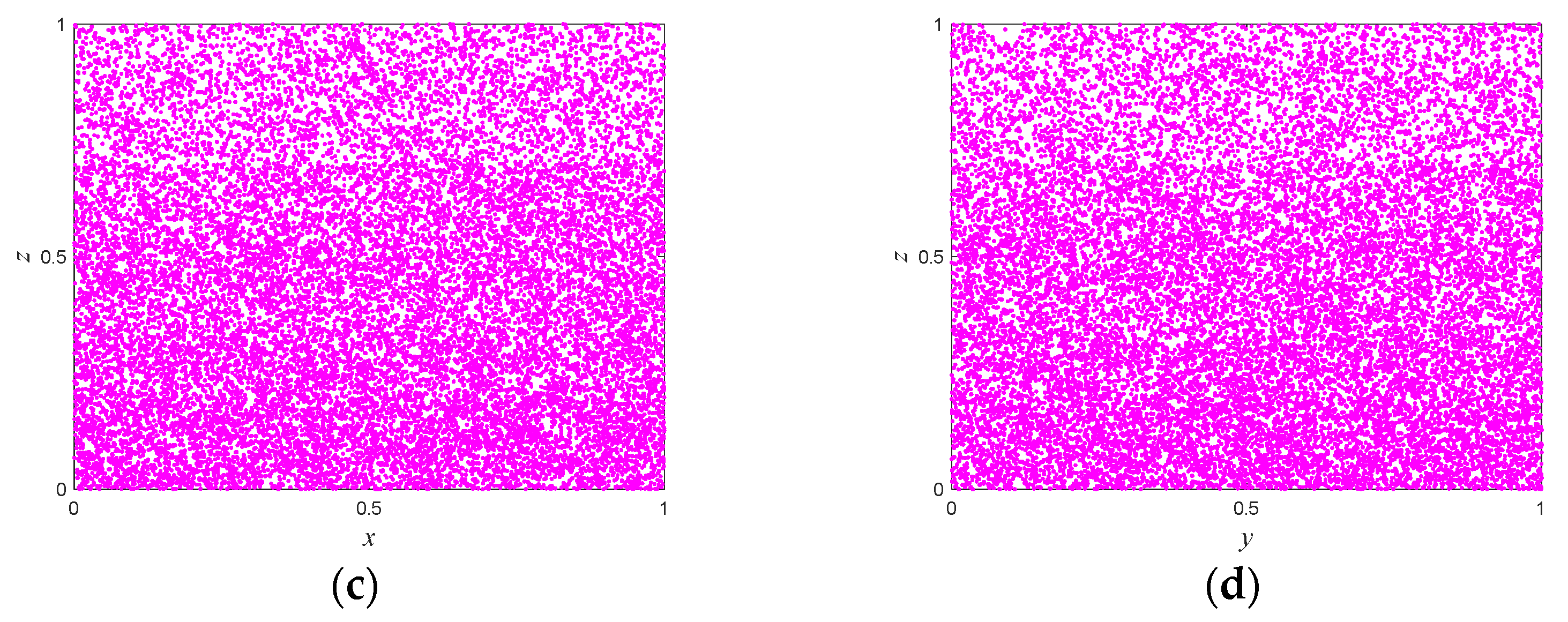
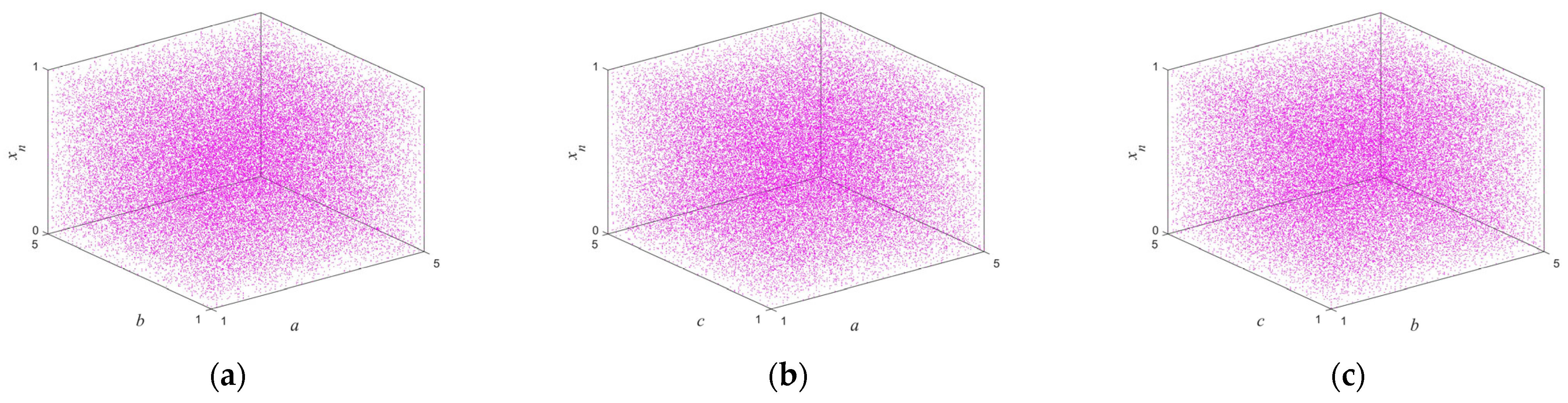
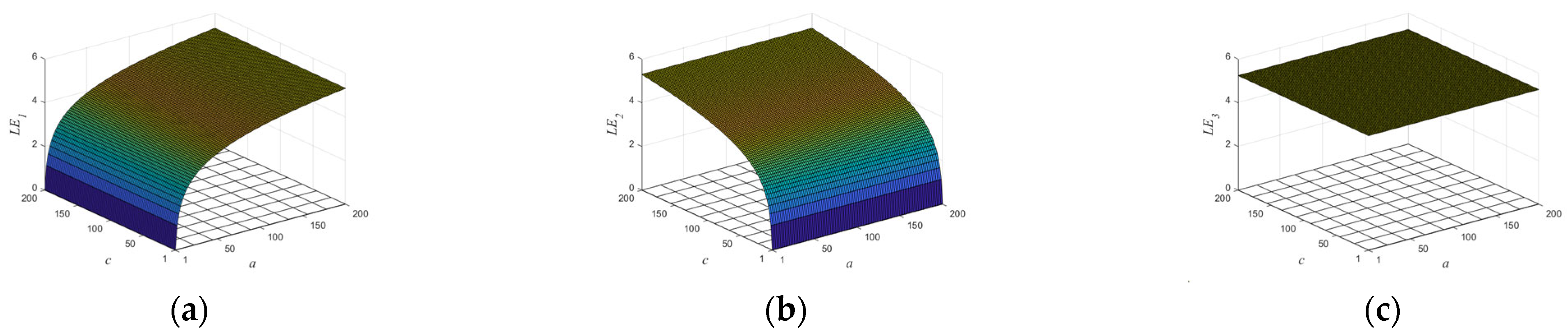






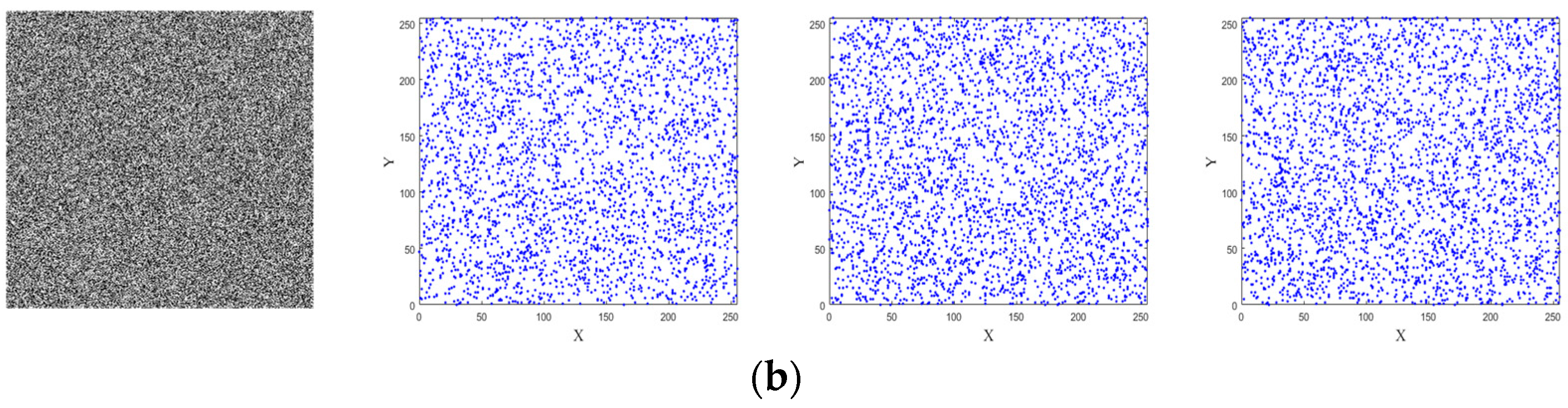
| Test Suites | p-Value | Result | |||
|---|---|---|---|---|---|
| 1 | Frequency | 0.554320 | 0.326810 | 0.457832 | Pass |
| 2 | Block frequency | 0.834570 | 0.577802 | 0.758221 | Pass |
| 3 | Runs | 0.547600 | 0.197506 | 0.421572 | Pass |
| 4 | Longest run | 0.801265 | 0.792351 | 0.823451 | Pass |
| 5 | Rank | 0.972745 | 0.267811 | 0.765341 | Pass |
| 6 | FFT | 0.035687 | 0.948721 | 0.689521 | Pass |
| 7 | Non-overlapping template | 0.235874 | 0.478512 | 0.367876 | Pass |
| 8 | Overlapping template | 0.497832 | 0.089451 | 0.289765 | Pass |
| 9 | Universal | 0.935647 | 0.058974 | 0.321768 | Pass |
| 10 | Linear complexity | 0.798145 | 0.278945 | 0.614729 | Pass |
| 11 | Serial | 0.754612 | 0.845971 | 0.792635 | Pass |
| 12 | Approximate entropy | 0.616784 | 0.089451 | 0.1976217 | Pass |
| 13 | Cumulative sums | 0.168745 | 0.944513 | 0.7122319 | Pass |
| 14 | Random excursions | 0.654123 | 0.087945 | 0.0933683 | Pass |
| 15 | Random excursions variant | 0.565209 | 0.058799 | 0.3548823 | Pass |
| Images | Lena | Gray | Ruler | Boat | Pepper |
|---|---|---|---|---|---|
| 242.042 | 230.458 | 237.344 | 246.341 | 224.633 |
| File Name | Original Image | Encrypted Image |
|---|---|---|
| 5.1.09.tiff | 6.7093 | 7.9975 |
| 5.1.13.tiff | 1.5483 | 7.9986 |
| 5.3.01.tiff | 7.5237 | 7.9991 |
| boat.512 | 7.1914 | 7.9992 |
| ruler.512 | 0.5000 | 7.9977 |
| gray21.512 | 4.3923 | 7.9990 |
| Mean value | 4.6442 | 7.9986 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Dong, W.; Zhang, J.; Ding, Q. An Image Encryption Transmission Scheme Based on a Polynomial Chaotic Map. Entropy 2023, 25, 1005. https://doi.org/10.3390/e25071005
Zhang Y, Dong W, Zhang J, Ding Q. An Image Encryption Transmission Scheme Based on a Polynomial Chaotic Map. Entropy. 2023; 25(7):1005. https://doi.org/10.3390/e25071005
Chicago/Turabian StyleZhang, Yanpeng, Wenjie Dong, Jing Zhang, and Qun Ding. 2023. "An Image Encryption Transmission Scheme Based on a Polynomial Chaotic Map" Entropy 25, no. 7: 1005. https://doi.org/10.3390/e25071005
APA StyleZhang, Y., Dong, W., Zhang, J., & Ding, Q. (2023). An Image Encryption Transmission Scheme Based on a Polynomial Chaotic Map. Entropy, 25(7), 1005. https://doi.org/10.3390/e25071005




