From Geometry of Hamiltonian Dynamics to Topology of Phase Transitions: A Review
Abstract
1. Introduction
2. Riemannian Geometric Formulation of Hamiltonian Dynamics
2.1. The Jacobi Metric in Configuration Space
2.2. The Eisenhart Metric in Enlarged Configuration Space
2.3. Geodesic Spread Equation to Tackle Dynamical (In)Stability
2.3.1. Curvature of the Mechanical Manifolds
2.3.2. The Jacobi–Levi–Civita Equation for the Jacobi Metric
2.3.3. The Jacobi–Levi–Civita Equation for the Eisenhart Metric
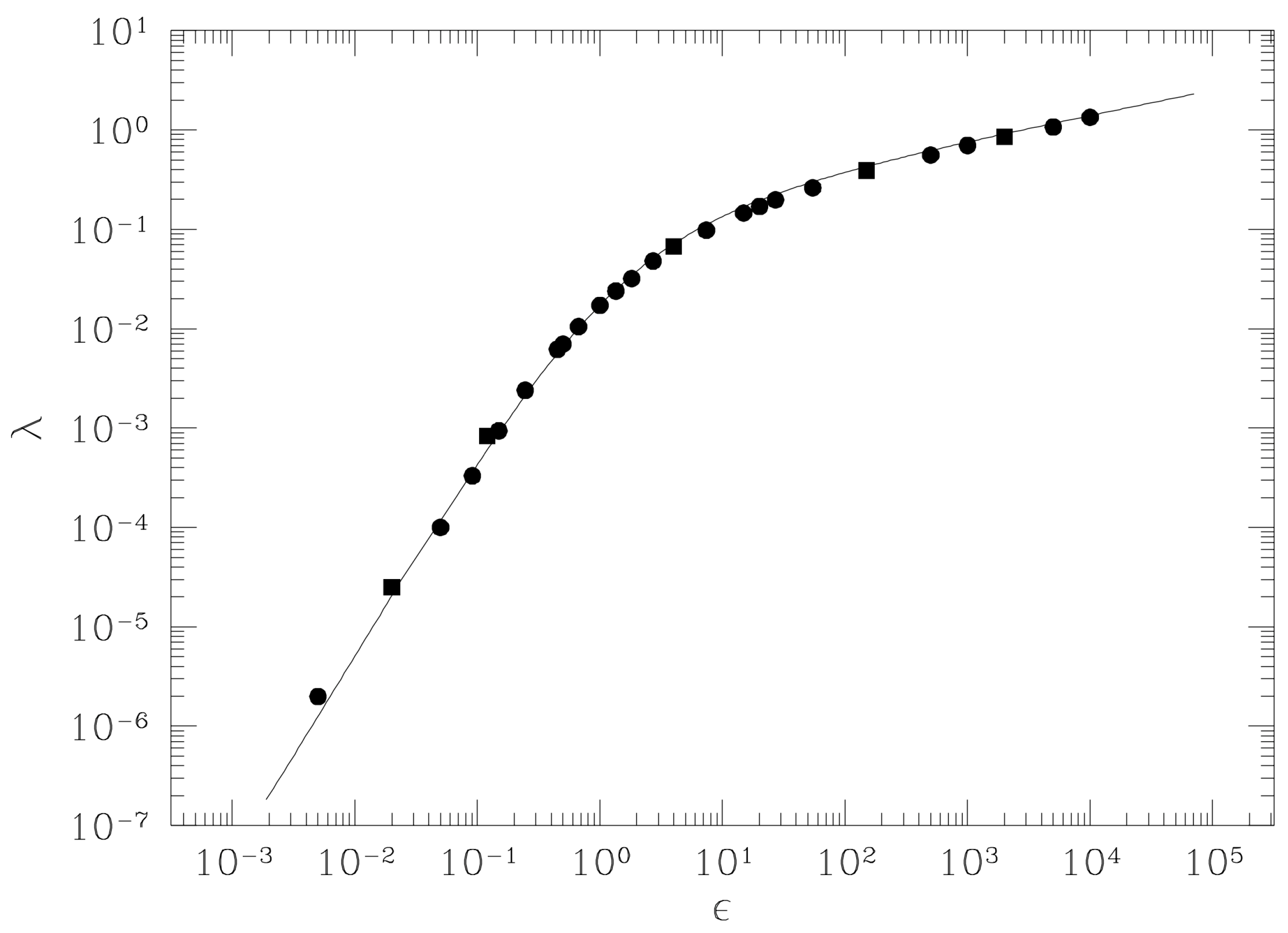
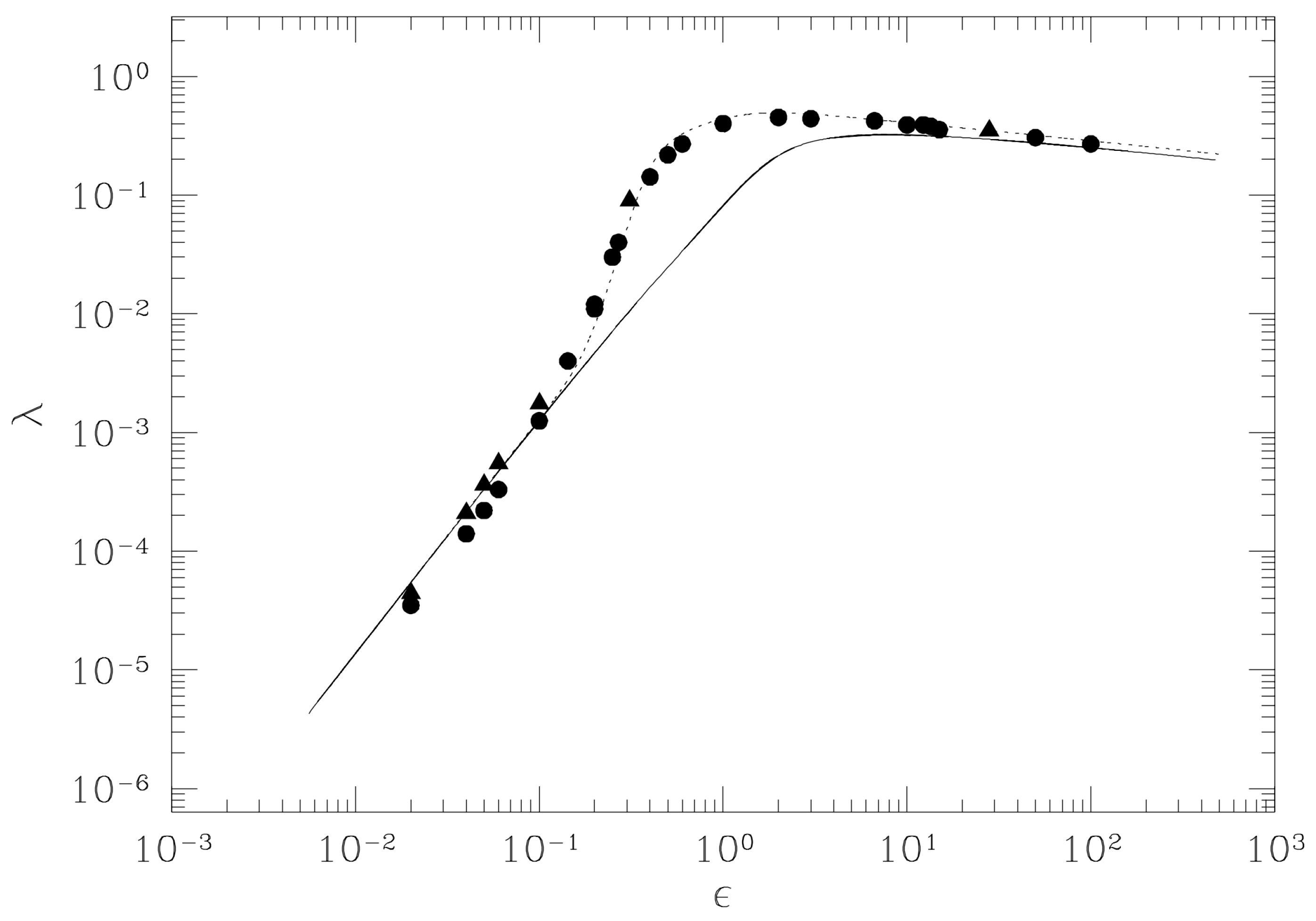
2.4. Analytic Computation of the Largest Lyapunov Exponent
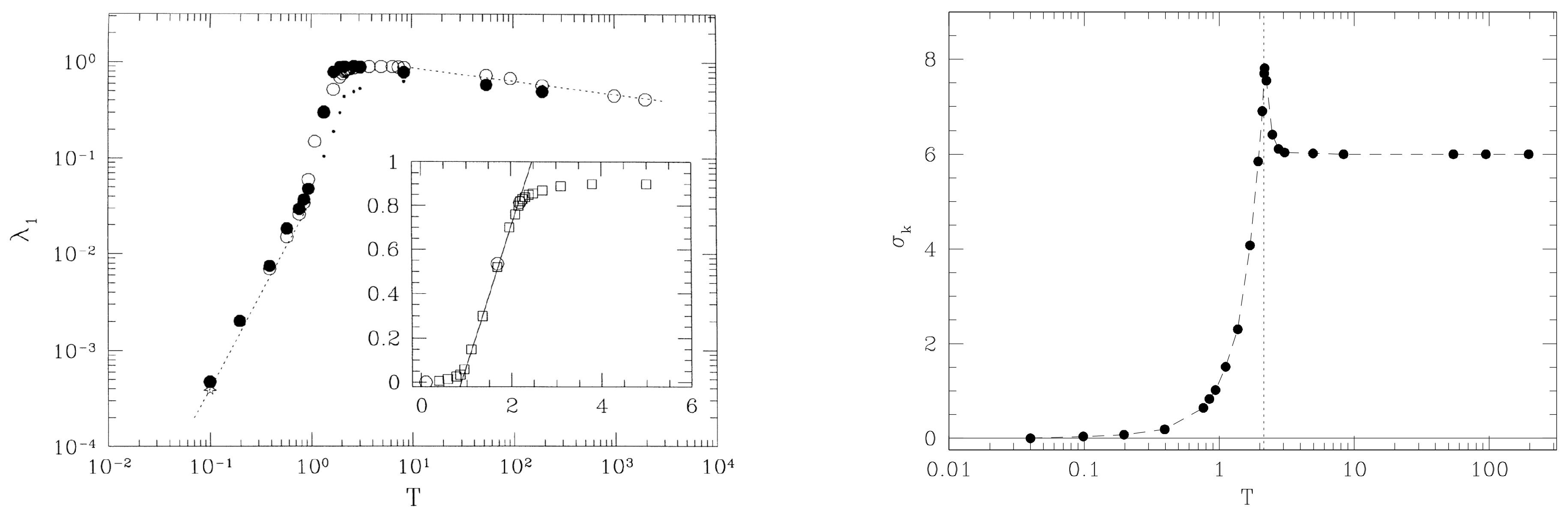
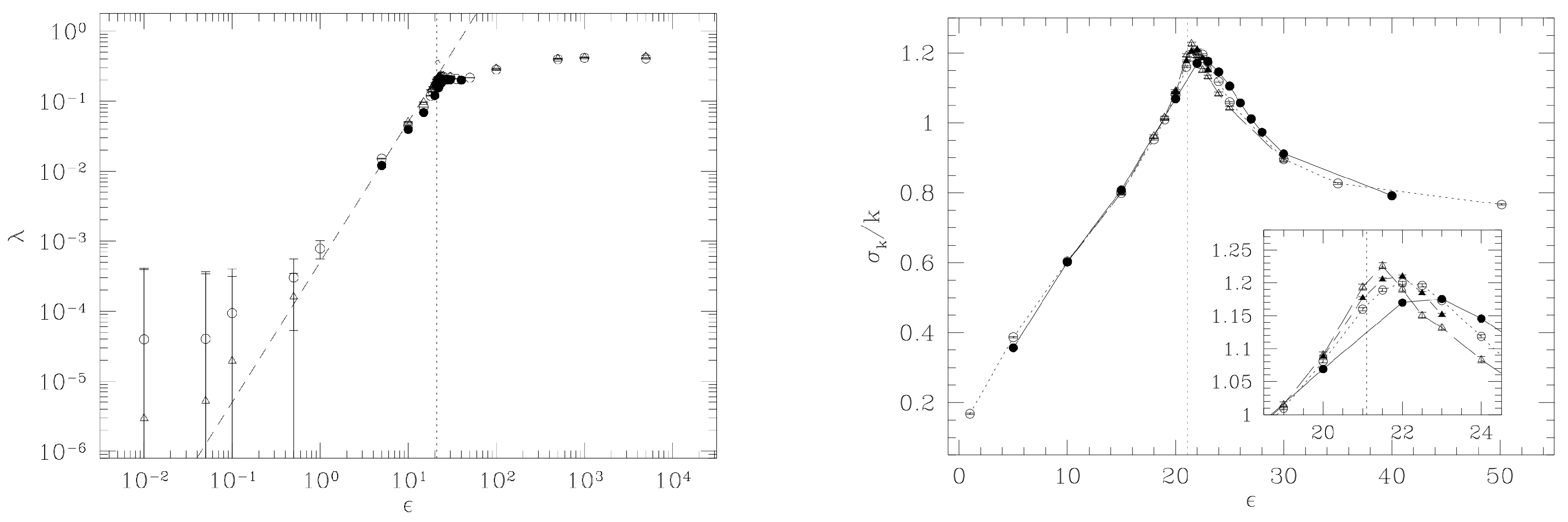
3. Geometry and Chaos at Phase Transitions
Lyapunov Exponents and Configuration Space Topology
4. Topology and Phase Transitions
4.1. Rigorous Results
4.1.1. Two Exactly Computable Models
4.1.2. A Necessity Theorem
4.2. Applications
4.2.1. Phase Transitions in Small N Systems
4.2.2. Phase Transitions in the Absence of Symmetry Breaking
4.2.3. Prospective Applications to Phase Transitions in Quantum Systems
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Landau, L.D. On the Theory of Phase Transitions. Zh. Eksp. Teor. Fiz. 1937, 7, 926. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Statistical Physics; Elsevier: Amsterdam, The Netherlands, 2013; Volume 5. [Google Scholar]
- Yang, C.N.; Lee, T.D. Statistical theory of equations of state and phase transitions I. Theory of condensation. Phys. Rev. 1952, 87, 404–409. [Google Scholar] [CrossRef]
- Lee, T.D.; Yang, C.N. Statistical theory of equations of state and phase transitions II. Lattice gas and Ising model. Phys. Rev. 1952, 87, 410–419. [Google Scholar] [CrossRef]
- De Gruyter. A comprehensive account of the Dobrushin-Lanford-Ruelle theory and of its developments can be found in: H.O. Georgii. In Gibbs Measures and Phase Transitions, 2nd ed.; De Gruyter: Berlin, Germany, 2011. [Google Scholar]
- Fermi, E.; Pasta, J.; Ulam, S.; Tsingou, M. Studies of Nonlinear Problems I; Los Alamos report LA-1940, reprinted in Collected Papers of Enrico Fermi; Segré, E., Ed.; University of Chicago: Chicago, IL, USA, 1965; Volume 2, p. 978. [Google Scholar]
- Caiani, L.; Casetti, L.; Clementi, C.; Pettini, M. Geometry of dynamics, Lyapunov exponents and phase transitions. Phys. Rev. Lett. 1997, 79, 4361. [Google Scholar] [CrossRef]
- Caiani, L.; Casetti, L.; Clementi, C.; Pettini, G.; Pettini, M.; Gatto, R. Geometry of dynamics and phase transitions in classical lattice φ4 theories. Phys. Rev. E 1998, 57, 3886. [Google Scholar] [CrossRef]
- Caiani, L.; Casetti, L.; Pettini, M. Hamiltonian dynamics of the two-dimensional lattice φ4 model. J. Phys. A Math. Gen. 1998, 31, 3357. [Google Scholar] [CrossRef][Green Version]
- Cerruti-Sola, M.; Clementi, C.; Pettini, M. Hamiltonian dynamics and geometry of phase transitions in classical XY models. Phys. Rev. E 2000, 61, 5171. [Google Scholar] [CrossRef]
- Cerruti-Sola, M.; Cipriani, P.; Pettini, M. On the clustering phase transition in self-gravitating N-body systems. Mon. Not. Roy. Astron. Soc. 2001, 328, 339. [Google Scholar] [CrossRef][Green Version]
- Krylov, N.S. Works on the Foundations of Statistical Physics; Princeton University Press: Princeton, NJ, USA, 1979. [Google Scholar]
- Abraham, R.; Marsden, J.E. Foundations of Mechanics; Addison-Wesley: Redwood City, CA, USA, 1987. [Google Scholar]
- Pettini, M. Geometrical hints for a nonperturbative approach to Hamiltonian dynamics. Phys. Rev. E 1993, 47, 828. [Google Scholar] [CrossRef]
- Casetti, L.; Pettini, M.; Cohen, E.G.D. Geometric approach to Hamiltonian dynamics and statistical mechanics. Phys. Rep. 2000, 337, 237–342. [Google Scholar] [CrossRef]
- Pettini, M. Geometry and Topology in Hamiltonian Dynamics and Statistical Mechanics; IAM Series n.33; Springer: New York, NY, USA, 2007. [Google Scholar]
- Eisenhart, L.P. Dynamical trajectories and geodesics. Ann. Math. 1928, 30, 591. [Google Scholar] [CrossRef]
- Lichnerowicz, A. Théories Rélativistes de la Gravitation et de l’Eléctromagnétisme; Masson: Paris, France, 1955. [Google Scholar]
- Cerruti-Sola, M.; Franzosi, R.; Pettini, M. Lyapunov exponents from geodesic spread in configuration space. Phys. Rev. E 1997, 56, 4872. [Google Scholar] [CrossRef]
- Gonzalez Leon, M.A.; Hernandez Pastora, J.L. On the Jacobi-metric stability criterion. In Proceedings of the XV International Workshop on Geometry and Physics, Puerto de la Cruz, Tenerife, Spain, 11–16 September 2006. [Google Scholar]
- Cuervo-Reyes, E.; Movassagh, R. Non-affine geometrization can lead to non-physical instabilities. J. Phys. A Math. Theor. 2015, 48, 075101. [Google Scholar] [CrossRef][Green Version]
- Cairano, L.D.; Gori, M.; Pettini, M. Coherent Riemannian-geometric description of Hamiltonian order and chaos with Jacobi metric. Chaos 2019, 29, 123134. [Google Scholar] [CrossRef] [PubMed]
- Hénon, H.; Heiles, C. The applicability of the third integral of motion. Astron. J. 1964, 69, 73. [Google Scholar] [CrossRef]
- Hadamard, J. Les surfaces à courbures opposées et leurs lignes géodésiques. J. Math. Pur. Appl. 1898, 4, 27. [Google Scholar]
- Hedlund, G.A. The dynamics of geodesic flows. Bull. Amer. Math. Soc. 1939, 45, 241. [Google Scholar] [CrossRef]
- Hopf, E. Complete transitivity and the ergodic principle. Proc. Natl. Acad. Sci. USA 1932, 18, 204. [Google Scholar] [CrossRef]
- Anosov, V.I. Geodesic flows on closed Riemannian manifolds of negative curvature. Proc. Steklov Math. Inst. 1967, 90, 3–210. [Google Scholar]
- MacKay, R.S.; Meiss, J.D. (Eds.) Hamiltonian Systems: A Reprint Selection; Adam Hilger: Bristol, UK, 1990. [Google Scholar]
- Arnold, V.I. Mathematical Methods of Classical Mechanics; Springer: Berlin/Heidelberg, Germany, 1978. [Google Scholar]
- Cerruti-Sola, M.; Pettini, M. Geometric description of chaos in two-degrees-of-freedom Hamiltonian systems. Phys. Rev. E 1996, 53, 179. [Google Scholar] [CrossRef]
- Casetti, L.; Clementi, C.; Pettini, M. Riemannian theory of Hamiltonian chaos and Lyapunov exponents. Phys. Rev. E 1996, 54, 5969. [Google Scholar] [CrossRef] [PubMed]
- van Kampen, N.G. Stochastic Differential Equations. Phys. Rep. 1976, 24, 171. [Google Scholar] [CrossRef]
- Hirsch, M.W. Differential Topology; Springer: New York, NY, USA, 1976. [Google Scholar]
- Milnor, J. Morse Theory; Annals of the Mathematics Studies; Princeton University Press: Princeton, NJ, USA, 1963; Volume 51. [Google Scholar]
- Morse, M.; Cairns, S.S. Critical Point Theory in Global Analysis and Differential Topology; Academic Press: New York, NY, USA, 1969. [Google Scholar]
- Nakahara, M. Geometry, Topology and Physics; Adam Hilger: Bristol, UK, 1991. [Google Scholar]
- Franzosi, R.; Pettini, M. Theorem on the origin of Phase Transitions. Phys. Rev. Lett. 2004, 92, 060601. [Google Scholar] [CrossRef] [PubMed]
- Franzosi, R.; Pettini, M.; Spinelli, L. Topology and Phase Transitions I. Preliminary results. Nucl. Phys. B 2007, 782, 189. [Google Scholar] [CrossRef]
- Kastner, M.; Mehta, D. Phase Transitions Detached from Stationary Points of the Energy Landscape. Phys. Rev. Lett. 2011, 107, 160602. [Google Scholar] [CrossRef]
- Gori, M.; Franzosi, R.; Pettini, M. Topological origin of phase transitions in the absence of critical points of the energy landscape. J. Stat. Mech. 2018, 2018, 093204. [Google Scholar] [CrossRef]
- Pettini, G.; Gori, M.; Franzosi, R.; Clementi, C.; Pettini, M. On the origin of phase transitions in the absence of symmetry-breaking. Physica A 2019, 516, 376. [Google Scholar] [CrossRef]
- Gori, M.; Franzosi, R.; Pettini, G.; Pettini, M. Topological Theory of Phase Transitions. J. Phys. A Math. Theor. 2022, 55, 37002. [Google Scholar] [CrossRef]
- Franzosi, R.; Pettini, M. Topology and Phase Transitions II. Theorem on a necessary relation. Nucl. Phys. B 2007, 782, 219. [Google Scholar] [CrossRef][Green Version]
- Cairano, L.D.; Gori, M.; Pettini, M. Topology and phase transitions: A first analytical step towards the definition of sufficient conditions. Entropy 2021, 23, 1414. [Google Scholar] [CrossRef]
- Chern, S.S.; Lashof, R.K. On the total curvature of immersed manifolds. Am. J. Math. 1957, 79, 306. [Google Scholar] [CrossRef]
- Chern, S.S.; Lashof, R.K. On the total curvature of immersed manifolds II. Michigan Math. J. 1958, 5, 5. [Google Scholar] [CrossRef]
- Pinkall, U. Inequalities of Willmore type for submanifolds. Math. Z. 1986, 193, 241. [Google Scholar] [CrossRef]
- Overholt, M. Fluctuation of sectional curvature for closed hypersurfaces. Rocky Mount. Math. 2002, 32, 385. [Google Scholar] [CrossRef]
- Cairano, L.D.; Capelli, R.; Bel-Hadj-Aissa, G.; Pettini, M. Topological origin of protein folding transition. Phys. Rev. E 2022, 106, 054134. [Google Scholar] [CrossRef]
- Clementi, C.; Nymeyer, H.; Onuchic, J.N. Topological and energetic factors: What determines the structural details of the transition state ensemble and “en-route” intermediates for protein folding? An investigation for small globular proteins. J. Mol. Biol. 2000, 298, 937. [Google Scholar] [CrossRef]
- Noel, J.K.; Levi, M.; Raghunathan, M.; Lammert, H.; Hayes, R.L.; Onuchic, J.N.; Whitford, P.C. SMOG 2: A versatile software package for generating structure based models. PLoS Comput. Biol. 2016, 12, e1004794. [Google Scholar] [CrossRef]
- Kogut, J. An introduction to lattice gauge theory and spin systems. Rev. Mod. Phys. 1979, 51, 659. [Google Scholar] [CrossRef]
- Elitzur, S. Impossibility of spontaneously breaking local symmetries. Phys. Rev. D 1975, 12, 3978. [Google Scholar] [CrossRef]
- Kramer, P.; Saraceno, M. Geometry of the time-dependent variational principle in quantum mechanics. In Group Theoretical Methods in Physics; Springer: New York, NY, USA, 1980; pp. 112–121. [Google Scholar]
- Kramer, P. A review of the time-dependent variational principle. J. Phys. Conf. Ser. 2008, 99, 012009. [Google Scholar] [CrossRef]
- Jauslin, H.-R.; Sugny, D. Dynamics of mixed classical-quantum systems, geometric quantization and coherent states. In Mathematical Horizons for Quantum Physics; Araki, H., Englert, B.-G., Kwek, L.-C., Suzuki, J., Eds.; IMS-NUS Lecture Notes Series; World Scientific: Singapore, 2010; Volume 20. [Google Scholar]
- Callaway, D.J.E.; Rahman, A. Lattice gauge theory in the microcanonical ensemble. Phys. Rev. D 1983, 28, 1506. [Google Scholar] [CrossRef]
- Cairano, L.D.; Gori, M.; Sarkis, M.; Tkatchenko, A. Detecting phase transitions in lattice gauge theories: Production and dissolution of topological defects in 4D compact electrodynamics. Phys. Rev. D 2024, in press. [CrossRef]
- Pradzynski, C.C.; Forck, R.M.; Zeuch, T.; Slavicek, P.; Buck, U. A fully size-resolved perspective on the crystallization of water clusters. Science 2012, 337, 1529. [Google Scholar] [CrossRef] [PubMed]
- Leggett, A.J. Bose–Einstein condensation in the alkali gases: Some fundamental concepts. Rev. Mod. Phys. 2001, 73, 307, Erratum in Rev. Mod. Phys. 2003, 75, 1083. [Google Scholar] [CrossRef]
- Lifshitz, I.M.; Grosberg, A.Y.; Khokhlov, A.R. Some problems of the statistical physics of polymer chains with volume interaction. Rev. Mod. Phys. 1978, 50, 683. [Google Scholar] [CrossRef]
- Dill, K.A.; Ozkan, S.B.; Shell, M.S.; Weikl, T.R. The protein folding problem. Annu. Rev. Biophys. 2008, 37, 289. [Google Scholar] [CrossRef]
- Qi, K.; Bachmann, M. Classification of phase transitions by microcanonical inflection-point analysis. Phys. Rev. Lett. 2018, 120, 180601. [Google Scholar] [CrossRef]
- Bachmann, M. Thermodynamics and Statistical Mechanics of Macromolecular Systems; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Mermin, N.D.; Wagner, H. Absence of ferromagnetism or antiferromagnetism in one- or two-dimensional isotropic Heisenberg models. Phys. Rev. Lett. 1966, 17, 1133. [Google Scholar] [CrossRef]
- Mermin, N.D. Crystalline Order in Two Dimensions. Phys. Rev. 1968, 176, 250. [Google Scholar] [CrossRef]
- Carlsson, G.; Gorham, J.; Kahle, M.; Mason, J. Computational topology for configuration spaces of hard disks. Phys. Rev. E 2012, 85, 011303. [Google Scholar] [CrossRef]
- Baryshnikov, Y.; Bubenik, P.; Kahle, M. Min-type Morse theory for configuration spaces of hard spheres. Int. Math. Res. Not. 2013, 2014, 2577. [Google Scholar] [CrossRef]
- Brody, D.C.; Hook, D.W.; Hughston, L.P. Quantum phase transitions without thermodynamic limits. Proc. R. Soc. A 2007, 463, 2021. [Google Scholar] [CrossRef]
- Buonsante, P.; Franzosi, R.; Smerzi, A. Phase transitions at high energy vindicate negative microcanonical temperature. Phys. Rev. E 2017, 95, 052135. [Google Scholar] [CrossRef] [PubMed]
- Volovik, G.E. Quantum Phase Transitions from Topology in Momentum Space Quantum Analogues: From Phase Transitions to Black Holes and Cosmology; Springer: Berlin/Heidelberg, Germany, 2007; pp. 31–73. [Google Scholar]
- Angelani, L.; Leonardo, R.D.; Parisi, G.; Ruocco, G. Topological description of the aging dynamics in simple glasses. Phys. Rev. Lett. 2001, 87, 055502. [Google Scholar] [CrossRef] [PubMed]
- Debenedetti, P.G.; Stillinger, F.H. Supercooled liquids and the glass transition Nature. Nature 2001, 410, 259. [Google Scholar] [CrossRef]
- Risau-Gusman, S.; Ribeiro-Teixeira, A.C.; Stariolo, D.A. Topology, phase transitions, and the spherical model. Phys. Rev. Lett. 2005, 95, 145702. [Google Scholar] [CrossRef]
- Santos, F.A.N.; da Silva, L.C.B.; Coutinho-Filho, M.D. Topological approach to microcanonical thermodynamics and phase transition of interacting classical spins. J. Stat. Mech. 2017, 2017, 013202. [Google Scholar] [CrossRef][Green Version]
- Garanin, D.A.; Schilling, R.; Scala, A. Saddle index properties, singular topology, and its relation to thermodynamic singularities for a φ4 mean-field model. Phys. Rev. E 2004, 70, 036125. [Google Scholar] [CrossRef]
- Cimasoni, D.; Delabays, R. The topological hypothesis for discrete spin models. J. Stat. Mech. 2019, 2019, 033216. [Google Scholar] [CrossRef]
- Grinza, P.; Mossa, A. Topological origin of the phase transition in a model of DNA denaturation. Phys. Rev. Lett. 2004, 92, 158102. [Google Scholar] [CrossRef]
- Becker, O.M.; Karplus, M. The topology of multidimensional potential energy surfaces: Theory and application to peptide structure and kinetics. J. Chem. Phys. 1997, 106, 1495. [Google Scholar] [CrossRef]
- Brooks, C.L.; Onuchic, J.N.; Wales, D.J. Taking a walk on a landscape. Science 2001, 293, 612. [Google Scholar] [CrossRef] [PubMed]
- Wales, D.J. A microscopic basis for the global appearance of energy landscapes. Science 2001, 293, 2067. [Google Scholar] [CrossRef] [PubMed]
- Santos, F.A.N.; Raposo, E.P.; Coutinho-Filho, M.D.; Copelli, M.; Stam, C.J.; Douw, L. Topological phase transitions in functional brain networks. Phys. Rev. E 2019, 100, 032414. [Google Scholar] [CrossRef]


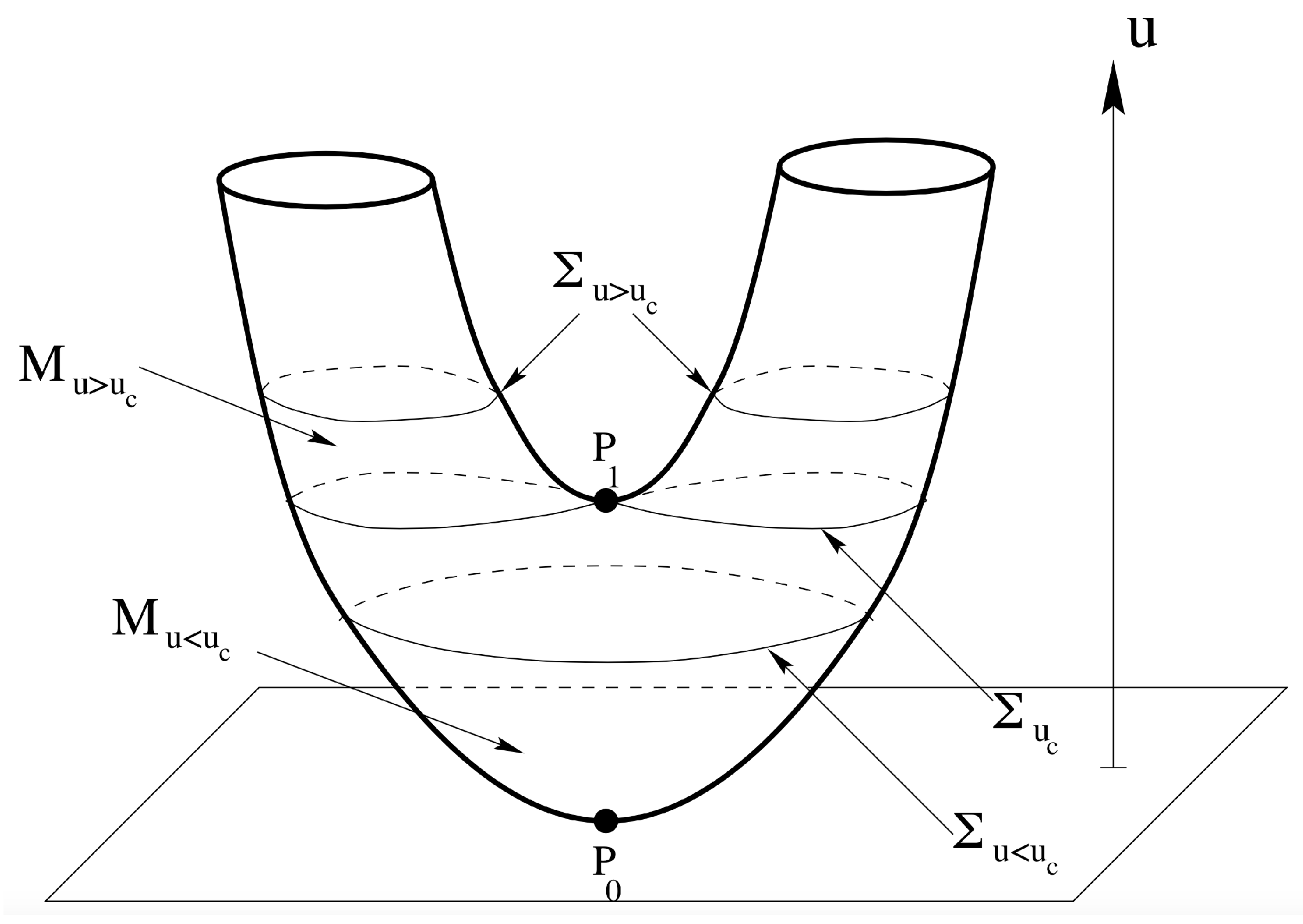
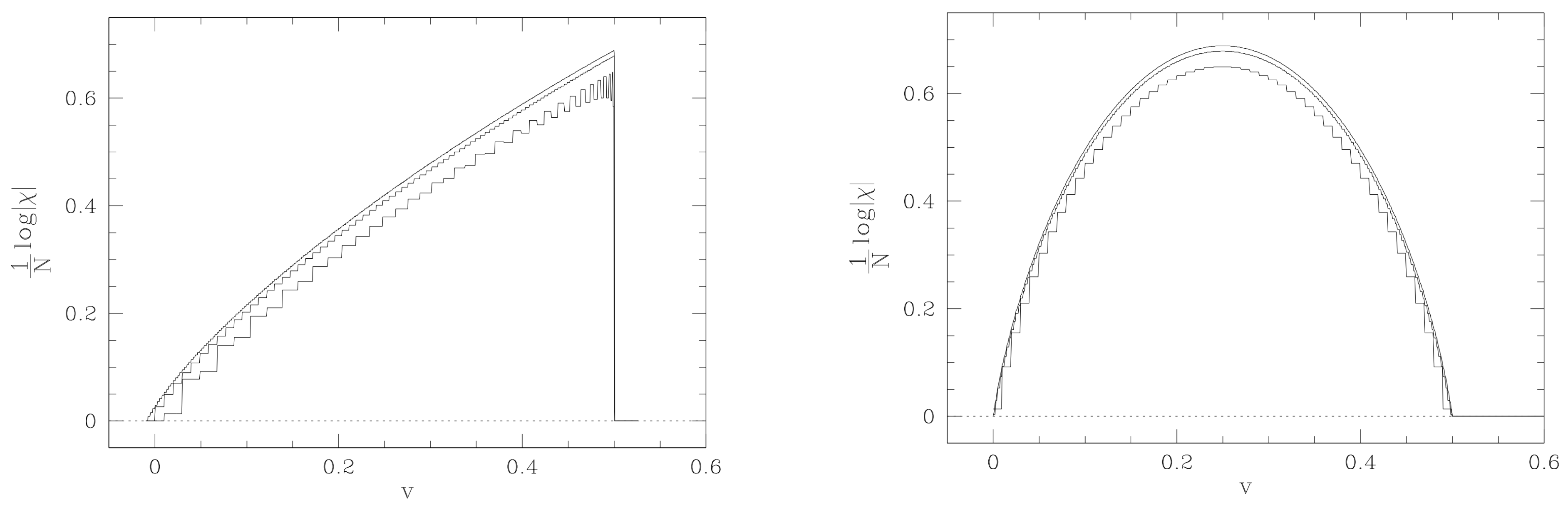
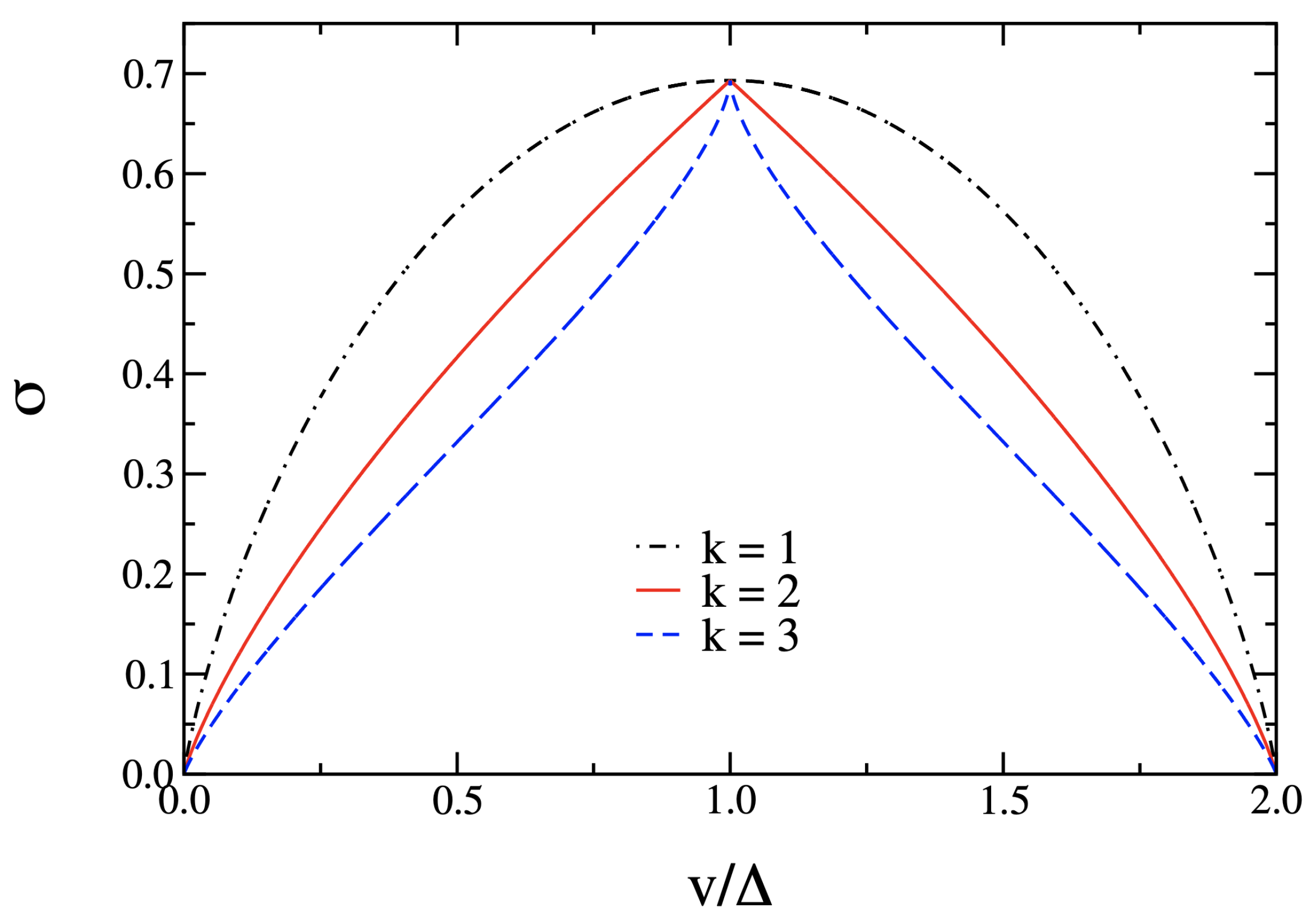
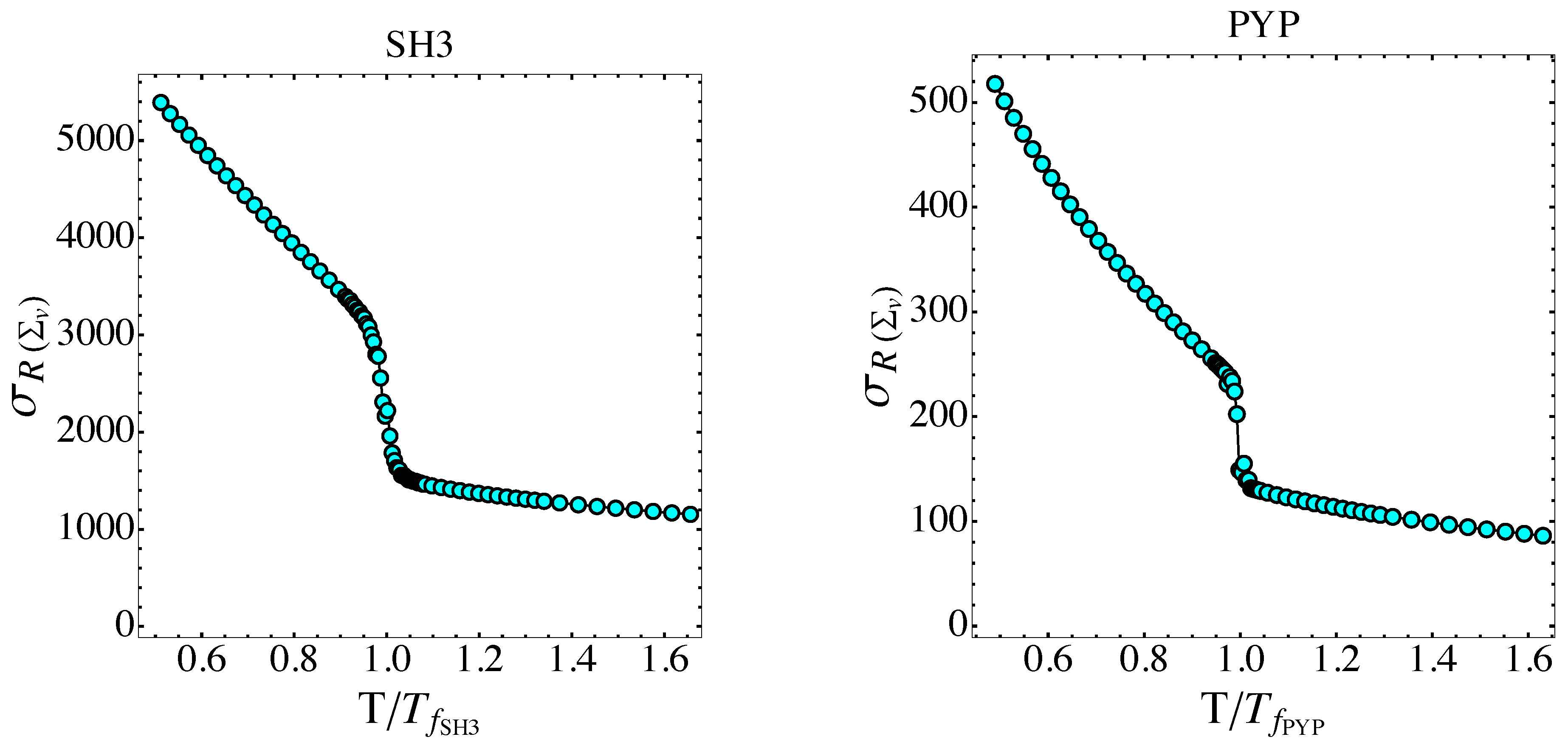
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pettini, G.; Gori, M.; Pettini, M. From Geometry of Hamiltonian Dynamics to Topology of Phase Transitions: A Review. Entropy 2024, 26, 840. https://doi.org/10.3390/e26100840
Pettini G, Gori M, Pettini M. From Geometry of Hamiltonian Dynamics to Topology of Phase Transitions: A Review. Entropy. 2024; 26(10):840. https://doi.org/10.3390/e26100840
Chicago/Turabian StylePettini, Giulio, Matteo Gori, and Marco Pettini. 2024. "From Geometry of Hamiltonian Dynamics to Topology of Phase Transitions: A Review" Entropy 26, no. 10: 840. https://doi.org/10.3390/e26100840
APA StylePettini, G., Gori, M., & Pettini, M. (2024). From Geometry of Hamiltonian Dynamics to Topology of Phase Transitions: A Review. Entropy, 26(10), 840. https://doi.org/10.3390/e26100840






