Quantum Information Scrambling in Adiabatically Driven Critical Systems
Abstract
:1. Introduction
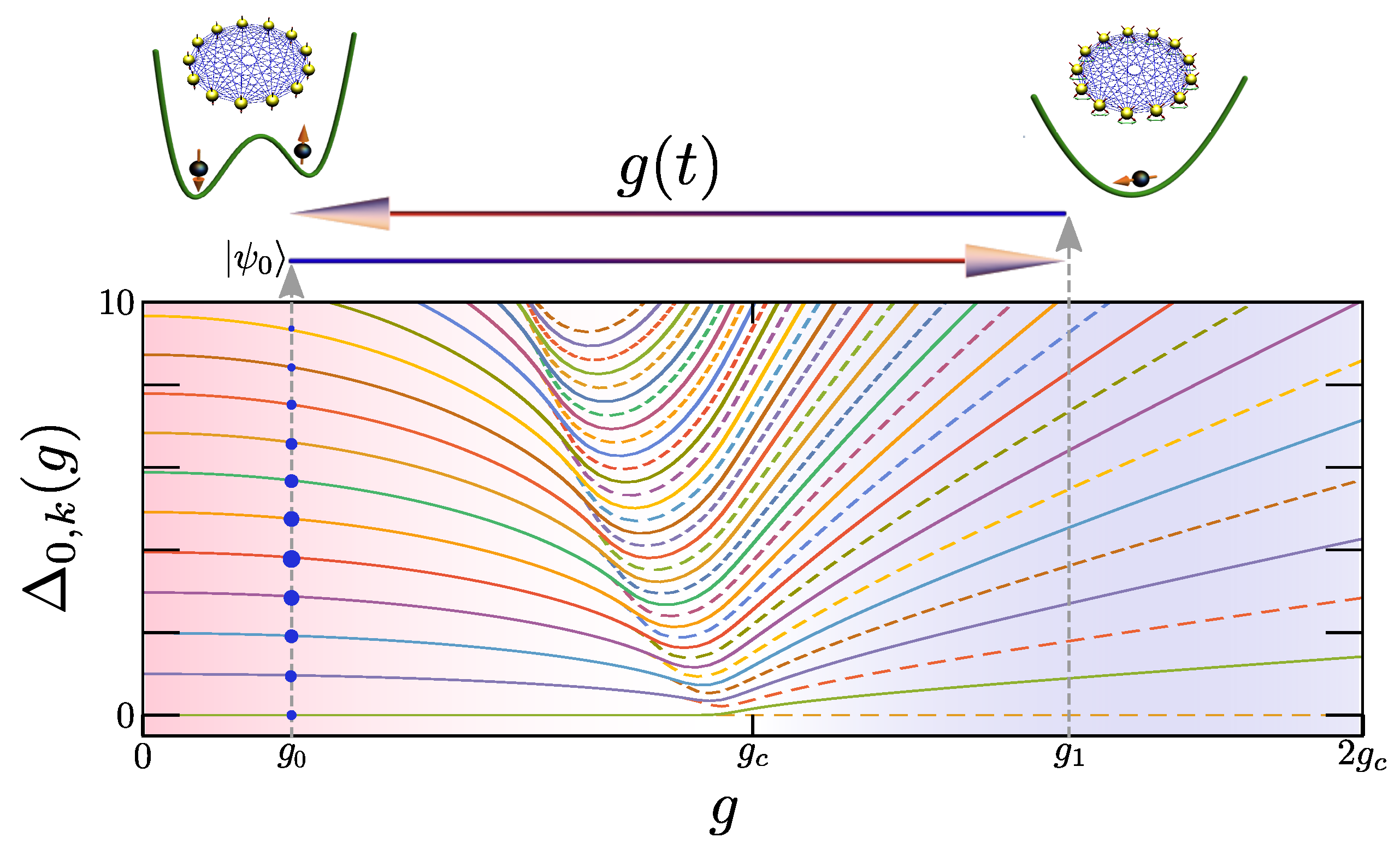
2. Adiabatic Quantum Information Scrambling
3. Lipkin–Meshkov–Glick Model
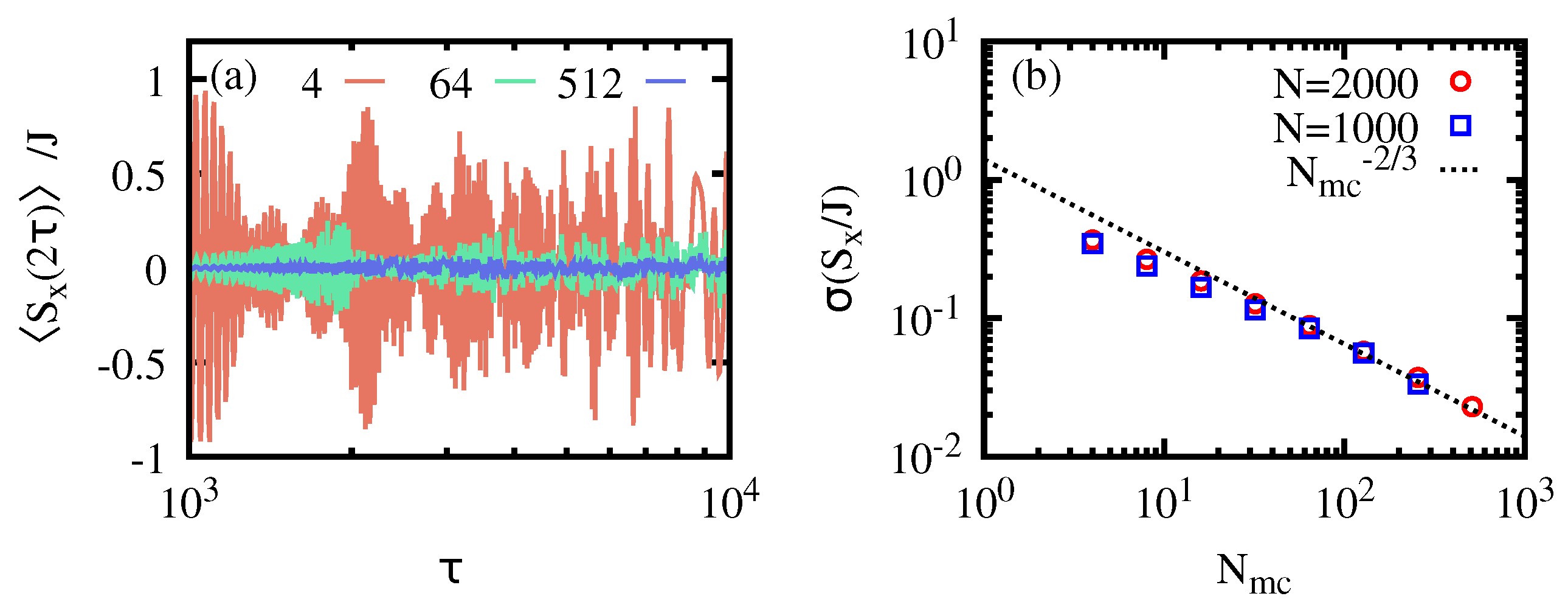
3.1. Effectiveness of the Quantum Information Scrambling
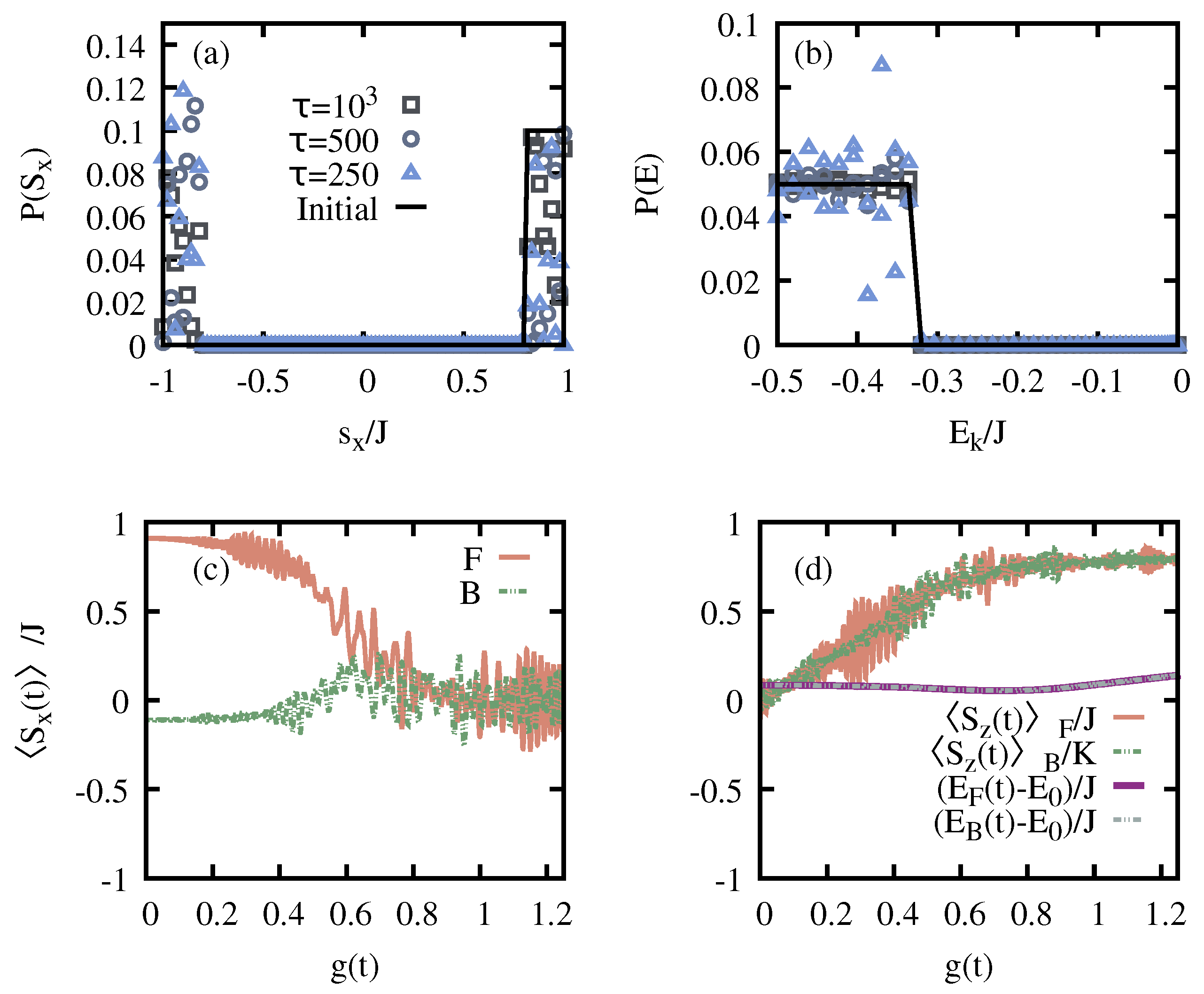
3.2. Loschmidt Echo and Out-of-Time-Ordered Correlator
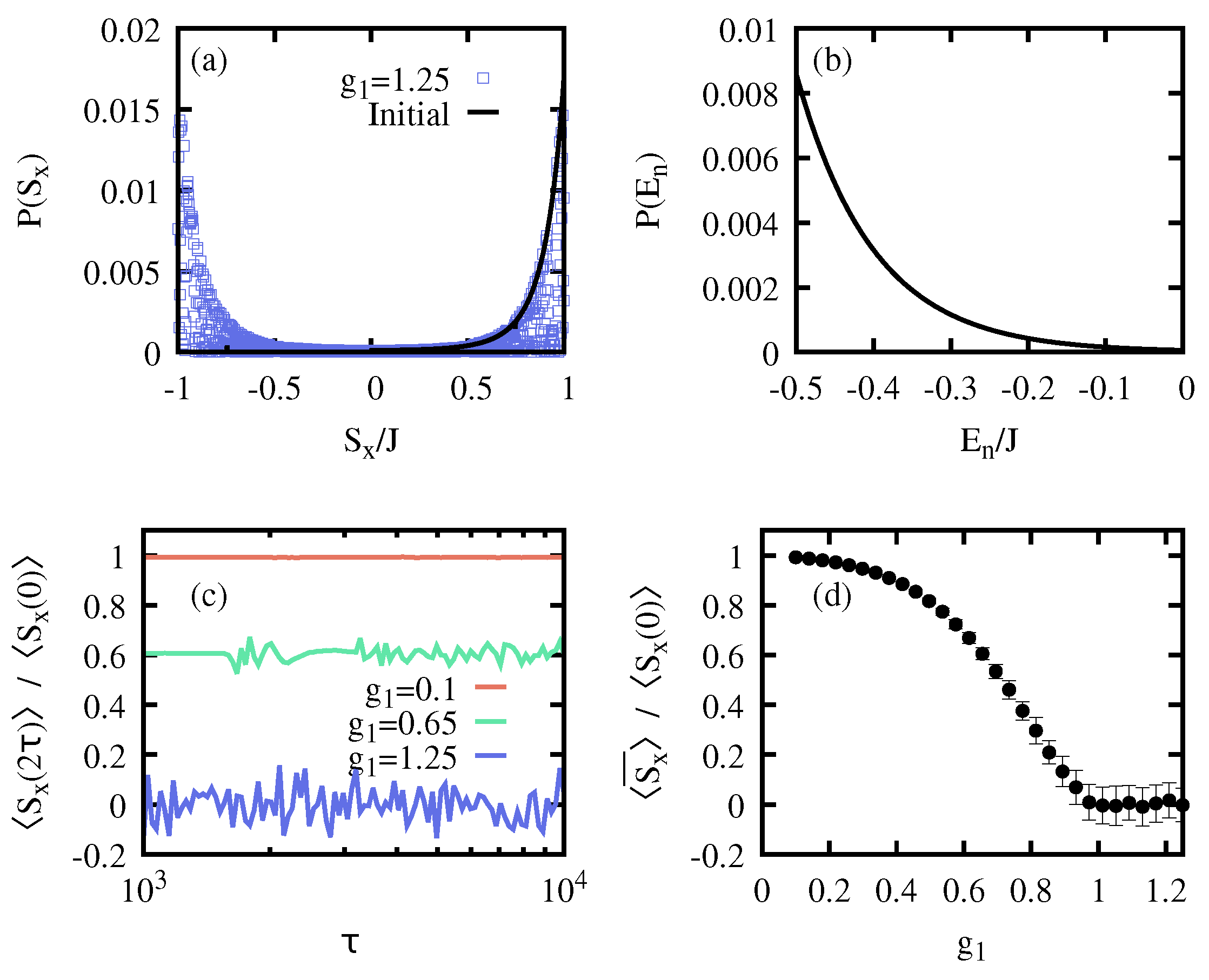
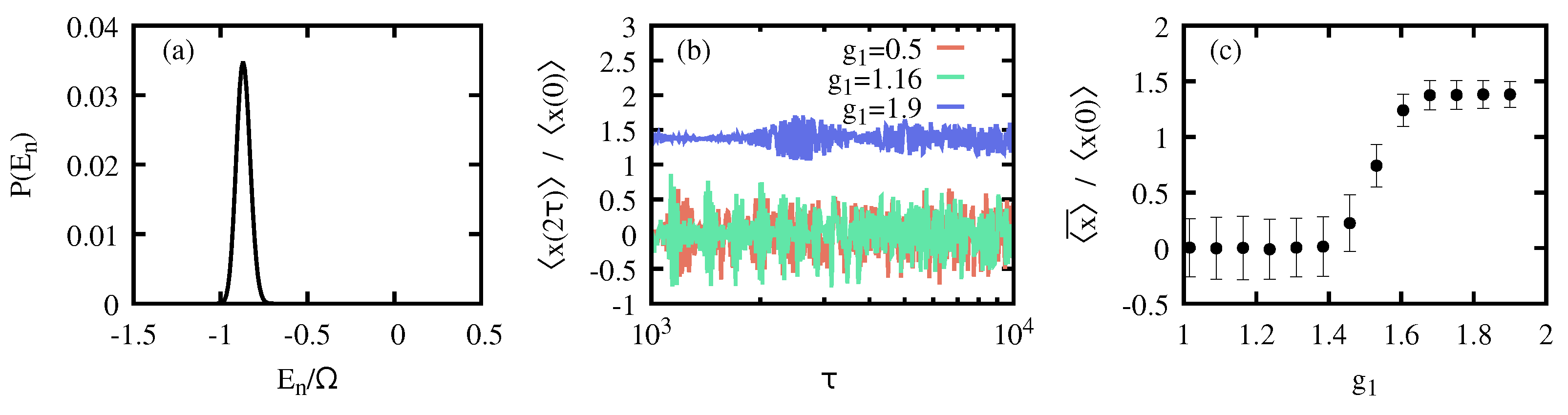
3.3. Symmetry-Breaking Thermal States
4. Quantum Rabi Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Swingle, B.; Bentsen, G.; Schleier-Smith, M.; Hayden, P. Measuring the scrambling of quantum information. Phys. Rev. A 2016, 94, 040302. [Google Scholar] [CrossRef]
- Swingle, B. Unscrambling the physics of out-of-time-order correlators. Nat. Phys. 2018, 14, 988–990. [Google Scholar] [CrossRef]
- Xu, S.; Swingle, B. Scrambling Dynamics and Out-of-Time-Ordered Correlators in Quantum Many-Body Systems. PRX Quantum 2024, 5, 010201. [Google Scholar] [CrossRef]
- Deutsch, J.M. Quantum statistical mechanics in a closed system. Phys. Rev. A 1991, 43, 2046–2049. [Google Scholar] [CrossRef] [PubMed]
- Touil, A.; Deffner, S. Information Scrambling versus Decoherence—Two Competing Sinks for Entropy. PRX Quantum 2021, 2, 010306. [Google Scholar] [CrossRef]
- Touil, A.; Deffner, S. Information scrambling—A quantum thermodynamic perspective. Europhys. Lett. 2024, 146, 48001. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Mezei, M.; Stanford, D. On entanglement spreading in chaotic systems. J. High Energy Phys. 2017, 2017, 65. [Google Scholar] [CrossRef]
- Chenu, A.; Molina-Vilaplana, J.; del Campo, A. Work Statistics, Loschmidt Echo and Information Scrambling in Chaotic Quantum Systems. Quantum 2019, 3, 127. [Google Scholar] [CrossRef]
- Campisi, M.; Goold, J. Thermodynamics of quantum information scrambling. Phys. Rev. E 2017, 95, 62127. [Google Scholar] [CrossRef] [PubMed]
- Deffner, S.; Campbell, S. Quantum Thermodynamics; Morgan & Claypool Publishers: San Rafael, CA, USA, 2019; pp. 2053–2571. [Google Scholar] [CrossRef]
- Maldacena, J.; Shenker, S.H.; Stanford, D. A bound on chaos. J. High Energy Phys. 2016, 2016, 106. [Google Scholar] [CrossRef]
- Polkovnikov, A.; Sengupta, K.; Silva, A.; Vengalattore, M. Colloquium: Nonequilibrium dynamics of closed interacting quantum systems. Rev. Mod. Phys. 2011, 83, 863–883. [Google Scholar] [CrossRef]
- Eisert, J.; Friesdorf, M.; Gogolin, C. Quantum many-body systems out of equilibrium. Nat. Phys. 2015, 11, 124–130. [Google Scholar] [CrossRef]
- Sachdev, S. Quantum Phase Transitions, 2nd ed.; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Srednicki, M. Chaos and quantum thermalization. Phys. Rev. E 1994, 50, 888–901. [Google Scholar] [CrossRef] [PubMed]
- Kaufman, A.M.; Tai, M.E.; Lukin, A.; Rispoli, M.; Schittko, R.; Preiss, P.M.; Greiner, M. Quantum thermalization through entanglement in an isolated many-body system. Science 2016, 353, 794–800. [Google Scholar] [CrossRef]
- Rigol, M.; Dunjko, V.; Olshanii, M. Thermalization and its mechanism for generic isolated quantum systems. Nature 2008, 452, 854–858. [Google Scholar] [CrossRef]
- Mi, X.; Roushan, P.; Quintana, C.; Mandrà, S.; Marshall, J.; Neill, C.; Arute, F.; Arya, K.; Atalaya, J.; Babbush, R.; et al. Information scrambling in quantum circuits. Science 2021, 374, 1479–1483. [Google Scholar] [CrossRef]
- Zhu, Q.; Sun, Z.H.; Gong, M.; Chen, F.; Zhang, Y.R.; Wu, Y.; Ye, Y.; Zha, C.; Li, S.; Guo, S.; et al. Observation of Thermalization and Information Scrambling in a Superconducting Quantum Processor. Phys. Rev. Lett. 2022, 128, 160502. [Google Scholar] [CrossRef]
- Gómez-Ruiz, F.J.; Mendoza-Arenas, J.J.; Rodríguez, F.J.; Tejedor, C.; Quiroga, L. Universal two-time correlations, out-of-time-ordered correlators, and Leggett-Garg inequality violation by edge Majorana fermion qubits. Phys. Rev. B 2018, 97, 235134. [Google Scholar] [CrossRef]
- Landsman, K.A.; Figgatt, C.; Schuster, T.; Linke, N.M.; Yoshida, B.; Yao, N.Y.; Monroe, C. Verified quantum information scrambling. Nature 2019, 567, 61–65. [Google Scholar] [CrossRef]
- Monaco, G.L.; Innocenti, L.; Cilluffo, D.; Chisholm, D.A.; Lorenzo, S.; Palma, G.M. Quantum scrambling via accessible tripartite information. Quantum Sci. Technol. 2023, 8, 035006. [Google Scholar] [CrossRef]
- Seshadri, A.; Madhok, V.; Lakshminarayan, A. Tripartite mutual information, entanglement, and scrambling in permutation symmetric systems with an application to quantum chaos. Phys. Rev. E 2018, 98, 052205. [Google Scholar] [CrossRef]
- Gärttner, M.; Bohnet, J.G.; Safavi-Naini, A.; Wall, M.L.; Bollinger, J.J.; Rey, A.M. Measuring out-of-time-order correlations and multiple quantum spectra in a trapped-ion quantum magnet. Nat. Phys. 2017, 13, 781–786. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Huang, Y.; Chen, X. Information scrambling in chaotic systems with dissipation. Phys. Rev. B 2019, 99, 014303. [Google Scholar] [CrossRef]
- Huang, Y.; Brandão, F.G.S.L.; Zhang, Y.L. Finite-Size Scaling of Out-of-Time-Ordered Correlators at Late Times. Phys. Rev. Lett. 2019, 123, 010601. [Google Scholar] [CrossRef]
- Alba, V.; Calabrese, P. Quantum information scrambling after a quantum quench. Phys. Rev. B 2019, 100, 115150. [Google Scholar] [CrossRef]
- Wang, J.H.; Cai, T.Q.; Han, X.Y.; Ma, Y.W.; Wang, Z.L.; Bao, Z.H.; Li, Y.; Wang, H.Y.; Zhang, H.Y.; Sun, L.Y.; et al. Information scrambling dynamics in a fully controllable quantum simulator. Phys. Rev. Res. 2022, 4, 043141. [Google Scholar] [CrossRef]
- Omanakuttan, S.; Chinni, K.; Blocher, P.D.; Poggi, P.M. Scrambling and quantum chaos indicators from long-time properties of operator distributions. Phys. Rev. A 2023, 107, 032418. [Google Scholar] [CrossRef]
- Heyl, M.; Pollmann, F.; Dóra, B. Detecting Equilibrium and Dynamical Quantum Phase Transitions in Ising Chains via Out-of-Time-Ordered Correlators. Phys. Rev. Lett. 2018, 121, 016801. [Google Scholar] [CrossRef]
- Sun, Z.; Cai, J.; Tang, Q.; Hu, Y.; Fan, H. Out-of-Time-Order Correlators and Quantum Phase Transitions in the Rabi and Dicke Models. Annalen der Physik 2020, 532, 1900270. [Google Scholar] [CrossRef]
- Wei, B.B.; Sun, G.; Hwang, M.J. Dynamical scaling laws of out-of-time-ordered correlators. Phys. Rev. B 2019, 100, 195107. [Google Scholar] [CrossRef]
- Dağ, C.B.; Sun, K.; Duan, L.M. Detection of Quantum Phases via Out-of-Time-Order Correlators. Phys. Rev. Lett. 2019, 123, 140602. [Google Scholar] [CrossRef] [PubMed]
- Dorner, R.; Goold, J.; Cormick, C.; Paternostro, M.; Vedral, V. Emergent Thermodynamics in a Quenched Quantum Many-Body System. Phys. Rev. Lett. 2012, 109, 160601. [Google Scholar] [CrossRef] [PubMed]
- Varizi, A.D.; Vieira, A.P.; Cormick, C.; Drumond, R.C.; Landi, G.T. Quantum coherence and criticality in irreversible work. Phys. Rev. Res. 2020, 2, 033279. [Google Scholar] [CrossRef]
- Bayat, A.; Apollaro, T.J.G.; Paganelli, S.; De Chiara, G.; Johannesson, H.; Bose, S.; Sodano, P. Nonequilibrium critical scaling in quantum thermodynamics. Phys. Rev. B 2016, 93, 201106. [Google Scholar] [CrossRef]
- Abah, O.; De Chiara, G.; Paternostro, M.; Puebla, R. Harnessing nonadiabatic excitations promoted by a quantum critical point: Quantum battery and spin squeezing. Phys. Rev. Res. 2022, 4, L022017. [Google Scholar] [CrossRef]
- Vijayan, V.; Chotorlishvili, L.; Ernst, A.; Katsnelson, M.I.; Parkin, S.S.P.; Mishra, S.K. Plasmonic skyrmion quantum thermodynamics. arXiv 2023, arXiv:2312.05656. [Google Scholar]
- Cejnar, P.; Macek, M.; Heinze, S.; Jolie, J.; Dobeš, J. Monodromy and excited-state quantum phase transitions in integrable systems: Collective vibrations of nuclei. J. Phys. A Math. Theor. 2006, 39, L515. [Google Scholar] [CrossRef]
- Caprio, M.; Cejnar, P.; Iachello, F. Excited state quantum phase transitions in many-body systems. Ann. Phys. 2008, 323, 110–1135. [Google Scholar] [CrossRef]
- Brandes, T. Excited-state quantum phase transitions in Dicke superradiance models. Phys. Rev. E 2013, 88, 032133. [Google Scholar] [CrossRef]
- Stránský, P.; Macek, M.; Cejnar, P. Excited-state quantum phase transitions in systems with two degrees of freedom: Level density, level dynamics, thermal properties. Ann. Phys. 2014, 345, 73–97. [Google Scholar] [CrossRef]
- Stránský, P.; Macek, M.; Leviatan, A.; Cejnar, P. Excited-state quantum phase transitions in systems with two degrees of freedom: II. Finite-size effects. Ann. Phys. 2015, 356, 57–82. [Google Scholar] [CrossRef]
- Cejnar, P.; Stránský, P.; Macek, M.; Kloc, M. Excited-state quantum phase transitions. J. Phys. A Math. Theor. 2021, 54, 133001. [Google Scholar] [CrossRef]
- Puebla, R.; Relaño, A.; Retamosa, J. Excited-state phase transition leading to symmetry-breaking steady states in the Dicke model. Phys. Rev. A 2013, 87, 023819. [Google Scholar] [CrossRef]
- Puebla, R.; Relaño, A. Non-thermal excited-state quantum phase transitions. Europhys. Lett. 2013, 104, 50007. [Google Scholar] [CrossRef]
- Puebla, R.; Relaño, A. Irreversible processes without energy dissipation in an isolated Lipkin-Meshkov-Glick model. Phys. Rev. E 2015, 92, 012101. [Google Scholar] [CrossRef]
- Corps, A.L.; Relaño, A. Constant of Motion Identifying Excited-State Quantum Phases. Phys. Rev. Lett. 2021, 127, 130602. [Google Scholar] [CrossRef]
- Corps, A.L.; Relaño, A. Dynamical and excited-state quantum phase transitions in collective systems. Phys. Rev. B 2022, 106, 024311. [Google Scholar] [CrossRef]
- Corps, A.L.; Relaño, A. Theory of Dynamical Phase Transitions in Quantum Systems with Symmetry-Breaking Eigenstates. Phys. Rev. Lett. 2023, 130, 100402. [Google Scholar] [CrossRef]
- Gómez-Ruiz, F.J.; Acevedo, O.L.; Rodríguez, F.J.; Quiroga, L.; Johnson, N.F. Pulsed Generation of Quantum Coherences and Non-classicality in Light-Matter Systems. Front. Phys. 2018, 6, 92. [Google Scholar] [CrossRef]
- Gómez-Ruiz, F.; Acevedo, O.; Quiroga, L.; Rodríguez, F.; Johnson, N. Quantum Hysteresis in Coupled Light–Matter Systems. Entropy 2016, 18, 319. [Google Scholar] [CrossRef]
- Lipkin, H.; Meshkov, N.; Glick, A. Validity of many-body approximation methods for a solvable model. Nucl. Phys. 1965, 62, 188–198. [Google Scholar] [CrossRef]
- Dusuel, S.; Vidal, J. Finite-size scaling exponents of the Lipkin-Meshkov-Glick model. Phys. Rev. Lett. 2004, 93, 237204. [Google Scholar] [CrossRef] [PubMed]
- Leyvraz, F.; Heiss, W.D. Large-N scaling behavior of the Lipkin-Meshkov-Glick Model. Phys. Rev. Lett. 2005, 95, 050402. [Google Scholar] [CrossRef] [PubMed]
- Vidal, J.; Dusuel, S.; Barthel, T. Entanglement entropy in collective models. J. Stat. Mech. 2007, 2007, P01015. [Google Scholar] [CrossRef]
- Ribeiro, P.; Vidal, J.; Mosseri, R. Thermodynamical limit of the Lipkin-Meshkov-Glick model. Phys. Rev. Lett. 2007, 99, 050402. [Google Scholar] [CrossRef]
- Ribeiro, P.; Vidal, J.; Mosseri, R. Exact spectrum of the Lipkin-Meshkov-Glick model in the thermodynamic limit and finite-size corrections. Phys. Rev. E 2008, 78, 021106. [Google Scholar] [CrossRef]
- Dicke, R.H. Coherence in Spontaneous Radiation Processes. Phys. Rev. 1954, 93, 99–110. [Google Scholar] [CrossRef]
- Emary, C.; Brandes, T. Quantum Chaos Triggered by Precursors of a Quantum Phase Transition: The Dicke Model. Phys. Rev. Lett. 2003, 90, 044101. [Google Scholar] [CrossRef]
- Hwang, M.J.; Puebla, R.; Plenio, M.B. Quantum phase transition and universal dynamics in the Rabi model. Phys. Rev. Lett. 2015, 115, 180404. [Google Scholar] [CrossRef]
- Puebla, R.; Hwang, M.J.; Plenio, M.B. Excited-state quantum phase transition in the Rabi model. Phys. Rev. A 2016, 94, 023835. [Google Scholar] [CrossRef]
- Bakemeier, L.; Alvermann, A.; Fehske, H. Quantum phase transition in the Dicke model with critical and noncritical entanglement. Phys. Rev. A 2012, 85, 043821. [Google Scholar] [CrossRef]
- Puebla, R. Finite-component dynamical quantum phase transitions. Phys. Rev. B 2020, 102, 220302. [Google Scholar] [CrossRef]
- Felicetti, S.; Le Boité, A. Universal Spectral Features of Ultrastrongly Coupled Systems. Phys. Rev. Lett. 2020, 124, 040404. [Google Scholar] [CrossRef]
- Bastarrachea-Magnani, M.A.; Lerma-Hernández, S.; Hirsch, J.G. Comparative quantum and semiclassical analysis of atom-field systems. II. Chaos and regularity. Phys. Rev. A 2014, 89, 032102. [Google Scholar] [CrossRef]
- Relaño, A.; Bastarrachea-Magnani, M.A.; Lerma-Hernández, S. Approximated integrability of the Dicke model. Europhys. Lett. 2017, 116, 50005. [Google Scholar] [CrossRef]
- Lóbez, C.M.; Relaño, A. Entropy, chaos, and excited-state quantum phase transitions in the Dicke model. Phys. Rev. E 2016, 94, 012140. [Google Scholar] [CrossRef]
- Corps, Á.L.; Molina, R.A.; Relaño, A. Chaos in a deformed Dicke model. J. Phys. A Math. Theor. 2022, 55, 084001. [Google Scholar] [CrossRef]
- Zibold, T.; Nicklas, E.; Gross, C.; Oberthaler, M.K. Classical Bifurcation at the Transition from Rabi to Josephson Dynamics. Phys. Rev. Lett. 2010, 105, 204101. [Google Scholar] [CrossRef]
- Jurcevic, P.; Shen, H.; Hauke, P.; Maier, C.; Brydges, T.; Hempel, C.; Lanyon, B.P.; Heyl, M.; Blatt, R.; Roos, C.F. Direct observation of dynamical quantum phase transitions in an interacting many-body system. Phys. Rev. Lett. 2017, 119, 080501. [Google Scholar] [CrossRef]
- Caneva, T.; Fazio, R.; Santoro, G.E. Adiabatic quantum dynamics of the Lipkin-Meshkov-Glick model. Phys. Rev. B 2008, 78, 104426. [Google Scholar] [CrossRef]
- Kwok, H.M.; Ning, W.Q.; Gu, S.J.; Lin, H.Q. Quantum criticality of the Lipkin-Meshkov-Glick model in terms of fidelity susceptibility. Phys. Rev. E 2008, 78, 032103. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Z.G.; Zhang, P.; Li, S.S.; Jing, J.; Kong, L.B. Scaling of the Berry phase close to the excited-state quantum phase transition in the Lipkin model. Phys. Rev. A 2012, 85, 044102. [Google Scholar] [CrossRef]
- Acevedo, O.L.; Quiroga, L.; Rodríguez, F.J.; Johnson, N.F. New dynamical scaling universality for quantum networks across adiabatic quantum phase transitions. Phys. Rev. Lett. 2014, 112, 030403. [Google Scholar] [CrossRef]
- Salvatori, G.; Mandarino, A.; Paris, M.G.A. Quantum metrology in Lipkin-Meshkov-Glick critical systems. Phys. Rev. A 2014, 90, 022111. [Google Scholar] [CrossRef]
- Campbell, S.; De Chiara, G.; Paternostro, M.; Palma, G.M.; Fazio, R. Shortcut to Adiabaticity in the Lipkin-Meshkov-Glick Model. Phys. Rev. Lett. 2015, 114, 177206. [Google Scholar] [CrossRef]
- Campbell, S. Criticality revealed through quench dynamics in the Lipkin-Meshkov-Glick model. Phys. Rev. B 2016, 94, 184403. [Google Scholar] [CrossRef]
- Defenu, N.; Enss, T.; Kastner, M.; Morigi, G. Dynamical Critical Scaling of Long-Range Interacting Quantum Magnets. Phys. Rev. Lett. 2018, 121, 240403. [Google Scholar] [CrossRef]
- Puebla, R.; Smirne, A.; Huelga, S.F.; Plenio, M.B. Universal Anti-Kibble-Zurek Scaling in Fully Connected Systems. Phys. Rev. Lett. 2020, 124, 230602. [Google Scholar] [CrossRef]
- Mzaouali, Z.; Puebla, R.; Goold, J.; El Baz, M.; Campbell, S. Work statistics and symmetry breaking in an excited-state quantum phase transition. Phys. Rev. E 2021, 103, 032145. [Google Scholar] [CrossRef]
- Garbe, L.; Abah, O.; Felicetti, S.; Puebla, R. Critical quantum metrology with fully-connected models: From Heisenberg to Kibble–Zurek scaling. Quantum Sci. Technol. 2022, 7, 035010. [Google Scholar] [CrossRef]
- Gamito, J.; Khalouf-Rivera, J.; Arias, J.M.; Pérez-Fernández, P.; Pérez-Bernal, F. Excited-state quantum phase transitions in the anharmonic Lipkin-Meshkov-Glick model: Static aspects. Phys. Rev. E 2022, 106, 044125. [Google Scholar] [CrossRef] [PubMed]
- Garbe, L.; Abah, O.; Felicetti, S.; Puebla, R. Exponential time-scaling of estimation precision by reaching a quantum critical point. Phys. Rev. Res. 2022, 4, 043061. [Google Scholar] [CrossRef]
- Santini, A.; Lumia, L.; Collura, M.; Giachetti, G. Semiclassical Quantum Trajectories in the Monitored Lipkin-Meshkov-Glick Model. arXiv 2024, arXiv:2407.20314. [Google Scholar]
- Cejnar, P.; Stránský, P. Impact of quantum phase transitions on excited-level dynamics. Phys. Rev. E 2008, 78, 031130. [Google Scholar] [CrossRef]
- Pérez-Fernández, P.; Relaño, A. From thermal to excited-state quantum phase transition: The Dicke model. Phys. Rev. E 2017, 96, 012121. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Puebla, R.; Gómez-Ruiz, F.J. Quantum Information Scrambling in Adiabatically Driven Critical Systems. Entropy 2024, 26, 951. https://doi.org/10.3390/e26110951
Puebla R, Gómez-Ruiz FJ. Quantum Information Scrambling in Adiabatically Driven Critical Systems. Entropy. 2024; 26(11):951. https://doi.org/10.3390/e26110951
Chicago/Turabian StylePuebla, Ricardo, and Fernando J. Gómez-Ruiz. 2024. "Quantum Information Scrambling in Adiabatically Driven Critical Systems" Entropy 26, no. 11: 951. https://doi.org/10.3390/e26110951
APA StylePuebla, R., & Gómez-Ruiz, F. J. (2024). Quantum Information Scrambling in Adiabatically Driven Critical Systems. Entropy, 26(11), 951. https://doi.org/10.3390/e26110951






