Random Walk on T-Fractal with Stochastic Resetting
Abstract
1. Introduction
2. Network Model and Some Properties
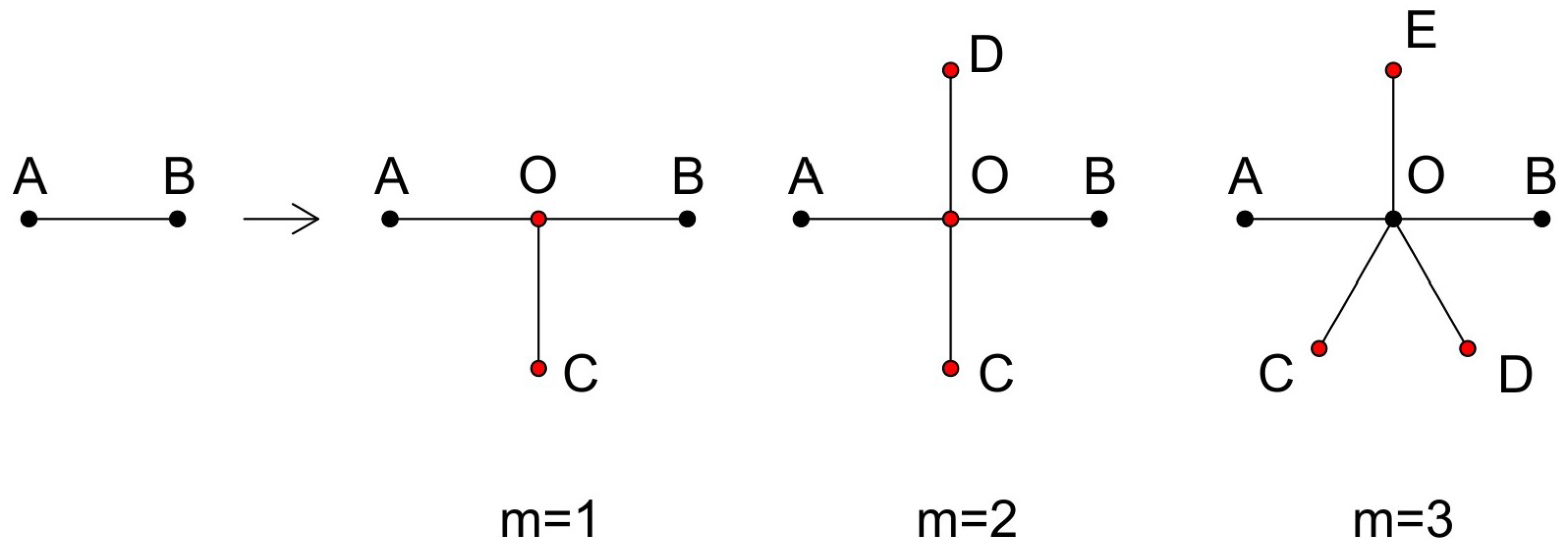
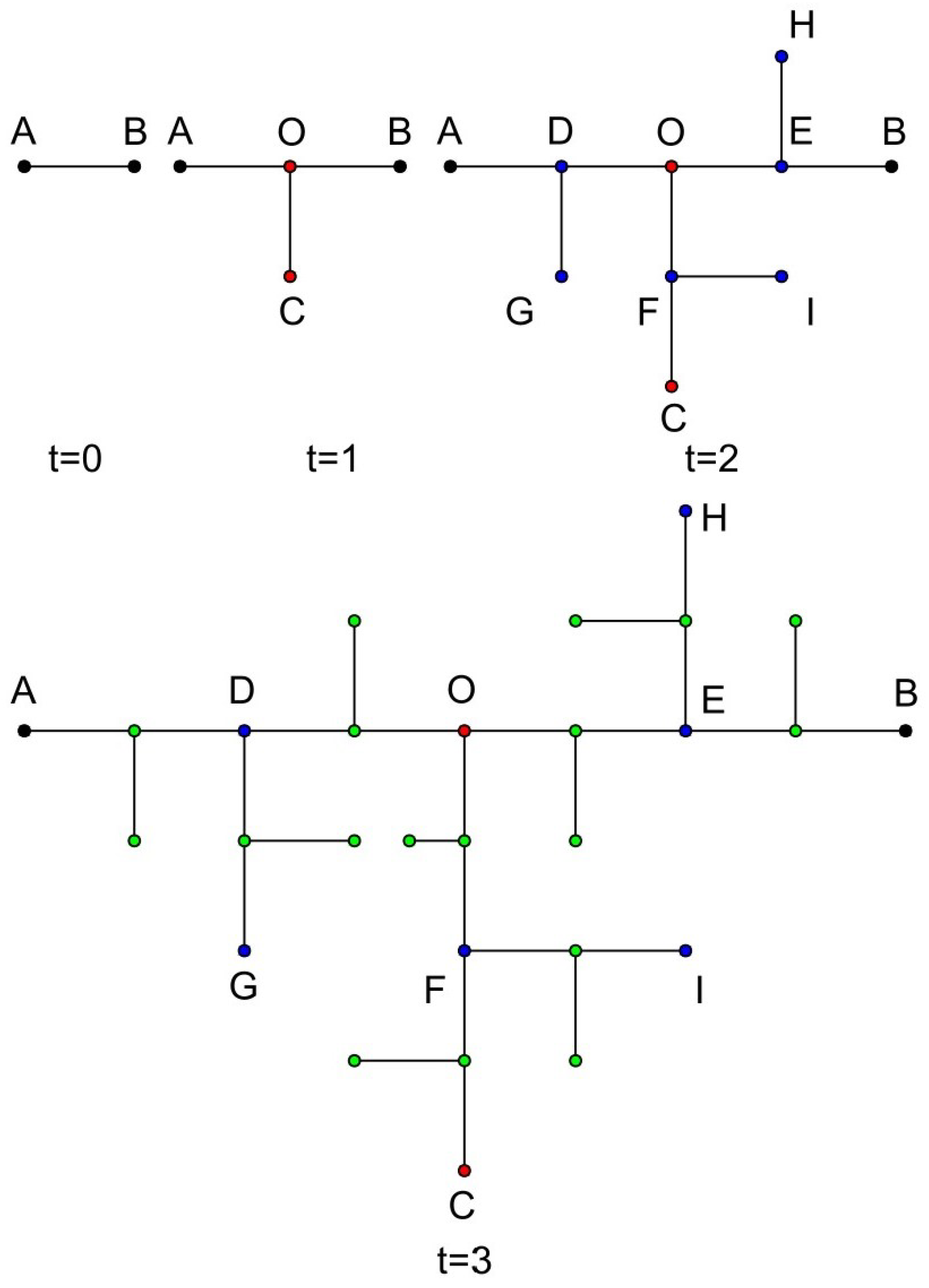
2.1. The Construction of Tree-like Fractals
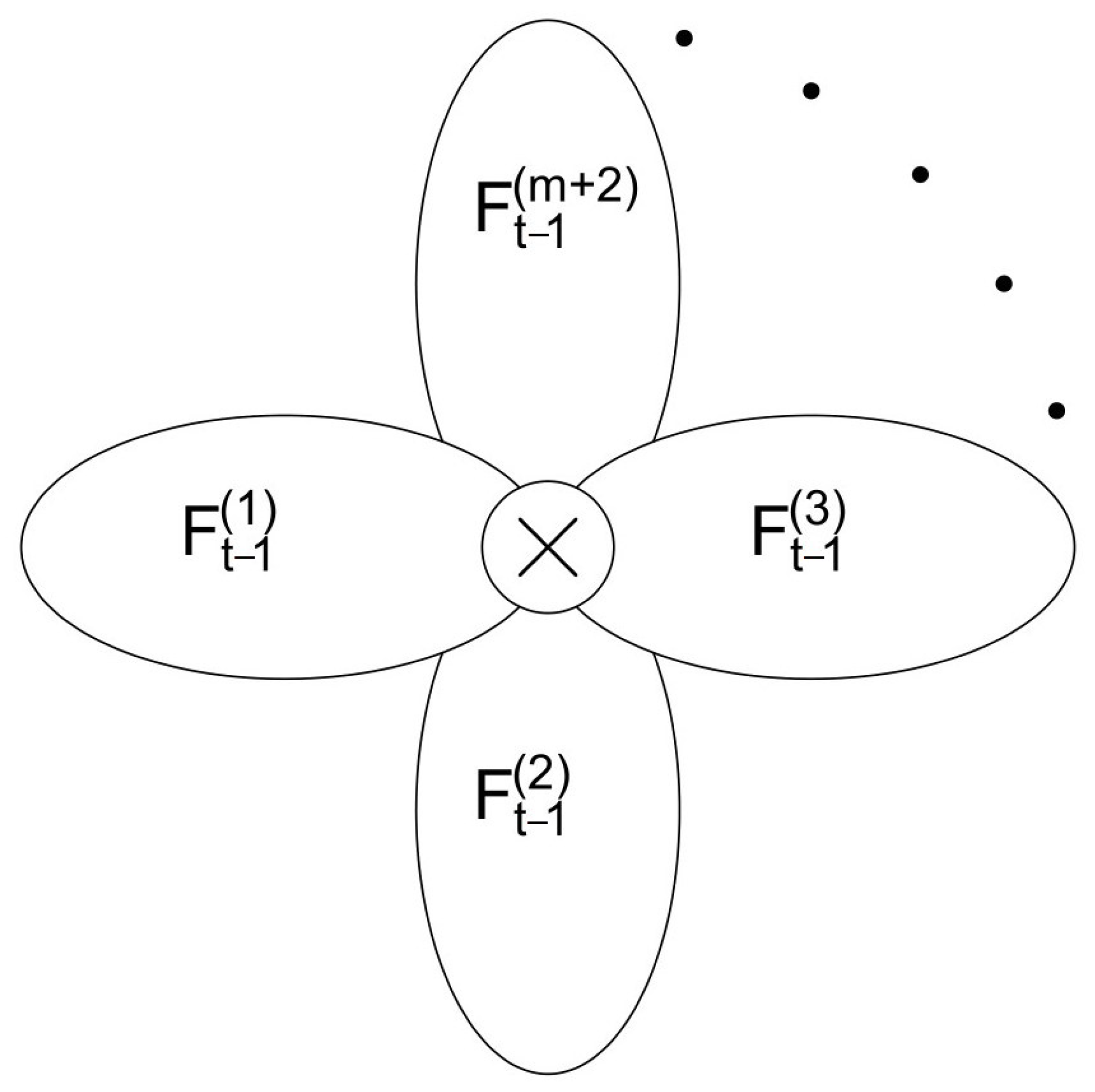
2.2. Some Basic Properties of Tree-like Fractals
3. Random Walk on T-Fractal
3.1. Random Walk from A to B
3.2. Random Walk from D to E
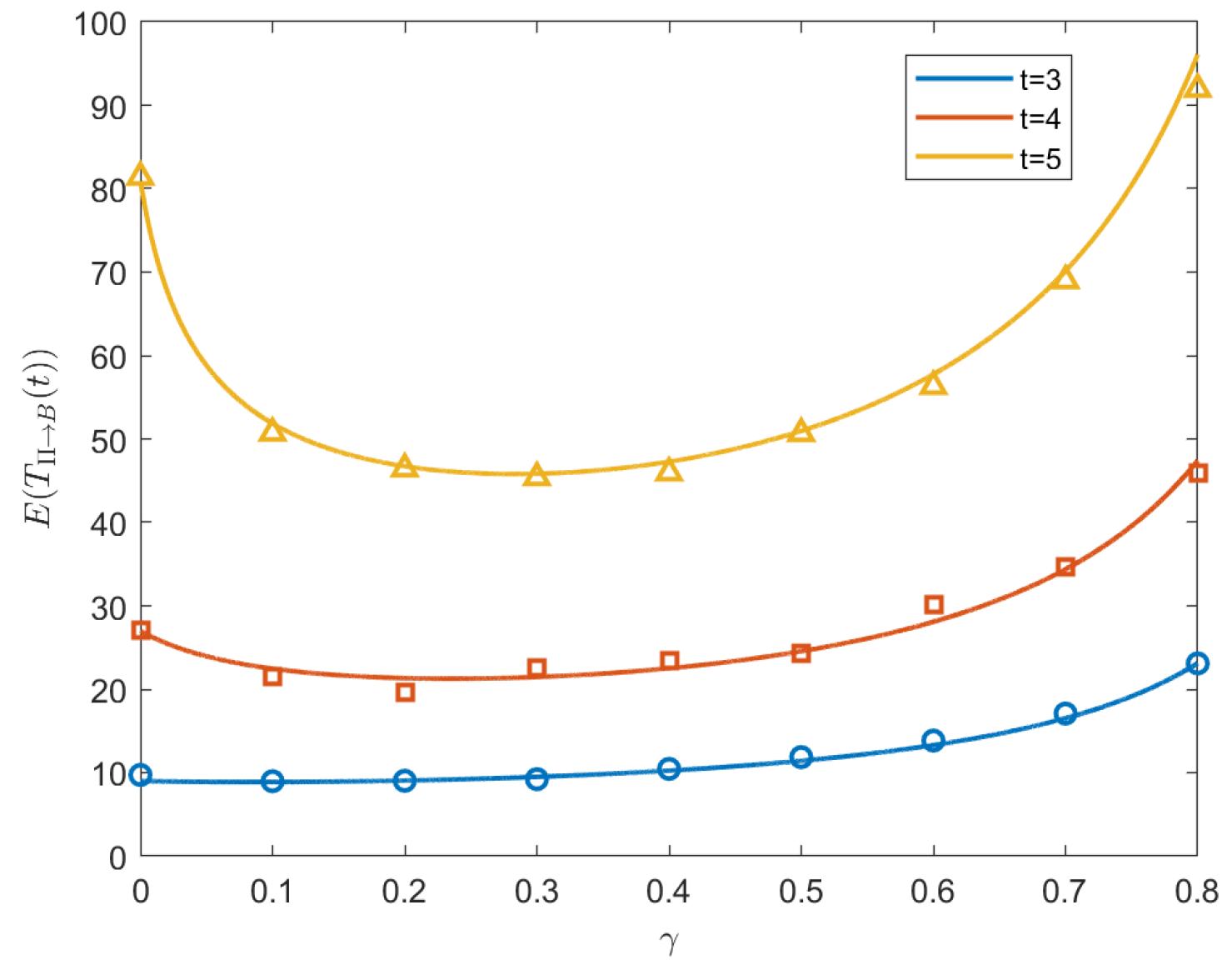
3.3. Random Walk from O to B
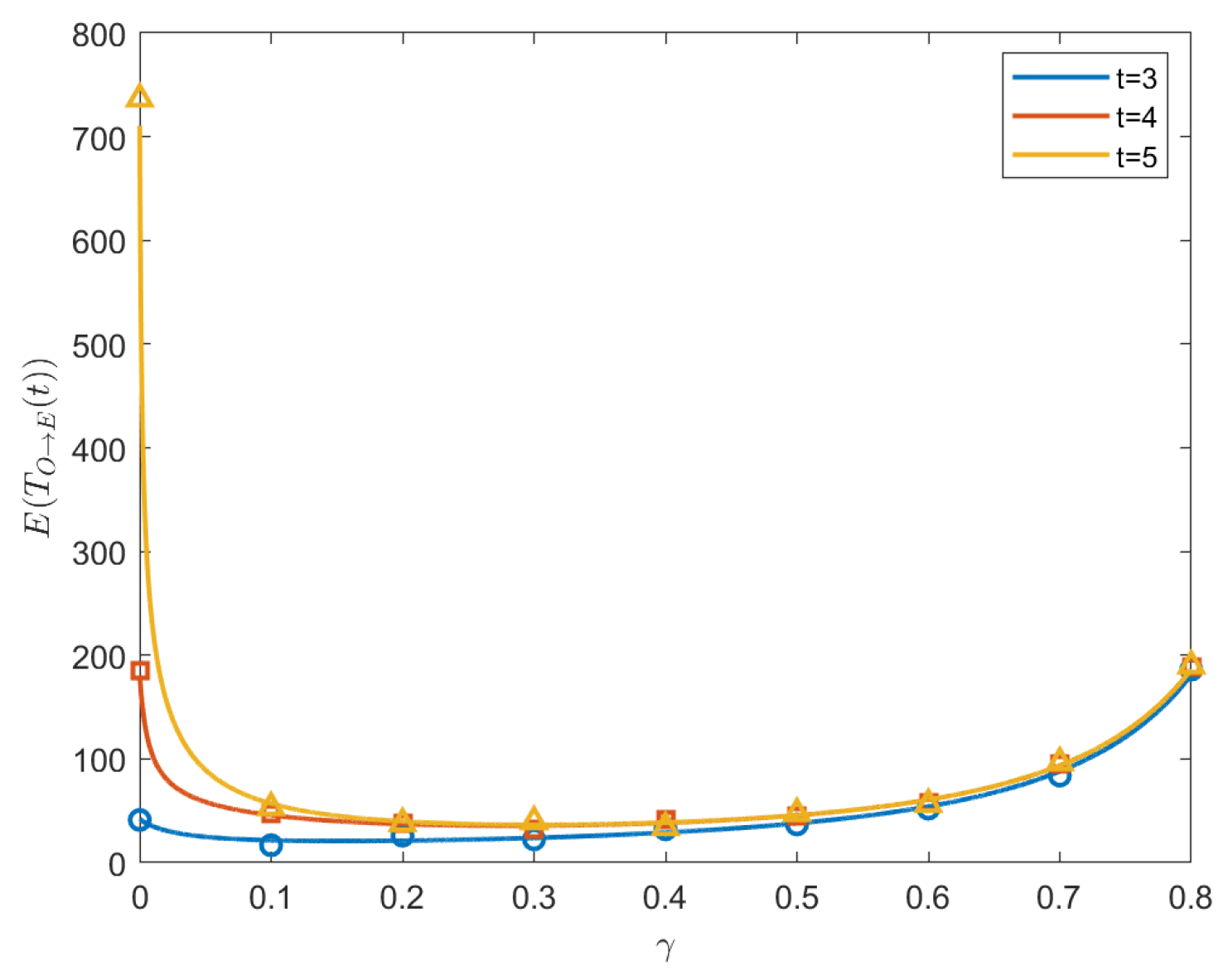
3.4. Random Walk from O to E
3.5. Random Walk to B with the Starting Node Selected Randomly
4. Random Walk on Network with Stochastic Resetting
4.1. MFPT for the Discrete-Time First Passage Process Under Resetting
4.2. MFPT for a Random Walk on a Network with a Fixed Resetting Rate
5. Random Walk on T-Fractal with Stochastic Resetting
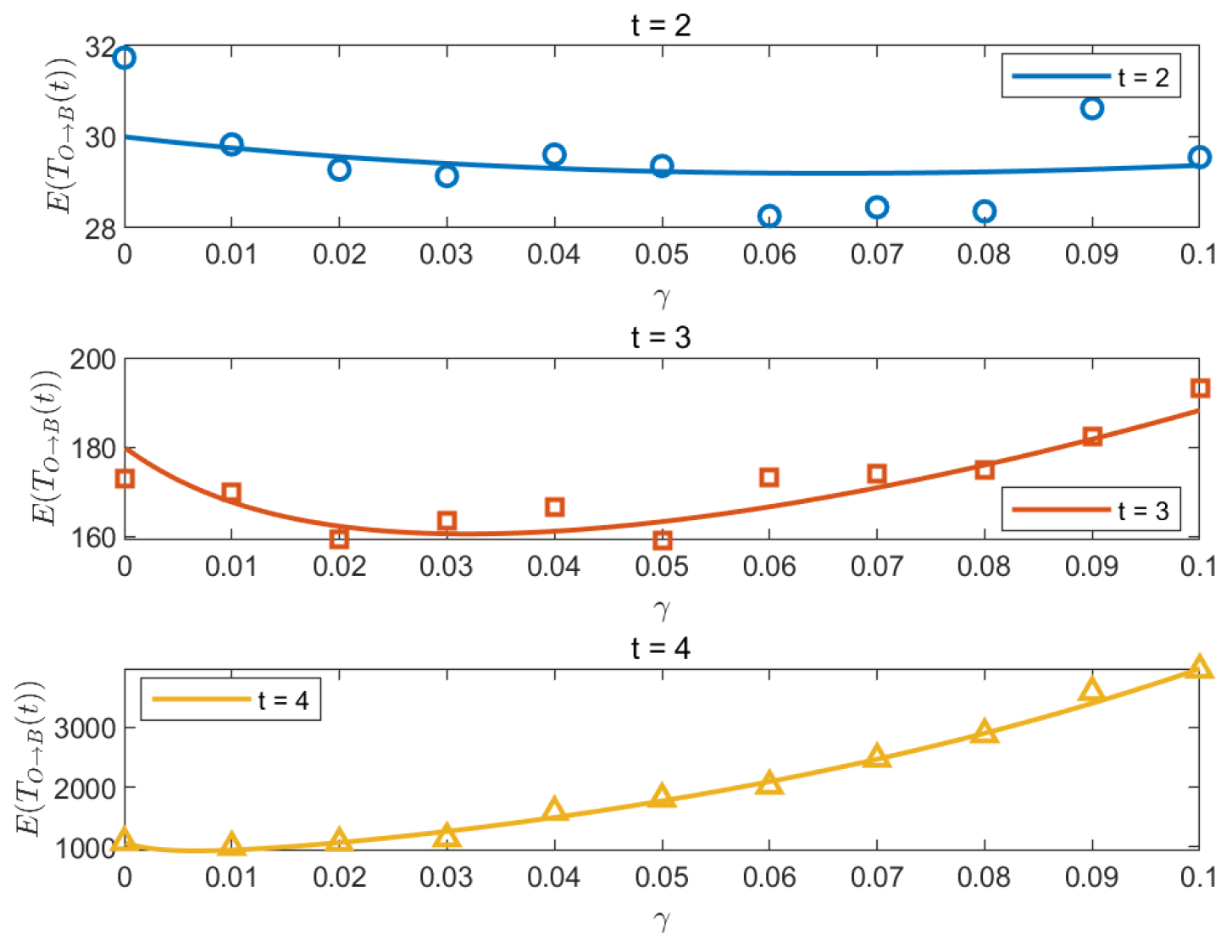
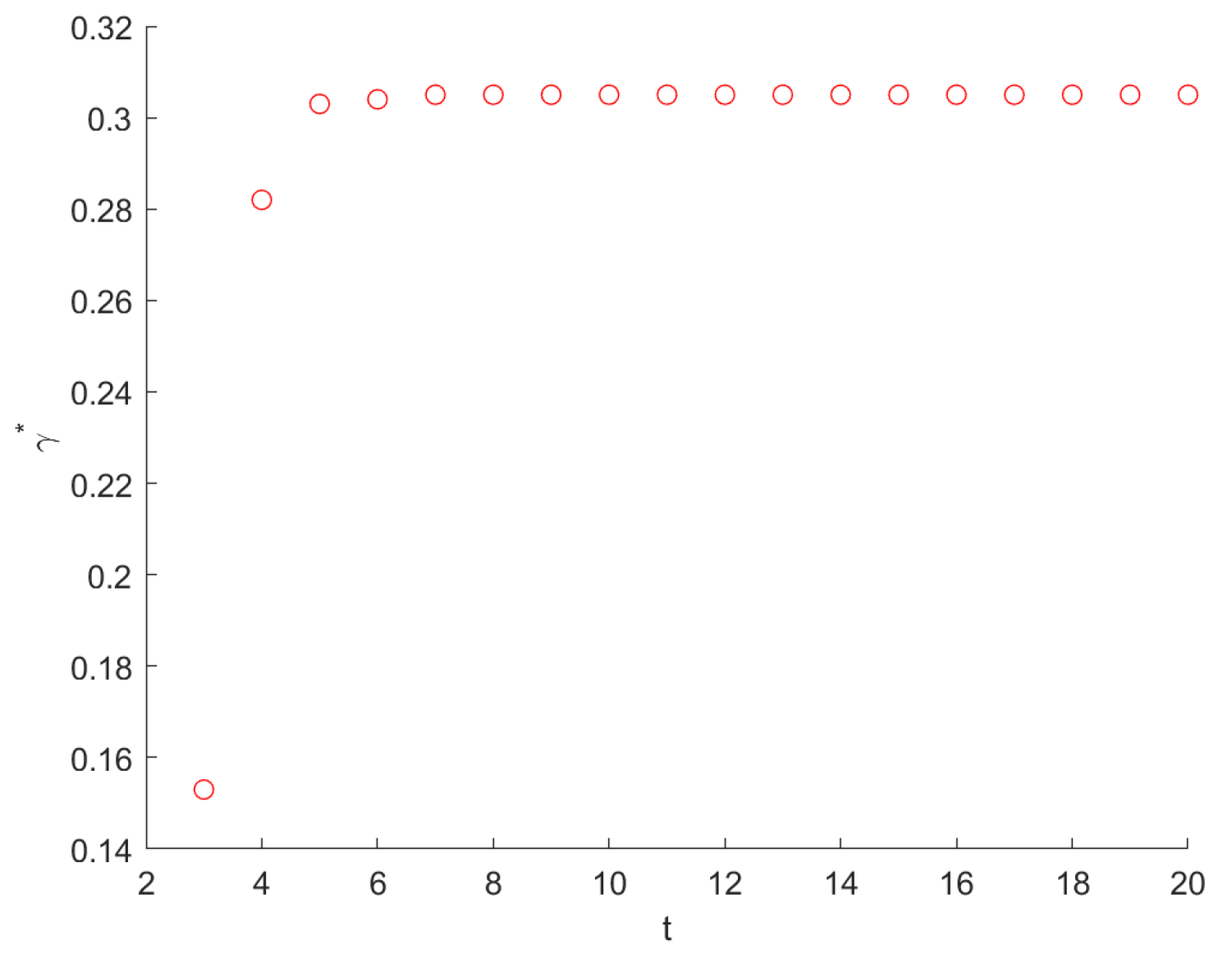
5.1. Random Walk with Resetting from O to B
5.2. Random Walk with Resetting from O to E
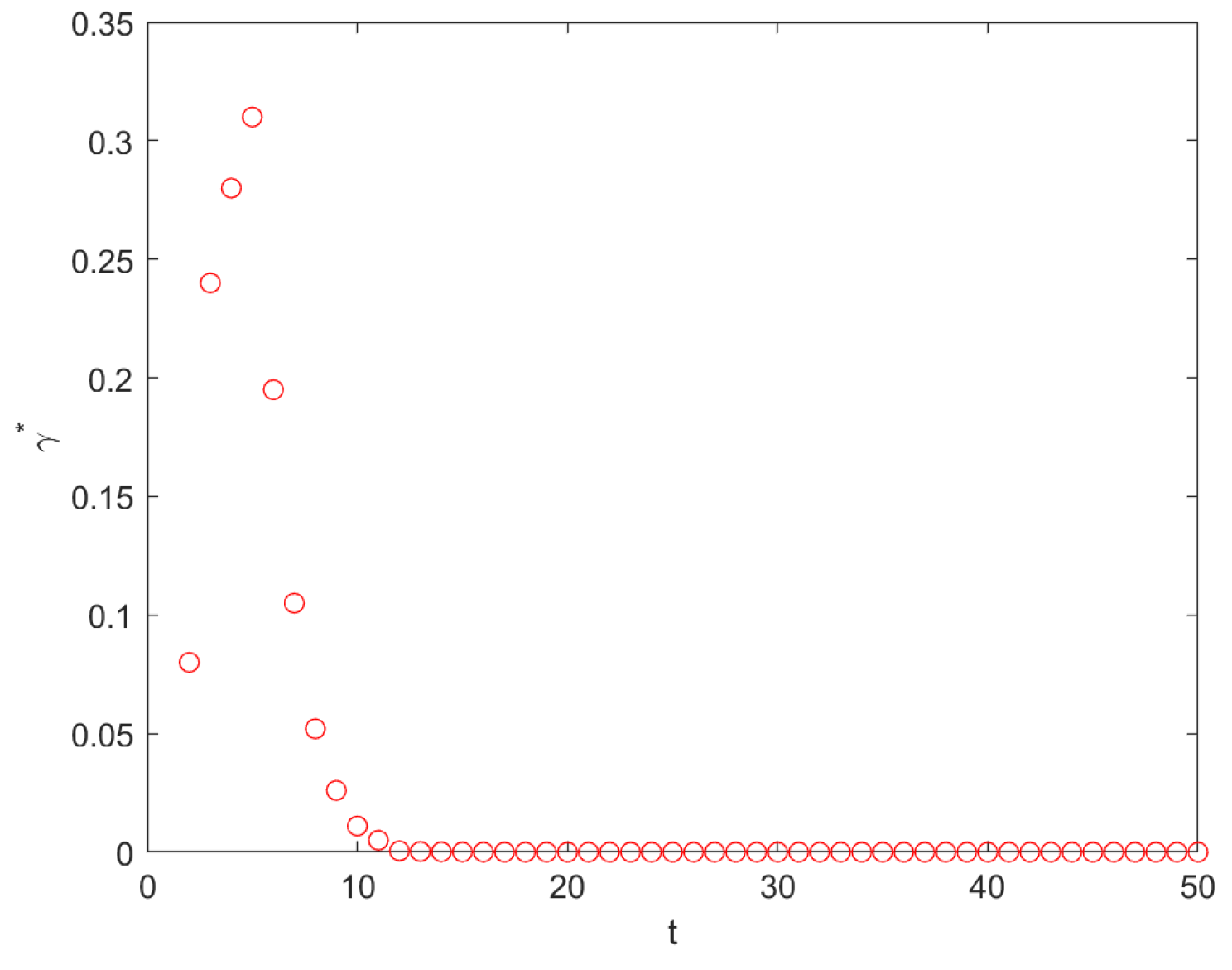
5.3. MFPT for a Random Walk on a T-Fractal with the Resetting Position Selected Randomly
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MFPT | Mean first passage time |
| FFP | First passage probability |
| FPT | First passage time |
Appendix A. Some Basic Properties of the Generating Function
Appendix B. The Calculation of the Initial Condition
Appendix C. The Derivation of Equations (10), (14) and (18) in Section 3
Appendix D. The Derivation of Equations (26) and (27)
References
- Evans, M.R.; Majumdar, S.N. Diffusion with stochastic resetting. Phys. Rev. Lett. 2011, 106, 160601. [Google Scholar] [CrossRef] [PubMed]
- Kuśmierz, Ł.; Majumdar, S.N.; Sabhapandit, S.; Schehr, G. First order transition for the optimal search time of Lévy flights with resetting. Phys. Rev. Lett. 2014, 113, 220602. [Google Scholar] [CrossRef] [PubMed]
- Pal, A.; Kundu, A.; Evans, M.R. Diffusion under time-dependent resetting. J. Phys. A Math. Theor. 2016, 49, 225001. [Google Scholar] [CrossRef]
- Bhat, U.; Bacco, C.D.; Redner, S. Stochastic search with Poisson and deterministic resetting. J. Stat. Mech. Theory Exp. 2016, 2016, 083401. [Google Scholar] [CrossRef]
- Masuda, N.; Porter, M.A.; Lambiotte, R. Random walks and diffusion on networks. Phys. Rep. 2017, 716, 1–58. [Google Scholar] [CrossRef]
- Pal, A.; Prasad, V.V. First passage under stochastic resetting in an interval. Phys. Rev. E 2019, 99, 032123. [Google Scholar] [CrossRef]
- Giuggioli, L.; Gupta, S.; Chase, M. Comparison of two models of tethered motion. J. Phys. A Math. Theor. 2020, 53, 155001. [Google Scholar] [CrossRef]
- Evans, M.R.; Majumdar, S.N.; Schehr, G. Stochastic resetting and applications. J. Phys. A Math. Theor. 2020, 53, 193001. [Google Scholar] [CrossRef]
- Reuveni, S. Optimal stochastic restart renders fluctuations in first passage times universal. Phys. Rev. Lett. 2016, 116, 170601. [Google Scholar] [CrossRef]
- Evans, M.R.; Majumdar, S.N. Diffusion with optimal resetting. J. Phys. A Math. Theor. 2011, 44, 435001. [Google Scholar] [CrossRef]
- Riascos, A.P.; Boyer, D.; Herringer, P.; Mateos, J.L. Random walks on networks with stochastic resetting. Phys. Rev. E 2020, 101, 062147. [Google Scholar] [CrossRef] [PubMed]
- González, F.H.; Riascos, A.P.; Boyer, D. Diffusive transport on networks with stochastic resetting to multiple nodes. Phys. Rev. E 2021, 103, 062126. [Google Scholar] [CrossRef]
- Wang, S.; Chen, H.; Huang, F. Random walks on complex networks with multiple resetting nodes: A renewal approach. Chaos 2021, 31, 062147. [Google Scholar] [CrossRef]
- Ye, Y.; Chen, H. Random walks on complex networks under node-dependent stochastic resetting. J. Stat. Mech. Theory Exp. 2022, 2022, 053201. [Google Scholar] [CrossRef]
- Chen, H.; Ye, Y. Random walks on complex networks under time-dependent stochastic resetting. Phys. Rev. E 2022, 106, 044139. [Google Scholar] [CrossRef] [PubMed]
- Huang, F.; Chen, H. Random walks on complex networks with first-passage resetting. Phys. Rev. E 2021, 103, 062132. [Google Scholar] [CrossRef]
- Chen, J.; Bin, F.; Ge, X.; Li, Q.; Wang, C.-X. A dual-directional path-loss model in 5G wireless fractal small cell networks. arXiv 2016, arXiv:1612.04463. [Google Scholar]
- Ge, X.; Chen, J.; Bin, F.; Li, Q.; Wang, C.-X. Small-cell networks with fractal coverage characteristics. IEEE Trans. Veh. Technol. 2018, 67, 7853–7867. [Google Scholar] [CrossRef]
- Ge, X.; Chen, J.; Li, Q.; Wang, C.-X. Wireless fractal cellular networks. IEEE Wirel. Commun. 2016, 23, 110–119. [Google Scholar] [CrossRef]
- Losa, G.A.; Merlini, D.; Nonnenmacher, T.F.; Weibel, E.R. Fractals in Biology and Medicine; Mathematics and Biosciences in Interaction Series; Birkhäuser: Basel, Switzerland, 2005; Volume 4. [Google Scholar]
- Goldberger, A.L. Fractal dynamics in physiology: Alterations with disease and aging. Proc. Natl. Acad. Sci. USA 2002, 99 (Suppl. S1), 2466–2472. [Google Scholar] [CrossRef]
- Buehler, M.J. Materiomics: Biological protein materials, from nano to macro. Prog. Mater. Sci. 2013, 58, 1686–1720. [Google Scholar] [CrossRef] [PubMed]
- Fratzl, P.; Weinkamer, R. Nature’s hierarchical materials. Prog. Mater. Sci. 2007, 52, 1263–1334. [Google Scholar] [CrossRef]
- Gao, H.; Bower, B.J. Fractal-based hierarchical materials: Fundamentals and applications. Adv. Mater. 2015, 27, 3641–3650. [Google Scholar]
- Molz, F.J.; Rajaram, H.; Lu, S. Stochastic fractal-based models of heterogeneity in subsurface hydrology: Origins, applications, limitations, and future research questions. Rev. Geophys. 2004, 42, RG1002. [Google Scholar] [CrossRef]
- Lorenz, W.E. Fractals and fractal architecture. In Industrial and Civil Construction 2022; Springer: Cham, Switzerland, 2002. [Google Scholar]
- Balakrishnan, V. Random walks on fractals. Mater. Sci. Eng. B 1995, 32, 201–210. [Google Scholar] [CrossRef]
- Goldstein, S. Random walks and diffusions on fractals. In Percolation Theory and Ergodic Theory of Infinite Particle Systems; Springer: New York, NY, USA, 1987; pp. 121–129. [Google Scholar]
- Ma, F.; Wang, P.; Yao, B. Random walks on Fibonacci treelike models: Emergence of power law. arXiv 2019, arXiv:1904.11314. [Google Scholar]
- Brandes, U. Network Analysis: Methodological Foundations; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Kantz, H. Dynamics and Statistical Physics Division Fachverband Dynamik und Statistische Physik (DY). 2023. Available online: https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=a92b9055852b6330a81ac49fabdd74cb6054c51c (accessed on 20 November 2024).
- Weng, T.; Zhang, J.; Khajehnejad, M.; Small, M.; Zheng, R.; Hui, P. Navigation by anomalous random walks on complex networks. Sci. Rep. 2016, 6, 37547. [Google Scholar] [CrossRef][Green Version]
- Lin, Y.; Wu, B.; Zhang, Z. Determining mean first-passage time on a class of treelike regular fractals. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2010, 82, 031140. [Google Scholar] [CrossRef]
- Peng, J.; Shao, R.; Chen, L.; Stanley, H.E. Moments of global first passage time and first return time on tree-like fractals. J. Stat. Mech. Theory Exp. 2018, 2018, 093205. [Google Scholar] [CrossRef]
- Agliari, E. Exact mean first-passage time on the T-graph. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2008, 77, 011128. [Google Scholar] [CrossRef]
- Havlin, S.; Weissman, H. Mapping between hopping on hierarchical structures and diffusion on a family of fractals. J. Phys. A Math. Gen. 1986, 19, L1021. [Google Scholar] [CrossRef]
- Kahng, B.; Redner, S. Scaling of the first-passage time and the survival probability on exact and quasi-exact self-similar structures. J. Phys. A Math. Gen. 1989, 22, 887. [Google Scholar] [CrossRef]
- Zhang, Z.; Qi, Y.; Zhou, S.; Wang, B.; Guan, J. Mean first-passage time for random walks on the T-fractal structure. New J. Phys. 2009, 11, 103043. [Google Scholar] [CrossRef]
- Bonomo, O.L.; Pal, A. The Polya and Sisyphus lattice random walks with resetting—A first passage under restart approach. arXiv 2021, arXiv:2106.14036. [Google Scholar]
- Bonomo, I.; Roldán, É. First passage under restart for discrete space and time: Application to one-dimensional confined lattice random walks. Phys. Rev. E 2021, 103, 052129. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, X.; Li, A.; Zhu, S.; Zhu, F. Random Walk on T-Fractal with Stochastic Resetting. Entropy 2024, 26, 1034. https://doi.org/10.3390/e26121034
Sun X, Li A, Zhu S, Zhu F. Random Walk on T-Fractal with Stochastic Resetting. Entropy. 2024; 26(12):1034. https://doi.org/10.3390/e26121034
Chicago/Turabian StyleSun, Xiaohan, Anlin Li, Shaoxiang Zhu, and Feng Zhu. 2024. "Random Walk on T-Fractal with Stochastic Resetting" Entropy 26, no. 12: 1034. https://doi.org/10.3390/e26121034
APA StyleSun, X., Li, A., Zhu, S., & Zhu, F. (2024). Random Walk on T-Fractal with Stochastic Resetting. Entropy, 26(12), 1034. https://doi.org/10.3390/e26121034







