Modification of Premises for the Black Hole Information Paradox Caused by Topological Constraints in the Event Horizon Vicinity
Abstract
:1. Introduction
2. Methods
2.1. Change in Trajectory Homotopy Class When Passing the Photon Sphere Rim
2.2. Quantum Statistics Transition in Multi-Particle Systems Passing the Photon Sphere Rim of a Black Hole
3. Results
3.1. Collapse of Fermi Spheres in Dense Systems of Fermions Passing the Photon Sphere Rim
3.2. Spectrum and Timing of Short Giant Gamma-Ray Burst at Unstable Neutron Star Merger Collapse
3.3. The Radiation Efficiency of Fermi Sphere Decay in Plasma at Varying Particle Concentrations
4. Discussion
4.1. Upgrade of Premises for Information Paradox
4.2. Astrophysical Observations Which Support Quantum Statistics Transition at Photon Sphere Rim of Black Holes
- AT 2020neh: A rapidly brightening tidal disruption event (TDE) candidate, originating from a dwarf galaxy SDSSJ152120.07+140410.5 at a redshift of . The central black hole within this galaxy possesses a mass of approximately solar masses [54]. AT 2020neh has been under continuous observation since June 2020, with its peak luminosity occurring in July and persisting for approximately 20 days. Concurrent observations in optical, ultraviolet, and X-ray wavelengths have revealed an X-ray component reaching a maximum of W, comparable to other TDEs [55]. The overall peak luminosity attained W. By employing conventional hydrodynamic models [56], it has been estimated the rate at which stellar debris from the disrupted star (assumed to be a main sequence star with a mass of solar masses) is accreting onto the black hole. The observed optical and ultraviolet spectra have been successfully fitted using a black body temperature model, exhibiting a cooling rate of approximately K per 20 days. While no definitive mechanism for the X-ray component has been identified, post-flare observations and prior survey data have ruled out the presence of a gaseous accretion disk around the host galaxy’s black hole. However, by applying Equation (10) to the disrupted stellar debris during the peak luminosity phase and considering the maximum energy of observed X-ray photons (10 keV), we find that the contribution to the luminosity primarily in the X-ray range is approximately W due to the decay of Fermi spheres within the ionized debris consumed by the black hole. This result is consistent with the observed spectra of TDEs [54,55].
- AT2021lwx: Located at a redshift of , AT2021lwx exhibited a temporal increase in radiation luminosity to W, commencing in April 2021 and lasting over a year [57]. This event represents the most energetic non-quasar transient ever observed, with no prior emission detected in the preceding several years. The optical and ultraviolet spectral energy distribution of AT2021lwx indicates a black-body temperature of K. This transient is believed to be the result of a massive gaseous cloud accreting onto a black hole (this black hole mass has been estimated to be between and solar masses), rather than TDE. The observed X-ray component, spanning the energy range of to 10 keV with a luminosity of W, has proven challenging to explain using conventional models at such a low temperature. However, by incorporating the emission arising from the decay of Fermi spheres within compressed fermion systems passing through the photon sphere rim of the central black hole, we can reconcile the Fermi momentum (related to the compression level via Equation (9) and linked to the maximum observed photon energy) and a realistic supply of matter at the accretion site to achieve a luminosity of approximately W. This contribution effectively supplements the total luminosity of AT2021lwx and provides an explanation for the observed X-ray component at this event.
- Transient AGN 1ES 1927+654: Located at a redshift of , this active galactic nucleus (AGN) underwent a 100-fold brightening event lasting for one year, beginning in December 2017. The optical and ultraviolet spectral components increased during this period, while the gamma-ray flux exhibited a decline. By July 2018, the X-ray coronal emission had vanished, only to reappear a few months later [58]. The source subsequently returned to its pre-changing-look state after approximately one year in the optical, ultraviolet, and X-ray ranges. Previous interpretations [58] suggested that the puzzling behavior of gamma-ray radiation in AGN 1ES 1927+654 was due to the temporary quenching of jets from a spinning black hole caused by the consumption of an oppositely magnetized gas cloud during a changing-look episode. However, the quantum statistics transition at photon sphere rim of the black hole offers an alternative explanation for the observed behavior without relying on such speculations about jet quenching. In the case of AGN 1ES 1927+654, the source of gamma radiation is believed to be associated with electrons and positrons accelerated by the magnetic field within the jets of the spinning black hole, in accordance with the Blandford–Znajek model of jet formation [59]. This model explains the formation of jets for spinning Kerr-like black holes, where the dragging of the reference frame in the Kerr metric causes the magnetic field frozen within the accretion matter to rotate. This results in an outgoing flux of angular momentum, extracting energy from the system and propelling jets into outer space. The rotating magnetic field within these jets accelerates electrons and positrons, leading to the production of gamma-ray radiation. The source of electron–positron pairs in the Blandford–Znajek model is a strong electric field generated by the rotating magnetic field frozen within the ergosphere. In the case of the AGN 1ES 1927+654 transient, the decay of Fermi spheres of electrons and protons from the occasionally captured gas cloud produces sub-MeV radiation (at most 2 keV, consistent with X-ray observations [58]) due to the relatively low plasma compression at the photon sphere rim. These photons are unable to excite additional electron–positron pairs within the ergosphere but can exert a force on existing pairs created according to the Blandford–Znajek mechanism, pushing them towards the event horizon. This ultimately leads to a reduction in the supply of electrons and positrons to the jets (via diffusion to jets across nodes in the ergosphere of a Kerr-like black hole), resulting in a temporary quenching of gamma-ray radiation without the need to speculate on the demagnetization of the AGN by an oppositely magnetized gas cloud during this episode [58].
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Quantum Statistics and Trajectories Entering Feynman Path Integrals
Appendix B. Quantum Statistics and Spin: A Topological Perspective
References
- Hawking, S.W. Black hole explosions? Nature 1974, 248, 30–31. [Google Scholar] [CrossRef]
- Bekenstein, A. Black holes and the second law. Lett. Al Nuovo Cimento 1972, 4, 737–740. [Google Scholar] [CrossRef]
- Almheiri, A.; Hartman, T.; Maldacena, J.; Shaghoulian, E.; Tajdini, A. The entropy of Hawking radiation. Rev. Mod. Phys. 2021, 93, 035002. [Google Scholar] [CrossRef]
- Unruh, W.G. Notes on black-hole evaporation. Phys. Rev. D 1976, 14, 870. [Google Scholar] [CrossRef]
- Hawking, S.W. Breakdown of predictability in gravitational collapse. Phys. Rev. D 1976, 14, 2460. [Google Scholar] [CrossRef]
- Almheiri, A.; Marolf, D.; Polchinski, J.; Sully, J. Black holes: Complementarity or firewalls. J. High Energy Phys. 2013, 2013, 62. [Google Scholar] [CrossRef]
- Merali, Z. LIGO black hole echoes hint at general-relativity breakdown. Nature 2016. [Google Scholar] [CrossRef]
- Westerweck, J.; Nielsen, A.; Fischer-Birnholtz, O.; Cabero, M.; Capano, C.; Dent, T.; Krishnan, B.; Meadors, G.; Nitz, A. Low significance of evidence for black hole echoes in gravitational wave data. Phys. Rev. D 2018, 97, 124037. [Google Scholar] [CrossRef]
- Svidzinsky, A. Nonthermal radiation of evaporating black holes. Phys. Rev. D 2023, 107, 024038. [Google Scholar] [CrossRef]
- Calmet, X.; Hsu, S.D.H. Quantum hair and black hole information. Phys. Lett. B 2022, 827, 136995. [Google Scholar] [CrossRef]
- Mathur, S.D. The information paradox: A pedagogical introduction. Class. Quantum Gravity 2009, 26, 224001. [Google Scholar] [CrossRef]
- Zhang, B.; Cai, Q.; Zhan, M.; You, L. Information conservation is fundamental: Recovering the lost information in Hawking radiation. Int. J. Mod. Phys. D 2013, 22, 1341014. [Google Scholar] [CrossRef]
- Vaz, C. Black holes as gravitational atoms. Int. J. Mod. Phys. D 2014, 23, 1441002. [Google Scholar] [CrossRef]
- Corda, C. Schrödinger and Klein–Gordon theories of black holes from the quantization of the Oppenheimer and Snyder gravitational collapse. Commun. Theor. Phys. 2023, 75, 095405. [Google Scholar] [CrossRef]
- Jacak, J.E. Topology-induced quantum transition in multi-particle systems in vicinity of a black hole. Class. Quantum Gravity 2024, 41, 035006. [Google Scholar] [CrossRef]
- Tolman, R.C. Static Solutions of Einstein’s Field Equations for Spheres of Fluid. Phys. Rev. 1939, 55, 364. [Google Scholar] [CrossRef]
- Oppenheimer, J.R.; Volkoff, G.M. On Massive Neutron Cores. Phys. Rev. 1939, 55, 374. [Google Scholar] [CrossRef]
- Brightman, M.; Bachetti, M.; Earnshaw, H.P.; Fürst, F.; García, J.; Grefenstette, B.; Heida, M.; Kara, E.; Madsen, K.K.; Middleton, M.J.; et al. Breaking the limit: Super-Eddington accretion onto black holes and neutron stars. Bull. Am. Astron. Soc. 2019, 51, 352. [Google Scholar] [CrossRef]
- Shapiro, S.L.; Lightman, A.P.; Eardley, D.M. A two-temperature accretion disk model for Cygnus X-1: Structure and spectrum. Astrophys. J. 1976, 204, 187. [Google Scholar] [CrossRef]
- Fragile, P.C.; Etheridge, S.M.; Anninos, P.; Mishra, B.; Kluźniak, W. Relativistic, Viscous, Radiation Hydrodynamic Simulations of Geometrically Thin Disks. I. Thermal and Other Instabilities. Astrophys. J. 2018, 857, 1. [Google Scholar] [CrossRef]
- Dexter, J.; Scepi, N.; Begelman, M.C. Radiation GRMHD Simulations of the Hard State of Black Hole X-Ray Binaries and the Collapse of a Hot Accretion Flow. Astrophys. J. Lett. 2021, 919, L20. [Google Scholar] [CrossRef]
- Jacak, J. Quantum contribution to luminosity of quasars. J. Cosmol. Astropart. Phys. 2022, 10, 092. [Google Scholar] [CrossRef]
- Spanier, E. Algebraic Topology; Springer: Berlin, Germany, 1966. [Google Scholar]
- Ryder, J.H. Quantum Field Theory; Cambridge UP: Cambridge, UK, 1966. [Google Scholar]
- Mermin, N.D. The topological theory of defects in ordered media. Rev. Mod. Phys. 1979, 51, 591. [Google Scholar] [CrossRef]
- Birman, J.S. Braids, Links and Mapping Class Groups; Princeton UP: Princeton, NJ, USA, 1974. [Google Scholar]
- Laidlaw, M.G.; DeWitt, C.M. Feynman functional integrals for systems of indistinguishable particles. Phys. Rev. D 1971, 3, 1375. [Google Scholar] [CrossRef]
- Imbo, T.D.; Imbo, C.S.; Sudarshan, C.S. Identical particles, exotic statistics and braid groups. Phys. Lett. B 1990, 234, 103–107. [Google Scholar] [CrossRef]
- Wu, Y.S. General theory for quantum statistics in two dimensions. Phys. Rev. Lett. 1984, 52, 2103. [Google Scholar] [CrossRef]
- Artin, E. Theory of braids. Ann. Math. 1947, 48, 101. [Google Scholar] [CrossRef]
- Wilczek, F. Fractional Statistics and Anyon Superconductivity; World Scientific: Singapore, 1990. [Google Scholar]
- Sudarshan, E.; Imbo, T.D.; Govindarajan, T. Configuration space topology and quantum internal symmetries. Phys. Lett. B 1988, 213, 471–476. [Google Scholar] [CrossRef]
- Feynman, R.P. The Principle of Least Action in Quantum Mechanics. Ph.D. Thesis, Princeton University, Princeton, NJ, USA, 1942. [Google Scholar]
- Feynman, R.P.; Hibbs, A.R. Quantum Mechanics and Path Integrals; McGraw-Hill: New York, NY, USA, 1964. [Google Scholar]
- Schwarzschild, K. Über das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie. Sitzungsberichte Der Königlich Preuss. Akad. Der Wissenschaften 1916, 7, 189. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. The Classical Theory of Fields; Pergamon Press Ltd.: Oxford, UK, 1971. [Google Scholar]
- Kruskal, M.D. Maximal Extension of Schwarzschild Metric. Phys. Rev. 1960, 119, 1743. [Google Scholar] [CrossRef]
- Szekeres, G. On the singularities of a Riemannian manifold. Publ. Math. Debr. 1960, 7, 285–301. [Google Scholar] [CrossRef]
- Novikov, I.D.; Thorne, K.S. Black Holes (Les Astres Occlus) by C. DeWitt and B. S. DeWitt; Gordon and Breach Science Publishers: London, UK, 1973. [Google Scholar]
- Leinaas, J.M.; Myrheim, J. On the theory of identical particles. Nuovo Cimento 1977, 37B, 1–23. [Google Scholar] [CrossRef]
- Chaichian, M.; Demichev, A. Path Integrals in Physics Volume I Stochastic Processes and Quantum Mechanics; IOP Publishing Ltd.: Bristol, UK; Philadelphia, PA, USA, 2001. [Google Scholar]
- Chaichian, M.; Demichev, A. Path Integrals in Physics Volume II Quantum Field Theory, Statistical Physics and other Modern Applications; IOP Publishing Ltd.: Bristol, UK; Philadelphia, PA, USA, 2001. [Google Scholar]
- Jacak, J.E. Forbidden trajectories for path integrals. Phys. Rev. A 2023, 107, 032207. [Google Scholar] [CrossRef]
- Wiener, N. The Average of an Analytic Functional. Proc. Natl. Acad. Sci. USA 1921, 7, 253. [Google Scholar] [CrossRef]
- Jacak, J.E. Quantum mechanism of extremely high energy processes at neutron star collapse and of quasar luminosity. J. High Energy Phys. 2022, 2022, 2. [Google Scholar] [CrossRef]
- Chandrasekhar, S. The Maximum Mass of Ideal White Dwarfs. Astrophys. J. 1931, 74, 81. [Google Scholar] [CrossRef]
- Yakovlev, D.G.; Haensel, P.; Baym, G.; Pethick, C. Lev Landau and the concept of neutron stars. Physics-Uspekhi 2013, 56, 289. [Google Scholar] [CrossRef]
- Abrikosov, A.A.; Gorkov, L.P.; Dzialoshinskii, I.E. Methods of Quantum Field Theory in Statistical Physics; Dover Publ. Inc.: Dover, DE, USA, 1975. [Google Scholar]
- Luttinger, J.M. Fermi Surface and Some Simple Equilibrium Properties of a System of Interacting Fermions. Phys. Rev. 1960, 119, 1153. [Google Scholar] [CrossRef]
- Shakura, N.I.; Sunyaev, R.A. Black holes in binary systems. Observational appearance. Astron. Astrophys. 1973, 24, 337–355. [Google Scholar]
- Farrah, D.; Efstathiou, A.; Afonso, J.; Bernard-Salas, J.; Cairns, J.; Clements, D.; Croker, K.; Hatziminaoglou, E.; Joyce, M.; Lacy, M.; et al. Stellar and black hole assembly in z < 0.3 infrared-luminous mergers: Intermittent starbursts vs. super-Eddington accretion. Mon. Not. R. Astron. Soc. 2022, 513, 4770–4786. [Google Scholar] [CrossRef]
- Merloni, A.; Fabian, A.C.; Ross, R.R. On the interpretation of the multicolour disc model for black hole candidates. Mon. Not. R. Astron. Soc. 2000, 313, 193–197. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics: Non-Relativistic Theory; Pergamon Press Ltd.: Oxford, UK, 1965. [Google Scholar]
- Angus, C.R.; Baldassare, V.F.; Mockler, B.; Foley, R.J.; Ramirez-Ruiz, E.; Raimundo, S.I.; French, K.D.; Auchettl, K.; Pfister, H.; Gall, C.; et al. A fast-rising tidal disruption event from a candidate intermediate-mass black hole. Nat. Astron. 2022, 6, 1452–1463. [Google Scholar] [CrossRef]
- Rees, M.J. Tidal disruption of stars by black holes of 106–108 solar masses in nearby galaxies. Nature 1988, 333, 523–528. [Google Scholar] [CrossRef]
- van Velzen, S.; Gezari, S.; Hammerstein, E.; Roth, N.; Frederick, S.; Ward, C.; Hung, T.; Cenko, S.B.; Stein, R.; Perley, D.A.; et al. Seventeen Tidal Disruption Events from the First Half of ZTF Survey Observations: Entering a New Era of Population Studies. Astrophys. J. 2021, 908, 4. [Google Scholar] [CrossRef]
- Wiseman, P.; Wang, Y.; Hönig, S.; Castro-Segura, N.; Clark, P.; Frohmaier, C.; Fulton, M.D.; Leloudas, G.; Middleton, M.; Müller-Bravo, T.E.; et al. Multiwavelength observations of the extraordinary accretion event AT2021lwx. Mon. Not. R. Astron. Soc. 2023, 522, 3992–4002. [Google Scholar] [CrossRef]
- Laha, S.; Meyer, E.; Roychowdhury, A.; Becerra Gonzalez, J.; Acosta–Pulido, J.A.; Thapa, A.; Ghosh, R.; Behar, E.; Gallo, L.C.; Kriss, G.A.; et al. A Radio, Optical, UV, and X-Ray View of the Enigmatic Changing-look Active Galactic Nucleus 1ES 1927+654 from Its Pre- to Postflare States. Astrophys. J. 2022, 931, 5. [Google Scholar] [CrossRef]
- Blandford, R.D.; Znajek, R.L. Electromagnetic extraction of energy from Kerr black holes. Mon. Not. R. Astron. Soc. 1977, 179, 433–456. [Google Scholar] [CrossRef]
- Pauli, W. The Connection Between Spin and Statistics. Phys. Rev. 1940, 58, 716. [Google Scholar] [CrossRef]
- Duck, I.; Sudarshan, E.C.G. Toward an understanding of the spin-statistics theorem. Am. J. Phys. 1998, 66, 284–303. [Google Scholar] [CrossRef]
- Duck, I.; Sudarshan, E.C.G. Pauli and the Spin-Statistics Theorem; World Scientific: Singapore, 1997. [Google Scholar]
- Rumer, Y.R.; Fet, A.I. Theory of Unitary Symmetry; Nauka: Moscow, Russia, 1970. [Google Scholar]
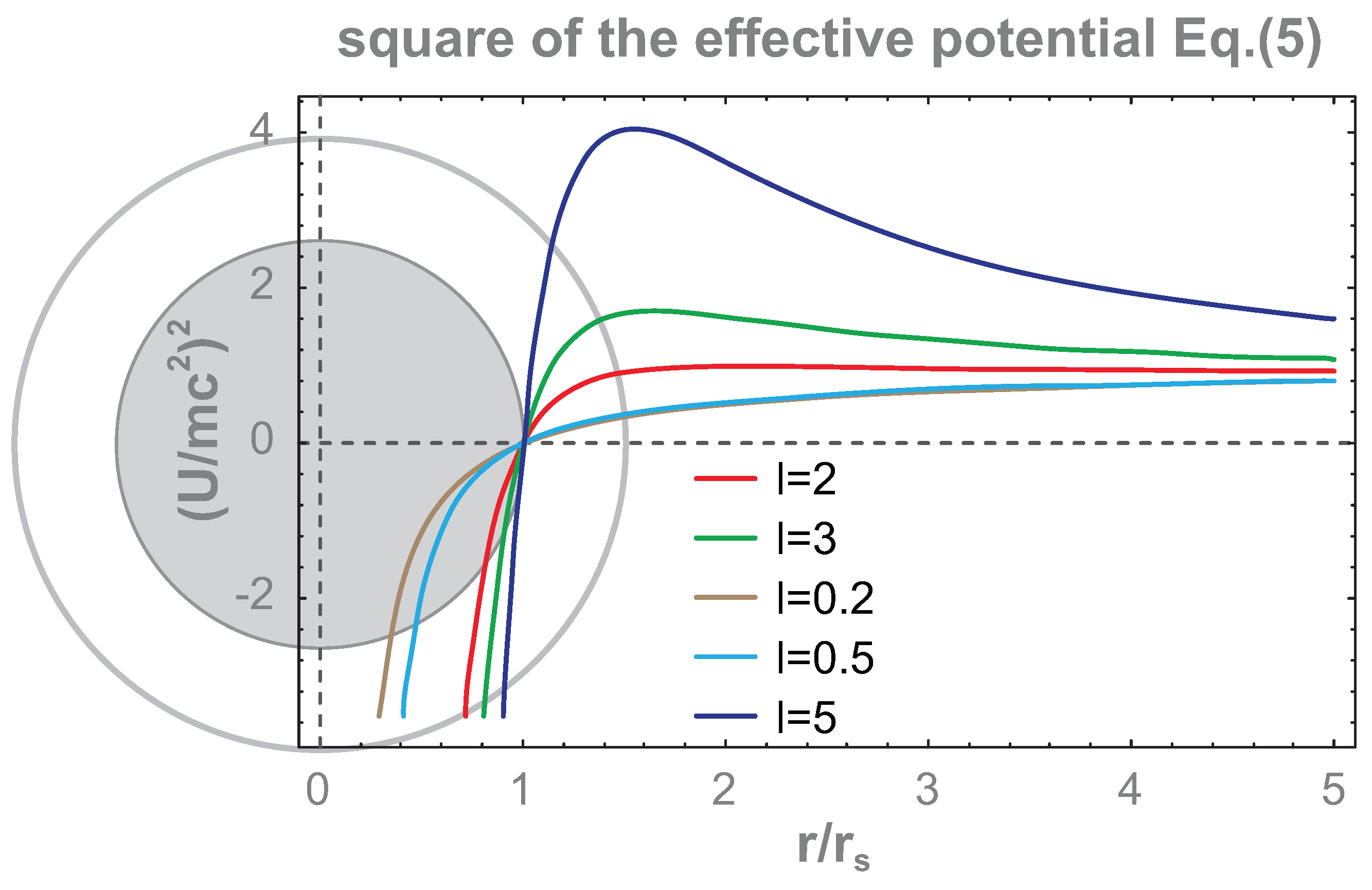
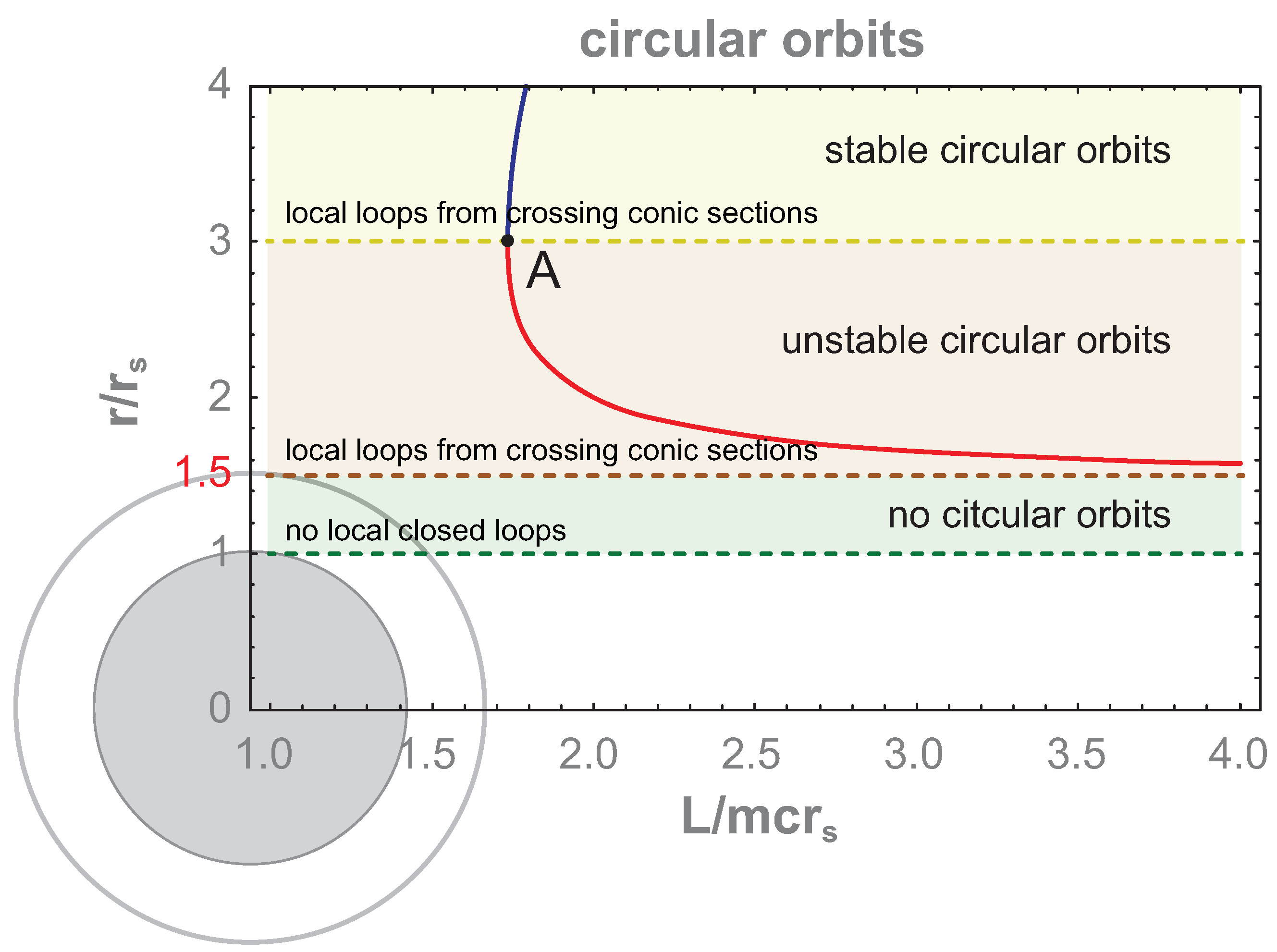


| Radius r | , | [kg m/s] | E [J] | ||
|---|---|---|---|---|---|
| 6 km | 1/m3 | kg/m3 | J | ||
| 8 km | 1/m3 | kg/m3 | J | ||
| 10 km | 1/m3 | kg/m3 | J |
| Electrons | Protons | |||
|---|---|---|---|---|
| [eV] | [1/s] | [s] | [1/s] | [s] |
| GeV | ||||
| 1 MeV | ||||
| 1 keV | ||||
| [eV] | [kg m/s] | [1/m3] | [%] | Luminosity |
|---|---|---|---|---|
| 2 keV | W | |||
| 10 keV | W | |||
| 100 keV | W | |||
| 1 MeV | W | |||
| 10 MeV | W | |||
| 100 MeV | 4 | W | ||
| GeV | 20 | W | ||
| GeV | 29 | W | ||
| 1 GeV | 35 | W |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jacak, J.E. Modification of Premises for the Black Hole Information Paradox Caused by Topological Constraints in the Event Horizon Vicinity. Entropy 2024, 26, 1035. https://doi.org/10.3390/e26121035
Jacak JE. Modification of Premises for the Black Hole Information Paradox Caused by Topological Constraints in the Event Horizon Vicinity. Entropy. 2024; 26(12):1035. https://doi.org/10.3390/e26121035
Chicago/Turabian StyleJacak, Janusz Edward. 2024. "Modification of Premises for the Black Hole Information Paradox Caused by Topological Constraints in the Event Horizon Vicinity" Entropy 26, no. 12: 1035. https://doi.org/10.3390/e26121035
APA StyleJacak, J. E. (2024). Modification of Premises for the Black Hole Information Paradox Caused by Topological Constraints in the Event Horizon Vicinity. Entropy, 26(12), 1035. https://doi.org/10.3390/e26121035








