Word Length in Political Public Speaking: Distribution and Time Evolution
Abstract
:1. Introduction
2. Data for Analysis
3. Analysis of the Word Length Distribution Law
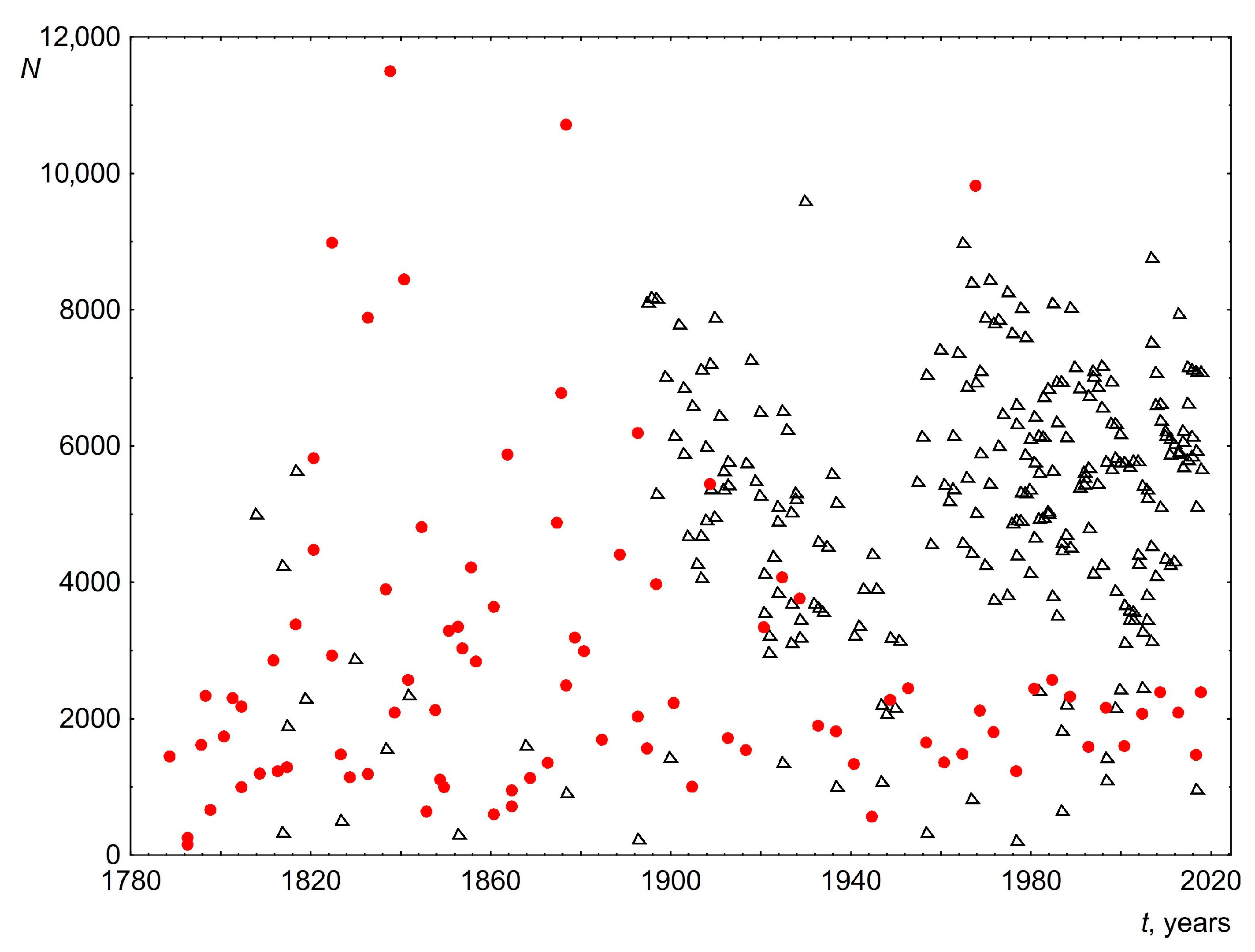
4. Change in Word Length over Time
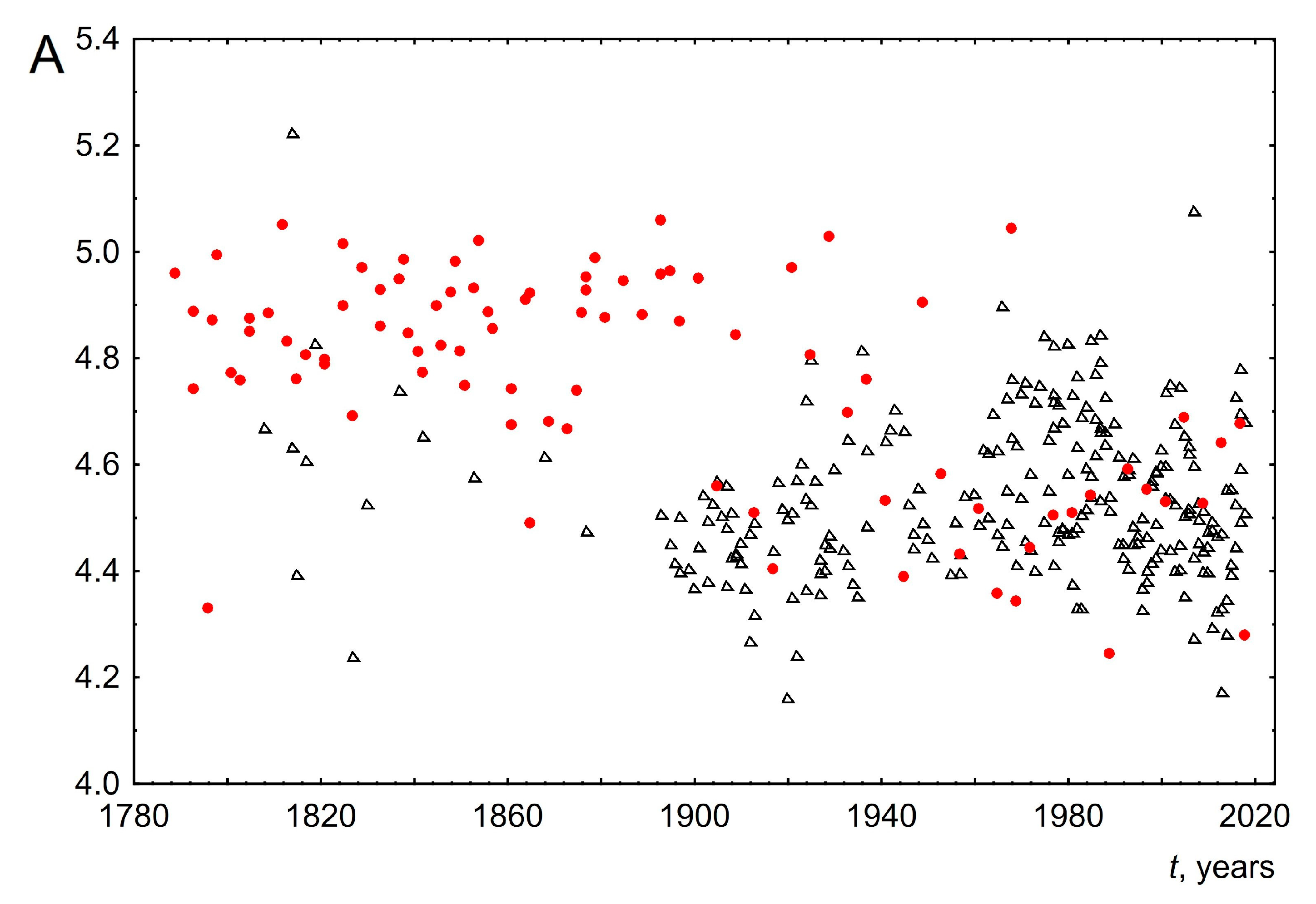
- The average word length. To calculate this parameter, the total number of letters in a speech is divided by the number of words. The change in this parameter over time is shown in Figure 5. As can be seen from the graph, the average word length for UK speeches has remained almost unchanged over two hundred years and is about 4.5. For USA speeches, the result is more complicated. So, from 1789 to about 1950, the average length of words practically did not change and was about 4.9. However, then there is a small stepwise change in the average word length to 4.5. As a result, from 1950 to the present, the average length of words for both the USA and the UK is the same. Within quantitative linguistics it is impossible to understand the reasons for such behavior. However, based on historical facts, we will put forward the following hypotheses to explain this behavior. (1) Initially, USA presidents made speeches only before Congress; other citizens became acquainted with their speeches through newspapers. Such speeches only began to be fully broadcasted on radio and television after the Second World War. This may have led to the observed decrease in average word length. (2) The unchanged average word length for the UK can be explained, apparently, by the fact that the speeches were made before members of Parliament, a rather conservative representative body with strong centuries-old traditions. Adherence to tradition is a quality that is often used to describe British society as a whole. This is illustrated by the result obtained in the work about the unchanged average length of words of parliamentarians over more than two hundred years. (3) It was after the Second World War that a special relationship emerged between the USA and the UK. The term “special relationship” publicly emerged in Winston Churchill’s “Iron Curtain” speech of 1946. The special relationship is a term that is often used to describe the close historic, political, military, economic and cultural relations between USA and UK political leaders and elites. This could be the reason that the vocabulary of USA and UK politicians became very close after the war and, as a consequence, the average length of words is the same.
- 2.
- The median of the word length distribution for all speeches was found to be four and did not change over time.
- 3.
- The maximum word length of speeches delivered over 200 years also did not change and was in the range from 14 to 16. Examples of these most common words for the USA: accountability, administration, constitutional, accomplishment, irresponsibility. For the UK, these words are responsibility, congratulation, disestablishment, apprenticeship, discrimination, internationalism.
- 4.
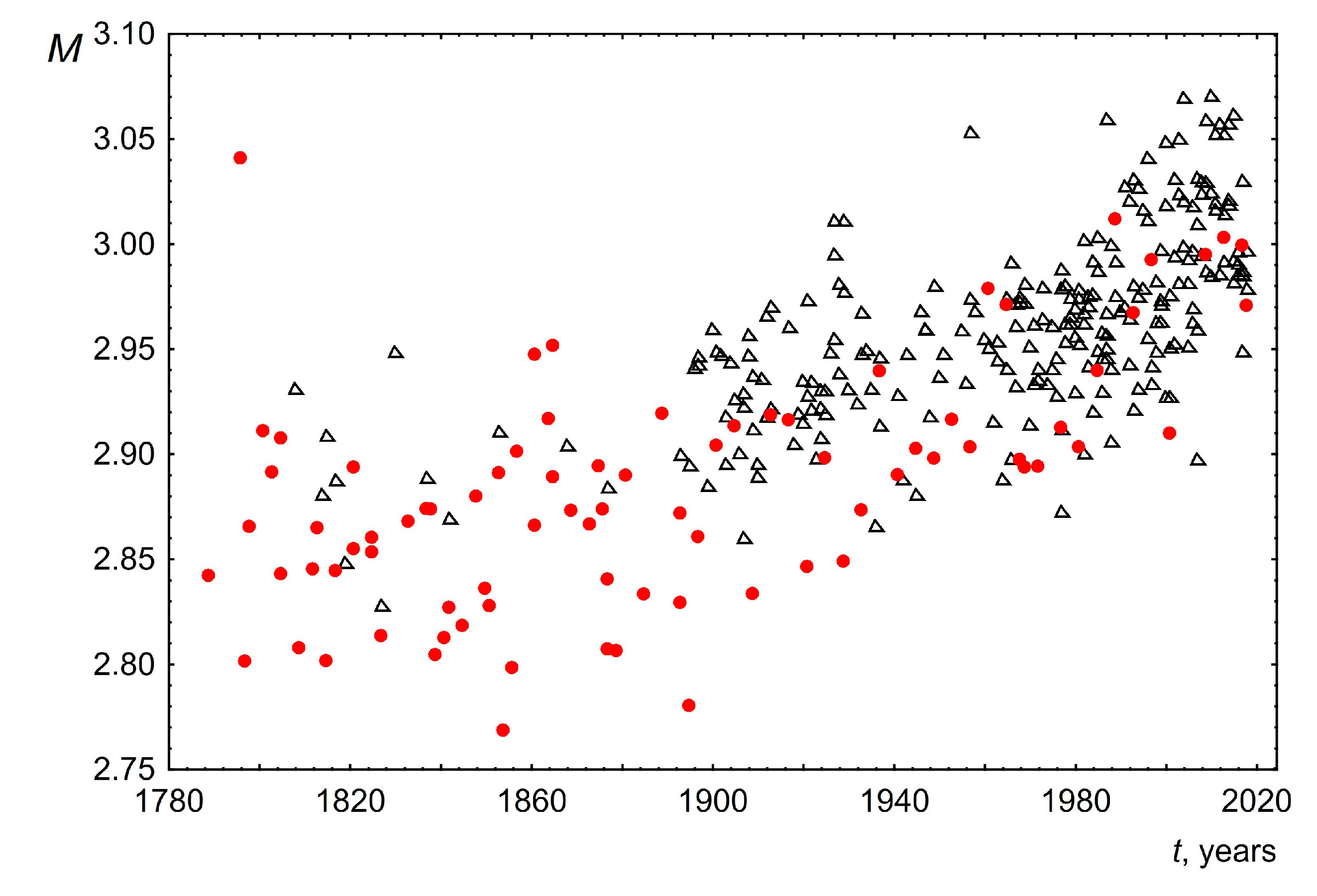
- The mode for each of the speeches was calculated based on the averaging of the three most probable word lengths. The averaging was performed taking into account the probabilities of occurrence of these three values in the text. This was performed to make this parameter more sensitive to the shape and width of the length distribution near the maximum. The change in the mode of the word length distribution over time is shown in Figure 6. As can be seen, the mode of word lengths of public speeches for both the USA and the UK increases slightly over 200 years from 2.85 to 3.02. This change is approximately linear with a slope of 0.0005± 0.0002 for the USA and 0.0006 ± 0.0001 for the UK.
- 5.
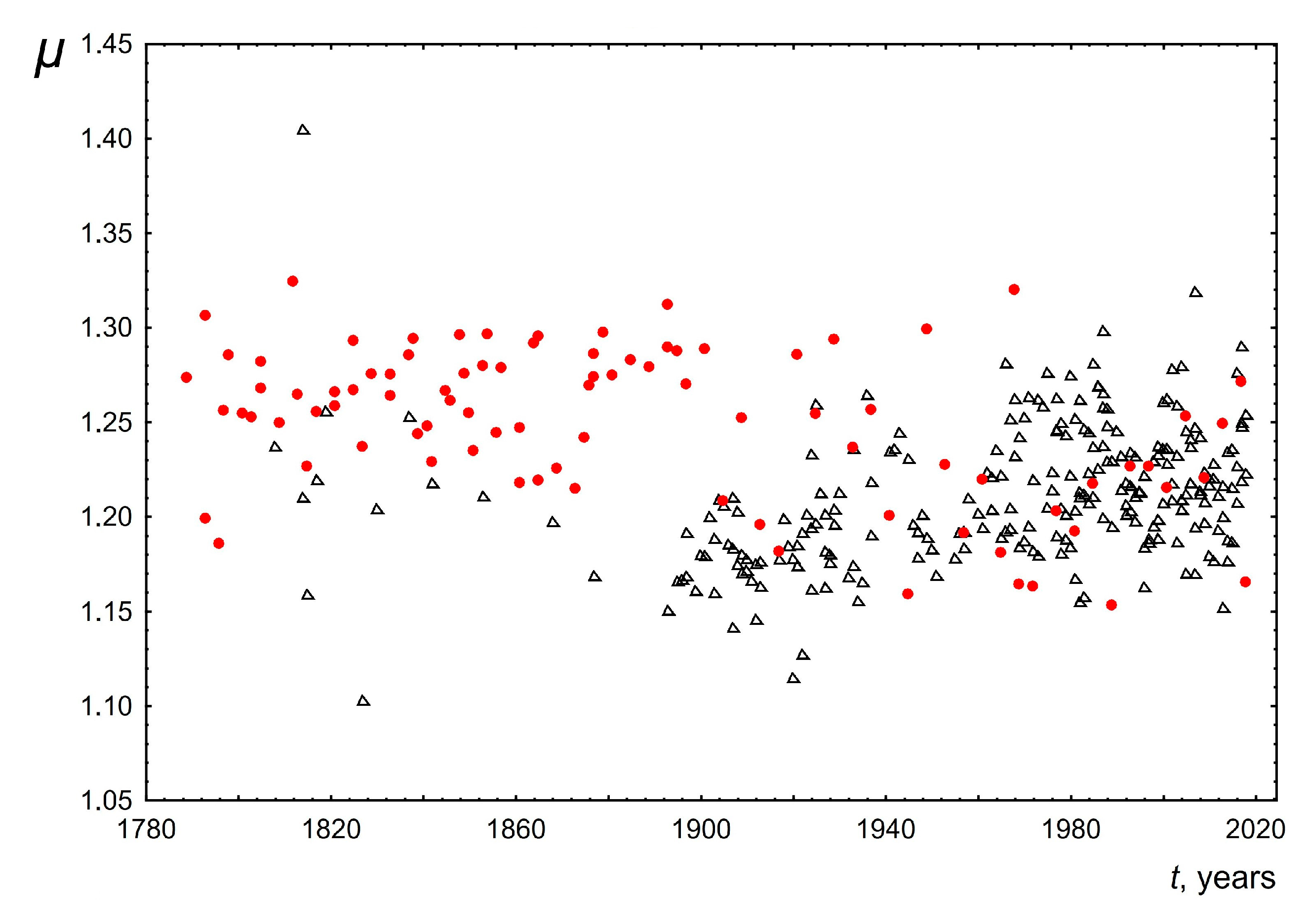
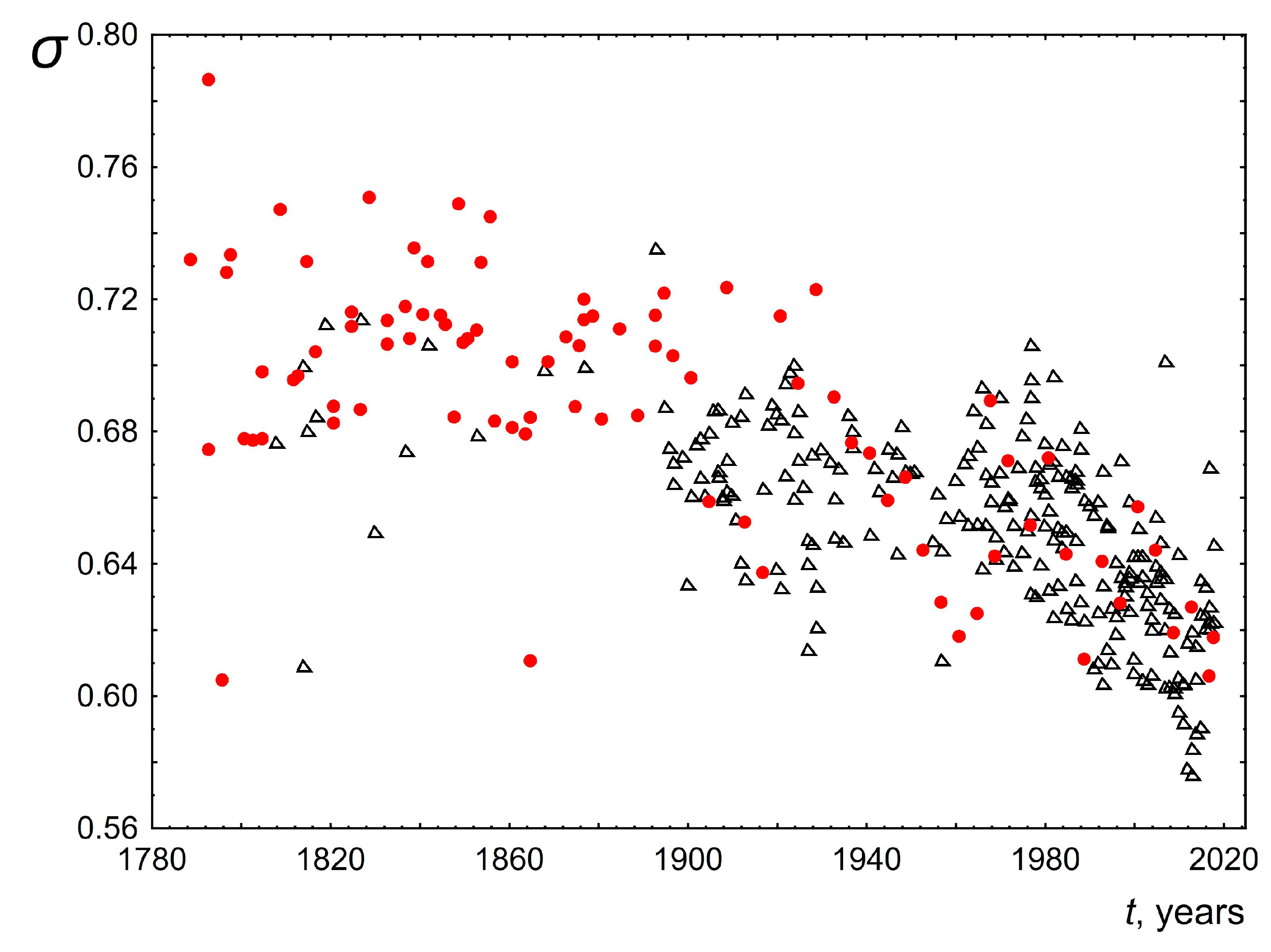
- Figure 7 and Figure 8 show the dependence of the parameters of the lognormal distribution µ, σ on time. As can be seen, µ does not depend on time, remaining approximately equal to 1.25. At the same time, the parameter σ slightly decreases over 200 years from 0.74 to 0.62. These results are consistent with the results presented in Figure 5 and Figure 6. Indeed, as we know, the mean value for a lognormal distribution is related to µ, σ as . As a consequence, when µ is constant and σ decreases the mean value will decrease. On the other hand, since the mode is related to µ, σ as , then when µ remains constant and σ decreases, the mode should increase. The above agreement in the behavior of the parameters of the lognormal distribution µ, σ (Figure 7 and Figure 8) with the results based on the analysis of directly empirical histograms (Figure 5 and Figure 6) provides an additional argument for the applicability of the lognormal distribution to describe the distribution of word lengths.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Year, Party | I Place, R2 | II Place, R2 | III Place, R2 |
|---|---|---|---|
| 1789 | Lognormal, 0.995 | Weibull, 0.993 | Folded normal, 0.987 |
| 1796 | Lognormal, 0.998 | Weibull, 0.996 | Rayleigh, 0.992 |
| 1797 | Weibull, 0.993 | Lognormal, 0.992 | Folded normal, 0.989 |
| 1798 | Lognormal, 0.989 | Weibull, 0.988 | Folded normal, 0.981 |
| 1801 | Lognormal, 0.997 | Weibull, 0.994 | Folded normal, 0.985 |
| 1803 | Lognormal, 0.996 | Weibull, 0.994 | Folded normal 0.985 |
| 1805 | Lognormal, 0.996 | Weibull, 0.995 | Folded normal, 0.988 |
| 1805 | Weibull, 0.994 | Lognormal, 0.994 | Folded normal, 0.988 |
| 1809 | Lognormal, 0.993 | Weibull, 0.992 | Folded normal, 0.987 |
| 1812 | Weibull, 0.996 | Lognormal, 0.992 | Folded normal, 0.991 |
| 1813 | Lognormal, 0.995 | Weibull, 0.994 | Folded normal, 0.987 |
| 1815 | Lognormal, 0.993 | Weibull, 0.992 | Folded normal, 0.986 |
| 1817 | Lognormal, 0.994 | Weibull, 0.994 | Folded normal, 0.987 |
| 1821 | Lognormal, 0.996 | Weibull, 0.995 | Folded normal, 0.987 |
| 1821 | Lognormal, 0.994 | Weibull, 0.994 | Folded normal, 0.986 |
| 1825 | Lognormal, 0.992 | Weibull, 0.992 | Folded normal, 0.986 |
| 1825 | Lognormal, 0.993 | Weibull, 0.991 | Folded normal, 0.984 |
| 1827 | Lognormal, 0.994 | Weibull, 0.992 | Folded normal, 0.984 |
| 1833 | Lognormal, 0.993 | Weibull, 0.992 | Folded normal, 0.985 |
| 1837 | Weibull, 0.994 | Lognormal, 0.991 | Folded normal, 0.989 |
| 1838 | Weibull, 0.993 | Lognormal, 0.992 | Folded normal, 0.988 |
| 1839 | Lognormal, 0.993 | Weibull 0.992 | Folded normal, 0.987 |
| 1841 | Lognormal, 0.993 | Weibull, 0.993 | Folded normal, 0.987 |
| 1842 | Lognormal, 0.993 | Weibull, 0.993 | Folded normal, 0.987 |
| 1845 | Lognormal, 0.993 | Weibull, 0.993 | Folded normal, 0.987 |
| 1848 | Weibull, 0.995 | Lognormal, 0.993 | Folded normal, 0.99 |
| 1850 | Lognormal, 0.993 | Weibull, 0.993 | Folded normal, 0.986 |
| 1851 | Lognormal, 0.993 | Weibull, 0.992 | Folded normal, 0.985 |
| 1853 | Lognormal, 0.994 | Weibull, 0.994 | Folded normal, 0.988 |
| 1854 | Weibull, 0.991 | Lognormal, 0.988 | Folded normal, 0.986 |
| 1856 | Lognormal, 0.99 | Weibull, 0.988 | Folded normal, 0.982 |
| 1857 | Weibull, 0.995 | Lognormal, 0.995 | Folded normal, 0.989 |
| 1861 | Lognormal, 0.996 | Weibull, 0.994 | Folded normal, 0.986 |
| 1861 | Lognormal, 0.997 | Weibull, 0.993 | Folded normal, 0.983 |
| 1864 | Lognormal, 0.994 | Weibull, 0.994 | Folded normal, 0.987 |
| 1865 | Lognormal, 0.998 | Weibull, 0.993 | Rayleigh, 0.989 |
| 1865 | Lognormal, 0.992 | Weibull, 0.99 | Folded normal, 0.982 |
| 1868 | Weibull, 0.994 | Lognormal, 0.992 | Folded normal, 0.989 |
| 1869 | Weibull, 0.995 | Lognormal, 0.994 | Folded normal, 0.99 |
| 1873 | Lognormal, 0.995 | Weibull, 0.994 | Folded normal, 0.987 |
| 1875 | Lognormal, 0.996 | Weibull, 0.994 | Folded normal 0.986 |
| 1876 | Lognormal, 0.994 | Weibull, 0.994 | Folded normal, 0.987 |
| 1877 | Weibull, 0.993 | Lognormal, 0.992 | Folded normal, 0.989 |
| 1877 | Weibull, 0.992 | Lognormal, 0.991 | Folded normal, 0.987 |
| 1879 | Weibull, 0.992 | Lognormal, 0.989 | Folded normal, 0.986 |
| 1881 | Lognormal, 0.995 | Weibull, 0.992 | Folded normal, 0.984 |
| 1885 | Lognormal, 0.992 | Weibull, 0.992 | Folded normal, 0.985 |
| 1889 | Lognormal, 0.995 | Weibull, 0.994 | Folded normal, 0.986 |
| 1893 | Weibull, 0.993 | Lognormal, 0.991 | Folded normal, 0.988 |
| 1893 | Weibull, 0.993 | Lognormal, 0.992 | Folded normal, 0.987 |
| 1895 | Weibull, 0.992 | Lognormal, 0.99 | Folded normal, 0.987 |
| 1897 | Lognormal, 0.992 | Weibull, 0.992 | Folded normal, 0.986 |
| 1901 | Lognormal, 0.993 | Weibull, 0.992 | Folded normal, 0.984 |
| 1905 | Lognormal, 0.998 | Weibull, 0.994 | Folded normal, 0.985 |
| 1909 | Weibull, 0.993 | Lognormal, 0.992 | Folded normal, 0.987 |
| 1913 | Lognormal, 0.998 | Weibull, 0.994 | Rayleigh, 0.984 |
| 1917 | Lognormal, 0.998 | Weibull, 0.994 | Rayleigh, 0.987 |
| 1921 | Lognormal, 0.993 | Weibull, 0.993 | Folded normal, 0.987 |
| 1925 | Lognormal, 0.995 | Weibull, 0.993 | Folded normal, 0.986 |
| 1929 | Weibull, 0.993 | Lognormal, 0.993 | Folded normal, 0.987 |
| 1933 | Weibull, 0.996 | Lognormal, 0.996 | Folded normal, 0.989 |
| 1937 | Lognormal, 0.996 | Weibull, 0.996 | Folded normal, 0.989 |
| 1941 | Lognormal, 0.997 | Weibull, 0.993 | Folded normal, 0.984 |
| 1945 | Lognormal, 0.999 | Weibull, 0.995 | Folded normal, 0.986 |
| 1949 | Weibull, 0.996 | Lognormal, 0.995 | Folded normal, 0.991 |
| 1953 | Lognormal, 0.997 | Weibull, 0.995 | Folded normal, 0.987 |
| 1957 | Lognormal, 0.998 | Weibull, 0.995 | Rayleigh, 0.99 |
| 1961 | Lognormal, 0.998 | Weibull, 0.996 | Rayleigh, 0.992 |
| 1965 | Lognormal, 0.997 | Weibull, 0.996 | Rayleigh, 0.99 |
| 1969 | Lognormal, 0.998 | Weibull, 0.996 | Rayleigh, 0.988 |
| 1973 | Lognormal, 0.999 | Weibull, 0.993 | Folded normal, 0.983 |
| 1977 | Lognormal, 0.998 | Weibull, 0.996 | Folded normal, 0.988 |
| 1981 | Lognormal, 0.997 | Weibull, 0.995 | Folded normal, 0.987 |
| 1985 | Lognormal, 0.998 | Weibull, 0.996 | Folded normal, 0.988 |
| 1989 | Lognormal, 0.999 | Weibull, 0.996 | Rayleigh, 0.993 |
| 1993 | Lognormal, 0.997 | Weibull, 0.994 | Rayleigh, 0.986 |
| 1997 | Lognormal, 0.998 | Weibull, 0.995 | Rayleigh, 0.989 |
| 2001 | Weibull, 0.996 | Lognormal, 0.995 | Folded normal, 0.99 |
| 2009 | Lognormal, 0.998 | Weibull, 0.995 | Rayleigh, 0.99 |
| 2013 | Lognormal, 0.998 | Weibull, 0.996 | Rayleigh, 0.99 |
| 2017 | Lognormal, 0.997 | Weibull, 0.995 | Rayleigh, 0.992 |
| 2021 | Lognormal, 0.998 | Weibull, 0.996 | Rayleigh, 0.992 |
| Year, Party | I Place, R2 | II Place, R2 | III Place, R2 |
|---|---|---|---|
| 1808 | Lognormal, 0.996 | Weibull, 0.996 | Folded normal, 0.989 |
| 1814 | Lognormal, 0.996 | Weibull, 0.993 | Folded normal, 0.985 |
| 1815 | Lognormal, 0.998 | Weibull, 0.996 | Folded normal, 0.988 |
| 1817 | Lognormal, 0.995 | Weibull, 0.995 | Folded normal, 0.987 |
| 1819 | Lognormal, 0.993 | Weibull, 0.993 | Folded normal, 0.986 |
| 1827 | Lognormal, 0.996 | Weibull, 0.995 | Folded normal, 0.987 |
| 1830 | Lognormal, 0.998 | Weibull, 0.995 | Rayleigh, 0.987 |
| 1837 | Lognormal, 0.996 | Weibull, 0.994 | Folded normal, 0.985 |
| 1842 | Weibull, 0.995 | Lognormal, 0.994 | Folded normal, 0.99 |
| 1853 | Lognormal, 0.995 | Weibull, 0.994 | Folded normal, 0.985 |
| 1868 | Lognormal, 0.998 | Weibull, 0.993 | Folded normal, 0.985 |
| 1877 | Lognormal, 0.996 | Weibull, 0.992 | Folded normal, 0.984 |
| 1893 | Lognormal, 0.993 | Weibull, 0.987 | Half Normal, 0.979 |
| 1895 Liberal | Lognormal, 0.998 | Weibull, 0.995 | Folded normal, 0.986 |
| 1896 Liberal | Lognormal, 0.998 | Weibull, 0.995 | Folded normal, 0.986 |
| 1897 Conservative | Lognormal, 0.998 | Weibull, 0.995 | Folded normal, 0.986 |
| 1897 Liberal | Lognormal, 0.998 | Weibull, 0.995 | Folded normal, 0.986 |
| 1899 Liberal | Lognormal, 0.998 | Weibull, 0.993 | Folded normal, 0.984 |
| 1900 Conservative | Lognormal, 0.998 | Weibull, 0.996 | Rayleigh, 0.988 |
| 1901 Liberal | Lognormal, 0.998 | Weibull, 0.994 | Folded normal, 0.984 |
| 1902 Conservative | Lognormal, 0.997 | Weibull, 0.996 | Folded normal, 0.988 |
| 1903 Conservative | Lognormal, 0.998 | Weibull, 0.997 | Folded normal, 0.99 |
| 1903 Liberal | Lognormal, 0.998 | Weibull, 0.994 | Folded normal, 0.984 |
| 1904 Conservative | Lognormal, 0.997 | Weibull, 0.996 | Folded normal, 0.989 |
| 1905 Liberal | Lognormal, 0.997 | Weibull, 0.995 | Folded normal, 0.987 |
| 1906 Conservative | Lognormal, 0.997 | Weibull, 0.994 | Folded normal, 0.987 |
| 1907 | Lognormal, 0.998 | Weibull 0.994 | Folded normal, 0.986 |
| 1907 Conservative | Lognormal, 0.998 | Weibull, 0.996 | Folded normal, 0.988 |
| 1907 Liberal | Lognormal, 0.998 | Weibull, 0.995 | Folded normal, 0.986 |
| 1908 Conservative | Lognormal, 0.998 | Weibull, 0.995 | Folded normal, 0.986 |
| 1908 Liberal | Lognormal, 0.998 | Weibull, 0.995 | Folded normal, 0.986 |
| 1909 Conservative | Lognormal, 0.998 | Weibull, 0.996 | Folded normal, 0.988 |
| 1909 Liberal | Lognormal, 0.998 | Weibull, 0.994 | Folded normal, 0.985 |
| 1910 Conservative | Lognormal, 0.998 | Weibull, 0.996 | Folded normal, 0.989 |
| 1910 Liberal | Lognormal, 0.998 | Weibull, 0.995 | Folded normal, 0.987 |
| 1911 Conservative | Lognormal, 0.998 | Weibull, 0.996 | Folded normal, 0.988 |
| 1912 Conservative | Lognormal, 0.999 | Weibull, 0.996 | Rayleigh, 0.989 |
| 1912 Liberal | Lognormal, 0.997 | Weibull, 0.995 | Folded normal, 0.987 |
| 1913 Conservative | Lognormal, 0.999 | Weibull, 0.996 | Rayleigh, 0.989 |
| 1913 Liberal | Lognormal, 0.997 | Weibull, 0.994 | Folded normal, 0.986 |
| 1917 | Lognormal 0.999 | Weibull, 0.996 | Folded normal, 0.988 |
| 1918 Liberal | Lognormal, 0.998 | Weibull, 0.994 | Folded normal, 0.986 |
| 1919 Liberal | Lognormal, 0.997 | Weibull, 0.995 | Folded normal, 0.987 |
| 1920 Conservative | Lognormal, 0.999 | Weibull, 0.995 | Rayleigh, 0.988 |
| 1920 Liberal | Lognormal, 0.997 | Weibull, 0.993 | Folded normal, 0.985 |
| 1921 Conservative | Lognormal, 0.999 | Weibull, 0.997 | Rayleigh, 0.99 |
| 1921 Liberal | Lognormal, 0.998 | Weibull, 0.995 | Folded normal, 0.986 |
| 1922 Conservative | Lognormal, 0.998 | Weibull, 0.996 | Folded normal, 0.989 |
| 1922 Liberal | Lognormal, 0.997 | Weibull, 0.993 | Folded normal, 0.984 |
| 1923 Liberal | Lognormal, 0.996 | Weibull, 0.993 | Folded normal, 0.984 |
| 1924 Conservative | Lognormal, 0.998 | Weibull, 0.995 | Folded normal, 0.987 |
| 1924 Labour | Lognormal, 0.997 | Weibull, 0.993 | Folded normal, 0.984 |
| 1924 Liberal | Lognormal, 0.995 | Weibull, 0.993 | Folded normal, 0.985 |
| 1925 Conservative | Lognormal, 0.997 | Weibull, 0.994 | Folded normal, 0.985 |
| 1925 Liberal | Lognormal, 0.995 | Weibull, 0.993 | Folded normal, 0.985 |
| 1926 Conservative | Lognormal, 0.998 | Weibull, 0.995 | Folded normal, 0.986 |
| 1927 | Lognormal, 0.999 | Weibull, 0.996 | Rayleigh, 0.988 |
| 1927 Conservative | Lognormal, 0.998 | Weibull, 0.996 | Rayleigh, 0.988 |
| 1927 Liberal | Lognormal, 0.999 | Weibull, 0.996 | Rayleigh, 0.991 |
| 1928 Conservative | Lognormal, 0.998 | Weibull, 0.996 | Folded normal, 0.988 |
| 1928 Liberal | Lognormal, 0.998 | Weibull, 0.994 | Folded normal, 0.984 |
| 1929 Conservative | Lognormal, 0.998 | Weibull, 0.995 | Rayleigh, 0.988 |
| 1929 Liberal | Lognormal, 0.999 | Weibull, 0.994 | Rayleigh, 0.989 |
| 1930 Liberal | Lognormal, 0.997 | Weibull, 0.995 | Folded normal, 0.987 |
| 1932 Conservative | Lognormal, 0.998 | Weibull, 0.993 | Folded normal, 0.984 |
| 1932 Liberal | Lognormal, 0.997 | Weibull, 0.995 | Rayleigh, 0.984 |
| 1933 Conservative | Lognormal, 0.999 | Weibull, 0.993 | Rayleigh, 0.985 |
| 1934 Conservative | Lognormal, 0.998 | Weibull, 0.993 | Folded normal, 0.983 |
| 1935 Conservative | Lognormal, 0.998 | Weibull, 0.996 | Folded normal, 0.988 |
| 1936 Liberal | Lognormal, 0.994 | Weibull, 0.993 | Folded normal, 0.986 |
| 1937 | Lognormal, 0.997 | Weibull, 0.996 | Folded normal, 0.989 |
| 1937 Liberal | Lognormal, 0.996 | Weibull, 0.994 | Folded normal, 0.985 |
| 1941 Liberal | Lognormal, 0.998 | Weibull, 0.994 | Rayleigh, 0.985 |
| 1942 Liberal | Lognormal, 0.996 | Weibull, 0.995 | Folded normal, 0.987 |
| 1943 Liberal | Lognormal, 0.997 | Weibull, 0.994 | Folded normal, 0.986 |
| 1945 Liberal | Lognormal, 0.996 | Weibull, 0.994 | Folded normal, 0.986 |
| 1946 Labour | Lognormal, 0.998 | Weibull, 0.994 | Folded normal, 0.984 |
| 1947 | Lognormal 0.998 | Weibull, 0.996 | Folded normal, 0.988 |
| 1947 Labour | Lognormal, 0.998 | Weibull, 0.993 | Folded normal, 0.984 |
| 1948 Labour | Lognormal, 0.997 | Weibull, 0.995 | Folded normal, 0.986 |
| 1949 Labour | Lognormal, 0.998 | Weibull, 0.994 | Folded normal, 0.985 |
| 1950 Labour | Lognormal, 0.998 | Weibull, 0.995 | Folded normal, 0.985 |
| 1951 Labour | Lognormal, 0.998 | Weibull, 0.994 | Folded normal, 0.985 |
| 1955 Conservative | Lognormal, 0.998 | Weibull, 0.995 | Folded normal, 0.987 |
| 1956 Conservative | Lognormal, 0.998 | Weibull, 0.994 | Folded normal, 0.985 |
| 1957 | Lognormal 0.999 | Weibull, 0.994 | Rayleigh, 0.99 |
| 1957 Conservative | Lognormal, 0.998 | Weibull, 0.994 | Rayleigh, 0.986 |
| 1958 Conservative | Lognormal, 0.998 | Weibull, 0.995 | Folded normal, 0.986 |
| 1960 Conservative | Lognormal, 0.998 | Weibull, 0.993 | Folded normal, 0.983 |
| 1961 Conservative | Lognormal, 0.998 | Weibull, 0.995 | Folded normal, 0.986 |
| 1962 Conservative | Lognormal, 0.997 | Weibull, 0.994 | Folded normal, 0.985 |
| 1963 Conservative | Lognormal, 0.997 | Weibull, 0.994 | Folded normal, 0.985 |
| 1963 Liberal | Lognormal, 0.998 | Weibull, 0.996 | Folded normal, 0.987 |
| 1964 Labour | Lognormal, 0.996 | Weibull, 0.995 | Folded normal, 0.989 |
| 1965 Conservative | Lognormal, 0.999 | Weibull, 0.995 | Folded normal, 0.986 |
| 1965 Labour | Lognormal, 0.997 | Weibull, 0.995 | Folded normal, 0.988 |
| 1966 Conservative | Lognormal, 0.998 | Weibull, 0.994 | Rayleigh, 0.986 |
| 1966 Labour | Weibull, 0.995 | Lognormal, 0.994 | Folded normal, 0.988 |
| 1967 | Lognormal, 0.997 | Weibull, 0.995 | Folded normal, 0.988 |
| 1967 Conservative | Lognormal, 0.998 | Weibull, 0.994 | Rayleigh, 0.984 |
| 1967 Labour | Lognormal, 0.997 | Weibull, 0.995 | Folded normal, 0.986 |
| 1968 Conservative | Lognormal, 0.998 | Weibull, 0.994 | Folded normal, 0.985 |
| 1968 Labour | Lognormal, 0.997 | Weibull, 0.996 | Folded normal, 0.988 |
| 1969 Conservative | Lognormal, 0.998 | Weibull, 0.996 | Rayleigh, 0.988 |
| 1969 Labour | Lognormal, 0.997 | Weibull, 0.996 | Folded normal, 0.989 |
| 1970 Conservative | Lognormal, 0.997 | Weibull, 0.991 | Folded normal, 0.981 |
| 1970 Labour | Lognormal, 0.997 | Weibull, 0.995 | Folded normal, 0.987 |
| 1971 Conservative | Lognormal, 0.998 | Weibull, 0.995 | Rayleigh, 0.987 |
| 1971 Labour | Lognormal, 0.998 | Weibull, 0.996 | Folded normal, 0.989 |
| 1972 Conservative | Lognormal, 0.998 | Weibull, 0.995 | Folded normal, 0.986 |
| 1972 Labour | Lognormal, 0.998 | Weibull, 0.996 | Folded normal, 0.988 |
| 1973 Conservative | Lognormal, 0.998 | Weibull, 0.994 | Rayleigh, 0.986 |
| 1973 Labour | Lognormal, 0.997 | Weibull, 0.997 | Folded normal, 0.99 |
| 1974 Labour | Lognormal, 0.996 | Weibull, 0.995 | Folded normal, 0.988 |
| 1975 Conservative | Lognormal, 0.998 | Weibull, 0.995 | Rayleigh, 0.986 |
| 1975 Labour | Lognormal, 0.996 | Weibull, 0.995 | Folded normal, 0.987 |
| 1976 Conservative | Lognormal, 0.998 | Weibull, 0.994 | Folded normal, 0.985 |
| 1976 Labour | Lognormal, 0.997 | Weibull, 0.996 | Folded normal, 0.988 |
| 1977 Conservative | Lognormal, 0.998 | Weibull, 0.995 | Rayleigh, 0.988 |
| 1977 Liberal a | Weibull, 0.995 | Lognormal, 0.995 | Folded normal, 0.989 |
| 1977 Liberal b | Weibull, 0.995 | Lognormal, 0.995 | Folded normal, 0.989 |
| 1978 Conservative | Lognormal, 0.999 | Weibull, 0.996 | Rayleigh, 0.989 |
| 1978 Labour | Lognormal, 0.998 | Weibull, 0.995 | Folded normal, 0.986 |
| 1978 Liberal | Lognormal, 0.997 | Weibull, 0.996 | Folded normal, 0.989 |
| 1979 Conservative | Lognormal, 0.998 | Weibull, 0.995 | Rayleigh, 0.987 |
| 1979 Labour | Lognormal, 0.998 | Weibull, 0.995 | Folded normal, 0.985 |
| 1979 Liberal | Lognormal, 0.997 | Weibull, 0.995 | Folded normal, 0.987 |
| 1980 Conservative | Lognormal, 0.998 | Weibull, 0.996 | Folded normal, 0.988 |
| 1980 Labour | Lognormal, 0.998 | Weibull, 0.994 | Folded normal, 0.985 |
| 1980 Liberal | Weibull, 0.996 | Lognormal, 0.995 | Folded normal, 0.989 |
| 1981 Conservative | Lognormal, 0.998 | Weibull, 0.996 | Rayleigh, 0.989 |
| 1981 Labour | Lognormal, 0.998 | Weibull, 0.995 | Folded normal, 0.987 |
| 1981 Liberal | Lognormal, 0.997 | Weibull, 0.995 | Folded normal, 0.986 |
| 1982 Conservative | Lognormal, 0.998 | Weibull, 0.996 | Rayleigh, 0.99 |
| 1982 Labour | Lognormal, 0.999 | Weibull, 0.994 | Rayleigh, 0.986 |
| 1982 Liberal | Lognormal, 0.996 | Weibull, 0.995 | Folded normal, 0.988 |
| 1982 SDP-Liberal Alliance | Lognormal, 0.995 | Weibull, 0.993 | Folded normal, 0.985 |
| 1983 Conservative | Lognormal, 0.998 | Weibull, 0.995 | Rayleigh, 0.988 |
| 1983 Labour | Lognormal, 0.998 | Weibull, 0.995 | Folded normal, 0.987 |
| 1983 Liberal | Lognormal, 0.996 | Weibull, 0.996 | Folded normal, 0.988 |
| 1984 Conservative | Lognormal, 0.998 | Weibull, 0.995 | Rayleigh, 0.987 |
| 1984 Labour | Lognormal, 0.997 | Weibull, 0.993 | Folded normal, 0.983 |
| 1984 Liberal | Lognormal, 0.996 | Weibull, 0.995 | Folded normal, 0.988 |
| 1985 Conservative | Lognormal, 0.998 | Weibull, 0.996 | Rayleigh, 0.989 |
| 1985 Labour | Lognormal, 0.998 | Weibull, 0.995 | Folded normal, 0.986 |
| 1985 Liberal | Lognormal, 0.996 | Weibull, 0.996 | Folded normal, 0.988 |
| 1986 Conservative | Weibull, 0.997 | Lognormal, 0.997 | Rayleigh, 0.992 |
| 1986 Labour | Lognormal, 0.997 | Weibull, 0.994 | Folded normal, 0.986 |
| 1986 Liberal | Weibull, 0.996 | Lognormal, 0.996 | Folded normal, 0.99 |
| 1987 Conservative | Lognormal, 0.997 | Weibull, 0.997 | Rayleigh, 0.989 |
| 1987 | Weibull 0.997 | Lognormal, 0.996 | Folded normal 0.991 |
| 1987 Labour | Lognormal, 0.998 | Weibull, 0.993 | Folded normal, 0.984 |
| 1987 SDP-Liberal Alliance a | Lognormal, 0.997 | Weibull, 0.994 | Folded normal, 0.985 |
| 1987 SDP-Liberal Alliance b | Lognormal, 0.997 | Weibull, 0.995 | Folded normal, 0.987 |
| 1988 Conservative | Lognormal, 0.997 | Weibull, 0.996 | Rayleigh, 0.989 |
| 1988 Labour | Lognormal, 0.996 | Weibull, 0.994 | Folded normal, 0.987 |
| 1988 Liberal | Weibull, 0.996 | Lognormal, 0.996 | Folded normal, 0.99 |
| 1989 Conservative | Lognormal, 0.998 | Weibull, 0.996 | Rayleigh, 0.991 |
| 1989 Labour | Lognormal, 0.998 | Weibull, 0.993 | Folded normal, 0.983 |
| 1990 Labour | Lognormal, 0.996 | Weibull, 0.994 | Folded normal, 0.986 |
| 1991 Conservative | Lognormal, 0.999 | Weibull, 0.997 | Rayleigh, 0.993 |
| 1991 Labour | Lognormal, 0.996 | Weibull, 0.995 | Folded normal, 0.987 |
| 1992 Conservative | Lognormal, 0.999 | Weibull, 0.996 | Rayleigh, 0.992 |
| 1992 Labour | Lognormal, 0.997 | Weibull, 0.995 | Folded normal, 0.988 |
| 1992 Liberal Democrat | Lognormal, 0.999 | Weibull, 0.996 | Rayleigh, 0.99 |
| 1993 Conservative | Lognormal, 0.999 | Weibull, 0.997 | Rayleigh, 0.993 |
| 1993 Labour | Lognormal, 0.998 | Weibull, 0.996 | Rayleigh, 0.989 |
| 1993 Liberal Democrat | Lognormal, 0.998 | Weibull, 0.996 | Folded normal, 0.988 |
| 1994 Conservative | Lognormal, 0.998 | Weibull, 0.997 | Rayleigh, 0.992 |
| 1994 Labour | Lognormal, 0.998 | Weibull, 0.996 | Folded normal, 0.988 |
| 1994 Liberal Democrat | Lognormal, 0.998 | Weibull, 0.996 | Folded normal, 0.988 |
| 1995 Conservative | Lognormal, 0.999 | Weibull, 0.997 | Rayleigh, 0.993 |
| 1995 Labour | Weibull, 0.998 | Lognormal, 0.997 | Rayleigh, 0.992 |
| 1996 Conservative | Lognormal, 0.998 | Weibull, 0.997 | Rayleigh, 0.991 |
| 1996 Labour | Lognormal, 0.999 | Weibull, 0.996 | Rayleigh, 0.989 |
| 1996 Liberal Democrat | Lognormal, 0.998 | Weibull, 0.996 | Rayleigh, 0.991 |
| 1997 Conservative | Lognormal, 0.998 | Weibull, 0.997 | Rayleigh, 0.991 |
| 1997 | Lognormal, 0.996 | Weibull, 0.994 | Folded normal 0.986 |
| 1997 Labour | Lognormal, 0.998 | Weibull, 0.996 | Folded normal, 0.988 |
| 1997 Labour | Lognormal, 0.998 | Weibull, 0.997 | Rayleigh, 0.99 |
| 1998 Conservative | Lognormal, 0.998 | Weibull, 0.996 | Rayleigh, 0.99 |
| 1998 Labour | Lognormal, 0.997 | Weibull, 0.997 | Rayleigh, 0.99 |
| 1998 Liberal Democrat | Lognormal, 0.998 | Weibull, 0.996 | Rayleigh, 0.99 |
| 1999 Conservative | Lognormal, 0.998 | Weibull, 0.996 | Rayleigh, 0.989 |
| 1999 Labour | Lognormal, 0.998 | Weibull, 0.996 | Rayleigh, 0.99 |
| 1999 Liberal Democrat a | Lognormal, 0.999 | Weibull, 0.994 | Folded normal, 0.984 |
| 1999 Liberal Democrat b | Lognormal, 0.997 | Weibull, 0.996 | Rayleigh, 0.989 |
| 2000 Conservative | Lognormal, 0.999 | Weibull, 0.995 | Rayleigh, 0.992 |
| 2000 Labour | Lognormal, 0.997 | Weibull, 0.997 | Folded normal, 0.99 |
| 2000 Liberal Democrat | Lognormal, 0.998 | Weibull, 0.996 | Rayleigh, 0.992 |
| 2001 Conservative | Lognormal, 0.997 | Weibull, 0.997 | Folded normal, 0.989 |
| 2001 Labour | Lognormal, 0.997 | Weibull, 0.997 | Folded normal, 0.99 |
| 2001 Liberal Democrat | Lognormal, 0.997 | Weibull, 0.996 | Folded normal, 0.987 |
| 2002 Conservative | Lognormal, 0.999 | Weibull, 0.996 | Rayleigh, 0.993 |
| 2002 Labour | Lognormal, 0.998 | Weibull, 0.996 | Folded normal, 0.988 |
| 2002 Liberal Democrat | Lognormal, 0.997 | Weibull, 0.997 | Folded normal, 0.989 |
| 2003 Conservative | Lognormal, 0.999 | Weibull, 0.996 | Rayleigh, 0.992 |
| 2003 Labour | Lognormal, 0.998 | Weibull, 0.995 | Rayleigh, 0.988 |
| 2003 Liberal Democrat | Lognormal, 0.998 | Weibull, 0.996 | Rayleigh, 0.99 |
| 2004 Conservative | Lognormal, 0.999 | Weibull, 0.997 | Rayleigh, 0.993 |
| 2004 Labour | Lognormal, 0.998 | Weibull, 0.996 | Rayleigh, 0.991 |
| 2004 Liberal Democratl | Lognormal, 0.998 | Weibull, 0.996 | Rayleigh, 0.991 |
| 2005 Conservative | Lognormal, 0.999 | Weibull, 0.995 | Rayleigh, 0.989 |
| 2005 Labour | Lognormal, 0.998 | Weibull, 0.996 | Rayleigh, 0.988 |
| 2005 Liberal Democrat | Lognormal, 0.997 | Weibull, 0.997 | Folded normal, 0.989 |
| 2006 Conservative a | Lognormal, 0.999 | Weibull, 0.997 | Rayleigh, 0.99 |
| 2006 Conservative b | Lognormal, 0.999 | Weibull, 0.996 | Rayleigh, 0.99 |
| 2006 Labour | Lognormal, 0.998 | Weibull, 0.997 | Rayleigh, 0.989 |
| 2006 Liberal Democrat | Lognormal, 0.997 | Weibull, 0.995 | Folded normal, 0.987 |
| 2007 | Weibull, 0.995 | Lognormal, 0.994 | Folded normal, 0.989 |
| 2007 Conservative | Lognormal, 0.999 | Weibull, 0.997 | Rayleigh, 0.994 |
| 2007 Labour | Lognormal, 0.998 | Weibull, 0.996 | Rayleigh, 0.989 |
| 2007 Liberal Democrat | Lognormal, 0.998 | Weibull, 0.997 | Rayleigh, 0.991 |
| 2008 Conservative | Lognormal, 0.999 | Weibull, 0.996 | Rayleigh, 0.99 |
| 2008 Labour | Lognormal, 0.998 | Weibull, 0.997 | Rayleigh, 0.992 |
| 2008 Liberal Democratl | Lognormal, 0.998 | Weibull, 0.998 | Rayleigh, 0.994 |
| 2009 Conservative | Lognormal, 0.999 | Weibull, 0.996 | Rayleigh, 0.993 |
| 2009 Labour | Lognormal, 0.999 | Weibull, 0.995 | Rayleigh, 0.992 |
| 2009 Liberal Democrat | Lognormal, 0.998 | Weibull, 0.997 | Rayleigh, 0.991 |
| 2010 Conservative | Lognormal, 0.999 | Weibull, 0.996 | Rayleigh, 0.994 |
| 2010 Labour | Lognormal, 0.998 | Weibull, 0.995 | Rayleigh, 0.987 |
| 2010 Liberal Democratl | Lognormal, 0.999 | Weibull, 0.996 | Rayleigh, 0.993 |
| 2011 Conservative | Lognormal, 0.999 | Weibull, 0.996 | Rayleigh, 0.993 |
| 2011 Labour | Lognormal, 0.999 | Weibull, 0.996 | Rayleigh, 0.994 |
| 2011 Liberal Democrat | Lognormal, 0.999 | Weibull, 0.997 | Rayleigh, 0.994 |
| 2012 Conservative | Lognormal, 0.999 | Weibull, 0.996 | Rayleigh, 0.995 |
| 2012 Liberal Democrat | Lognormal, 0.999 | Weibull, 0.996 | Rayleigh, 0.992 |
| 2013 Conservative | Lognormal, 0.999 | Weibull, 0.997 | Rayleigh, 0.996 |
| 2013 Labour | Lognormal, 0.999 | Weibull, 0.997 | Rayleigh, 0.996 |
| 2013 Liberal Democrat | Lognormal, 0.998 | Weibull, 0.997 | Rayleigh, 0.992 |
| 2014 Conservative | Lognormal, 0.999 | Weibull, 0.997 | Rayleigh, 0.995 |
| 2014 Labour | Lognormal, 0.999 | Weibull, 0.997 | Rayleigh, 0.993 |
| 2014 Liberal Democrat | Lognormal, 0.999 | Weibull, 0.996 | Rayleigh, 0.991 |
| 2015 Conservative | Lognormal, 0.998 | Weibull, 0.998 | Rayleigh, 0.996 |
| 2015 Labour | Lognormal, 0.997 | Weibull, 0.997 | Rayleigh, 0.991 |
| 2015 Liberal Democrat | Lognormal, 0.998 | Weibull, 0.997 | Rayleigh, 0.99 |
| 2016 Conservative | Lognormal, 0.998 | Weibull, 0.997 | Rayleigh, 0.992 |
| 2016 Labour | Weibull, 0.997 | Lognormal, 0.997 | Folded normal, 0.991 |
| 2016 Liberal Democrat | Lognormal, 0.998 | Weibull, 0.998 | Rayleigh, 0.992 |
| 2017 | Lognormal 0.997 | Weibull 0.996 | Rayleigh 0.991 |
| 2017 Conservative | Lognormal, 0.998 | Weibull, 0.997 | Rayleigh, 0.992 |
| 2017 Labour | Weibull, 0.997 | Lognormal, 0.997 | Rayleigh, 0.991 |
| 2017 Liberal Democrat | Weibull, 0.997 | Lognormal, 0.996 | Folded normal, 0.991 |
| 2018 Conservative | Lognormal, 0.998 | Weibull, 0.997 | Rayleigh, 0.993 |
| 2018 Labour | Lognormal, 0.997 | Weibull, 0.996 | Folded normal, 0.989 |
Appendix B
| Year | R2 | µ | σ |
|---|---|---|---|
| 1789 | 0.995 | 1.27 | 0.73 |
| 1796 | 0.998 | 1.19 | 0.60 |
| 1797 | 0.992 | 1.26 | 0.73 |
| 1798 | 0.989 | 1.29 | 0.73 |
| 1801 | 0.997 | 1.25 | 0.68 |
| 1803 | 0.996 | 1.25 | 0.68 |
| 1805 | 0.994 | 1.27 | 0.70 |
| 1805 | 0.996 | 1.28 | 0.68 |
| 1809 | 0.993 | 1.25 | 0.75 |
| 1812 | 0.992 | 1.32 | 0.70 |
| 1813 | 0.995 | 1.26 | 0.70 |
| 1815 | 0.993 | 1.23 | 0.73 |
| 1817 | 0.994 | 1.26 | 0.70 |
| 1821 | 0.994 | 1.26 | 0.69 |
| 1821 | 0.996 | 1.27 | 0.68 |
| 1825 | 0.993 | 1.27 | 0.71 |
| 1825 | 0.992 | 1.29 | 0.72 |
| 1827 | 0.994 | 1.24 | 0.69 |
| 1833 | 0.993 | 1.26 | 0.71 |
| 1837 | 0.991 | 1.29 | 0.72 |
| 1838 | 0.992 | 1.29 | 0.71 |
| 1839 | 0.993 | 1.24 | 0.74 |
| 1841 | 0.993 | 1.25 | 0.71 |
| 1842 | 0.993 | 1.23 | 0.73 |
| 1845 | 0.993 | 1.27 | 0.71 |
| 1848 | 0.993 | 1.30 | 0.68 |
| 1850 | 0.993 | 1.25 | 0.71 |
| 1851 | 0.993 | 1.23 | 0.71 |
| 1853 | 0.994 | 1.28 | 0.71 |
| 1854 | 0.988 | 1.30 | 0.73 |
| 1856 | 0.990 | 1.24 | 0.74 |
| 1857 | 0.995 | 1.28 | 0.68 |
| 1861 | 0.997 | 1.25 | 0.68 |
| 1861 | 0.996 | 1.22 | 0.70 |
| 1864 | 0.994 | 1.29 | 0.68 |
| 1865 | 0.992 | 1.30 | 0.68 |
| 1865 | 0.998 | 1.22 | 0.61 |
| 1868 | 0.992 | 1.32 | 0.69 |
| 1869 | 0.994 | 1.23 | 0.70 |
| 1873 | 0.995 | 1.21 | 0.71 |
| 1875 | 0.996 | 1.24 | 0.69 |
| 1876 | 0.994 | 1.27 | 0.71 |
| 1877 | 0.991 | 1.29 | 0.71 |
| 1877 | 0.992 | 1.27 | 0.72 |
| 1879 | 0.989 | 1.30 | 0.71 |
| 1881 | 0.995 | 1.27 | 0.68 |
| 1885 | 0.992 | 1.28 | 0.71 |
| 1889 | 0.995 | 1.28 | 0.68 |
| 1893 | 0.992 | 1.29 | 0.71 |
| 1893 | 0.991 | 1.31 | 0.71 |
| 1895 | 0.990 | 1.29 | 0.72 |
| 1897 | 0.992 | 1.27 | 0.70 |
| 1901 | 0.993 | 1.29 | 0.70 |
| 1905 | 0.998 | 1.21 | 0.66 |
| 1909 | 0.992 | 1.25 | 0.72 |
| 1913 | 0.998 | 1.20 | 0.65 |
| 1917 | 0.998 | 1.18 | 0.64 |
| 1921 | 0.993 | 1.29 | 0.71 |
| 1925 | 0.995 | 1.25 | 0.69 |
| 1929 | 0.993 | 1.29 | 0.72 |
| 1933 | 0.996 | 1.24 | 0.69 |
| 1937 | 0.996 | 1.26 | 0.68 |
| 1941 | 0.997 | 1.20 | 0.67 |
| 1945 | 0.999 | 1.16 | 0.66 |
| 1949 | 0.995 | 1.30 | 0.67 |
| 1953 | 0.997 | 1.23 | 0.64 |
| 1957 | 0.998 | 1.19 | 0.63 |
| 1961 | 0.998 | 1.22 | 0.62 |
| 1965 | 0.997 | 1.18 | 0.62 |
| 1969 | 0.998 | 1.16 | 0.64 |
| 1973 | 0.999 | 1.16 | 0.67 |
| 1977 | 0.998 | 1.20 | 0.65 |
| 1981 | 0.997 | 1.19 | 0.67 |
| 1985 | 0.998 | 1.22 | 0.64 |
| 1989 | 0.999 | 1.15 | 0.61 |
| 1993 | 0.997 | 1.23 | 0.64 |
| 1997 | 0.998 | 1.23 | 0.63 |
| 2001 | 0.995 | 1.22 | 0.66 |
| 2009 | 0.998 | 1.22 | 0.62 |
| 2013 | 0.998 | 1.25 | 0.63 |
| 2017 | 0.997 | 1.27 | 0.61 |
| 2021 | 0.998 | 1.17 | 0.62 |
| Year | R2 | µ | σ |
|---|---|---|---|
| 1808 | 0.996 | 1.24 | 0.68 |
| 1814 | 0.996 | 1.21 | 0.70 |
| 1815 | 0.998 | 1.16 | 0.68 |
| 1817 | 0.995 | 1.22 | 0.68 |
| 1819 | 0.993 | 1.26 | 0.71 |
| 1827 | 0.996 | 1.10 | 0.71 |
| 1830 | 0.998 | 1.20 | 0.65 |
| 1837 | 0.996 | 1.25 | 0.67 |
| 1842 | 0.994 | 1.22 | 0.71 |
| 1853 | 0.995 | 1.21 | 0.68 |
| 1868 | 0.998 | 1.20 | 0.70 |
| 1877 | 0.996 | 1.17 | 0.70 |
| 1893 | 0.993 | 1.15 | 0.73 |
| 1895 Liberal | 0.998 | 1.17 | 0.69 |
| 1896 Liberal | 0.998 | 1.17 | 0.67 |
| 1897 Liberal | 0.998 | 1.17 | 0.66 |
| 1897 Conservative | 0.998 | 1.19 | 0.67 |
| 1899 Liberal | 0.998 | 1.16 | 0.67 |
| 1900 Conservative | 0.998 | 1.18 | 0.63 |
| 1901 Liberal | 0.998 | 1.18 | 0.66 |
| 1902 Conservative | 0.997 | 1.20 | 0.68 |
| 1903 Conservative | 0.998 | 1.19 | 0.68 |
| 1903 Liberal | 0.998 | 1.16 | 0.67 |
| 1904 Conservative | 0.997 | 1.21 | 0.66 |
| 1905 Liberal | 0.997 | 1.21 | 0.68 |
| 1906 Conservative | 0.997 | 1.19 | 0.69 |
| 1907 | 0.998 | 1.14 | 0.69 |
| 1907 Conservative | 0.998 | 1.21 | 0.67 |
| 1907 Liberal | 0.998 | 1.18 | 0.67 |
| 1908 Liberal | 0.998 | 1.17 | 0.66 |
| 1908 Conservative | 0.998 | 1.20 | 0.66 |
| 1909 Liberal | 0.998 | 1.17 | 0.67 |
| 1909 Conservative | 0.998 | 1.18 | 0.66 |
| 1910 Liberal | 0.998 | 1.17 | 0.68 |
| 1910 Conservative | 0.998 | 1.18 | 0.66 |
| 1911 Conservative | 0.998 | 1.17 | 0.65 |
| 1912 Liberal | 0.997 | 1.17 | 0.68 |
| 1912 Conservative | 0.999 | 1.15 | 0.64 |
| 1913 Conservative | 0.999 | 1.16 | 0.63 |
| 1913 Liberal | 0.997 | 1.18 | 0.69 |
| 1917 | 0.999 | 1.18 | 0.66 |
| 1918 Liberal | 0.998 | 1.20 | 0.68 |
| 1919 Liberal | 0.997 | 1.18 | 0.69 |
| 1920 Liberal | 0.997 | 1.18 | 0.69 |
| 1920 Conservative | 0.999 | 1.11 | 0.64 |
| 1921 Liberal | 0.998 | 1.18 | 0.68 |
| 1921 Conservative | 0.999 | 1.17 | 0.63 |
| 1922 Liberal | 0.997 | 1.19 | 0.69 |
| 1922 Conservative | 0.998 | 1.13 | 0.67 |
| 1923 Liberal | 0.996 | 1.20 | 0.70 |
| 1924 Liberal | 0.995 | 1.23 | 0.70 |
| 1924 Labour | 0.997 | 1.19 | 0.68 |
| 1924 Conservative | 0.998 | 1.16 | 0.66 |
| 1925 Liberal | 0.995 | 1.26 | 0.69 |
| 1925 Conservative | 0.997 | 1.20 | 0.67 |
| 1926 Conservative | 0.998 | 1.21 | 0.66 |
| 1927 | 0.999 | 1.16 | 0.65 |
| 1927 Liberal | 0.999 | 1.20 | 0.61 |
| 1927 Conservative | 0.998 | 1.18 | 0.64 |
| 1928 Liberal | 0.998 | 1.18 | 0.67 |
| 1928 Conservative | 0.998 | 1.18 | 0.65 |
| 1929 Liberal | 0.999 | 1.20 | 0.62 |
| 1929 Conservative | 0.998 | 1.20 | 0.63 |
| 1930 Liberal | 0.997 | 1.21 | 0.67 |
| 1932 Conservative | 0.998 | 1.17 | 0.67 |
| 1932 Liberal | 0.997 | 1.24 | 0.66 |
| 1933 Conservative | 0.999 | 1.17 | 0.65 |
| 1934 Conservative | 0.998 | 1.16 | 0.67 |
| 1935 Conservative | 0.998 | 1.17 | 0.65 |
| 1936 Liberal | 0.994 | 1.26 | 0.68 |
| 1937 | 0.997 | 1.19 | 0.67 |
| 1937 Liberal | 0.996 | 1.22 | 0.68 |
| 1941 Liberal | 0.998 | 1.23 | 0.65 |
| 1942 Liberal | 0.996 | 1.24 | 0.67 |
| 1943 Liberal | 0.997 | 1.24 | 0.66 |
| 1945 Liberal | 0.996 | 1.23 | 0.67 |
| 1946 Labour | 0.998 | 1.20 | 0.67 |
| 1947 | 0.998 | 1.19 | 0.64 |
| 1947 Labour | 0.998 | 1.18 | 0.67 |
| 1948Labour | 0.997 | 1.20 | 0.68 |
| 1949 Labour | 0.998 | 1.19 | 0.67 |
| 1950 Labour | 0.998 | 1.18 | 0.67 |
| 1951 Labour | 0.998 | 1.17 | 0.67 |
| 1955 Conservative | 0.998 | 1.18 | 0.65 |
| 1956 Conservative | 0.998 | 1.19 | 0.66 |
| 1957 | 0.999 | 1.19 | 0.61 |
| 1957 Conservative | 0.998 | 1.18 | 0.64 |
| 1958 Conservative | 0.998 | 1.21 | 0.65 |
| 1960 Conservative | 0.998 | 1.20 | 0.67 |
| 1961 Conservative | 0.998 | 1.19 | 0.65 |
| 1962 Conservative | 0.997 | 1.22 | 0.67 |
| 1963 Liberal | 0.998 | 1.20 | 0.65 |
| 1963 Conservative | 0.997 | 1.22 | 0.67 |
| 1964 Labour | 0.996 | 1.24 | 0.69 |
| 1965 Labour | 0.997 | 1.22 | 0.68 |
| 1965 Conservative | 0.999 | 1.19 | 0.65 |
| 1966 Labour | 0.994 | 1.28 | 0.69 |
| 1966 Conservative | 0.998 | 1.19 | 0.64 |
| 1967 | 0.997 | 1.20 | 0.68 |
| 1967 Labour | 0.997 | 1.25 | 0.67 |
| 1967 Conservative | 0.998 | 1.19 | 0.65 |
| 1968 Labour | 0.997 | 1.26 | 0.66 |
| 1968 Conservative | 0.998 | 1.23 | 0.66 |
| 1969 Labour | 0.997 | 1.24 | 0.65 |
| 1969 Conservative | 0.998 | 1.18 | 0.64 |
| 1970 Labour | 0.997 | 1.25 | 0.67 |
| 1970 Conservative | 0.997 | 1.19 | 0.69 |
| 1971 Conservative | 0.998 | 1.19 | 0.64 |
| 1971 Labour | 0.998 | 1.26 | 0.66 |
| 1972 Conservative | 0.998 | 1.18 | 0.66 |
| 1972 Labour | 0.998 | 1.22 | 0.66 |
| 1973 Conservative | 0.998 | 1.18 | 0.64 |
| 1973 Labour | 0.997 | 1.26 | 0.65 |
| 1974 Labour | 0.996 | 1.26 | 0.67 |
| 1975 Conservative | 0.998 | 1.20 | 0.64 |
| 1975 Labour | 0.996 | 1.28 | 0.68 |
| 1976 Conservative | 0.998 | 1.21 | 0.65 |
| 1976 Labour | 0.997 | 1.22 | 0.68 |
| 1977 Conservative | 0.998 | 1.19 | 0.63 |
| 1997 Labour | 0.998 | 1.25 | 0.65 |
| 1977 Liberal a | 0.995 | 1.25 | 0.69 |
| 1977 Liberal b | 0.995 | 1.26 | 0.70 |
| 1978 Conservative | 0.999 | 1.20 | 0.63 |
| 1978 Labour | 0.998 | 1.18 | 0.67 |
| 1978 Liberal | 0.997 | 1.25 | 0.66 |
| 1979 Conservative | 0.998 | 1.20 | 0.64 |
| 1979 Labour | 0.998 | 1.19 | 0.66 |
| 1979 Liberal | 0.997 | 1.24 | 0.67 |
| 1980 Conservative | 0.998 | 1.22 | 0.65 |
| 1980 Labour | 0.998 | 1.18 | 0.66 |
| 1980 Liberal | 0.995 | 1.27 | 0.68 |
| 1981 Conservative | 0.998 | 1.20 | 0.63 |
| 1981 Labour | 0.998 | 1.17 | 0.66 |
| 1981 Liberal | 0.997 | 1.25 | 0.67 |
| 1982 SDP-Liberal Alliance | 0.995 | 1.21 | 0.70 |
| 1982 Conservative | 0.998 | 1.21 | 0.62 |
| 1982 Labour | 0.999 | 1.15 | 0.65 |
| 1982 Liberal | 0.996 | 1.26 | 0.67 |
| 1983 Conservative | 0.998 | 1.21 | 0.63 |
| 1983 Labour | 0.998 | 1.16 | 0.65 |
| 1983 Liberal | 0.996 | 1.25 | 0.67 |
| 1984 Conservative | 0.998 | 1.21 | 0.64 |
| 1984 Labour | 0.997 | 1.22 | 0.65 |
| 1984 Liberal | 0.996 | 1.24 | 0.68 |
| 1985 Conservative | 0.998 | 1.24 | 0.63 |
| 1985 Labour | 0.998 | 1.21 | 0.65 |
| 1985 Liberal | 0.996 | 1.28 | 0.67 |
| 1986 Conservative | 0.997 | 1.27 | 0.62 |
| 1986 Labour | 0.997 | 1.22 | 0.66 |
| 1986 Liberal | 0.996 | 1.27 | 0.67 |
| 1987 | 0.996 | 1.30 | 0.65 |
| 1987 Conservative | 0.997 | 1.26 | 0.63 |
| 1987 Labour | 0.998 | 1.20 | 0.67 |
| 1987 SDP-Liberal Alliance a | 0.997 | 1.24 | 0.66 |
| 1987 SDP-Liberal Alliance b | 0.997 | 1.27 | 0.67 |
| 1988 Conservative | 0.997 | 1.26 | 0.63 |
| 1988 Labour | 0.996 | 1.25 | 0.67 |
| 1988 Liberal | 0.996 | 1.23 | 0.68 |
| 1989 Conservative | 0.998 | 1.23 | 0.62 |
| 1989 Labour | 0.998 | 1.19 | 0.66 |
| 1990 Labour | 0.996 | 1.24 | 0.66 |
| 1991 Conservative | 0.999 | 1.21 | 0.61 |
| 1991 Labour | 0.996 | 1.23 | 0.65 |
| 1992 Conservative | 0.999 | 1.21 | 0.61 |
| 1992 Labour | 0.997 | 1.22 | 0.66 |
| 1992 Liberal Democrat | 0.999 | 1.20 | 0.63 |
| 1993 Conservative | 0.999 | 1.20 | 0.60 |
| 1993 Labour | 0.998 | 1.23 | 0.63 |
| 1993 Liberal Democrat | 0.998 | 1.22 | 0.67 |
| 1994 Conservative | 0.998 | 1.21 | 0.61 |
| 1994 Labour | 0.998 | 1.20 | 0.65 |
| 1994 Liberal Democrat | 0.998 | 1.23 | 0.65 |
| 1995 Conservative | 0.999 | 1.21 | 0.61 |
| 1995 Labour | 0.997 | 1.21 | 0.63 |
| 1996 Conservative | 0.998 | 1.18 | 0.62 |
| 1996 Labour | 0.999 | 1.16 | 0.64 |
| 1996 Liberal Democrat | 0.998 | 1.22 | 0.62 |
| 1997 | 0.996 | 1.19 | 0.67 |
| 1997 Conservative | 0.998 | 1.19 | 0.63 |
| 1997 Labour | 0.998 | 1.19 | 0.64 |
| 1998 Conservative | 0.998 | 1.23 | 0.63 |
| 1998 Labour | 0.997 | 1.19 | 0.63 |
| 1998 Liberal Democrat | 0.998 | 1.23 | 0.63 |
| 1999 Conservative | 0.998 | 1.23 | 0.64 |
| 1999 Labour | 0.998 | 1.20 | 0.63 |
| 1999 Liberal Democrat a | 0.999 | 1.19 | 0.66 |
| 1999 Liberal Democrat b | 0.997 | 1.24 | 0.64 |
| 2000 Conservative | 0.999 | 1.21 | 0.61 |
| 2000 Labour | 0.997 | 1.24 | 0.64 |
| 2000 Liberal Democrat | 0.998 | 1.26 | 0.61 |
| 2001 Conservative | 0.997 | 1.23 | 0.63 |
| 2001 Labour | 0.997 | 1.24 | 0.64 |
| 2001 Liberal Democrat | 0.997 | 1.26 | 0.65 |
| 2002 Conservative | 0.999 | 1.21 | 0.60 |
| 2002 Labour | 0.998 | 1.22 | 0.64 |
| 2002 Liberal Democrat | 0.997 | 1.28 | 0.64 |
| 2003 Conservative | 0.999 | 1.23 | 0.60 |
| 2003 Labour | 0.998 | 1.19 | 0.63 |
| 2003 Liberal Democrat | 0.998 | 1.26 | 0.63 |
| 2004 Conservative | 0.999 | 1.20 | 0.61 |
| 2004 Labour | 0.998 | 1.21 | 0.62 |
| 2004 Liberal Democrat | 0.998 | 1.28 | 0.62 |
| 2005 Conservative | 0.999 | 1.17 | 0.63 |
| 2005 Labour | 0.998 | 1.21 | 0.64 |
| 2005 Liberal Democrat | 0.997 | 1.24 | 0.65 |
| 2006 Conservative a | 0.999 | 1.24 | 0.64 |
| 2006 Conservative b | 0.999 | 1.22 | 0.63 |
| 2006 Labour | 0.998 | 1.22 | 0.64 |
| 2006 Liberal Democrat | 0.997 | 1.24 | 0.65 |
| 2007 | 0.994 | 1.32 | 0.70 |
| 2007 Conservative | 0.999 | 1.17 | 0.60 |
| 2007 Labour | 0.998 | 1.19 | 0.64 |
| 2007 Liberal Democrat | 0.998 | 1.25 | 0.62 |
| 2008 Conservative | 0.999 | 1.21 | 0.63 |
| 2008 Labour | 0.998 | 1.21 | 0.61 |
| 2008 Liberal Democratl | 0.998 | 1.24 | 0.60 |
| 2009 Conservative | 0.999 | 1.20 | 0.60 |
| 2009 Labour | 0.999 | 1.21 | 0.60 |
| 2009 Liberal Democrat | 0.998 | 1.22 | 0.62 |
| 2010 Conservative | 0.999 | 1.22 | 0.60 |
| 2010 Labour | 0.998 | 1.18 | 0.64 |
| 2010 Liberal Democratl | 0.999 | 1.22 | 0.61 |
| 2011 Conservative | 0.999 | 1.22 | 0.60 |
| 2011 Labour | 0.999 | 1.18 | 0.59 |
| 2011 Liberal Democrat | 0.999 | 1.23 | 0.60 |
| 2012 Conservative | 0.999 | 1.19 | 0.58 |
| 2012 Liberal Democrat | 0.999 | 1.21 | 0.62 |
| 2013 Conservative | 0.999 | 1.20 | 0.58 |
| 2013 Labour | 0.999 | 1.15 | 0.58 |
| 2013 Liberal Democrat | 0.998 | 1.22 | 0.62 |
| 2014 Conservative | 0.999 | 1.18 | 0.59 |
| 2014 Labour | 0.999 | 1.19 | 0.60 |
| 2014 Liberal Democrat | 0.999 | 1.23 | 0.61 |
| 2015 Conservative | 0.998 | 1.21 | 0.59 |
| 2015 Labour | 0.997 | 1.24 | 0.62 |
| 2015 Liberal Democrat | 0.998 | 1.19 | 0.63 |
| 2016 Conservative | 0.998 | 1.23 | 0.62 |
| 2016 Labour | 0.997 | 1.28 | 0.63 |
| 2016 Liberal Democrat | 0.998 | 1.21 | 0.62 |
| 2017 | 0.997 | 1.25 | 0.62 |
| 2017 Conservative | 0.998 | 1.22 | 0.62 |
| 2017 Labour | 0.997 | 1.29 | 0.63 |
| 2017 Liberal Democrat | 0.996 | 1.25 | 0.67 |
| 2018 Conservative | 0.998 | 1.22 | 0.62 |
| 2018 Labour | 0.997 | 1.25 | 0.65 |
References
- Altmann, G. Prolegomena to Menzerath’s law. Glottometrika 1980, 2, 1–10. [Google Scholar]
- Zipf, G.K. Human Behavior and the Principle of Least Effort: An Introduction to Human Ecology; Addison-Wesley Publishing: Cambridge, UK, 1949. [Google Scholar]
- Popescu, I.; Naumann, S.; Kelih, E.; Rovenchak, A.; Overbeck, A.; Sanada, H.; Smith, R.D.; Čech, R.; Mohanty, P.; Wilson, A. Word length: Aspects and languages. Issues Quant. Linguist. 2013, 3, 224–281. [Google Scholar]
- Grzybek, P. (Ed.) Contributions to the Science of Text and Language: Word Length Studies and Related Issues; Springer Science & Business Media: Dordrecht, The Netherlands, 2006; Volume 31. [Google Scholar]
- Rottmann, O.A. On Word Length in German and Polish. Glottometrics 2018, 42, 13–20. [Google Scholar]
- Vieira, D.S.; Picoli, S.; Mendes, R.S. Robustness of sentence length measures in written texts. Phys. A Stat. Mech. Its Appl. 2018, 506, 749–754. [Google Scholar] [CrossRef]
- Milička, J. Average Word Length from the Diachronic Perspective: The Case of Arabic. Linguist. Front. 2018, 1, 81–89. [Google Scholar] [CrossRef]
- Liberman, M. Real Trends in Word and Sentence Length. 2011. Available online: http://languagelog.ldc.upenn.edu/nll (accessed on 25 December 2023).
- Tsizhmovska, N.L.; Martyushev, L.M. Principle of least effort and sentence length in public speaking. Entropy 2021, 23, 1023. [Google Scholar] [CrossRef]
- Tucker, E.C.; Capps, C.J.; Shamir, L. A data science approach to 138 years of congressional speeches. Heliyon 2020, 6, e04417. [Google Scholar] [CrossRef] [PubMed]
- Bochkarev, V.V.; Shevlyakova, A.V.; Solovyev, V.D. The average word length dynamics as an indicator of cultural changes in society. Soc. Evol. Hist. 2015, 14, 153–175. [Google Scholar]
- Lenard, D.B. Gender differences in the length of words and sentences on the corpus of congressional speeches. Imp. J. Interdiscip. Res. 2016, 2, 1417–1424. [Google Scholar]
- Corral, Á.; Serra, I. The brevity law as a scaling law, and a possible origin of zipf’s law for word frequencies. Entropy 2020, 22, 224. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Liu, H. A diachronic study of Chinese word length distribution. Glottometrics 2014, 29, 81–94. [Google Scholar]
- Sigurd, B.; Eeg-Olofsson, M.; Van de Weijer, J. Word length, sentence length and frequency—Zipf revisited. Stud. Linguist. 2004, 58, 37–52. [Google Scholar] [CrossRef]
- Grzybek, P. Word Length. In The Oxford Handbook of the Word; Taylor, J.R., Ed.; Oxford Academic: Oxford, UK, 2015. [Google Scholar]
- Torre, I.G.; Luque, B.; Lacasa, L.; Kello, C.T.; Hernández-Fernández, A. On the physical origin of linguistic laws and lognormality in speech. R. Soc. Open Sci. 2019, 6, 191023. [Google Scholar] [CrossRef] [PubMed]
- Rosen, K.M. Analysis of speech segment duration with the lognormal distribution: A basis for unification and comparison. J. Phon. 2005, 33, 411–426. [Google Scholar] [CrossRef]
- Kosmidis, K.; Kalampokis, A.; Argyrakis, P. Language time series analysis. Phys. A Stat. Mech. Its Appl. 2006, 370, 808–816. [Google Scholar] [CrossRef]
- University of Virginia. Famous Presidential Speeches of the United States. Available online: https://millercenter.org/the-presidency/presidential-speeches (accessed on 1 January 2022).
- Inaugural Addresses of the Presidents of the United States. Available online: https://www.bartleby.com/124/ (accessed on 25 July 2021).
- British Political Speech; Swansea University: Swansea, UK. Available online: http://britishpoliticalspeech.org/index.htm (accessed on 25 July 2021).
- UK Parliament 2023. Hansard. Available online: https://hansard.parliament.uk/ (accessed on 1 January 2022).
- Montemurro, M.A.; Pury, P.A. Long-range fractal correlations in literary corpora. Fractals 2002, 10, 451–461. [Google Scholar] [CrossRef]
- Grzybek, P. History and Methodology of Word Length Studies: The State of the Art; Springer: Dordrecht, The Netherlands, 2007; pp. 15–90. [Google Scholar]
- Tsizhmovska, N.L. Word Length in Public Speaking; Ural Federal University: Yekaterinburg, Russia, 2023; Available online: https://github.com/Kototiapa/Word-Length-in-Public-Speaking (accessed on 1 January 2022).
- Sobkowicz, P.; Thelwall, M.; Buckley, K.; Paltoglou, G.; Sobkowicz, A. Lognormal distributions of user post lengths in Internet discussions—A consequence of the Weber-Fechner law? EPJ Data Sci. 2013, 2, 1–20. [Google Scholar] [CrossRef]

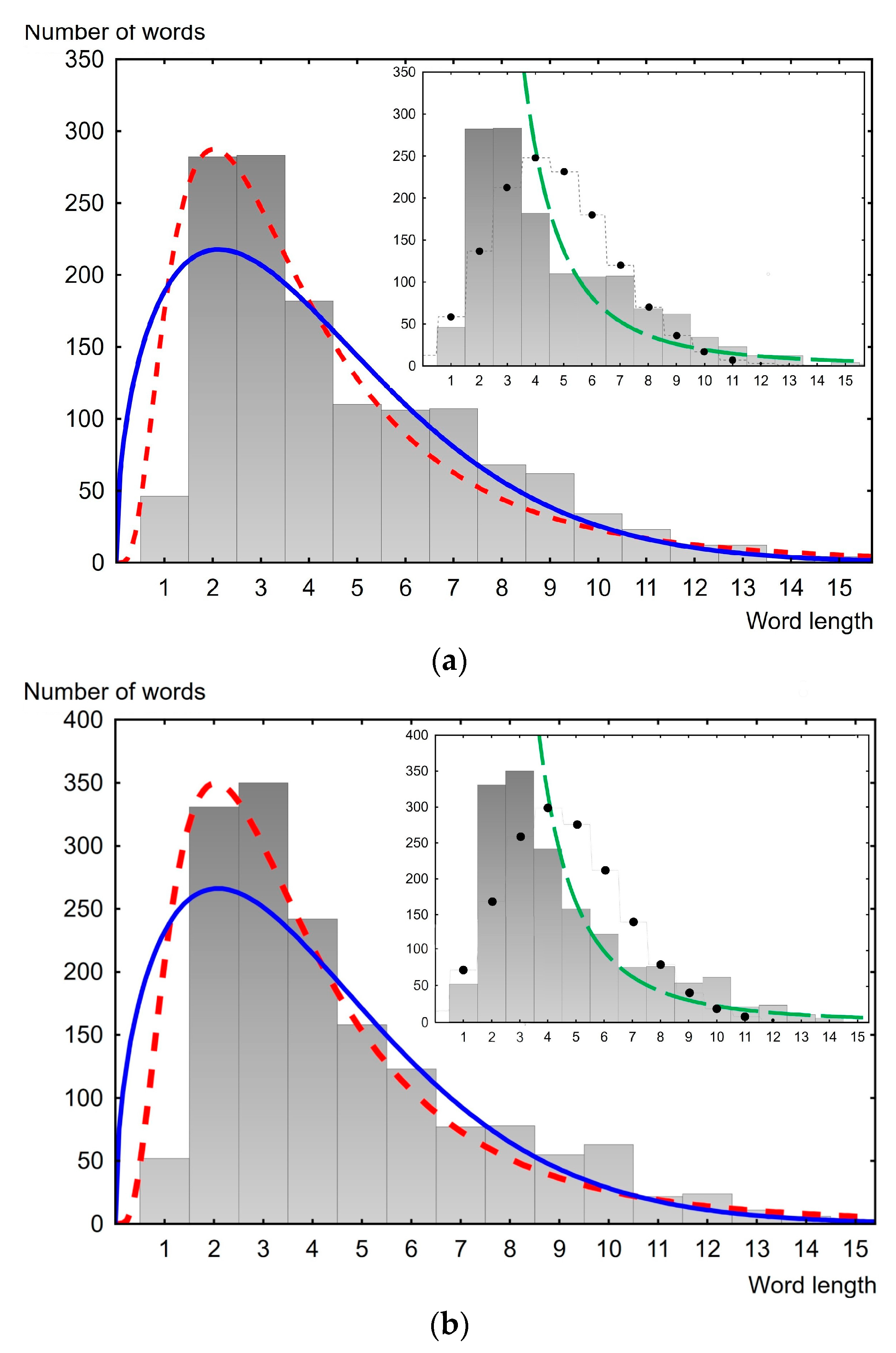
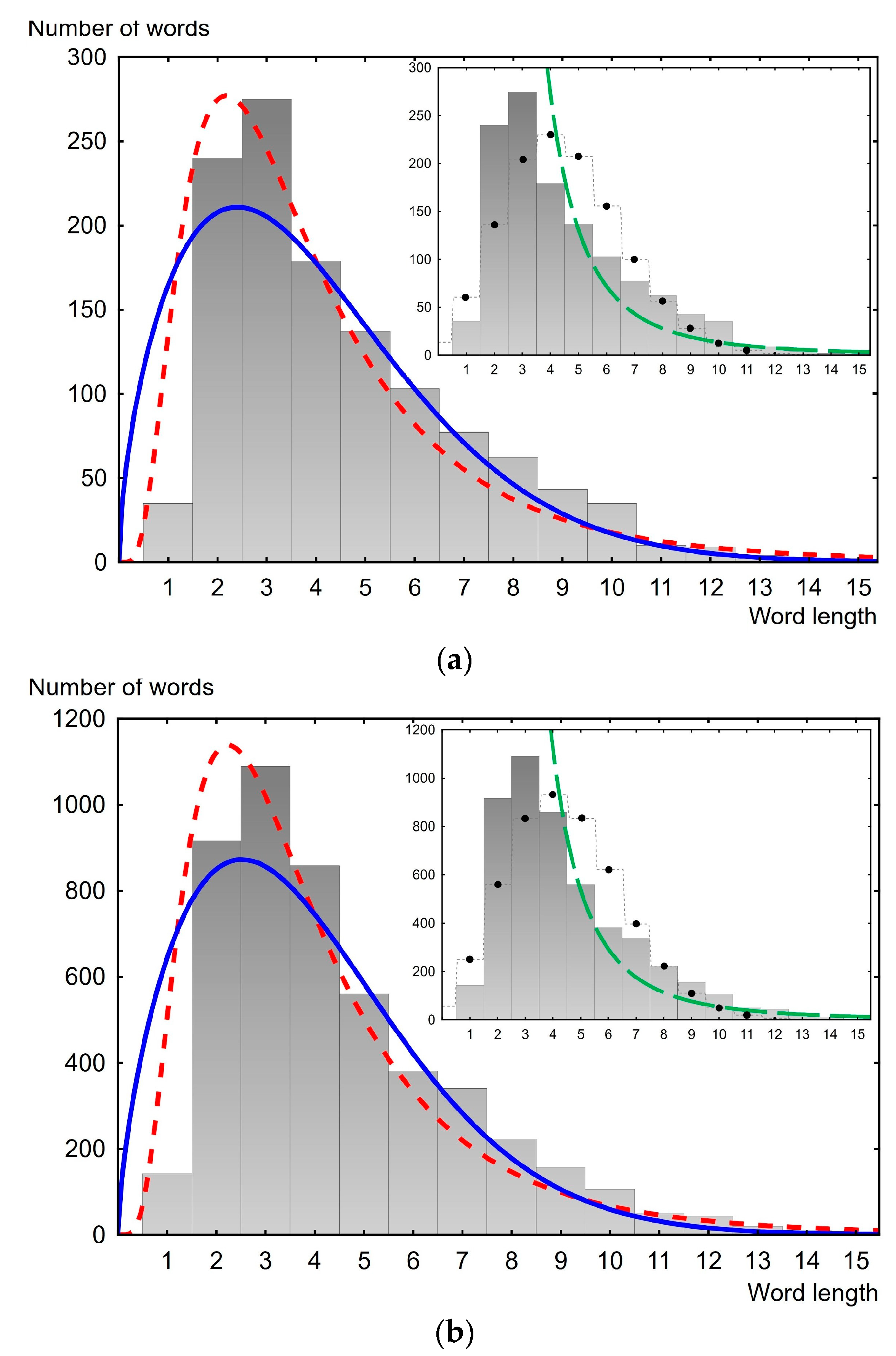

| Place | Lognormal | Weibull | Folded Normal | Rayleigh | Half Normal |
|---|---|---|---|---|---|
| 1 | 58 | 24 | 0 | 0 | 0 |
| 2 | 24 | 58 | 0 | 0 | 0 |
| 3 | 0 | 0 | 67 | 15 | 0 |
| 4 | 0 | 0 | 15 | 9 | 58 |
| 5 | 0 | 0 | 0 | 14 | 68 |
| 6 | 0 | 0 | 0 | 44 | 38 |
| Place | Lognormal | Weibull | Folded Normal | Rayleigh | Half Normal |
|---|---|---|---|---|---|
| 1 | 230 | 15 | 0 | 0 | 0 |
| 2 | 14 | 230 | 1 | 0 | 0 |
| 3 | 0 | 0 | 145 | 99 | 1 |
| 4 | 0 | 0 | 99 | 83 | 63 |
| 5 | 0 | 0 | 0 | 37 | 208 |
| 6 | 1 | 0 | 0 | 26 | 218 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsizhmovska, N.L.; Martyushev, L.M. Word Length in Political Public Speaking: Distribution and Time Evolution. Entropy 2024, 26, 180. https://doi.org/10.3390/e26030180
Tsizhmovska NL, Martyushev LM. Word Length in Political Public Speaking: Distribution and Time Evolution. Entropy. 2024; 26(3):180. https://doi.org/10.3390/e26030180
Chicago/Turabian StyleTsizhmovska, Natalia L., and Leonid M. Martyushev. 2024. "Word Length in Political Public Speaking: Distribution and Time Evolution" Entropy 26, no. 3: 180. https://doi.org/10.3390/e26030180
APA StyleTsizhmovska, N. L., & Martyushev, L. M. (2024). Word Length in Political Public Speaking: Distribution and Time Evolution. Entropy, 26(3), 180. https://doi.org/10.3390/e26030180






