Fault Diagnosis Method for Space Fluid Loop Systems Based on Improved Evidence Theory
Abstract
1. Introduction
2. Preliminaries
3. Materials and Methods
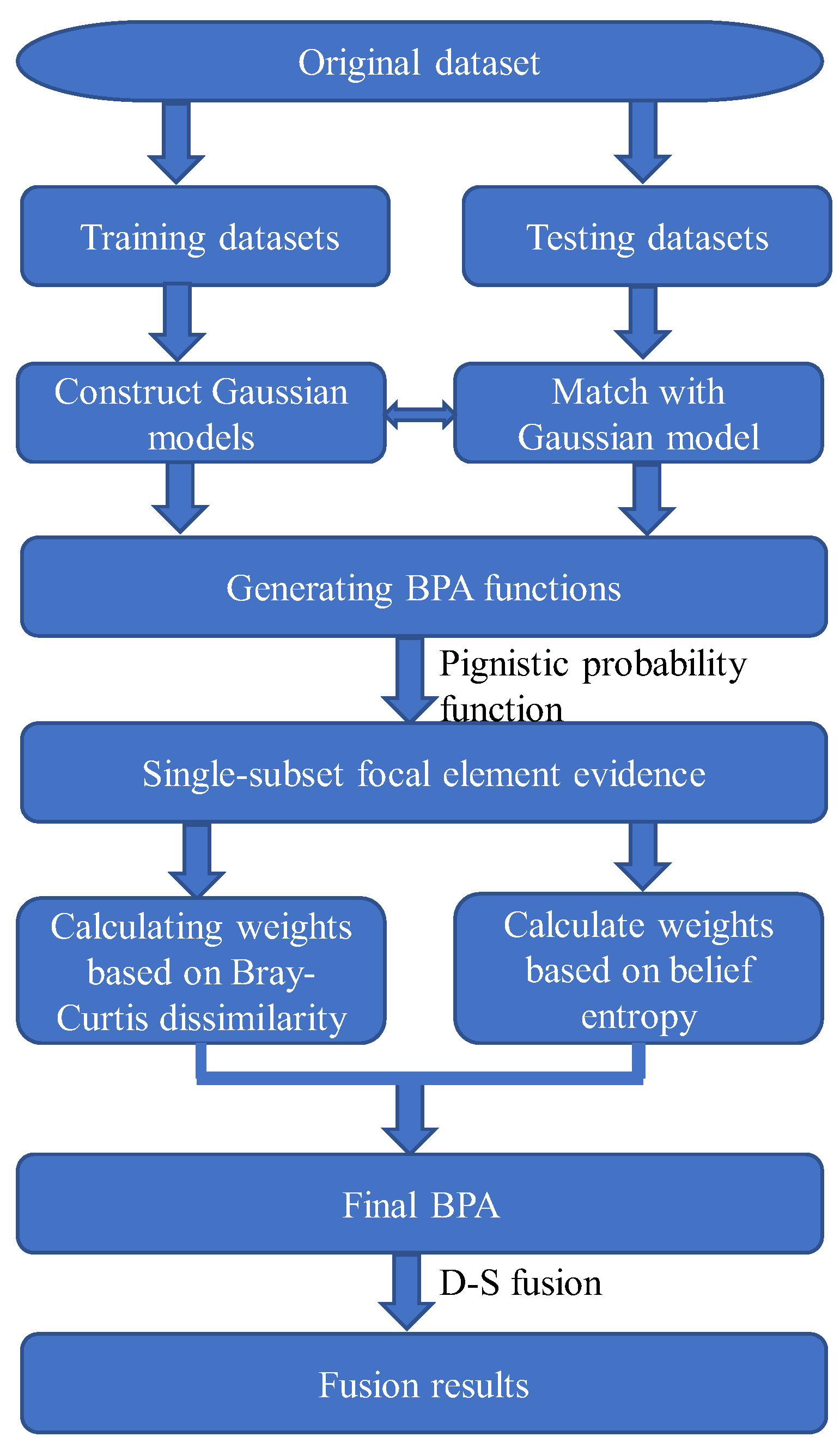
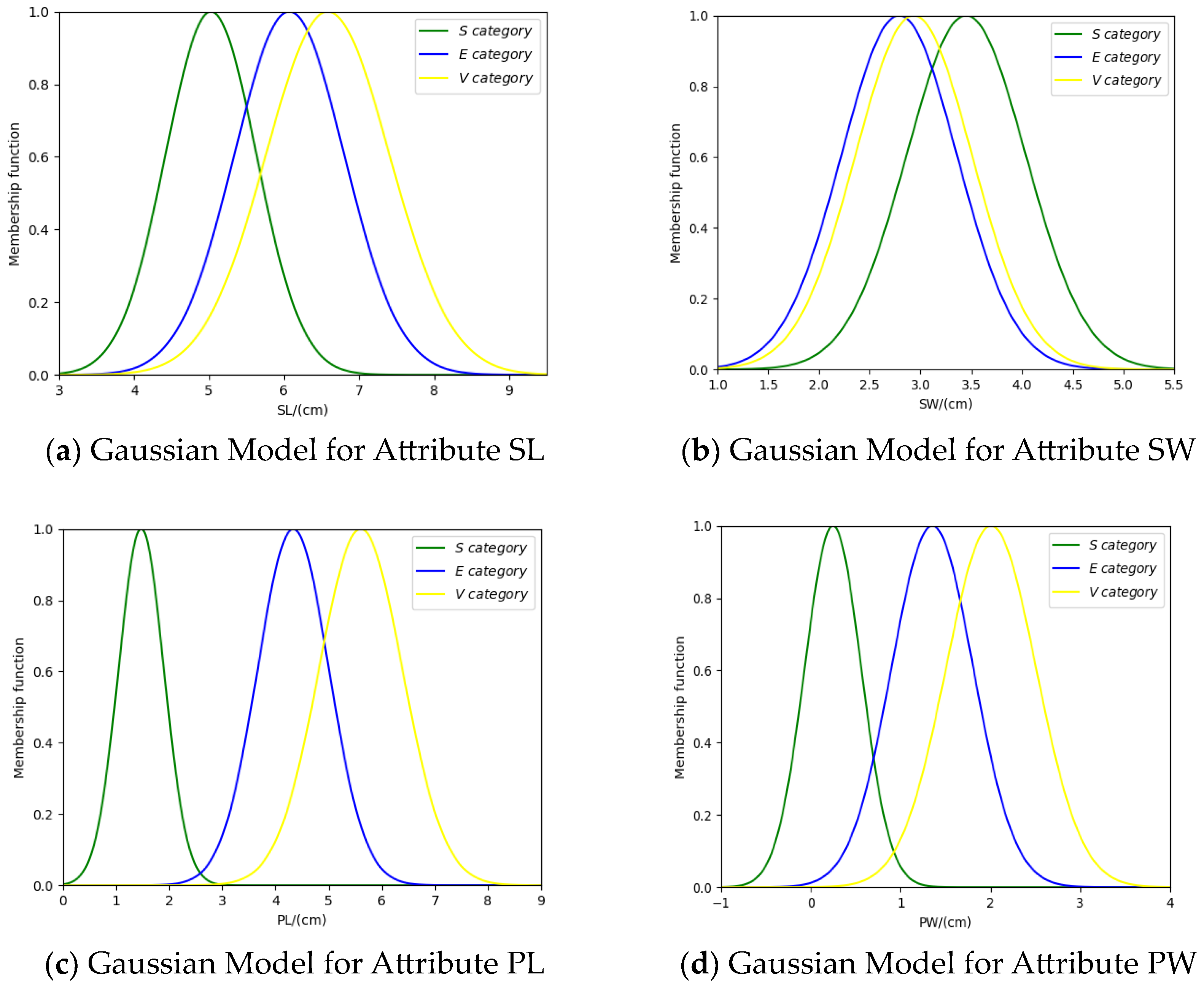
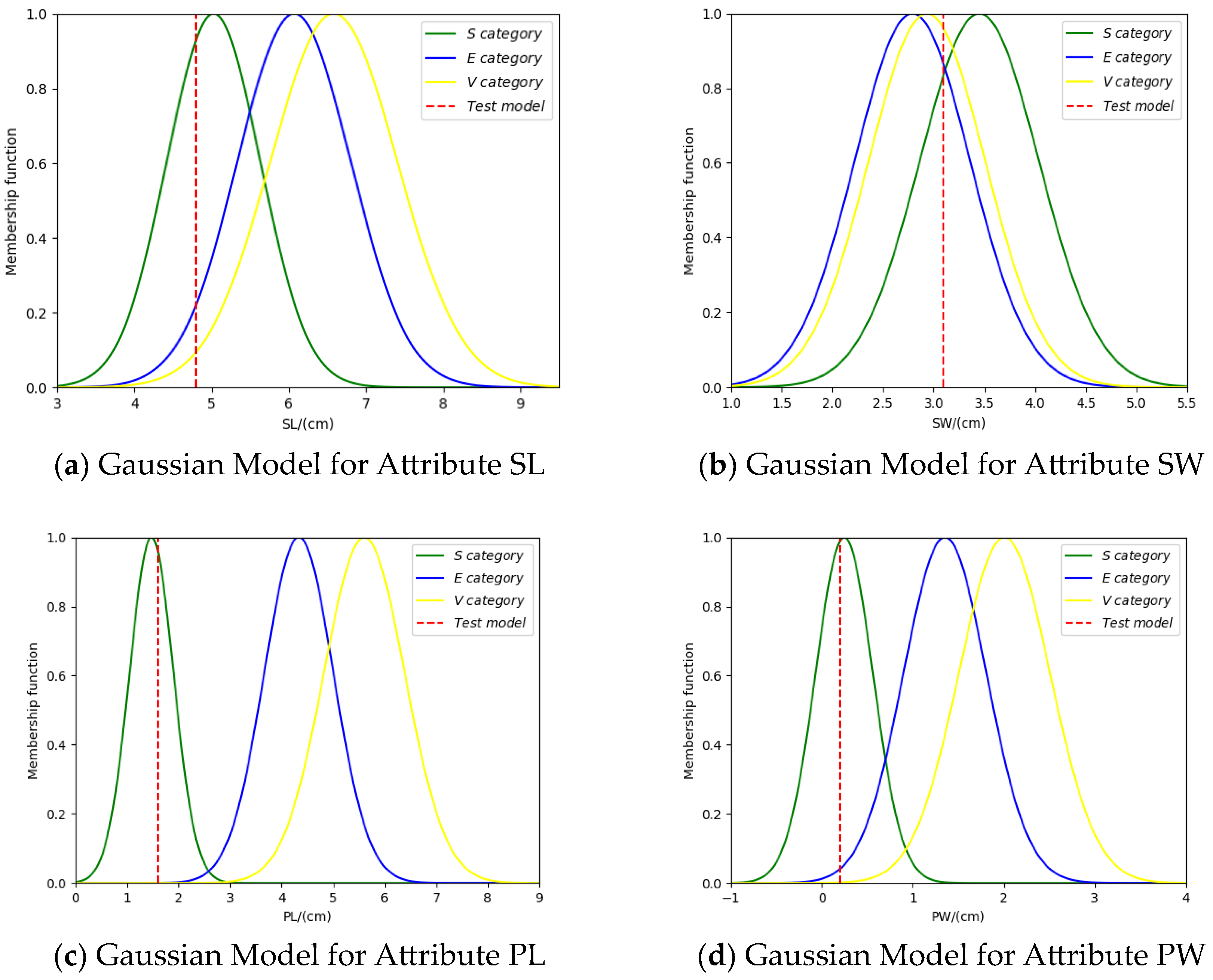
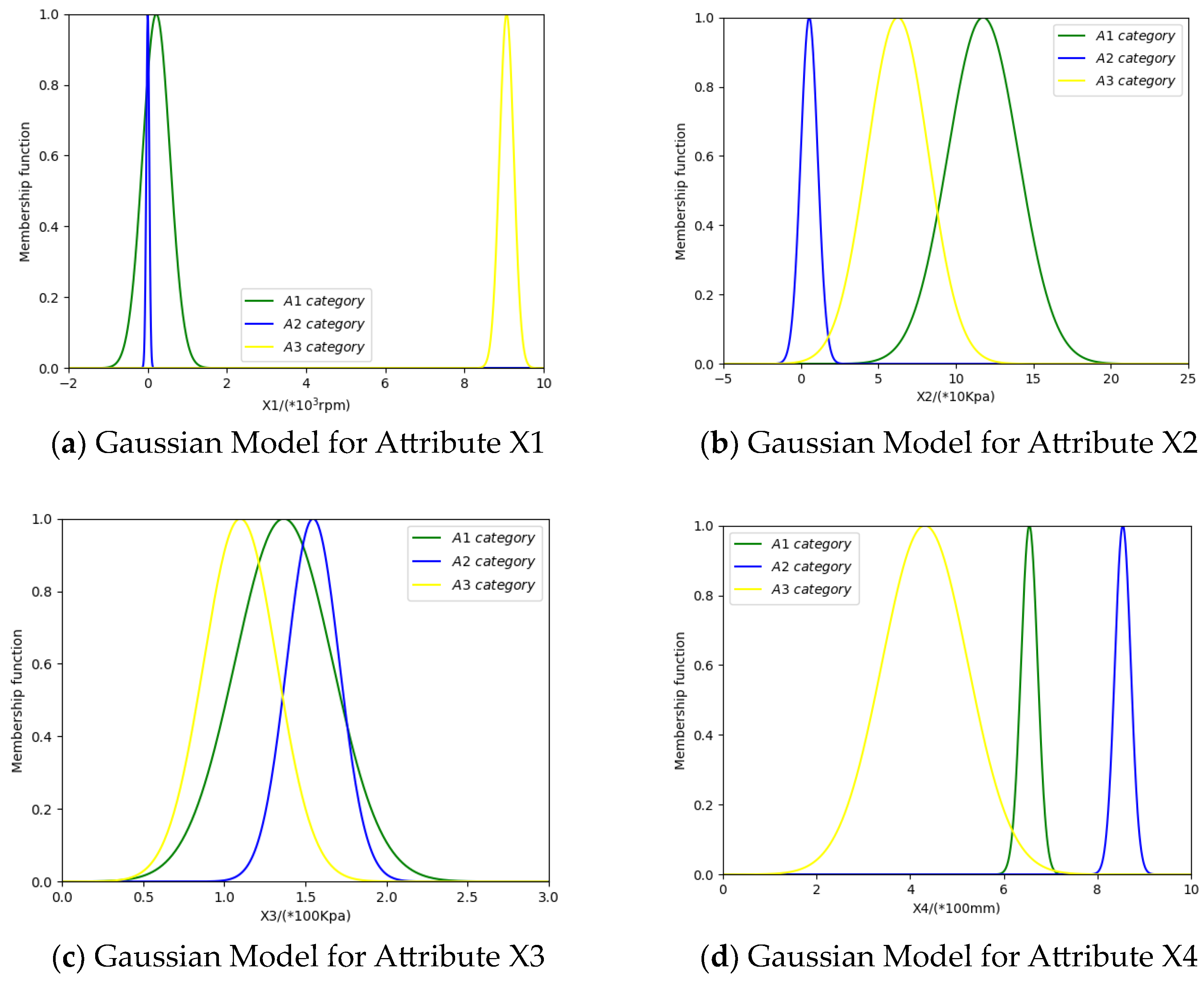
3.1. Method for BPA Generation Based on Gaussian Affiliation Function
3.2. Pignistic Probability Function
3.3. Weight Determination Based on Credibility and Uncertainty
3.3.1. Evidence Similarity Based on the Bray–Curtis Dissimilarity
3.3.2. Evidence Uncertainty Based on Entropy
3.3.3. Evidence Fusion Based on the Dempster Rule
3.4. The Proposed Fault Diagnosis Method
4. Experiments
4.1. Iris Data Set Classification
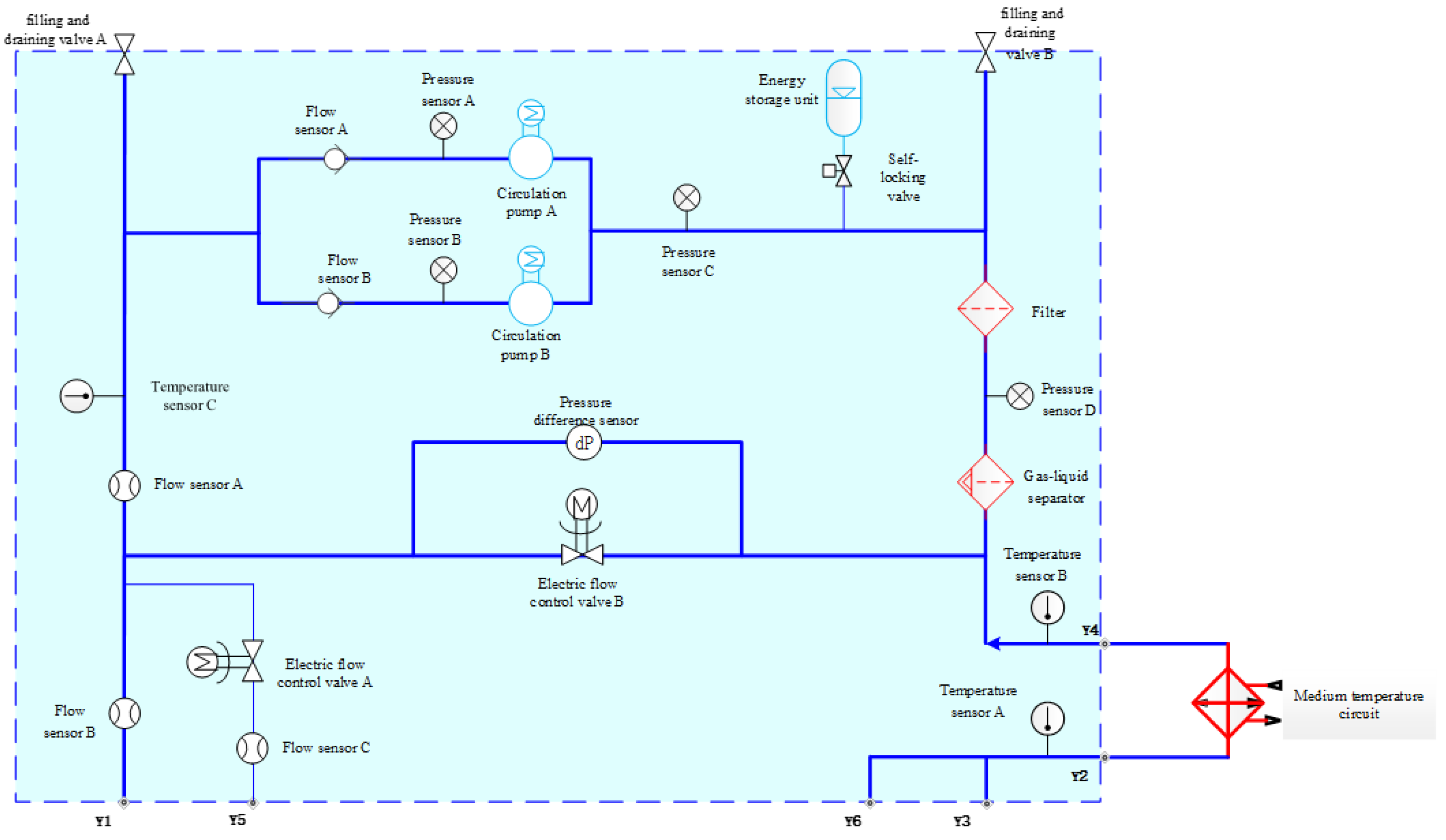
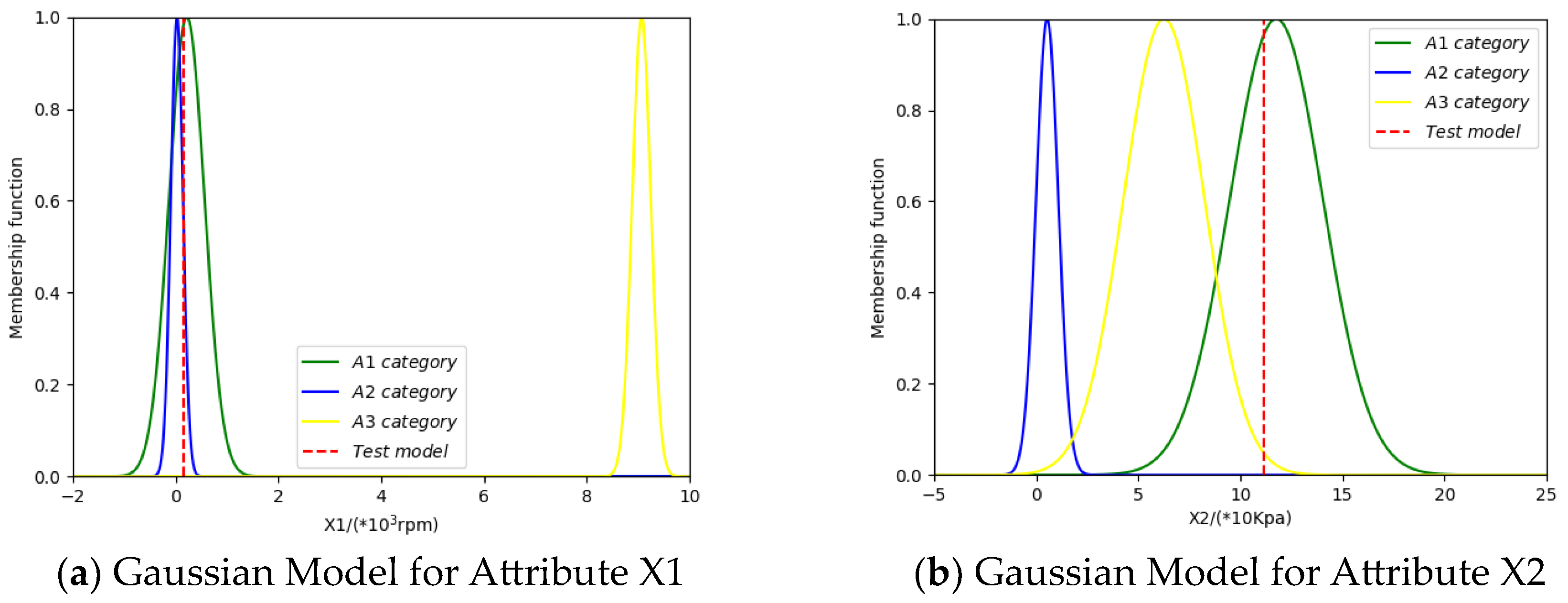
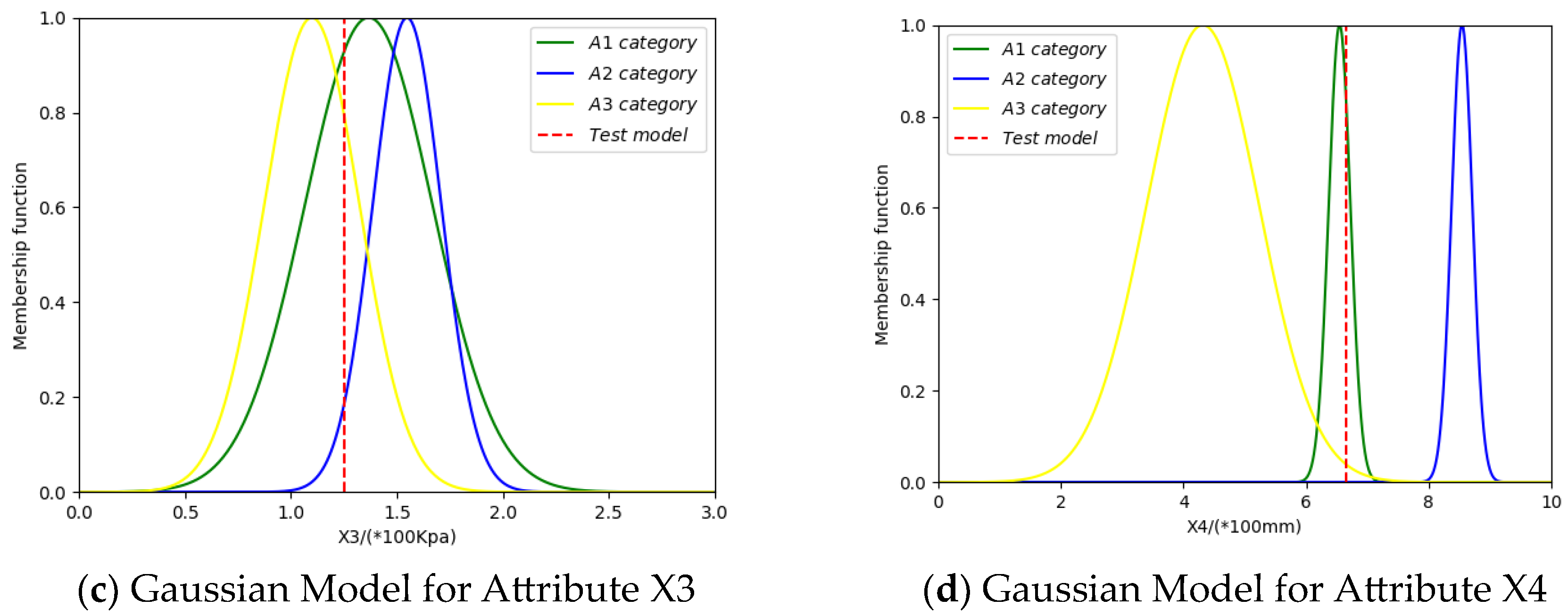
4.2. Application in Fault Diagnosis of Fluid Circuit Loop Pumps
5. Conclusions
- (1)
- Addressing the ambiguity of sensor signals in the practical working environment of spatially applied fluid circuit loop pumps by introducing Gaussian models to determine BPA functions for each attribute. This enables the quantitative representation of sensor signals and facilitates more accurate fault identification through the conversion of multi-subset focal element evidence to single-subset focal element evidence using the pignistic probability function.
- (2)
- Proposing a conflict evidence fusion method based on Bray–Curtis dissimilarity and belief entropy for handling conflicting evidence in D-S evidence theory. This method integrates the assessment of evidence similarity and information content to determine evidence credibility and uncertainty, respectively. Weighting correction coefficients for evidence are then determined based on this comprehensive assessment, leading to the final fault diagnosis using D-S evidence theory.
- (3)
- The fault diagnosis method for space fluid circuit loop pumps based on the improved D-S evidence theory effectively addresses the ambiguity of sensor signals and the conflict after signal interference in the equipment environment, thus aligning well with the actual operating conditions of spatially applied fluid circuit loop pumps and demonstrating strong robustness.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, F.; Wu, S.; Zheng, W.; Yuan, Y.; Tian, Q.; Fan, P.; Wu, M.; Zhang, T.; Yu, L.; Wang, J. Research and Development of Cell Culture Devices Aboard the Chinese Space Station. Microgravity Sci. Technol. 2023, 36, 1. [Google Scholar] [CrossRef]
- Rojas-Alva, U.; Jomaas, G. A historical overview of experimental solid combustion research in microgravity. Acta Astronaut. 2022, 194, 363–375. [Google Scholar] [CrossRef]
- Liu, Q.; Liu, R. Influence of high-frequency vibration on the Rayleigh–Marangoni instability in a two-layer system. Phys. Fluids 2011, 23, 034105. [Google Scholar] [CrossRef]
- Liu, C.J.; Yang, X.; Mao, Y.; Zhang, X.X.; Wu, X.T.; Wang, S.H.; Fan, Y.B.; Sun, W.E. The alteration of advanced glycation end products and its potential role on bone loss under microgravity. Acta Astronaut. 2023, 206, 114–122. [Google Scholar] [CrossRef]
- Xue, T.; Liang, D.; Pang, W.; Shen, D.; Niamat, A.; Liu, J.; Zhou, J. Ignition and combustion of metal fuels under microgravity: A short review. FirePhysChem 2022, 2, 340–356. [Google Scholar] [CrossRef]
- Liu, L.J.; Fan, Y.B.; Wang, S.H.; Wu, X.T.; Yang, X.; Sun, L.W. Enhanced osteogenic potential of periosteal stem cells maintained cortical bone relatively stable under microgravity. Acta Astronaut. 2023, 205, 163–171. [Google Scholar] [CrossRef]
- Cao, Z.; Zhang, J.; Li, Z.; Zhao, X.; Guo, D.; Fu, H. Study on Prognostics and Health Management of Fluid Loop System for Space Application. J. Phys. Conf. Ser. 2022, 2184, 012059. [Google Scholar] [CrossRef]
- Sasiadek, J.Z. Sensor fusion. Annu. Rev. Control. 2002, 26, 203–228. [Google Scholar] [CrossRef]
- Fan, X.; Zuo, M.J. Fault diagnosis of machines based on D–S evidence theory. Part 1: D–S evidence theory and its improvement. Pattern Recognit. Lett. 2006, 27, 366–376. [Google Scholar] [CrossRef]
- Castanedo, F. A review of data fusion techniques. Sci. World J. 2013, 2013, 704504. [Google Scholar] [CrossRef]
- Kashinath, S.A.; Mostafa, S.A.; Mustapha, A.; Mahdin, H.; Lim, D.; Mahmoud, M.A.; Mohammed, M.A.; Al-Rimy, B.A.S.; Fudzee, M.F.M.; Yang, T. Review of data fusion methods for real-time and multi-sensor traffic flow analysis. IEEE Access 2021, 9, 51258–51276. [Google Scholar] [CrossRef]
- Meng, T.; Jing, X.; Yan, Z.; Pedrycz, W. A survey on machine learning for data fusion. Inf. Fusion 2020, 57, 115–129. [Google Scholar] [CrossRef]
- Yeong, D.J.; Velasco-Hernandez, G.; Barry, J.; Walsh, J. Sensor and sensor fusion technology in autonomous vehicles: A review. Sensors 2021, 21, 2140. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.F.; Wang, H.; Sun, M. ChatGPT-like large-scale foundation models for prognostics and health management: A survey and roadmaps. Reliab. Eng. Syst. Saf. 2023, 243, 109850. [Google Scholar] [CrossRef]
- Gu, Y.; Zhang, Y.; Yang, M.; Li, C. Motor on-line fault diagnosis method research based on 1D-CNN and multi-sensor information. Appl. Sci. 2023, 13, 4192. [Google Scholar] [CrossRef]
- Wan, S.; Li, T.; Fang, B.; Yan, K.; Hong, J.; Li, X. Bearing Fault Diagnosis Based on Multi-Sensor Information Coupling and Attentional Feature Fusion. IEEE Trans. Instrum. Meas. 2023, 72, 3514412. [Google Scholar] [CrossRef]
- Oukhellou, L.; Debiolles, A.; Denœux, T.; Aknin, P. Fault diagnosis in railway track circuits using Dempster–Shafer classifier fusion. Eng. Appl. Artif. Intell. 2010, 23, 117–128. [Google Scholar] [CrossRef]
- Chen, L.; Diao, L.; Sang, J. Weighted evidence combination rule based on evidence distance and uncertainty measure: An application in fault diagnosis. Math. Probl. Eng. 2018, 2018, 5858272. [Google Scholar] [CrossRef]
- Jiang, W.; Hu, W.; Xie, C. A new engine fault diagnosis method based on multi-sensor data fusion. Applied Sciences 2017, 7, 280. [Google Scholar] [CrossRef]
- Jiang, W.; Xie, C.; Zhuang, M.; Shou, Y.; Tang, Y. Sensor data fusion with z-numbers and its application in fault diagnosis. Sensors 2016, 16, 1509. [Google Scholar] [CrossRef]
- Liu, J.; Chen, A.; Zhao, N. An intelligent fault diagnosis method for bogie bearings of metro vehicles based on weighted improved DS evidence theory. Energies 2018, 11, 232. [Google Scholar] [CrossRef]
- Jiang, D.; Wang, Z. Research on mechanical equipment fault diagnosis method based on deep learning and information fusion. Sensors 2023, 23, 6999. [Google Scholar] [CrossRef] [PubMed]
- Huo, Z.; Martinez-Garcia, M.; Zhang, Y.; Shu, L. A multisensor information fusion method for high-reliability fault diagnosis of rotating machinery. IEEE Trans. Instrum. Meas. 2021, 71, 3500412. [Google Scholar] [CrossRef]
- Ghosh, N.; Saha, S.; Paul, R. iDCR: Improved Dempster Combination Rule for multisensor fault diagnosis. Eng. Appl. Artif. Intell. 2021, 104, 104369. [Google Scholar] [CrossRef]
- Jia, R.S.; Liu, C.; Sun, H.M.; Yan, X.H. A situation assessment method for rock burst based on multi-agent information fusion. Comput. Electr. Eng. 2015, 45, 22–32. [Google Scholar] [CrossRef]
- Liu, Z.G.; Pan, Q.; Dezert, J.; Martin, A. Adaptive imputation of missing values for incomplete pattern classification. Pattern Recognit. 2016, 52, 85–95. [Google Scholar] [CrossRef]
- Khan, M.N.; Anwar, S. Paradox elimination in Dempster–Shafer combination rule with novel entropy function: Application in decision-level multi-sensor fusion. Sensors 2019, 19, 4810. [Google Scholar] [CrossRef] [PubMed]
- Belmahdi, F.; Lazri, M.; Ouallouche, F.; Labadi, K.; Absi, R.; Ameur, S. Application of Dempster-Shafer theory for optimization of precipitation classification and estimation results from remote sensing data using machine learning. Remote Sens. Appl. Soc. Environ. 2023, 29, 100906. [Google Scholar] [CrossRef]
- Hamid, R.A.; Albahri, A.S.; Albahri, O.S.; Zaidan, A.A. Dempster–Shafer theory for classification and hybridised models of multi-criteria decision analysis for prioritisation: A telemedicine framework for patients with heart diseases. J. Ambient. Intell. Humaniz. Comput. 2022, 13, 4333–4367. [Google Scholar] [CrossRef]
- Zadeh, L.A. Review of a mathematical theory of evidence. AI Mag. 1984, 5, 81. [Google Scholar]
- Murphy, C.K. Combining belief functions when evidence conflicts. Decis. Support Syst. 2000, 29, 1–9. [Google Scholar] [CrossRef]
- Yong, D.; Shi, W.; Zhu, Z.; Liu, Q. Combining belief functions based on distance of evidence. Decis. Support Syst. 2004, 38, 489–493. [Google Scholar] [CrossRef]
- Lin, Y.; Wang, C.; Ma, C.; Dou, Z.; Ma, X. A new combination method for multisensor conflict information. J. Supercomput. 2016, 72, 2874–2890. [Google Scholar] [CrossRef]
- Liu, Y.; Zou, T.; Fu, H. A Conflict Evidence Fusion Method Based on Bray–Curtis Dissimilarity and the Belief Entropy. Symmetry 2024, 16, 75. [Google Scholar] [CrossRef]
- Fei, L.; Xia, J.; Feng, Y.; Liu, L. A novel method to determine basic probability assignment in Dempster–Shafer theory and its application in multi-sensor information fusion. Int. J. Distrib. Sens. Netw. 2019, 15, 1550147719865876. [Google Scholar] [CrossRef]
- Numbers, U.F. Determination of Basic Belief Assignment Using Fuzzy Numbers. Adv. Appl. DSmT Inf. Fusion 2023, 623, 1–6. [Google Scholar]
- Xu, P.; Deng, Y.; Su, X.; Mahadevan, S. A new method to determine basic probability assignment from training data. Knowl. Based Syst. 2013, 46, 69–80. [Google Scholar] [CrossRef]
- Fu, W.; Yu, S.; Wang, X. A novel method to determine basic probability assignment based on AdaBoost and its application in classification. Entropy 2021, 23, 812. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Qinghai, Y. Target recognition method based on BP neural networks and improved DS evidence theory. Comput. Appl. Softw. 2018, 35, 151–156. [Google Scholar]
- Dempster, A.P. Upper and Lower Probabilities Induce by a Multiplicand Mapping. Ann. Math. Stat. 1967, 38, 325–339. [Google Scholar] [CrossRef]
- Glenn, S. A Mathematical Theory of Evidence; Princeton University Press: Princeton, NJ, USA, 1976; Volume 42. [Google Scholar]
- Pal, N.R.; Bezdek, J.C.; Hemasinha, R. Uncertainty measures for evidential reasoning I: A review. Int. J. Approx. Reason. 1992, 7, 165–183. [Google Scholar] [CrossRef]
- George, T.; Pal, N.R. Quantification of conflict in Dempster-Shafer framework: A new approach. Int. J. Gen. Syst. 1996, 24, 407–423. [Google Scholar] [CrossRef]
- Barnard, G.A. Statistical inference. J. R. Stat. Society. Ser. B (Methodol.) 1949, 11, 115–149. [Google Scholar] [CrossRef]
- Smets, P.; Kennes, R. The transferable belief model. Class. Work. Dempster-Shafer Theory Belief Funct. 2008, 219, 693–736. [Google Scholar]
- Bray, J.R.; Curtis, J.T. An ordination of the upland forest communities of southern Wisconsin. Ecol. Monogr. 1957, 27, 326–349. [Google Scholar] [CrossRef]
- Ricotta, C.; Podani, J. On some properties of the Bray-Curtis dissimilarity and their ecological meaning. Ecol. Complex. 2017, 31, 201–205. [Google Scholar] [CrossRef]
- Ricotta, C.; Pavoine, S. A new parametric measure of functional dissimilarity: Bridging the gap between the Bray-Curtis dissimilarity and the Euclidean distance. Ecol. Model. 2022, 466, 109880. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. ACM Sigmobile Mob. Comput. Commun. Rev. 2001, 5, 3–55. [Google Scholar] [CrossRef]
- Deng, Y. Deng Entropy: A Generalized Shannon Entropy to Measure Uncertainty. Available online: https://fs.unm.edu/DengEntropyAGeneralized.pdf (accessed on 31 January 2015).
- Fisher, R.A. The use of multiple measurements in taxonomic problems. Ann. Eugen. 1936, 7, 179–188. [Google Scholar] [CrossRef]
| Category | ||||
|---|---|---|---|---|
| S | ||||
| E | ||||
| V |
| Category | |||||||
|---|---|---|---|---|---|---|---|
| 0.9320 | 0.0000 | 0.0000 | 0.2219 | 0.0000 | 0.0000 | 0.0950 | |
| 0.0000 | 0.0000 | 0.9606 | 0.0000 | 0.0000 | 0.8596 | 0.8391 | |
| 0.9569 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0003 | |
| 0.9887 | 0.0000 | 0.0000 | 0.0412 | 0.0000 | 0.0000 | 0.0003 |
| Category | |||
|---|---|---|---|
| 0.8601 | 0.1145 | 0.0254 | |
| 0.1052 | 0.2668 | 0.6280 | |
| 0.9998 | 0.0001 | 0.0001 | |
| 0.9798 | 0.0201 | 0.0001 |
| Fusion Results | |||
|---|---|---|---|
| 0.9938 | 0.0030 | 0.0032 | |
| 0.9996 | 0.0002 | 0.0002 | |
| 1.0000 | 0.0000 | 0.0000 |
| Project Name | Fault Mode | Fault Diagnosis Method | Telemetry Available for Fault Diagnosis |
|---|---|---|---|
| Space Application Fluid Circuit Loop Pump | (Circulation Pump speed reduction) | Decrease in Circulation Pump Speed, decrease in Internal Pressure Circulation pump | A rotational speed value, Pressure sensor A pressure value, Pressure sensor C pressure value, Energy storage tank gauge value |
(Circulation Pump Shutdown) | Gradual decrease in circulation pump speed to zero, decrease in internal pressure | ||
(Circulation Pump Leakage) | Decrease in circulation pump speed, decrease in internal pressure, decrease in system flow rate |
| Category | |||||||
|---|---|---|---|---|---|---|---|
| 0.978 | 0.0000 | 0.0000 | 0.538 | 0.0000 | 0.0000 | 0.0000 | |
| 0.972 | 0.0000 | 0.0000 | 0.0000 | 0.052 | 0.0000 | 0.0000 | |
| 0.932 | 0.0000 | 0.0000 | 0.0000 | 0.783 | 0.0000 | 0.1928 | |
| 0.845 | 0.0000 | 0.0000 | 0.0000 | 0.0395 | 0.0000 | 0.0015 |
| Category | |||
|---|---|---|---|
| 0.8226 | 0.1774 | 0.0000 | |
| 0.9746 | 0.0000 | 0.0254 | |
| 0.7274 | 0.0337 | 0.2389 | |
| 0.9766 | 0.0006 | 0.0228 |
| Fusion Results | |||
|---|---|---|---|
| 0.9989 | 0.0001 | 0.0010 | |
| 0.9999 | 0.0000 | 0.0001 | |
| 1.0000 | 0.0000 | 0.0000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Li, Z.; Zhang, L.; Fu, H. Fault Diagnosis Method for Space Fluid Loop Systems Based on Improved Evidence Theory. Entropy 2024, 26, 427. https://doi.org/10.3390/e26050427
Liu Y, Li Z, Zhang L, Fu H. Fault Diagnosis Method for Space Fluid Loop Systems Based on Improved Evidence Theory. Entropy. 2024; 26(5):427. https://doi.org/10.3390/e26050427
Chicago/Turabian StyleLiu, Yue, Zhenxiang Li, Lu Zhang, and Hongyong Fu. 2024. "Fault Diagnosis Method for Space Fluid Loop Systems Based on Improved Evidence Theory" Entropy 26, no. 5: 427. https://doi.org/10.3390/e26050427
APA StyleLiu, Y., Li, Z., Zhang, L., & Fu, H. (2024). Fault Diagnosis Method for Space Fluid Loop Systems Based on Improved Evidence Theory. Entropy, 26(5), 427. https://doi.org/10.3390/e26050427





