Entropy Production in Reaction–Diffusion Systems Confined in Narrow Channels
Abstract
:1. Introduction
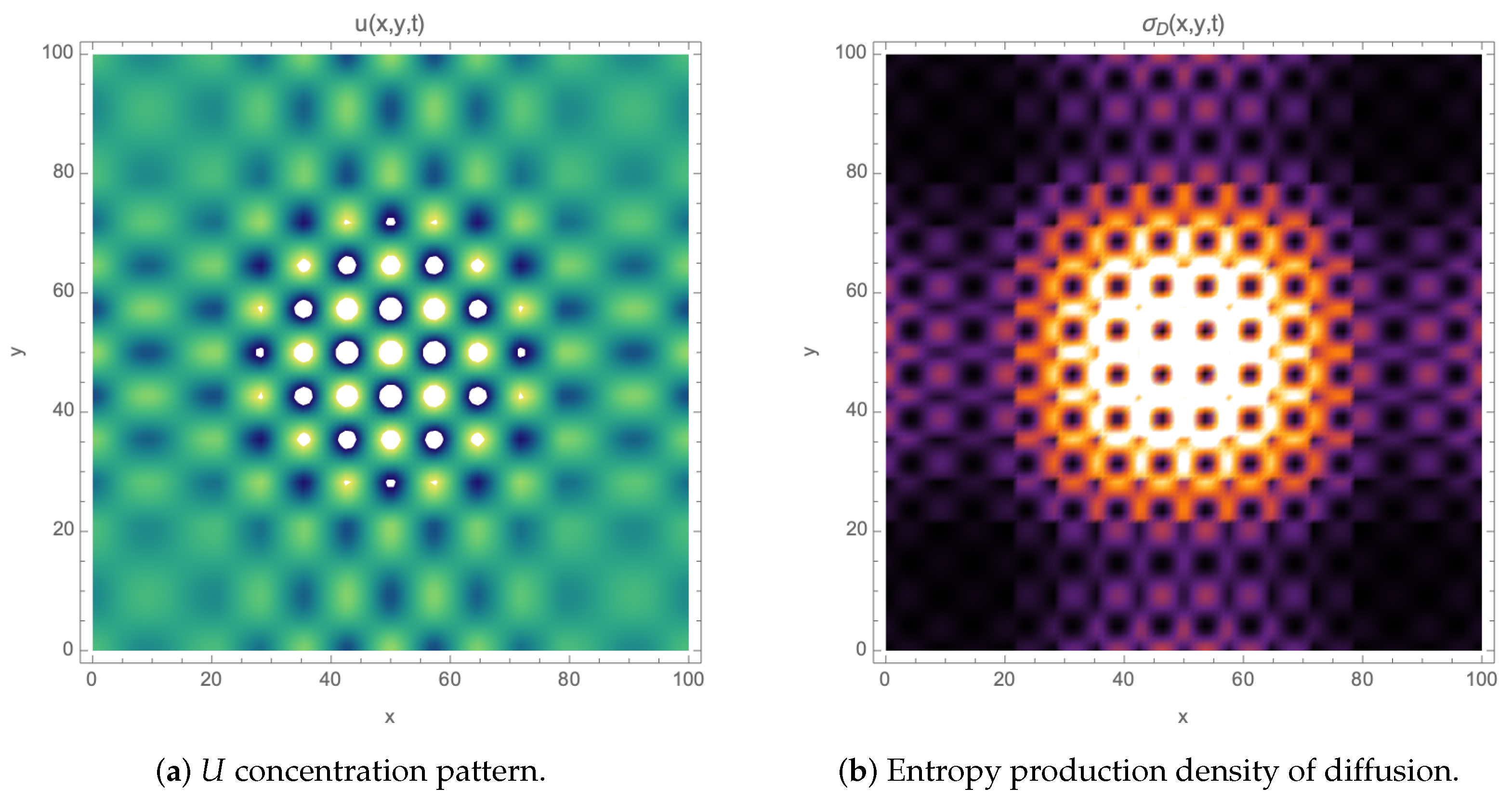
2. Entropy Production in 2D Reaction–Diffusion Systems
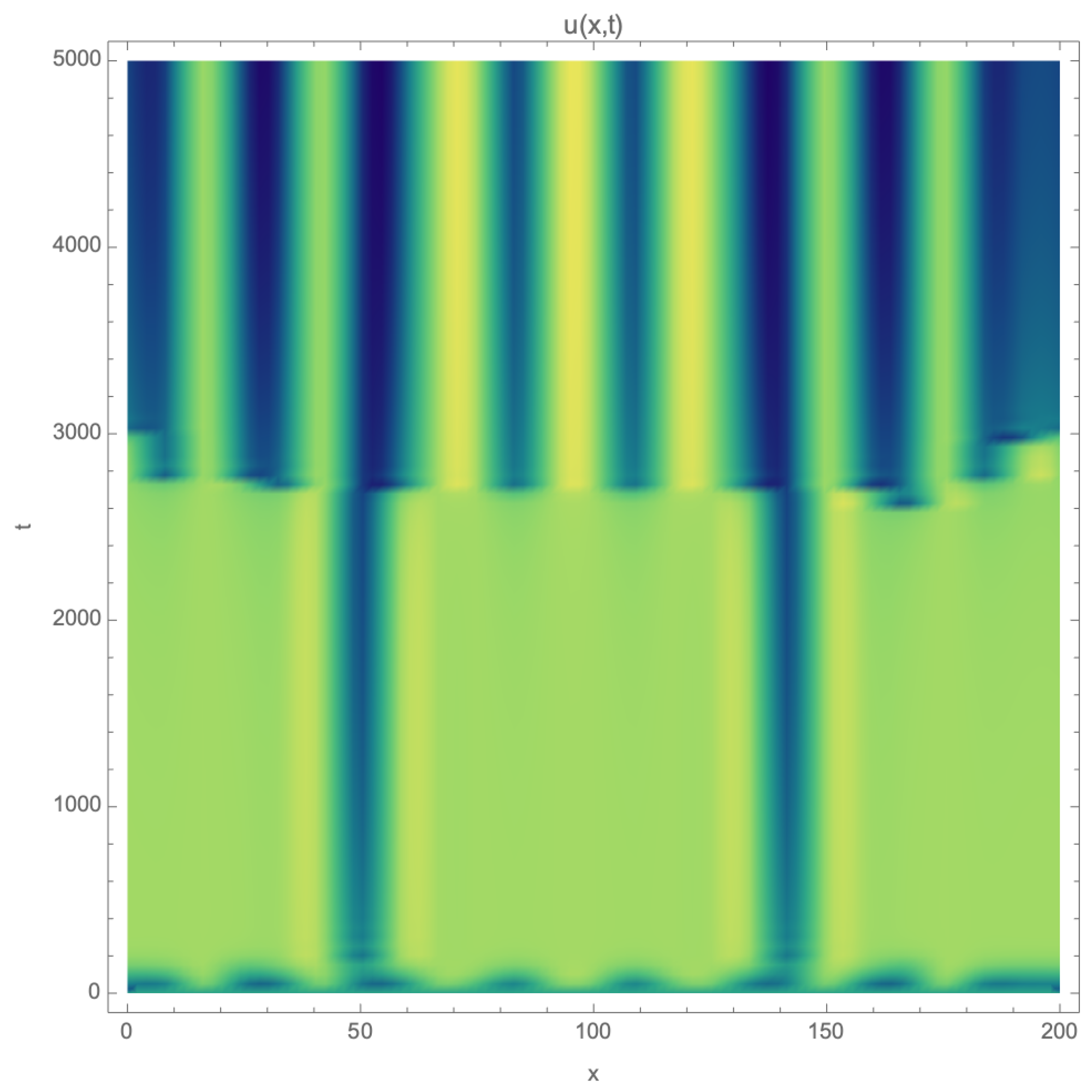
3. Pattern Formation in Reaction–Diffusion on Narrow Channels
4. Effect of Channel Geometry on Entropy Production
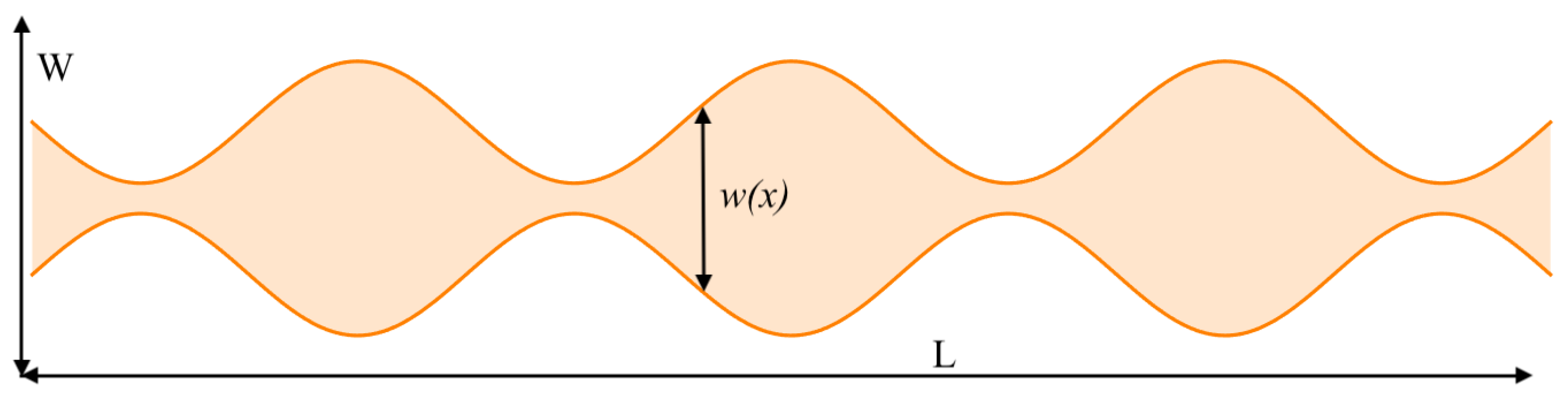
4.1. Fick–Jacobs Approximation for Reaction–Diffusion Equations and Entropy Production
4.2. Effective Diffusion Coefficient in Terms of Availability, Tortuosity, and Constriction
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Turing, A.M. The chemical basis of morphogenesis. Philos. Trans. R. Soc. Lond. Ser. B 1952, 237, 37. [Google Scholar]
- Murray, J.D.L. Mathematical Biology II: Spatial Models and Biomedical Applications, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Mahara, H.; Suematsu, N.J.; Yamaguchi, T.; Ohgane, K.; Nishiura, Y.; Shimomura, M. Three-variable reversible Gray–Scott model. J. Chem. Phys. 2004, 121, 8968. [Google Scholar] [CrossRef] [PubMed]
- Glansdorff, P.; Prigogine, I. Thermodynamic Theory of Structure, Stability and Fluctuations; Wiley: New York, NY, USA, 1971. [Google Scholar]
- Nicolis, G.; Prigogine, I. Self-Organization in Non-Equilibrium System; Wiley: New York, NY, USA, 1977. [Google Scholar]
- Kondepudi, D. Introduction to Modern Thermodynamics; John Wiley & Sons, Ltd.: Chichester, UK, 1998. [Google Scholar]
- Hanson, M.P. Spatial structures in dissipative systems. J. Chem. Phys. 1974, 60, 3210. [Google Scholar] [CrossRef]
- Irvin, B.R.; Ross, J. Calculation of the rate of entropy production for a model chemical reaction. J. Chem. Phys. 1988, 89, 1064. [Google Scholar] [CrossRef]
- Kagan, E. Turing Systems, Entropy, and Kinetic Models for Self-Healing Surfaces. Entropy 2010, 12, 554–569. [Google Scholar] [CrossRef]
- López-Agudelo, V.A.; Barragán, D. Entropy production in oscillatory processes during photosynthesis. Photochem. Photobiol. Sci. 2014, 13, 23–31. [Google Scholar] [CrossRef] [PubMed]
- Gray, P.; Scott, S.K. Chemical Oscillations and Instabilities, Nonlinear Chemical Kinetics; Clarendon: Oxford, UK, 1990. [Google Scholar]
- Gray, P.; Scott, S.K. Autocatalytic reactions in the isothermal, continuous stirred tank reactor: Isolas and other forms of multistability. Chem. Eng. Sci. 1983, 38, 29–43. [Google Scholar] [CrossRef]
- Escher, C.; Ross, J. Multiranges of flow rate with bistability and limit cycles for Schlögl’s mechanism in a CSTR. J. Chem. Phys. 1983, 79, 3773. [Google Scholar] [CrossRef]
- Yoshida, N. Entropy production in a chemical system involving an autocatalytic reaction in an isothermal, continuous stirred tank reactor. J. Chem. Phys. 1990, 92, 2593. [Google Scholar] [CrossRef]
- Mahara, H.; Susuki, K.; Jahan, R.A.; Yamaguchi, T. Coexisting stable patterns in a reaction-diffusion system with reversible Gray–Scott dynamics. Phys. Rev. E 2008, 78, 066210. [Google Scholar] [CrossRef] [PubMed]
- Kalantarova, J.; Uğrlu, D. Structural stability and stabilization of solutions of the reversible three-component Gray-Scott system. Math. Meth. Appl. Sci. 2019, 42, 3687–3699. [Google Scholar] [CrossRef]
- Mahara, H.; Yamaguchi, T.; Shimomura, M. Entropy production in a two-dimensional reversible Gray-Scott system. Chaos 2005, 15, 047508. [Google Scholar] [CrossRef] [PubMed]
- Mahara, H.; Yamaguchi, T. Entropy balance in distributed reversible Gray–Scott model. Phys. D 2010, 239, 729–734. [Google Scholar] [CrossRef]
- Mahara, H.; Yamaguchi, T. Calculation of the Entropy Balance Equation in a Non-equilibrium Reaction-Diffusion System. Entropy 2010, 12, 2436–2449. [Google Scholar] [CrossRef]
- Huang, W.-L.; Li, J. Compromise between minimization and maximization of entropy production in reversible Gray–Scott model. Chem. Eng. Sci. 2016, 155, 233–238. [Google Scholar] [CrossRef]
- Serna, H.; Muñuzuri, A.P.; Barragán, D. Thermodynamic and morphological characterization of Turing patterns in non-isothermal reaction–diffusion systems. Phys. Chem. Chem. Phys. 2017, 19, 14401. [Google Scholar] [CrossRef] [PubMed]
- Silva-Dias, L.; Lopez-Castillo, A. Turing patterns modulation by chemical gradient in isothermal and non-isothermal conditions. Phys. Chem. Chem. Phys. 2020, 22, 7507. [Google Scholar] [CrossRef]
- Mátyás, L.; Gaspard, P. Entropy production in diffusion-reaction systems: The reactive random Lorentz gas. Phys. Rev. E 2005, 71, 036147. [Google Scholar] [CrossRef]
- Serdyukov, S. Macroscopic Entropy of Non-Equilibrium Systems and Postulates of Extended Thermodynamics: Application to Transport Phenomena and Chemical Reactions in Nanoparticles. Entropy 2018, 20, 802. [Google Scholar] [CrossRef]
- Berezhkovskii, A.; Hummer, G. Single-File Transport of Water Molecules through a Carbon Nanotube. Phys. Rev. Lett. 2002, 89, 064503. [Google Scholar] [CrossRef]
- Chester, A.W.; Derouane, E.G. Zeolite Characterization and Catalysis; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Keyser, U.; Koeleman, B.; Dorp, S.V.; Krapf, D.; Smeets, R.; Lemay, S.; Dekker, N.; Dekker, C. Direct force measurements on DNA in a solid-state nanopore. Nat. Phys. 2006, 2, 473–477. [Google Scholar] [CrossRef]
- Hille, B. Ion Channels of Excitable Membranes, 3rd ed.; Sinauer Associates, Inc.: Sunderland, MA, USA, 2001. [Google Scholar]
- Gouaux, E.; MacKinnon, R. Principles of selective ion transport in channels and pumps. Science 2005, 310, 1461. [Google Scholar] [CrossRef] [PubMed]
- Malgaretti, P.; IPagonabarraga, I.; Rubí, J.M. Entropic Electrokinetics: Recirculation, Particle Separation, and Negative Mobility. Phys. Rev. Lett. 2014, 113, 128301. [Google Scholar] [CrossRef]
- Hänggi, P.; Marchesoni, F. Artificial Brownian motors: Controlling transport on the nanoscale. Rev. Mod. Phys. 2009, 81, 387–442. [Google Scholar] [CrossRef]
- Malgaretti, P.; Pagonabarraga, I.; Rubí, J.M. Confined brownian ratchets. Front. Phys. 2013, 68, 1–21. [Google Scholar] [CrossRef]
- Dagdug, L.; Peña, J.; Pompa-García, I. Diffusion under Confinement. A Journey through Counterintuition; Springer Nature: Cham, Switzerland, 2024. [Google Scholar]
- Zwanzig, R. Diffusion Past an Entropy Barrier. J. Phys. Chem. 1992, 96, 3926–3930. [Google Scholar] [CrossRef]
- Reguera, D.; Rubi, J.M. Kinetic equations for diffusion in the presence of entropic barriers. Phys. Rev. E 2001, 64, 061106. [Google Scholar] [CrossRef] [PubMed]
- Kalinay, P.; Percus, J.K. Projection of two-dimensional diffusion in a narrow channel onto the longitudinal dimension. J. Chem. Phys. 2005, 122, 204701. [Google Scholar] [CrossRef] [PubMed]
- Kalinay, P.; Percus, J.K. Corrections to the Fick-Jacobs equation. Phys. Rev. E 2006, 74, 041203. [Google Scholar] [CrossRef] [PubMed]
- Bradley, R.M. Diffusion in a two-dimensional channel with curved midline and varying width: Reduction to an effective one-dimensional description. Phys. Rev. E 2009, 80, 061142. [Google Scholar] [CrossRef] [PubMed]
- Berezhkovskii, A.M.; Szabo, A. Time scale separation leads to position-dependent diffusion along a slow coordinate. J. Chem. Phys. 2011, 135, 074108. [Google Scholar] [CrossRef] [PubMed]
- Dagdug, L.; Pineda, I. Projection of two-dimensional diffusion in a curved midline and narrow varying width channel onto the longitudinal dimension. J. Chem. Phys. 2012, 137, 024107. [Google Scholar] [CrossRef] [PubMed]
- Ogawa, N. Diffusion in a curved tube. Phys. Lett. A 2013, 377, 2465. [Google Scholar] [CrossRef]
- Dagdug, L.; García-Chung, A.A.; Chacón-Acosta, G. On the description of Brownian particles in confinement on a non-Cartesian coordinates basis. J. Chem. Phys. 2016, 145, 074105. [Google Scholar] [CrossRef] [PubMed]
- Chávez, Y.; Chacón-Acosta, G.; Dagdug, L. Unbiased diffusion of Brownian particles in a helical tube. J. Chem. Phys. 2018, 148, 214106. [Google Scholar] [CrossRef] [PubMed]
- Chacón-Acosta, G.; Pineda, I.; Dagdug, L. Diffusion in narrow channels on curved manifolds. J. Chem. Phys. 2013, 139. [Google Scholar] [CrossRef] [PubMed]
- Pineda, I.; Chacón-Acosta, G.; Dagdug, L. Diffusion coefficients for two-dimensional narrow asymmetric channels embedded on flat and curved surfaces. Eur. Phys. J. Spec. Top. 2014, 223, 3045. [Google Scholar] [CrossRef]
- Ledesma-Durán, A.; León-Velasco, D.A.; Chacón-Acosta, G.; Juárez-Valencia, L.H. Surface diffusion in narrow channels on curved domains. Phys. Rev. E 2023, 107, 034801. [Google Scholar] [CrossRef]
- Ledesma-Durán, A.; Hernéz-Hernéz, S.I.; Santamaría-Holek, I. Generalized Fick-Jacobs Approach for Describing Adsorption-Desorption Kinetics in Irregular Pores under Nonequilibrium Conditions. J. Phys. Chem. C 2016, 120, 7810. [Google Scholar] [CrossRef]
- Chacón-Acosta, G.; Núñez-López, M.; Pineda, I. Turing instability conditions in confined systems with an effective position-dependent diffusion-coefficient. J. Chem. Phys. 2020, 152, 024101. [Google Scholar] [CrossRef]
- Núñez-López, M.; Chacón-Acosta, G. Pattern formation in a predator-prey system with finite interaction range in a channel-like region using the Fick-Jacobs diffusion approach. Phys. D 2022, 433, 133194. [Google Scholar] [CrossRef]
- Chacón-Acosta, G.; León-Ramírez, A.; González-Gaxiola, O. Biharmonic Fick–Jacobs diffusion in narrow channels. Phys. A 2023, 628, 129155. [Google Scholar] [CrossRef]
- Carusela, M.F.; Rubi, J.M. Entropy production and rectifcation efficiency in colloid transport along a pulsating channel. J. Phys. Condens. Matter 2018, 30, 244001. [Google Scholar] [CrossRef] [PubMed]
- Burada, P.S.; Hänggi, P.; Marchesoni, F.; Schmid, G.; Talkner, P. Diffusion in Confined Geometries. ChemPhysChem 2009, 10, 45–54. [Google Scholar] [CrossRef] [PubMed]
- Lifson, S.; Jackson, J.L. On the Self-Diffusion of Ions in a Polyelectrolyte Solution. J. Chem. Phys. 1962, 36, 2410. [Google Scholar] [CrossRef]
- Ledesma-Durán, A.; Hernández, S.I.; Santamaría-Holek, I. Relation between the porosity and tortuosity of a membrane formed by disconnected irregular pores and the spatial diffusion coefficient of the Fick-Jacobs model. Phys. Rev. E 2017, 95, 052804. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chacón-Acosta, G.; Núñez-López, M. Entropy Production in Reaction–Diffusion Systems Confined in Narrow Channels. Entropy 2024, 26, 463. https://doi.org/10.3390/e26060463
Chacón-Acosta G, Núñez-López M. Entropy Production in Reaction–Diffusion Systems Confined in Narrow Channels. Entropy. 2024; 26(6):463. https://doi.org/10.3390/e26060463
Chicago/Turabian StyleChacón-Acosta, Guillermo, and Mayra Núñez-López. 2024. "Entropy Production in Reaction–Diffusion Systems Confined in Narrow Channels" Entropy 26, no. 6: 463. https://doi.org/10.3390/e26060463




