Design of a Robust Synchronization-Based Topology Observer for Complex Delayed Networks with Fixed and Adaptive Coupling Strength
Abstract
:1. Introduction
2. Problem Formulation
2.1. Model Description
2.2. Topology Identification Based on Synchronization
3. Main Results
3.1. Complex Delayed Networks with Fixed Coupling Strength
3.2. Complex Delayed Networks with Adaptive Coupling Strength
4. Illustrative Examples
4.1. Identification Topology of Complex Networks with Fixed Coupling Strength
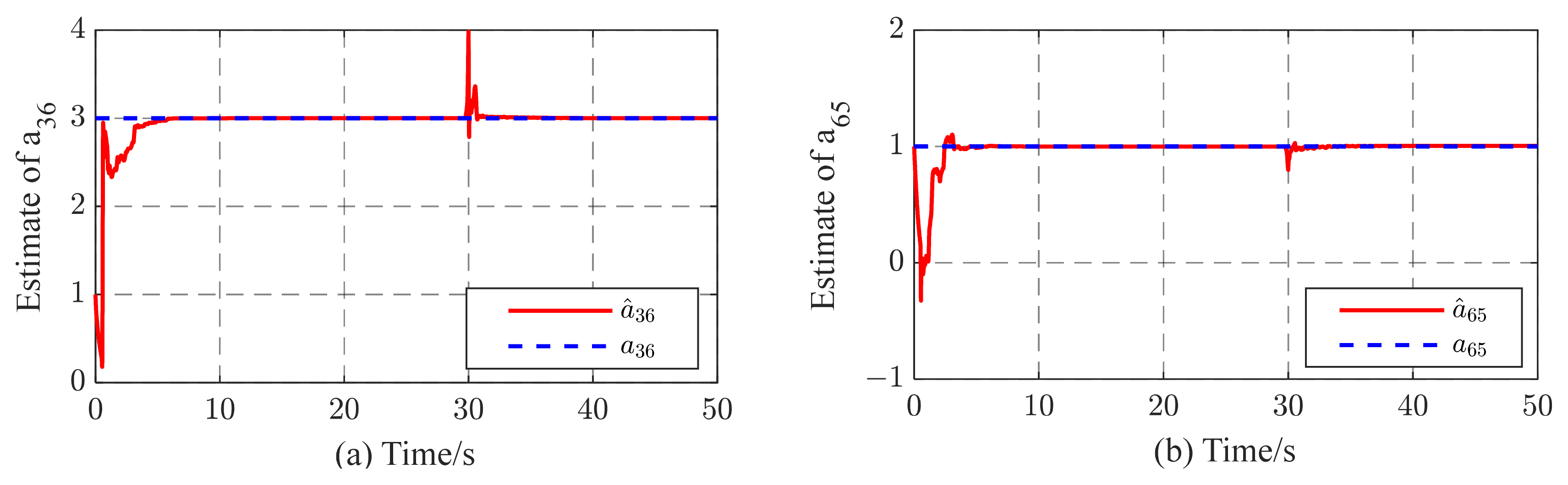
4.1.1. The Effectiveness of the Proposed STO
4.1.2. Comparison with Other Methods
- (i)
- Performance indices
- Minimum identification time (): the time needed for successful identification when decreases to a specific value . In this study, we adopt a value of .
- The integral of the identification error () is calculated as follows:where
- The final error result of the identification topology is given by the steady-state error ():
- (ii)
- Identification results
4.2. Identification Topology of Complex Networks with Adaptive Coupling Strength
4.3. Robustness Test for Topology Identification
4.3.1. Complex Networks with Fixed Coupling Strength
- Case 1: robustness to parameter variation
- Case 2: robustness to external disturbances
4.3.2. Complex Networks with Adaptive Coupling Strength
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Albert, R.; Barabasi, A.L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 26, 1–54. [Google Scholar] [CrossRef]
- Ping, L.; Lam, J. Synchronization in networks of genetic oscillators with delayed coupling. Asian J. Control 2011, 13, 713–725. [Google Scholar]
- Gu, H.; Liu, K.; Zhu, G.; Lü, J. Leader-following consensus of stochastic dynamical multi-agent systems with fixed and switching topologies under proportional-integral protocols. Asian J. Control 2023, 25, 662–676. [Google Scholar] [CrossRef]
- Huang, W.; Liu, T.; Liu, H.; Huang, Y.; Chen, S. Robust consensus of heterogeneous multiagent systems with switching topologies: A time-delay case. Asian J. Control 2023, 25, 1336–1349. [Google Scholar] [CrossRef]
- Baruch, I.S.; Quintana, V.A.; Reynaud, E.P. Complex-valued neural network topology and learning applied for identification and control of nonlinear systems. Neurocomputing 2017, 233, 104–115. [Google Scholar] [CrossRef]
- Kazemy, A. Synchronization analysis of complex dynamical networks with hybrid coupling with application to Chua’s circuit. J. Control 2020, 14, 53–61. [Google Scholar] [CrossRef]
- Dkhichi, F.; Oukarfi, B.; Fakkar, A.; Belbounaguia, N. Parameter identification of solar cell model using Levenberg–Marquardt algorithm combined with simulated annealing. Sol. Energy 2014, 110, 781–788. [Google Scholar] [CrossRef]
- Peng, H.; Li, L.; Kurths, J.; Li, S.; Yang, Y. Topology Identification of Complex Network via Chaotic Ant Swarm Algorithm. Math. Probl. Eng. 2013, 2013, 401983. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, B.; Zhou, S. An improved cuckoo search optimization algorithm for the problem of chaotic systems pa-rameter estimation. Comput. Intel. Neurosci. 2016, 25, 2959370. [Google Scholar]
- Tian, Z.; Wu, W.; Zhang, B. A Mixed Integer Quadratic Programming Model for Topology Identification in Distribution Network. IEEE Trans. Power Syst. 2016, 31, 823–824. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, W.; Zang, C.; Liu, L. Multiagent System-Based Integrated Solution for Topology Identification and State Estimation. IEEE Trans. Ind. Inform. 2017, 13, 714–724. [Google Scholar] [CrossRef]
- Wei, Y.; Stanford, R.J. Parameter identification of solid oxide fuel cell by Chaotic Binary Shark Smell Optimization method. Energy 2019, 188, 115770. [Google Scholar] [CrossRef]
- Li, G.; Wu, X.; Liu, J.; Lu, J.-A.; Guo, C. Recovering network topologies via Taylor expansion and compressive sensing. Chaos 2015, 25, 043102. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Li, N.; Liu, S.; Wu, X. Compressive sensing-based topology identification of multilayer networks. Chaos 2019, 29, 053117. [Google Scholar] [CrossRef] [PubMed]
- Babakmehr, M.; Simoes, M.G.; Wakin, M.B.; Harirchi, F. Compressive Sensing-Based Topology Identification for Smart Grids. IEEE Trans. Ind. Inform. 2016, 12, 532–543. [Google Scholar] [CrossRef]
- Jahandari, S.; Materassi, D. Topology Identification of Dynamical Networks via Compressive Sensing. IFAC-PapersOnLine 2018, 51, 575–580. [Google Scholar] [CrossRef]
- Wu, X.; Zhao, X.; Lu, J.; Tang, L.; Lu, J.-A. Identifying topologies of complex dynamical networks with stochastic perturbations. IEEE Trans. Control Netw. Syst. 2017, 3, 379–389. [Google Scholar] [CrossRef]
- Lü, L.; Li, C.; Bai, S.; Li, G.; Rong, T.; Gao, Y.; Yan, Z. Synchronization of uncertain time-varying network based on sliding mode control technique. Physica A 2017, 482, 808–817. [Google Scholar] [CrossRef]
- Behinfaraz, R.; Ghaemi, S.; Khanmohammadi, S.; Badamchizadeh, M.A. Time-varying parameters identification and synchronization of switching complex networks using the adaptive fuzzy-impulsive control with an application to secure communication. Asian J. Control 2022, 24, 377–387. [Google Scholar] [CrossRef]
- Wang, X.; Gu, H.; Wang, Q.; Lü, J. Identifying topologies and system parameters of uncertain time-varying delayed complex networks. Sci. China Technol. Sci. 2019, 62, 94–105. [Google Scholar] [CrossRef]
- Duan, W.; Du, B.; You, J.; Zou, Y. Synchronization criteria for neutral complex dynamic networks with internal time-vary coupling delays. Asian J. Control 2013, 15, 1385–1396. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, J.; Tang, W. Parameters and structure identification of complex delayed networks via pinning control. Trans. Inst. Meas. Control 2013, 35, 619–624. [Google Scholar] [CrossRef]
- Chen, Z.; Yuan, X.; Yuan, Y.; Iu, H.H.-C.; Fernando, T. Parameter identification of chaotic and hyper-chaotic systems using synchronization-based parameter observer. IEEE Trans. Circuits Syst. I Regul. Pap. 2016, 63, 1464–1475. [Google Scholar] [CrossRef]
- Zheng, Y.; Wu, X.; Fan, Z.; Wang, W. Identifying topology and system parameters of fractional-order complex dynamical networks. Appl. Math. Comput. 2022, 414, 126666. [Google Scholar] [CrossRef]
- Xu, Y.; Zhou, W.; Zhang, J.; Sun, W.; Tong, D. Topology identification of complex delayed dynamical networks with multiple response systems. Nonlinear Dyn. 2017, 88, 2969–2981. [Google Scholar] [CrossRef]
- Wang, F.X.; Zhang, J.; Shu, Y.J.; Liu, X.G. Stability analysis for fractional-order neural networks with time-varying delay. Asian J. Control 2023, 25, 1488–1498. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, X.; Duan, P. Observer-based sliding mode control for synchronization of delayed chaotic neural networks with unknown disturbance. Neural Netw. 2019, 117, 268–273. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Li, H.; Li, C.; Li, Z.; Yang, X. Fixed-time synchronization criteria for complex networks via quantized pinning control. ISA Trans. 2019, 91, 151–156. [Google Scholar] [CrossRef] [PubMed]
- Grzybowski, J.; Macau, E.; Yoneyama, T. The Lyapunov–Krasovskii theorem and a sufficient criterion for local stability of isochronal synchronization in networks of delay-coupled oscillators. Physica D 2017, 346, 28–36. [Google Scholar] [CrossRef]
- Liu, X.; Chen, T. Synchronization of Complex Networks via Aperiodically Intermittent Pinning Control. IEEE Trans. Autom. Control 2015, 60, 3316–3321. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, Z.; Lin, C.; Chen, J. Fixed-time synchronization for complex-valued BAM neural networks with time-varying delays via pinning control and adaptive pinning control. Chaos Solitons Fractals 2021, 153, 111583. [Google Scholar] [CrossRef]
- Xiang, L.Y.; Yu, Y.Y.; Zhu, J.W. Moment-based analysis of pinning synchronization in complex networks. Asian J. Control 2022, 24, 669–685. [Google Scholar] [CrossRef]
- Zhu, S.; Zhou, J.; Lu, J.-A. Identifying partial topology of complex dynamical networks via a pinning mechanism. Chaos 2018, 28, 043108. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Zhou, J.; Qu, F.; Song, C.; Zhu, S. Identifying partial topology of complex networks with stochastic perturbations and time delay. Commun. Nonlinear Sci. Numer. Simul. 2022, 115, 106779. [Google Scholar] [CrossRef]
- Yue, C.-X.; Wang, L.; Hu, X.; Tang, H.-A.; Duan, S. Pinning control for passivity and synchronization of coupled memristive reaction–diffusion neural networks with time-varying delay. Neurocomputing 2020, 381, 113–129. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, J.; Zhang, D.; Shao, X. Synchronization and tracking of multi-spacecraft formation attitude control using adaptive sliding mode. Asian J. Control 2019, 21, 832–846. [Google Scholar] [CrossRef]
- Wu, H.Y.; Wang, L.; Zhao, L.H.; Wang, J.L. Topology identification of coupled neural networks with multiple weights. Neurocomputing 2021, 457, 254–264. [Google Scholar] [CrossRef]
- Tan, F.; Zhou, L.; Lu, J.; Chu, Y.; Li, Y. Fixed-time outer synchronization under double-layered multiplex networks with hybrid links and time-varying delays via delayed feedback control. Asian J. Control 2022, 24, 137–148. [Google Scholar] [CrossRef]
- Wu, D.; Zhu, S.; Luo, X.; Wu, L. Effects of adaptive coupling on stochastic resonance of small-world networks. Phys. Rev. E 2011, 84, 021102. [Google Scholar] [CrossRef] [PubMed]
- Huang, D.; Fan, X.; Yu, Z.; Jiang, H. On Multitracking of First-Order MASs with Adaptive Coupling Strength. Discret. Dyn. Nat. Soc. 2020, 2020, 8897487. [Google Scholar] [CrossRef]
- Wu, Y.; Li, Y.; Li, W. Synchronization of random coupling delayed complex networks with random and adaptive coupling strength. Nonlinear Dyn. 2019, 96, 2393–2412. [Google Scholar] [CrossRef]

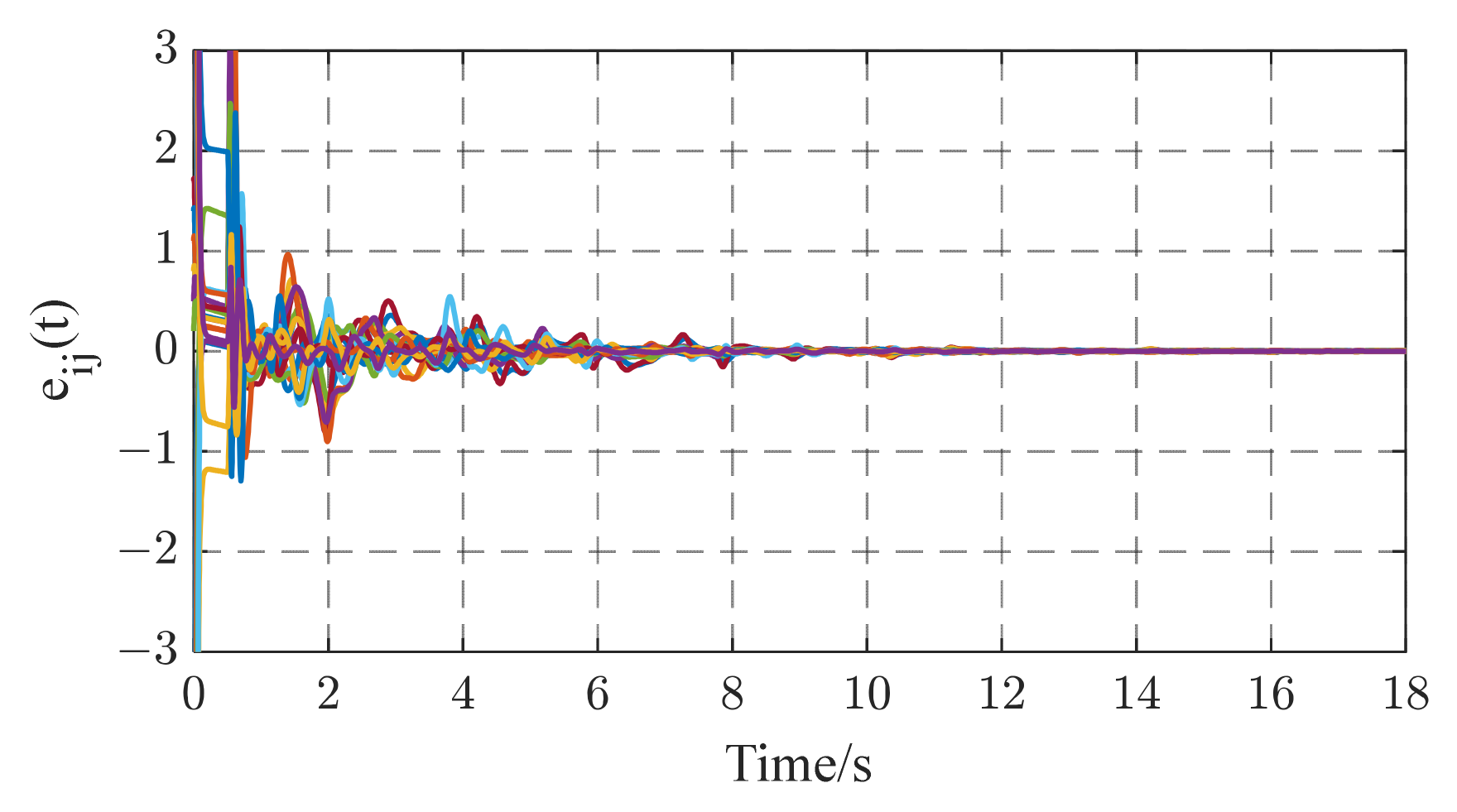

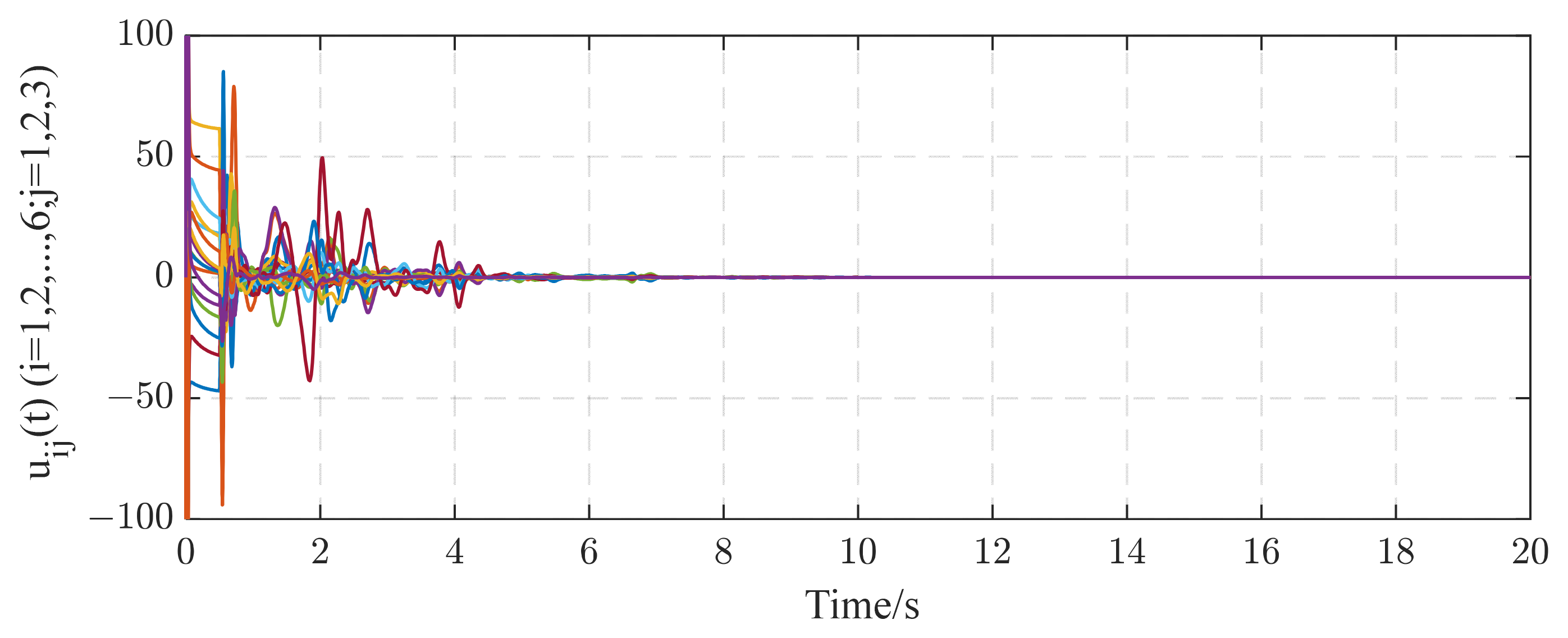


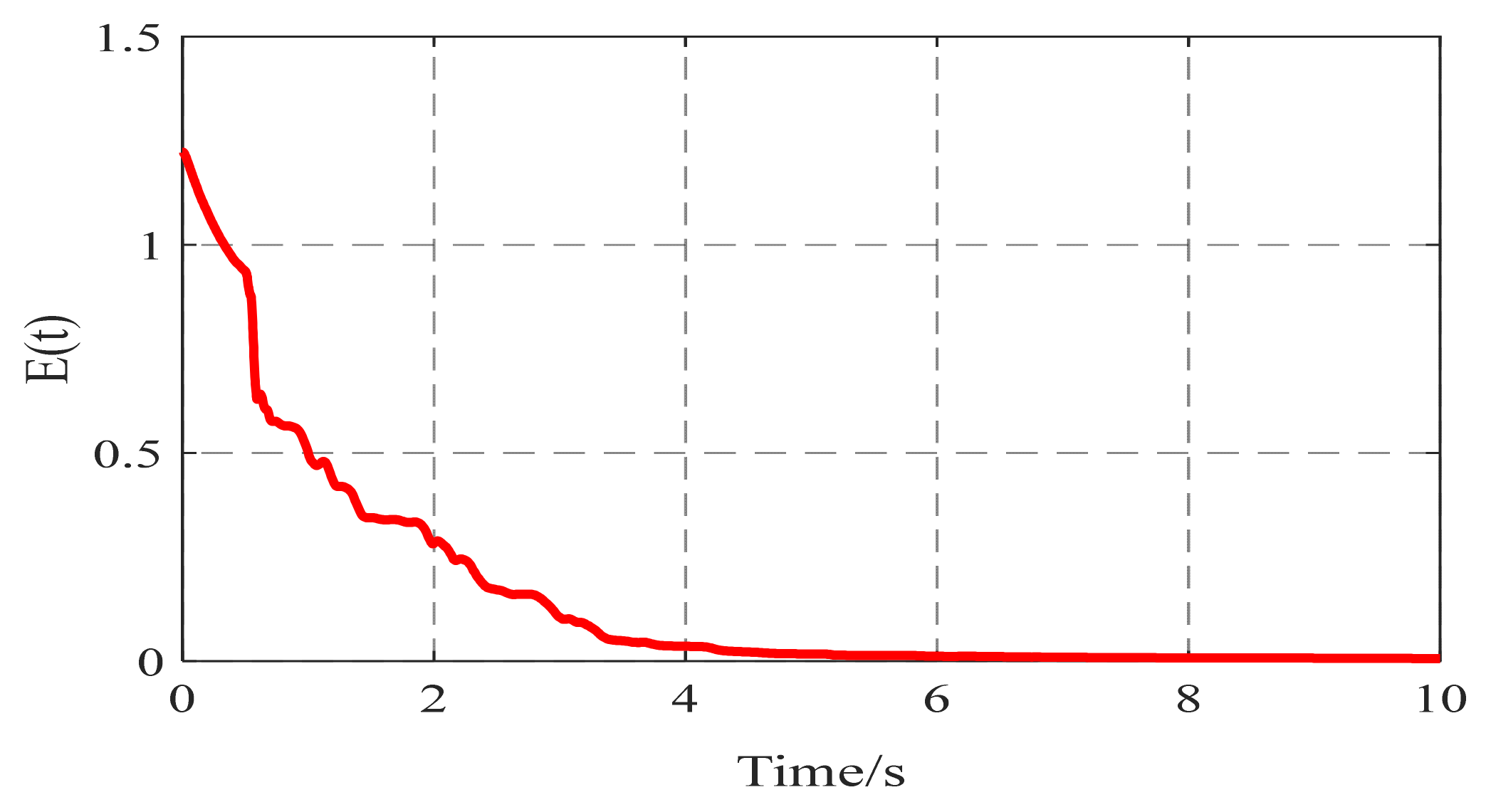



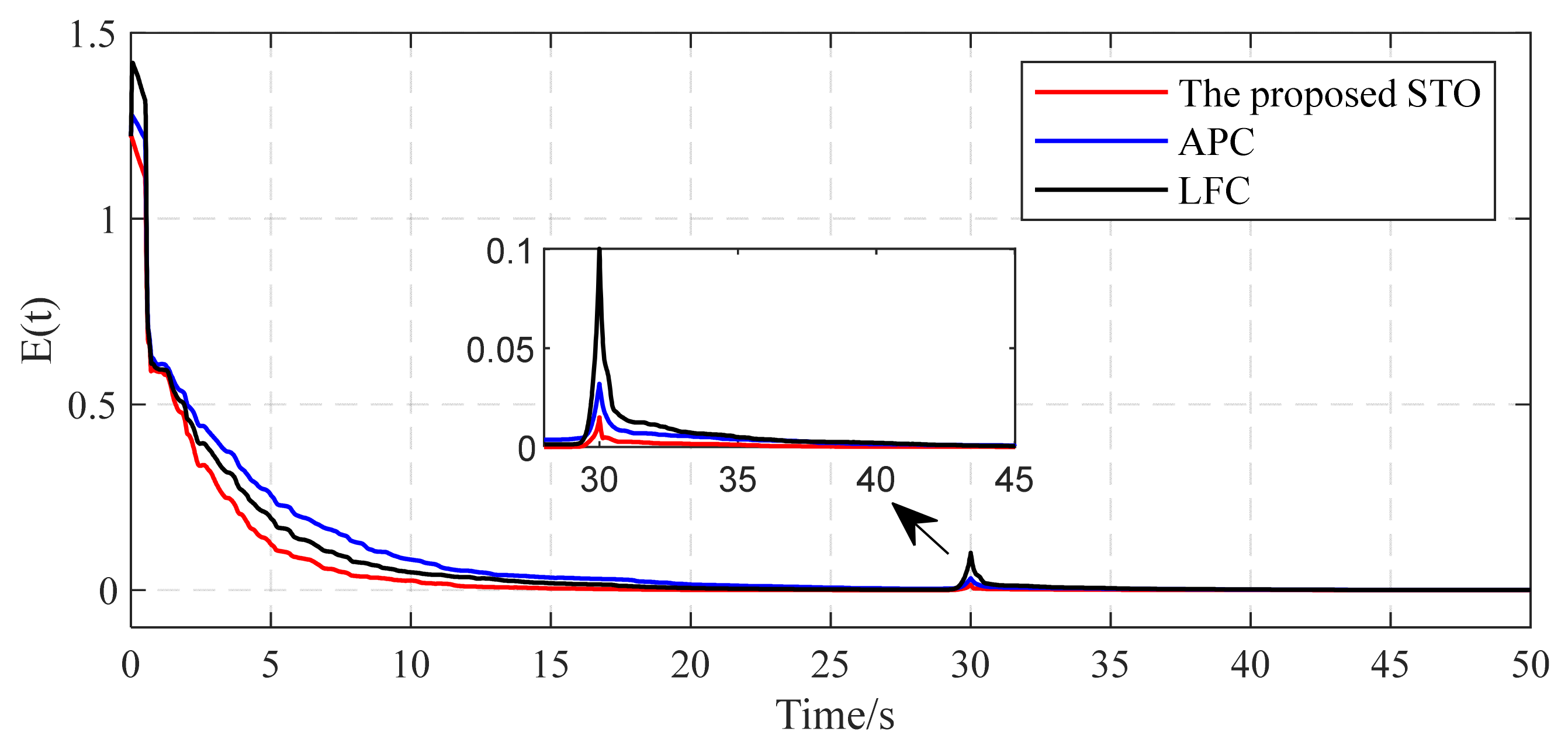

| Method Indices | |||
|---|---|---|---|
| The proposed STO | 2.5540 (65.77%) * | 5.6230 × 10−5 (2.129%) | 18.3301 (61.96%) |
| LFC [24] | 3.8829 (100.0%) | 2.6411 × 10−3 (100.0%) | 29.5825 (100.0%) |
| APC [35] | 3.2815 (84.50%) | 1.1611 × 10−3 (43.96%) | 22.8965 (77.39%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Wu, H.; Chen, Z.; Chen, Y.; Zheng, X. Design of a Robust Synchronization-Based Topology Observer for Complex Delayed Networks with Fixed and Adaptive Coupling Strength. Entropy 2024, 26, 525. https://doi.org/10.3390/e26060525
Sun Y, Wu H, Chen Z, Chen Y, Zheng X. Design of a Robust Synchronization-Based Topology Observer for Complex Delayed Networks with Fixed and Adaptive Coupling Strength. Entropy. 2024; 26(6):525. https://doi.org/10.3390/e26060525
Chicago/Turabian StyleSun, Yanqin, Huaiyu Wu, Zhihuan Chen, Yang Chen, and Xiujuan Zheng. 2024. "Design of a Robust Synchronization-Based Topology Observer for Complex Delayed Networks with Fixed and Adaptive Coupling Strength" Entropy 26, no. 6: 525. https://doi.org/10.3390/e26060525





