The Area Law of Molecular Entropy: Moving beyond Harmonic Approximation
Abstract
1. Introduction
1.1. Computational Techniques to Calculate the Entropy of a Single Molecule
1.2. Area Law—An Alternate Way of Calculating Entropy
1.3. Thermal Entropy of a Single Molecule and Area Law
1.4. Estimating Molecular Entropy Using the Area Law
- 1.
- Surface deformations, curvature with an value other than 1, add to the MI of the system’s microstates. Note that value 1 indicates a perfectly spherical surface.
- 2.
- Positive (0 ≤ < 1) and negative (−1 ≤ < 0) deformations change the MI of the system independently.
2. Materials and Methods
2.1. Data Curation
2.2. Molecular Structure Calculation
2.3. Theoretical Entropy Calculation
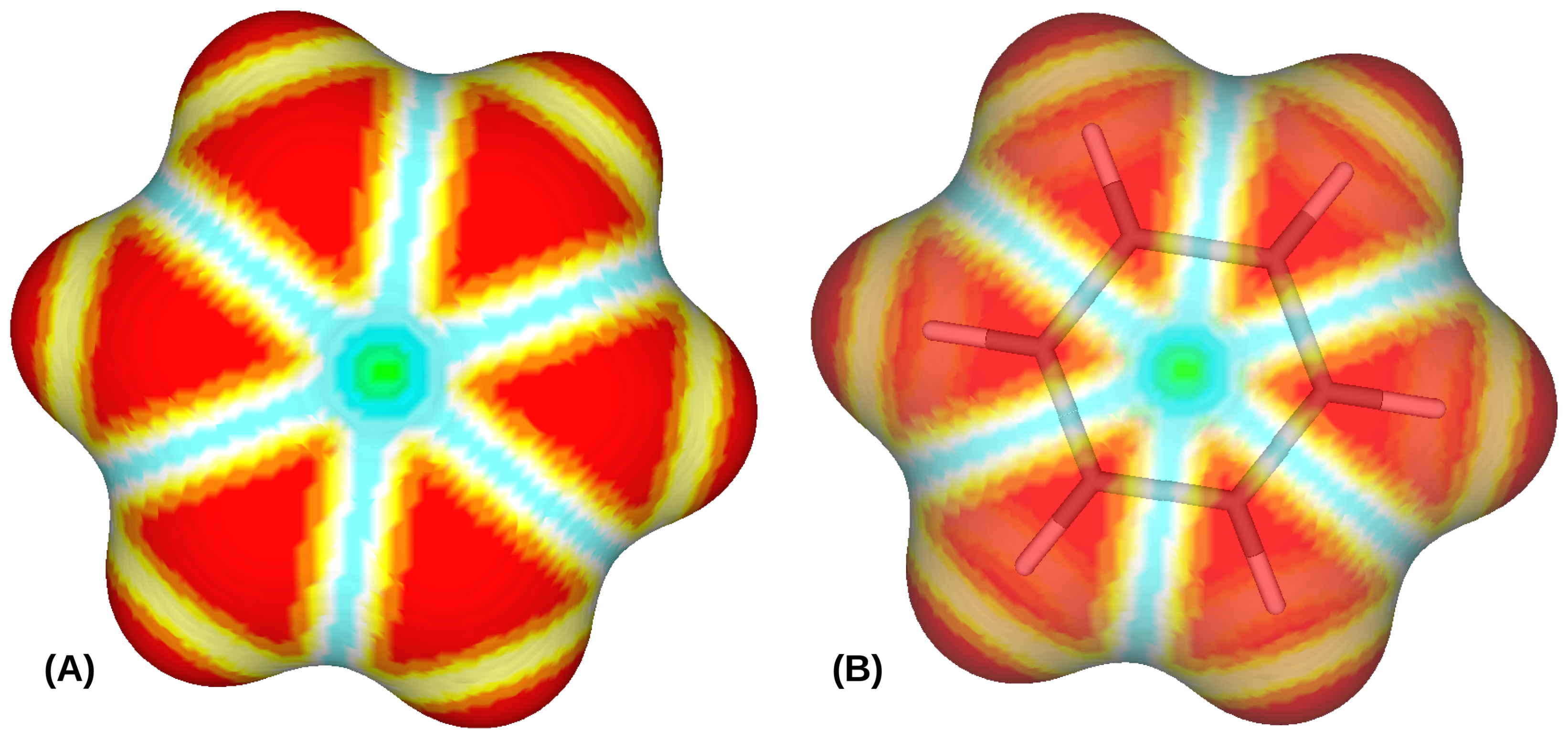
2.4. Molecular Surface Calculation
2.5. Surface Curvature
2.6. Shape Index Probabilities
- Calculate the shape index (see Equation (11)) at the center of each triangle as the mean of shape index values at the vertices. Divide the data into positive and negative groups (<0).
- Calculate the normalized histogram counts for shape index distributions with respect to a predefined number of bins. The probabilities for each bin are given by , where is the number of triangles (i.e., shape index values) allotted to the ith bin.
2.7. Data Fitting
3. Results and Discussion
3.1. Gas-Phase Entropy Varies Linearly with Shape Entropy
3.2. The Impact of Positive and Negative Curvature on the Entropy
3.3. The Coefficient of Ultraviolet Cutoff—Connecting , , and
3.4. Comparison with Entropies Calculated Using RRHO Approximation
3.5. Prediction of Relative Entropies
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CPU | Central Processing Unit |
| DCOR | Distance Correlation |
| GA | Genetic Algorithm |
| LIGO | Laser Interferometer Gravitational-wave Observatory |
| MAPE | Mean Average Percentage Error |
| MI | Missing Information |
| NMA | Normal Mode Analysis |
| OPFF | Open Force Field Toolkit |
| RMSD | Root Mean Square Deviation |
| RMSE | Root Mean Square Error |
| RRHO | Rigid Rotor Harmonic Oscillators |
| SHM | Simple Harmonic Oscillators |
| UFF | Universal Force Field |
| VDW | van der Waal |
References
- Clausius, R. The Mechanical Theory of Heat; Macmillan: New York, NY, USA, 1879. [Google Scholar]
- Jaynes, E.T. Gibbs vs Boltzmann entropies. Am. J. Phys. 1965, 33, 391–398. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information theory and statistical mechanics. Phys. Rev. 1957, 106, 620. [Google Scholar] [CrossRef]
- Rosenkrantz, R. Where do we stand on maximum entropy? In ET Jaynes: Papers on Probability, Statistics and Statistical Physics; Springer: Cham, Switzerland, 1989; pp. 210–314. [Google Scholar]
- Kabo, G.J.; Blokhin, A.V.; Paulechka, E.; Roganov, G.N.; Frenkel, M.; Yursha, I.A.; Diky, V.; Zaitsau, D.; Bazyleva, A.; Simirsky, V.V.; et al. Thermodynamic properties of organic substances: Experiment, modeling, and technological applications. J. Chem. Thermodyn. 2019, 131, 225–246. [Google Scholar] [CrossRef] [PubMed]
- Littlejohn, R.G.; Reinsch, M. Gauge fields in the separation of rotations andinternal motions in the n-body problem. Rev. Mod. Phys. 1997, 69, 213. [Google Scholar] [CrossRef]
- Karplus, M.; Ichiye, T.; Pettitt, B. Configurational entropy of native proteins. Biophys. J. 1987, 52, 1083–1085. [Google Scholar] [CrossRef] [PubMed]
- Van Gunsteren, W.; Luque, F.; Timms, D.; Torda, A. Molecular mechanics in biology: From structure to function, taking account of solvation. Annu. Rev. Biophys. Biomol. Struct. 1994, 23, 847–863. [Google Scholar] [CrossRef] [PubMed]
- Chan, L.; Morris, G.M.; Hutchison, G.R. Understanding conformational entropy in small molecules. J. Chem. Theory Comput. 2021, 17, 2099–2106. [Google Scholar] [CrossRef] [PubMed]
- Christiansen, O. Selected new developments in vibrational structure theory: Potential construction and vibrational wave function calculations. Phys. Chem. Chem. Phys. 2012, 14, 6672–6687. [Google Scholar] [CrossRef] [PubMed]
- Ma, J. Usefulness and limitations of normal mode analysis in modeling dynamics of biomolecular complexes. Structure 2005, 13, 373–380. [Google Scholar] [CrossRef] [PubMed]
- Murray, C.W.; Verdonk, M.L. The consequences of translational and rotational entropy lost by small molecules on binding to proteins. J.-Comput.-Aided Mol. Des. 2002, 16, 741–753. [Google Scholar] [CrossRef] [PubMed]
- Bekenstein, J.D. Black holes and entropy. Phys. Rev. D 1973, 7, 2333. [Google Scholar] [CrossRef]
- Hawking, S.W. Black holes and thermodynamics. Phys. Rev. D 1976, 13, 191. [Google Scholar] [CrossRef]
- Isi, M.; Farr, W.M.; Giesler, M.; Scheel, M.A.; Teukolsky, S.A. Testing the black-hole area law with GW150914. Phys. Rev. Lett. 2021, 127, 011103. [Google Scholar] [CrossRef] [PubMed]
- Eisert, J.; Cramer, M.; Plenio, M.B. Area laws for the entanglement entropy—A review. arXiv 2008, arXiv:0808.3773. [Google Scholar]
- Bombelli, L.; Koul, R.K.; Lee, J.; Sorkin, R.D. Quantum source of entropy for black holes. Phys. Rev. D 1986, 34, 373. [Google Scholar] [CrossRef] [PubMed]
- Srednicki, M. Entropy and area. Phys. Rev. Lett. 1993, 71, 666. [Google Scholar] [CrossRef] [PubMed]
- Herdman, C.; Roy, P.N.; Melko, R.; Maestro, A.D. Entanglement area law in superfluid 4 He. Nat. Phys. 2017, 13, 556–558. [Google Scholar] [CrossRef]
- Caruso, F.; Tsallis, C. Nonadditive entropy reconciles the area law in quantum systems with classical thermodynamics. Phys. Rev. E-Stat. Nonlinear Soft Matter Phys. 2008, 78, 021102. [Google Scholar] [CrossRef] [PubMed]
- Wienen-Schmidt, B.; Schmidt, D.; Gerber, H.D.; Heine, A.; Gohlke, H.; Klebe, G. Surprising non-additivity of methyl groups in drug—kinase interaction. ACS Chem. Biol. 2019, 14, 2585–2594. [Google Scholar] [CrossRef] [PubMed]
- Tsallis, C. The nonadditive entropy Sq and its applications in physics and elsewhere: Some remarks. Entropy 2011, 13, 1765–1804. [Google Scholar] [CrossRef]
- Tsallis, C. Entropy. Encyclopedia 2022, 2, 264–300. [Google Scholar] [CrossRef]
- Guthrie, J.P. Use of DFT Methods for the Calculation of the Entropy of Gas Phase Organic Molecules: An Examination of the Quality of Results from a Simple Approach. J. Phys. Chem. A 2001, 105, 8495–8499. [Google Scholar] [CrossRef]
- Ghahremanpour, M.M.; van Maaren, P.J.; Ditz, J.C.; Lindh, R.; van der Spoel, D. Large-scale calculations of gas phase thermochemistry: Enthalpy of formation, standard entropy, and heat capacity. J. Chem. Phys. 2016, 145, 114305. [Google Scholar] [CrossRef]
- van der Spoel, D.; Ghahremanpour, M.M.; Lemkul, J.A. Small Molecule Thermochemistry: A Tool for Empirical Force Field Development. J. Phys. Chem. A 2018, 122, 8982–8988. [Google Scholar] [CrossRef] [PubMed]
- Raychaudhury, C.; Rizvi, I.; Pal, D. Predicting gas phase entropy of select hydrocarbon classes through specific information-theoretical molecular descriptors. SAR QSAR Environ. Res. 2019, 30, 491–505. [Google Scholar] [CrossRef]
- Bains, W.; Petkowski, J.J.; Zhan, Z.; Seager, S. A Data Resource for Prediction of Gas-Phase Thermodynamic Properties of Small Molecules. Data 2022, 7, 33. [Google Scholar] [CrossRef]
- Landrum, G. RDKit: Open-Source Cheminformatics Software, RDKit Version 2020.09.1.0. 2020.
- O’Boyle, N.M.; Banck, M.; James, C.A.; Morley, C.; Vandermeersch, T.; Hutchison, G.R. Open Babel: An open chemical toolbox. J. Cheminform. 2011, 3, 33. [Google Scholar] [CrossRef] [PubMed]
- Rappe, A.K.; Casewit, C.J.; Colwell, K.S.; Goddard, W.A.; Skiff, W.M. UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations. J Am. Chem. Soc. 1992, 114, 10024–10035. [Google Scholar] [CrossRef]
- Ebejer, J.P.; Morris, G.M.; Deane, C.M. Freely Available Conformer Generation Methods: How Good Are They? J. Chem. Inf. Model. 2012, 52, 1146–1158. [Google Scholar] [CrossRef] [PubMed]
- Dewar, M.J.S.; Zoebisch, E.G.; Healy, E.F.; Stewart, J.J.P. Development and use of quantum mechanical molecular models. 76. AM1: A new general purpose quantum mechanical molecular model. J. Am. Chem. Soc. 1985, 107, 3902–3909. [Google Scholar] [CrossRef]
- Stewart, J.J.P. MOPAC2016; Stewart Computational Chemistry: Colorado Springs, CO, USA, 2016; Available online: http://OpenMOPAC.net (accessed on 2 November 2020).
- Curtiss, L.A.; Redfern, P.C.; Raghavachari, K. Gaussian-4 theory. J. Chem. Phys. 2007, 126, 084108. [Google Scholar] [CrossRef]
- Ghahremanpour, M.M.; van Maaren, P.J.; van der Spoel, D. The Alexandria library, a quantum-chemical database of molecular properties for force field development. Sci. Data 2018, 5. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09 Revision B.01, 2009; Gaussian Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Qiu, Y.; Smith, D.G.A.; Boothroyd, S.; Jang, H.; Hahn, D.F.; Wagner, J.; Bannan, C.C.; Gokey, T.; Lim, V.T.; Stern, C.D.; et al. Development and Benchmarking of Open Force Field v1.0.0—The Parsley Small-Molecule Force Field. J. Chem. Theory Comput. 2021, 17, 6262–6280. [Google Scholar] [CrossRef] [PubMed]
- Morado, J.; Mortenson, P.N.; Nissink, J.W.M.; Essex, J.W.; Skylaris, C.K. Does a Machine-Learned Potential Perform Better Than an Optimally Tuned Traditional Force Field? A Case Study on Fluorohydrins. J. Chem. Inf. Model. 2023, 63, 2810–2827. [Google Scholar] [CrossRef] [PubMed]
- Salomon-Ferrer, R.; Case, D.; Walker, R. An overview of the Amber biomolecular simulation package. WIREs Comput. Mol. Sci. 2013, 3, 198–210. [Google Scholar] [CrossRef]
- Wang, J.; Wang, W.; Kollman, P.A.; Case, D.A. Antechamber: An accessory software package for molecular mechanical calculations. J. Am. Chem. Soc 2001, 222, 2001. [Google Scholar]
- Abraham, M.; Alekseenko, A.; Bergh, C.; Blau, C.; Briand, E.; Doijade, M.; Fleischmann, S.; Gapsys, V.; Garg, G.; Gorelov, S.; et al. GROMACS 2023.3 Manual. 2023. Available online: https://zenodo.org/records/10017699 (accessed on 2 November 2020).
- Gabdoulline, R.; Wade, R. Analytically defined surfaces to analyze molecular interaction properties. J. Mol. Graph. 1996, 14, 341–353. [Google Scholar] [CrossRef] [PubMed]
- Whitley, D.C. Chapter 8. Analysing Molecular Surface Properties. In Drug Design Strategies; Royal Society of Chemistry: London, UK, 2012; pp. 184–209. [Google Scholar] [CrossRef]
- Sigg, C. Representation and Rendering of Implicit Surfaces. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 2006. [Google Scholar]
- Liu, T.; Chen, M.; Lu, B. Parameterization for molecular Gaussian surface and a comparison study of surface mesh generation. J. Mol. Model. 2015, 21, 113. [Google Scholar] [CrossRef]
- Vega, D.; Abache, J.; Coll, D. A Fast and Memory Saving Marching Cubes 33 Implementation with the Correct Interior Test. J. Comput. Graph. Tech. JCGT 2019, 8, 1–18. [Google Scholar]
- do Carmo, M.P. Differential Geometry of Curves and Surfaces; Prentice Hall: Hoboken, NJ, USA, 1976; pp. I–VIII, 1–503. [Google Scholar]
- Goldman, R. Curvature formulas for implicit curves and surfaces. Comput. Aided Geom. Des. 2005, 22, 632–658, Geometric Modelling and Differential Geometry. [Google Scholar] [CrossRef]
- Xia, K.; Feng, X.; Chen, Z.; Tong, Y.; Wei, G.W. Multiscale geometric modeling of macromolecules I: Cartesian representation. J. Comput. Phys. 2014, 257, 912–936. [Google Scholar] [CrossRef] [PubMed]
- Koenderink, J.J.; van Doorn, A.J. Surface shape and curvature scales. Image Vis. Comput. 1992, 10, 557–564. [Google Scholar] [CrossRef]
- Scrucca, L. GA: A Package for Genetic Algorithms in R. J. Stat. Softw. 2013, 53, 1–37. [Google Scholar] [CrossRef]
- Scrucca, L. On some extensions to GA package: Hybrid optimisation, parallelisation and islands evolution. R J. 2017, 9, 187–206. [Google Scholar] [CrossRef]
- Chernick, M.R. Bootstrap Methods: A Guide for Practitioners and Researchers; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007. [Google Scholar] [CrossRef]
- Mantina, M.; Chamberlin, A.C.; Valero, R.; Cramer, C.J.; Truhlar, D.G. Consistent van der Waals radii for the whole main group. J. Phys. Chem. A 2009, 113, 5806–5812. [Google Scholar] [CrossRef] [PubMed]
- Jaynes, E.T. Information theory and statistical mechanics. ii. Phys. Rev. 1957, 108, 171. [Google Scholar] [CrossRef]
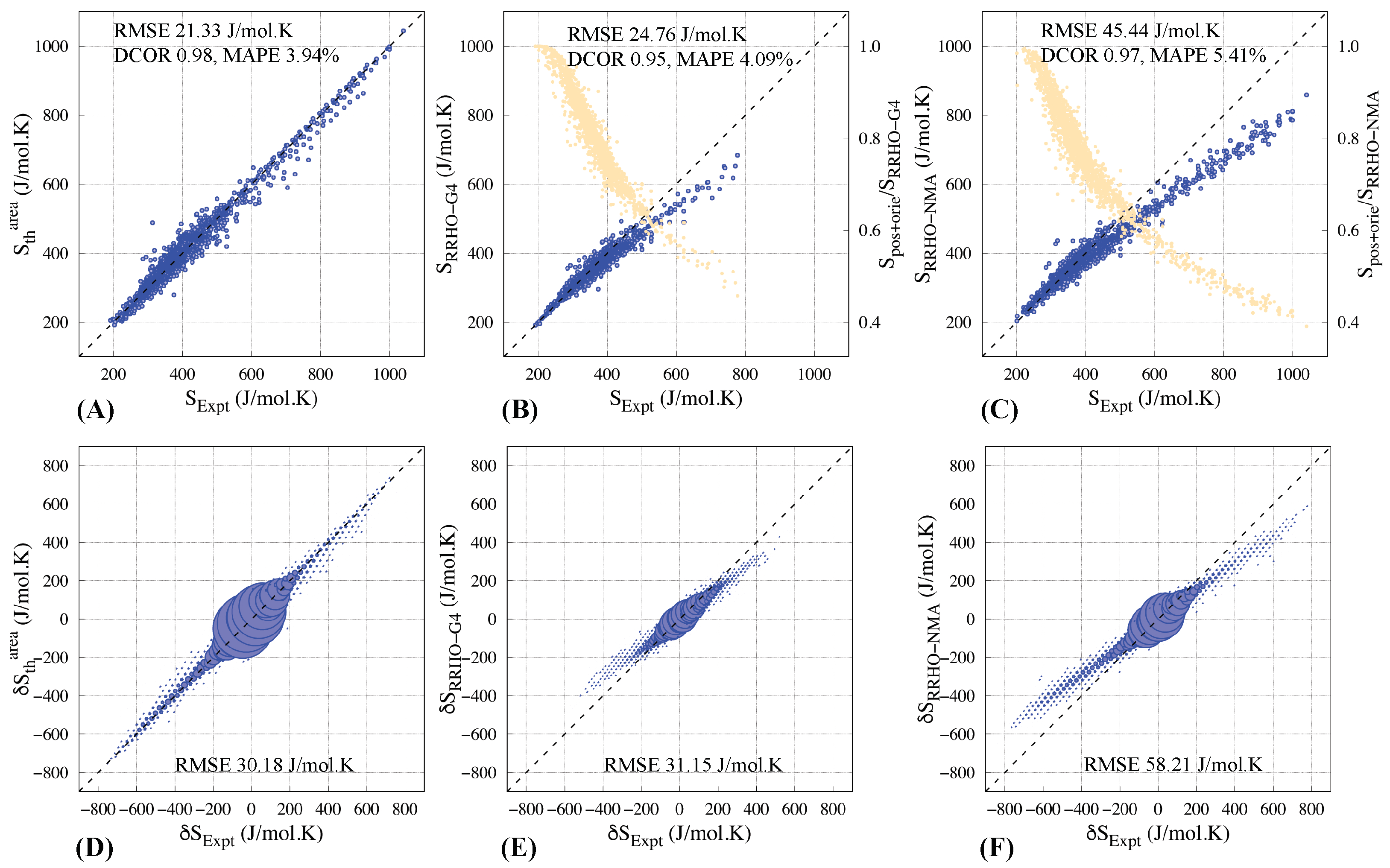
| SRRHO-G4 | SRRHO-NMA | ||
|---|---|---|---|
| ∩ SRRHO-G4 ∩ SRRHO-NMA (1326) | 20.91 | 23.38 | 26.21 |
| ∩ SRRHO-NMA (1665) | 20.93 | – | 45.44 |
| ∩ SRRHO-G4 (1529) | 21.47 | 24.76 | – |
| Method | = (J/mol·K) | RMSE (J/mol·K) | MAPE % | |
|---|---|---|---|---|
| Area | 5.42 | |||
| Area + deformation | 3.94 | |||
| G4 NMA | 4.09 5.41 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roy, A.; Ali, T.; Venkatraman, V. The Area Law of Molecular Entropy: Moving beyond Harmonic Approximation. Entropy 2024, 26, 688. https://doi.org/10.3390/e26080688
Roy A, Ali T, Venkatraman V. The Area Law of Molecular Entropy: Moving beyond Harmonic Approximation. Entropy. 2024; 26(8):688. https://doi.org/10.3390/e26080688
Chicago/Turabian StyleRoy, Amitava, Tibra Ali, and Vishwesh Venkatraman. 2024. "The Area Law of Molecular Entropy: Moving beyond Harmonic Approximation" Entropy 26, no. 8: 688. https://doi.org/10.3390/e26080688
APA StyleRoy, A., Ali, T., & Venkatraman, V. (2024). The Area Law of Molecular Entropy: Moving beyond Harmonic Approximation. Entropy, 26(8), 688. https://doi.org/10.3390/e26080688






