Random Quantum Ising Model with Three-Spin Couplings
Abstract
1. Introduction
2. Basic Idea of Block Renormalization
3. Block Renormalization Approach of the Model
3.1. Pure Model
3.2. Random Model
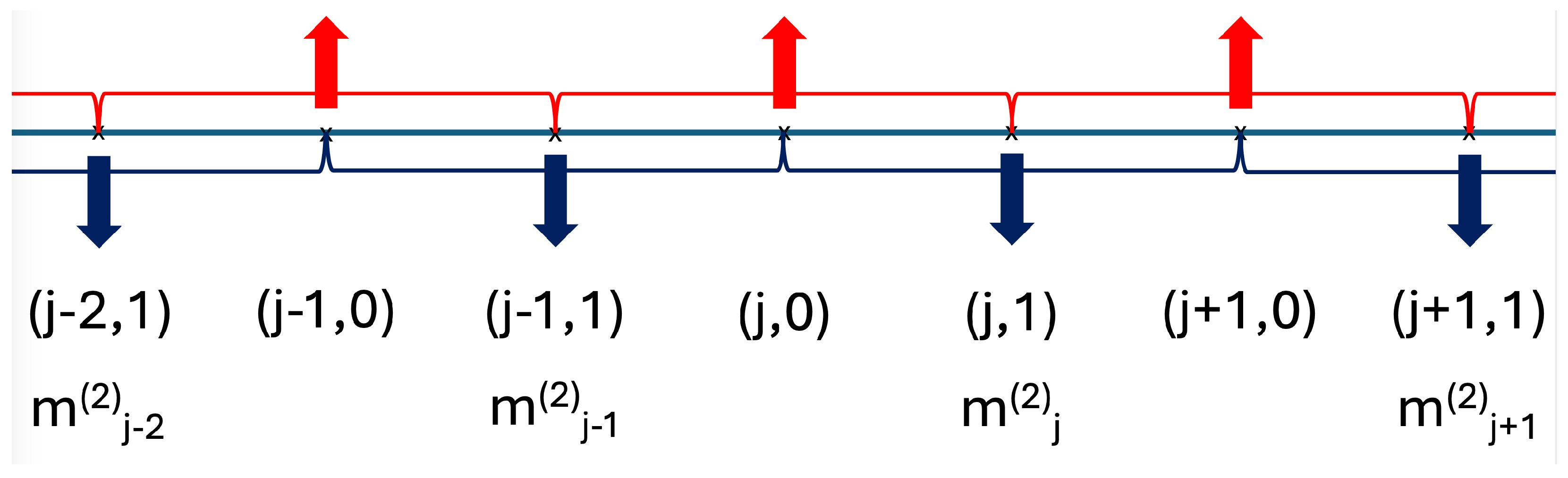
4. Block Renormalization Approach of the Model
4.1. Pure Model
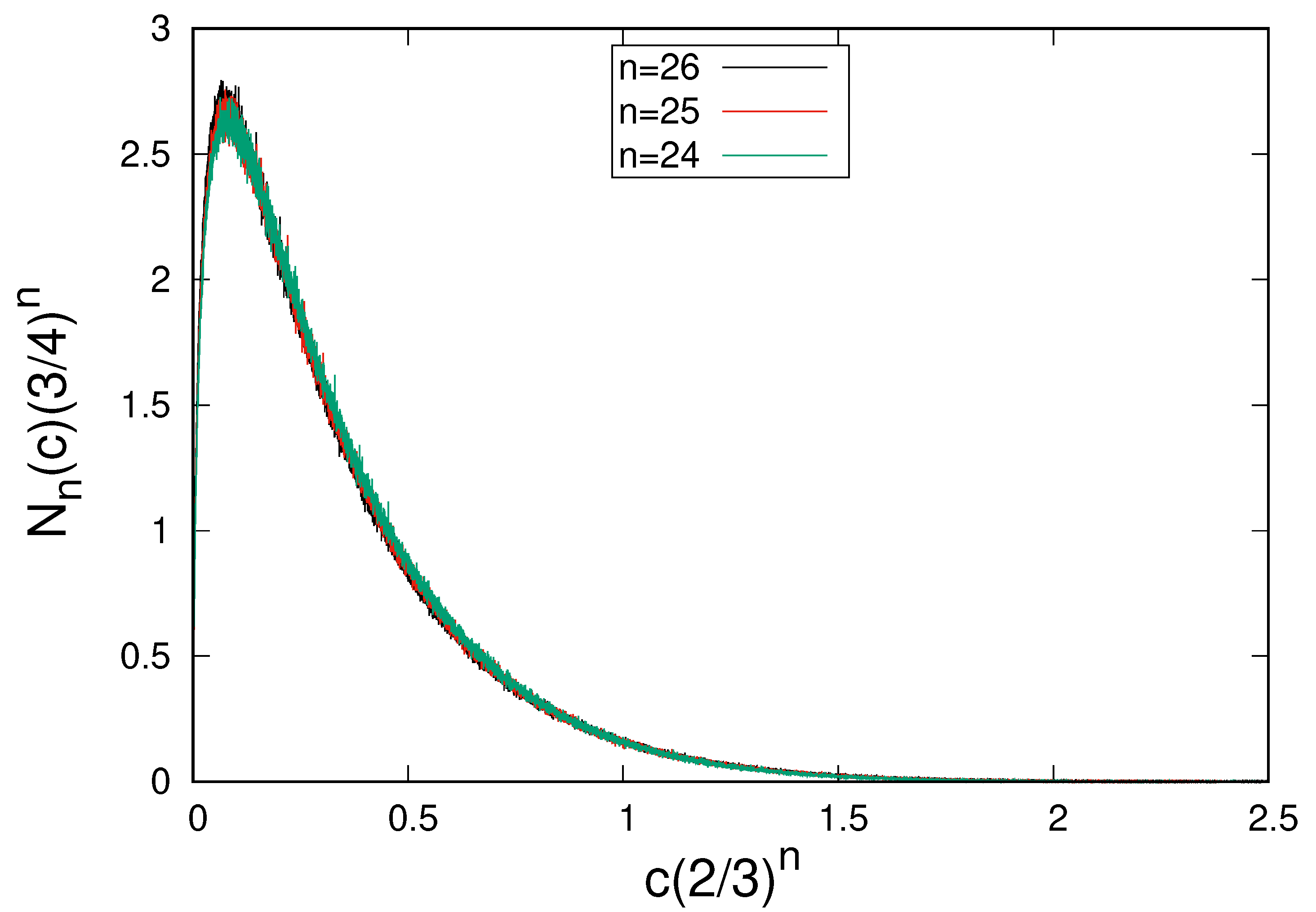
4.2. Random Model
5. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sachdev, S. Quantum Phase Transitions, 2nd ed.; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Kogut, B. An introduction to lattice gauge theory and spin systems. Rev. Mod. Phys. 1979, 51, 659. [Google Scholar] [CrossRef]
- Cardy, J. Scaling and Renormalization in Statistical Physics; Cambridge Lecture Notes in Physics; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Iglói, F.; Monthus, C. Strong disorder rg approach of random systems. Phys. Rep. 2005, 412, 277. [Google Scholar] [CrossRef]
- Iglói, F.; Monthus, C. Strong disorder rg approach—A short review of recent developments. Eur. Phys. J. B 2018, 91, 290. [Google Scholar] [CrossRef]
- Fisher, D.S. Phase transitions and singularities in random quantum systems. Phys. A Stat. Mech. Its Appl. 1999, 263, 222. [Google Scholar] [CrossRef]
- Ma, S.-K.; Dasgupta, C.; Hu, C.-K. Random antiferromagnetic chain. Phys. Rev. Lett. 1979, 43, 1434. [Google Scholar] [CrossRef]
- Dasgupta, C.; Ma, S.-K. Low-temperature properties of the random heisenberg antiferromagnetic chain. Phys. Rev. B 1980, 22, 1305. [Google Scholar] [CrossRef]
- Fisher, D.S. Random transverse field ising spin chains. Phys. Rev. Lett. 1992, 69, 534. [Google Scholar] [CrossRef] [PubMed]
- Fisher, D.S. Critical behavior of random transverse-field ising spin chains. Phys. Rev. B 1995, 51, 6411. [Google Scholar] [CrossRef]
- Fisher, D.S. Random antiferromagnetic quantum spin chains. Phys. Rev. B 1994, 50, 3799. [Google Scholar] [CrossRef]
- Senthil, T.; Majumdar, S.N. Critical properties of random quantum potts and clock models. Phys. Rev. Lett. 1996, 76, 3001. [Google Scholar] [CrossRef]
- Monthus, C.; Golinelli, O.; Jolicœur, T. Percolation transition in the random antiferromagnetic spin-1 chain. Phys. Rev. Lett. 1997, 79, 3254. [Google Scholar] [CrossRef]
- Hyman, R.A.; Yang, K. Impurity driven phase transition in the antiferromagnetic spin-1 chain. Phys. Rev. Lett. 1997, 78, 1783. [Google Scholar] [CrossRef]
- Carlon, E.; Lajkó, P.; Iglói, F. Disorder induced cross-over effects at quantum critical points. Phys. Rev. Lett. 2001, 87, 277201. [Google Scholar] [CrossRef]
- Motrunich, O.; Mau, S.-C.; Huse, D.A.; Fisher, D.S. Infinite-randomness quantum ising critical fixed points. Phys. Rev. B 2000, 61, 1160. [Google Scholar] [CrossRef]
- Lin, Y.-C.; Kawashima, N.; Iglói, F.; Rieger, H. Numerical Renormalization Group Study of Random Transverse Ising Models in One and Two Space Dimensions. Prog. Theor. Phys. Suppl. 2000, 138, 479. [Google Scholar] [CrossRef]
- Karevski, D.; Lin, Y.-C.; Rieger, H.; Kawashima, N.; Iglói, F. Random quantum magnets with broad disorder distribution. Eur. Phys. J. B-Condens. Matter Complex Syst. 2001, 20, 267. [Google Scholar] [CrossRef]
- Lin, Y.-C.; Iglói, F.; Rieger, H. Entanglement entropy at infinite-randomness fixed points in higher dimensions. Phys. Rev. Lett. 2007, 99, 147202. [Google Scholar] [CrossRef]
- Yu, R.; Saleur, H.; Haas, S. Entanglement entropy in the two-dimensional random transverse field ising model. Phys. Rev. B 2008, 77, 140402. [Google Scholar] [CrossRef]
- Kovács, I.A.; Iglói, F. Critical behavior and entanglement of the random transverse-field ising model between one and two dimensions. Phys. Rev. B 2009, 80, 214416. [Google Scholar] [CrossRef]
- Kovács, I.A.; Iglói, F. Renormalization group study of the two-dimensional random transverse-field ising model. Phys. Rev. B 2010, 82, 054437. [Google Scholar] [CrossRef]
- Kovács, I.A.; Iglói, F. Infinite-disorder scaling of random quantum magnets in three and higher dimensions. Phys. Rev. B 2011, 83, 174207. [Google Scholar] [CrossRef]
- Kovács, I.A.; Iglói, F. Renormalization group study of random quantum magnets. J. Phys. Condens. Matter 2011, 23, 404204. [Google Scholar] [CrossRef] [PubMed]
- Hooyberghs, J.; Iglói, F.; Vanderzande, C. Strong disorder fixed point in absorbing-state phase transitions. Phys. Rev. Lett. 2003, 90, 100601. [Google Scholar] [CrossRef]
- Hooyberghs, J.; Iglói, F.; Vanderzande, C. Absorbing state phase transitions with quenched disorder. Phys. Rev. E 2004, 69, 066140. [Google Scholar] [CrossRef] [PubMed]
- Vojta, T.; Dickison, M. Critical behavior and griffiths effects in the disordered contact process. Phys. Rev. E 2005, 72, 036126. [Google Scholar] [CrossRef] [PubMed]
- Juhász, R.; Kovács, I.A.; Iglói, F. Random transverse-field ising chain with long-range interactions. Europhys. Lett. 2014, 107, 47008. [Google Scholar] [CrossRef]
- Kovács, I.A.; Juhász, R.; Iglói, F. Long-range random transverse-field ising model in three dimensions. Phys. Rev. B 2016, 93, 184203. [Google Scholar] [CrossRef]
- Turban, L. Self-dual ising chain in a transverse field with multispin interactions. J. Phys. C Solid State Phys. 1982, 15, L65. [Google Scholar] [CrossRef]
- Penson, K.A.; Jullien, R.; Pfeuty, P. Phase transitions in systems with multispin interactions. Phys. Rev. B 1982, 26, 6334. [Google Scholar] [CrossRef]
- Igloi, F.; Kapor, D.V.; Skrinjar, M.; Solyom, J. The critical behaviour of a quantum spin problem with thee-spin coupling. J. Phys. A Math. Gen. 1983, 16, 4067. [Google Scholar] [CrossRef]
- Igloi, F.; Kapor, D.V.; Skrinjar, M.; Solyom, J. Series expansion study of first- and second-order phase transitions in a model with multispin coupling. J. Phys. A Math. Gen. 1986, 19, 1189. [Google Scholar] [CrossRef]
- Blöte, H.; Compagner, A.; Cornelissen, P.; Hoogland, A.; Mallezie, F.; Vanderzande, C. Critical behaviour of two ising models with multispin interactions. Phys. A Stat. Mech. Its Appl. 1986, 139, 395. [Google Scholar] [CrossRef]
- Alcaraz, F.C. Order of phase transition for systems with multispin interactions: Monte carlo simulations. Phys. Rev. B 1986, 34, 4885. [Google Scholar] [CrossRef] [PubMed]
- Kolb, M.; Penson, K.A. Conformal invariance and the phase transition of a spin chain with three-spin interaction. J. Phys. A Math. Gen. 1986, 19, L779. [Google Scholar] [CrossRef]
- Blote, H.W.J. Equivalence of an ising model with two- and three-spin interactions with the four-state potts model. J. Phys. A Math. Gen. 1987, 20, L35. [Google Scholar] [CrossRef]
- Vanderzande, C.; Igloi, F. Critical behaviour and logarithmic corrections of a quantum model with three-spin interaction. J. Phys. A Math. Gen. 1987, 20, 4539. [Google Scholar] [CrossRef]
- Igloi, F. Conformal invariance and surface critical behaviour of a quantum chain with three-spin interaction. J. Phys. A Math. Gen. 1987, 20, 5319. [Google Scholar] [CrossRef]
- Fernandez-Pacheco, A. Comment on the slac renormalization-group approach to the ising chain in a transverse magnetic field. Phys. Rev. D 1979, 19, 3173. [Google Scholar] [CrossRef]
- Horn, D.; Karliner, M.; Yankielowicz, S. Self-dual renormalization group analysis of the potts models. Nucl. Phys. B 1980, 170, 467. [Google Scholar] [CrossRef]
- Hu, B. Critical exponents of the four-state potts model. J. Phys. A Math. Gen. 1980, 13, L321. [Google Scholar] [CrossRef]
- Sólyom, J.; Pfeuty, P. Renormalization-group study of the hamiltonian version of the potts model. Phys. Rev. B 1981, 24, 218. [Google Scholar] [CrossRef]
- Sólyom, J. Duality of the block transformation and decimation for quantum spin systems. Phys. Rev. B 1981, 24, 230. [Google Scholar] [CrossRef]
- Iglói, F.; Sólyom, J. Renormalization-group study of the hamiltonian version of the potts model. ii. self-dual renormalization-group treatment. Phys. Rev. B 1983, 28, 2785. [Google Scholar] [CrossRef]
- Iglói, F.; Sólyom, J. Phase diagram and critical properties of the (1+1)-dimensional ashkin-teller model. J. Phys. A Math. Gen. 1984, 17, 1531. [Google Scholar] [CrossRef]
- Iglói, F. Renormalization for quantum systems: Generalized block transformations in the large-l limit. Phys. Rev. B 1993, 48, 58. [Google Scholar] [CrossRef] [PubMed]
- Epele, L.N.; Fanchiotti, H.; Canal, C.A.G. Ferromagnetism and antiferromagnetism in the quantum ising model. Phys. Rev. B 1981, 24, 310. [Google Scholar] [CrossRef]
- Miyazaki, R.; Nishimori, H.; Ortiz, G. Real-space renormalization group for the transverse-field ising model in two and three dimensions. Phys. Rev. E 2011, 83, 051103. [Google Scholar] [CrossRef] [PubMed]
- Miyazaki, R.; Nishimori, H. Real-space renormalization-group approach to the random transverse-field ising model in finite dimensions. Phys. Rev. E 2013, 87, 032154. [Google Scholar] [CrossRef]
- Monthus, C. Block renormalization for quantum ising models in dimension d = 2: Applications to the pure and random ferromagnet, and to the spin-glass. J. Stat. Mech. Theory Exp. 2015, 2015, P01023. [Google Scholar] [CrossRef]
- Jullien, R. Transitions de phases a t=0 dans les systemes quantiques par le groupe de renormalisation dans l’espace reel. Can. J. Phys. 1981, 59, 605. [Google Scholar] [CrossRef]
- Pfeuty, P.; Jullien, R.; Penson, K.A. Renormalization for quantum systems. In Real-Space Renormalization; Burkhardt, T.W., van Leeuwen, J.M.J., Eds.; Springer: Berlin/Heidelberg, Germany, 1982; pp. 119–147. [Google Scholar] [CrossRef]
- Peschel, I. Surface magnetization in inhomogeneous two-dimensional ising lattices. Phys. Rev. B 1984, 30, 6783. [Google Scholar] [CrossRef]
- Iglói, F.; Rieger, H. Random transverse ising spin chain and random walks. Phys. Rev. B 1998, 57, 11404. [Google Scholar] [CrossRef]
- Griffiths, R.B. Nonanalytic behavior above the critical point in a random ising ferromagnet. Phys. Rev. Lett. 1969, 23, 17. [Google Scholar] [CrossRef]
- McCoy, B.M. Incompleteness of the critical exponent description for ferromagnetic systems containing random impurities. Phys. Rev. Lett. 1969, 23, 383. [Google Scholar] [CrossRef]
- Kesten, H. Random difference equations and Renewal theory for products of random matrices. Acta Math. 1973, 131, 207. [Google Scholar] [CrossRef]
- Iglói, F.; Rieger, H. Anomalous diffusion in disordered media and random quantum spin chains. Phys. Rev. E 1998, 58, 4238. [Google Scholar] [CrossRef]
- Iglói, F.; Juhász, R.; Lajkó, P. Griffiths-mccoy singularities in random quantum spin chains: Exact results through renormalization. Phys. Rev. Lett. 2001, 86, 1343. [Google Scholar] [CrossRef]
- Iglói, F. Exact renormalization of the random transverse-field ising spin chain in the strongly ordered and strongly disordered griffiths phases. Phys. Rev. B 2022, 65, 064416. [Google Scholar] [CrossRef]
- Berche, B.; Ellis, T.; Holovatch, Y.; Kenna, R. Phase transitions above the upper critical dimension. SciPost Phys. Lect. Notes 2022, 60. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iglói, F.; Lin, Y.-C. Random Quantum Ising Model with Three-Spin Couplings. Entropy 2024, 26, 709. https://doi.org/10.3390/e26080709
Iglói F, Lin Y-C. Random Quantum Ising Model with Three-Spin Couplings. Entropy. 2024; 26(8):709. https://doi.org/10.3390/e26080709
Chicago/Turabian StyleIglói, Ferenc, and Yu-Cheng Lin. 2024. "Random Quantum Ising Model with Three-Spin Couplings" Entropy 26, no. 8: 709. https://doi.org/10.3390/e26080709
APA StyleIglói, F., & Lin, Y.-C. (2024). Random Quantum Ising Model with Three-Spin Couplings. Entropy, 26(8), 709. https://doi.org/10.3390/e26080709






