Synergy Makes Direct Perception Inefficient
Abstract
1. Introduction
2. The Direct Perception of Affordances
3. Multi-Modal Perception and Synergistic Affordances
4. Information Theory and Lossy Communication
4.1. Basic Concepts
4.2. PID and Synergistic Information
4.3. Communication
4.4. Lossy Compression
4.5. Spatial Entropy
5. Methods
5.1. Model Description
5.2. Encoding Strategies
5.3. Encoder Optimization
| Algorithm 1 Encoder Optimization |
|
5.4. Information-Theoretic Measures
5.5. Data
6. Results
6.1. Toy Example
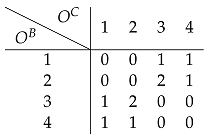
6.1.1. Direct Encoding

6.1.2. Indirect Encoding

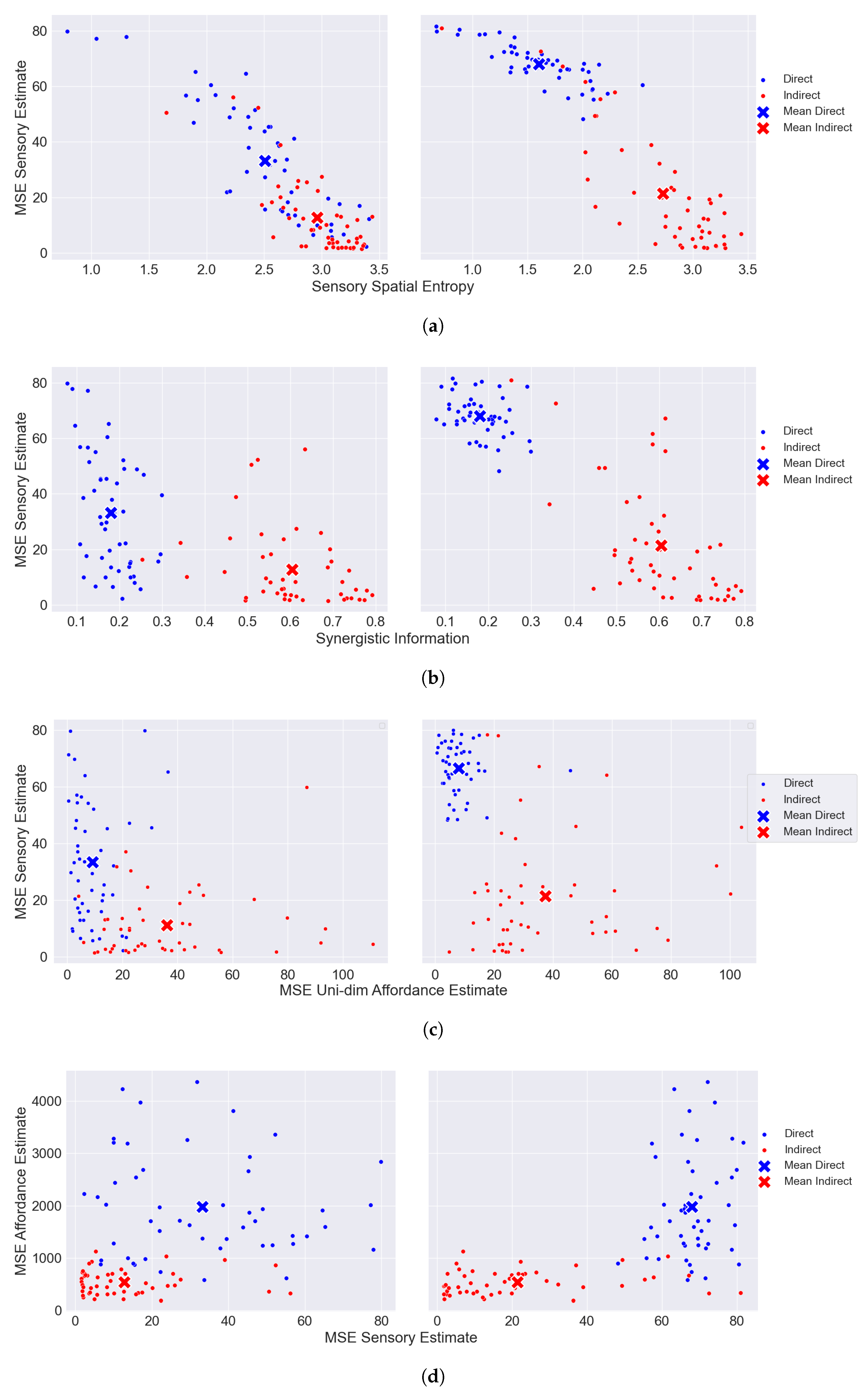
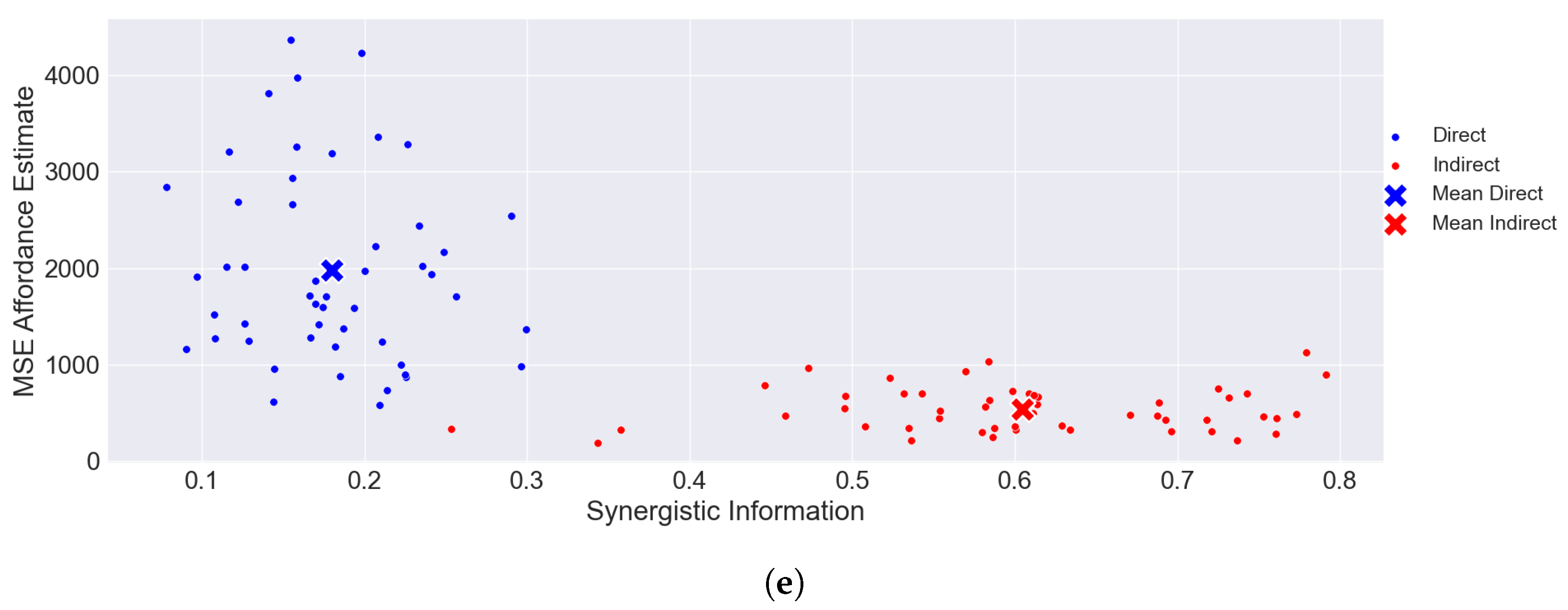
6.2. CIFAR-100
7. Discussion
7.1. Direct Perception and Synergistic Information in Nature
7.2. Direct Perception and the Global Array
7.3. Real Multimodal Data to Study Information Interaction
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Akagi, M. Cognition as the Sensitive Management of an Agent’s Behavior. Philos. Psychol. 2022, 35, 718–741. [Google Scholar] [CrossRef]
- Barack, D.L.; Krakauer, J.W. Two Views on the Cognitive Brain. Nat. Rev. Neurosci. 2021, 22, 359–371. [Google Scholar] [CrossRef]
- Anderson, J.R. The Adaptive Character of Thought; Lawrence Erlbaum Associates, Publishers: Hillsdale, NJ, USA, 1990. [Google Scholar]
- Favela, L.H.; Machery, E. Investigating the Concept of Representation in the Neural and Psychological Sciences. Front. Psychol. 2023, 14, 1165622. [Google Scholar]
- Fodor, J.A. The Language of Thought, 1st ed.; Harvard University Press: Cambridge, MA, USA, 1980. [Google Scholar]
- Millikan, R.G. Language, Thought and Other Biological Categories; The MIT Press: Cambridge, MA, USA, 1984. [Google Scholar]
- Shea, N. Representation in Cognitive Science; Oxford University Press: Oxford, UK, 2018. [Google Scholar]
- Quilty-Dunn, J.; Porot, N.; Mandelbaum, E. The Best Game in Town: The Reemergence of the Language-of-Thought Hypothesis across the Cognitive Sciences. Behav. Brain Sci. 2023, 46, e261. [Google Scholar] [CrossRef]
- Chemero, A. Radical Embodied Cognitive Science; MIT Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Wilson, A.D.; Golonka, S. Embodied Cognition Is Not What You Think It Is. Front. Psychol. 2013, 4, 58. [Google Scholar] [CrossRef]
- Newen, A.; Bruin, L.D.; Gallagher, S. (Eds.) The Oxford Handbook of 4E Cognition; Oxford Library of Psychology, Oxford University Press: Oxford, UK, 2018. [Google Scholar]
- Fajen, B.R.; Riley, M.A.; Turvey, M.T. Information, Affordances, and the Control of Action in Sport. Int. J. Sport Psychol. 2008, 40, 79–107. [Google Scholar]
- Beer, R.D.; Williams, P.L. Information Processing and Dynamics in Minimally Cognitive Agents. Cogn. Sci. 2015, 39, 1–38. [Google Scholar] [CrossRef]
- Stephen, D.G.; Boncoddo, R.A.; Magnuson, J.S.; Dixon, J.A. The Dynamics of Insight: Mathematical Discovery as a Phase Transition. Mem. Cogn. 2009, 37, 1132–1149. [Google Scholar] [CrossRef]
- Gibson, J.J. The Ecological Approach to Visual Perception: Classic Edition; Psychology Press: London, UK, 2014. [Google Scholar]
- Turvey, M.T.; Shaw, R.E.; Reed, E.S.; Mace, W.M. Ecological Laws of Perceiving and Acting: In Reply to Fodor and Pylyshyn (1981). Cognition 1981, 9, 237–304. [Google Scholar] [PubMed]
- Heras-Escribano, M. The Philosophy of Affordances; Springer International Publishing: Berlin, Germany, 2019. [Google Scholar] [CrossRef]
- Stoffregen, T.A.; Bardy, B.G. On Specification and the Senses. Behav. Brain Sci. 2001, 24, 195–213. [Google Scholar] [CrossRef]
- Bruineberg, J.; Chemero, A.; Rietveld, E. General ecological information supports engagement with affordances for ‘higher’cognition. Synthese 2019, 196, 5231–5251. [Google Scholar] [PubMed]
- Mace, W.M. JJ Gibson’s Ecological Theory of Information Pickup: Cognition from the Ground Up. In Approaches to Cognition: Contrasts and Controversies; Knapp, T.J., Robertson, L.C., Eds.; Lawrence Erlbaum Associates, Publishers: Hillsdale, NJ, USA, 1986; pp. 137–157. [Google Scholar]
- Shaw, R.; Turvey, M.T.; Mace, W.M. Ecological Psychology: The Consequence of a Commitment to Realism. In Cognition and the Symbolic Processes; Weimer, W., Palermo, D., Eds.; Lawrence Erlbaum Associates, Inc.: Hillsdale, NJ, USA, 1982; Volume 2, pp. 159–226. [Google Scholar]
- Gibson, J. The Senses Considered as Perceptual Systems. In The Senses Considered as Perceptual Systems; Houghton Mifflin: Boston, MA, USA, 1966. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Ehrlich, D.A.; Schneider, A.C.; Priesemann, V.; Wibral, M.; Makkeh, A. A Measure of the Complexity of Neural Representations Based on Partial Information Decomposition. arXiv 2023, arXiv:2209.10438. [Google Scholar]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar]
- Williams, P.L.; Beer, R.D. Nonnegative decomposition of multivariate information. arXiv 2010, arXiv:1004.2515. [Google Scholar]
- Griffith, V.; Koch, C. Quantifying Synergistic Mutual Information. In Guided Self-Organization: Inception; Prokopenko, M., Ed.; Emergence, Complexity and Computation; Springer: Berlin/Heidelberg, Germany, 2014; pp. 159–190. [Google Scholar] [CrossRef]
- Bertschinger, N.; Rauh, J.; Olbrich, E.; Jost, J.; Ay, N. Quantifying Unique Information. Entropy 2014, 16, 2161–2183. [Google Scholar] [CrossRef]
- Jaynes, E.T. On the rationale of maximum-entropy methods. Proc. IEEE 1982, 70, 939–952. [Google Scholar]
- Chechik, G.; Globerson, A.; Anderson, M.; Young, E.; Nelken, I.; Tishby, N. Group redundancy measures reveal redundancy reduction in the auditory pathway. In Advances in Neural Information Processing Systems; NIPS: Cambridge, MA, USA, 2001; Volume 14. [Google Scholar]
- McGill, W. Multivariate Information Transmission. Trans. IRE Prof. Group Inf. Theory 1954, 4, 93–111. [Google Scholar] [CrossRef]
- Rosas, F.E. Quantifying High-Order Interdependencies via Multivariate Extensions of the Mutual Information. Phys. Rev. E 2019, 100, 032305. [Google Scholar] [CrossRef] [PubMed]
- Varley, T.F.; Pope, M.; Faskowitz, J.; Sporns, O. Multivariate Information Theory Uncovers Synergistic Subsystems of the Human Cerebral Cortex. Commun. Biol. 2023, 6, 1–12. [Google Scholar] [CrossRef]
- Sims, C.R. Rate–Distortion Theory and Human Perception. Cognition 2016, 152, 181–198. [Google Scholar]
- Genewein, T.; Leibfried, F.; Grau-Moya, J.; Braun, D.A. Bounded rationality, abstraction, and hierarchical decision-making: An information-theoretic optimality principle. Front. Robot. AI 2015, 2, 27. [Google Scholar]
- Lieder, F.; Griffiths, T.L. Resource-rational analysis: Understanding human cognition as the optimal use of limited computational resources. Behav. Brain Sci. 2020, 43, e1. [Google Scholar]
- Zhou, D.; Lynn, C.W.; Cui, Z.; Ciric, R.; Baum, G.L.; Moore, T.M.; Roalf, D.R.; Detre, J.A.; Gur, R.C.; Gur, R.E.; et al. Efficient coding in the economics of human brain connectomics. Netw. Neurosci. 2022, 6, 234–274. [Google Scholar]
- Shannon, C.E. Coding theorems for a discrete source with a fidelity criterion. IRE Nat. Conv. Rec. 1959, 4, 1. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley: New York, NY, USA, 2006. [Google Scholar]
- Claramunt, C. A spatial form of diversity. In Proceedings of the Spatial Information Theory: International Conference, COSIT 2005, Ellicottville, NY, USA, 14–18 September 2005; Proceedings 7; Springer: Berlin, Germany, 2005; pp. 218–231. [Google Scholar]
- James, R.G.; Ellison, C.J.; Crutchfield, J.P. dit: A Python package for discrete information theory. J. Open Source Softw. 2018, 3, 738. [Google Scholar] [CrossRef]
- Altieri, L.; Cocchi, D.; Roli, G. Spatentropy: Spatial entropy measures in r. arXiv 2018, arXiv:1804.05521. [Google Scholar]
- Krizhevsky, A.; Hinton, G. Learning Multiple Layers of Features from Tiny Images; University of Toronto: Toronto, ON, Canada, 2009. [Google Scholar]
- Laughlin, S. A Simple Coding Procedure Enhances a Neuron’s Information Capacity. Zeitschrift für Naturforschung C 1981, 36, 910–912. [Google Scholar] [CrossRef]
- Barlow, H.B. Possible Principles Underlying the Transformation of Sensory Messages; MIT Press: Cambridge, MA, USA, 1961; Volume 1, pp. 217–234. [Google Scholar]
- Campbell, S.A.; Borden, J.H. Additive and synergistic integration of multimodal cues of both hosts and non-hosts during host selection by woodboring insects. Oikos 2009, 118, 553–563. [Google Scholar]
- Nikbakht, N.; Tafreshiha, A.; Zoccolan, D.; Diamond, M.E. Supralinear and supramodal integration of visual and tactile signals in rats: Psychophysics and neuronal mechanisms. Neuron 2018, 97, 626–639. [Google Scholar] [PubMed]
- Noppeney, U. Perceptual inference, learning, and attention in a multisensory world. Annu. Rev. Neurosci. 2021, 44, 449–473. [Google Scholar]
- Chen, Y.; Spence, C. Assessing the role of the ‘unity assumption’ on multisensory integration: A review. Front. Psychol. 2017, 8, 445. [Google Scholar]
- Choi, I.; Lee, J.Y.; Lee, S.H. Bottom-up and top-down modulation of multisensory integration. Curr. Opin. Neurobiol. 2018, 52, 115–122. [Google Scholar] [PubMed]
- Stein, B.E.; Stanford, T.R. Multisensory integration: Current issues from the perspective of the single neuron. Nat. Rev. Neurosci. 2008, 9, 255–266. [Google Scholar] [PubMed]
- Watkins, S.; Shams, L.; Tanaka, S.; Haynes, J.D.; Rees, G. Sound Alters Activity in Human V1 in Association with Illusory Visual Perception. NeuroImage 2006, 31, 1247–1256. [Google Scholar] [CrossRef]
- Ernst, M.O.; Bülthoff, H.H. Merging the senses into a robust percept. Trends Cogn. Sci. 2004, 8, 162–169. [Google Scholar]



| Y | ||
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
| Strategy | ||||||
|---|---|---|---|---|---|---|
| Direct | 0.44 | 0.25 | 0 | 0 | 1 | 1 |
| Indirect | 0.09 | 1 | 1 | 1 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Llanza Varona, M.; Martínez, M. Synergy Makes Direct Perception Inefficient. Entropy 2024, 26, 708. https://doi.org/10.3390/e26080708
de Llanza Varona M, Martínez M. Synergy Makes Direct Perception Inefficient. Entropy. 2024; 26(8):708. https://doi.org/10.3390/e26080708
Chicago/Turabian Stylede Llanza Varona, Miguel, and Manolo Martínez. 2024. "Synergy Makes Direct Perception Inefficient" Entropy 26, no. 8: 708. https://doi.org/10.3390/e26080708
APA Stylede Llanza Varona, M., & Martínez, M. (2024). Synergy Makes Direct Perception Inefficient. Entropy, 26(8), 708. https://doi.org/10.3390/e26080708






