Research on a Transformer Vibration Fault Diagnosis Method Based on Time-Shift Multiscale Increment Entropy and CatBoost
Abstract
1. Introduction
2. TSMIE–CatBoost
2.1. Theory Background
2.1.1. Incremental Entropy
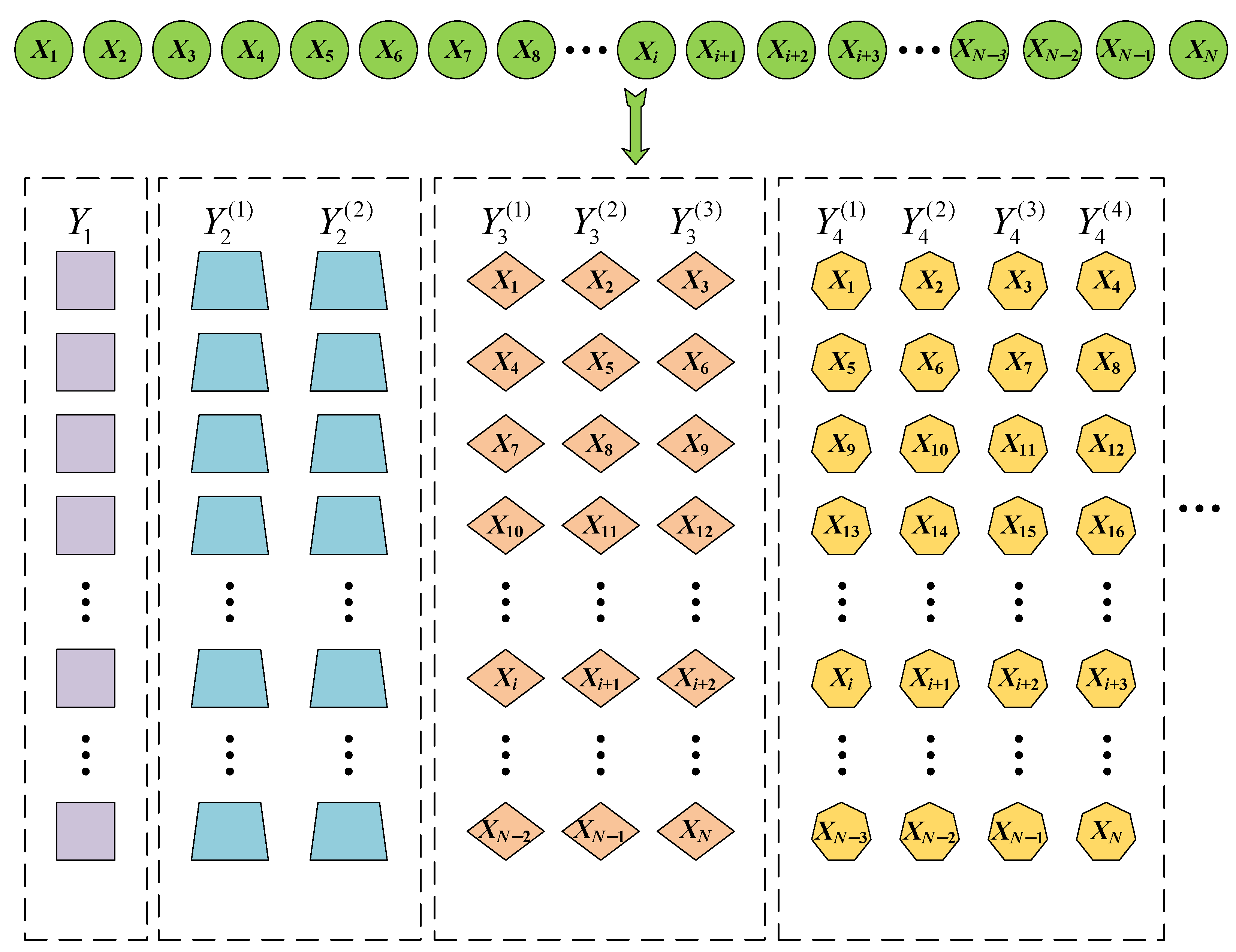
2.1.2. Multiscale Increment Entropy
2.1.3. Time-Shift Multiscale Increment Entropy
| Algorithm 1 Time-shift multiscale increment entropy. |
| Input: (1) : Time series (2) : Embedding dimension (3) : Resolution parameter (4) : Scale factor |
| Running process: |
| 1 for do |
| 2 Construct time shifted subsequences , obtaining the set of time shifted sequences |
| 3 for do |
| 4 Construct incremental time series in each time shifted sequence set |
| 5 Divide incremental time series into incremental vectors |
| 6 Map to |
| 7 Calculate the relative frequency of each unique character |
| 8 Calculate the IE |
| 9 end for |
| 10 Calculate TSMIE |
| 11 end for |
| Output: TSMIE values |
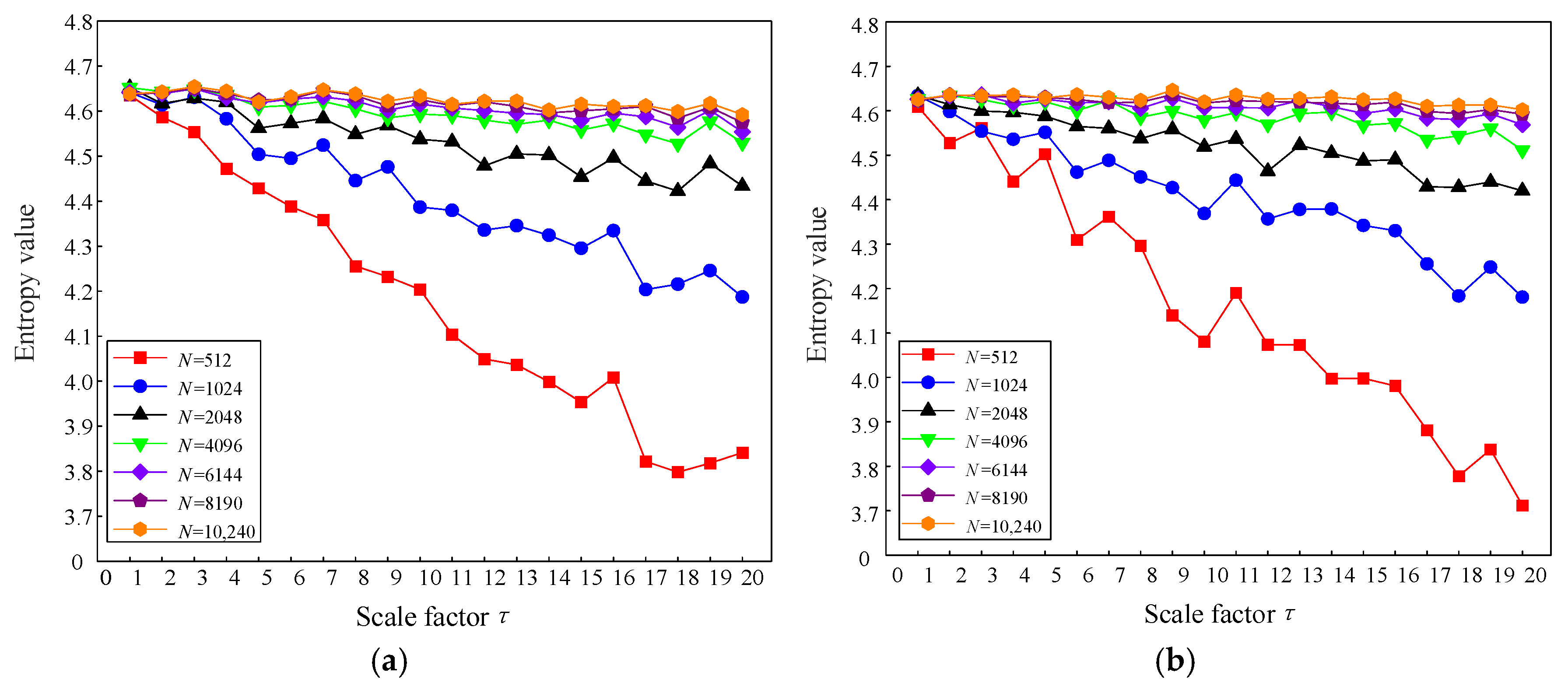
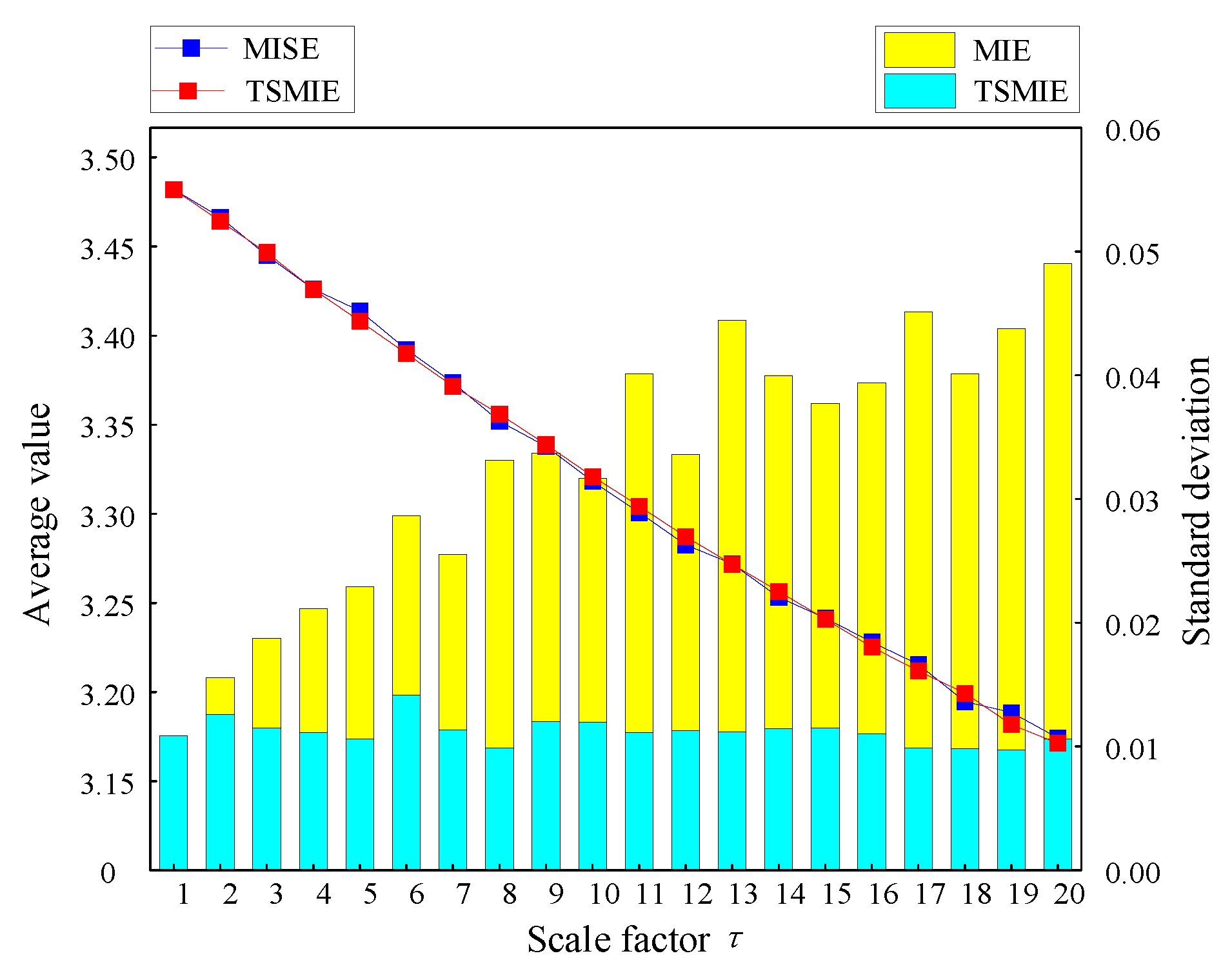
2.2. Influence Analysis of TSMIE Parameters
2.3. CatBoost Model
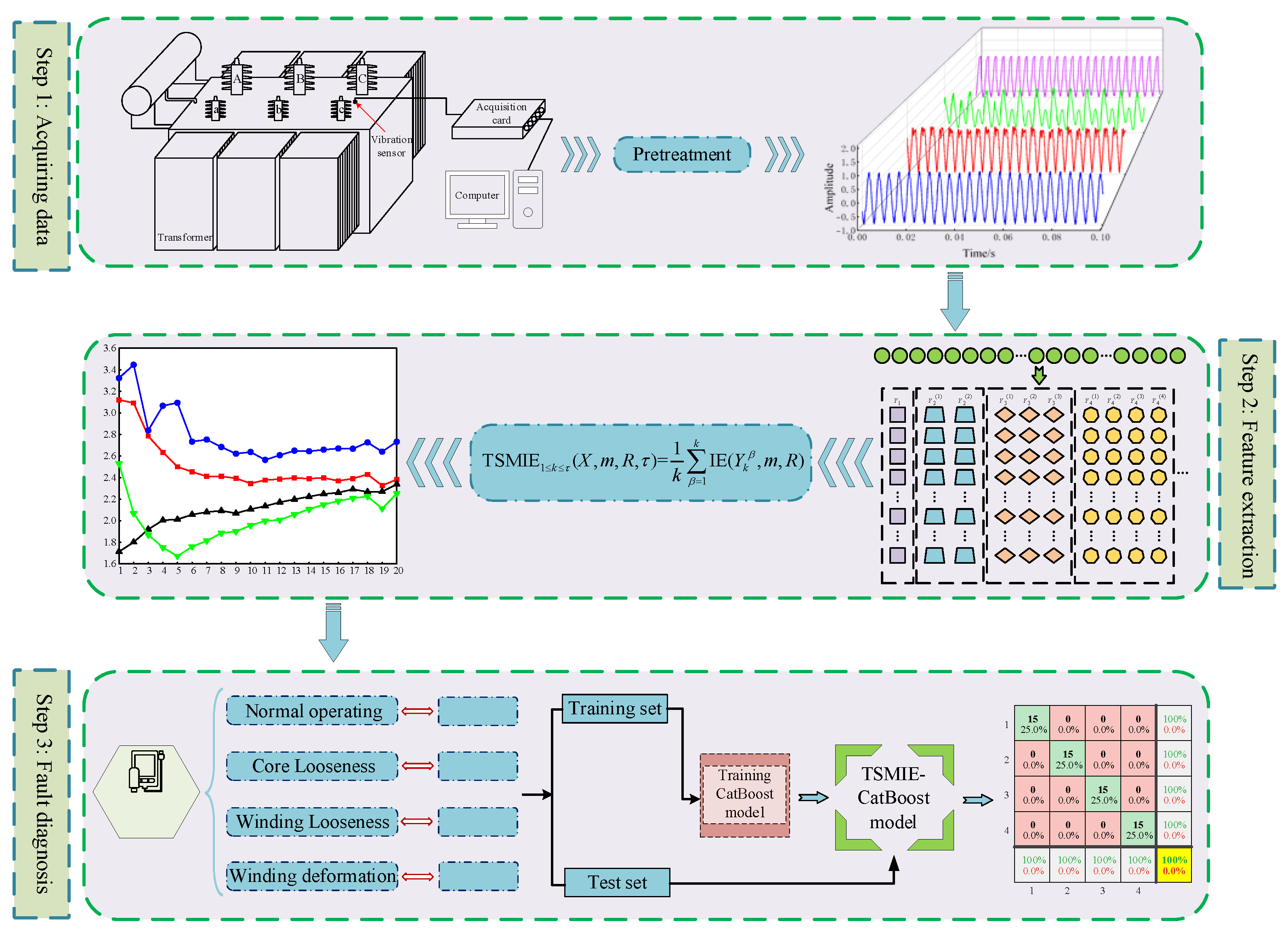
3. A Transformer Fault Diagnosis Model Based on TSMIE–CatBoost
4. Signal Analysis
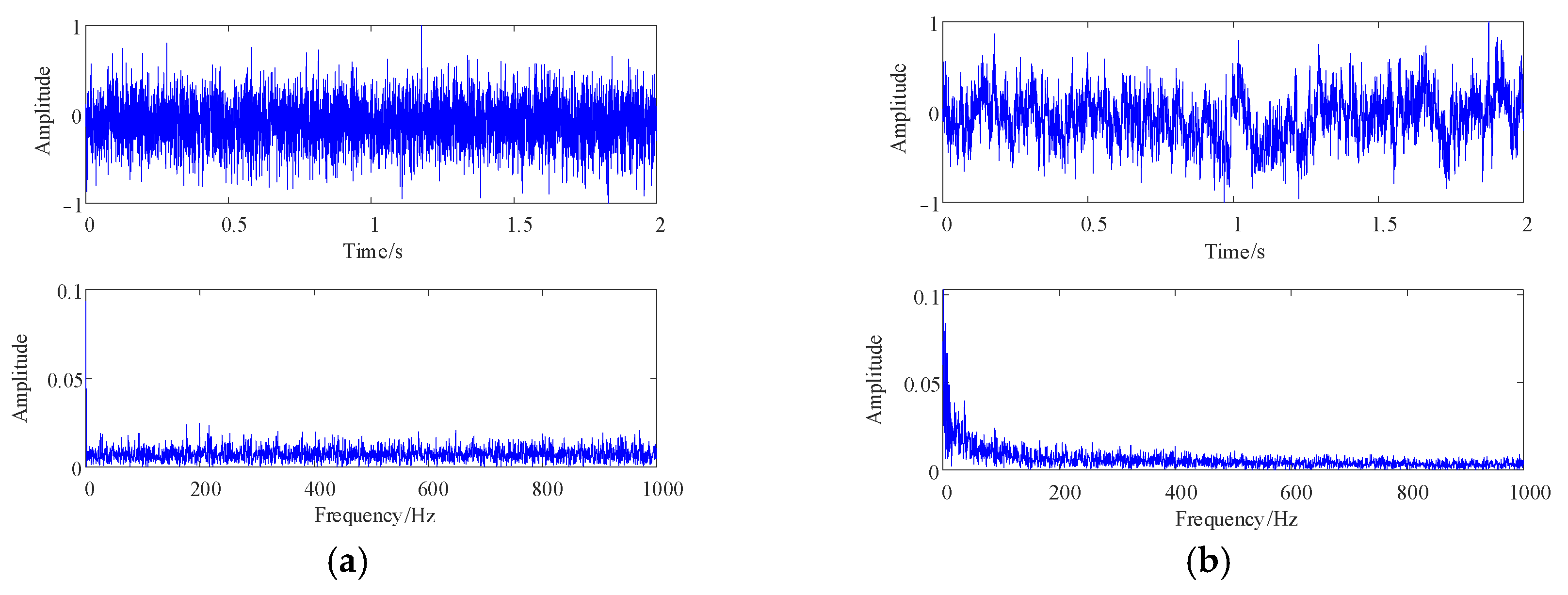
4.1. Transformer Vibration Signal Collection
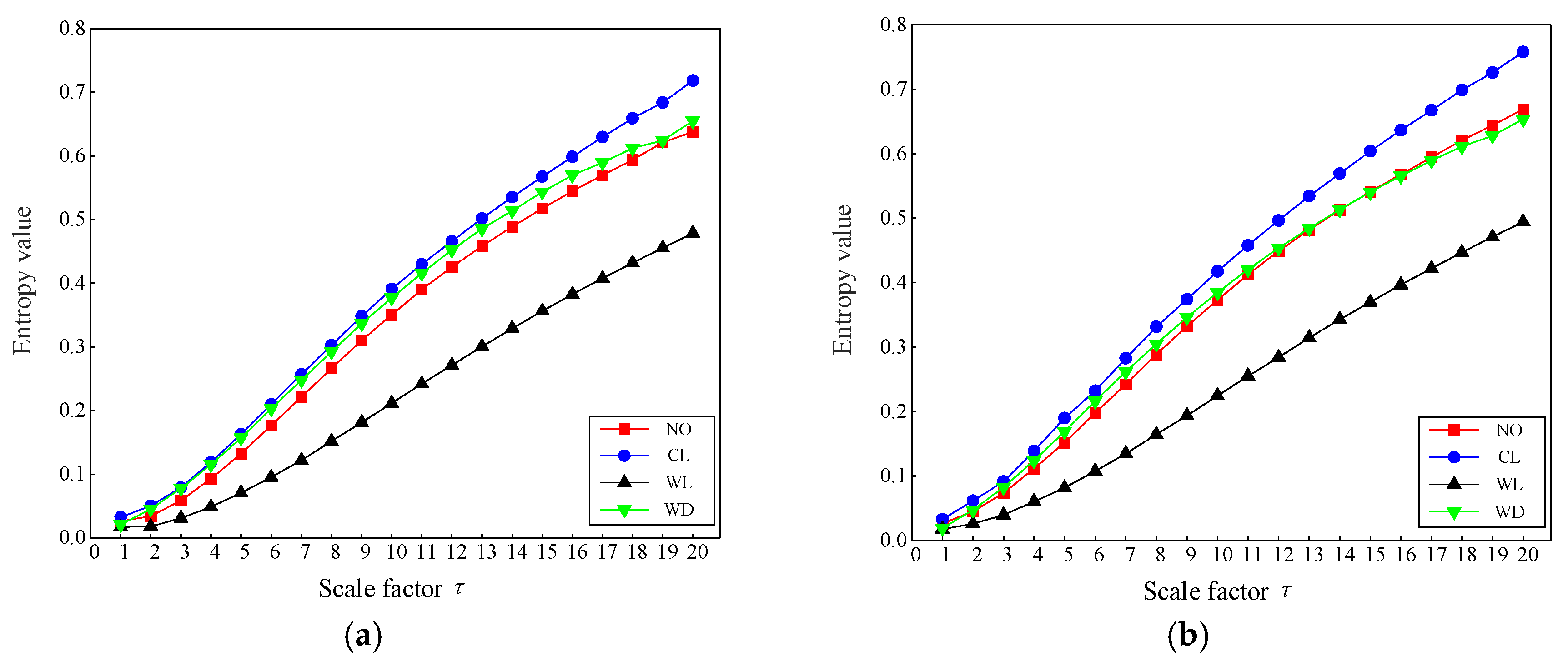
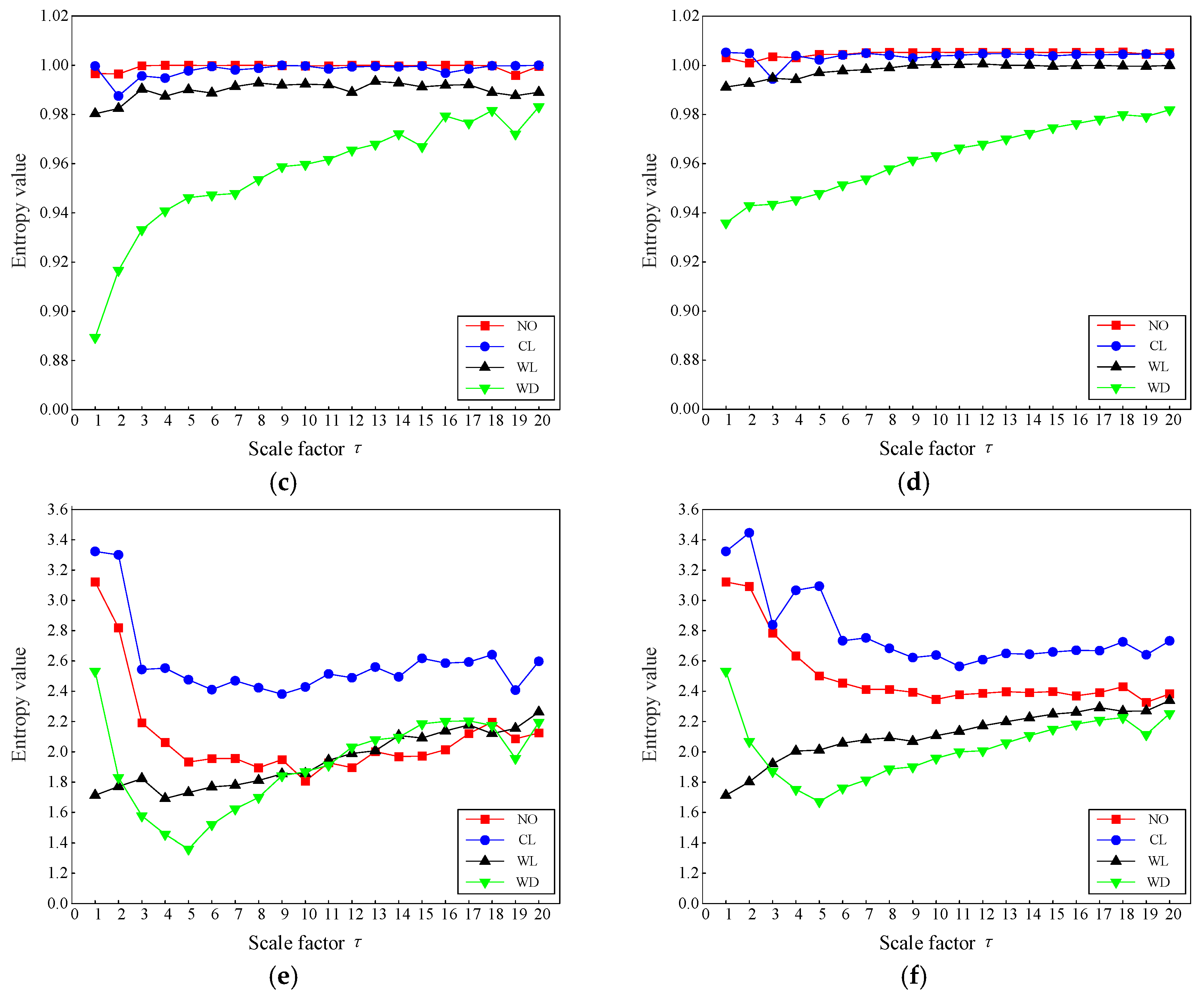
4.2. TSMIE Feature Extraction
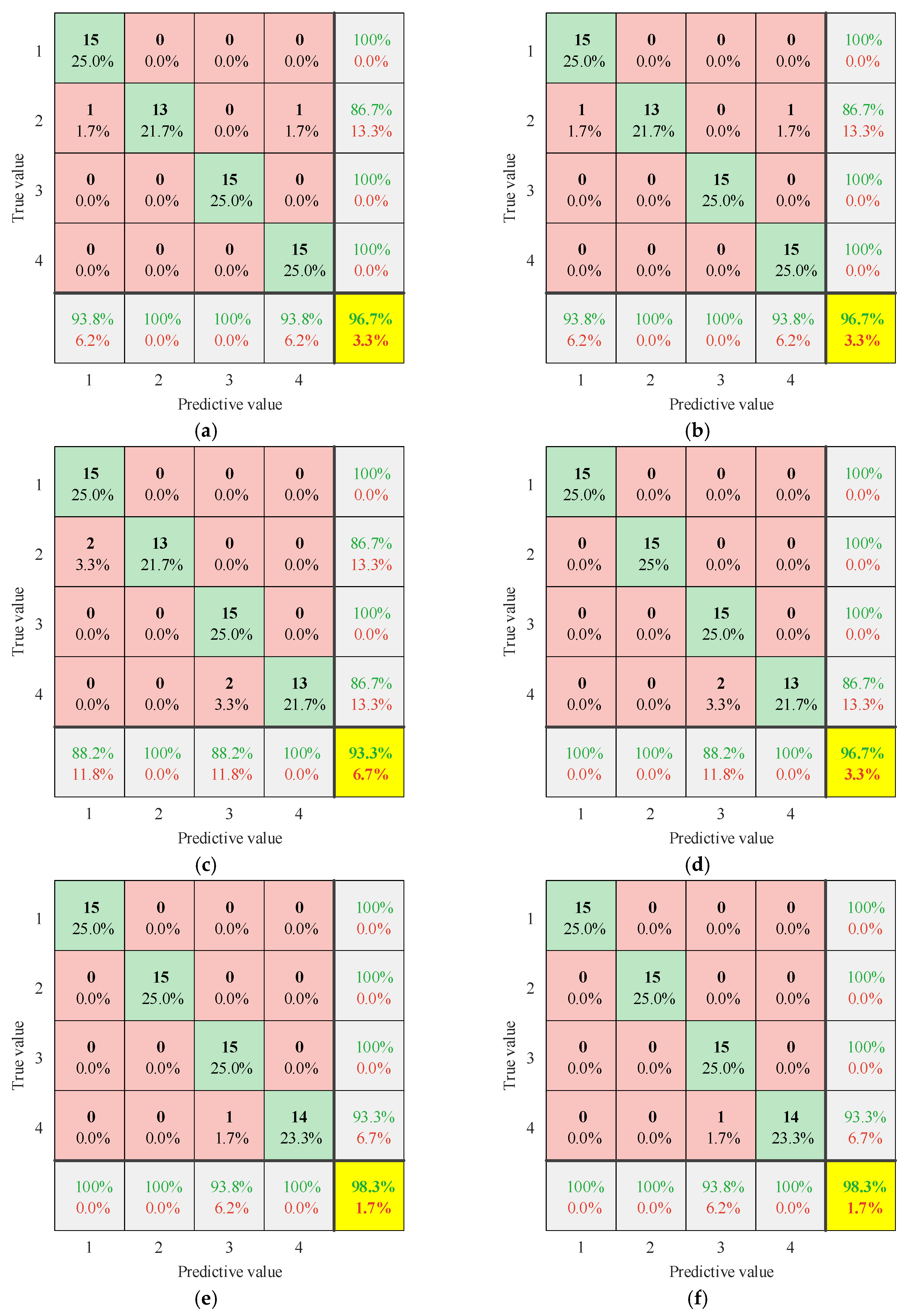
4.3. Transformer Vibration Signal Fault Diagnosis
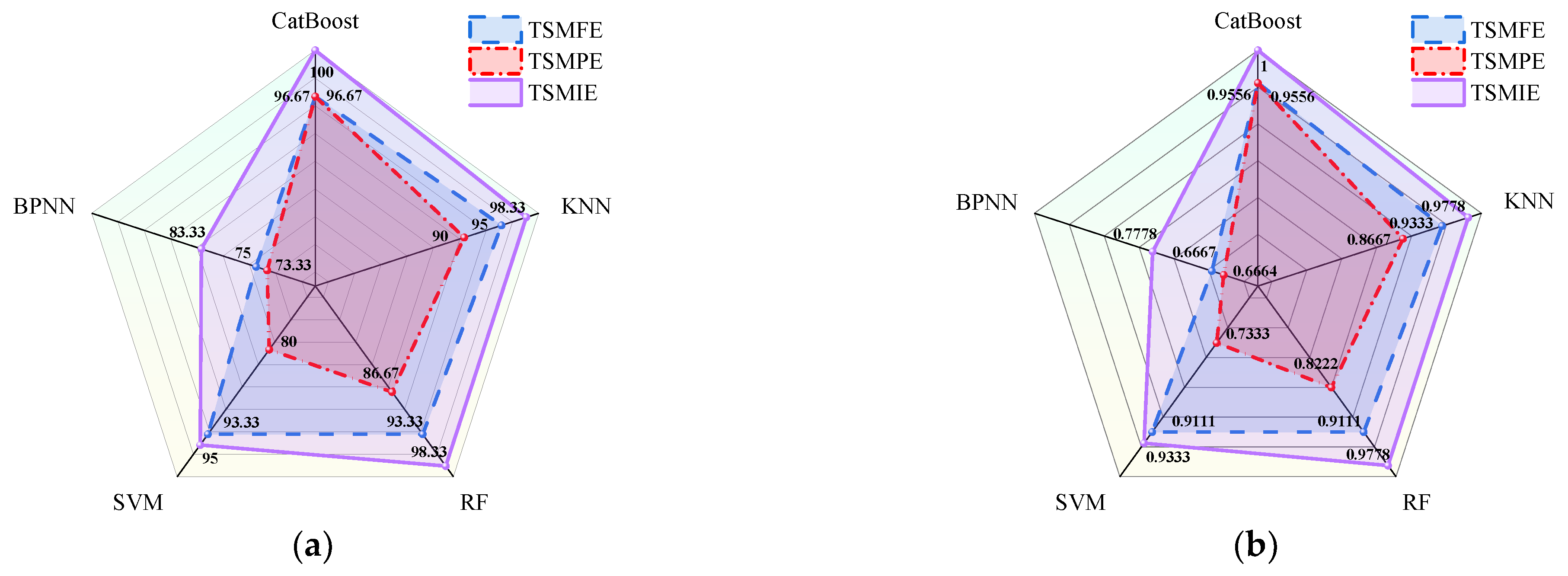
4.4. Comparative Analysis of Different Fault Diagnosis Models
5. Conclusions
- By addressing the issue of signal loss and incomplete feature extraction in the coarse-graining process of MIE, this paper introduces TSMIE by integrating the concept of time-shift. The influence of different parameters on TSMIE was analyzed by applying simulation signals, and its optimal parameters were determined. Finally, a comparison was made with MIE in terms of the means and standard deviations. The results showed that TSMIE had a much smaller standard deviation than MIE, which could provide a more stable description of signal dynamic changes, verifying TSMIE’s good signal feature extraction ability and stability.
- By utilizing TSMIE for feature extraction from vibration signals under normal and fault conditions of a transformer, comparative analyses were conducted with MFE, TSMFE, MPE, TSMPE, and MIE in terms of the entropy distribution, dimension reduction visualization, and noise robustness. The results showed that, compared with other entropy values, TSMIE can effectively distinguish normal operation, iron core looseness, winding looseness, and winding deformation faults in a transformer. After a T-SNE dimensionality reduction, the data aggregation degree of TSMIE was the best, and it could effectively distinguish the four situations. Moreover, TSMIE had the shortest running time and the highest diagnostic accuracy under different noise conditions, verifying the accuracy and noise robustness of TSMIE in extracting features from transformer vibration signals.
- CatBoost was integrated with TSMIE for the transformer vibration fault diagnosis. Comparative analyses were conducted with the MFE–CatBoost, TSMFE–CatBoost, MPE–CatBoost, TSMPE–CatBoost, and MIE–CatBoost models. BPNN, SVM, RF, KNN, and CatBoost were also compared for transformer fault diagnoses. The results showed that the TSMIE–CatBoost model exhibited a good performance in its accuracy and Kappa coefficient, as well as its recall rate, precision rate, false negative rate, and false positive rate in the confusion matrix, verifying the superiority of the proposed model for transformer fault diagnoses. This indicates that the fault diagnosis model proposed in this paper is an excellent method and provides new ideas for transformer fault diagnoses.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Hong, K.; Jin, M.; Huang, H. Transformer winding fault diagnosis using vibration image and deep learning. IEEE Trans. Power Deliv. 2021, 36, 676–685. [Google Scholar] [CrossRef]
- Li, C.; Chen, J.; Yang, C.; Yang, J.; Liu, Z.; Davari, P. Convolutional neural network-based transformer fault diagnosis using vibration signals. Sensors 2023, 23, 4781. [Google Scholar] [CrossRef]
- Pan, C.; Zhao, T.; Cai, G.W.; Li, G.T.; Yang, R.Y. Electromagnetic Vibration Characteristics Of Three-Phase Transformer Windings In AC/DC Hybrid Environment. J. Northeast Electr. Power Univ. 2023, 43, 45–54. [Google Scholar]
- Borucki, S. Diagnosis of technical condition of power transformers based on the analysis of vibroacoustic signals measured in transient operating conditions. IEEE Trans. Power Deliv. 2012, 27, 670–676. [Google Scholar] [CrossRef]
- Yoon, J.T.; Youn, B.D.; Park, K.M.; Lee, W.R. Vibration-based robust health diagnostics for mechanical failure modes of power transformers. In Proceedings of the IEEE Conference on Prognostics and Health Management, Gaithersburg, MD, USA, 24–27 June 2013; pp. 1–5. [Google Scholar]
- Huerta-Rosales, J.R.; Granados-Lieberman, D.; García-Pérez, A.; Camarena-Martinez, D.; Amezquita-Sanchez, J.P.; Valtierra-Rodriguez, M. Short-circuited turn fault diagnosis in transformers by using vibration signals, statistical time features, and support vector machines on FPGA. Sensors 2021, 21, 3598. [Google Scholar] [CrossRef]
- Liu, X.; He, Y.; Wang, L. Adaptive transfer learning based on a two-stream densely connected residual shrinkage network for transformer fault diagnosis over vibration signals. Electronics 2021, 10, 2130. [Google Scholar] [CrossRef]
- Liu, X.; He, Y. Hierarchical dynamic aggregation graph modeling of vibration for semi-supervised fault diagnosis of power transformer. Meas. Sci. Technol. 2024, 35, 025019. [Google Scholar] [CrossRef]
- Li, L.; Zhu, Y.; Song, Y. Feature research of vibration signal of power transformer using multiscale entropy. J. Vib. Meas. Diagn. 2015, 35, 757–762+802–803. [Google Scholar]
- Shannon, C.E. A Mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol.-Heart Circ. Physiol. 2000, 278, 2039–2049. [Google Scholar] [CrossRef]
- Chen, W.; Wang, Z.; Xie, H.; Yu, W. Characterization of surface EMG signal based on fuzzy entropy. IEEE Trans. Neural Syst. Rehabil. Eng. 2007, 15, 266–272. [Google Scholar] [CrossRef]
- Jiang, J.; Shang, P.; Zhang, Z.; Li, X. Permutation entropy analysis based on Gini-Simpson index for financial time series. Phys. A Stat. Mech. Its Appl. 2017, 486, 273–283. [Google Scholar] [CrossRef]
- Rostaghi, M.; Ashory, M.R.; Azami, H. Application of dispersion entropy to status characterization of rotary machines. J. Sound Vib. 2019, 438, 291–308. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of biological signals. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2005, 71, 021906. [Google Scholar] [CrossRef]
- Zhu, X.; Zheng, J.; Pan, H.; Bao, J.; Han, M. Time-shift multiscale fuzzy entropy and Laplacian support vector machine based rolling bearing fault diagnosis. Entropy 2018, 20, 602. [Google Scholar] [CrossRef]
- Ye, Y.; Zhang, Y.; Wang, Q.; Wang, Z.; Teng, Z.; Zang, H. Fault diagnosis of high-speed train suspension systems using multiscale permutation entropy and linear local tangent space alignment. Mech. Syst. Signal Process. 2020, 138, 106565. [Google Scholar] [CrossRef]
- Chakraborty, S.M.; Mitra, D. Automated detection of epileptic seizures using multiscale and refined composite multiscale dispersion entropy. Chaos Solitons Fractals Appl. Sci. Eng. Interdiscip. J. Nonlinear Sci. 2021, 146, 110939. [Google Scholar]
- Liu, X.; Jiang, A.; Xu, N.; Xue, J. Increment entropy as a measure of complexity for time series. Entropy 2016, 18, 22. [Google Scholar] [CrossRef]
- Liu, X.; Wang, X.; Zhou, X.; Jiang, A. Appropriate use of the increment entropy for electrophysiological time series. Comput. Biol. Med. 2018, 95, 13–23. [Google Scholar] [CrossRef]
- Wang, X.; Liu, X.; Pang, W.; Jiang, A. multiscale increment entropy: An approach for quantifying the physiological complexity of biomedical time series. Inf. Sci. Int. J. 2022, 586, 279–293. [Google Scholar] [CrossRef]
- Pham, T.D. Time-Shift multiscale entropy analysis of physiological signals. Entropy 2017, 19, 257. [Google Scholar] [CrossRef]
- Jin, Y.; Wu, H.; Zheng, J.; Zhang, J.; Liu, Z. Power transformer fault diagnosis based on improved BP neural Network. Electronics 2023, 12, 3526. [Google Scholar] [CrossRef]
- Hong, K.S.; Huang, H.; Zhou, J.; Shen, Y.; Li, Y. A method of real-time fault diagnosis for power transformers based on vibration analysis. Meas. Sci. Technol. 2015, 26, 115011. [Google Scholar] [CrossRef]
- Malik, H.; Mishra, S. Selection of most relevant input parameters using principle component analysis for extreme learning machine based power transformer fault diagnosis model. Electr. Power Compon. Syst. 2017, 45, 1339–1352. [Google Scholar] [CrossRef]
- Kherif, O.; Benmahamed, Y.; Teguar, M.; Boubakeur, A.; Ghoneim, S.S.M. Accuracy improvement of power transformer faults diagnostic using KNN classifier with decision tree principle. IEEE Access 2021, 9, 81693–81701. [Google Scholar] [CrossRef]
- Zhang, M.; Chen, W.; Zhang, Y.; Liu, F.; Yu, D.; Zhang, C.; Gao, L. Fault diagnosis of oil-immersed power transformer based on Difference-mutation Brain Storm Optimized Catboost model. IEEE Access 2021, 9, 168767–168782. [Google Scholar] [CrossRef]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. Catboost: Unbiased boosting with categorical features. Adv. Neural Inf. Process. Syst. 2018, 31, 121–128. [Google Scholar]
- Huang, G.; Wu, L.; Ma, X.; Zhang, W.; Fan, J.; Zeng, W.; Zhou, H. Evaluation of Catboost method for prediction of reference evapotranspiration in humid regions. J. Hydrol. 2019, 574, 1029–1041. [Google Scholar] [CrossRef]
- Anowar, F.; Sadaoui, S.; Selim, B. Conceptual and empirical comparison of dimensionality reduction algorithms (PCA, KPCA, LDA, MDS, SVD, LLE, ISOMAP, LE, ICA, t-SNE). Comput. Sci. Rev. 2021, 40, 100378. [Google Scholar] [CrossRef]





| Method | Advantages | Disadvantages |
|---|---|---|
| BPNN | Strong non-linear mapping capability; capable of handling non-linear and complex problems; excellent adaptability and versatility | Long training time; slow convergence speed; prone to local optima; sensitive to parameters; requires manual setting of network structure |
| SVM | Strong generalization ability; suitable for small-size, non-linear, and high-dimensional data | Long learning time; sensitive to parameters; requires data preprocessing |
| ELM | Fewer parameters; fast training speed; strong generalization ability; robust to noise | Weak stability; limited ability to process complex nonlinear data; unsuitable for data with special distributions |
| KNN | Requires no repeated model training; robust to noise | Sensitive to data dimensions; poor performance in handling high-dimensional and imbalanced data; slow convergence speed |
| Parameter | Values |
|---|---|
| Model | SZ-20,000/35 |
| Type | Three-phase |
| Rated Power | 20,000 kVA |
| Rated Voltage | 35 ± 3 × 2.5%/10 kV |
| No-load current | 0.43% |
| Impedance voltage | 8% |
| Category | Embedding Dimension m | Similarity Tolerance r | Gradient Parameter n | Time Delay d | Resolution Parameter R |
|---|---|---|---|---|---|
| MFE | 2 | 0.15 SD | 2 | 1 | — |
| TSMFE | 2 | 0.15 SD | 2 | 1 | — |
| MPE | 2 | — | — | 1 | — |
| TSMPE | 2 | — | — | 1 | — |
| MIE | 3 | — | — | — | 3 |
| TSMIE | 3 | — | — | — | 3 |
| MFE | MPE | MIE | TSMFE | TSMPE | TSMIE | |
|---|---|---|---|---|---|---|
| Noiseless | 274.89 | 10.92 | 8.56 | 824.78 | 93.70 | 85.17 |
| SNR = 15 dB | 278.95 | 9.73 | 8.93 | 824.45 | 100.56 | 94.78 |
| SNR = 20 dB | 291.12 | 10.07 | 8.98 | 883.72 | 89.58 | 88.39 |
| SNR = 25 dB | 292.78 | 10.25 | 8.73 | 883.63 | 84.18 | 85.78 |
| Diagnostic Model | SNR = 15 | SNR = 20 | SNR = 25 |
|---|---|---|---|
| MFE–CatBoost | 88.33% | 93.33% | 93.33% |
| TSMFE–CatBoost | 88.33% | 96.67% | 96.67% |
| MPE–CatBoost | 86.67% | 86.67% | 91.67% |
| TSMPE–CatBoost | 93.33% | 96.67% | 96.67% |
| MIE–CatBoost | 96.67% | 96.67% | 96.67% |
| TSMIE–CatBoost | 96.67% | 98.33% | 98.33% |
| Parameters | BPNN | SVM | RF | KNN |
|---|---|---|---|---|
| Network structure | 20-2-4 | - | - | - |
| Iterations | 1000 | - | - | - |
| Learning rate | 0.01 | - | - | - |
| Target training error | 0.000001 | - | - | - |
| Kernel function | - | RBF | - | - |
| Kernel function parameter | - | 0.01 | - | - |
| Penalty factor | - | 10 | - | - |
| Number of decision trees | - | - | 10 | - |
| Minimum number of leaves | - | - | 5 | - |
| Number of nearest neighbor samples | - | - | - | 4 |
| Diagnostic Model | Recall Rate | Precision Rate | False Negative Rate | False Positive Rate |
|---|---|---|---|---|
| TSMFE–BPNN | 75% | 60.45% | 25% | 14.55% |
| TSMPE–BPNN | 73.33% | 60.51% | 26.67% | 14.49% |
| TSMIE–BPNN | 83.33% | 90% | 16.67% | 10% |
| TSMFE–SVM | 93.33% | 94.12% | 6.67% | 5.88% |
| TSMPE–SVM | 80% | 83.77% | 20% | 16.23% |
| TSMIE–SVM | 95% | 95.83% | 5% | 4.17% |
| TSMFE–RF | 93.33% | 94.27% | 6.67% | 5.73% |
| TSMPE–RF | 86.67% | 89.58% | 13.33% | 10.42% |
| TSMIE–RF | 98.33% | 98.44% | 1.67% | 1.56% |
| TSMFE–KNN | 95% | 95.5% | 5% | 4.5% |
| TSMPE–KNN | 90% | 91.8% | 10% | 8.21% |
| TSMIE–KNN | 98.33% | 98.44% | 1.67% | 1.56% |
| TSMFE–CatBoost | 96.67% | 96.88% | 3.33% | 3.13% |
| TSMPE–CatBoost | 96.67% | 97.06% | 3.33% | 2.94% |
| TSMIE–CatBoost | 100% | 100% | 0% | 0% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shang, H.; Huang, T.; Wang, Z.; Li, J.; Zhang, S. Research on a Transformer Vibration Fault Diagnosis Method Based on Time-Shift Multiscale Increment Entropy and CatBoost. Entropy 2024, 26, 721. https://doi.org/10.3390/e26090721
Shang H, Huang T, Wang Z, Li J, Zhang S. Research on a Transformer Vibration Fault Diagnosis Method Based on Time-Shift Multiscale Increment Entropy and CatBoost. Entropy. 2024; 26(9):721. https://doi.org/10.3390/e26090721
Chicago/Turabian StyleShang, Haikun, Tao Huang, Zhiming Wang, Jiawen Li, and Shen Zhang. 2024. "Research on a Transformer Vibration Fault Diagnosis Method Based on Time-Shift Multiscale Increment Entropy and CatBoost" Entropy 26, no. 9: 721. https://doi.org/10.3390/e26090721
APA StyleShang, H., Huang, T., Wang, Z., Li, J., & Zhang, S. (2024). Research on a Transformer Vibration Fault Diagnosis Method Based on Time-Shift Multiscale Increment Entropy and CatBoost. Entropy, 26(9), 721. https://doi.org/10.3390/e26090721






