Effects of Particle Migration on the Relaxation of Shock Wave Collisions
Abstract
:1. Introduction
2. Computational Details
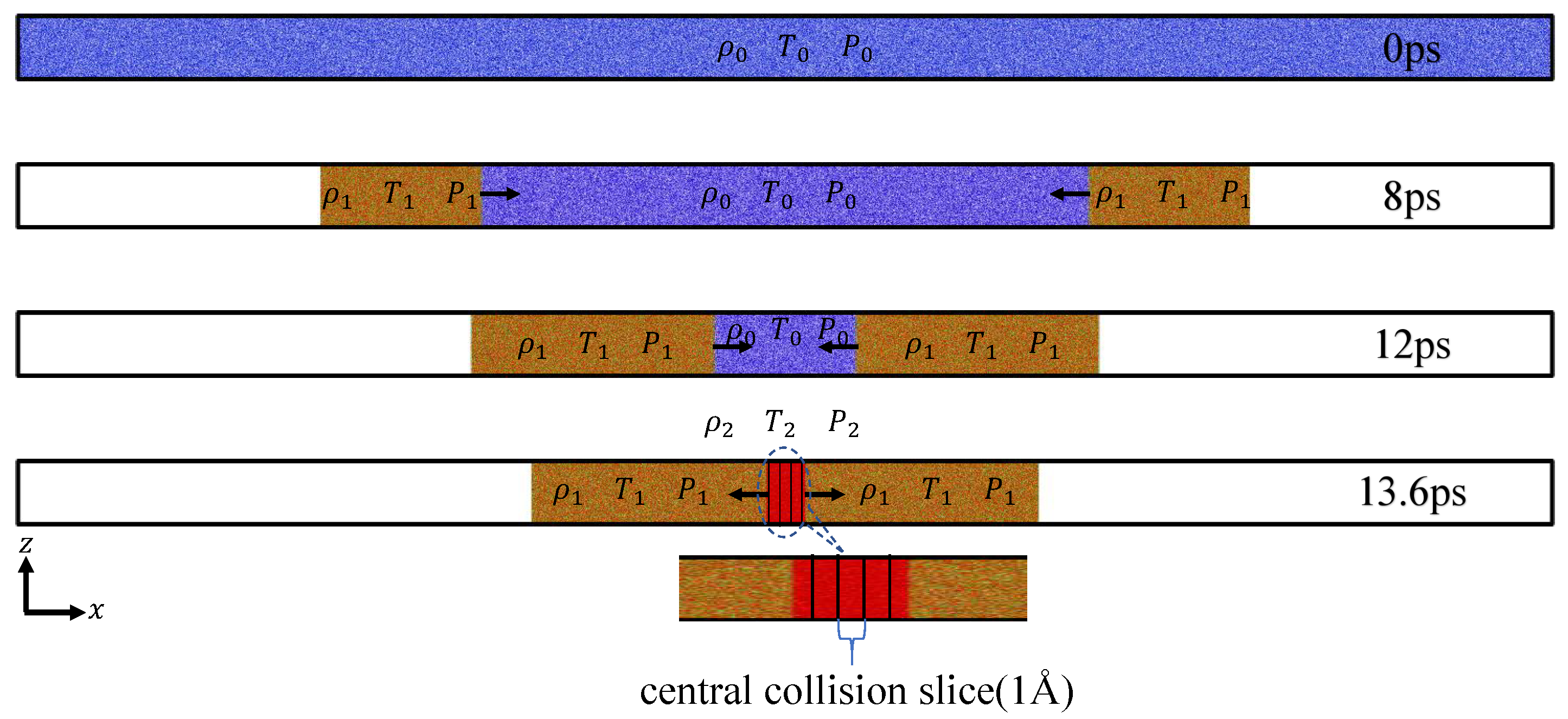
2.1. NEMD Configurations
2.2. Thermodynamic Statistical Methodologies
3. Results and Discussion
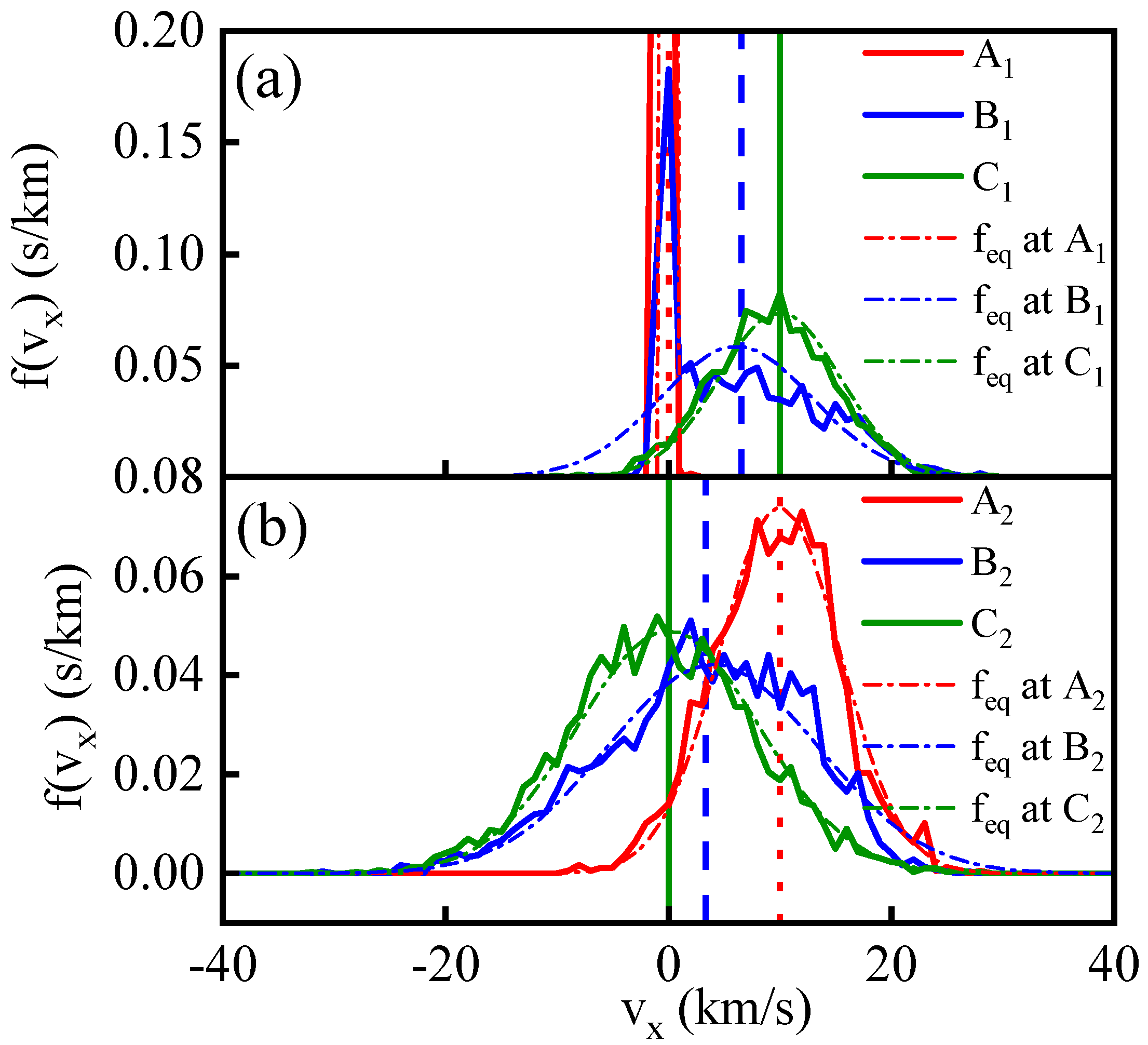
3.1. Overshoot Structure and Velocity Distribution
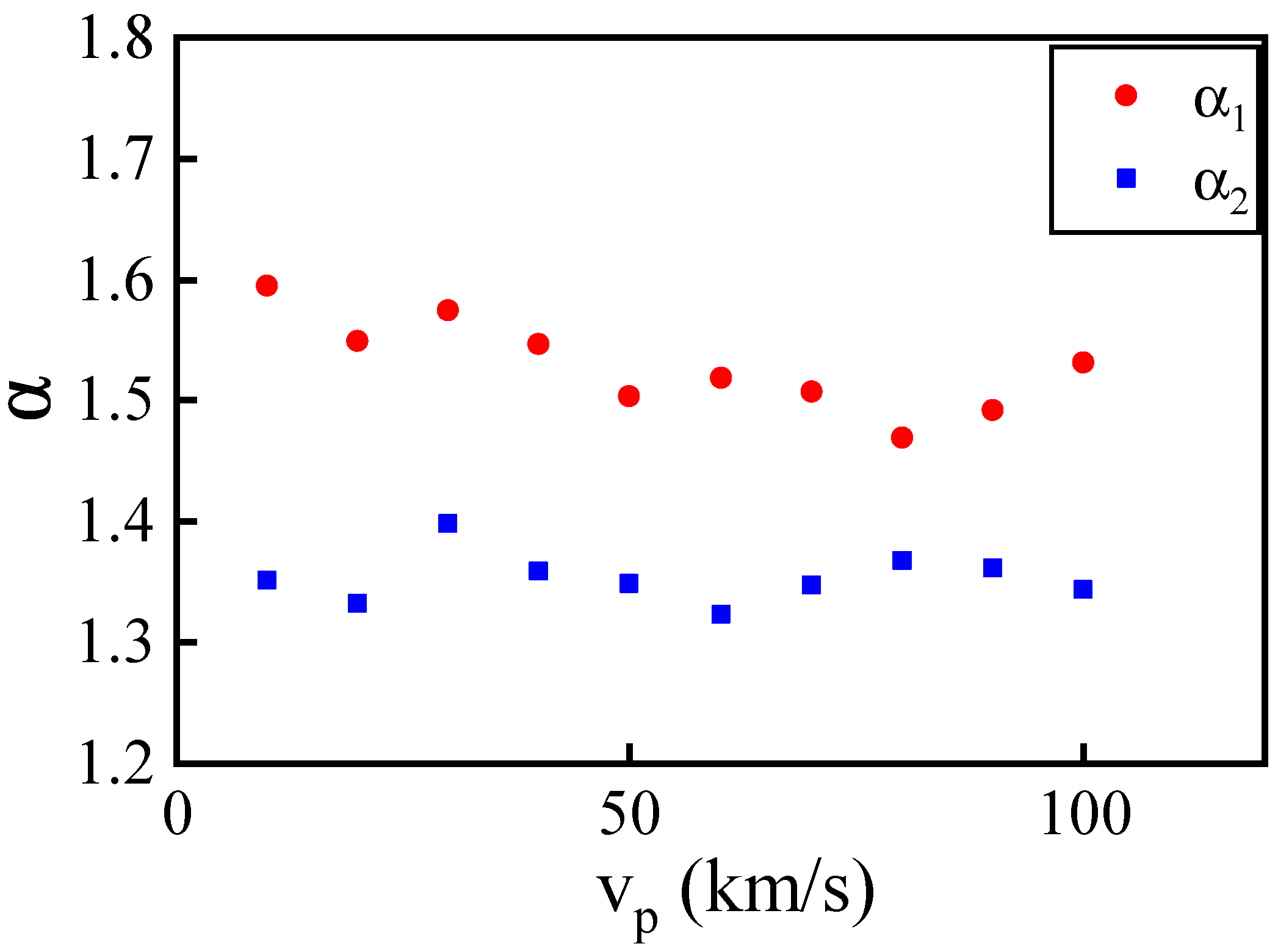
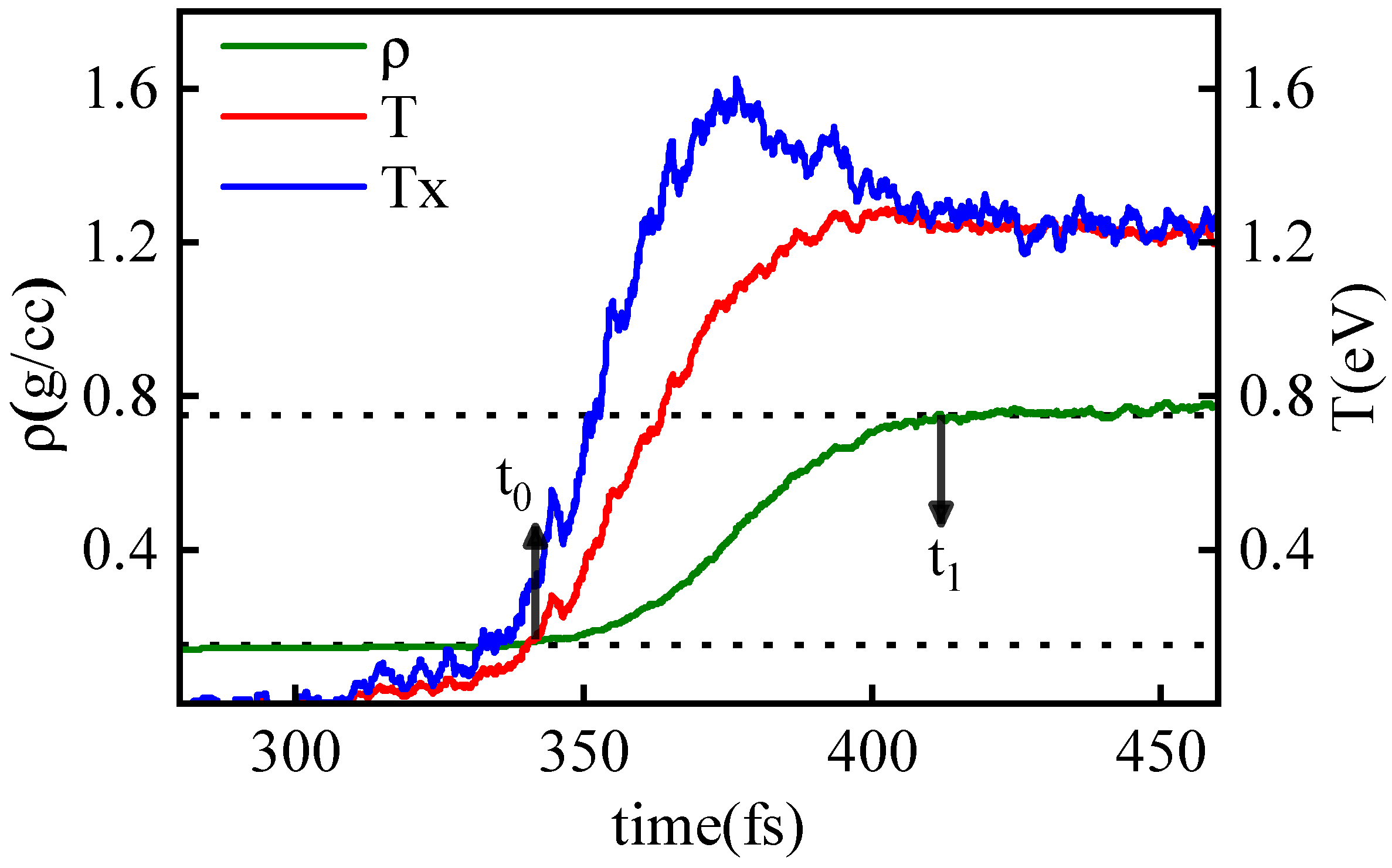
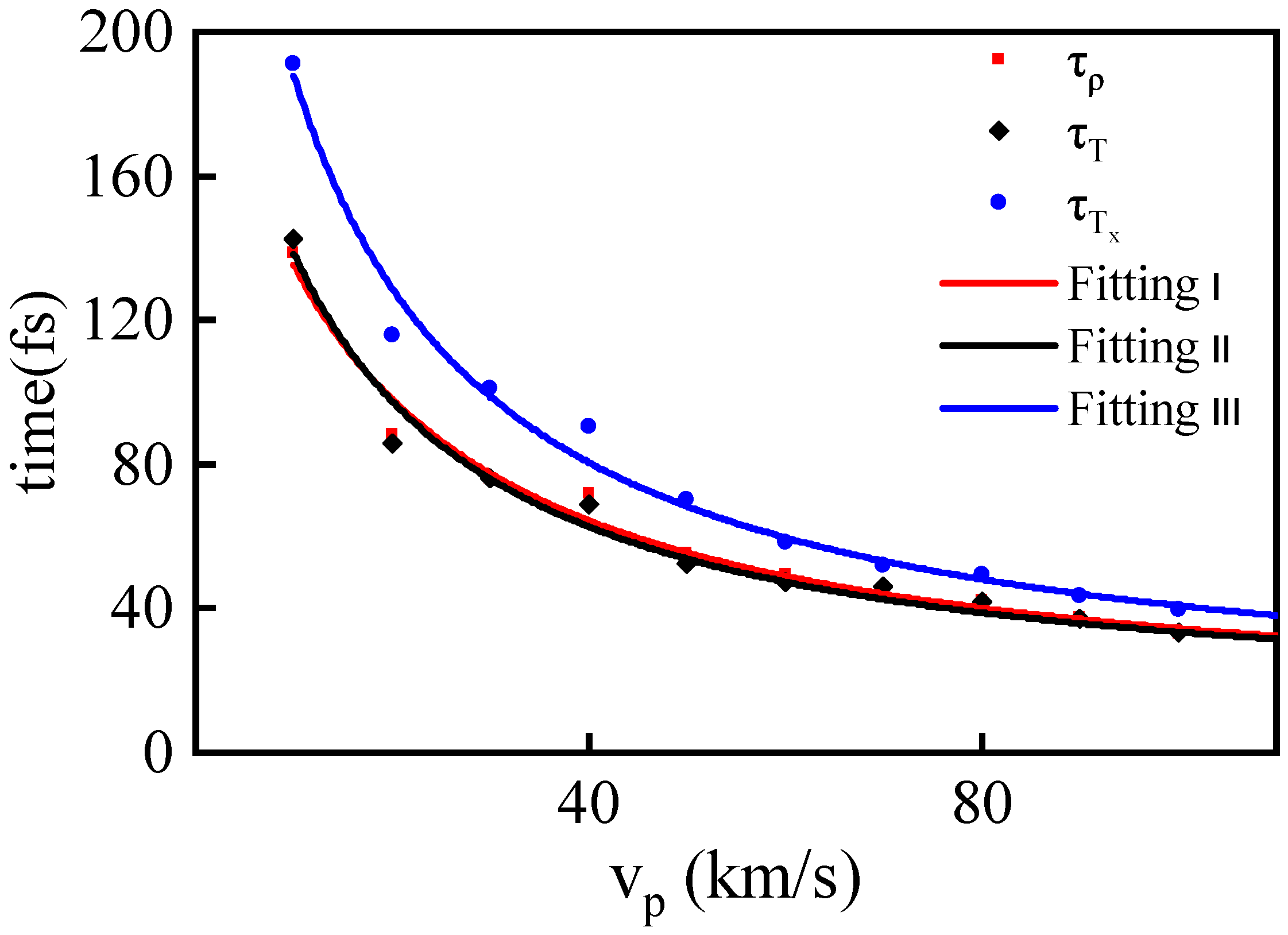
3.2. Relaxation Time under Shock Collision
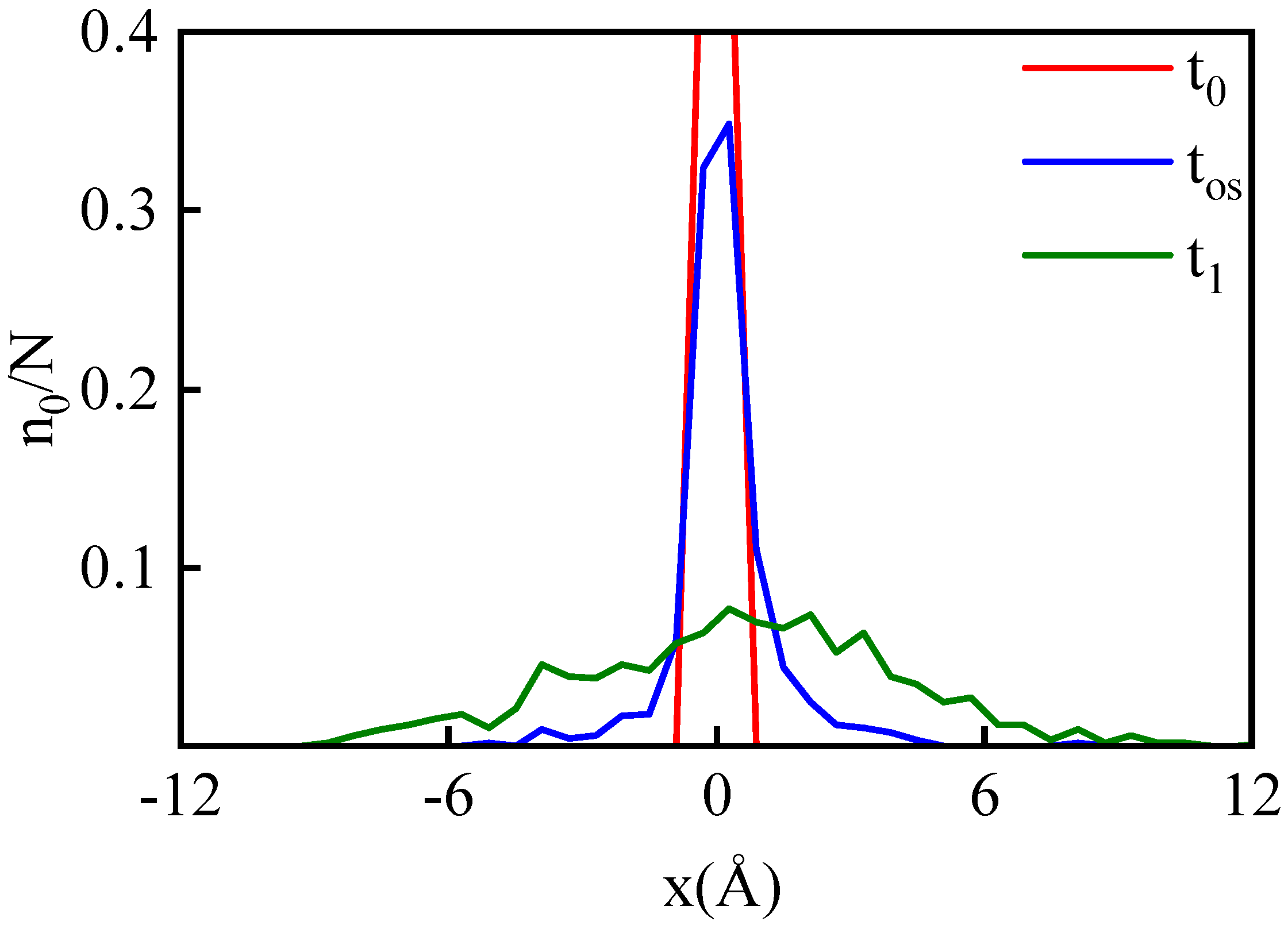
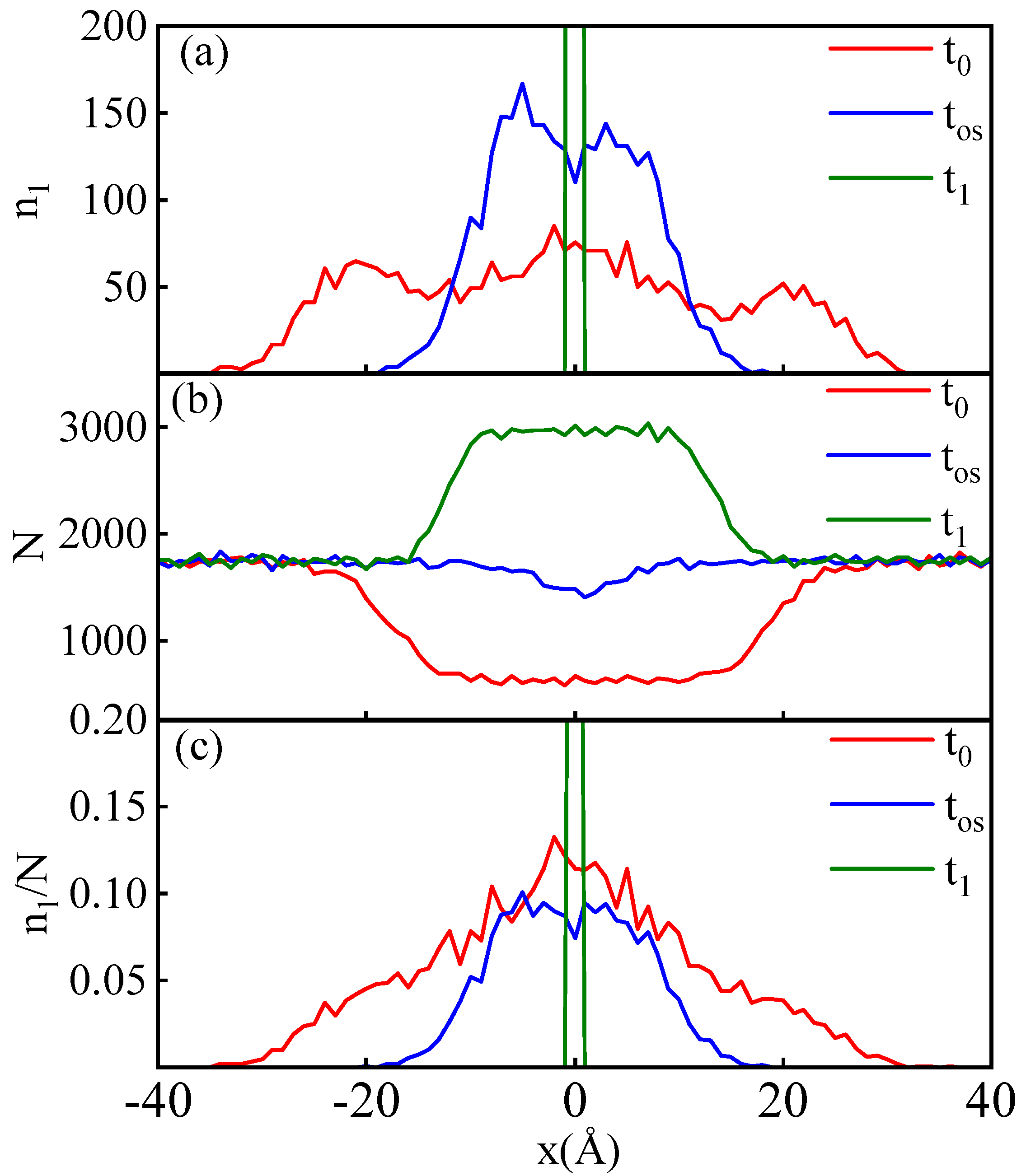
3.3. Particle Migration During Relaxation
- : the starting point of the relaxation process.
- : the ending point of the relaxation process.
- : the moment when reaches the peak of the overshoot.
- G0 or G1: the group of particles located within the collision slice at time or .
- or : the number of G0 or G1 particles in a slice.
- N: the total number of all particles in a slice.
3.4. Changes in Particle Kinetic Energy during the Relaxation Process
- or : the average kinetic energy of particles in G0 or G1.
- or : the component of average kinetic energy along axis x (the parallel direction) for particles in G0 or G1.
- or : the component of average kinetic energy along axis y (the perpendicular direction) for particles in G0 or G1.
- : the average kinetic energy of particles located within the collision slice.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Collins, T.J.B.; Poludnenko, A.; Cunningham, A.; Frank, A. Shock propagation in deuterium-tritium-saturated foam. Phys. Plasmas 2005, 12, 062705. [Google Scholar] [CrossRef]
- Scott, R.H.H.; Barlow, D.; Trickey, W.; Ruocco, A.; Glize, K.; Antonelli, L.; Khan, M.; Woolsey, N.C. Shock-Augmented Ignition Approach to Laser Inertial Fusion. Phys. Rev. Lett. 2022, 129, 195001. [Google Scholar] [CrossRef]
- Nilsen, J.; Kritcher, A.; Martin, M.; Tipton, R.; Whitley, H.; Swift, D.; Döppner, T.; Bachmann, B.L.; Lazicki, A.E.; Kostinski, N.B.; et al. Understanding the effects of radiative preheat and self-emission from shock heating on equation of state measurement at 100s of Mbar using spherically converging shock waves in a NIF hohlraum. Matter Radiat. Extrem. 2020, 5, 018401. [Google Scholar] [CrossRef]
- Shang, W.L.; Betti, R.; Hu, S.X.; Woo, K.; Hao, L.; Ren, C.; Christopherson, A.R.; Bose, A.; Theobald, W. Electron Shock Ignition of Inertial Fusion Targets. Phys. Rev. Lett. 2017, 119, 195001. [Google Scholar] [CrossRef]
- Bell, A.R. The acceleration of cosmic rays in shock fronts. Mon. Not. R. Astron. Soc. 1978, 182, 147–156. [Google Scholar] [CrossRef]
- Schwartz, S.J.; Henley, E.; Mitchell, J.; Krasnoselskikh, V. Electron Temperature Gradient Scale at Collisionless Shocks. Phys. Rev. Lett. 2011, 107, 215002. [Google Scholar] [CrossRef]
- Hansen, J.; Edwards, M.; Froula, D.; Gregori, G.; Edens, A.; Ditmire, T. Laboratory Simulations of Supernova Shockwave Propagation. In High Energy Density Laboratory Astrophysics; Kyrala, G., Ed.; Springer: Dordrecht, The Netherlands, 2005; pp. 61–67. [Google Scholar] [CrossRef]
- Guidry, M.; Messer, B. The Physics and Astrophysics of Type Ia Supernova Explosions. Front. Phys. 2013, 8, 111–115. [Google Scholar] [CrossRef]
- Wang, J.; Shi, Y.; Wang, L.P.; Xiao, Z.; He, X.; Chen, S. Effect of shocklets on the velocity gradients in highly compressible isotropic turbulence. Phys. Fluids 2011, 23, 125103. [Google Scholar] [CrossRef]
- Wang, J.; Shi, Y.; Wang, L.P.; Xiao, Z.; He, X.T.; Chen, S. Effect of compressibility on the small-scale structures in isotropic turbulence. J. Fluid Mech. 2012, 713, 588–631. [Google Scholar] [CrossRef]
- Rotman, D. Shock wave effects on a turbulent flow. Phys. Fluids A 1991, 3, 1792–1806. [Google Scholar] [CrossRef]
- Belonoshko, A.B.; Rosengren, A.; Skorodumova, N.V.; Bastea, S.; Johansson, B. Shock wave propagation in dissociating low-Z liquids: D2. J. Chem. Phys. 2005, 122, 124503. [Google Scholar] [CrossRef] [PubMed]
- Kadau, K.; Germann, T.C.; Lomdahl, P.S.; Holian, B.L. Atomistic simulations of shock-induced transformations and their orientation dependence in bcc Fe single crystals. Phys. Rev. B 2005, 72, 064120. [Google Scholar] [CrossRef]
- Brenner, D.W.; Robertson, D.H.; Elert, M.L.; White, C.T. Detonations at nanometer resolution using molecular dynamics. Phys. Rev. Lett. 1993, 70, 2174–2177. [Google Scholar] [CrossRef]
- Hamilton, B.W.; Sakano, M.N.; Li, C.; Strachan, A. Chemistry Under Shock Conditions. Annu. Rev. Mater. Sci. 2021, 51, 101–130. [Google Scholar] [CrossRef]
- Betti, R.; Zhou, C.D.; Anderson, K.S.; Perkins, L.J.; Theobald, W.; Solodov, A.A. Shock Ignition of Thermonuclear Fuel with High Areal Density. Phys. Rev. Lett. 2007, 98, 155001. [Google Scholar] [CrossRef]
- Betti, R.; Theobald, W.; Zhou, C.D.; Anderson, K.S.; McKenty, P.W.; Skupsky, S.; Shvarts, D.; Goncharov, V.N.; Delettrez, J.A.; Radha, P.B.; et al. Shock ignition of thermonuclear fuel with high areal densities. J. Phys. Conf. Ser. 2008, 112, 022024. [Google Scholar] [CrossRef]
- Perkins, L.J.; Betti, R.; LaFortune, K.N.; Williams, W.H. Shock Ignition: A New Approach to High Gain Inertial Confinement Fusion on the National Ignition Facility. Phys. Rev. Lett. 2009, 103, 045004. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, W.; Yang, X.; Wu, D.; Ma, Y.; Jiao, J.; Zhang, Z.; Wu, F.; Yuan, X.; Li, Y.; et al. Double-cone ignition scheme for inertial confinement fusion. Philos. Trans. R. Soc. 2020, 378, 20200015. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Wang, J.; Shi, Y.; Chen, S.; He, X.T. A Hybrid Numerical Simulation of Supersonic Isotropic Turbulence. Commun. Comput. Phys. 2019, 25, 189–217. [Google Scholar] [CrossRef]
- Mott-Smith, H.M. The Solution of the Boltzmann Equation for a Shock Wave. Phys. Rev. 1951, 82, 885–892. [Google Scholar] [CrossRef]
- Comisar, G.G. Bimodal Distributions and Plasma Shock Wave Structure. Phys. Fluids 1963, 6, 1263–1267. [Google Scholar] [CrossRef]
- Muckenfuss, C. Some Aspects of Shock Structure According to the Bimodal Model. Phys. Fluids 1962, 5, 1325–1336. [Google Scholar] [CrossRef]
- Zhakhovskii, V.; Nishihara, K.; Anisimov, S. Shock wave structure in dense gases. JETP Lett. 1997, 66, 99–105. [Google Scholar] [CrossRef]
- Holian, B. Atomistic computer simulations of shock waves. Shock Waves 1995, 5, 149–157. [Google Scholar] [CrossRef]
- Holian, B.L.; Hoover, W.G.; Moran, B.; Straub, G.K. Shock-wave structure via nonequilibrium molecular dynamics and Navier-Stokes continuum mechanics. Phys. Rev. A 1980, 22, 2798. [Google Scholar] [CrossRef]
- Döntgen, M. Theory and simulation of shock waves freely propagating through monoatomic non-Boltzmann gas. Theor. Comput. Fluid Dyn. 2024, 38, 61–74. [Google Scholar] [CrossRef]
- Hoover, W.G.; Hoover, C.G.; Travis, K.P. Shock-Wave Compression and Joule-Thomson Expansion. Phys. Rev. Lett. 2014, 112, 144504. [Google Scholar] [CrossRef]
- Hoover, W.G. Structure of a Shock-Wave Front in a Liquid. Phys. Rev. Lett. 1979, 42, 1531–1534. [Google Scholar] [CrossRef]
- Hoover, W.G.; Hoover, C.G. Shockwaves and Local Hydrodynamics: Failure of the Navier-Stokes Equations. In New Trends in Statistical Physics; World Scientific: Hackensack, NJ, USA, 2010; pp. 15–26. [Google Scholar] [CrossRef]
- Holian, B.L.; Mareschal, M. Heat-flow equation motivated by the ideal-gas shock wave. Phys. Rev. E 2010, 82, 026707. [Google Scholar] [CrossRef]
- Holian, B.L.; Mareschal, M.; Ravelo, R. Test of a new heat-flow equation for dense-fluid shock waves. J. Chem Phy. 2010, 133, 114502. [Google Scholar] [CrossRef]
- Holian, B.L.; Patterson, C.W.; Mareschal, M.; Salomons, E. Modeling shock waves in an ideal gas: Going beyond the Navier-Stokes level. Phys. Rev. E 1993, 47, R24–R27. [Google Scholar] [CrossRef] [PubMed]
- Zhakhovskiĭ, V.V.; Zybin, S.V.; Nishihara, K.; Anisimov, S.I. Shock Wave Structure in Lennard-Jones Crystal via Molecular Dynamics. Phys. Rev. Lett. 1999, 83, 1175–1178. [Google Scholar] [CrossRef]
- Holian, B.L.; Lomdahl, P.S. Plasticity induced by shock waves in nonequilibrium molecular-dynamics simulations. Science 1998, 280, 2085–2088. [Google Scholar] [CrossRef]
- Budzevich, M.M.; Zhakhovsky, V.V.; White, C.T.; Oleynik, I.I. Evolution of Shock-Induced Orientation-Dependent Metastable States in Crystalline Aluminum. Phys. Rev. Lett. 2012, 109, 125505. [Google Scholar] [CrossRef]
- Zhakhovsky, V.V.; Migdal, K.P.; Inogamov, N.A.; Anisimov, S.I. MD simulation of steady shock-wave fronts with phase transition in single-crystal iron. AIP Conf. Proc. 2017, 1793, 070003. [Google Scholar] [CrossRef]
- Gu, Y.J.; Zhao, K.; Liu, H.; Li, G.J.; Wang, Z.Q.; Chen, Q.F. Shock-induced volume-collapse phase transition in a Ce-La alloy dynamically compressed up to 20 GPa. Phys. Rev. B 2023, 108, 144105. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, Y.; Kang, W.; Zhang, P.; Duan, H.; He, X.T. Molecular dynamics simulation of strong shock waves propagating in dense deuterium, taking into consideration effects of excited electrons. Phys. Rev. E 2017, 95, 023201. [Google Scholar] [CrossRef]
- Liu, H.; Zhou, H.; Kang, W.; Zhang, P.; Duan, H.; Zhang, W.; He, X.T. Dynamics of bond breaking and formation in polyethylene near shock front. Phys. Rev. E 2020, 102, 023207. [Google Scholar] [CrossRef]
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; Veld, P.J.i.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; et al. LAMMPS—A flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Computer. Phys. Commun. 2022, 271, 108171. [Google Scholar] [CrossRef]
- Nellis, W.J.; Holmes, N.C.; Mitchell, A.C.; Trainor, R.J.; Governo, G.K.; Ross, M.; Young, D.A. Shock Compression of Liquid Helium to 56 GPa (560 kbar). Phys. Rev. Lett. 1984, 53, 1248–1251. [Google Scholar] [CrossRef]
- Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef]
- Shinoda, W.; Shiga, M.; Mikami, M. Rapid estimation of elastic constants by molecular dynamics simulation under constant stress. Phys. Rev. B 2004, 69, 134103. [Google Scholar] [CrossRef]
- Mamedov, B.; Somuncu, E. Analytical treatment of second virial coefficient over Lennard-Jones (2n-n) potential and its application to molecular systems. J. Mol. Struct. 2014, 1068, 164–169. [Google Scholar] [CrossRef]
- Beck, D. A new interatomic potential function for helium. Mol. Phys. 1968, 14, 311–315. [Google Scholar] [CrossRef]
- Kovalenko, M.A.; Kupryazhkin, A.Y.; Gupta, S.K. Influence of defects on the diffusion of helium in uranium dioxide: Molecular dynamics study. AIP Conf. Proc. 2019, 2142, 020002. [Google Scholar] [CrossRef]
- Liu, H.; Kang, W.; Zhang, Q.; Zhang, Y.; Duan, H.; He, X. Molecular dynamics simulations of microscopic structure of ultra strong shock waves in dense helium. Front. Phys. 2016, 11, 115206. [Google Scholar] [CrossRef]
- Irving, J.; Kirkwood, J.G. The statistical mechanical theory of transport processes. IV. The equations of hydrodynamics. J. Chem. Phys. 1950, 18, 817–829. [Google Scholar] [CrossRef]
- Pearson, K. The problem of the random walk. Nature 1905, 72, 294. [Google Scholar] [CrossRef]






| km/s | g/cm3 | ev | GPa | km/s | g/cm3 | ev | GPa | km/s |
|---|---|---|---|---|---|---|---|---|
| 10 | 0.396 | 1.206 | 21.32 | 14.8 | 0.693 | 2.757 | 112.1 | 13.4 |
| 20 | 0.426 | 4.998 | 82.32 | 28.2 | 0.787 | 12.06 | 458.9 | 23.7 |
| 30 | 0.443 | 11.20 | 178.6 | 42.3 | 0.850 | 26.71 | 1017 | 32.8 |
| 40 | 0.455 | 20.68 | 320.8 | 55.8 | 0.886 | 47.39 | 1792 | 41.9 |
| 50 | 0.464 | 31.88 | 486.6 | 68.4 | 0.921 | 74.97 | 2764 | 50.4 |
| 60 | 0.470 | 46.53 | 707.2 | 82.3 | 0.946 | 112.0 | 4154 | 59.6 |
| 70 | 0.473 | 63.77 | 957.0 | 96.2 | 0.964 | 146.5 | 5404 | 67.1 |
| 80 | 0.478 | 83.59 | 1243 | 109 | 0.973 | 198.2 | 7149 | 76.8 |
| 90 | 0.483 | 103.4 | 1544 | 122 | 0.998 | 249.9 | 9112 | 83.9 |
| 100 | 0.488 | 129.3 | 1920 | 135 | 1.01 | 310.2 | 11253 | 93.6 |
| km/s | fs | fs | fs | fs |
|---|---|---|---|---|
| 10 | 138.80 | 142.50 | 191.30 | 138.30 |
| 20 | 88.30 | 85.94 | 115.78 | 93.07 |
| 30 | 76.24 | 75.96 | 101.24 | 68.40 |
| 40 | 72.08 | 68.76 | 90.41 | 64.15 |
| 50 | 55.41 | 52.53 | 70.17 | 50.69 |
| 60 | 49.39 | 47.52 | 58.34 | 46.45 |
| 70 | 45.23 | 45.97 | 52.08 | 43.24 |
| 80 | 42.13 | 41.86 | 49.31 | 41.67 |
| 90 | 37.62 | 37.09 | 43.37 | 38.98 |
| 100 | 32.77 | 33.59 | 39.80 | 33.45 |
| a (fs−1) | b (Å) | c (fs/Å2) | |
|---|---|---|---|
| (km/s) | Collisions (%) | Migration (%) |
|---|---|---|
| 10 | 40.2 | 59.8 |
| 20 | 36.9 | 63.1 |
| 30 | 38.6 | 61.4 |
| 40 | 52.5 | 47.5 |
| 50 | 46.7 | 53.3 |
| 60 | 40.3 | 59.7 |
| 70 | 39.5 | 60.5 |
| 80 | 42.3 | 57.7 |
| 90 | 34.9 | 65.1 |
| 100 | 48.6 | 51.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Xu, B.; Yan, Z.; Zhang, X.; Mo, C.; Xue, Q.; Xiao, X.; Liu, H. Effects of Particle Migration on the Relaxation of Shock Wave Collisions. Entropy 2024, 26, 724. https://doi.org/10.3390/e26090724
Li H, Xu B, Yan Z, Zhang X, Mo C, Xue Q, Xiao X, Liu H. Effects of Particle Migration on the Relaxation of Shock Wave Collisions. Entropy. 2024; 26(9):724. https://doi.org/10.3390/e26090724
Chicago/Turabian StyleLi, Hao, Bo Xu, Zixiang Yan, Xinyu Zhang, Chongjie Mo, Quanxi Xue, Xiazi Xiao, and Hao Liu. 2024. "Effects of Particle Migration on the Relaxation of Shock Wave Collisions" Entropy 26, no. 9: 724. https://doi.org/10.3390/e26090724







