Chaos in Optomechanical Systems Coupled to a Non-Markovian Environment
Abstract
:1. Introduction
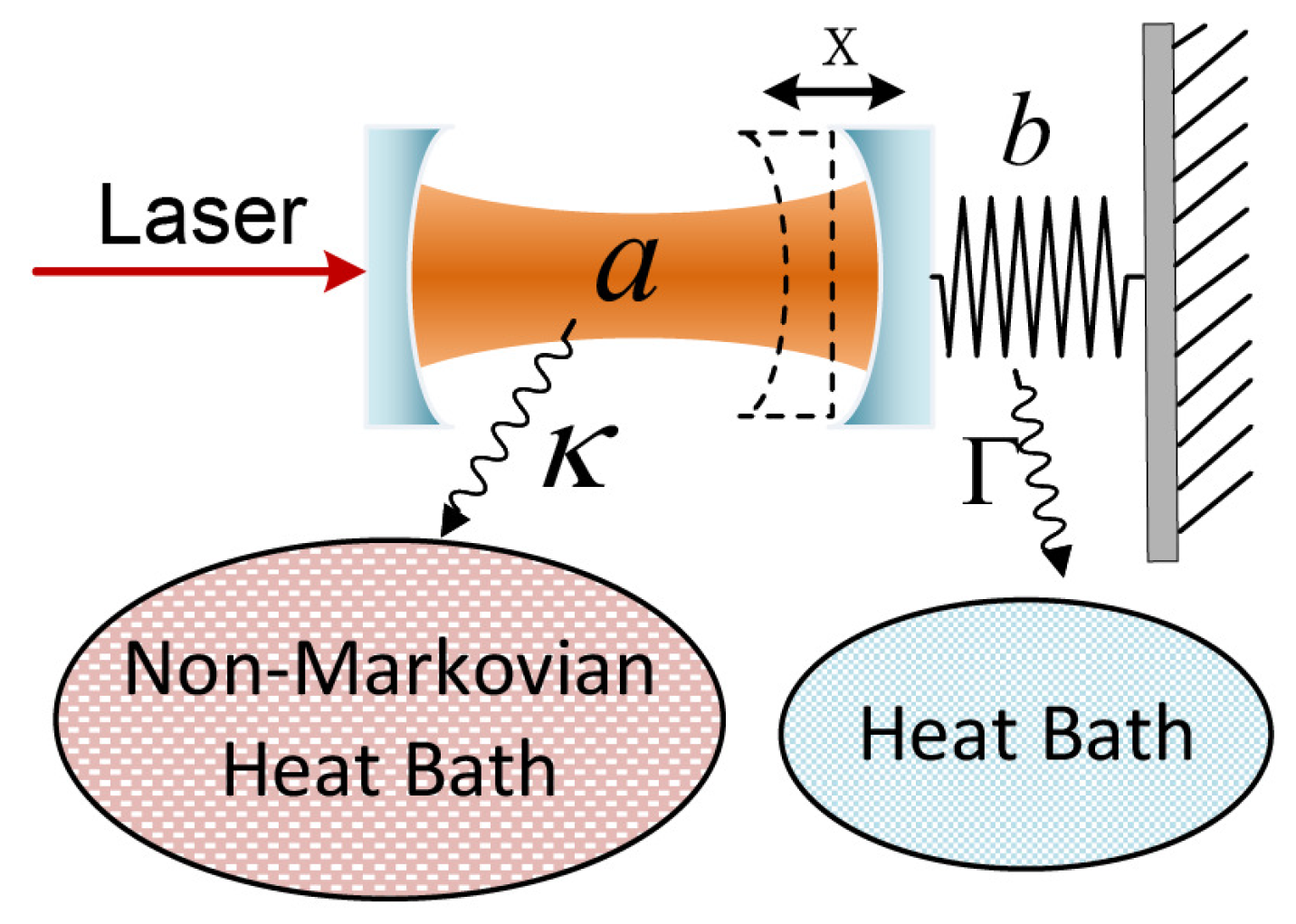
2. Optomechanical Model Coupled to a Non-Markovian Environment
3. Chaos in Non-Markovian Environments
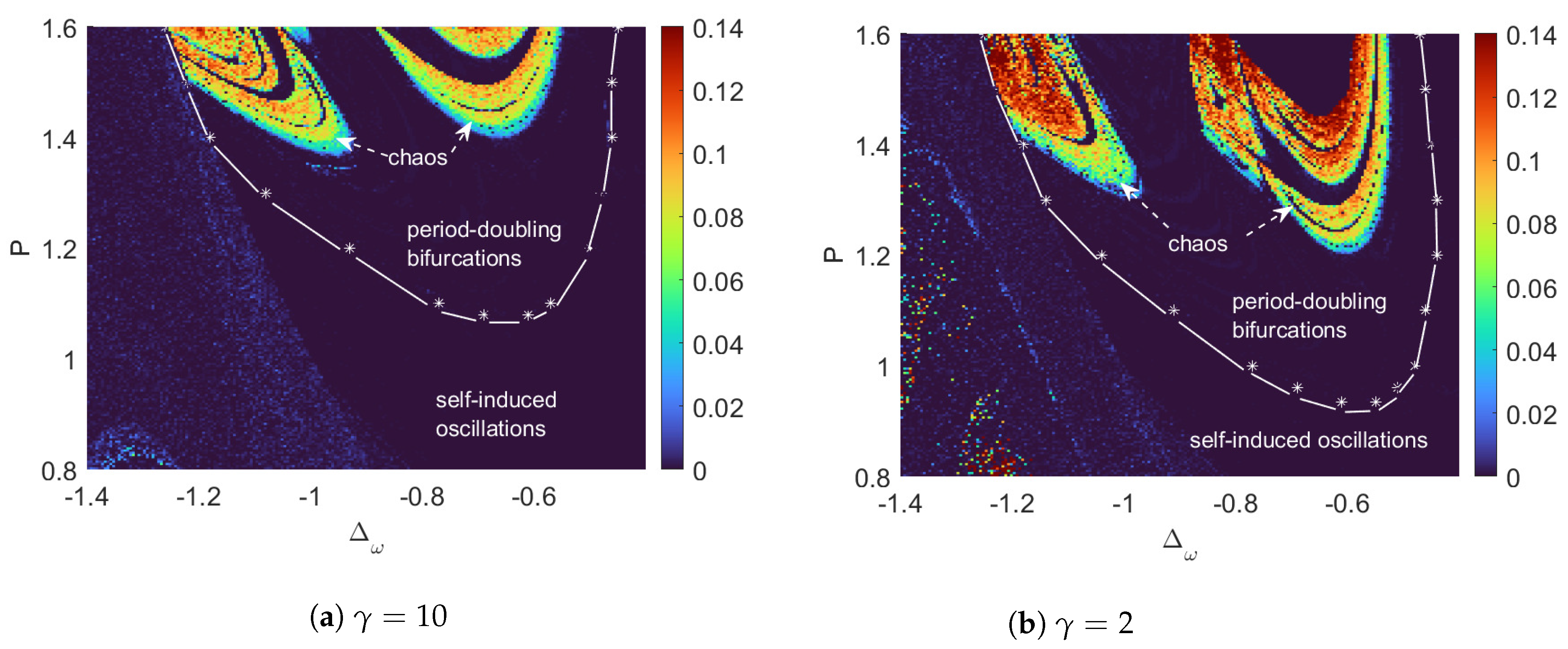
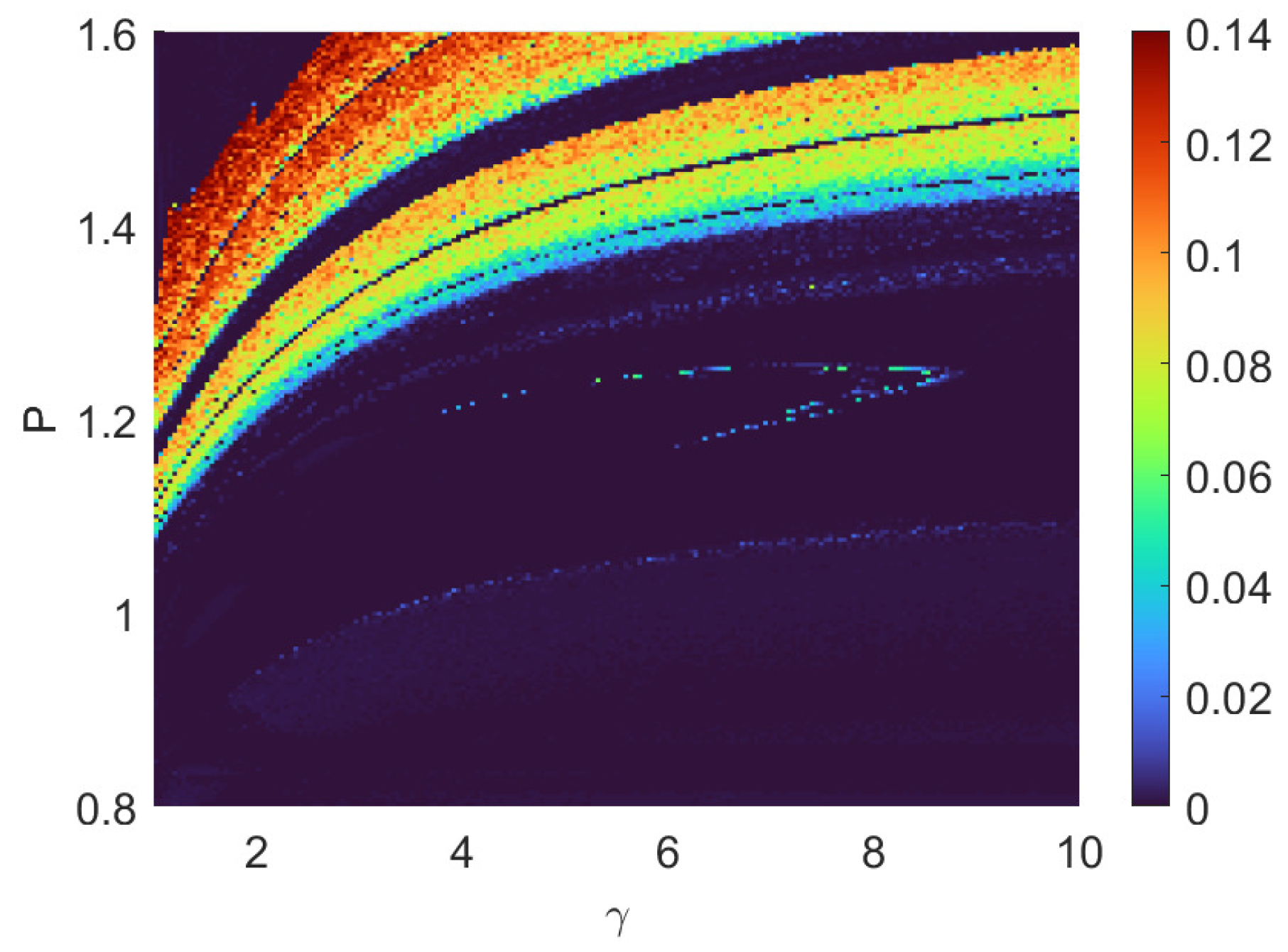
3.1. Simulation Results
3.2. The Comparison between Markov and Non-Markovian Regimes
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. The Non-Markovian Quantum State Diffusion (NMQSD) and Master Equation
References
- Aspelmeyer, M.; Kippenberg, T.J.; Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 2014, 86, 1391. [Google Scholar] [CrossRef]
- Carmon, T.; Cross, M.C.; Vahala, K.J. Chaotic Quivering of Micron-Scaled On-Chip Resonators Excited by Centrifugal Optical Pressure. Phys. Rev. Lett. 2007, 98, 167203. [Google Scholar] [CrossRef]
- Yang, N.; Zhang, J.; Wang, H.; Liu, Y.X.; Wu, R.B.; Liu, L.Q.; Li, C.W.; Nori, F. Noise suppression of on-chip mechanical resonators by chaotic coherent feedback. Phys. Rev. A 2015, 92, 033812. [Google Scholar] [CrossRef]
- Jiang, X.F.; Shao, L.B.; Zhang, S.X.; Yi, X.; Wiersig, J.; Wang, L.; Gong, Q.H.; Loncar, M.; Yang, L.; Xiao, Y.F. Chaos-assisted broadband momentum transformation in optical microresonators. Science 2017, 358, 344. [Google Scholar] [CrossRef] [PubMed]
- Monifi, F.; Zhang, J.; Özdemir, S.K.; Peng, B.; Liu, Y.X.; Bo, F.; Nori, F.; Yang, L. Optomechanically induced stochastic resonance and chaos transfer between optical fields. Nat. Photon. 2016, 10, 399. [Google Scholar] [CrossRef]
- Larson, J.; Horsdal, M. Photonic Josephson effect, phase transitions, and chaos in optomechanical systems. Phys. Rev. A 2011, 84, 021804(R). [Google Scholar] [CrossRef]
- Wang, G.L.; Huang, L.; Lai, Y.C.; Grebogi, C. Nonlinear Dynamics and Quantum Entanglement in Optomechanical Systems. Phys. Rev. Lett. 2014, 112, 110406. [Google Scholar] [CrossRef]
- Yang, X.; Yin, H.-J.; Zhang, F.; Nie, J. Macroscopic entanglement generation in optomechanical system embedded in non-Markovian environment. Laser Phys. Lett. 2022, 20, 015205. [Google Scholar] [CrossRef]
- Walter, S.; Marquardt, F. Classical dynamical gauge fields in optomechanics. New J. Phys. 2016, 18, 113029. [Google Scholar] [CrossRef]
- Lü, X.Y.; Jing, H.; Ma, J.Y.; Wu, Y. PT-Symmetry-Breaking Chaos in Optomechanics. Phys. Rev. Lett. 2015, 114, 253601. [Google Scholar] [CrossRef]
- Sciamanna, M. Vibrations copying optical chaos. Nat. Photon. 2016, 10, 366. [Google Scholar] [CrossRef]
- Navarro-Urrios, D.; Capuj, N.E.; Colombano, M.F.; Garcia, P.D.; Sledzinska, M.; Alzina, F.; Griol, A.; Martinez, A.; Sotomayor-Torres, C.M. Nonlinear dynamics and chaos in an optomechanical beam. Nat. Commun. 2017, 8, 14965. [Google Scholar] [CrossRef]
- Lee, S.B.; Yang, J.; Moon, S.; Lee, S.Y.; Shim, J.B.; Kim, S.W.; Lee, J.H.; An, K. Observation of an Exceptional Point in a Chaotic Optical Microcavity. Phys. Rev. Lett. 2009, 103, 134101. [Google Scholar] [CrossRef]
- Sun, Y.; Sukhorukov, A.A. Chaotic oscillations of coupled nanobeam cavities with tailored optomechanical potentials. Opt. Lett. 2014, 39, 3543. [Google Scholar] [CrossRef]
- Piazza, F.; Ritsch, H. Self-Ordered Limit Cycles, Chaos, and Phase Slippage with a Superfluid inside an Optical Resonator. Phys. Rev. Lett. 2015, 115, 163601. [Google Scholar] [CrossRef]
- Zhang, D.; You, C.; Lü, X. Intermittent chaos in cavity optomechanics. Phys. Rev. A 2020, 101, 053851. [Google Scholar] [CrossRef]
- Wang, G.L.; Lai, Y.C.; Grebogi, C. Transient chaos—A resolution of breakdown of quantum-classical correspondence in optomechanics. Sci. Rep. 2016, 6, 35381. [Google Scholar] [CrossRef] [PubMed]
- Bakemeier, L.; Alvermann, A.; Fehske, H. Route to chaos in optomechanics. Phys. Rev. Lett. 2015, 114, 013601. [Google Scholar] [CrossRef]
- Nakamura, K. Quantum Chaos: A New Paradigm of Nonlinear Dynamics; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Heller, E.J. Bound-state eigenfunctions of classically chaotic Hamiltonian systems: Scars of periodic orbits. Phys. Rev. Lett. 1984, 53, 1515. [Google Scholar] [CrossRef]
- Heller, E.J. The Semiclassical Way to Dynamics and Spectroscopy; Princeton University Press: Princeton, NJ, USA, 2018. [Google Scholar]
- Gutzwiller, M.C. Chaos in Classical and Quantum Mechanics; Springer: New York, NY, USA, 1990. [Google Scholar]
- Ullmo, D. Many-body physics and quantum chaos. Rep. Prog. Phys. 2008, 71, 026001. [Google Scholar] [CrossRef]
- Wright, M.; Weaver, R. New Directions in Linear Acoustics and Vibration: Quantum Chaos, Random Matrix Theory and Complexity; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- García-Mata, I.; Jalabert, R.A.; Wisniacki, D.A. Out-of-time-order correlators and quantum chaos. arXiv 2022, arXiv:2209.07965. [Google Scholar]
- Novotnỳ, J.; Stránskỳ, P. Relative asymptotic oscillations of the out-of-time-ordered correlator as a quantum chaos indicator. Phys. Rev. E 2023, 107, 054220. [Google Scholar] [CrossRef]
- Roque, T.F.; Marquardt, F.; Yevtushenko, O.M. Nonlinear dynamics of weakly dissipative optomechanical systems. New J. Phys. 2020, 22, 013049. [Google Scholar] [CrossRef]
- Breuer, H.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: Cary, NC, USA, 2002. [Google Scholar]
- Weiss, U. Quantum Dissipative Systems; World Scientific: Singapore, 2012. [Google Scholar]
- De Vega, I.; Alonso, D. Dynamics of non-Markovian open quantum systems. Rev. Mod. Phys. 2017, 89, 015001. [Google Scholar] [CrossRef]
- Miki, D.; Matsumoto, N.; Matsumura, A.; Shichijo, T.; Sugiyama, Y.; Yamamoto, K.; Yamamoto, N. Generating quantum entanglement between macroscopic objects with continuous measurement and feedback control. Phys. Rev. A 2023, 107, 032410. [Google Scholar] [CrossRef]
- Liu, J.X.; Jiao, Y.F.; Li, Y.; Xu, X.W.; He, Q.Y.; Jing, H. Phase-controlled asymmetric optomechanical entanglement against optical backscattering. Sci. China Phys. Mech. Astron. 2023, 66, 230312. [Google Scholar] [CrossRef]
- Strunz, W.T.; Diósi, L.; Gisin, N. Open system dynamics with non-Markovian quantum trajectories. Phys. Rev. Lett. 1999, 82, 1801. [Google Scholar] [CrossRef]
- Yu, T.; Diósi, L.; Gisin, N.; Strunz, W.T. Non-Markovian quantum-state diffusion: Perturbation approach. Phys. Rev. A 1999, 60, 91. [Google Scholar] [CrossRef]
- Diósi, L.; Gisin, N.; Strunz, W.T. Non-Markovian quantum state diffusion. Phys. Rev. A 1998, 58, 1699. [Google Scholar] [CrossRef]
- Strunz, W.T.; Yu, T. Convolutionless non-Markovian master equations and quantum trajectories: Brownian motion. Phys. Rev. A 2004, 69, 052115. [Google Scholar] [CrossRef]
- Yu, T. Non-Markovian quantum trajectories versus master equations: Finite-temperature heat bath. Phys. Rev. A 2004, 69, 062107. [Google Scholar] [CrossRef]
- Jing, J.; Yu, T. Non-Markovian relaxation of a three-level system: Quantum trajectory approach. Phys. Rev. Lett. 2010, 105, 240403. [Google Scholar] [CrossRef]
- Yang, H.; Miao, H.; Chen, Y. Nonadiabatic elimination of auxiliary modes in continuous quantum measurements. Phys. Rev. A 2012, 85, 040101. [Google Scholar] [CrossRef]
- Chen, Y.; You, J.Q.; Yu, T. Exact non-Markovian master equations for multiple qubit systems: Quantum-trajectory approach. Phys. Rev. A 2014, 90, 052104. [Google Scholar] [CrossRef]
- Xu, J.; Zhao, X.; Jing, J.; Wu, L.A.; Yu, T. Perturbation methods for the non-Markovian quantum state diffusion equation. J. Phys. A Math. Theor. 2014, 47, 435301. [Google Scholar] [CrossRef]
- Dalibard, J.; Castin, Y.; Mølmer, K. Wave-function approach to dissipative processes in quantum optics. Phys. Rev. Lett. 1992, 68, 580. [Google Scholar] [CrossRef]
- Gisin, N.; Percival, I.C. The quantum-state diffusion model applied to open systems. J. Phys. A Math. Gen. 1992, 25, 5677. [Google Scholar] [CrossRef]
- Carmichael, H. An Open Systems Approach to Quantum Optics Springer-Verlag; Springer: Berlin/Heidelberg, Geramny, 1993. [Google Scholar]
- Wiseman, H.M.; Milburn, G.J. Interpretation of quantum jump and diffusion processes illustrated on the Bloch sphere. Phys. Rev. A 1993, 47, 1652. [Google Scholar] [CrossRef]
- Plenio, M.B.; Knight, P.L. The quantum-jump approach to dissipative dynamics in quantum optics. Rev. Mod. Phys. 1998, 70, 101. [Google Scholar] [CrossRef]
- Liu, B.H.; Li, L.; Huang, Y.F.; Li, C.F.; Guo, G.C.; Laine, E.M.; Breuer, H.P.; Piilo, J. Experimental control of the transition from Markovian to non-Markovian dynamics of open quantum systems. Nat. Phys. 2011, 7, 931. [Google Scholar] [CrossRef]
- Marquardt, F.; Harris, J.G.E.; Girvin, S.M. Dynamical Multistability Induced by Radiation Pressure in High-Finesse Micromechanical Optical Cavities. Phys. Rev. Lett. 2006, 96, 103901. [Google Scholar] [CrossRef] [PubMed]
- Ludwig, M.; Kubala, B.; Marquardt, F. The optomechanical instability in the quantum regime. New J. Phys. 2008, 10, 095013. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D 1985, 16, 285. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, X.; Yu, T. Memory-effect-induced macroscopic-microscopic entanglement. Phys. Rev. A 2016, 94, 012334. [Google Scholar] [CrossRef]
- Harayama, T.; Sunada, S.; Yoshimura, K.; Davis, P.; Tsuzuki, K.; Uchida, A. Fast nondeterministic random-bit generation using on-chip chaos lasers. Phys. Rev. A 2011, 83, 031803. [Google Scholar] [CrossRef]
- Shen, B.; Shu, H.; Xie, W.; Chen, R.; Liu, Z.; Ge, Z.; Zhang, X.; Wang, Y.; Zhang, Y.; Cheng, B.; et al. Harnessing microcomb-based parallel chaos for random number generation and optical decision making. Nat. Commun. 2023, 14, 4590. [Google Scholar] [CrossRef]
- Sun, Z.-H.; Cai, J.-Q.; Tang, Q.-C.; Hu, Y.; Fan, H. Out-of-Time-Order Correlators and Quantum Phase Transitions in the Rabi and Dicke Models. Ann. Phys. 2020, 532, 1900270. [Google Scholar] [CrossRef]
- Chávez-Carlos, J.; López-del Carpio, B.; Bastarrachea-Magnani, M.A.; Stránskỳ, P.; Lerma-Hernández, S.; Santos, L.F.; Hirsch, J.G. Quantum and classical Lyapunov exponents in atom-field interaction systems. Phys. Rev. Lett. 2019, 122, 024101. [Google Scholar] [CrossRef]
- Buijsman, W.; Gritsev, V.; Sprik, R. Nonergodicity in the anisotropic dicke model. Phys. Rev. Lett. 2017, 118, 080601. [Google Scholar] [CrossRef]
- Scala, G.; Słowik, K.; Facchi, P.; Pascazio, S.; Pepe, F.V. Beyond the Rabi model: Light interactions with polar atomic systems in a cavity. Phys. Rev. A 2021, 104, 013722. [Google Scholar] [CrossRef]
- Burgarth, D.; Facchi, P.; Hillier, R.; Ligabò, M. Taming the Rotating Wave Approximation. arXiv 2023, arXiv:2301.02269. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, P.; Yang, N.; Couvertier, A.; Ding, Q.; Chatterjee, R.; Yu, T. Chaos in Optomechanical Systems Coupled to a Non-Markovian Environment. Entropy 2024, 26, 742. https://doi.org/10.3390/e26090742
Chen P, Yang N, Couvertier A, Ding Q, Chatterjee R, Yu T. Chaos in Optomechanical Systems Coupled to a Non-Markovian Environment. Entropy. 2024; 26(9):742. https://doi.org/10.3390/e26090742
Chicago/Turabian StyleChen, Pengju, Nan Yang, Austen Couvertier, Quanzhen Ding, Rupak Chatterjee, and Ting Yu. 2024. "Chaos in Optomechanical Systems Coupled to a Non-Markovian Environment" Entropy 26, no. 9: 742. https://doi.org/10.3390/e26090742





