Exploring Limit Cycles of Differential Equations through Information Geometry Unveils the Solution to Hilbert’s 16th Problem
Abstract
:1. Introduction
In connection with this purely algebraic problem, I wish to bring forward a question which, it seems to me, may be attacked by the same method of continuous variations of coefficients, and whose answer is of corresponding value for the topology of families of curves defined by differential equations. This is the question as to the maximum number and position of Poincaré’s boundary cycles (limit cycles) for a differential equation of the first order and degree of the formwhere X and Y are rational integral functions of the nth degree in x and y.
2. General Theory
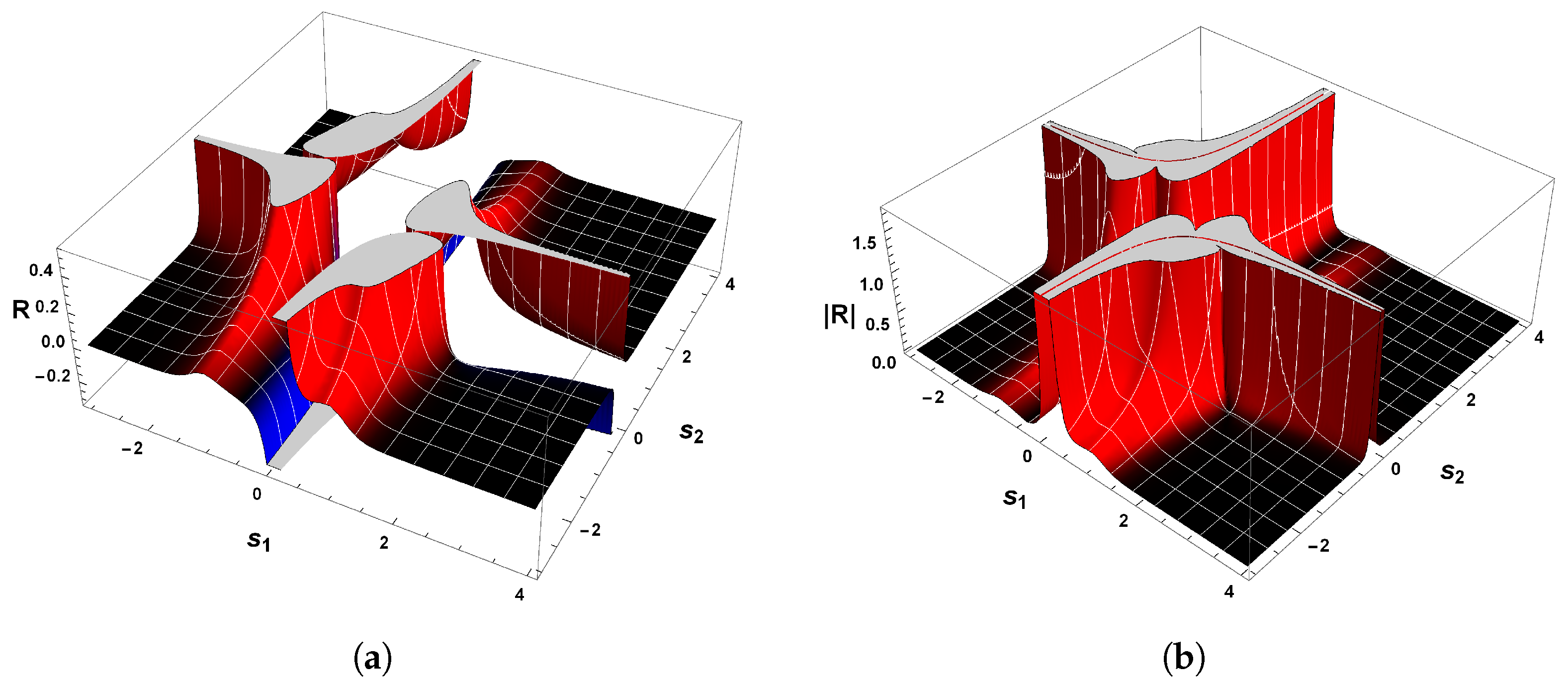
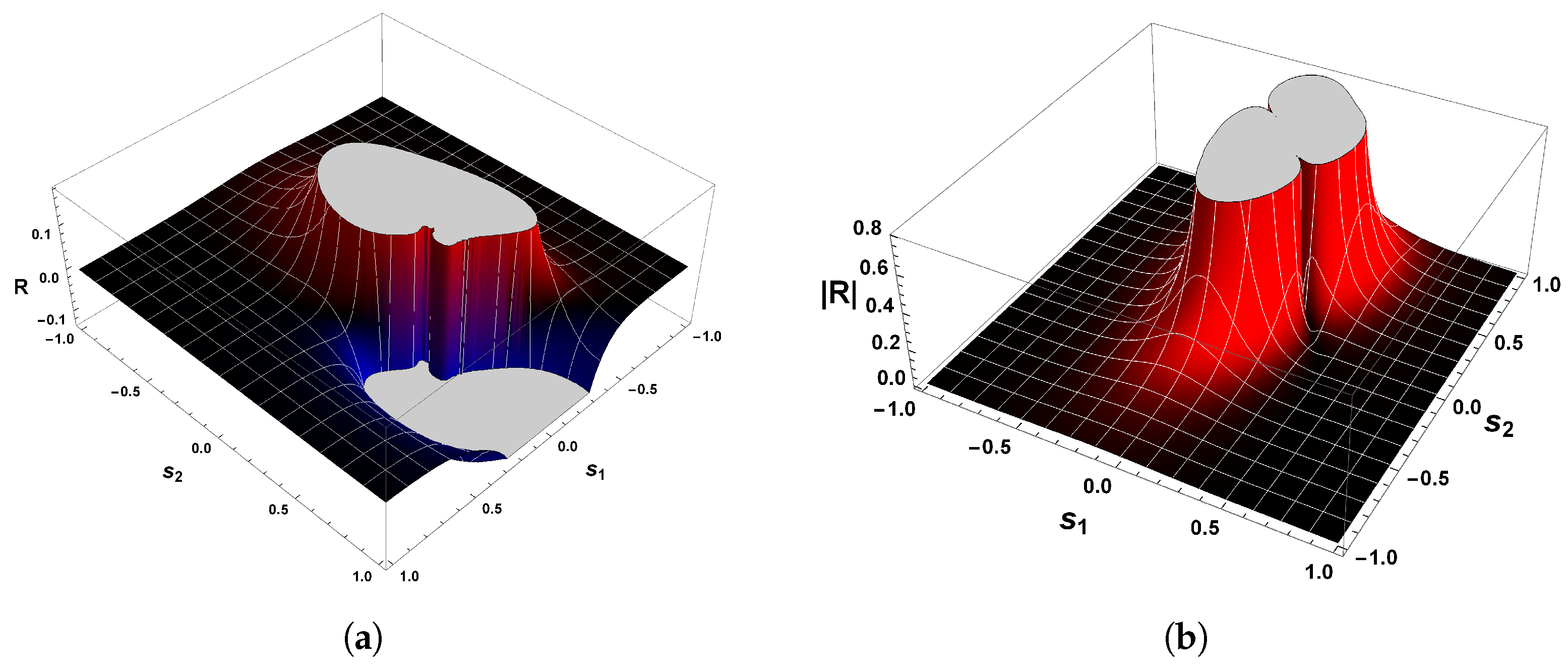
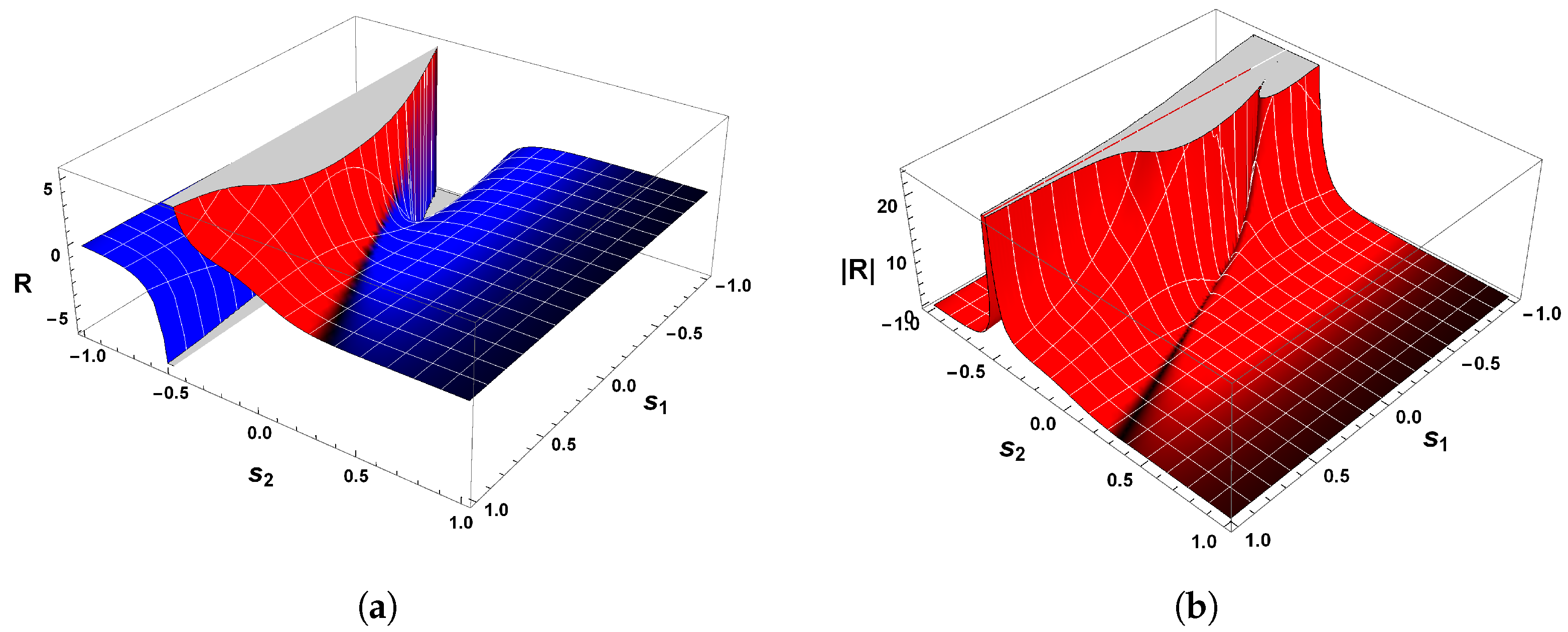
The Geometrical Properties of R Sign
3. Definition of Limit Cycles
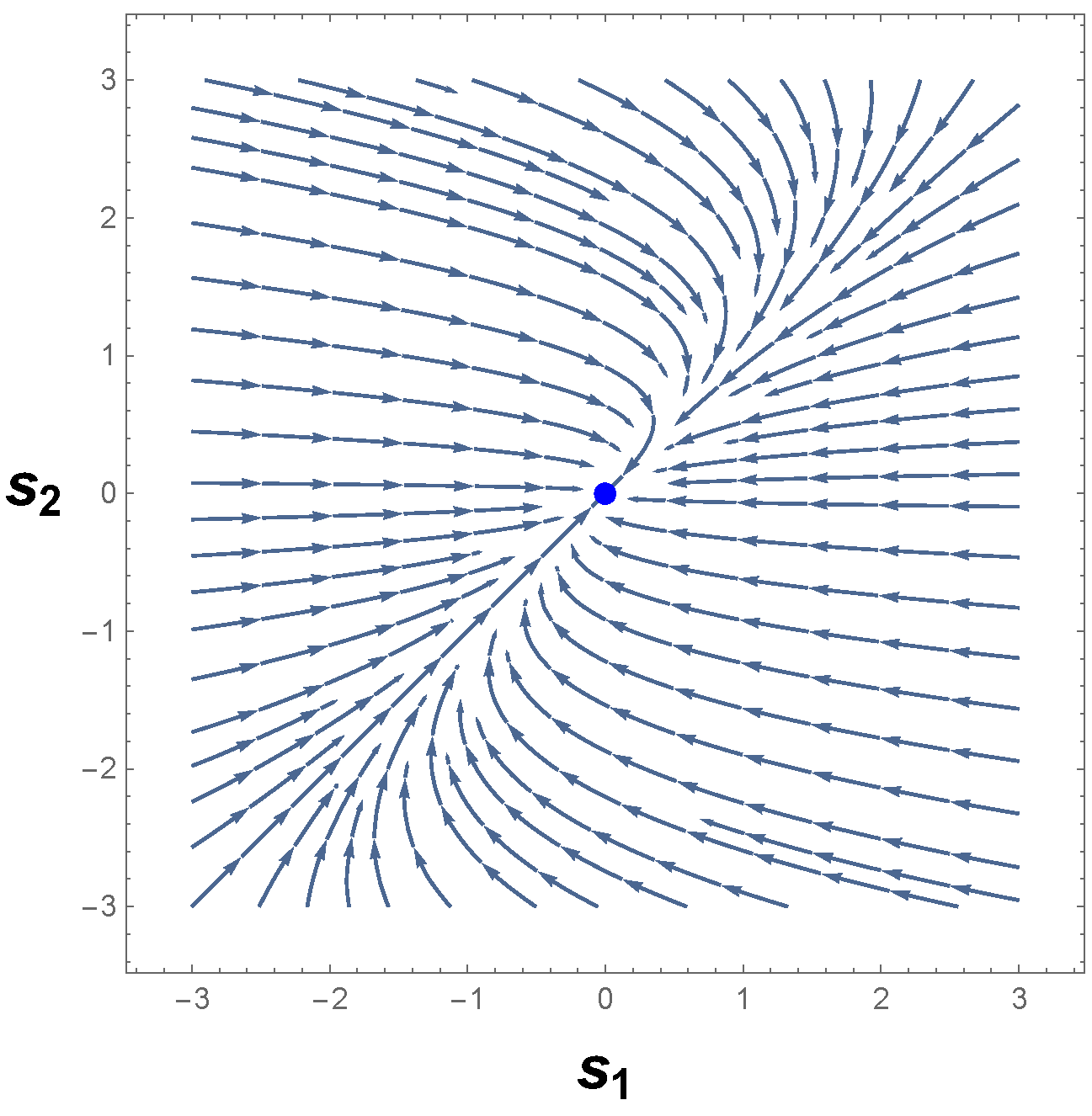
3.1. Systems without Limit Cycles
3.1.1. First Example
3.1.2. Second Example
3.1.3. Third Example
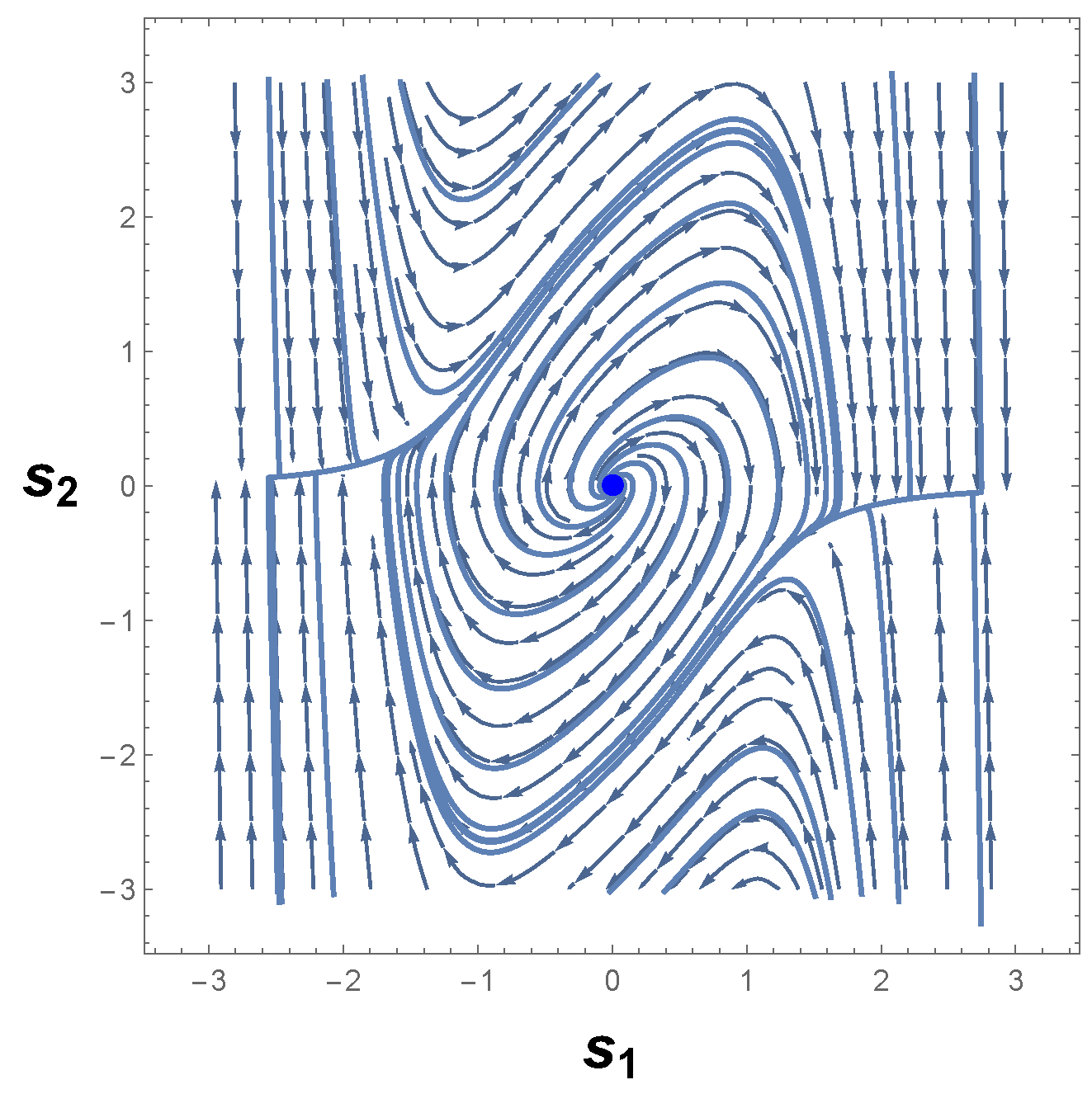
3.2. Systems with Only One Limit Cycle
3.2.1. First Example
3.2.2. Second Example
3.2.3. Third Example
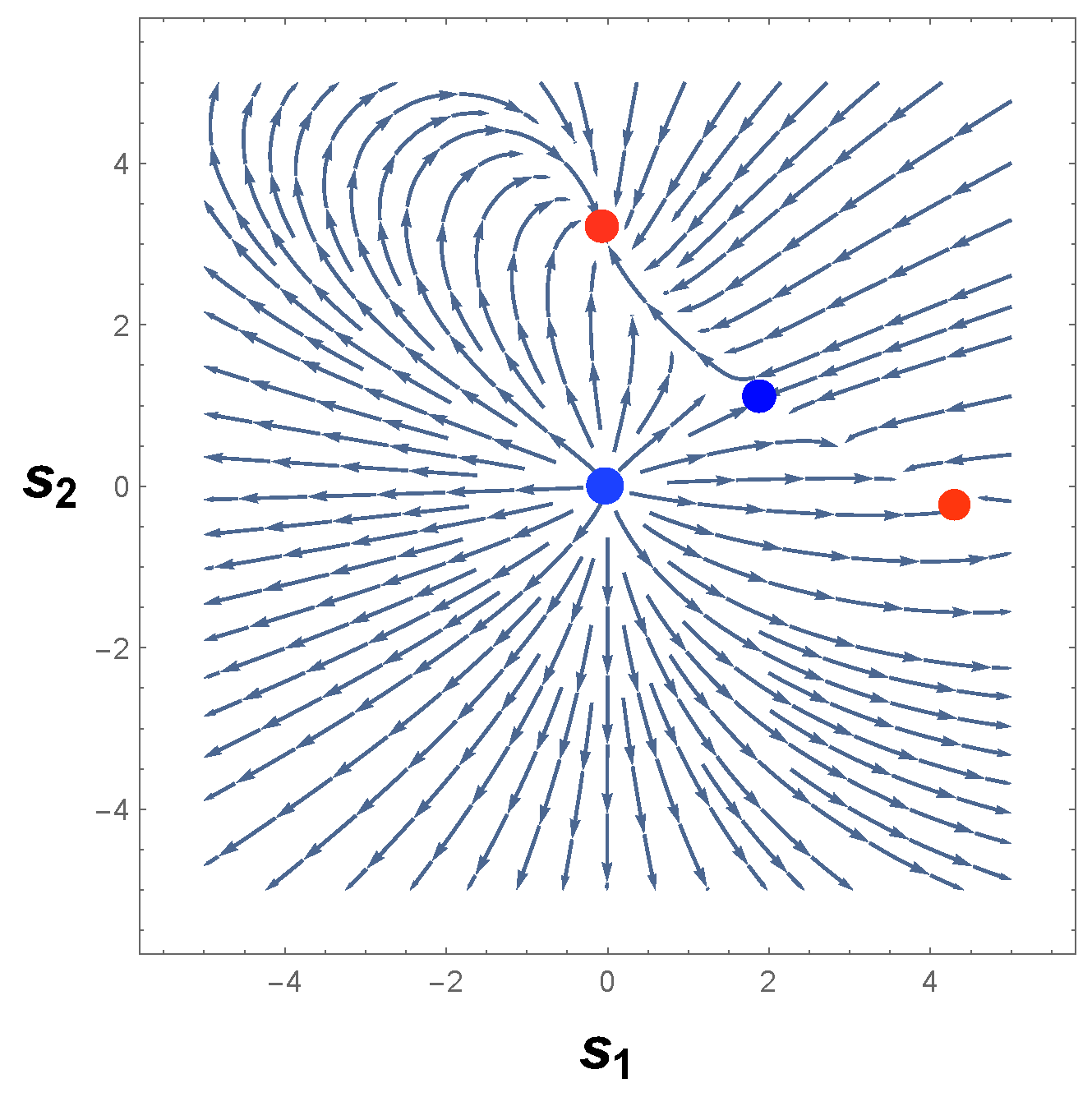
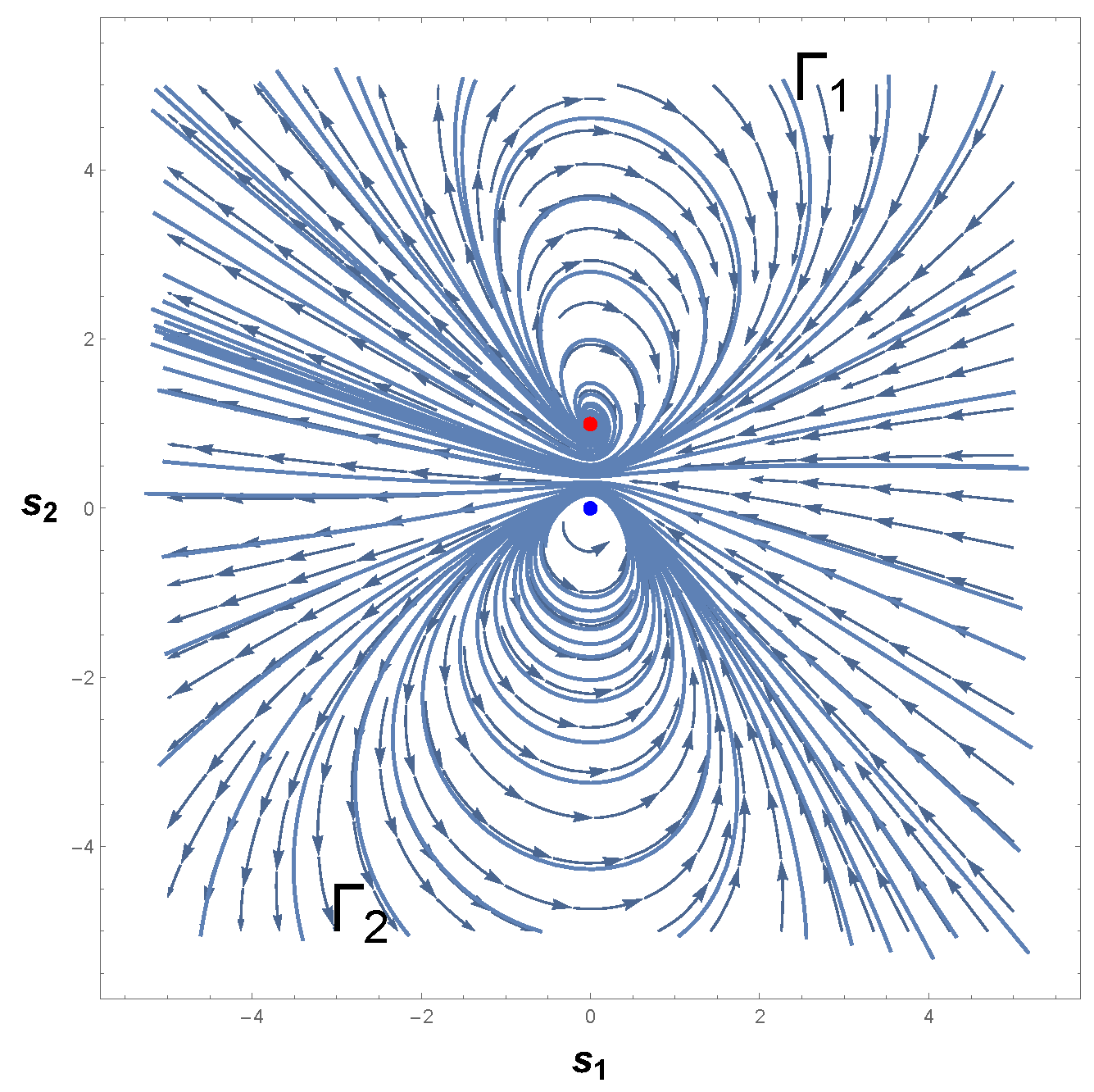
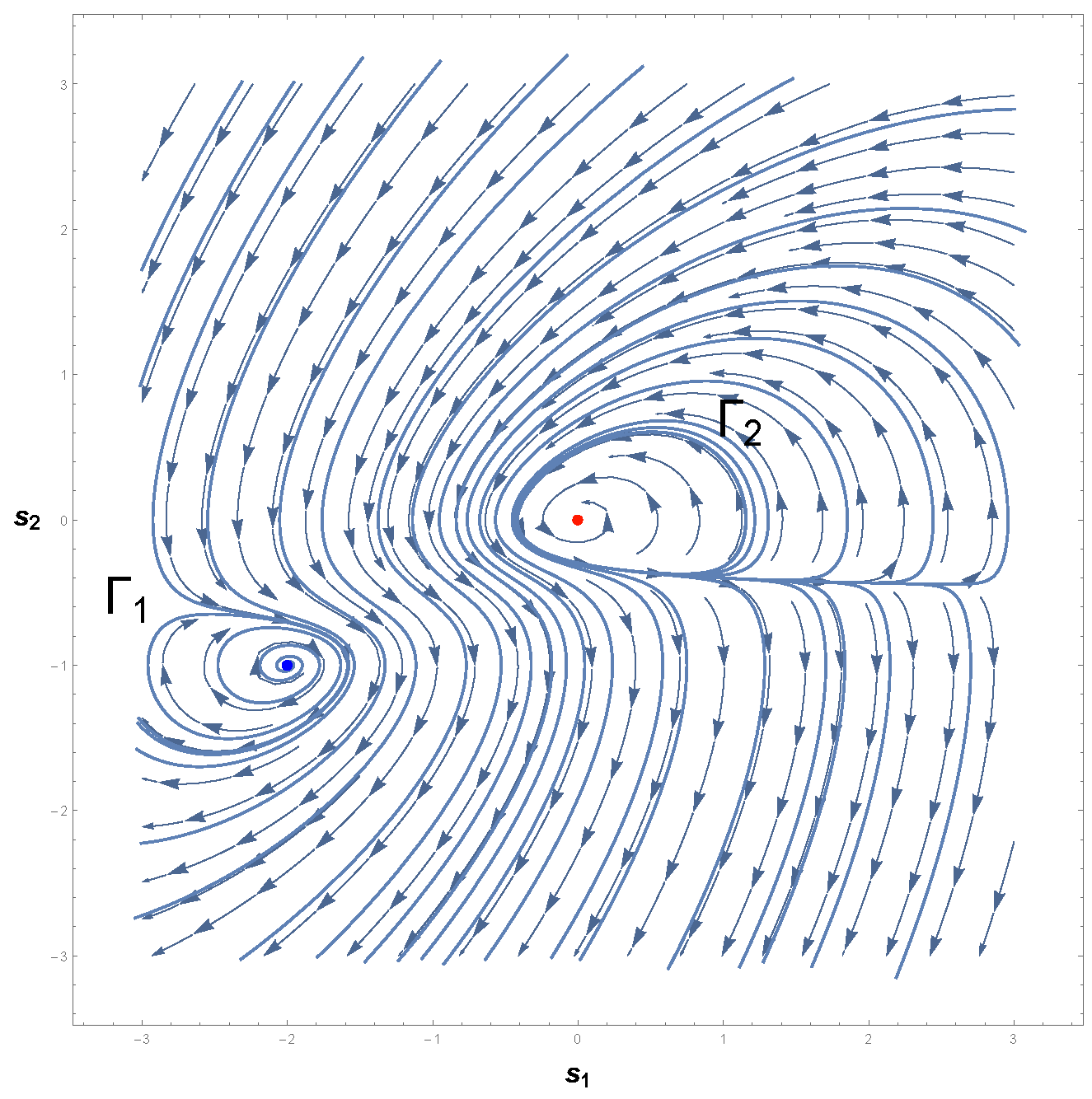
3.3. Systems with More than One Limit Cycle
3.3.1. First Example
3.3.2. Second Example
3.3.3. Final Example
4. The Sixteenth Problem of Hilbert
4.1. Second-Degree Polynomial Systems
4.2. nth-Degree Polynomial Systems
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. The Method of Geometric Characteristics
References
- Hilbert, D. Mathematical problems. Bull. Amer. Math. Soc. 2000, 37, 407–436. [Google Scholar] [CrossRef]
- Zoladek, H.; Murillo, R. Qualitative Theory of Odes: An Introduction to Dynamical Systems Theory; World Scientific Publishing Company: Singapore, 2022. [Google Scholar]
- European Mathematical Society. Limit cycle; Encyclopedia of Mathematics. Available online: http://encyclopediaofmath.org/index.php?title=Limit_cycle&oldid=54065 (accessed on 9 December 2022).
- Robinson, R.C. An Introduction to Dynamical Systems: Continuous and Discrete; American Mathematical Society: Providence, RI, USA, 2012. [Google Scholar]
- Jordan, D.; Smith, P. Nonlinear Ordinary Differential Equations: An Introduction for Scientists and Engineers; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Perko, L. Multiple Limit Cycle Bifurcation Surfaces and Global Families of Multiple Limit Cycles. J. Differ. Equ. 1995, 122, 89–113. [Google Scholar] [CrossRef]
- Chen, T.; Huang, L.; Yu, P. Center condition and bifurcation of limit cycles for quadratic switching systems with a nilpotent equilibrium point. J. Differ. Equ. 2021, 303, 326–368. [Google Scholar] [CrossRef]
- Liu, S.; Han, M. Bifurcation theory of limit cycles by higher order Melnikov functions and applications. J. Differ. Equ. 2024, 403, 29–66. [Google Scholar] [CrossRef]
- Yan, X.; Zhang, C. Properties of Hopf bifurcation to a reaction-diffusion population model with nonlocal delayed effect. J. Differ. Equ. 2024, 385, 155–182. [Google Scholar] [CrossRef]
- Lin, G.; Wang, L.; Yu, J. Basins of attraction and paired Hopf bifurcations for delay differential equations with bistable nonlinearity and delay-dependent coefficient. J. Differ. Equ. 2023, 354, 183–206. [Google Scholar] [CrossRef]
- Yan, S.; Du, Z. Hopf bifurcation in a Lotka-Volterra competition-diffusion-advection model with time delay. J. Differ. Equ. 2023, 344, 74–101. [Google Scholar] [CrossRef]
- Geng, D.; Wang, H. Normal form formulations of double-Hopf bifurcation for partial functional differential equations with nonlocal effect. J. Differ. Equ. 2022, 309, 741–785. [Google Scholar] [CrossRef]
- Luo, A.C.J. Global Transversality, Resonance and Chaotic Dynamics; World Scientific: Singapore, 2008. [Google Scholar]
- Tsarin, Y.A.; Ryabov, V.B.; Variv, D.M. Problems of the application of Melnikov method for chaos forecast in Dissipative dynamical systems. In Proceedings of the First International Conference on Unsolved Problems of Noise in Physics, Biology, Electronic Technology and Information Technology, 1st ed.; Doering, C.R., Kiss, L.B., Shlesinger, M.F., Eds.; World Scientific: Singapore, 1996; Volume 1, pp. 251–259. [Google Scholar]
- Luo, A.C.J.; Hamidzadeh, H.R.; Dai, L. (Eds.) Nonlinear Science And Complexity—Proceedings of the Conference; World Scientific Publishing Company: Singapore, 2006. [Google Scholar]
- Monteiro, L.H.A. Sistemas Dinâmicos; Livraria da Física: São Paulo, Brazil, 2002. [Google Scholar]
- Lynch, S. Dynamical Systems with Applications Using Mathematica; Springer International Publishing: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Kocak, H.; Hale, J.K. Dynamics and Bifurcations; Springer: New York, NY, USA, 2012. [Google Scholar]
- Boutelle, J.C.; Cronin, J. Mathematical Aspects of Hodgkin-Huxley Neural Theory; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Jones, D.; Plank, M.; Sleeman, B. Differential Equations and Mathematical Biology; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Gaiko, V. Global Bifurcation Theory and Hilbertś Sixteenth Problem; Springer: New York, NY, USA, 2013. [Google Scholar]
- Schlomiuk, D. Algebraic particular integrals, integrability and the problem of the center. Trans. Am. Math. Soc. 1993, 338, 799–841. [Google Scholar] [CrossRef]
- Schlomiuk, D. Aspects of Planar Polynomial Vector Fields: Global versus Local, Real versus Complex, Analytic versus Algebraic and Geometric; Kluwer Academic Publishers: Montreal, QC, Canada, 2004; Volume 134, pp. 471–509. [Google Scholar]
- da Silva, V.B.; Vieira, J.P.; Leonel, E.D. Information geometry theory of bifurcations? A covariant formulation. Chaos 2022, 32, 023119. [Google Scholar] [CrossRef] [PubMed]
- da Silva, V.B.; Vieira, J.P.; Leonel, E.D. Fisher information of the Kuramoto model: A geometric reading on synchronization. Phys. D Nonlinear Phenom. 2021, 423, 132926. [Google Scholar] [CrossRef]
- Hale, J.K. Ordinary Differential Equations; Dover Publications: Mineola, NY, USA, 2009. [Google Scholar]
- Afrajmovich, V.; Ilyashenko, Y.; Shilnikov, L.; Arnold, V.; Kazarinoff, N. Dynamical Systems V: Bifurcation Theory and Catastrophe Theory; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Kielhöfer, H. Bifurcation Theory: An Introduction with Applications to Partial Differential Equations; Springer-Verlag: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Janke, W.; Johnston, D.A.; Kenna, R. Information geometry and phase transitions. Physica A 2004, 336, 181–186. [Google Scholar] [CrossRef]
- Abdel-All, N.H.; Abd-Ellah, H.; Mostafa, H. Information geometry and statistical manifold. Chaos Solit. Fractals 2003, 15, 161–172. [Google Scholar] [CrossRef]
- Deza, M.M.; Deza, E. Encyclopedia of Distances; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Murray, M.K.; Rice, J.W. Differential Geometry and Statistics; CRC Press: Boca Raton, FL, USA, 1993. [Google Scholar]
- Kreyszig, E. Differential Geometry; Dover Publications: Mineola, NY, USA, 2013. [Google Scholar]
- Ruppeiner, G. Thermodynamic curvature measures interactions. Am. J. Phys 2010, 78, 1170. [Google Scholar] [CrossRef]
- Weinberg, S. Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity; Wiley & Sons: Hoboken, NJ, USA, 1972. [Google Scholar]
- Janyszek, H.; Mrugała, R. Riemannian geometry and stability of ideal quantum gases. J. Phys. A Math. Gen. 1990, 23, 467. [Google Scholar] [CrossRef]
- Ubriaco, M.R. The role of curvature in quantum statistical mechanics. J. Phys. Conf. Ser. 2016, 766, 012007. [Google Scholar] [CrossRef]
- Ruppeiner, G. Thermodynamic curvature from the critical point to the triple point. Phys. Rev. E 2012, 86, 021130. [Google Scholar] [CrossRef]
- Ruppeiner, G.; Dyjack, N.; McAloon, A.; Stoops, J. Solid-like features in dense vapors near the fluid critical point. J. Chem. Phys. 2017, 146, 224501. [Google Scholar] [CrossRef] [PubMed]
- Ruppeiner, G. Riemannian geometric theory of critical phenomena. Phys. Rev. A. 1991, 44, 3583–3595. [Google Scholar] [CrossRef]
- Basnarkov, L.; Urumov, V. Phase transitions in the Kuramoto model. Phys. Rev. E. 2007, 76, 057201–057204. [Google Scholar] [CrossRef] [PubMed]
- Dietert, H.; Fernandez, B. The mathematics of asymptotic stability in the Kuramoto model. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2018, 474, 20180467. [Google Scholar] [CrossRef]
- Hsia, C.H.; Jung, C.Y.; Kwon, B. On the synchronization theory of Kuramoto oscillators under the effect of inertia. J. Differ. Equ. 2019, 267, 742–775. [Google Scholar] [CrossRef]
- Horwitz, L.; Zion, Y.B.; Lewkowicz, M.; Schiffer, M.; Levitan, J. Geometry of Hamiltonian chaos. Phys. Rev. Lett. 2007, 98, 234301. [Google Scholar] [CrossRef] [PubMed]
- Arnol’d, V. Mathematical Methods of Classical Mechanics; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Landau, L.D.; Lifshitz, E. Mechanics; Elsevier Science: Amsterdam, The Netherlands, 1982. [Google Scholar]
- Janyszek, H.; Mrugała, R. Geometrical structure of the state space in classical statistical and phenomenological thermodynamics. Rep. Math. Phys. 1989, 27, 145–159. [Google Scholar] [CrossRef]
- Oprea, J. Differential Geometry and Its Applications; Mathematical Association of America: Washington, DC, USA, 2007. [Google Scholar]
- Prussing, J.; Conway, B. Orbital Mechanics; Oxford University Press: Oxford, UK, 1993. [Google Scholar]
- Newell, A. Nonlinear Optics; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Elnashaie, S.S.; Elshishini, E.H. Dynamic Modelling, Bifurcation and Chaotic Behaviour of Gas-Solid Catalytic Reactors; Taylor & Francis: Abingdon, UK, 1996. [Google Scholar]
- Tam, P.C. Object Recognition; IntechOpen: London, UK, 2011. [Google Scholar]
- McCauley, J.L. Classical Mechanics: Transformations, Flows, Integrable, and Chaotic Dynamics; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Okninski, A. Catastrophe Theory; Elsevier Science: Amsterdam, The Netherlands, 1992. [Google Scholar]
- Ottino, J.M. The Kinematics of Mixing: Stretching, Chaos, and Transport; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Verhulst, F. Nonlinear Differential Equations and Dynamical Systems; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- European Mathematical Society. Bendixson criterion; Encyclopedia of Mathematics. Available online: http://encyclopediaofmath.org/index.php?title=Bendixson_criterion&oldid=44727 (accessed on 9 December 2022).
- Lakshmanan, M.; Rajaseekar, S. Nonlinear Dynamics: Integrability, Chaos and Patterns; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Leonel, E.D. Scaling Laws in Dynamical Systems; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Dobrushkin, V.A. Applied Differential Equations: The Primary Course; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Espinar, J.M.; Espinar Garcia, J.M.; Viana, M. Differential Equations: A Dynamical Systems Approach to Theory and Practice; American Mathematical Society: Providence, RI, USA, 2021. [Google Scholar]
- Irwin, M.C. Smooth Dynamical Systems; World Scientific: Singapore, 2001. [Google Scholar]
- Lam, K.S. Fundamental Principles of Classical Mechanics: A Geometrical Perspective; World Scientific Publishing Company: Singapore, 2014. [Google Scholar]
- Renteln, P. Manifolds, Tensors, and Forms: An Introduction for Mathematicians and Physicists; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Hotz, I.; Masood, T.B.; Sadlo, F.; Tierny, J. (Eds.) Topological Methods in Data Analysis and Visualization VI: Theory, Applications, and Software; Springer International Publishing: Cham, Switzerland, 2021. [Google Scholar]
- Do Carmo, M. Differential Forms and Applications; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Kinsey, L. Topology of Surfaces; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Farmakis, I.; Moskowitz, M.A. Fixed Point Theorems and Their Applications; World Scientific Publishing Company: Singapore, 2013. [Google Scholar]
- Weinstein, T. An Introduction to Lorentz Surfaces; De Gruyter: Berlin, Germany, 2011. [Google Scholar]
- Enns, R.H.; McGuire, G. Nonlinear Physics with Mathematica for Scientists and Engineers; Birkhäuser: Basel, Switzerland, 2012. [Google Scholar]
- Thompson, D.E. Design Analysis: Mathematical Modeling of Nonlinear Systems; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Vepa, R. Nonlinear Control of Robots and Unmanned Aerial Vehicles: An Integrated Approach; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- European Mathematical Society. Van der Pol equation; Encyclopedia of Mathematics. Available online: http://encyclopediaofmath.org/index.php?title=Van_der_Pol_equation&oldid=52372 (accessed on 9 December 2022).
- Frame, M. Mathematical Models in the Biosciences I; Yale University Press: New Haven, CT, USA, 2021. [Google Scholar]
- Ye, Y.Q.; Lo, C.Y. Theory of Limit Cycles; American Mathematical Society: Providence, RI, USA, 1986. [Google Scholar]
- Weisstein, E.W. Concise Encyclopedia of Mathematics; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Nebel, B.; Freksa, C.; Hegarty, M.; Barkowsky, T. (Eds.) Spatial Cognition IX: International Conference, Spatial Cognition, September 15–19 in Proceedings, Bremen, Germany, 2014; Springer International Publishing: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Willett, R.; Yu, G. Higher Index Theory; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar]
- Blackadar, B. K-Theory for Operator Algebras; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Kriete, T.L.; Bourdon, P.; MacCluer, B.D. Differential Equations: Techniques, Theory, and Applications; American Mathematical Society: Providence, RI, USA, 2019. [Google Scholar]
- Mirza, B.; Talaei, Z. Thermodynamic geometry of a Kagome Ising model in a magnetic field. Phys. Lett. A 2013, 377, 513–517. [Google Scholar] [CrossRef]
- Taneja, H.C. Advanced Engineering Mathematics; International Publishing House Pvt. Limited: New Delhi, India, 2010. [Google Scholar]
- Shikin, E.V. Handbook and Atlas of Curves; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Srivastava, A.C. Engineering Mathematics; Prentice-Hall of India Pvt. Limited: New Delhi, India, 2010. [Google Scholar]
- Sheil-Small, T. Complex Polynomials; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Ram, B. Engineering Mathematics; Pearson: London, UK, 2009. [Google Scholar]
- Aluf, O. Advance Elements of Optoisolation Circuits: Nonlinearity Applications in Engineering; Springer International Publishing: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Izhikevich, E.M.; Hoppensteadt, F.C. Weakly Connected Neural Networks; Springer: New York, NY, USA, 2012. [Google Scholar]
- Rossa, F.D.; Dercole, F.; Rinaldi, S.; Landi, P.; Gragnani, A. Modeling Love Dynamics; World Scientific Publishing Company: Singapore, 2015. [Google Scholar]
- Scott, S.K. Chemical Chaos; Clarendon Press: Oxford, UK, 1993. [Google Scholar]
- Zhang, Z. Qualitative Theory of Differential Equations; American Mathematical Society: Providence, RI, USA, 1992. [Google Scholar]
- Bossel, H. Modeling and Simulation; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Sinha, N.K.; Ananthkrishnan, N. Advanced Flight Dynamics with Elements of Flight Control; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Larter, R.; Showalter, K. Computational Studies in Nonlinear Dynamics. In Reviews in Computational Chemistry; Lipkowitz, K.B., Boyd, D.B., Eds.; Wiley: Berlin, Germany, 2009; Volume 10, pp. 177–266. [Google Scholar]
- Cai, G.; Zhu, W. Elements of Stochastic Dynamics; World Scientific: Singapore, 2016. [Google Scholar]
- Christopher, C.; Li, C. Limit Cycles of Differential Equations; Springer: Basel, Switzerland, 2007. [Google Scholar]
- Arnold, V.; Atiyah, M.; Lax, P.; Mazur, B. Mathematics: Frontiers and Perspectives; American Mathematical Society: Providence, RI, USA, 2000. [Google Scholar]
- Castañeda, J.; Humanez, P.; Marcellán, F. Differential Algebra, Complex Analysis and Orthogonal Polynomials: Jairo Charris Seminar 2007–2008, Escuela de Matemáticas, Universidad Sergio Arboleda, Bogotá, Colombia; Contemporary mathematics—American Mathematical Society: Providence, RI, USA, 2010. [Google Scholar]
- Roussarie, R. Bifurcations of Planar Vector Fields and Hilbert’s Sixteenth Problem; Springer: Basel, Switzerland, 2013. [Google Scholar]
- Shi, S.L. A concrete example of the existence of four limit cycles for plane quadratic systems. Sci. Sin. 1980, 23, 153–158. [Google Scholar]
- Leonov, G. Effective methods for investigation of limit cycles in dynamical systems. Appl. Math. Mech. 2010, 21, 37–73. [Google Scholar]
- Leonov, G.; Kuznetsova, O. Lyapunov quantities and limit cycles of two-dimensional dynamical systems. Analytical methods and symbolic computation. Regul. Chaotic Dyn. 2010, 15, 354–377. [Google Scholar] [CrossRef]
- Ghorpade, S.R.; Limaye, B.V. A Course in Multivariable Calculus and Analysis; Springer: New York, NY, USA, 2010. [Google Scholar]
- Sverdlove, R. Critical points with asymmetric schemes Journal of Mathematical Analysis and Applications. J. Math. Anal. Appl 1982, 88, 452–463. [Google Scholar] [CrossRef]
- Oshea, D.; Cox, D.A.; Little, J. Using Algebraic Geometry; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Scottile, F. Computations in Algebraic Geometry with Macaulay 2, 1st ed.; Sturmfels, B., Grayson, D.R., Eisenbud, D., Stillman, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 2, Chapter 7; pp. 63–64. [Google Scholar]
- Hazewinkel, M. Encyclopaedia of Mathematics: Heaps and Semi-Heaps-Moments, Method of (in Probability Theory); Springer: Dordrecht, The Netherlands, 2013; Volume 3. [Google Scholar]
- Tsai, L. Robot Analysis: The Mechanics of Serial and Parallel Manipulators; Wiley: Hoboken, NJ, USA, 1999. [Google Scholar]
- Gleen, J. Mathematics Dictionary; Springer: Dordrecht, The Netherlands, 1992. [Google Scholar]
- Milovanovic, G.V.; Rassias, T.M.; Mitrinovic, D.S. Topics in Polynomials: Extremal Problems, Inequalities, Zeros; World Scientific Publishing Company: Singapore, 1994. [Google Scholar]
- Ackermann, J. Robust Control: The Parameter Space Approach; Springer: London, UK, 2012. [Google Scholar]
- Sommese, A.J.; Wampler, C.W. The Numerical Solution of Systems of Polynomials Arising in Engineering and Science; World Scientific: Singapore, 2005. [Google Scholar]
- Kaszkurewicz, E.; Bhaya, A. Applications of Computational Algebraic Geometry; American Mathematical Society: Providence, RI, USA, 2006. [Google Scholar]
- Epp, S.S. Discrete Mathematics: Introduction to Mathematical Reasoning; Cengage Learning: Boston, MA, USA, 2014. [Google Scholar]
- Gunderson, D.S. Handbook of Mathematical Induction: Theory and Applications; Taylor & Francis: Abingdon, UK, 2011. [Google Scholar]
- Ilyashenko, Y.; Yakovenko, S. Concerning the Hilbert 16th Problem; American Mathematical Society: Providence, RI, USA, 1995. [Google Scholar]
- Ecalle, J.; Martinet, J.M.; Ramis, J. Non-accumulation des cycles-limites I. C. R. Acad. Sci. Paris Sér. 1997, 304, 375–377. [Google Scholar]
- Ilyashenko, Y. Finiteness Theorems for Limit Cycles; American Mathematical Society: Providence, RI, USA, 1991. [Google Scholar]
- Klambauer, G. Aspects of Calculus; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Kazaryan, M.E.; Prasolov, V.V.; Lando, S.K. Algebraic Curves: Towards Moduli Spaces; Springer International Publishing: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Furdui, O.; Pop, V. Square Matrices of Order 2: Theory, Applications, and Problems; Springer International Publishing: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Weil, A. Oeuvres Scientifiques/Collected Papers II (1951–1964), 2nd ed.; Springer Collected Works in Mathematics; Springer: Berlin/Heidelberg, Germany, 2009; Volume 2. [Google Scholar]
- Rutter, J. Geometry of Curves; Taylor & Francis: Abingdon, UK, 2000. [Google Scholar]
- Bénéteau, C.; Hudson, N. A Survey on the Maximal Number of Solutions of Equations Related to Gravitational Lensing. In Complex Analysis and Dynamical Systems: New Trends and Open Problems, 1st ed.; Agranovsky, M., Golberg, A., Jacobzon, F., Shoikhet, D., Zalcman, L., Eds.; Number 23 in Trends in Mathematics, Birkhöuser; Springer: Cham, Switzerland, 2018; Chapter 3; pp. 179–183. [Google Scholar]
- Wilmshurst, A.S. Complex Harmonic Polynomials and the Valence of Harmonic Polynomials. Ph.D. Dissertation, University of York, York, UK, 1994. [Google Scholar]
- Wilmshurst, A. The valence of harmonic polynomials. Proc. Am. Math. Soc. 1998, 126, 2077–2081. [Google Scholar] [CrossRef]

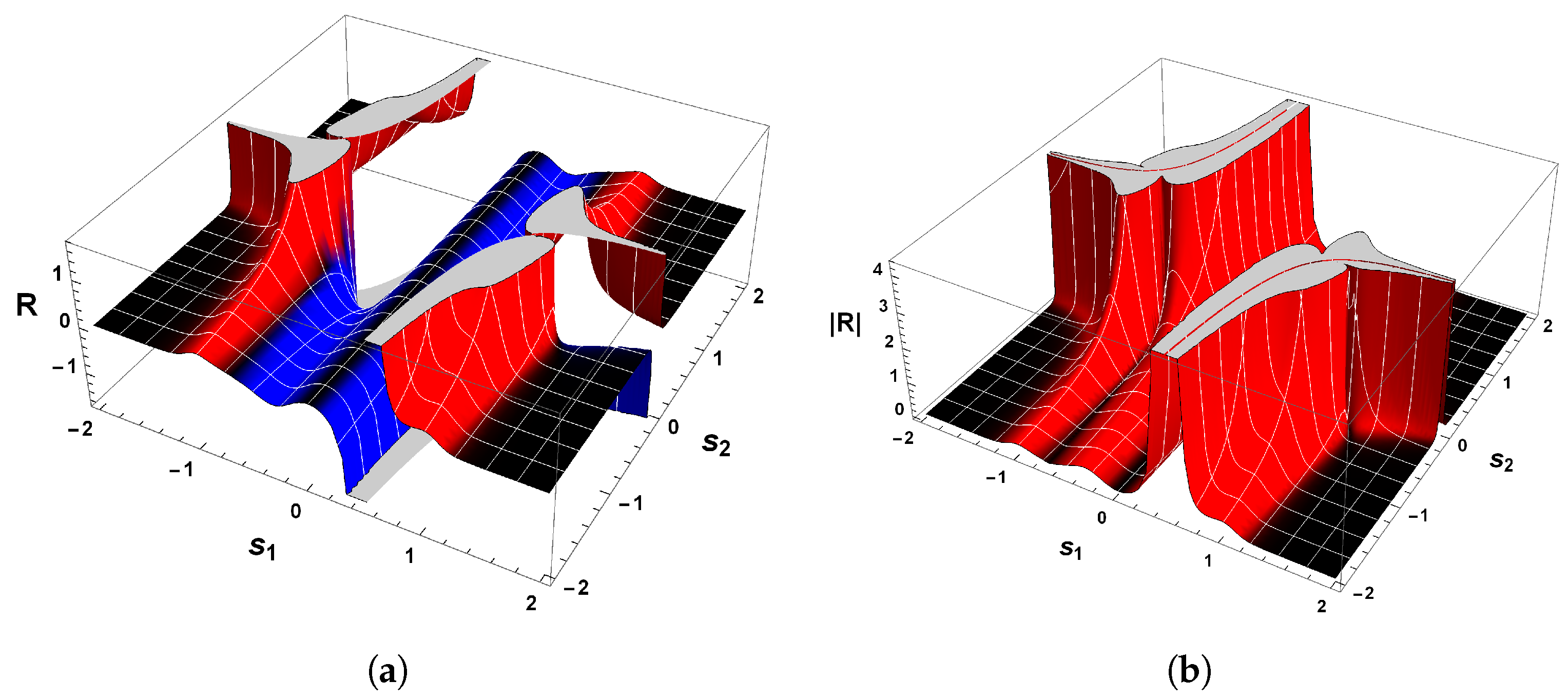
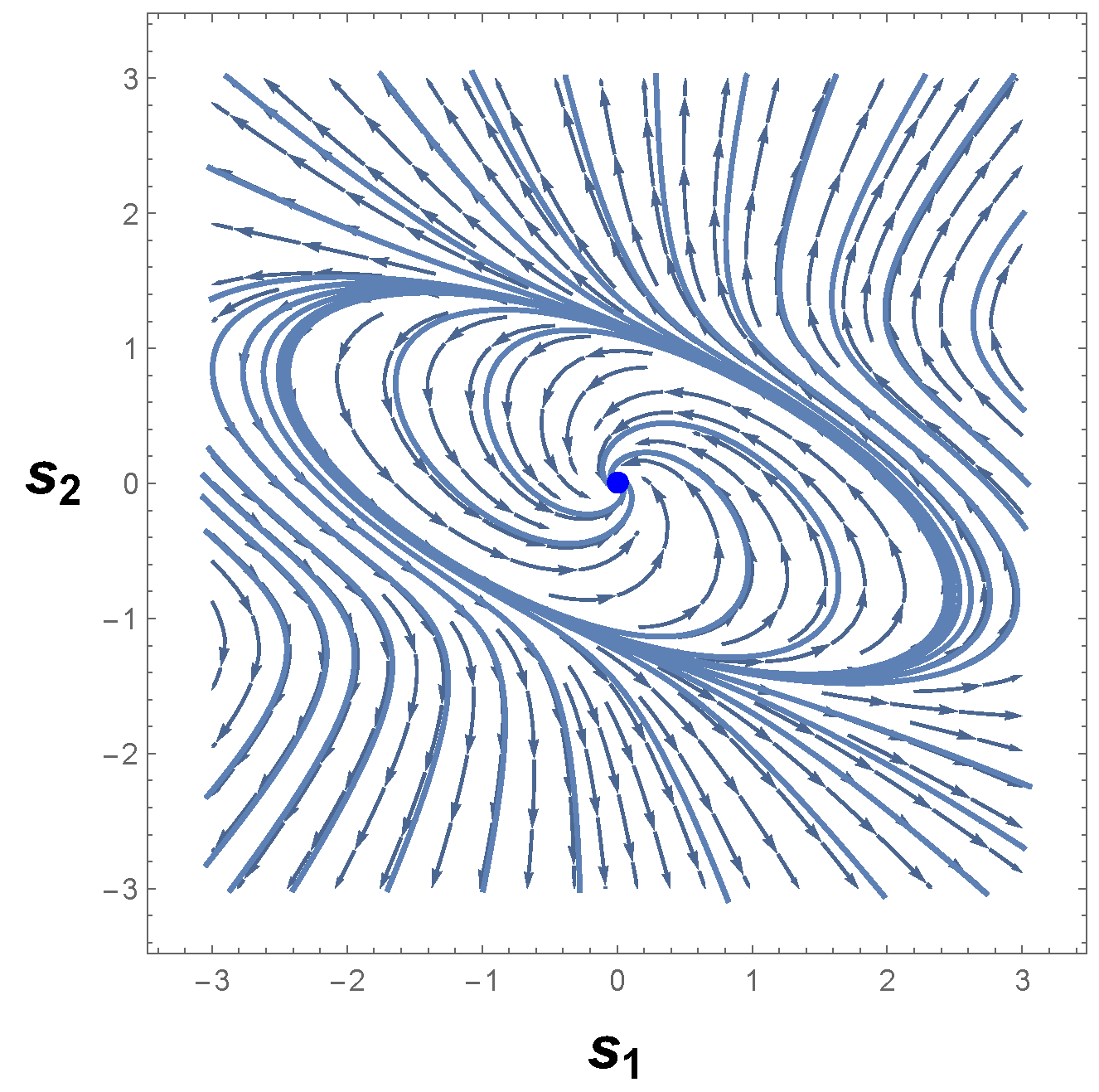
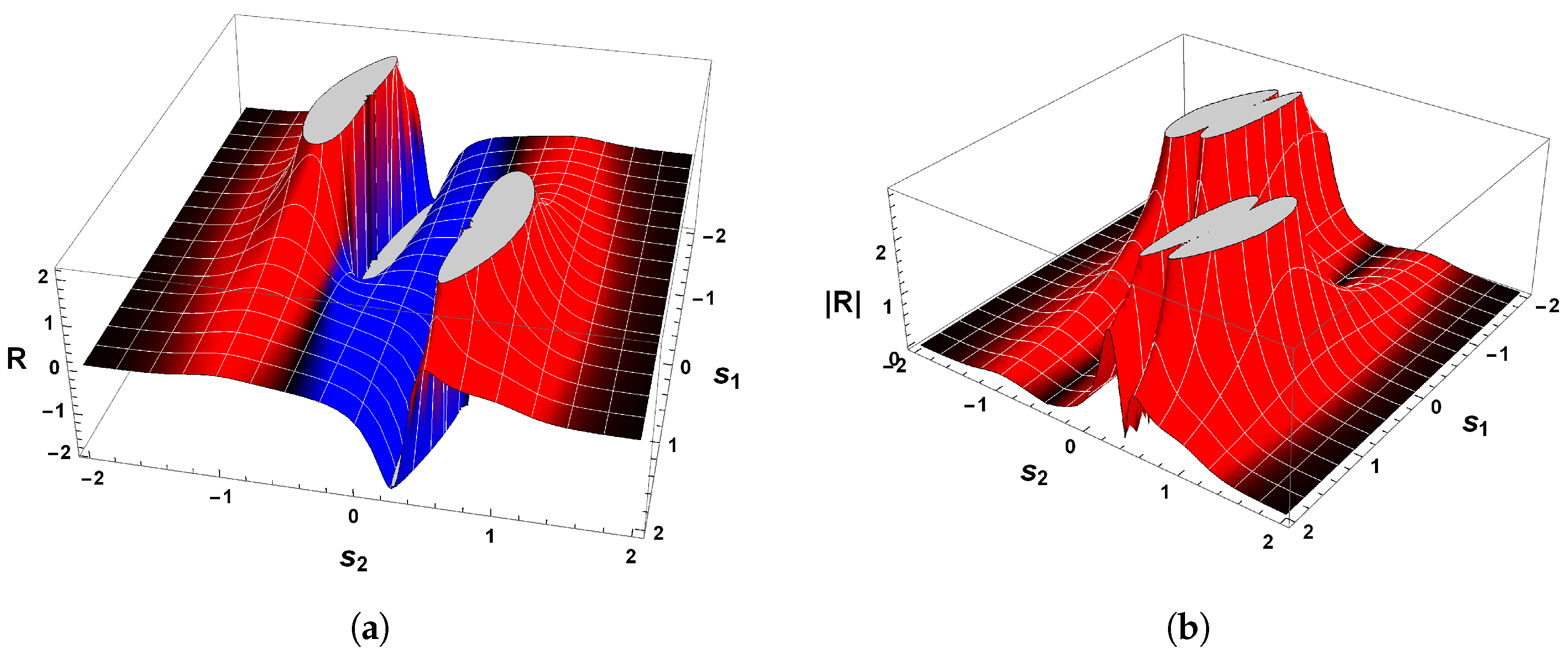
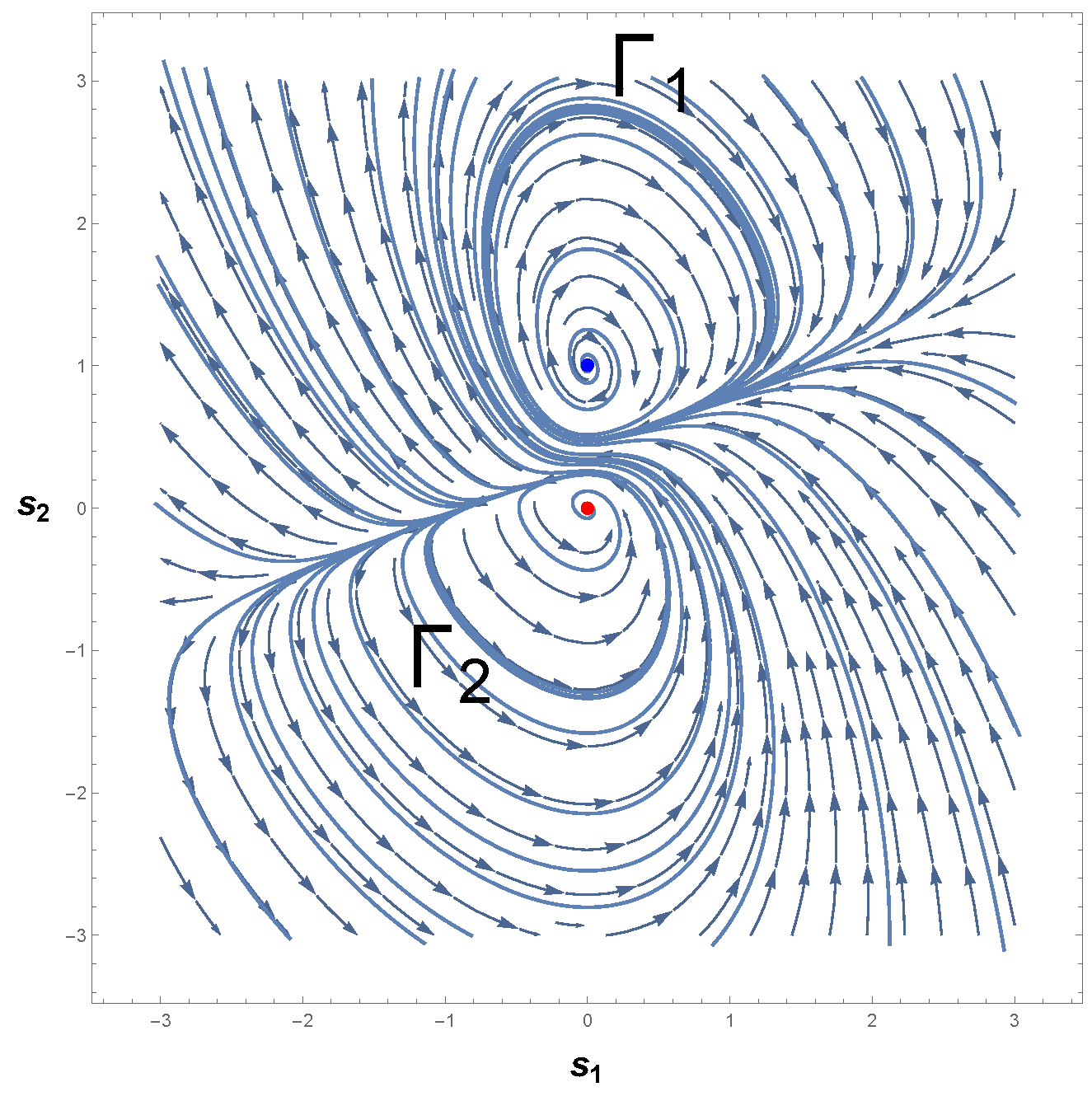

| Notation | Meaning |
|---|---|
| Rational integral functions | |
| Real variables | |
| r | Dimension of the parameter space X |
| Time | |
| Momenta | |
| Order parameters | |
| Control parameters | |
| Equilibrium points | |
| Critical/singular points of R | |
| Det | Determinant |
| Jacobian matrix | |
| Generalized Gaussian probability density | |
| T | Period of time |
| Family of probability distributions | |
| X | Parameter space |
| Riemannian manifold | |
| Fisher covariant symmetric tensor | |
| Metric elements | |
| G | Determinant of |
| Fourth-rank Riemannian curvature tensor | |
| R | Scalar curvature |
| Magnitude of scalar curvature | |
| Dulac function | |
| Index of | |
| Euler–Poincaré characteristic of | |
| Trace | |
| Saddle value/quantity | |
| Eigenvalues | |
| Resultant |
| Bifurcations | r | R Sign | Local Structural Stability | Divergence |
|---|---|---|---|---|
| Saddle-node [25] | 2 | − | Unstable | Bifurcation point |
| Transcritical [25] | 2 | − | Unstable | Bifurcation point |
| Supercritical pitchfork [25] | 2 | Stable/unstable | Bifurcation point | |
| Subcritical pitchfork [25] | 2 | Unstable/stable | Bifurcation point | |
| Homoclinic [25] (unperturbed oscillator) | 3 | + | Stable | Bifurcation point |
| Homoclinic [25] (perturbed oscillator) | 3 | + | Stable | Bifurcation point |
| Saddle-node [26] (2D Kuramoto model) | 2 | − | Unstable | Bifurcation point |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
da Silva, V.B.; Vieira, J.P.; Leonel, E.D. Exploring Limit Cycles of Differential Equations through Information Geometry Unveils the Solution to Hilbert’s 16th Problem. Entropy 2024, 26, 745. https://doi.org/10.3390/e26090745
da Silva VB, Vieira JP, Leonel ED. Exploring Limit Cycles of Differential Equations through Information Geometry Unveils the Solution to Hilbert’s 16th Problem. Entropy. 2024; 26(9):745. https://doi.org/10.3390/e26090745
Chicago/Turabian Styleda Silva, Vinícius Barros, João Peres Vieira, and Edson Denis Leonel. 2024. "Exploring Limit Cycles of Differential Equations through Information Geometry Unveils the Solution to Hilbert’s 16th Problem" Entropy 26, no. 9: 745. https://doi.org/10.3390/e26090745
APA Styleda Silva, V. B., Vieira, J. P., & Leonel, E. D. (2024). Exploring Limit Cycles of Differential Equations through Information Geometry Unveils the Solution to Hilbert’s 16th Problem. Entropy, 26(9), 745. https://doi.org/10.3390/e26090745






