The Joint Solvation Interaction
Abstract
1. Introduction
2. The Mixture Expansion











3. The Interaction Expansion



4. The Joint Solvation Interaction




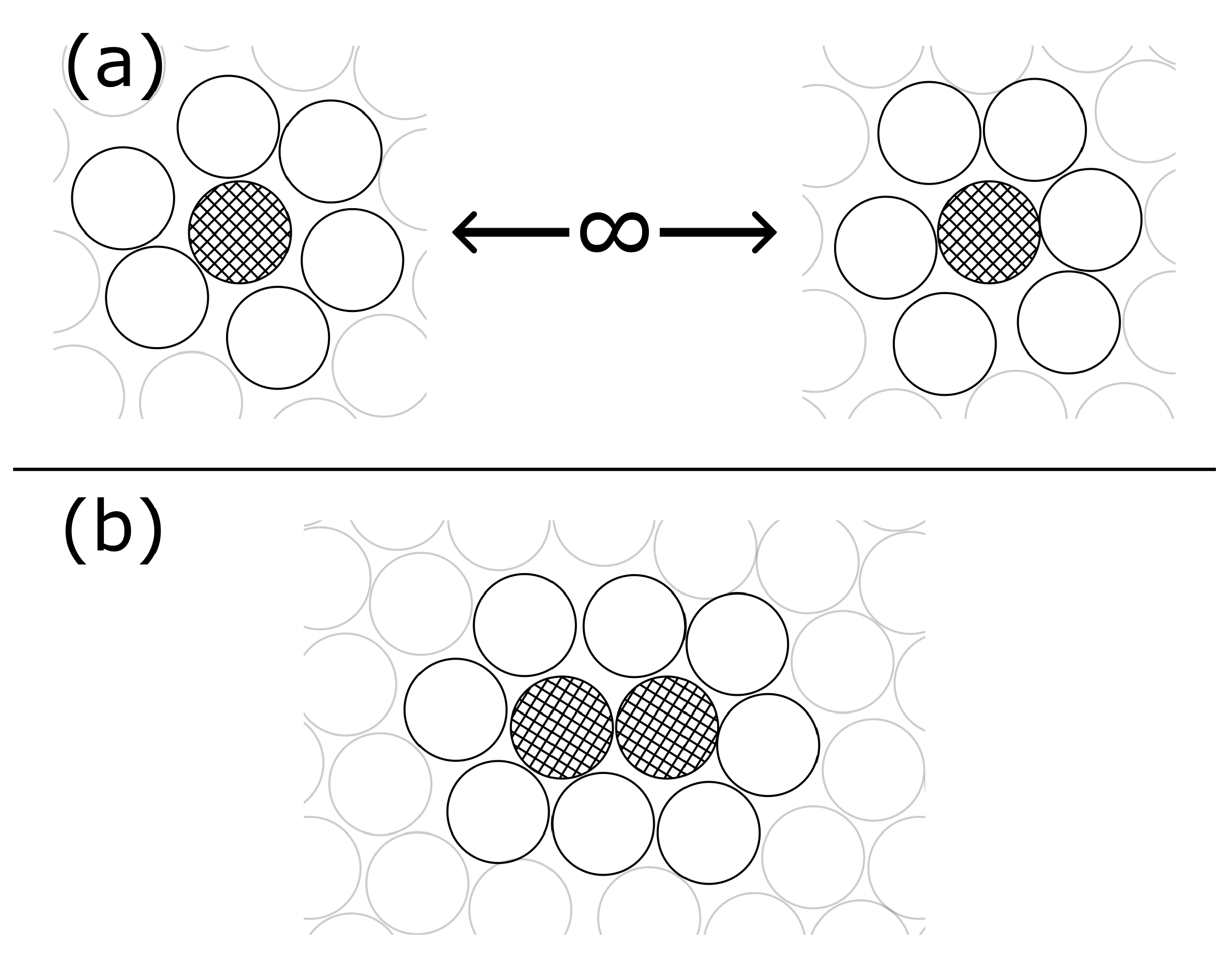
5. Equivalence of the Joint Solvation Interaction with the Solvent-Induced Interaction for Rigid Solutes





6. Comparison with the Cavity Interaction







7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SII | solvent-induced interaction |
| JSI | joint solvation interaction |
| ME | mixture expansion |
| CE | cluster expansion |
| MD | molecular dynamics |
| PCMD | partially connected molecular dynamics |
| CV | collective variable |
| CCF | cluster cumulant function |
Appendix A. Connection to the Microscopic Cluster Expansion










Appendix B. Convergence Properties of the Joint Solvation Interaction


References
- Durell, S.R.; Brooks, B.R.; Ben-Naim, A. Solvent-induced forces between two hydrophilic groups. J. Phys. Chem. 1994, 98, 2198–2202. [Google Scholar] [CrossRef]
- Yam, V.W.W.; Wong, K.M.C.; Zhu, N. Solvent-induced aggregation through metal⋯metal/π⋯π interactions: Large solvatochromism of luminescent organoplatinum (ii) terpyridyl complexes. J. Am. Chem. Soc. 2002, 124, 6506–6507. [Google Scholar] [CrossRef]
- Chandler, D. Interfaces and the driving force of hydrophobic assembly. Nature 2005, 437, 640–647. [Google Scholar] [CrossRef] [PubMed]
- Buisine, E.; de Villiers, K.; Egan, T.J.; Biot, C. Solvent-induced effects: Self-association of positively charged π systems. J. Am. Chem. Soc. 2006, 128, 12122–12128. [Google Scholar] [CrossRef]
- Korevaar, P.A.; Schaefer, C.; de Greef, T.F.; Meijer, E. Controlling chemical self-assembly by solvent-dependent dynamics. J. Am. Chem. Soc. 2012, 134, 13482–13491. [Google Scholar] [CrossRef] [PubMed]
- Tidor, B.; Karplus, M. The contribution of vibrational entropy to molecular association: The dimerization of insulin. J. Mol. Biol. 1994, 238, 405–414. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Ben-Naim, A. A possible involvement of solvent-induced interactions in drug design. J. Med. Chem. 1996, 39, 1531–1539. [Google Scholar] [CrossRef] [PubMed]
- Anfinsen, C.B. Principles that govern the folding of protein chains. Science 1973, 181, 223–230. [Google Scholar] [CrossRef]
- Vaiana, S.; Manno, M.; Emanuele, A.; Palma-Vittorelli, M.; Palma, M. The role of solvent in protein folding and in aggregation. J. Biol. Phys. 2001, 27, 133–145. [Google Scholar] [CrossRef]
- Zhou, R. Free energy landscape of protein folding in water: Explicit vs. implicit solvent. Proteins Struct. Funct. Bioinf. 2003, 53, 148–161. [Google Scholar] [CrossRef]
- Prabhu, N.; Sharp, K. Protein-solvent interactions. Chem. Rev. 2006, 106, 1616–1623. [Google Scholar] [CrossRef] [PubMed]
- Porter, L.L.; Looger, L.L. Extant fold-switching proteins are widespread. Proc. Natl. Acad. Sci. USA 2018, 115, 5968–5973. [Google Scholar] [CrossRef]
- Kauzmann, W. Some factors in the interpretation of protein denaturation. In Advances in Protein Chemistry; Elsevier: Amsterdam, The Netherlands, 1959; Volume 14, pp. 1–63. [Google Scholar]
- Ben-Naim, A. Statistical mechanical study of hydrophobic interaction. I. Interaction between two identical nonpolar solute particles. J. Chem. Phys. 1971, 54, 1387–1404. [Google Scholar] [CrossRef]
- Pratt, L.R.; Chandler, D. Theory of the hydrophobic effect. J. Chem. Phys. 1977, 67, 3683–3704. [Google Scholar] [CrossRef]
- Franks, F. Hydrophobic interactions—A historical perspective. Faraday Symp. Chem. Soc. 1982, 17, 7–10. [Google Scholar] [CrossRef]
- Ben-Naim, A. Solvent-induced interactions: Hydrophobic and hydrophilic phenomena. J. Chem. Phys. 1989, 90, 7412–7425. [Google Scholar] [CrossRef]
- Ben-Amotz, D.; Underwood, R. Unraveling water’s entropic mysteries: A unified view of nonpolar, polar, and ionic hydration. Acc. Chem. Res. 2008, 41, 957–967. [Google Scholar] [CrossRef] [PubMed]
- Egan, C.K.; Hassanali, A. Free energy decompositions illuminate synergistic effects in interfacial binding thermodynamics of mixed surfactant systems. J. Chem. Phys. 2023, 159, 104703. [Google Scholar] [CrossRef]
- Morita, T.; Hiroike, K. A new approach to the theory of classical fluids. III: General treatment of classical systems. Prog. Theor. Phys. 1961, 25, 537–578. [Google Scholar] [CrossRef]
- Stell, G.; Frisch, H.; Lebowitz, J. The Equilibrium Theory of Classical Fluids; Frisch, H.L., Lebowitz, J.L., Eds.; Benjamin: New York, NY, USA, 1964; pp. 171–261. [Google Scholar]
- Hansen, J.P.; McDonald, I.R. Theory of Simple Liquids: With Applications to Soft Matter; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Goodstein, D.L. States of Matter; Courier Corporation: North Chelmsford, MA, USA, 2014. [Google Scholar]
- Salpeter, E.E. On Mayer’s theory of cluster expansions. Ann. Phys. 1958, 5, 183–223. [Google Scholar] [CrossRef]
- Ladanyi, B.M.; Chandler, D. New type of cluster theory for molecular fluids: Interaction site cluster expansion. J. Chem. Phys. 1975, 62, 4308–4324. [Google Scholar] [CrossRef]
- Chandler, D.; Pratt, L.R. Statistical mechanics of chemical equilibria and intramolecular structures of nonrigid molecules in condensed phases. J. Chem. Phys. 1976, 65, 2925–2940. [Google Scholar] [CrossRef]
- Sengupta, S.; Gera, R.; Egan, C.; Morzan, U.N.; Versluis, J.; Hassanali, A.; Bakker, H.J. Observation of strong synergy in the interfacial water response of binary ionic and nonionic surfactant mixtures. J. Phys. Chem. Lett. 2022, 13, 11391–11397. [Google Scholar] [CrossRef]
- Scott, R.L. Thermodynamic functions for mixing at “constant volume”. J. Phys. Chem. 1960, 64, 1241–1247. [Google Scholar] [CrossRef]
- Kubo, R. Generalized cumulant expansion method. J. Phys. Soc. Jpn. 1962, 17, 1100–1120. [Google Scholar] [CrossRef]
- Beck, T.L.; Paulaitis, M.E.; Pratt, L.R. The Potential Distribution Theorem and Models of Molecular Solutions; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Grayce, C.J.; Schweizer, K.S. Solvation potentials for macromolecules. J. Chem. Phys. 1994, 100, 6846–6856. [Google Scholar] [CrossRef]
- Smith, P.E.; van Gunsteren, W.F. When are free energy components meaningful? J. Phys. Chem. 1994, 98, 13735–13740. [Google Scholar] [CrossRef]
- Mark, A.E.; Van Gunsteren, W.F. Decomposition of the free energy of a system in terms of specific interactions: Implications for theoretical and experimental studies. J. Mol. Biol. 1994, 240, 167–176. [Google Scholar] [CrossRef]
- Brady, G.P.; Szabo, A.; Sharp, K.A. On the decomposition of free energies. J. Mol. Biol. 1996, 263, 123–125. [Google Scholar] [CrossRef][Green Version]
- Levy, R.M.; Gallicchio, E. Computer simulations with explicit solvent: Recent progress in the thermodynamic decomposition of free energies and in modeling electrostatic effects. Annu. Rev. Phys. Chem. 1998, 49, 531–567. [Google Scholar] [CrossRef]
- Bren, U.; Martínek, V.; Florián, J. Decomposition of the solvation free energies of deoxyribonucleoside triphosphates using the free energy perturbation method. J. Phys. Chem. B 2006, 110, 12782–12788. [Google Scholar] [CrossRef] [PubMed]
- Gallicchio, E.; Kubo, M.; Levy, R.M. Enthalpy-entropy and cavity decomposition of alkane hydration free energies: Numerical results and implications for theories of hydrophobic solvation. J. Phys. Chem. B 2000, 104, 6271–6285. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hassanali, A.; Egan, C.K. The Joint Solvation Interaction. Entropy 2024, 26, 749. https://doi.org/10.3390/e26090749
Hassanali A, Egan CK. The Joint Solvation Interaction. Entropy. 2024; 26(9):749. https://doi.org/10.3390/e26090749
Chicago/Turabian StyleHassanali, Ali, and Colin K. Egan. 2024. "The Joint Solvation Interaction" Entropy 26, no. 9: 749. https://doi.org/10.3390/e26090749
APA StyleHassanali, A., & Egan, C. K. (2024). The Joint Solvation Interaction. Entropy, 26(9), 749. https://doi.org/10.3390/e26090749






