Is Seeing Believing? A Practitioner’s Perspective on High-Dimensional Statistical Inference in Cancer Genomics Studies
Abstract
:1. Introduction
2. Materials and Methods
2.1. The Frequentist High-Dimensional Inference
2.1.1. Classical Large Sample Properties
2.1.2. Post-Selection Inference
2.1.3. Data Shuffling via Sample Splitting and Bootstrapping
2.1.4. The Knock-Off Procedures
2.1.5. Remarks on Model Assumptions, Robustness and Inference Measures
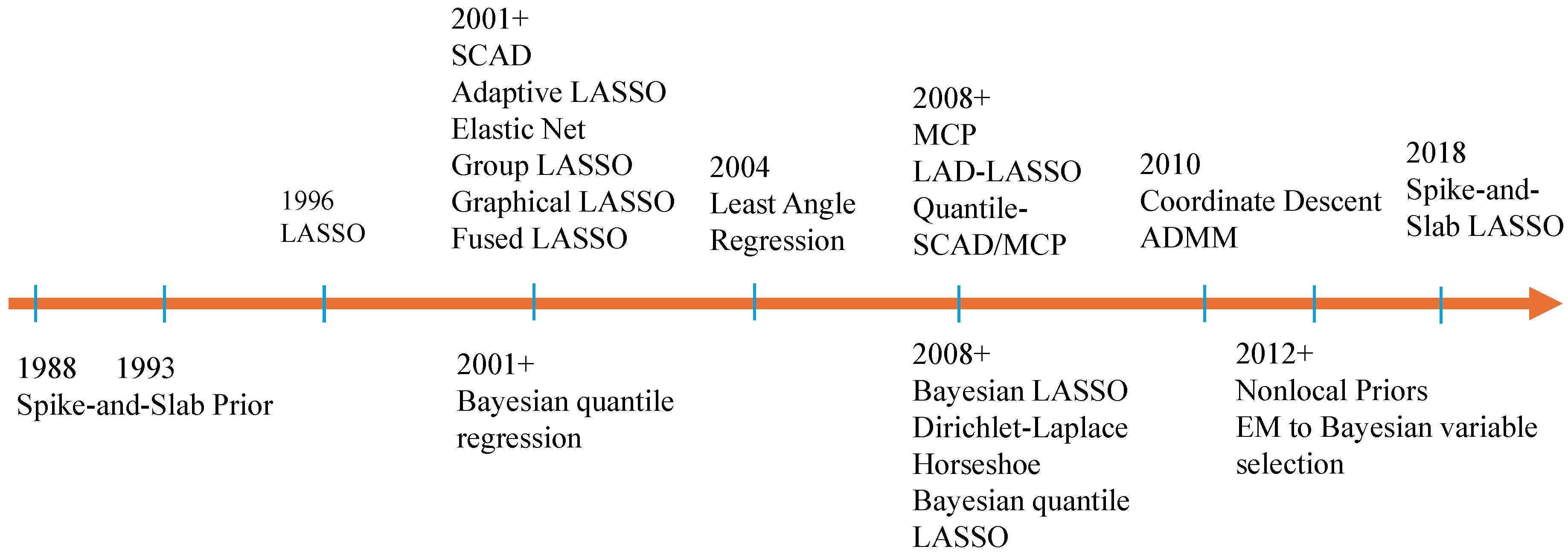
2.2. The Bayesian Inferences in High Dimensions
2.2.1. The Shrinkage Priors
2.2.2. The Robust Likelihood
2.3. Connections between High-Dimensional Frequentist and Bayesian Methods
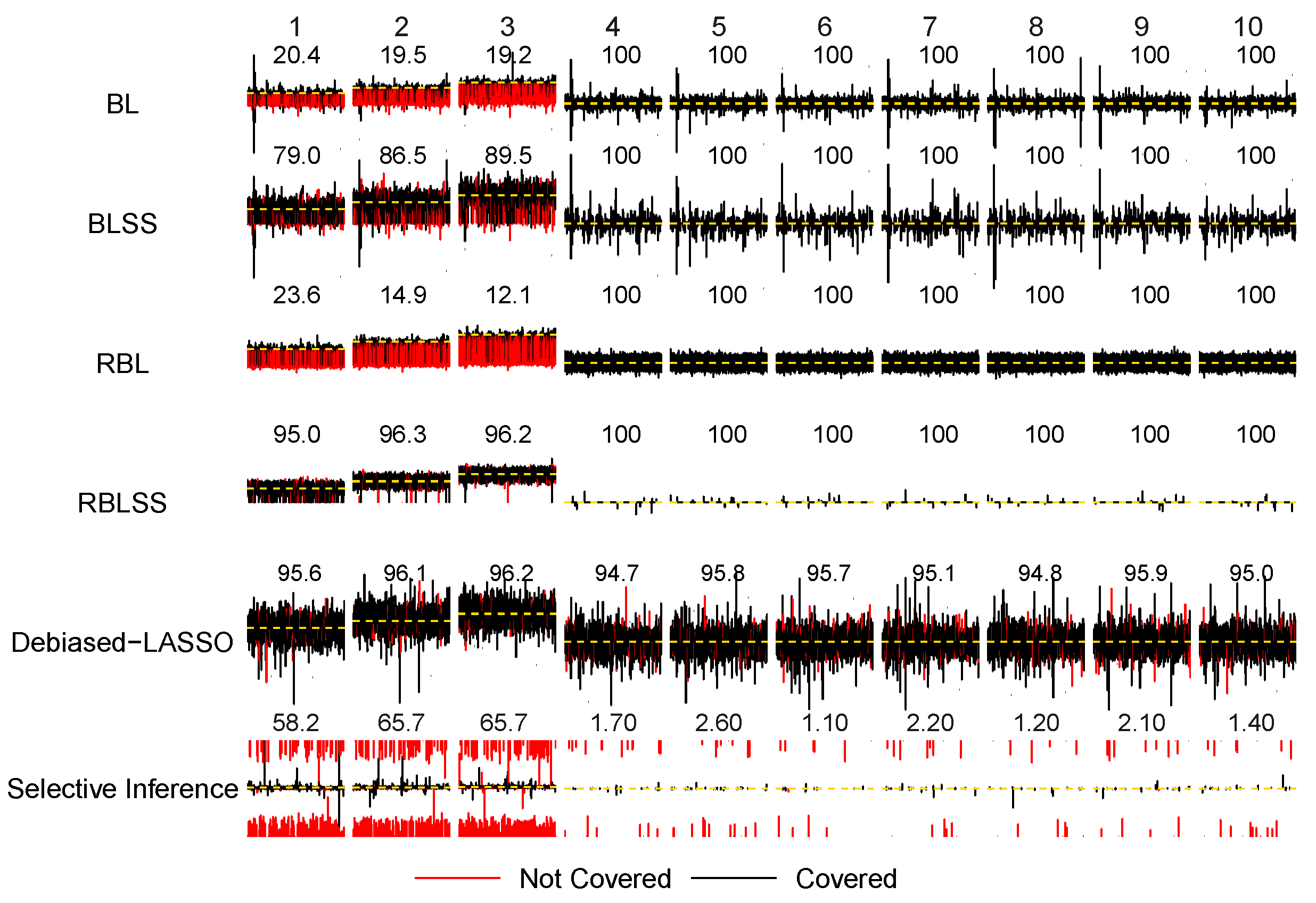
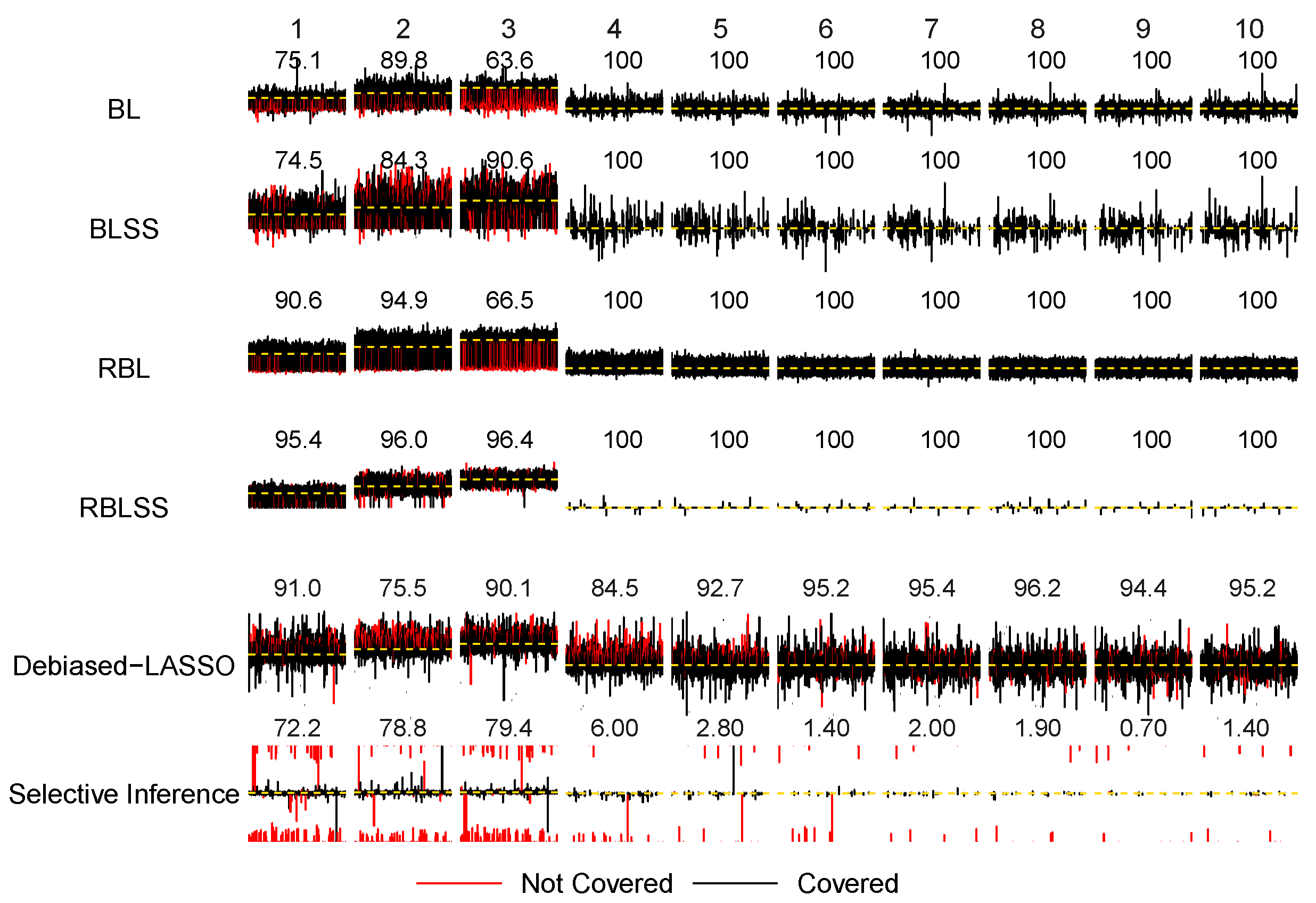
3. Simulation Study
4. Examples
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ADMM | Alternating direction method of multipliers |
| BL | Bayesian LASSO |
| BLSS | Bayesian LASSO with spike-and-slab prior |
| BMI | Body mass index |
| CI | Confidence interval |
| CV | Cross-validation |
| FDR | False discovery rate |
| GE | Gene expression |
| GWAS | Genome-wide association study |
| LAD | Least absolute deviation |
| LASSO | Least absolute shrinkage and selection operator |
| MCMC | Markov chain Monte Carlo |
| MCP | Minimax concave penalty |
| MPM | Median probability model |
| PGEE | Penalized generalized estimating |
| RBL | Robust Bayesian LASSO |
| RBLSS | Robust Bayesian LASSO with spike-and-slab prior |
| SCAD | Smoothly clipped absolute deviation |
| SNP | Single-nucleotide polymorphism |
Appendix A
Appendix A.1
| Methods | |||||||
|---|---|---|---|---|---|---|---|
| BL | BLSS | RBL | RBLSS | Debiased-LASSO | Selective Inference | ||
| Error 1 N(0,1) | error of | 1.773 | 0.250 | 2.898 | 0.274 | 1.038 | 0.718 |
| Standard deviation | 0.312 | 0.113 | 0.299 | 0.121 | 0.026 | 0.023 | |
| error of | 11.891 | 0.331 | 16.553 | 0.601 | 0.128 | 1.021 | |
| Standard deviation | 0.797 | 0.176 | 0.681 | 0.291 | 0.027 | 0.100 | |
| TP | 2.696 | 3.000 | 0.906 | 3.000 | 3.000 | 3.000 | |
| Standard deviation | 0.460 | 0.000 | 0.549 | 0.000 | 0.000 | 0.000 | |
| FP | 0.000 | 0.112 | 0.000 | 0.341 | 3.057 | 21.533 | |
| Standard deviation | 0.000 | 0.357 | 0.000 | 0.647 | 0.547 | 1.722 | |
| Coverage of | |||||||
| 0.138 | 0.957 | 0.167 | 0.939 | 0.938 | 0.725 | ||
| 0.153 | 0.950 | 0.087 | 0.920 | 0.945 | 0.725 | ||
| 0.166 | 0.943 | 0.079 | 0.927 | 0.943 | 0.725 | ||
| Average length | |||||||
| 0.789 | 0.412 | 1.030 | 0.416 | 0.458 | - | ||
| 0.901 | 0.411 | 1.309 | 0.413 | 0.456 | - | ||
| 0.908 | 0.410 | 1.607 | 0.412 | 0.457 | - | ||
| Coverage of | 0.995 | 0.994 | 0.998 | 0.994 | 0.957 | 0.020 | |
| Average length | 0.405 | 0.006 | 0.814 | 0.010 | 0.456 | - | |
| Error 2 t(2) | error of | 2.549 | 1.096 | 3.125 | 0.376 | 3.049 | 1.730 |
| Standard deviation | 0.551 | 0.881 | 0.372 | 0.285 | 0.103 | 0.081 | |
| error of | 27.124 | 8.645 | 23.650 | 0.390 | 0.067 | 2.099 | |
| Standard deviation | 39.807 | 40.405 | 3.622 | 0.229 | 0.021 | 0.213 | |
| TP | 1.581 | 2.611 | 0.474 | 2.972 | 1.996 | 2.731 | |
| Standard deviation | 0.793 | 0.610 | 0.558 | 0.208 | 0.117 | 0.066 | |
| FP | 0.007 | 15.999 | 0.000 | 0.039 | 0.849 | 19.204 | |
| Standard deviation | 0.083 | 78.785 | 0.000 | 0.223 | 0.247 | 1.632 | |
| Coverage of | |||||||
| 0.204 | 0.790 | 0.236 | 0.950 | 0.956 | 0.582 | ||
| 0.195 | 0.865 | 0.149 | 0.963 | 0.961 | 0.657 | ||
| 0.192 | 0.895 | 0.121 | 0.962 | 0.962 | 0.657 | ||
| Average length | |||||||
| 0.969 | 1.073 | 1.106 | 0.666 | 1.282 | - | ||
| 1.218 | 1.127 | 1.636 | 0.629 | 1.281 | - | ||
| 1.374 | 1.152 | 1.653 | 0.631 | 1.276 | - | ||
| Coverage of | 0.997 | 0.996 | 0.999 | 0.994 | 0.954 | 0.018 | |
| Average length | 0.703 | 0.208 | 0.923 | 0.007 | 1.282 | - | |

References
- Saeys, Y.; Inza, I.; Larranaga, P. A review of feature selection techniques in bioinformatics. Bioinformatics 2007, 23, 2507–2517. [Google Scholar] [CrossRef] [PubMed]
- Ma, S.; Huang, J. Penalized feature selection and classification in bioinformatics. Briefings Bioinform. 2008, 9, 392–403. [Google Scholar] [CrossRef] [PubMed]
- O’hara, R.B.; Sillanpää, M.J. A review of Bayesian variable selection methods: What, how and which. Bayesian Anal. 2009, 4, 85–117. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Wainwright, M. Statistical learning with sparsity. Monogr. Stat. Appl. Probab. 2015, 143, 8. [Google Scholar]
- Wu, Y.; Wang, L. A survey of tuning parameter selection for high-dimensional regression. Annu. Rev. Stat. Its Appl. 2020, 7, 209–226. [Google Scholar] [CrossRef]
- Breheny, P.J. Marginal false discovery rates for penalized regression models. Biostatistics 2019, 20, 299–314. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R. Sparse inverse covariance estimation with the graphical lasso. Biostatistics 2008, 9, 432–441. [Google Scholar] [CrossRef]
- Fan, J.; Liao, Y.; Liu, H. An overview of the estimation of large covariance and precision matrices. Econom. J. 2016, 19, C1–C32. [Google Scholar] [CrossRef]
- Meinshausen, N.; Bühlmann, P. Stability selection. J. R. Stat. Soc. Ser. Stat. Methodol. 2010, 72, 417–473. [Google Scholar] [CrossRef]
- Benjamini, Y.; Heller, R.; Yekutieli, D. Selective inference in complex research. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2009, 367, 4255–4271. [Google Scholar] [CrossRef]
- Gelman, A.; Loken, E. The statistical crisis in science. Am. Sci. 2014, 102, 460–465. [Google Scholar] [CrossRef]
- Benjamini, Y. Selective inference: The silent killer of replicability. Harv. Data Sci. Rev. 2020, 2. [Google Scholar] [CrossRef]
- Wang, H. Bayesian graphical lasso models and efficient posterior computation. Bayesian Anal. 2012, 7, 867–886. [Google Scholar] [CrossRef]
- Benjamini, Y.; Hochberg, Y. Controlling the false discovery rate: A practical and powerful approach to multiple testing. J. R. Stat. Soc. Ser. B (Methodol.) 1995, 57, 289–300. [Google Scholar] [CrossRef]
- Benjamini, Y.; Yekutieli, D. The control of the false discovery rate in multiple testing under dependency. Ann. Stat. 2001, 29, 1165–1188. [Google Scholar] [CrossRef]
- Wu, C.; Ma, S. A selective review of robust variable selection with applications in bioinformatics. Briefings Bioinform. 2015, 16, 873–883. [Google Scholar] [CrossRef]
- Zhou, F.; Ren, J.; Lu, X.; Ma, S.; Wu, C. Gene–environment interaction: A variable selection perspective. Epistasis Methods Protoc. 2021, 2212, 191–223. [Google Scholar]
- Noh, H.; Chung, K.; Van Keilegom, I. Variable selection of varying coefficient models in quantile regression. Electron. J. Stat. 2012, 6, 1220–1238. [Google Scholar] [CrossRef]
- Tang, Y.; Wang, H.J.; Zhu, Z.; Song, X. A unified variable selection approach for varying coefficient models. Stat. Sin. 2012, 601–628. [Google Scholar] [CrossRef]
- Zhou, F.; Ren, J.; Ma, S.; Wu, C. The Bayesian regularized quantile varying coefficient model. Comput. Stat. Data Anal. 2023, 107808. [Google Scholar] [CrossRef]
- Dezeure, R.; Bühlmann, P.; Meier, L.; Meinshausen, N. High-dimensional inference: Confidence intervals, p-values and R-software hdi. Stat. Sci. 2015, 30, 533–558. [Google Scholar] [CrossRef]
- Fan, J.; Li, R. Variable selection via nonconcave penalized likelihood and its oracle properties. J. Am. Stat. Assoc. 2001, 96, 1348–1360. [Google Scholar] [CrossRef]
- Cai, T.T.; Sun, W. Large-scale global and simultaneous inference: Estimation and testing in very high dimensions. Annu. Rev. Econ. 2017, 9, 411–439. [Google Scholar] [CrossRef]
- Kuchibhotla, A.K.; Kolassa, J.E.; Kuffner, T.A. Post-selection inference. Annu. Rev. Stat. Its Appl. 2022, 9, 505–527. [Google Scholar] [CrossRef]
- Chernozhukov, V.; Chetverikov, D.; Kato, K.; Koike, Y. High-dimensional data bootstrap. Annu. Rev. Stat. Its Appl. 2023, 10, 427–449. [Google Scholar] [CrossRef]
- Huang, Y.; Li, C.; Li, R.; Yang, S. An overview of tests on high-dimensional means. J. Multivar. Anal. 2022, 188, 104813. [Google Scholar] [CrossRef]
- Zhang, D.; Khalili, A.; Asgharian, M. Post-model-selection inference in linear regression models: An integrated review. Stat. Surv. 2022, 16, 86–136. [Google Scholar] [CrossRef]
- Heinze, G.; Wallisch, C.; Dunkler, D. Variable selection–A review and recommendations for the practicing statistician. Biom. J. 2018, 60, 431–449. [Google Scholar] [CrossRef]
- Bühlmann, P.; Kalisch, M.; Meier, L. High-dimensional statistics with a view toward applications in biology. Annu. Rev. Stat. Its Appl. 2014, 1, 255–278. [Google Scholar] [CrossRef]
- Farcomeni, A. A review of modern multiple hypothesis testing, with particular attention to the false discovery proportion. Stat. Methods Med. Res. 2008, 17, 347–388. [Google Scholar] [CrossRef]
- Lu, Z.; Lou, W. Bayesian approaches to variable selection: A comparative study from practical perspectives. Int. J. Biostat. 2022, 18, 83–108. [Google Scholar] [CrossRef] [PubMed]
- Fridley, B.L. Bayesian variable and model selection methods for genetic association studies. Genet. Epidemiol. Off. Publ. Int. Genet. Epidemiol. Soc. 2009, 33, 27–37. [Google Scholar] [CrossRef]
- Müller, P.; Parmigiani, G.; Rice, K. FDR and Bayesian Multiple Comparisons Rules. In Bayesian Statistics 8, Proceedings of the Eighth Valencia International Meeting, Valencia, Spain, 2–6 June 2006; Oxford University Press: Oxford, UK, 2007. [Google Scholar] [CrossRef]
- Bhadra, A.; Datta, J.; Polson, N.G.; Willard, B. Lasso meets horseshoe. Stat. Sci. 2019, 34, 405–427. [Google Scholar] [CrossRef]
- Shafer, G.; Vovk, V. A tutorial on conformal prediction. J. Mach. Learn. Res. 2008, 9, 371–421. [Google Scholar]
- Fontana, M.; Zeni, G.; Vantini, S. Conformal prediction: A unified review of theory and new challenges. Bernoulli 2023, 29, 1–23. [Google Scholar] [CrossRef]
- Angelopoulos, A.N.; Bates, S. Conformal prediction: A gentle introduction. Found. Trends Mach. Learn. 2023, 16, 494–591. [Google Scholar] [CrossRef]
- Fan, J.; Lv, J. A selective overview of variable selection in high dimensional feature space. Stat. Sin. 2010, 20, 101. [Google Scholar]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Rubin, D.B. Bayesian Data Analysis; Chapman and Hall/CRC, 1995. [Google Scholar]
- Bolstad, W.M.; Curran, J.M. Introduction to Bayesian Statistics; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Rousseeuw, P.; Yohai, V. Robust regression by means of S-estimators. In Proceedings of the Robust and Nonlinear Time Series Analysis: Proceedings of a Workshop Organized by the Sonderforschungsbereich 123 “Stochastische Mathematische Modelle”; Springer: Berlin/Heidelberg, Germany, 1984; pp. 256–272. [Google Scholar]
- Huber, P.J.; Ronchetti, E.M. Robust Statistics; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Yu, K.; Moyeed, R.A. Bayesian quantile regression. Stat. Probab. Lett. 2001, 54, 437–447. [Google Scholar] [CrossRef]
- Svensén, M.; Bishop, C.M. Robust Bayesian mixture modelling. Neurocomputing 2005, 64, 235–252. [Google Scholar] [CrossRef]
- Hjort, N.L.; Holmes, C.; Müller, P.; Walker, S.G. Bayesian Nonparametrics; Cambridge University Press: Cambridge, UK, 2010; Volume 28. [Google Scholar]
- Ghosal, S.; van der Vaart, A.W. Fundamentals of Nonparametric Bayesian Inference; Cambridge University Press: Cambridge, UK, 2017; Volume 44. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J.H.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: Berlin/Heidelberg, Germany, 2009; Volume 2. [Google Scholar]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B (Methodol.) 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Zhang, C.H. Nearly unbiased variable selection under minimax concave penalty. Ann. Stat. 2010, 38, 894–942. [Google Scholar] [CrossRef] [PubMed]
- Zou, H. The adaptive lasso and its oracle properties. J. Am. Stat. Assoc. 2006, 101, 1418–1429. [Google Scholar] [CrossRef]
- Sun, T.; Zhang, C.H. Scaled sparse linear regression. Biometrika 2012, 99, 879–898. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. Stat. Methodol. 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Tibshirani, R.; Saunders, M.; Rosset, S.; Zhu, J.; Knight, K. Sparsity and smoothness via the fused lasso. J. R. Stat. Soc. Ser. Stat. Methodol. 2005, 67, 91–108. [Google Scholar] [CrossRef]
- Tibshirani, R.J. The solution path of the generalized lasso. Ann. Stat. 2011, 39, 1335–1371. [Google Scholar] [CrossRef]
- Yuan, M.; Lin, Y. Model selection and estimation in regression with grouped variables. J. R. Stat. Soc. Ser. Stat. Methodol. 2006, 68, 49–67. [Google Scholar] [CrossRef]
- Meier, L.; Van De Geer, S.; Bühlmann, P. The group lasso for logistic regression. J. R. Stat. Soc. Ser. Stat. Methodol. 2008, 70, 53–71. [Google Scholar] [CrossRef]
- Huang, J.; Breheny, P.; Ma, S. A selective review of group selection in high-dimensional models. Stat. Sci. Rev. J. Inst. Math. Stat. 2012, 27. [Google Scholar] [CrossRef]
- Li, C.; Li, H. Network-constrained regularization and variable selection for analysis of genomic data. Bioinformatics 2008, 24, 1175–1182. [Google Scholar] [CrossRef]
- Huang, J.; Ma, S.; Li, H.; Zhang, C.H. The sparse Laplacian shrinkage estimator for high-dimensional regression. Ann. Stat. 2011, 39, 2021. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.; Zhang, Q.; Jiang, Y.; Ma, S. Robust network-based analysis of the associations between (epi) genetic measurements. J. Multivar. Anal. 2018, 168, 119–130. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.; Zhou, F.; Ren, J.; Li, X.; Jiang, Y.; Ma, S. A selective review of multi-level omics data integration using variable selection. High-Throughput 2019, 8, 4. [Google Scholar] [CrossRef] [PubMed]
- Meinshausen, N.; Bühlmann, P. High-dimensional graphs and variable selection with the lasso. Ann. Stat. 2006, 34, 1436–1462. [Google Scholar] [CrossRef]
- Rinaldo, A.; Wasserman, L.; G’Sell, M. Bootstrapping and sample splitting for high-dimensional, assumption-lean inference. Ann. Stat. 2019, 47, 3438–3469. [Google Scholar] [CrossRef]
- Lockhart, R.; Taylor, J.; Tibshirani, R.J.; Tibshirani, R. A significance test for the lasso. Ann. Stat. 2014, 42, 413. [Google Scholar] [CrossRef]
- Lee, J.D.; Sun, D.L.; Sun, Y.; Taylor, J.E. Exact post-selection inference, with application to the lasso. Ann. Stat. 2016, 44, 907–927. [Google Scholar] [CrossRef]
- Tibshirani, R.J.; Taylor, J.; Lockhart, R.; Tibshirani, R. Exact post-selection inference for sequential regression procedures. J. Am. Stat. Assoc. 2016, 111, 600–620. [Google Scholar] [CrossRef]
- Taylor, J.; Tibshirani, R.J. Statistical learning and selective inference. Proc. Natl. Acad. Sci. USA 2015, 112, 7629–7634. [Google Scholar] [CrossRef]
- Berk, R.; Brown, L.; Buja, A.; Zhang, K.; Zhao, L. Valid post-selection inference. Ann. Stat. 2013, 41, 802–837. [Google Scholar] [CrossRef]
- Bachoc, F.; Leeb, H.; Pötscher, B.M. Valid confidence intervals for post-model-selection predictors. Ann. Stat. 2019, 47, 1475–1504. [Google Scholar] [CrossRef]
- Bachoc, F.; Preinerstorfer, D.; Steinberger, L. Uniformly valid confidence intervals post-model-selection. Ann. Stat. 2020, 48, 440–463. [Google Scholar] [CrossRef]
- Javanmard, A.; Montanari, A. Confidence intervals and hypothesis testing for high-dimensional regression. J. Mach. Learn. Res. 2014, 15, 2869–2909. [Google Scholar]
- Bühlmann, P. Statistical significance in high-dimensional linear models. Bernoulli 2013, 19, 1212–1242. [Google Scholar] [CrossRef]
- Van de Geer, S.; Bühlmann, P.; Ritov, Y.; Dezeure, R. On asymptotically optimal confidence regions and tests for high-dimensional models. Ann. Stat. 2014, 42, 1166–1202. [Google Scholar] [CrossRef]
- Zhang, C.H.; Zhang, S.S. Confidence intervals for low dimensional parameters in high dimensional linear models. J. R. Stat. Soc. Ser. Stat. Methodol. 2014, 76, 217–242. [Google Scholar] [CrossRef]
- Song, Q.; Liang, F. Nearly optimal Bayesian shrinkage for high-dimensional regression. Sci. China Math. 2023, 66, 409–442. [Google Scholar] [CrossRef]
- Javanmard, A.; Javadi, H. False discovery rate control via debiased lasso. Electron. J. Stat. 2019, 13, 1212–1253. [Google Scholar] [CrossRef]
- Liang, W.; Zhang, Q.; Ma, S. Hierarchical false discovery rate control for high-dimensional survival analysis with interactions. Comput. Stat. Data Anal. 2024, 192, 107906. [Google Scholar] [CrossRef]
- Wasserman, L.; Roeder, K. High dimensional variable selection. Ann. Stat. 2009, 37, 2178. [Google Scholar] [CrossRef]
- Meinshausen, N.; Meier, L.; Bühlmann, P. P-values for high-dimensional regression. J. Am. Stat. Assoc. 2009, 104, 1671–1681. [Google Scholar] [CrossRef]
- Shah, R.D.; Samworth, R.J. Variable selection with error control: Another look at stability selection. J. R. Stat. Soc. Ser. Stat. Methodol. 2013, 75, 55–80. [Google Scholar] [CrossRef]
- Dai, C.; Lin, B.; Xing, X.; Liu, J.S. False discovery rate control via data splitting. J. Am. Stat. Assoc. 2023, 118, 2503–2520. [Google Scholar] [CrossRef]
- Dai, C.; Lin, B.; Xing, X.; Liu, J.S. A scale-free approach for false discovery rate control in generalized linear models. J. Am. Stat. Assoc. 2023, 118, 1551–1565. [Google Scholar] [CrossRef]
- Candes, E.; Fan, Y.; Janson, L.; Lv, J. Panning for gold:‘model-X’knockoffs for high dimensional controlled variable selection. J. R. Stat. Soc. Ser. Stat. Methodol. 2018, 80, 551–577. [Google Scholar] [CrossRef]
- Barber, R.F.; Candès, E.J. Controlling the false discovery rate via knockoffs. Ann. Stat. 2015, 43, 2055–2085. [Google Scholar] [CrossRef]
- Barber, R.F.; Candès, E.J. A knockoff filter for high-dimensional selective inference. Ann. Stat. 2019, 47, 2504–2537. [Google Scholar] [CrossRef]
- Barber, R.F.; Candès, E.J.; Samworth, R.J. Robust inference with knockoffs. Ann. Stat. 2020, 48, 1409–1431. [Google Scholar] [CrossRef]
- Romano, Y.; Sesia, M.; Candès, E. Deep knockoffs. J. Am. Stat. Assoc. 2020, 115, 1861–1872. [Google Scholar] [CrossRef]
- Jordon, J.; Yoon, J.; van der Schaar, M. KnockoffGAN: Generating knockoffs for feature selection using generative adversarial networks. In Proceedings of the International Conference on Learning Representations, Vancouver, Canada, 30 April–3 May 2018. [Google Scholar]
- Bates, S.; Candès, E.; Janson, L.; Wang, W. Metropolized knockoff sampling. J. Am. Stat. Assoc. 2021, 116, 1413–1427. [Google Scholar] [CrossRef]
- Sesia, M.; Sabatti, C.; Candès, E.J. Gene hunting with hidden Markov model knockoffs. Biometrika 2019, 106, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Huang, D.; Janson, L. Relaxing the assumptions of knockoffs by conditioning. Ann. Stat. 2020, 48, 3021–3042. [Google Scholar] [CrossRef]
- Sesia, M.; Katsevich, E.; Bates, S.; Candès, E.; Sabatti, C. Multi-resolution localization of causal variants across the genome. Nat. Commun. 2020, 11, 1093. [Google Scholar] [CrossRef] [PubMed]
- Dai, R.; Barber, R. The knockoff filter for FDR control in group-sparse and multitask regression. In Proceedings of the International Conference on Machine Learning, PMLR, New York, NY, USA, 19–24 June 2016; pp. 1851–1859. [Google Scholar]
- Dai, R.; Zheng, C. False discovery rate-controlled multiple testing for union null hypotheses: A knockoff-based approach. Biometrics 2023, 79, 3497–3509. [Google Scholar] [CrossRef]
- Zou, H.; Yuan, M. Composite quantile regression and the oracle model selection theory. Ann. Stat. 2008, 36, 1108–1126. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, Y. Variable selection in quantile regression. Stat. Sin. 2009, 19, 801–817. [Google Scholar]
- Fan, J.; Fan, Y.; Barut, E. Adaptive robust variable selection. Ann. Stat. 2014, 42, 324. [Google Scholar] [CrossRef]
- Kepplinger, D. Robust variable selection and estimation via adaptive elastic net S-estimators for linear regression. Comput. Stat. Data Anal. 2023, 183, 107730. [Google Scholar] [CrossRef]
- Belloni, A.; Chernozhukov, V.; Kato, K. Uniform post-selection inference for least absolute deviation regression and other Z-estimation problems. Biometrika 2015, 102, 77–94. [Google Scholar] [CrossRef]
- Belloni, A.; Chernozhukov, V.; Kato, K. Valid post-selection inference in high-dimensional approximately sparse quantile regression models. J. Am. Stat. Assoc. 2019, 114, 749–758. [Google Scholar] [CrossRef]
- Han, D.; Huang, J.; Lin, Y.; Shen, G. Robust post-selection inference of high-dimensional mean regression with heavy-tailed asymmetric or heteroskedastic errors. J. Econom. 2022, 230, 416–431. [Google Scholar] [CrossRef]
- He, X.; Pan, X.; Tan, K.M.; Zhou, W.X. Smoothed quantile regression with large-scale inference. J. Econom. 2023, 232, 367–388. [Google Scholar] [CrossRef] [PubMed]
- Huang, H. Controlling the false discoveries in LASSO. Biometrics 2017, 73, 1102–1110. [Google Scholar] [CrossRef] [PubMed]
- Su, W.; Bogdan, M.; Candes, E. False discoveries occur early on the lasso path. Ann. Stat. 2017, 2133–2150. [Google Scholar] [CrossRef]
- Bogdan, M.; Van Den Berg, E.; Sabatti, C.; Su, W.; Candès, E.J. SLOPE—Adaptive variable selection via convex optimization. Ann. Appl. Stat. 2015, 9, 1103. [Google Scholar] [CrossRef]
- Liang, W.; Ma, S.; Lin, C. Marginal false discovery rate for a penalized transformation survival model. Comput. Stat. Data Anal. 2021, 160, 107232. [Google Scholar] [CrossRef]
- Tadesse, M.G.; Vannucci, M. Handbook of Bayesian Variable Selection; Chapman & Hall: London, UK, 2021. [Google Scholar]
- Ickstadt, K.; Schäfer, M.; Zucknick, M. Toward integrative Bayesian analysis in molecular biology. Annu. Rev. Stat. Its Appl. 2018, 5, 141–167. [Google Scholar] [CrossRef]
- Mallick, H.; Yi, N. Bayesian methods for high dimensional linear models. J. Biom. Biostat. 2013, 1, 005. [Google Scholar]
- Park, T.; Casella, G. The bayesian lasso. J. Am. Stat. Assoc. 2008, 103, 681–686. [Google Scholar] [CrossRef]
- Casella, G.; Ghosh, M.; Gill, J.; Kyung, M. Penalized regression, standard errors, and Bayesian lassos. Bayesian Anal. 2010, 06, 369–411. [Google Scholar] [CrossRef]
- Simon, N.; Friedman, J.; Hastie, T.; Tibshirani, R. A sparse-group lasso. J. Comput. Graph. Stat. 2013, 22, 231–245. [Google Scholar] [CrossRef]
- Mitchell, T.J.; Beauchamp, J.J. Bayesian variable selection in linear regression. J. Am. Stat. Assoc. 1988, 83, 1023–1032. [Google Scholar] [CrossRef]
- George, E.I.; McCulloch, R.E. Variable selection via Gibbs sampling. J. Am. Stat. Assoc. 1993, 88, 881–889. [Google Scholar] [CrossRef]
- Barbieri, M.M.; Berger, J.O. Optimal predictive model selection. Ann. Stat. 2004, 32, 870–897. [Google Scholar] [CrossRef]
- Barbieri, M.M.; Berger, J.O.; George, E.I.; Ročková, V. The median probability model and correlated variables. Bayesian Anal. 2021, 16, 1085–1112. [Google Scholar] [CrossRef]
- Wasserman, L. Bayesian model selection and model averaging. J. Math. Psychol. 2000, 44, 92–107. [Google Scholar] [CrossRef]
- Hoeting, J.A.; Madigan, D.; Raftery, A.E.; Volinsky, C.T. Bayesian model averaging: A tutorial (with comments by M. Clyde, David Draper and EI George, and a rejoinder by the authors. Stat. Sci. 1999, 14, 382–417. [Google Scholar] [CrossRef]
- Xu, X.; Ghosh, M. Bayesian variable selection and estimation for group lasso. Bayesian Anal. 2015, 10, 909–936. [Google Scholar] [CrossRef]
- Ren, J.; Zhou, F.; Li, X.; Chen, Q.; Zhang, H.; Ma, S.; Jiang, Y.; Wu, C. Semiparametric Bayesian variable selection for gene-environment interactions. Stat. Med. 2020, 39, 617–638. [Google Scholar] [CrossRef]
- Bai, R.; Ročková, V.; George, E.I. Spike-and-slab meets LASSO: A review of the spike-and-slab LASSO. In Handbook of Bayesian Variable Selection; Chapman & Hall: London, UK, 2021; pp. 81–108. [Google Scholar]
- Carvalho, C.M.; Polson, N.G.; Scott, J.G. Handling sparsity via the horseshoe. In Proceedings of the Artificial Intelligence and Statistics, PMLR, Clearwater Beach, FL, USA, 16–18 April 2009; pp. 73–80. [Google Scholar]
- Ročková, V. Bayesian estimation of sparse signals with a continuous spike-and-slab prior. Ann. Stat. 2018, 46, 401–437. [Google Scholar] [CrossRef]
- Carvalho, C.M.; Polson, N.G.; Scott, J.G. The horseshoe estimator for sparse signals. Biometrika 2010, 97, 465–480. [Google Scholar] [CrossRef]
- Polson, N.G.; Scott, J.G. Shrink globally, act locally: Sparse Bayesian regularization and prediction. Bayesian Stat. 2010, 9, 105. [Google Scholar]
- Ročková, V.; George, E.I. EMVS: The EM approach to Bayesian variable selection. J. Am. Stat. Assoc. 2014, 109, 828–846. [Google Scholar] [CrossRef]
- Ročková, V.; George, E.I. The spike-and-slab lasso. J. Am. Stat. Assoc. 2018, 113, 431–444. [Google Scholar] [CrossRef]
- Fu, W.J. Penalized regressions: The bridge versus the lasso. J. Comput. Graph. Stat. 1998, 7, 397–416. [Google Scholar] [CrossRef]
- Wu, T.T.; Lange, K. Coordinate descent algorithms for lasso penalized regression. Ann. Appl. Stat. 2008, 2, 224–244. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R. Regularization paths for generalized linear models via coordinate descent. J. Stat. Softw. 2010, 33, 1. [Google Scholar] [CrossRef]
- Efron, B.; Hastie, T.; Johnstone, I.; Tibshirani, R. Least angle regression. Ann. Stat. 2004, 32, 407–499. [Google Scholar] [CrossRef]
- Tang, Y.; Wang, H.J.; Zhu, Z. Variable selection in quantile varying coefficient models with longitudinal data. Comput. Stat. Data Anal. 2013, 57, 435–449. [Google Scholar] [CrossRef]
- Tang, Z.; Shen, Y.; Zhang, X.; Yi, N. The spike-and-slab Lasso generalized linear models for prediction and associated genes detection. Genetics 2017, 205, 77–88. [Google Scholar] [CrossRef]
- Liu, Y.; Ren, J.; Ma, S.; Wu, C. The spike-and-slab quantile LASSO for robust variable selection in cancer genomics studies. Stat. Med. 2024. [Google Scholar] [CrossRef] [PubMed]
- Nie, L.; Ročková, V. Bayesian bootstrap spike-and-slab LASSO. J. Am. Stat. Assoc. 2023, 118, 2013–2028. [Google Scholar] [CrossRef]
- Newton, M.A.; Raftery, A.E. Approximate Bayesian inference with the weighted likelihood bootstrap. J. R. Stat. Soc. Ser. Stat. Methodol. 1994, 56, 3–26. [Google Scholar] [CrossRef]
- Kuo, L.; Mallick, B. Variable selection for regression models. Sankhyā Indian J. Stat. Ser. B 1998, 60, 65–81. [Google Scholar]
- Carlin, B.P.; Chib, S. Bayesian model choice via Markov chain Monte Carlo methods. J. R. Stat. Soc. Ser. Stat. Methodol. 1995, 57, 473–484. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Pati, D.; Pillai, N.S.; Dunson, D.B. Dirichlet–Laplace priors for optimal shrinkage. J. Am. Stat. Assoc. 2015, 110, 1479–1490. [Google Scholar] [CrossRef]
- Bhadra, A.; Datta, J.; Polson, N.G.; Willard, B. The horseshoe+ estimator of ultra-sparse signals. Bayesian Anal. 2017, 12, 1105–1131. [Google Scholar] [CrossRef]
- Johnson, V.E.; Rossell, D. On the use of non-local prior densities in Bayesian hypothesis tests. J. R. Stat. Soc. Ser. Stat. Methodol. 2010, 72, 143–170. [Google Scholar] [CrossRef]
- Shin, M.; Bhattacharya, A.; Johnson, V.E. Scalable Bayesian variable selection using nonlocal prior densities in ultrahigh-dimensional settings. Stat. Sin. 2018, 28, 1053. [Google Scholar]
- Yu, K.; Zhang, J. A three-parameter asymmetric Laplace distribution and its extension. Commun. Stat. Theory Methods 2005, 34, 1867–1879. [Google Scholar] [CrossRef]
- Li, Q.; Lin, N.; Xi, R. Bayesian regularized quantile regression. Bayesian Anal. 2010, 5, 533–556. [Google Scholar] [CrossRef]
- Lu, X.; Fan, K.; Ren, J.; Wu, C. Identifying gene–environment interactions with robust marginal Bayesian variable selection. Front. Genet. 2021, 12, 667074. [Google Scholar] [CrossRef] [PubMed]
- Ren, J.; Zhou, F.; Li, X.; Ma, S.; Jiang, Y.; Wu, C. Robust Bayesian variable selection for gene–environment interactions. Biometrics 2023, 79, 684–694. [Google Scholar] [CrossRef] [PubMed]
- Reich, B.J.; Bondell, H.D.; Wang, H.J. Flexible Bayesian quantile regression for independent and clustered data. Biostatistics 2010, 11, 337–352. [Google Scholar] [CrossRef]
- McLachlan, G.J.; Lee, S.X.; Rathnayake, S.I. Finite mixture models. Annu. Rev. Stat. Its Appl. 2019, 6, 355–378. [Google Scholar] [CrossRef]
- Neal, R.M. Markov chain sampling methods for Dirichlet process mixture models. J. Comput. Graph. Stat. 2000, 9, 249–265. [Google Scholar] [CrossRef]
- Li, Y.; Schofield, E.; Gönen, M. A tutorial on Dirichlet process mixture modeling. J. Math. Psychol. 2019, 91, 128–144. [Google Scholar] [CrossRef]
- Görür, D.; Edward Rasmussen, C. Dirichlet process gaussian mixture models: Choice of the base distribution. J. Comput. Sci. Technol. 2010, 25, 653–664. [Google Scholar] [CrossRef]
- Khalili, A. An overview of the new feature selection methods in finite mixture of regression models. J. Iran. Stat. Soc. 2022, 10, 201–235. [Google Scholar]
- Barcella, W.; De Iorio, M.; Baio, G. A comparative review of variable selection techniques for covariate dependent Dirichlet process mixture models. Can. J. Stat. 2017, 45, 254–273. [Google Scholar] [CrossRef]
- Peel, D.; McLachlan, G.J. Robust mixture modelling using the t distribution. Stat. Comput. 2000, 10, 339–348. [Google Scholar] [CrossRef]
- Wu, C.; Li, G.; Zhu, J.; Cui, Y. Functional mapping of dynamic traits with robust t-distribution. PLoS ONE 2011, 6, e24902. [Google Scholar] [CrossRef] [PubMed]
- Yao, W.; Wei, Y.; Yu, C. Robust mixture regression using the t-distribution. Comput. Stat. Data Anal. 2014, 71, 116–127. [Google Scholar] [CrossRef]
- Lee, S.; McLachlan, G.J. Finite mixtures of multivariate skew t-distributions: Some recent and new results. Stat. Comput. 2014, 24, 181–202. [Google Scholar] [CrossRef]
- Wang, H.; Li, G.; Jiang, G. Robust regression shrinkage and consistent variable selection through the LAD-Lasso. J. Bus. Econ. Stat. 2007, 25, 347–355. [Google Scholar] [CrossRef]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends® Mach. Learn. 2011, 3, 1–122. [Google Scholar]
- Wang, L.; Zhou, J.; Qu, A. Penalized generalized estimating equations for high-dimensional longitudinal data analysis. Biometrics 2012, 68, 353–360. [Google Scholar] [CrossRef]
- Zhou, F.; Ren, J.; Li, G.; Jiang, Y.; Li, X.; Wang, W.; Wu, C. Penalized variable selection for lipid–environment interactions in a longitudinal lipidomics study. Genes 2019, 10, 1002. [Google Scholar] [CrossRef]
- Zhou, F.; Lu, X.; Ren, J.; Fan, K.; Ma, S.; Wu, C. Sparse group variable selection for gene–environment interactions in the longitudinal study. Genet. Epidemiol. 2022, 46, 317–340. [Google Scholar] [CrossRef]
- Breheny, P.; Huang, J. Penalized methods for bi-level variable selection. Stat. Its Interface 2009, 2, 369. [Google Scholar] [CrossRef]
- Li, J.; Wang, Z.; Li, R.; Wu, R. Bayesian group lasso for nonparametric varying-coefficient models with application to functional genome-wide association studies. Ann. Appl. Stat. 2015, 9, 640. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.; Cui, Y.; Ma, S. Integrative analysis of gene–environment interactions under a multi-response partially linear varying coefficient model. Stat. Med. 2014, 33, 4988–4998. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.; Shi, X.; Cui, Y.; Ma, S. A penalized robust semiparametric approach for gene–environment interactions. Stat. Med. 2015, 34, 4016–4030. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.; Zhong, P.S.; Cui, Y. Additive varying-coefficient model for nonlinear gene-environment interactions. Stat. Appl. Genet. Mol. Biol. 2018, 17, 20170008. [Google Scholar] [CrossRef] [PubMed]
- Han, A.K. Non-parametric analysis of a generalized regression model: The maximum rank correlation estimator. J. Econom. 1987, 35, 303–316. [Google Scholar] [CrossRef]
- Khan, S.; Tamer, E. Partial rank estimation of duration models with general forms of censoring. J. Econom. 2007, 136, 251–280. [Google Scholar] [CrossRef]
- Steele, J.M.; Steiger, W.L. Algorithms and complexity for least median of squares regression. Discret. Appl. Math. 1986, 14, 93–100. [Google Scholar] [CrossRef]
- Alfons, A.; Croux, C.; Gelper, S. Sparse least trimmed squares regression for analyzing high-dimensional large data sets. Ann. Appl. Stat. 2013, 7, 226–248. [Google Scholar]
- She, Y.; Owen, A.B. Outlier detection using nonconvex penalized regression. J. Am. Stat. Assoc. 2011, 106, 626–639. [Google Scholar] [CrossRef]
- Wang, X.; Jiang, Y.; Huang, M.; Zhang, H. Robust variable selection with exponential squared loss. J. Am. Stat. Assoc. 2013, 108, 632–643. [Google Scholar] [CrossRef]
- Yu, C.; Yao, W. Robust linear regression: A review and comparison. Commun. Stat.-Simul. Comput. 2017, 46, 6261–6282. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, H.J.; He, X. Posterior inference in Bayesian quantile regression with asymmetric Laplace likelihood. Int. Stat. Rev. 2016, 84, 327–344. [Google Scholar] [CrossRef]
- Blei, D.M.; Kucukelbir, A.; McAuliffe, J.D. Variational inference: A review for statisticians. J. Am. Stat. Assoc. 2017, 112, 859–877. [Google Scholar] [CrossRef]
- Bishop, C.M.; Nasrabadi, N.M. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006; Volume 4. [Google Scholar]
- Wang, G.; Sarkar, A.; Carbonetto, P.; Stephens, M. A simple new approach to variable selection in regression, with application to genetic fine mapping. J. R. Stat. Soc. Ser. Stat. Methodol. 2020, 82, 1273–1300. [Google Scholar] [CrossRef] [PubMed]
- Logsdon, B.A.; Hoffman, G.E.; Mezey, J.G. A variational Bayes algorithm for fast and accurate multiple locus genome-wide association analysis. BMC Bioinform. 2010, 11, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Carbonetto, P.; Stephens, M. Scalable variational inference for Bayesian variable selection in regression, and its accuracy in genetic association studies. Bayesian Anal. 2012, 7, 73–108. [Google Scholar] [CrossRef]
- Sunnåker, M.; Busetto, A.G.; Numminen, E.; Corander, J.; Foll, M.; Dessimoz, C. Approximate bayesian computation. PLoS Comput. Biol. 2013, 9, e1002803. [Google Scholar] [CrossRef]
- Beaumont, M.A. Approximate bayesian computation. Annu. Rev. Stat. Its Appl. 2019, 6, 379–403. [Google Scholar] [CrossRef]
- Zhang, L.; Baladandayuthapani, V.; Mallick, B.K.; Manyam, G.C.; Thompson, P.A.; Bondy, M.L.; Do, K.A. Bayesian hierarchical structured variable selection methods with application to molecular inversion probe studies in breast cancer. J. R. Stat. Soc. Ser. C Appl. Stat. 2014, 63, 595–620. [Google Scholar] [CrossRef]
- Ren, J.; Zhou, F.; Li, X.; Wu, C. Package’roben’ 2020. Available online: https://cran.r-project.org/web/packages/roben/index.html (accessed on 23 July 2024).
- Xia, L.; Nan, B.; Li, Y. Debiased lasso for generalized linear models with a diverging number of covariates. Biometrics 2023, 79, 344–357. [Google Scholar] [CrossRef]
- Wang, L.; Li, H.; Huang, J.Z. Variable selection in nonparametric varying-coefficient models for analysis of repeated measurements. J. Am. Stat. Assoc. 2008, 103, 1556–1569. [Google Scholar] [CrossRef]
- Koenker, R.; Portnoy, S.; Ng, P.T.; Zeileis, A.; Grosjean, P.; Ripley, B.D. Package ‘Quantreg’. Reference Manual. 2018. Available online: https://cran.rproject.org/web/packages/quantreg/quantreg.pdf (accessed on 23 July 2024).
- Sherwood, B.; Maidman, A. Package ‘rqPen’. R Foundation for Statistical Computing; R Core Team: Vienna, Austria, 2017. [Google Scholar]
- Vilenchik, D. Simple statistics are sometime too simple: A case study in social media data. IEEE Trans. Knowl. Data Eng. 2019, 32, 402–408. [Google Scholar] [CrossRef]

| Reference | Type | Description | Inference Procedure | Numerical Study |
|---|---|---|---|---|
| Dezeure et al. (2015) [21] | Theory and frequentist | Provided a selective surveys on high-dimensional inference for frequentist regularization methods, which focuses on sample splitting, regularized projection and bias correction. R package hdi has also been introduced. | Confidence intervals and p-values in both linear and generalized linear models. Multiple testing correction included. | Both simulation and a case study on riboflavin data. |
| Fan and Lv (2010) [38] | Theory and frequentist | Systematically overviewed the theory, methods and application in high-dimensional variable selection. Topics on oracle property and ultra-high dimensional variable selection are included. | Discussed the oracle properties in both the classical and ultra-high dimensional setting. | No. |
| Cai and Sun (2017) [23] | Theory and frequentist | Surveyed recently developed large scale multiple testing with FDR control and examined efficient procedures to handle hierarchical, grouping and depedent structure. | Multiple testing with FDR control. | No. |
| Kuchibhotla et al. (2022) [24] | Theory and frequentist | Reviewed three categories of inference methods after variable selection: sample splitting, simultaneous inference and conditional selective inference. | Confidence intervals and p-values. | No simulation. Case studies on Boston Housing data. |
| Chernozhukov et al. (2023) [25] | Theory and frequentist | Reviewed recent development on high-dimensional bootstrap including high-dimensional central limit theorems, multiplier and empirical bootstrap and applications. | Confidence intervals and p-values. | Provided R codes to compute different versions of p-value on hedge fund data (n = 50, p = 2000). |
| Huang et al. (2022) [26] | Theory and frequentist | Surveyed statistical tests for high-dimensional mean problems, with a focus on testing two-sample means for differentially expressed gene expression analysis. | Power of tests and control on type 1 error. | Simulation. |
| Zhang et al. (2022) [27] | Theory and frequentist | A theoretical review on post selection inferences under linear models. | Examined the confidence intervals and coverage probabilities. | Simulation. |
| Heinze et al. (2018) [28] | Applied (for practicing statisticians) and frequentist | Focus on surveying variable selection methods for low-dimensional problems including backward/forward/stepwise/best subset selection and LASSO. | Inferences were not explicitly examined. Discussed model stability, resampling and bootstrap. | No simulation. Case study on body-fat data (n = 251, p = 13). |
| Bühlmann et al. (2014) [29] | Applied and frequentist | Reviewed uncertainty quantification using type 1 error and p-values on high-dimensional linear models (including generalized linear models and mixed models), graphical models, and causal inferences. | FDR and p-values. | No simulation. A case study on Riboflavin data with n = 71 and p = 4088. |
| Benjamini (2009) [10] | Applied and frequentist | Summarized the current success and future trend in inferences with FDR and multiple comparisons. | Discussed False discovery rates (FDR) and Family wise error rates (FWER). | No. |
| Farcomeni (2008) [30] | Applied and frequentist | Reviewed multiple hypothesis testing with control on different error measures related to FDR and its variants. | Assessed validity of controlling a variety of FDR related error measures in multiple hypothesis testing. | Simulation and two case studies on clinical trials with multiple endpoints and DNA microarrays. |
| O’hara and Sillanpöö (2009) [3] | Theory and Bayesian | Reviewed major categories of Bayesian variable selection methods, including indicator model selection, adaptive shrinkage, and stochastic search variable selection. | Posterior distributions of regression coefficients and posterior inclusion probabilities. | Both simulation and real data. |
| Lu and Lou (2022) [31] | Applied and Bayesian | Surveyed Bayesian variable selection under a variety shrinkage priors and conducted comprehensive comparative study. | Coverage probability on prediction assessed on real data. | Simulation and a case study on body-fat data (n = 251, p = 13). |
| Fridley (2009) [32] | Applied and Bayesian | Reviewed and compared Bayesian variable and model selection in genetic associations. | Posterior inclusion probability and credible intervals. | Both simulation and case studies on 17 SNPs genotyped from two genes. |
| Muller et al. (2007) [33] | Theory and Bayesian | Reviewed and compared Bayesian approaches to multiple testing. | Bayesian FDR and its variants. | Real data on DNA microarray studies. |
| Bhadra et al. (2019) [34] | Theory and Bayesian | Surveyed two major types of variable selection methods, LASSO and Horseshoe, in high-dimensional inference, efficiency and scalability. | Examined theoretical optimality in high-dimensional inference. | Used simulated data to check theoretical assumptions. |
| Methods | |||||||
|---|---|---|---|---|---|---|---|
| BL | BLSS | RBL | RBLSS | Debiased-LASSO | Selective Inference | ||
| Error 1 N(0,1) | error of | 0.951 | 0.305 | 1.713 | 0.329 | 0.688 | 0.497 |
| Standard deviation | 0.213 | 0.146 | 0.284 | 0.159 | 0.019 | 0.017 | |
| error of | 10.782 | 0.312 | 14.739 | 0.576 | 0.061 | 0.712 | |
| Standard deviation | 0.777 | 0.333 | 0.818 | 0.285 | 0.021 | 0.085 | |
| TP | 2.961 | 3.000 | 1.941 | 3.000 | 3.000 | 3.000 | |
| Standard deviation | 0.194 | 0.000 | 0.419 | 0.000 | 0.000 | 0.000 | |
| FP | 0.000 | 0.096 | 0.000 | 0.275 | 1.430 | 14.996 | |
| Standard deviation | 0.000 | 0.333 | 0.000 | 0.560 | 0.438 | 1.503 | |
| Coverage of | |||||||
| 0.774 | 0.942 | 0.946 | 0.920 | 0.913 | 0.788 | ||
| 0.966 | 0.945 | 0.990 | 0.931 | 0.775 | 0.790 | ||
| 0.740 | 0.949 | 0.795 | 0.932 | 0.911 | 0.784 | ||
| Average length | |||||||
| 0.937 | 0.472 | 1.369 | 0.476 | 0.483 | - | ||
| 1.075 | 0.526 | 1.892 | 0.531 | 0.482 | - | ||
| 1.008 | 0.471 | 1.892 | 0.477 | 0.481 | - | ||
| Coverage of | 0.994 | 0.994 | 0.996 | 0.994 | 0.956 | 0.015 | |
| Average length | 0.414 | 0.006 | 0.829 | 0.010 | 0.482 | - | |
| Error 2 t(2) | error of | 1.602 | 1.353 | 2.033 | 0.486 | 2.222 | 1.243 |
| Standard deviation | 0.784 | 0.941 | 0.451 | 0.331 | 0.103 | 0.065 | |
| error of | 25.542 | 4.911 | 23.405 | 0.383 | 0.025 | 1.416 | |
| Standard deviation | 0.063 | 14.225 | 4.082 | 0.225 | 0.017 | 0.176 | |
| TP | 2.200 | 2.437 | 1.350 | 2.948 | 2.409 | 2.856 | |
| Standard deviation | 0.784 | 0.612 | 0.720 | 0.222 | 0.093 | 0.047 | |
| FP | 0.004 | 10.376 | 0.000 | 0.042 | 0.329 | 13.183 | |
| Standard deviation | 0.063 | 62.511 | 0.000 | 0.186 | 0.212 | 1.357 | |
| Coverage of | |||||||
| 0.751 | 0.745 | 0.906 | 0.954 | 0.910 | 0.722 | ||
| 0.898 | 0.843 | 0.949 | 0.960 | 0.755 | 0.788 | ||
| 0.636 | 0.906 | 0.665 | 0.964 | 0.901 | 0.794 | ||
| Average length | |||||||
| 1.219 | 1.143 | 1.448 | 0.833 | 1.418 | - | ||
| 1.601 | 1.555 | 1.971 | 0.856 | 1.409 | - | ||
| 1.564 | 1.348 | 2.004 | 0.728 | 1.412 | - | ||
| Coverage of | 0.996 | 0.996 | 0.997 | 0.995 | 0.955 | 0.015 | |
| Average length | 0.704 | 0.120 | 0.953 | 0.008 | 1.414 | - | |
| Reference | Model | Inferences and Software | Case Study |
|---|---|---|---|
| Wang et al. (2012) [160] | Penalized Generalized Estimating Equation (PGEE) for longitudinal data | Confidence interval based on asymptotic property of Oracle estimator. R package PGEE (ver 1.5). | Yeast cell-cycle gene expression (GE) data. n = 297, p = 96. : log transformed time varying GE; : matching score of binding probability |
| Breheny (2019) [6] | Penalized regression (LASSO, SCAD and MCP) | Marginal FDR for penalized regression. R package ncvreg (ver 3.14.3). | (1) TCGA breast cancer data n = 536, p = 17,322. : BRCA1 expression, :GE; (2) Genetic association study of cardiac fibrosis n = 313, p = 66,0496 : ratio of cardiomyocytes to fibroblasts in the heart tissue on log scale. : SNP |
| Xia et al. (2023) [185] | De-biased LASSO in generalized linear models. | Confidence intervals based on refined de-biasing estimating approach. | Boston lung cancer data. : binary with 723 controls and 651 cases (n = 1374) : 103 SNPs and 4 clinical covariates |
| Meinshausen and Bühlmann (2010) [9] | Graphical LASSO and LASSO. | Error control on expected number of falsely selected edges from the graph. | Riboavin (vitamin gene-expression) data with n = 115 subjects and p = 160 GEs. No phenotype. |
| Zhang et al. (2014) [183] | Generalized hierarchical structured (bi-level) Bayesian variable selection | Bayesian credible intervals and FDR. | Breast cancer study. : binary. Case: 184 TNBC subtype. Control: 787 other and unclassified subtypes. (n = 971) : 167, 574 probes for copy number measurements |
| Zhou et al. (2023) [20] | Bayesian regularized quantile varying coefficient model. | Bayesian credible intervals on non-linear gene-environment interaction effects. R package pqrBayes (ver 1.0.2). | Type 2-diabetes data with SNP measurements. n = 1716 : BMI; : 53,408 SNPs |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, K.; Subedi, S.; Yang, G.; Lu, X.; Ren, J.; Wu, C. Is Seeing Believing? A Practitioner’s Perspective on High-Dimensional Statistical Inference in Cancer Genomics Studies. Entropy 2024, 26, 794. https://doi.org/10.3390/e26090794
Fan K, Subedi S, Yang G, Lu X, Ren J, Wu C. Is Seeing Believing? A Practitioner’s Perspective on High-Dimensional Statistical Inference in Cancer Genomics Studies. Entropy. 2024; 26(9):794. https://doi.org/10.3390/e26090794
Chicago/Turabian StyleFan, Kun, Srijana Subedi, Gongshun Yang, Xi Lu, Jie Ren, and Cen Wu. 2024. "Is Seeing Believing? A Practitioner’s Perspective on High-Dimensional Statistical Inference in Cancer Genomics Studies" Entropy 26, no. 9: 794. https://doi.org/10.3390/e26090794
APA StyleFan, K., Subedi, S., Yang, G., Lu, X., Ren, J., & Wu, C. (2024). Is Seeing Believing? A Practitioner’s Perspective on High-Dimensional Statistical Inference in Cancer Genomics Studies. Entropy, 26(9), 794. https://doi.org/10.3390/e26090794







