Improved Variational Bayes for Space-Time Adaptive Processing
Abstract
1. Introduction
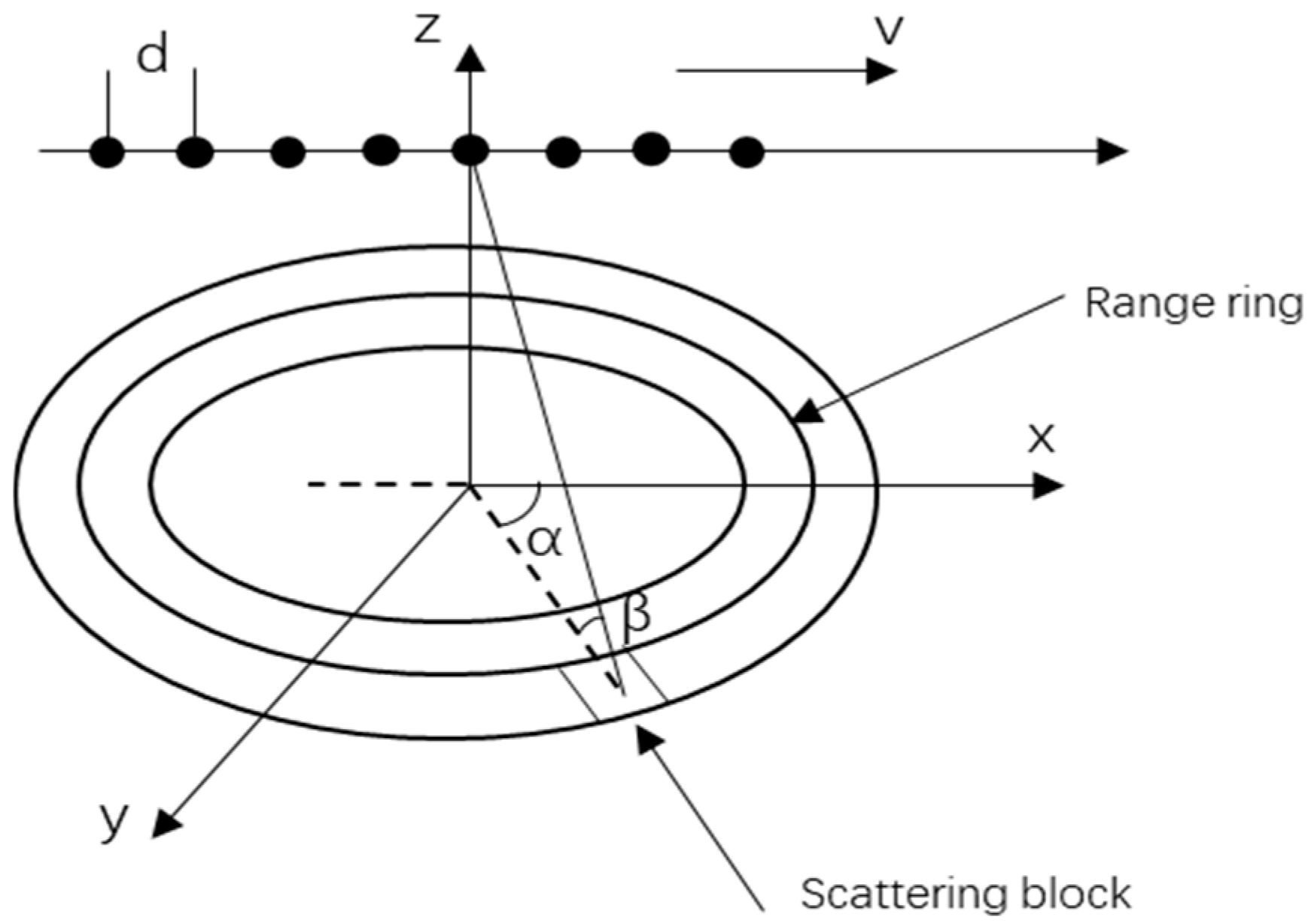
2. Signal Model
3. The Proposed Method
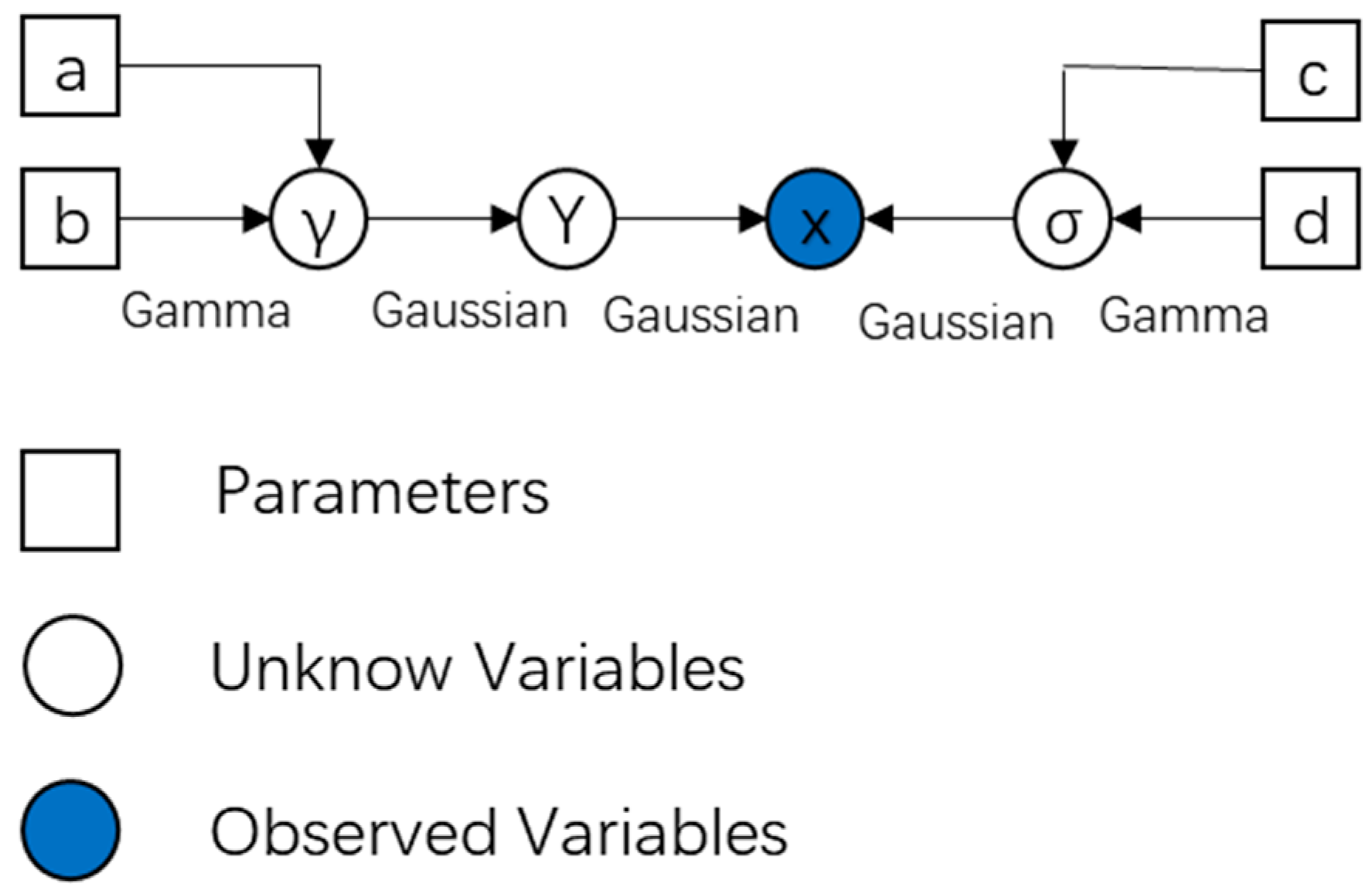
3.1. Bayesian Framework
3.2. Minimization of KL Divergence (Variational E-Step)
3.3. Maximization of the Lower Bound (M-Step)
| Algorithm 1. VB-SR-STAP algorithms. | |
| Stap1: | |
| Stap2: | respectively |
| Stap3: | respectively |
| Stap4: | |
| Stap5: | by 1 |
| Stap6: | , then return to Step 2 |
| Stap7: | Output the final result of μ(t) |
| Stap8: | |
3.4. Improved Variational Bayesian Inference
| Algorithm 2. IVB-SR-STAP algorithms. | |
| Stap1: | |
| Stap2: | |
| Stap3: | using Equation (47) |
| Stap4: | respectively |
| Stap5: | Update set A |
| Stap6: | |
| Stap7: | by 1 |
| Stap8: | , then return to Step 3 |
| Stap9: | Output the final result of μ(t) |
| Stap10: | |
3.5. Comparison of Computational Complexity
4. Experimental Simulation
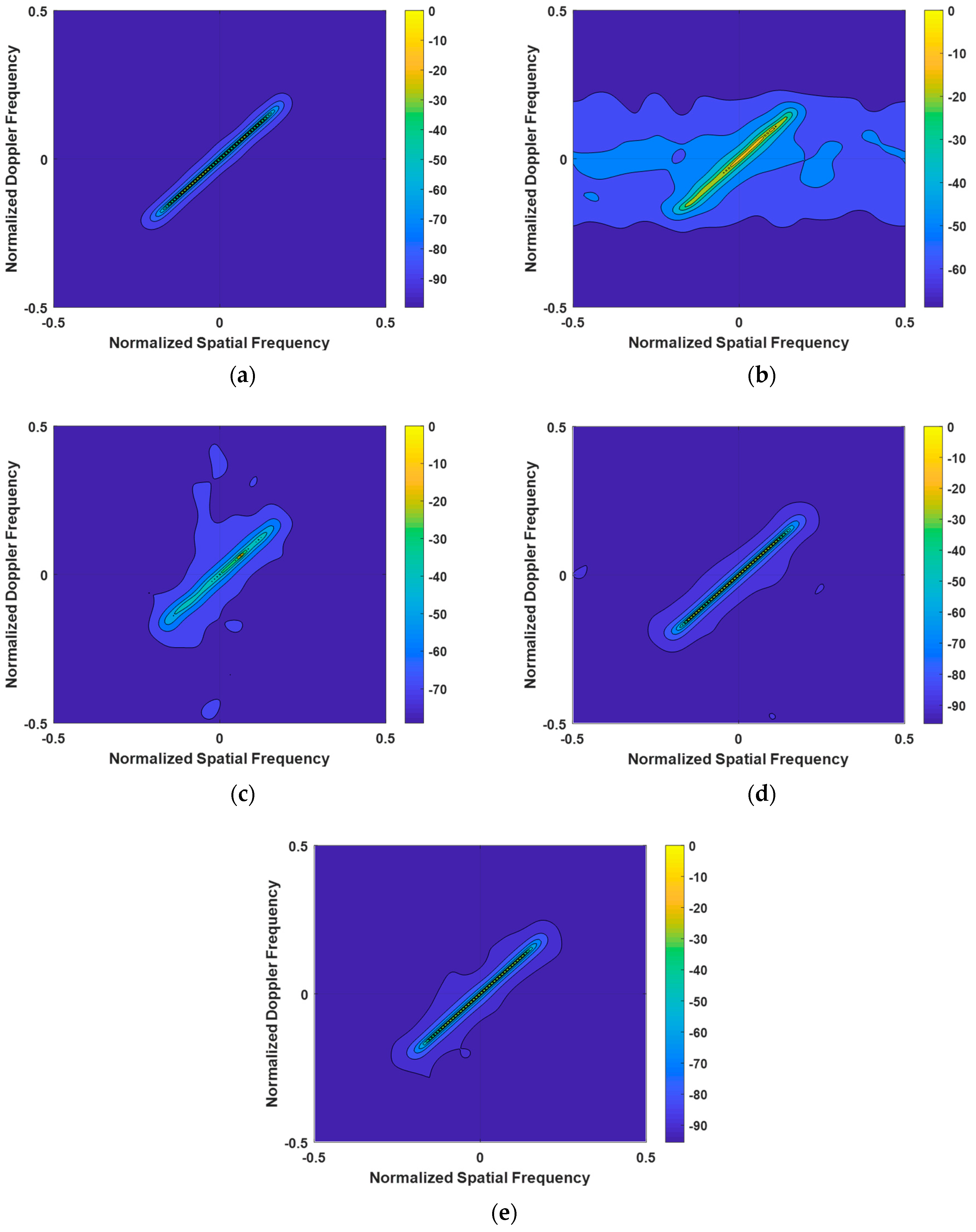
4.1. Analysis of Clutter Power Spectrum
4.1.1. Clutter Power Spectrum Under Ideal Conditions
4.1.2. Clutter Power Spectrum Under Array Element Error Conditions
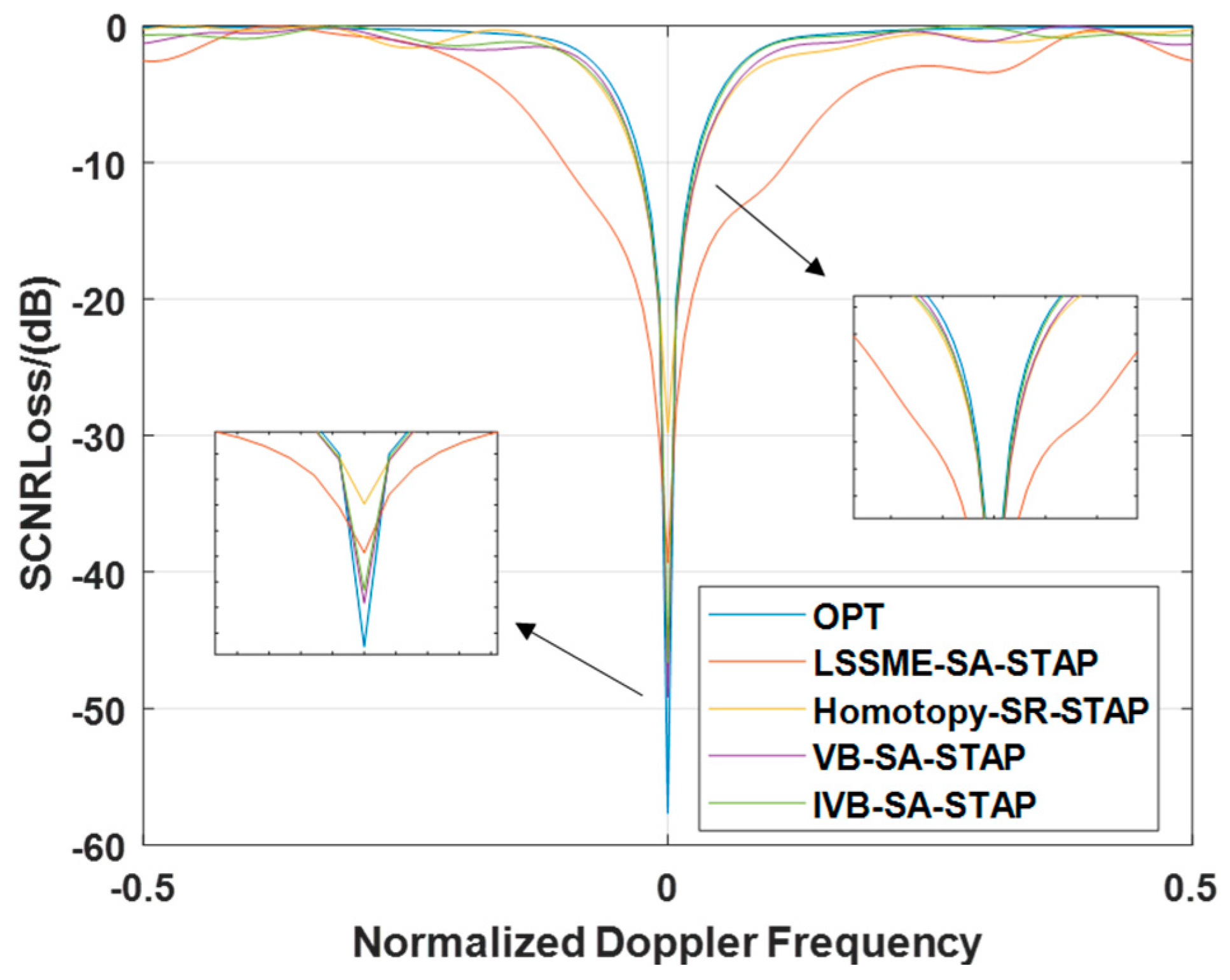
4.2. Analysis of Signal-to-Clutter-and-Noise Ratio Loss (SCNR Loss)
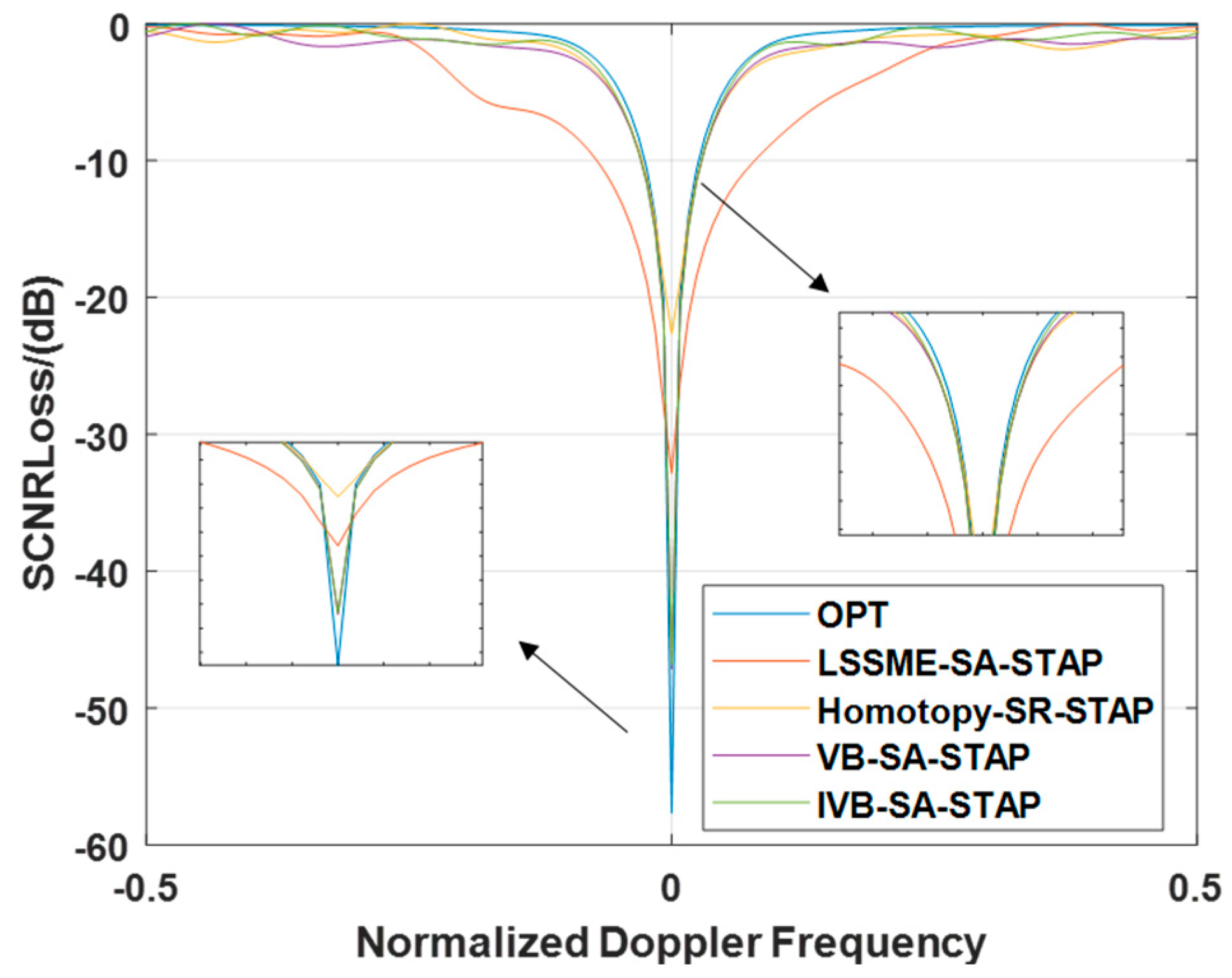
4.2.1. Signal-to-Clutter-and-Noise Ratio Loss Under Ideal Conditions
4.2.2. Signal-to-Clutter-and-Noise Ratio Loss Under Array Element Error Conditions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gao, Z.; Deng, W.; Huang, P.; Xu, W.; Tan, W. Airborne Radar Space–Time Adaptive Processing Algorithm Based on Dictionary and Clutter Power Spectrum Correction. Electronics 2024, 13, 2187. [Google Scholar] [CrossRef]
- Widrow, B.; Mantey, P.E.; Griffiths, L.J.; Goode, B.B. Adaptive antenna systems. Proc. IEEE 1967, 55, 2143–2159. [Google Scholar] [CrossRef]
- Brennan, L.E.; Reed, L.S. Theory of Adaptive Radar. IEEE Trans. Aerosp. Electron. Syst. 1973, AES-9, 237–252. [Google Scholar] [CrossRef]
- Melvin, W.L. A STAP overview. IEEE Aerosp. Electron. Syst. Mag. 2004, 19, 19–35. [Google Scholar] [CrossRef]
- Honig, M.L.; Goldstein, J.S. Adaptive reduced-rank interference suppression based on the multistage Wiener filter. IEEE Trans. Commun. 2002, 50, 986–994. [Google Scholar] [CrossRef]
- Wang, L.; Lamare, R.C.d. Adaptive reduced-rank LCMV beamforming algorithm based on the set-membership filtering framework. In Proceedings of the 2010 7th International Symposium on Wireless Communication Systems, York, UK, 19–22 September 2010; pp. 125–129. [Google Scholar]
- Cristallini, D.; Burger, W. A Robust Direct Data Domain Approach for STAP. IEEE Trans. Signal Process. 2012, 60, 1283–1294. [Google Scholar] [CrossRef]
- Cristallini, D.; Rosenberg, L.; Wojaczek, P. Complementary direct data domain STAP for multichannel airborne passive radar. In Proceedings of the 2021 IEEE Radar Conference (RadarConf21), Atlanta, GA, USA, 8–14 May 2021; pp. 1–6. [Google Scholar]
- Du, X.; Jing, Y.; Chen, X.; Cui, G.; Zheng, J. Clutter Covariance Matrix Estimation via KA-SADMM for STAP. IEEE Geosci. Remote Sens. Lett. 2024, 21, 1–5. [Google Scholar] [CrossRef]
- Tropp, J.A.; Wright, S.J. Computational Methods for Sparse Solution of Linear Inverse Problems. Proc. IEEE 2010, 98, 948–958. [Google Scholar] [CrossRef]
- Mallat, S.G.; Zhifeng, Z. Matching pursuits with time-frequency dictionaries. IEEE Trans. Signal Process. 1993, 41, 3397–3415. [Google Scholar] [CrossRef]
- Wang, J.; Shim, B. On the Recovery Limit of Sparse Signals Using Orthogonal Matching Pursuit. IEEE Trans. Signal Process. 2012, 60, 4973–4976. [Google Scholar] [CrossRef]
- Shaobo, L.; Yuanhua, R.; Xingping, S.; Zongben, X. Learning Capability of Relaxed Greedy Algorithms. IEEE Trans. Neural Networks Learn. Syst. 2013, 24, 1598–1608. [Google Scholar] [CrossRef] [PubMed]
- Zou, J.; Fu, Y.; Xie, S. A Block Fixed Point Continuation Algorithm for Block-Sparse Reconstruction. IEEE Signal Process. Lett. 2012, 19, 364–367. [Google Scholar] [CrossRef]
- Tipping, M.E. Sparse bayesian learning and the relevance vector machine. J. Mach. Learn. Res. 2001, 1, 211–244. [Google Scholar] [CrossRef]
- Zhang, L.; Dai, L. Image Reconstruction of Electrical Capacitance Tomography Based on an Efficient Sparse Bayesian Learning Algorithm. IEEE Trans. Instrum. Meas. 2022, 71, 1–14. [Google Scholar] [CrossRef]
- Cheng, L.; Xing, C.; Wu, Y.C. Irregular Array Manifold Aided Channel Estimation in Massive MIMO Communications. IEEE J. Sel. Top. Signal Process. 2019, 13, 974–988. [Google Scholar] [CrossRef]
- Xu, L.; Cheng, L.; Wong, N.; Wu, Y.C.; Poor, H.V. Overcoming Beam Squint in mmWave MIMO Channel Estimation: A Bayesian Multi-Band Sparsity Approach. IEEE Trans. Signal Process. 2024, 72, 1219–1234. [Google Scholar] [CrossRef]
- Duan, H.; Yang, L.; Fang, J.; Li, H. Fast Inverse-Free Sparse Bayesian Learning via Relaxed Evidence Lower Bound Maximization. IEEE Signal Process. Lett. 2017, 24, 774–778. [Google Scholar] [CrossRef]
- Thomas, C.K.; Slock, D. Save-space alternating variational estimation for sparse bayesian learning. In Proceedings of the 2018 IEEE Data Science Workshop (DSW), Lausanne, Switzerland, 4–6 June 2018; pp. 11–15. [Google Scholar]
- Al-Shoukairi, M.; Schniter, P.; Rao, B.D. A GAMP-Based Low Complexity Sparse Bayesian Learning Algorithm. IEEE Trans. Signal Process. 2018, 66, 294–308. [Google Scholar] [CrossRef]
- Zhou, W.; Zhang, H.-T.; Wang, J. An Efficient Sparse Bayesian Learning Algorithm Based on Gaussian-Scale Mixtures. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 3065–3078. [Google Scholar] [CrossRef] [PubMed]
- Ward, J. Space-time adaptive processing for airborne radar. In Proceedings of the 1995 International Conference on Acoustics, Speech, and Signal Processing, Detroit, MI, USA, 9–12 May 1995; Volume 2805, pp. 2809–2812. [Google Scholar]
- Lv, X.; Yuan, L.; Cheng, Z.; Zuo, L.; Yin, B.; He, Y.; Ding, C. An Improved Bayesian Learning Method for Distribution Grid Fault Location and Meter Deployment Optimization. IEEE Trans. Instrum. Meas. 2024, 73, 1–10. [Google Scholar] [CrossRef]
- Yang, Z.; Nie, L.; Huo, K.; Wang, H.; Li, X. Sparsity-based space-time adaptive processing using complex-valued homotopy technique. In Proceedings of the 2013 IEEE Radar Conference (RadarCon13), Ottawa, ON, Canada, 29 April–3 May 2013; pp. 1–6. [Google Scholar]
- Melvin, W.L.; Guerci, J.R. Knowledge-aided signal processing: A new paradigm for radar and other advanced sensors. IEEE Trans. Aerosp. Electron. Syst. 2006, 42, 983–996. [Google Scholar] [CrossRef]

| Parameters | Value |
|---|---|
| Number of Array Elements | 10 |
| Number of Pulses | 10 |
| Element Spacing (m) | 0.1 |
| Operating Wavelength (m) | 0.2 |
| Flight Speed (m/s) | 150 |
| Flight Altitude (m) | 4000 |
| Pulse Repetition Frequency (Hz) | 5000 |
| 4 | |
| 4 | |
| Training snapshot number | 10 |
| SNR (dB) | 30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, K.; Luo, J.; Li, P.; Liao, G.; Huang, Z.; Yang, L. Improved Variational Bayes for Space-Time Adaptive Processing. Entropy 2025, 27, 242. https://doi.org/10.3390/e27030242
Li K, Luo J, Li P, Liao G, Huang Z, Yang L. Improved Variational Bayes for Space-Time Adaptive Processing. Entropy. 2025; 27(3):242. https://doi.org/10.3390/e27030242
Chicago/Turabian StyleLi, Kun, Jinyang Luo, Peng Li, Guisheng Liao, Zhixiang Huang, and Lixia Yang. 2025. "Improved Variational Bayes for Space-Time Adaptive Processing" Entropy 27, no. 3: 242. https://doi.org/10.3390/e27030242
APA StyleLi, K., Luo, J., Li, P., Liao, G., Huang, Z., & Yang, L. (2025). Improved Variational Bayes for Space-Time Adaptive Processing. Entropy, 27(3), 242. https://doi.org/10.3390/e27030242









