Slot Allocation Protocol for UAV Swarm Ad Hoc Networks: A Distributed Coalition Formation Game Approach
Abstract
1. Introduction
- (1)
- We formulate the slot allocation problem of the UAV swarm ad hoc network based on the TDMA protocol as a coalition formation game among UAV nodes with different transmission time slots. Within the framework of the proposed game, UAV nodes with no interference from each other form a coalition, share their time slots, and transmit data packets simultaneously.
- (2)
- A simple distributed coalition formation algorithm based on the join-and-leave rule is proposed, through which each UAV node autonomously determines the most beneficial coalition to join. Subsequently, the whole network quickly converges to a final stable partition.
- (3)
- Based on the distributed time coalition formation algorithm, we design a TDMA MAC protocol (called DCFG-TDMA) for the UAV swarm ad hoc network. UAV nodes with a DCFG-TDMA protocol can achieve time slots adaptively with dynamically changing network topology.
2. Related Works
2.1. MAC Based on CSMA Mechanism
2.2. MAC Based on TDMA Mechanism
2.3. Method Based on Game Theory
2.4. Method Based on Reinforcement Learning
3. System Model and Problem Formulation
3.1. System Model
3.1.1. Channel Model
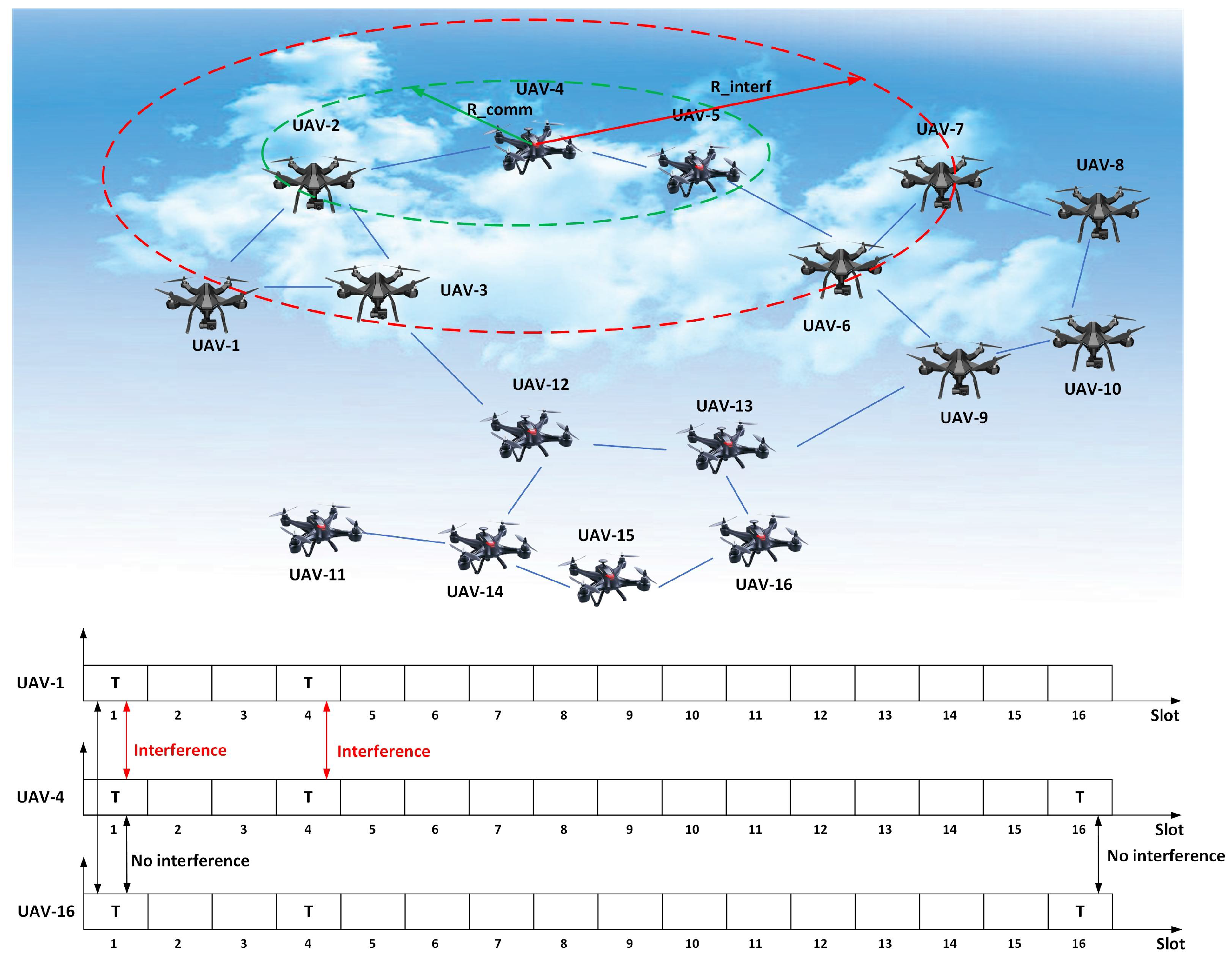
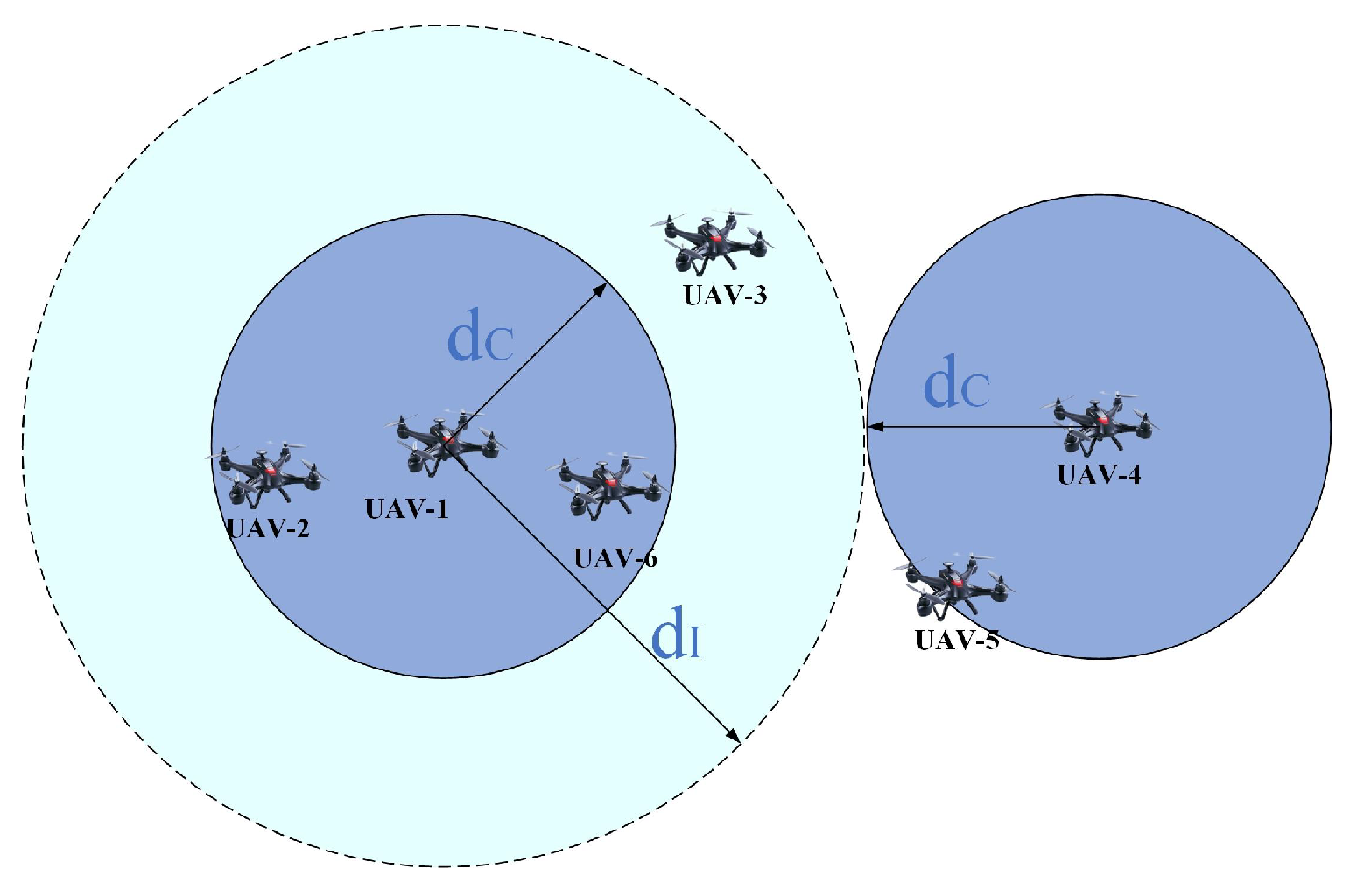
3.1.2. Analysis of Communication and Interference
3.1.3. Network Topology
3.2. Problem Formulation
4. The Coalition Formulation Game Model
4.1. Coalition Formation Basic Concepts
4.2. Distributed Coalition Formation Algorithm
| Algorithm 1 Procedure of Distributed Time Slot Coalition Formation Algorithm |
| 1 Phase 1: Discovery of neighbors |
| 2 Phase 2: Adaptive coalition formation |
| 3 Initialization: and |
| 4 Repeat |
| 5 (1) For each UAV-i calculates the , and , where ; |
| 6 (2) UAV-i randomly chooses a coalition to join, calculates , and , where denotes the coalition structure after UAV-i joining ; |
| 7 (3) If , then: UAV-i decides to join the coalition ; ; can be replaced to ; |
| 8 End if; |
| 9 (4) ; |
| 10 Until Convergence to a stable coalition structure. |
| 11 Phase 3: The UAVs in a coalition start transmitting packets at the sharing time slots simultaneously. |
4.3. Performance Analysis
5. Designs of TDMA Protocol-Based Distributed Coalition Formation Games
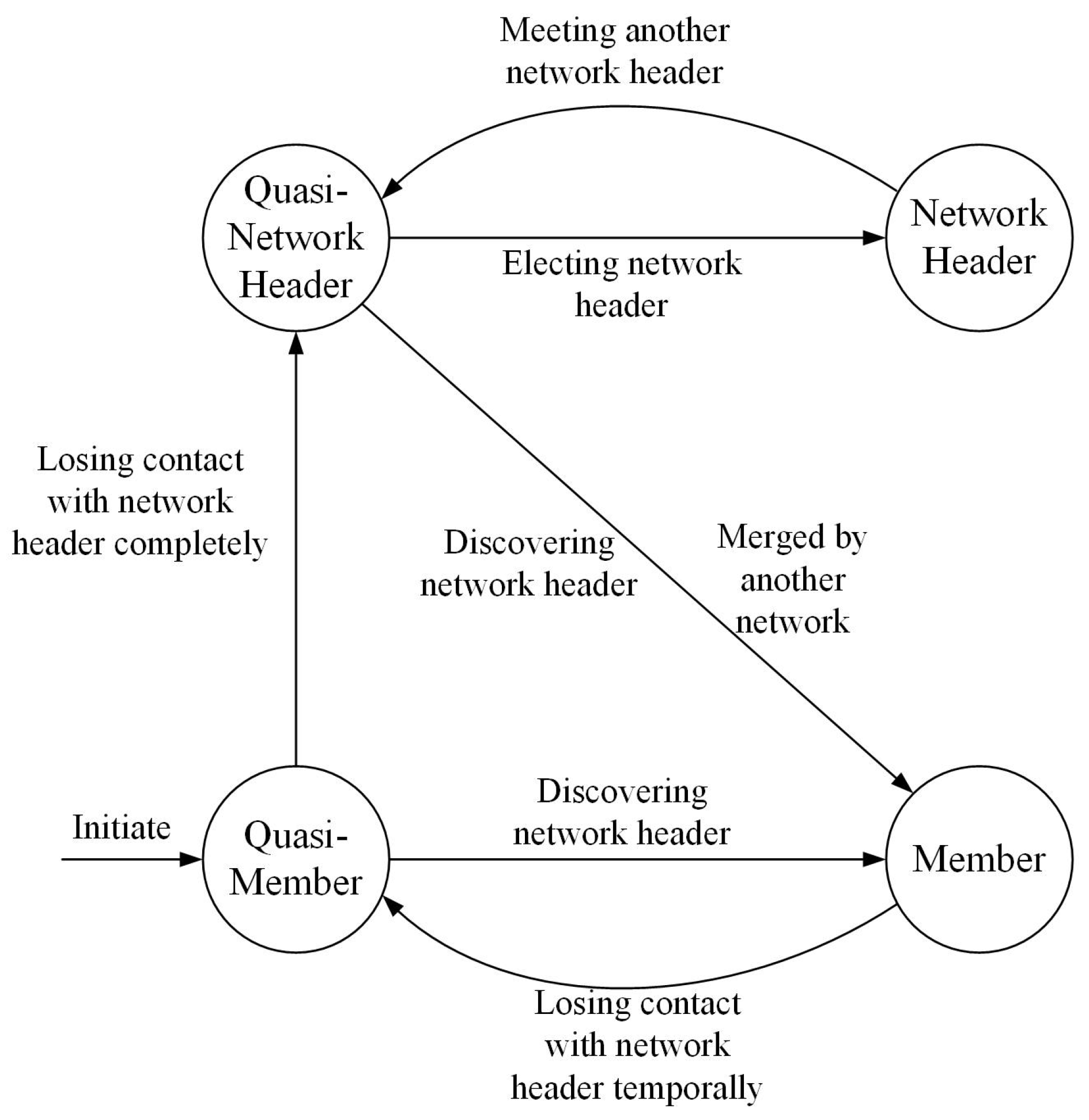
5.1. Network Configuration Protocol
- (1)
- Initiation: When a UAV node initially starts up, it enters the quasi-member state.
- (2)
- Discovering network header: When the quasi-member and quasi-network header UAV node receive the invite-to-join (ITJ) message from the network header again, they transform to the member state.
- (3)
- Losing contact with the network header temporally: When the member UAV node cannot receive the schedule assignment broadcast periodically from the network header over the limit time, the state of the UAV node changes from member to quasi-member.
- (4)
- Losing contact with network header completely: When the quasi-member UAV node cannot receive the schedule assignment ITJ message two consecutive times, the UAV node enters the quasi-network header state. The network header will delete this UAV node from the member list if it cannot receive packets from this UAV node three consecutive times.
- (5)
- Electing network header: When acting as a quasi-network header over a limited time, this UAV node elects itself as a network header and broadcasts the ITJ advertisement message periodically. The other quasi-network header UAV node joins its network and forwards the ITJ advertisement message when it receives the ITJ advertisement message.
- (6)
- Meeting another network header: When a network header receives another valid ITJ advertisement message, it enters the quasi-network header state and compares the node identification with another network header. The UAV network header with smaller identification then becomes a new network header.
- (7)
- Merging by another network: When a network header receives another valid ITJ advertisement message, the UAV network header with smaller identification merges another network. The UAV network header with larger identification joins the new network and changes to the member state.
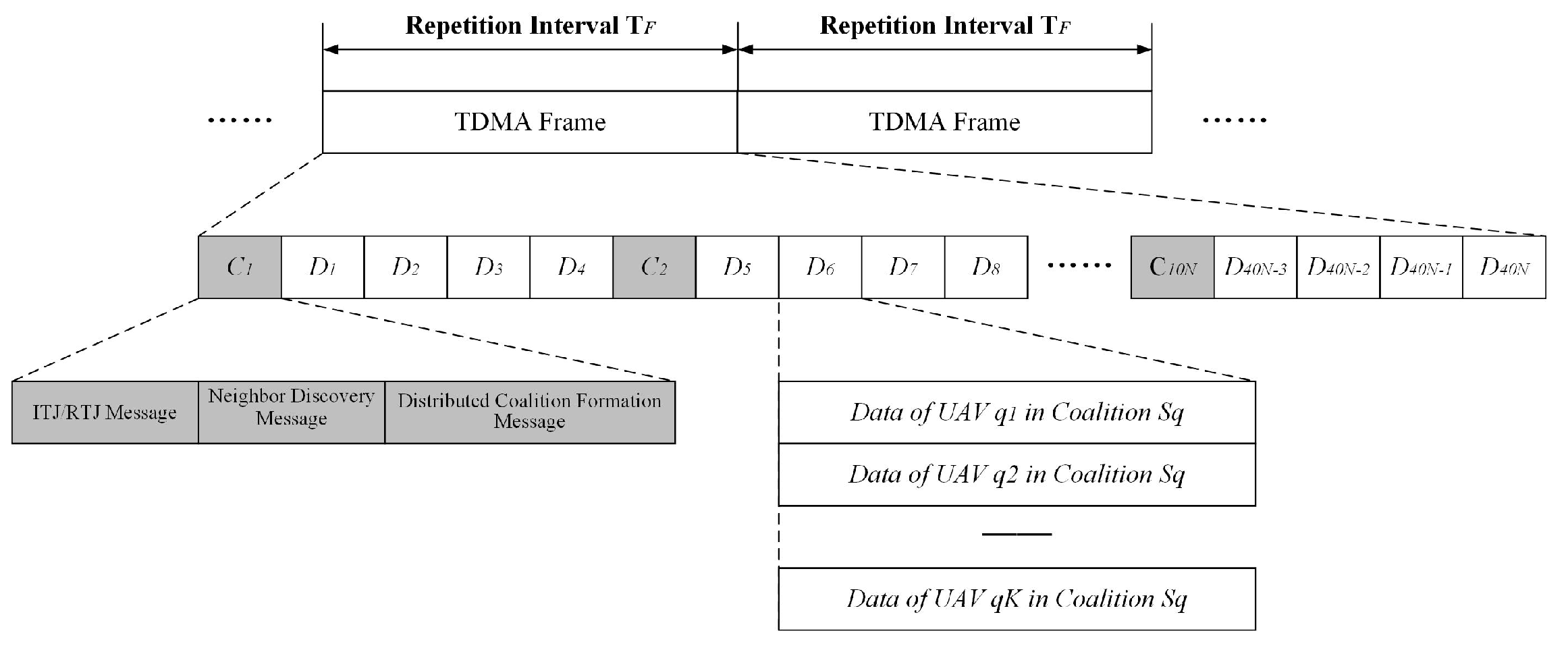
5.2. Time Frame Structure
5.3. Neighbor Discovery Protocol
5.4. Slot Allocation Protocol of DCF Game
- (1)
- The network header broadcasts the DCF message to the whole network in its control slot. The DCF message includes the current coalition structure with a sequence number, which is confirmed by the network header.
- (2)
- Every member node forwards the DCF message to other nodes once in the form of a broadcast at the pre-allocated control slot after it receives and stores the coalition structure . All UAV nodes transmit data packets in the data slots based on the slot allocation scheme defined by the coalition structure in the next repetition interval.
- (3)
- An ROC message is generated after operating the join-and-leave rule based on the coalition structure of the DCF message broadcast by the network header. Then, the member node sends the ROC message to the network header in the form of a broadcast.
- (4)
- Other member nodes forward the ROC message once in the form of a broadcast to ensure that it can be received by the network header.
- (5)
- After every member node has sent ROC messages, the network header decides the new coalition message structure based on the arrival order of ROC messages. Arriving earlier means the node is closer to the network header and its pre-allocated slot is in the front.
- (6)
- The network header broadcasts the new DCF message, which includes the new coalition structure, to the whole network.
- (7)
- Step 1 to step 6 are repeated in the whole network running time. The data packets are transmitted to the data slots allocated by the coalition structure simultaneously without waiting for the Algorithm 2 to converge.
| Algorithm 2 Procedure of DCFG-TDMA protocol | |
| 1 | UAV-i goes online; |
| 2 | Wait for the broadcast signaling ITJ of the network header; |
| 3 | If receive the ITJ broadcast signal from network header, then: |
| 4 | Join the network, enter in the member state, and get the current coalition partition; |
| 5 | Operate Algorithm 1, participate in the iterative process of DCFG-TDMA slot allocation; |
| 6 | Transmit data on the allocated time slot; |
| 7 | Else: |
| 8 | Continue waiting and enter the associate member status; |
| 9 | If receving a ITJ in two repetition intervals, then: |
| 10 | Join the network, enter the member state; |
| 11 | Repeat 2–6; |
| 12 | Else, donot receive a ITJ in 3 repetition intervals, then: |
| 13 | Enter quasi-network header state; |
| 14 | Broadcast ITJ signal; |
| 15 | If receive RTJ from other UAV nodes,then: |
| 16 | Enter the network header state, broadcast ITJ signal periodically; |
| 17 | Run Algorithm 1, maintain the time slot allocation process of the network; |
| 18 | Else if receive a ITJ from other network header, then: |
| 19 | Compare the node id of itself and other network header; |
| 20 | If my id smaller than another ITJ node, then: |
| 21 | I am the network header, continue broadcasting ITJ signal; |
| 22 | Else: |
| 23 | Join another network, and become a member; |
| 24 | Repeat 2–6. |
6. Numerical Results
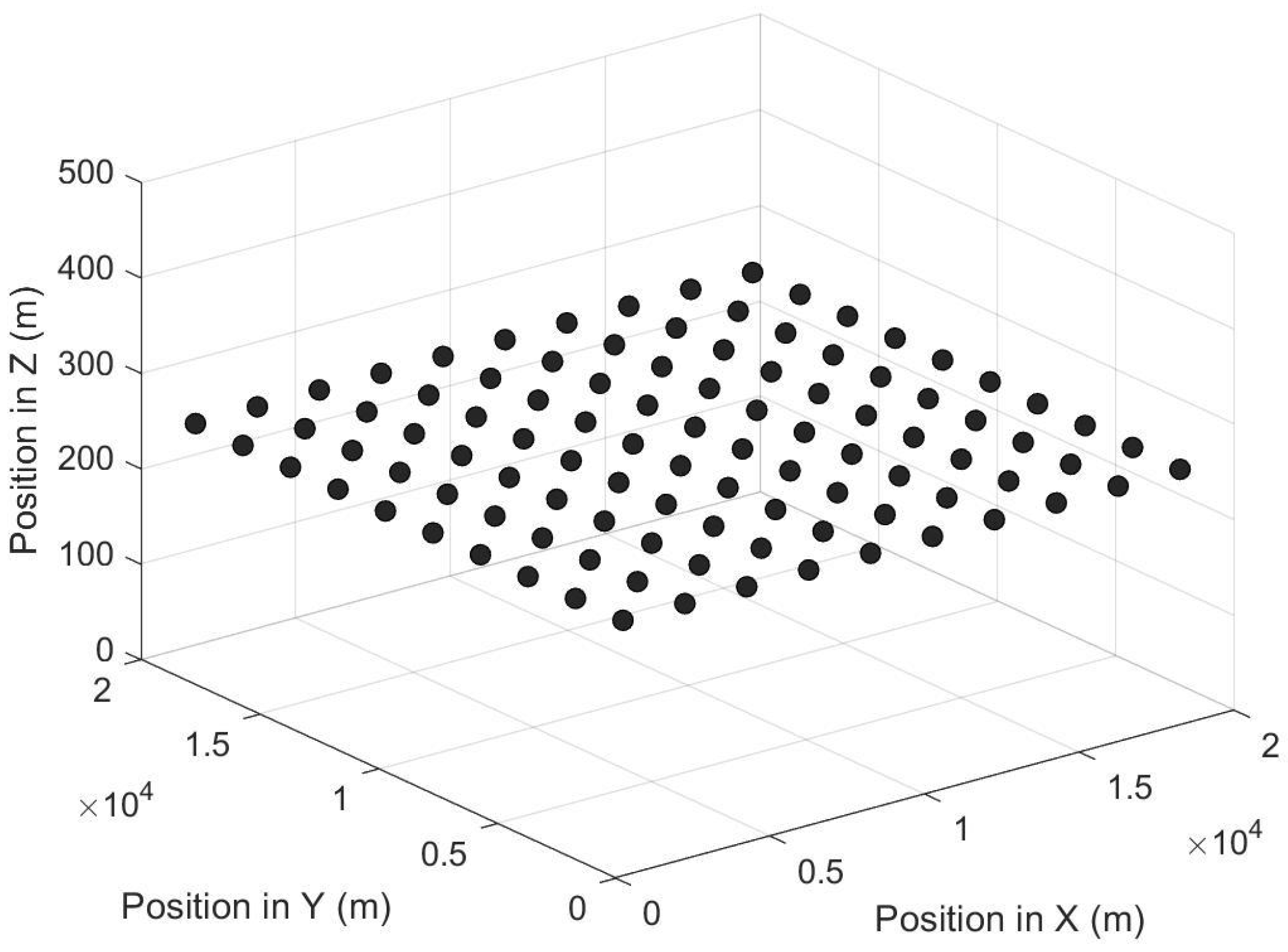
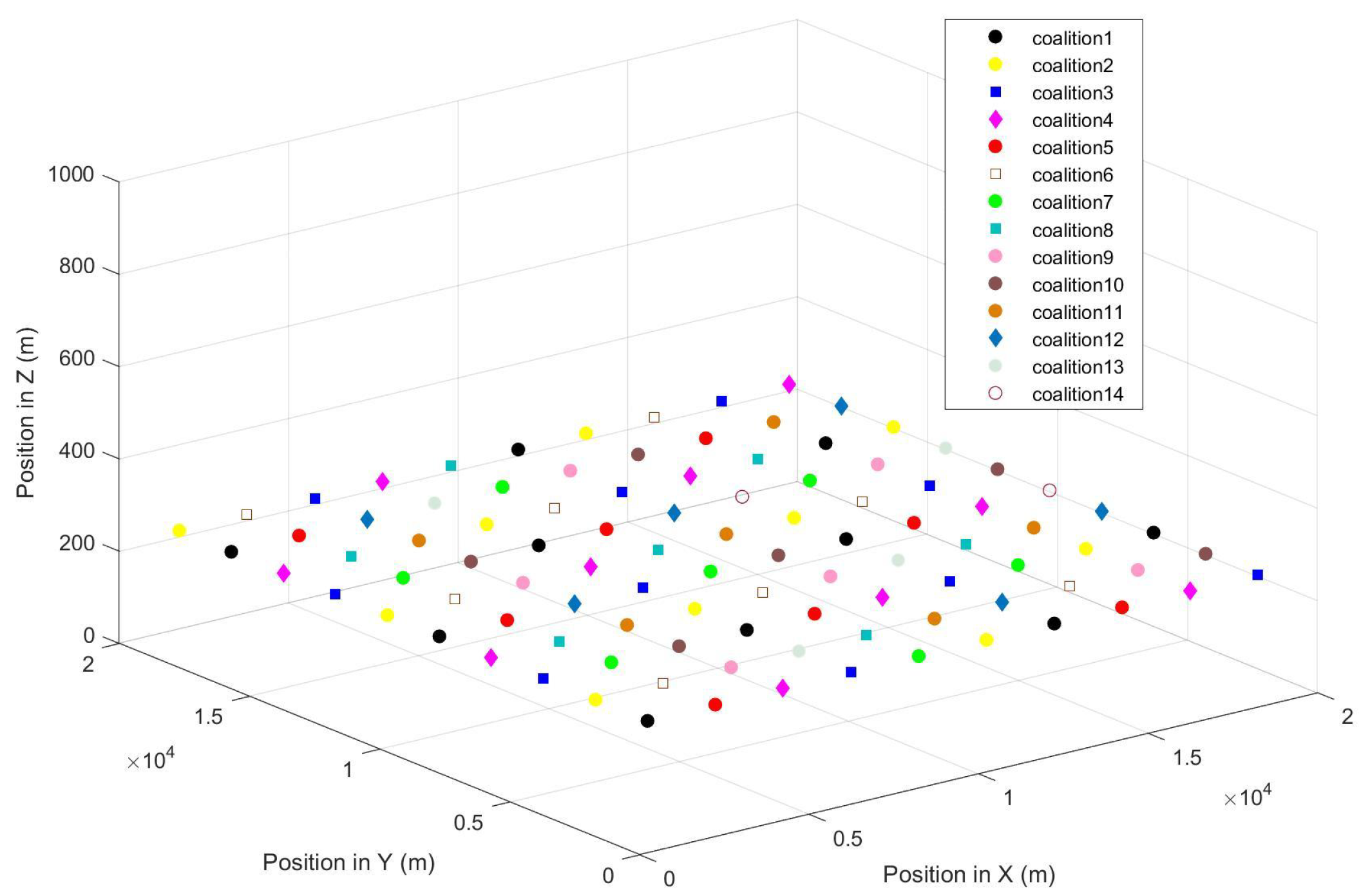
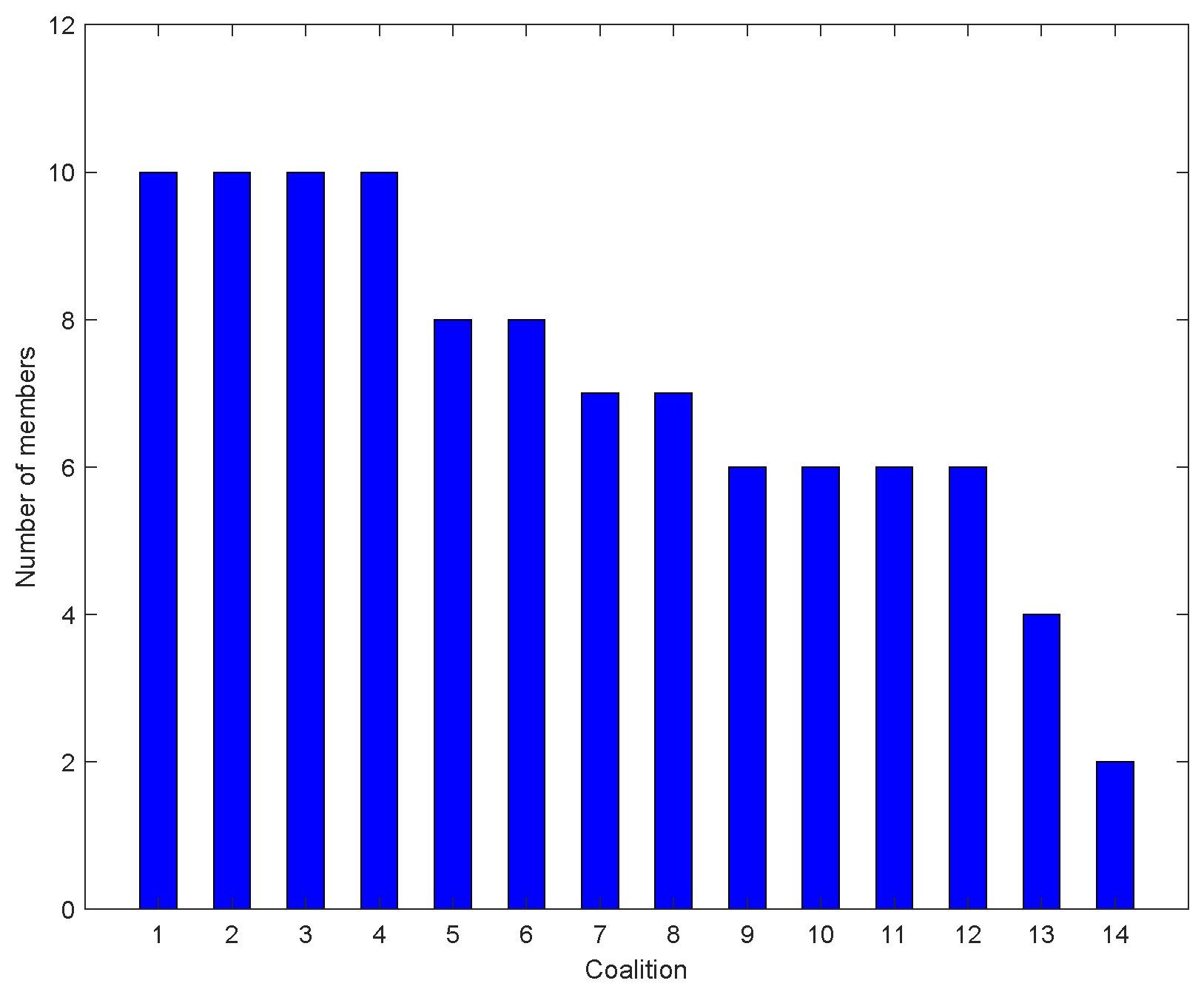
6.1. Static Grid Topology Environment
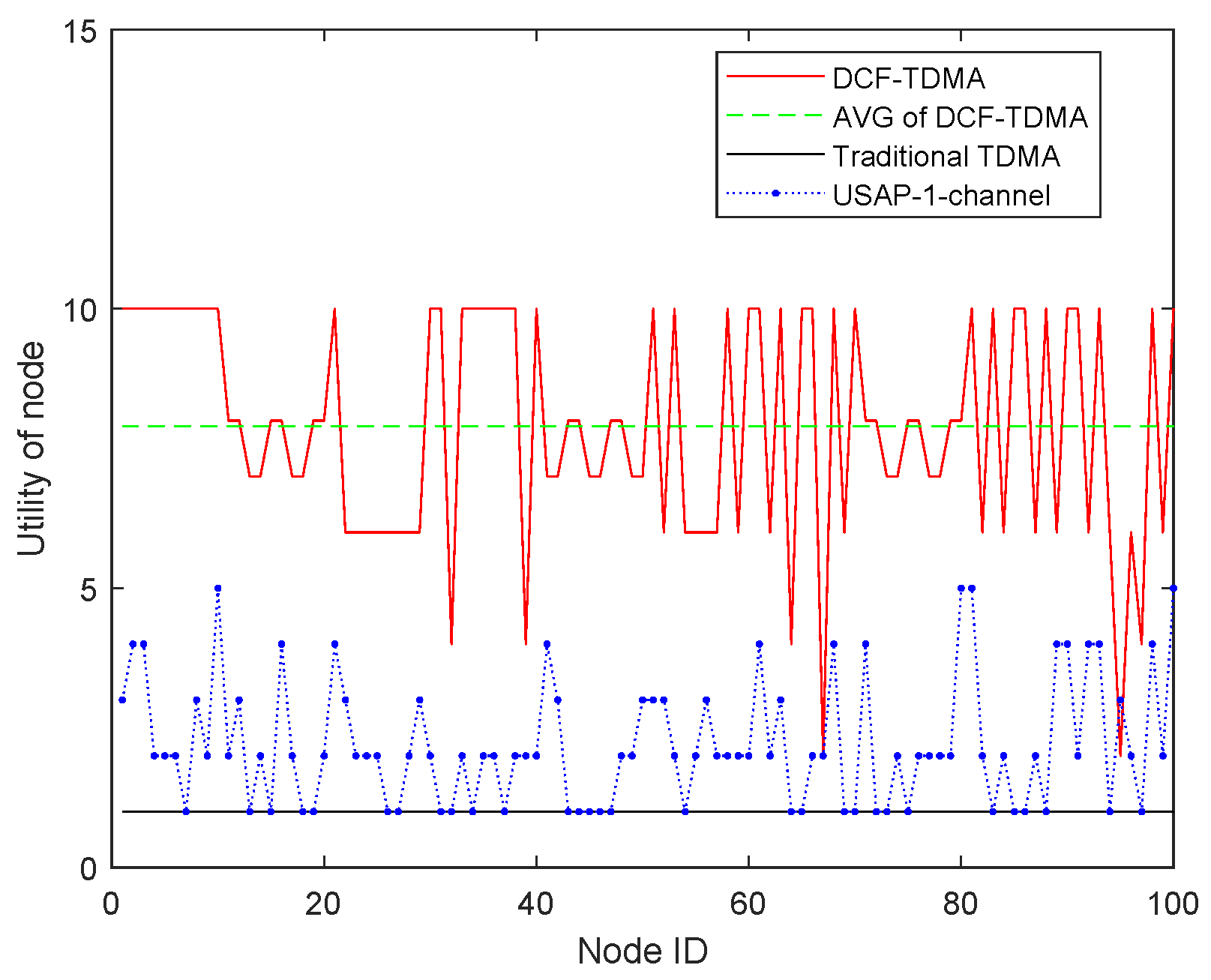
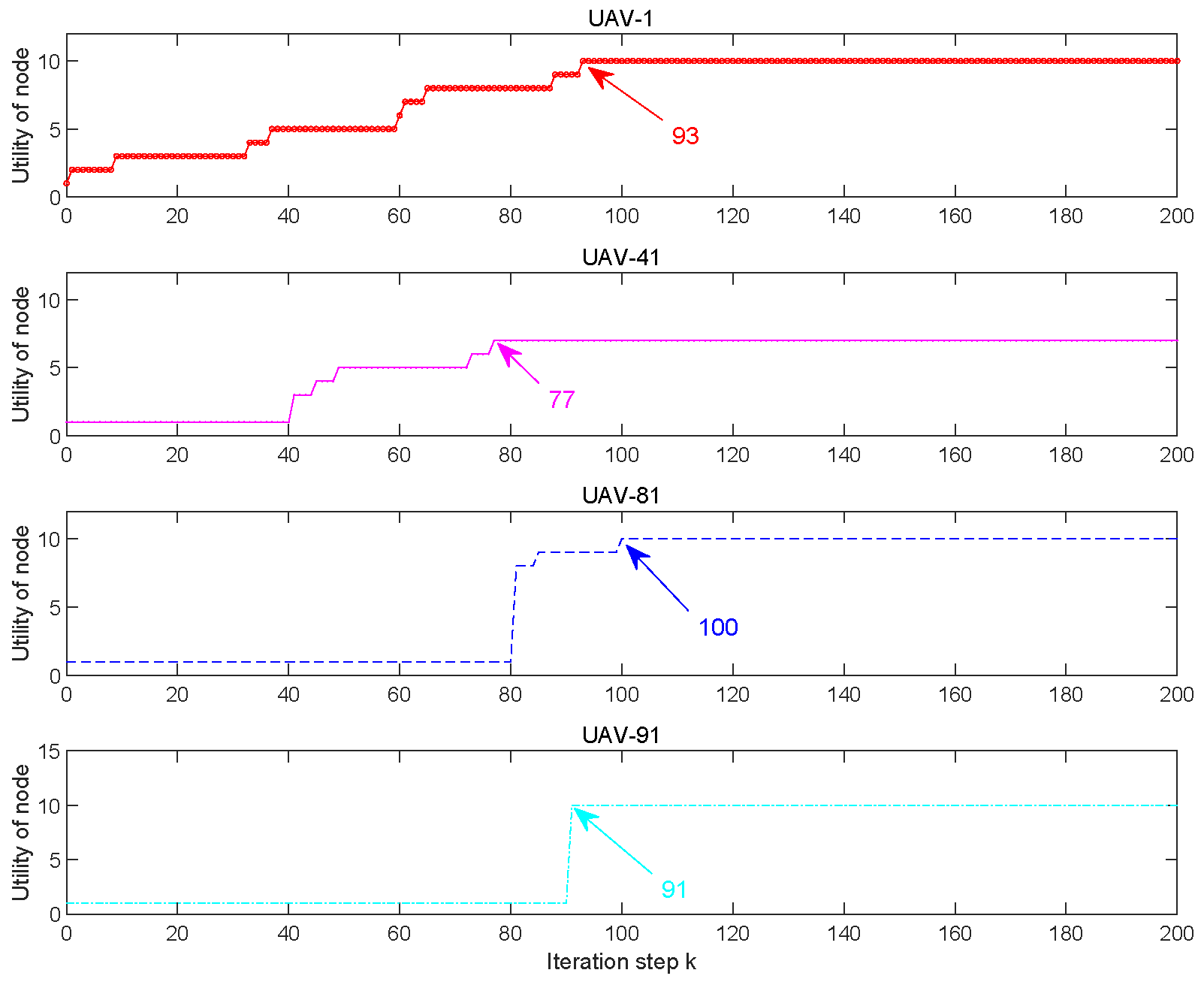
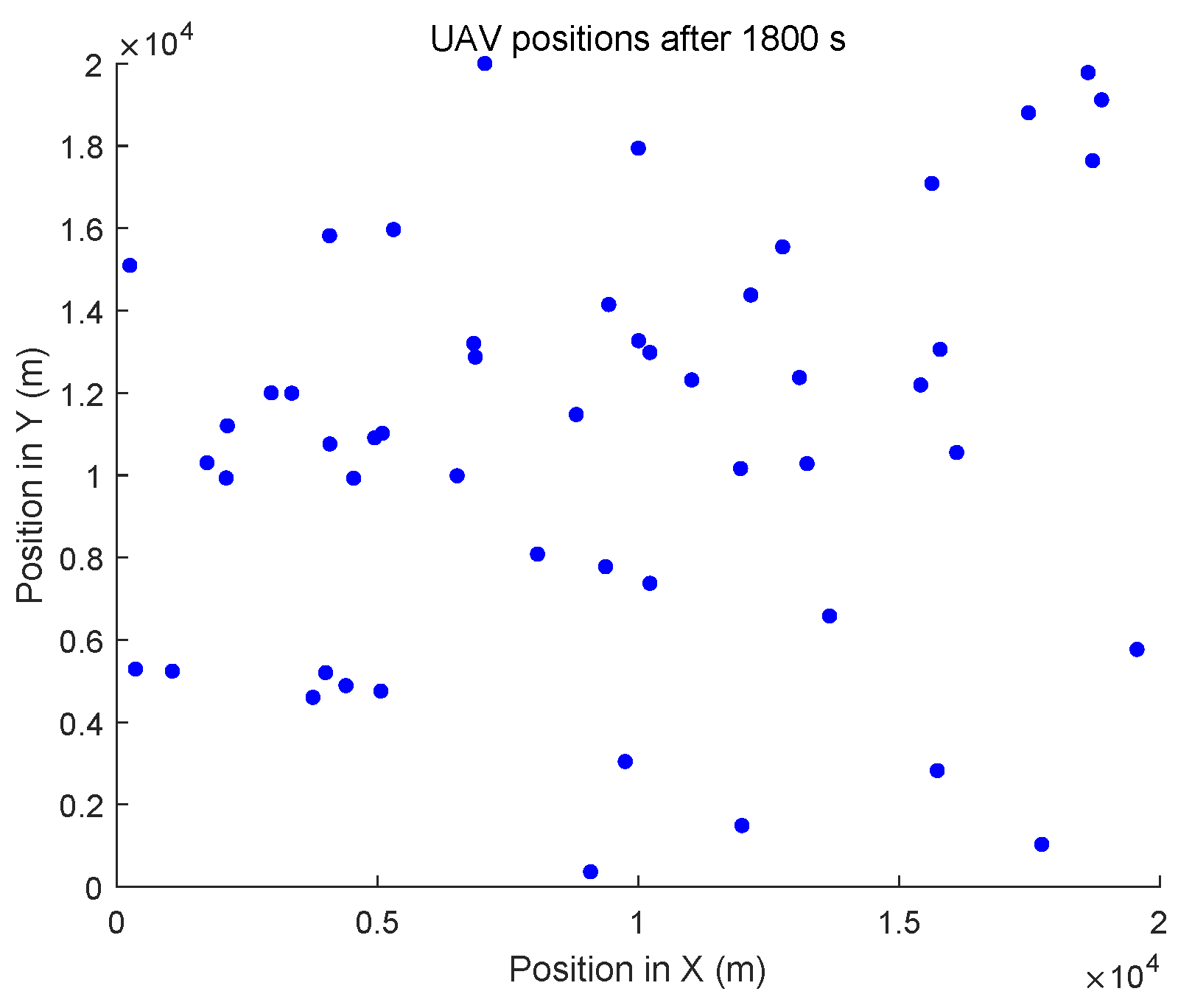
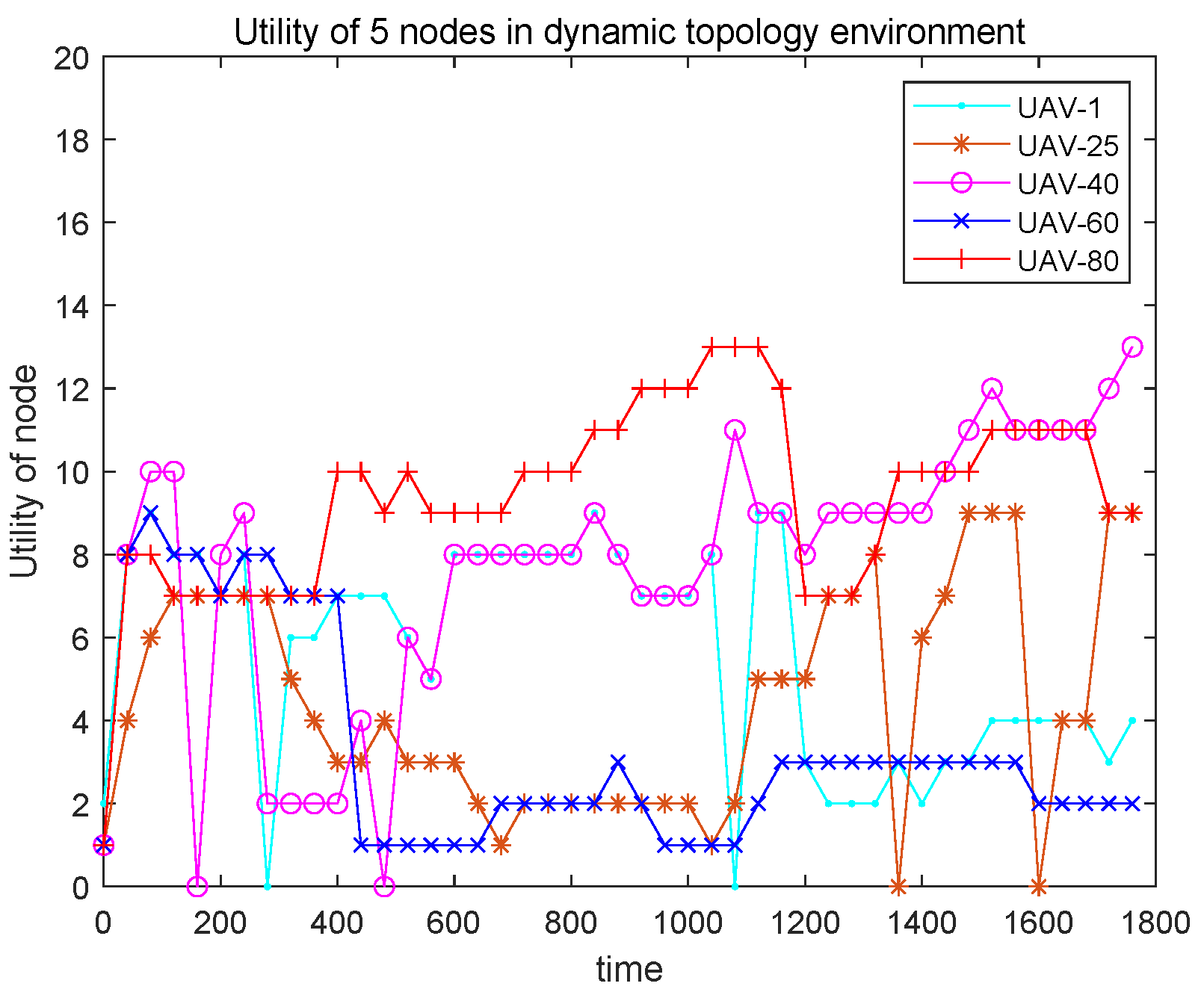
6.2. Dynamic Topology Environment
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Letaief, K.B.; Shi, Y.; Lu, J.; Lu, J. Edge rrtificial intelligence for 6G: Vision, enabling technologies, and applications. IEEE J. Sel. Areas Commun. 2022, 40, 5–36. [Google Scholar] [CrossRef]
- Zeng, Y.; Zhang, R.; Lim, T.J. Wireless communications with unmanned aerial vehicles: Opportunities and challenges. IEEE Commun. Mag. 2016, 54, 36–42. [Google Scholar] [CrossRef]
- Mozaffari, M.; Saad, W.; Bennis, M.; Nam, Y.-H.; Debbah, M. A tutorial on UAVs for wireless networks: Applications, challenges, and open problems. IEEE Commun. Surv. Tutorials 2019, 21, 2334–2360. [Google Scholar] [CrossRef]
- Khan, M.A.; Kumar, N.; Mohsan, S.A.H.; Khan, W.U.; Nasralla, M.M.; Alsharif, M.H. Swarm of UAVs for network management in 6G: A technical review. IEEE Trans. Netw. Serv. Manag. 2023, 20, 741–761. [Google Scholar] [CrossRef]
- Qi, F.; Zhu, X.; Mang, G.; Kadoch, M.; Li, W. UAV Network and IoT in the Sky for Future Smart Cities. IEEE Netw. 2019, 33, 96–101. [Google Scholar] [CrossRef]
- Chen, J.; Chen, P.; Wu, Q.; Xu, Y.; Qi, N.; Fang, T. A Game-theoretic Perspective on Resource Management for Large-scale UAV Communication Networks. China Commun. 2021, 18, 70–87. [Google Scholar] [CrossRef]
- Ding, G.; Wu, Q.; Zhang, L.; Lin, Y.; Tsiftsis, T.A.; Yao, Y.-D. An Amateur Drone Surveillance System Based on the Cognitive Internet of Things. IEEE Commun. Mag. 2018, 56, 29–35. [Google Scholar] [CrossRef]
- Zhao, J.; Gao, F.; Wu, Q.; Jin, S.; Wu, Y.; Jia, W. Beam Tracking for UAV Mounted SatCom on-the-Move with Massive Antenna Array. IEEE J. Sel. Areas Commun. 2018, 36, 363–375. [Google Scholar] [CrossRef]
- Zeng, Y.; Wu, Q.; Zhang, R. Accessing From the Sky: A Tutorial on UAV Communications for 5G and Beyond. Proc. IEEE 2019, 107, 2327–2375. [Google Scholar] [CrossRef]
- Wu, B.; Guo, D.; Zhang, B.; Zhang, X.; Wang, H.; Wang, H.; Jiang, H. Completion Time Minimization for UAV Enabled Data Collection with Communication Link Constrained. IET Commun. 2022, 16, 1025–1040. [Google Scholar] [CrossRef]
- Wang, H.; Wang, J.; Ding, G.; Chen, J.; Gao, F.; Han, Z. Completion Time Minimization with Path Planning for Fixed-wing UAV Communications. IEEE Trans. Wirel. Commun. 2019, 18, 3485–3499. [Google Scholar] [CrossRef]
- Wu, B.; Zhang, B.; Ma, W.; Xie, C.; Guo, D.; Jiang, H. Motion Planning in UAV-Aided Data Collection with Dynamic Jamming. Electronics 2023, 12, 1841. [Google Scholar] [CrossRef]
- Wu, B.; Zhang, B.; Guo, D.; Wang, H.; Jiang, H. Anti-jamming trajectory design for UAV-enabled wireless sensor networks using communication flight corridor. China Commun. 2022, 19, 37–52. [Google Scholar] [CrossRef]
- Gao, Y.; Wu, Y.; Cui, Z.; Yang, W.; Hu, G.; Xu, S. Robust Trajectory and Communication Design for Angle-constrained Multi-UAV Communications in the Presence of Jammers. China Commun. 2022, 19, 131–147. [Google Scholar] [CrossRef]
- Samir, M.; Sharafeddine, S.; Assi, C.M.; Nguyen, T.M.; Ghrayeb, A. UAV Trajectory Planning for Data Collection from Time-Constrained IoT Devices. IEEE Trans. Wirel. Commun. 2020, 19, 34–46. [Google Scholar] [CrossRef]
- Fei, B.L.Z.; Zhang, Y. UAV Communications for 5G and Beyond: Recent Advances and Future Trends. IEEE Internet Things J. 2019, 6, 2241–2263. [Google Scholar]
- Dorling, K.; Heinrichs, J.; Messier, G.G.; Magierowski, S. Vehicle Routing Problems for Drone Delivery. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 70–85. [Google Scholar] [CrossRef]
- Zhan, C.; Zeng, Y. Completion Time Minimization for Multi-UAV-Enabled Data Collection. IEEE Trans. Wirel. Commun. 2019, 18, 4859–4872. [Google Scholar] [CrossRef]
- Borgonovo, F.; Capone, A.; Cesana, M.; Fratta, L. ADHOC MAC: New MAC Architecture for Ad Hoc Networks Providing Efficient and Reliable Point-to-point and Broadcast Services. Wirel. Netw. 2004, 10, 359–366. [Google Scholar] [CrossRef]
- Omar, H.A.; Zhuang, W.; Li, L. VeMAC: A TDMA-based MAC protocol for reliable broadcast in VANETs. IEEE Trans. Mob. Comput. 2013, 12, 1724–1736. [Google Scholar] [CrossRef]
- Nguyen, V.; Dang, D.N.M.; Jang, S.; Hong, C.S. E-VeMAC: An Enhanced Vehicular MAC Protocol to Mitigate the Exposed Terminal Problem. In Proceedings of the 16th Asia-Pacific Network Operations and Management Symposium (APNOMS 16), Hsinchu, Taiwan, 17–19 September 2014; pp. 1–4. [Google Scholar]
- Zou, R.; Liu, Z.; Zhang, L.; Kamil, M. A near collision free reservation based MAC protocol for VANETs. In Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC), Istanbul, Turkey, 6–9 April 2014; pp. 1538–1543. [Google Scholar]
- Jiang, A.; Mi, Z.; Dong, C.; Wang, H. CF-MAC: A Collision-free MAC Protocol for UAVs Ad-Hoc Networks. In Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC), Doha, Qatar, 3–6 April 2016; pp. 1–6. [Google Scholar]
- Chua, M.Y.-K.; Yu, F.R.; Li, J.; Zhou, Y.; Lamont, L. Medium Access Control for Unmanned Aerial Vehicle (UAV) Ad-Hoc Networks With Full-Duplex Radios and Multipacket Reception Capability. IEEE Trans. Veh. Technol. 2013, 62, 390–394. [Google Scholar] [CrossRef]
- Wang, H.; Jiang, B.; Zhao, H.; Zhang, J.; Zhou, L.; Ma, D. Joint Resource Allocation on Slot, Space and Power Towards Concurrent Transmissions in UAV Ad Hoc Networks. IEEE Trans. Wirel. Commun. 2022, 21, 8698–8712. [Google Scholar] [CrossRef]
- Xu, Y.; Anpalagan, A.; Wu, Q.; Shen, L.; Gao, Z.; Wang, J. Decision-Theoretic Distributed Channel Selection for Opportunistic Spectrum Access: Strategies, Challenges and Solutions. IEEE Commun. Surv. Tutorials 2013, 15, 1689–1713. [Google Scholar] [CrossRef]
- Ahmed, M.; Peng, M.; Abana, M.; Yan, S.; Wang, C. Interference Coordination in Heterogeneous Small-Cell Networks: A Coalition Formation Game Approach. IEEE Syst. J. 2018, 12, 604–615. [Google Scholar] [CrossRef]
- Wang, B.; Wang, L.; Fu, G.; Liu, W.; Cui, J. A New Distributed Coalition Formation Algorithm for Cooperation in Ad Hoc Networks. In Proceedings of the 2018 IEEE 4th International Conference on Computer and Communications (ICCC), Chengdu, China, 7–10 December 2018; pp. 446–450. [Google Scholar]
- Li, T.; Li, C.; Yang, C.; Shao, J.; Zhang, Y.; Pang, L. A Mean Field Game-theoretic Cross-layer Optimization for Multi-hop Swarm UAV Communications. J. Commun. Netw. 2021, 24, 68–82. [Google Scholar] [CrossRef]
- Zhang, Z.; Atapattu, S.; Wang, Y.; Renzo, M.D. Distributed MAC for RIS-Assisted Multiuser Networks: CSMA/CA Protocol Design and Statistical Optimization. IEEE Trans. Mob. Comput. 2025; early access. [Google Scholar]
- Peng, G.; Fang, D.; Fu, B.; Zhang, N. NCSMA: A NOMA-Based CSMA/CA Protocol for Ad Hoc Networks. In Proceedings of the 2024 IEEE 35th International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC 24), Valencia, Spain, 2–5 September 2024; pp. 1–6. [Google Scholar]
- Young, C.D. USAP multiple access: Dynamic resource allocation for mobile multihop multichannel wireless networking. In Proceedings of the IEEE Military Communications 1999, Atlantic City, NJ, USA, 31 October–3 November 1999; pp. 271–275. [Google Scholar]
- Zhang, S.; Ni, Z.; Kuang, L.; Jiang, C.; Zhao, X. Load-Aware Distributed Resource Allocation for MF-TDMA Ad Hoc Networks: A Multi-Agent DRL Approach. IEEE Trans. Netw. Sci. Eng. 2022, 9, 4426–4443. [Google Scholar] [CrossRef]
- Zhao, X.; Wei, Z.; Zou, Y.; Ma, H.; Cui, Y.; Feng, Z. A dual-cluster-head based medium access control for large-scale UAV ad-hoc networks. China Commun. 2024, 21, 123–136. [Google Scholar]
- Sohaib, M.; Jeong, J.; Jeon, S.-W. Dynamic Multichannel Access via Multi-agent Reinforcement Learning: Throughput and Fairness Guarantees. IEEE Trans. Wirel. Commun. 2022, 21, 3994–4008. [Google Scholar] [CrossRef]
- Liu, X.; Xu, C.; Yu, H.; Zeng, P. Deep Reinforcement Learning-Based Multichannel Access for Industrial Wireless Networks With Dynamic Multiuser Priority. IEEE Trans. Ind. Inform. 2022, 18, 7048–7058. [Google Scholar] [CrossRef]
- Naeem, F.; Adam, N.; Kaddoum, G.; Waqar, O. Learning MAC Protocols in HetNets: A Cooperative Multi-Agent Deep Reinforcement Learning Approach. In Proceedings of the 2024 IEEE Wireless Communications and Networking Conference (WCNC), Dubai, United Arab Emirates, 21–24 April 2024; pp. 1–6. [Google Scholar]
- Li, X.; Yao, H.; Wang, J.; Xu, X.; Jiang, C.; Hanzo, L. A Near-Optimal UAV-Aided Radio Coverage Strategy for Dense Urban Areas. IEEE Trans. Veh. Technol. 2019, 68, 9098–9109. [Google Scholar] [CrossRef]


| Variables | Explanation |
|---|---|
| M | The number of coalitions |
| N | The number of UAVs and slots |
| The index set of the UAVs | |
| The set of the available time slot | |
| B | The bandwidth of a channel |
| The fixed data rate | |
| The transmit power of each UAV | |
| The communication range | |
| The interference range | |
| The received power of the signal | |
| The communication graph | |
| The collision graph | |
| A distributed coalition game with non-transferable utility | |
| The finite set of players (i.e., UAVs) | |
| A partition function | |
| A partition of | |
| The individual payoff of UAV i in coalition | |
| The utility function of the coalition | |
| The system payoff on | |
| The corresponding slots selected by UAV-n | |
| The throughput of the whole multi-UAV network |
| Parameter | Value |
|---|---|
| Carrier frequency f | 2.4 GHz |
| Bandwidth B | 20 MHz |
| Channel parameter | 1 |
| Variance of noise | W/Hz |
| UAV transmit power | 0.5 W |
| Data rate R | 20 Mbps |
| Communication range | 2225.4 m |
| Slot | 100 μs |
| Repetition interval | 500 ms |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, L.; Guo, D. Slot Allocation Protocol for UAV Swarm Ad Hoc Networks: A Distributed Coalition Formation Game Approach. Entropy 2025, 27, 256. https://doi.org/10.3390/e27030256
Song L, Guo D. Slot Allocation Protocol for UAV Swarm Ad Hoc Networks: A Distributed Coalition Formation Game Approach. Entropy. 2025; 27(3):256. https://doi.org/10.3390/e27030256
Chicago/Turabian StyleSong, Liubin, and Daoxing Guo. 2025. "Slot Allocation Protocol for UAV Swarm Ad Hoc Networks: A Distributed Coalition Formation Game Approach" Entropy 27, no. 3: 256. https://doi.org/10.3390/e27030256
APA StyleSong, L., & Guo, D. (2025). Slot Allocation Protocol for UAV Swarm Ad Hoc Networks: A Distributed Coalition Formation Game Approach. Entropy, 27(3), 256. https://doi.org/10.3390/e27030256







